扩展功能
文章信息
- 史焕杰, 曾钰宸, 许薛军
- SHI Huan-jie, ZENG Yu-chen, XU Xue-jun
- 基于节点重要度的旅游公路规划方法研究
- Study on Tourism Highway Planning Method Based on Node Importance
- 公路交通科技, 2019, 36(11): 97-103
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(11): 97-103
- 10.3969/j.issn.1002-0268.2019.11.013
-
文章历史
- 收稿日期: 2019-04-01
2. 华南理工大学 土木与交通学院, 广东 广州 510640
2. School of Transport and Civil Engineering, South China University of Technology, Guangzhou Guangdong 510640, China
随着旅游业的快速发展, 游客数量和需求的不断提高带来了日益严重的交通拥堵。旅游公路作为承担旅游交通的重要载体, 能否满足快速增长的旅游出行需求, 在新常态发展形势下逐渐成为旅游业面临的新挑战[1]。因此, 如何实现旅游和公路交通两个领域的深度融合, 实现旅游和交通的协同发展成为了当前旅游交通发展的关键[2-3]。
在承担旅游功能的国省干线公路网评价中, 部分学者倾向于采用定性指标, 但涉及的适应性因素多, 评价体系复杂, 又缺乏必要的数据支撑[4]。邓亚娟[5]等根据复杂网络中的节点度、接近中心性、中介中心性及网络连通可靠性4个指标, 进行了公路网结构分析和评价。赵俊红等将天津市公交网络看作随机网络[6]; 高中华等对城市道路网的复杂性进行了研究, 认为城市道路网具有小世界特性[7]。国外学者也做了相应研究, 如《匈牙利公路网规划的一种新的评价方法》主要介绍匈牙利公路网规划和预测系统[8]; 美国《德克萨斯湾海岸公路发展对旅游的影响的区域性分析》介绍了海岸地区的旅游模式和公路的发展模式, 评价了公路网对旅游业发展的满足程度[9]; 加拿大《75号省级干道路线位置分析》讨论了道路交通方面的问题和贸易与旅游的提升[10]。部分学者提出了构建以景区为核心的旅游交通公路网络, 并通过复杂网络理论及创新算法对其进行研究评价[11-14]。但计算过程相当繁琐, 计算量呈指数倍增长, 无法用于省级或全国范围内的路网计算。采用节点重要度计算法, 可以有效简化计算过程, 能客观定量地对公路网规划进行评价。本研究通过层次分析法[15], 提出了基于节点重要度的旅游公路规划方法, 并以广东省旅游公路现状为实例进行分析, 验证了该规划方法的可行性, 为旅游公路规划提供了理论依据和方法实践。
1 基于节点重要度的旅游公路规划方法 1.1 规划原则在现代化旅游交通路网的布局规划中, 优化布局是关键, 常采用的方法有节点重要度法、OD法、交通区位法、双层规划模型法等。旅游公路规划往往存在各发展指标区域性差异较大的难题, 为客观评价各指标的重要程度, 可采用主成分分析法、模糊聚类法、灰色关联度法对确定旅游节点重要度的因素进行分析。综合考虑规划可靠性和计算效率, 本研究将采用节点重要度法进行规划, 通过交通运营路线分析, 筛选出关键的交通转换节点, 利用综合性指标对节点重要度进行评价。在此过程中, 关键是因素及其权重的确定。
1.2 规划思路 1.2.1 节点确定针对旅游公路网的功能和特点, 规划节点主要分为区域内的旅游点和中心城镇。对于较广的研究区域, 可将中心城镇或主要城市抽象成路网中的节点。作为当地的政治、经济、文化中心和重要旅游客源地的同时, 也可以连接游客吸引点(旅游景点)和其它游客出发点(周边各大人口聚集地), 对旅游交通起到关键的集散作用, 往往具有综合性, 是旅游交通网络的核心。旅游点作为旅游的目的地, 通常具有丰富的旅游资源, 在旅游交通网络规划中通常包括现有和计划开发的旅游地。但在规划区域较广的情况下, 此类节点通常分布分散, 没有明显的地域分布规律, 因此在旅游公路规划中难以覆盖所有旅游点, 通常根据规模和游客数量选择有代表的景区群或名胜古迹, 作为旅游节点进行规划。
1.2.2 节点重要度计算旅游公路规划的节点重要度相关影响因素按节点进行统计和汇总, 可进行旅游节点重要度的计算。为消除量纲和数值对决策结果的影响, 首先对不同节点的各指标采用极值法[18]进行标准化处理, 具体方法见式(1)
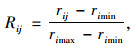
|
(1) |
式中, Rij为节点j的第i个指标的标准值, rij为节点j的第i个指标值, rijmax和rijmin分别为所有节点的第i个指标值的最大及最小值, 当该指标为正向指标时, 指标值可直接取该指标的数值, 当该指标为反向指标时, 指标值应取该指标的倒数。
旅游交通网络中各规划节点的重要度[2]计算见式(2)
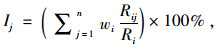
|
(2) |
式中, Ij为规划节点j的重要度, Ri为区域内各节点的第i个指标的标准值的算术平均值, wi为第i个指标综合格重。
2 基于节点重要度的旅游公路规划指标 2.1 规划指标确定旅游公路规划的节点重要度可以反映节点在该网络中的重要程度。重要度越大的节点对外界建立紧密交互联系的需求越大, 同时对旅游公路建设的依赖性也越大。确定旅游公路规划的节点重要度, 需要从构成吸引要素的影响因素出发, 对其原因进行深入分析, 且具备同时性和稳定性, 即能够真实有效地反映在同一时期内对相应节点的重要程度。因此, 分析应当综合考虑旅游与交通两个方面。
需要注意的是, 旅游资源为旅游公路规划的正向指标, 即与旅游公路规划的节点重要度正相关, 景区等级越高, 数目越多, 该节点对旅游公路规划的需求越强烈。而交通资源为旅游公路规划的反向指标, 即与旅游公路规划的节点重要度负相关, 与某旅游节点相关的交通资源指标(拥挤度除外, 拥挤度越大则说明交通资源越贫乏)越低, 该节点的旅游公路规划重要性越强, 重要度也越高。反之, 如该节点公路通达性越低, 该节点对旅游公路规划的需求表现为越强烈。
根据已知文献[2]选取旅游节点重要度的影响因素为依附旅游资源单体5A级景区数、依附旅游资源单体4A级景区数、重点发展景区数、节点周边国省干线公路数和公路长度、节点拥挤度、节点平均运行速度, 并对其进行层次划分如图 1。
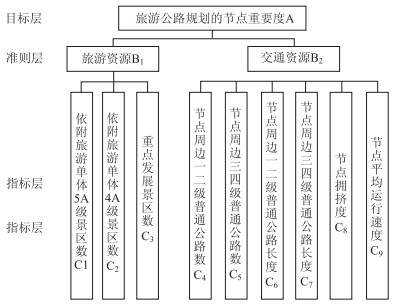
|
| 图 1 重要度因素 Fig. 1 Factors of Importance |
| |
2.2 规划指标计算 2.2.1 层次分析法
美国匹兹堡大学运筹学家T.L.Saaty在20世纪70年代初期提出了层次分析法(Analytical Hierarchy Process, 简称AHP)。该方法[16]通过模拟决策者的决策过程, 对复杂问题进行系统化和层次化处理, 解析得到若干层次的因素并进行相应的归类, 最终形成多层次结构。在各层次内, 根据一定标准规则对要素进行比较分析, 并建立矩阵进行数学计算, 实现不同因素的重要性及其优先顺序的量化描述。在此基础上, 不同因素重要性次序得到了模型化和数量化, 通过对不同要素的权重进行排序, 可以帮助最终确定总体目标下各要素的组合权重, 即权重向量, 从而为最优方案提供重要依据。近年来该方法在专利转化评估[17], 地震预测[18], 城市内涝影响分析[19]等各领域得到了广泛的应用, 并取得了较为理想的成果。文章考虑了旅游公路的多需求响应特性[20], 采用AHP法[16]计算旅游公路规划中的节点重要度影响因子。
通过向有关交通公路、旅游从业者、及景区游客、社会公众等相关人员发放调查问卷, 邀请专家学者展开专项调查, 研究确定影响旅游公路节点重要度的影响因子, 通过AHP方法计算各因素的权重。
2.2.2 计算步骤Step 1:对影响旅游节点重要度的要素进行梳理, 建立递阶层次结构模型, 包括目标层A、准则层B和指标层C;
Step 2:根据问卷调查和专项调查结论, 综合确定各层次结构对应的判断矩阵A。设因素i对因素j的对比度为aij, 则有式(3)所示关系, 指标详见表 1, 其中2、4、6、8分别代表对比度对应的中间值。
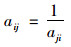
|
(3) |
| 对比度aij的标度值 | aij含义 |
| 1 | i与j同等重要 |
| 3 | i比j重要一些 |
| 5 | i比j重要较多 |
| 7 | i比j重要很多 |
| 9 | i比j重要特别多 |
Step 3:对判断矩阵进行一致性检验, 当一致性比例CR < 0.10时, 表明计算满足要求。CR表达式为:
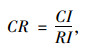
|
(4) |
其中, 一致性系数CI的取值见式(5), 平均随机一致性指标RI取值见表 2。
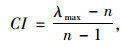
|
(5) |
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| RI | 0.52 | 0.89 | 1.12 | 1.24 | 1.36 | 1.41 | 1.46 |
式中, n为该判断矩阵所包含的因素个数, λmax为判断矩阵A的最大特征值。
Step 4:采用特征向量法计算各准则层结构内各指标的权重, 权重矩阵记为W, 计算式见式(6)。
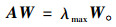
|
(6) |
Step 5:令准则层B和指标层C包含因素分别为Bi和Ci, 对应的层次权重值分别为bi和ci, i=1, 2, ……n, 层次权重值分别根据Step 4的结果, 采用式(7)计算目标层下各指标的综合权重wi
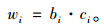
|
(7) |
Step 6:对层次总排序进行一致性检验, 总排序一致性比例CR'计算如式(8), 同理需满足CR < 0.10。
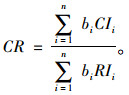
|
(8) |
普通国省干线公路在旅游中承担着衔接高速公路与景区间的旅游交通、作为高速公路的交通集散线路。为满足旅游需求, 研究旅游公路发展趋势, 本研究以广东省境内与旅游相关的普通国省干线公路为计算实例, 进一步验证了基于节点重要度的旅游公路规划方法的正确性和可行性。规划研究区域为广东省辖的21个地级市, 划分为珠三角经济创新、粤东潮汕文化、粤东北客家风情、粤北南岭生态、粤西滨海休闲五大区域旅游节点, 每个地级市(不含阳江市)为旅游发展的城市小节点, 分别计算了每个城市的旅游公路节点重要度, 可为未来旅游公路的规划提供理论支撑和重要参考。
准则层的旅游资源和交通资源判断矩阵由3位经验丰富的决策者共同确定, 若其中两名决策者给定分值相同时取相同值, 否则取三者平均值, 所得判断矩阵如表 3。由于准则层判断矩阵只有两个因素, 因此无需进行一致性分析。利用MATLAB中的eig命令分别求得判断矩阵的特征值和相应的特征矩阵, 将结果代入式(4), 计算出指标层中判断矩阵的一致性比例CR, 一致性检测效果较好, 结果见表 4; 将结果代入式(7), 可得各级权重计算结果, 见表 5。
| (a)准则层 | |||||||
| 准则层 | B1 | B2 | |||||
| B1 | 1.00 | 2.00 | |||||
| B2 | 0.50 | 1.00 | |||||
| (b)指标层B1 | |||||||
| 指标层(B1) | C1 | C2 | C3 | ||||
| C1 | 1.00 | 3.00 | 5.00 | ||||
| C2 | 0.33 | 1.00 | 3.00 | ||||
| C3 | 0.20 | 0.33 | 1.00 | ||||
| (c)指标层B2 | |||||||
| 指标层(B2) | C4 | C5 | C6 | C7 | C8 | C9 | |
| C4 | 1.00 | 5.00 | 3.00 | 5.00 | 1.00 | 3.00 | |
| C5 | 0.20 | 1.00 | 2.00 | 5.00 | 0.20 | 0.33 | |
| C6 | 0.33 | 0.50 | 1.00 | 2.00 | 0.33 | 1.00 | |
| C7 | 0.20 | 0.20 | 0.50 | 1.00 | 0.20 | 0.33 | |
| C8 | 1.00 | 5.00 | 3.00 | 5.00 | 1.00 | 3.00 | |
| C9 | 0.33 | 3.00 | 1.00 | 3.00 | 0.33 | 1.00 | |
| λmax | CI | RI | CR | 一致性检测结果 | |
| 指标层(B1) | 3.04 | 0.02 | 0.52 | 0.04 | 通过 |
| 指标层(B2) | 6.52 | 0.10 | 1.24 | 0.09 | 通过 |
| 层次总排序 | — | 0.05 | 0.76 | 0.06 | 通过 |
| 注:层次总排序中, CI和RI分别为式(18)的分子和分母, CR为式(8)计算值。 | |||||
| 目标层A | 准则层Bi | 权重bi | 决策层Ci | 权重ci | 综合权重wi |
| 旅游公路规划的节点重要度 | 旅游资源B1 | 0.666 7 | C1 | 0.637 0 | 0.424 7 |
| C2 | 0.258 3 | 0.172 2 | |||
| C3 | 0.104 7 | 0.069 8 | |||
| 交通资源B2 | 0.333 3 | C4 | 0.335 1 | 0.111 7 | |
| C5 | 0.131 0 | 0.043 7 | |||
| C6 | 0.079 1 | 0.026 4 | |||
| C7 | 0.040 6 | 0.013 5 | |||
| C8 | 0.335 1 | 0.111 7 | |||
| C9 | 0.079 1 | 0.026 4 |
根据结果可知, 影响旅游公路节点重要度的关键因素为依附旅游资源单体5A级景区数, 权重高达0.424 7, 其次分别为节点周边国省干线一二级公路数、节点拥挤度和依附旅游资源单体4A级景区数, 占比分别为0.1117、0.1117和0.1722。其他指标所占权重相差不大, 对旅游节点重要度的影响较为有限。主要原因是5A级景区的游客吸引量及辐射效应相对其他类型旅游资源较为显著, 对相应节点旅游交通吸引起到较为关键的作用。此外, 旅游公路节点周边的一二级公路数则反映了景区通达性, 路径选择越多, 出行的路径越灵活, 旅游公路的建设需求也相应降低。
在此基础上, 按式(1)对各节点指标采用极值标准化处理, 将所得综合权重代入式(2)进行旅游公路规划的节点重要度计算, 结果见表 6。
| 旅游片区 | 城市 | 依附旅游资源 单体5A 等级数 |
依附旅游 资源单体4A 等级数 |
重点发展 景区数 |
普通国省干线 公路数 |
普通国省干线 公路里程 |
节点 拥挤度 |
平均运行 速度 |
重要度 | |||
| 一二级 | 三四级 | 一二级 | 三四级 | |||||||||
| 珠三角经济创新旅游区 | 广州 | 1.000 0 | 1.000 0 | 1.000 0 | 0.000 0 | 0.166 7 | 0.027 5 | 0.125 0 | 0.429 5 | 0.681 2 | 0.742 3 | |
| 深圳 | 0.500 0 | 0.227 3 | 0.355 6 | 0.630 3 | 0.000 0 | 1.000 0 | 0.254 8 | 1.000 0 | 0.291 7 | 0.495 9 | ||
| 珠海 | 0.000 0 | 0.045 5 | 0.511 1 | 0.784 3 | 0.500 0 | 0.570 4 | 0.551 7 | 0.539 1 | 0.502 2 | 0.248 9 | ||
| 佛山 | 1.000 0 | 0.363 6 | 0.044 4 | 0.065 4 | 0.000 0 | 0.046 2 | 0.460 1 | 0.449 0 | 0.349 5 | 0.564 5 | ||
| 惠州 | 0.500 0 | 0.363 6 | 0.355 6 | 0.245 1 | 0.200 0 | 0.112 2 | 0.199 2 | 0.016 5 | 0.839 3 | 0.365 5 | ||
| 肇庆 | 0.000 0 | 0.136 4 | 0.133 3 | 0.110 3 | 0.333 3 | 0.013 0 | 0.133 1 | 0.147 0 | 0.494 2 | 0.091 3 | ||
| 江门 | 0.000 0 | 0.363 6 | 0.244 4 | 0.294 1 | 0.333 3 | 0.008 7 | 0.198 2 | 0.282 7 | 0.464 9 | 0.173 8 | ||
| 中山 | 0.000 0 | 0.000 0 | 0.000 0 | 1.000 0 | 1.000 0 | 0.688 3 | 1.000 0 | 0.411 8 | 0.446 0 | 0.244 8 | ||
| 东莞 | 0.000 0 | 0.409 1 | 0.111 1 | 0.630 3 | 0.000 0 | 0.287 4 | 0.000 0 | 0.628 2 | 1.000 0 | 0.252 7 | ||
| 粤东潮汕文化旅游区 | 汕头 | 0.000 0 | 0.181 8 | 0.155 6 | 0.294 1 | 1.000 0 | 0.350 9 | 0.699 3 | 0.498 9 | 0.412 8 | 0.204 0 | |
| 潮州 | 0.000 0 | 0.181 8 | 0.066 7 | 0.630 3 | 0.000 0 | 0.519 7 | 0.000 0 | 0.030 7 | 0.916 6 | 0.147 6 | ||
| 揭阳 | 0.000 0 | 0.090 9 | 0.044 4 | 0.294 1 | 0.000 0 | 0.217 6 | 0.000 0 | 0.296 8 | 0.758 9 | 0.110 5 | ||
| 汕尾 | 0.000 0 | 0.090 9 | 0.133 3 | 0.784 3 | 0.000 0 | 0.248 8 | 0.000 0 | 0.192 4 | 0.470 5 | 0.153 0 | ||
| 粤东北客家风情旅游区 | 河源 | 0.000 0 | 0.181 8 | 0.244 4 | 0.203 6 | 0.500 0 | 0.062 7 | 0.118 9 | 0.171 8 | 0.832 8 | 0.137 4 | |
| 梅州 | 0.500 0 | 0.318 2 | 0.400 0 | 0.168 1 | 0.200 0 | 0.022 4 | 0.079 1 | 0.091 4 | 0.894 1 | 0.358 0 | ||
| 粤北南岭生态旅游区 | 韶关 | 0.500 0 | 0.318 2 | 0.644 4 | 0.086 5 | 0.071 4 | 0.061 2 | 0.028 0 | 0.000 0 | 0.208 9 | 0.332 4 | |
| 清远 | 0.500 0 | 0.636 4 | 0.511 1 | 0.065 4 | 0.200 0 | 0.000 0 | 0.134 6 | 0.101 4 | 0.520 9 | 0.400 5 | ||
| 粤西滨海旅休闲游区 | 湛江 | 0.000 0 | 0.000 0 | 0.177 8 | 0.294 1 | 0.250 0 | 0.055 9 | 0.132 1 | 0.225 0 | 0.054 4 | 0.086 0 | |
| 茂名 | 0.000 0 | 0.090 9 | 0.200 0 | 0.294 1 | 0.125 0 | 0.144 1 | 0.068 0 | 0.288 9 | 0.000 0 | 0.104 9 | ||
从广东省五大区域旅游节点的研究分析看, 与旅游相关的普通国省干线公路中, 珠三角经济创新旅游区为一二级公路主要分布地, 覆盖了约52%的旅游景点。其中, 广州市比例最高的一二级公路数, 各类旅游资源单体数也在所有旅游节点中最高, 重要度高达0.742 3。主要原因是广州具有最为丰富的旅游资源, 三大旅游资源指标均位于全省之首, 但城市交通与旅游交通互相交织, 经常由于城市交通堵塞导致旅游交通的服务水平和同行能力下降, 需要加大规划建设满足旅游交通需要的旅游公路。由表中数据可以看出, 珠三角广府文化旅游区旅游公路规划的城市平均节点重要度位居第二, 说明该片区具备较高的建设需求, 但由于其包含城市群体数量较大, 且景区多离市区较近, 以改造现有国省干线公路满足旅游需要为旅游公路的发展方向。
粤北南岭生态旅游区的旅游公路规划的节点重要度平均达0.366 4, 原因是该区旅游资源丰富, 地形条件复杂, 现有国省干线公路网密度较低, 需要整体加强旅游公路的规划发展。
粤东北客家风情旅游区及粤东潮汕文化旅游区的旅游公路规划的节点重要度分别为第三、四位。粤西滨海休闲旅游区的旅游公路规划的节点重要度位于第五位, 该区域现有的国省干线公路的一、二公路的数量和等级可满足一定时期的旅游发展需要。
4 结论本研究提出了基于节点重要度的旅游公路规划方法, 通过区域划分确定旅游节点及规划指标, 采用层次分析法分析了影响旅游公路规划的主要因素, 以广东省旅游公路现状作为计算实例, 验证了规划方法的可行性。得出以下主要结论:
(1) 采用层次分析法对旅游公路的节点重要度因素进行了分析, 权重依次为:依附旅游资源单体5A级景区数、节点拥挤度、节点周边国省干线一二级公路数、依附旅游资源单体4A级景区数、节点周边国省干线三四级公路数、重点发展景区数、节点周边国省干线一二级公路里程、节点平均运行速度、节点周边国省干线三四级公路里程。
(2) 依附旅游资源单体5A级景区数是旅游公路节点重要度的最主要因素, 占所有因素的42.47%, 原因是5A级景区的游客吸引量及辐射效应较为显著。
(3) 案例分析了广东省旅游节点的区域特征, 提出的基于节点重要度的旅游公路规划方法具有较好的普适性, 可以为旅游公路规划提供理论参考。
后续将进一步研究其他因素对旅游公路节点重要度的影响。
| [1] |
方顺, 朱信山. 区域旅游公路网布局规划方法探讨[J]. 广东公路交通, 2016(1): 60-63. FANG Shun, ZHU Xin-shan. Discussion on Regional Tourism Highway Network Layout Planning Method-A Case Study of Huizhou City[J]. Guangdong Highway Communications, 2016(1): 60-63. |
| [2] |
马芸芸.内蒙古草原旅游公路网规划研究[D].呼和浩特: 内蒙古农业大学, 2007. MA Yun-yun. Study on Tourism Highway Network Planning in Grassland Region of Inner Mongolia[D]. Huhhot: Inner Mongolia Agricultural University, 2007. |
| [3] |
赵世元, 陈济丁, 孔亚平, 等. 环长白山旅游公路改扩建对景观格局的影响[J]. 公路交通科技, 2010, 27(12): 152-158. ZHAO Shi-yuan, CHEN Ji-ding, KONG Ya-ping, et al. Effect of Reconstruction and Expansion of Tourist Highway Circumscribing Changbai Mountain on Landscape Pattern[J]. Journal of Highway and Transportation Research and Development, 2010, 27(12): 152-158. |
| [4] |
高自友, 吴建军, 毛保华, 等. 交通运输网络复杂性及其相关问题的研究[J]. 交通运输系统工程与信息, 2005, 5(2): 79-84. GAO Zi-you, WU Jian-jun, MAO Bao-hua, et al. Study on the Complexity of Traffic Networks and Related Problems[J]. Journal of Transportation Systems Engineering and Information Technology, 2005, 5(2): 79-84. |
| [5] |
邓亚娟, 杨云峰, 马荣国. 基于复杂网络理论的公路网结构特征[J]. 中国公路学报, 2010, 23(1): 98-104. DENG Ya-juan, YANG Yun-feng, MA Rong-guo. Highway Network Structure Characteristics Based on Complex Network Theory[J]. China Journal of Highway and Transport, 2010, 23(1): 98-104. |
| [6] |
赵俊红, 马军海, 李瑞山. 基于天津市公共交通网络的复杂性研究[J]. 复杂系统与复杂性科学, 2009, 6(4): 76-82. ZHAO Jun-hong, MA Jun-hai, LI Rui-shan. Complexity Research Based on Public Transport Network of Tianjin[J]. Complex Systems and Complexity Science, 2009, 6(4): 76-82. |
| [7] |
高中华, 李满春, 陈振杰, 等. 城市道路网络的小世界特征研究[J]. 地理与地理信息科学, 2007, 23(4): 97-101. GAO Zhong-hua, LI Man-chun, CHEN Zhen-jie, et al. Research on Small World Characteristic of Urban Road Network[J]. Geography and Geo-information Science, 2007, 23(4): 97-101. |
| [8] |
Canada Transport Association. Provincial Trunk Highway 75 Route Location Study[M]. Ottawa: CTA, 1992.
|
| [9] |
FESENMAIER J, BURKE D. A Regional Analysis of the Effects of Highway Development on Tourism in the Texas Gulf Coast[R]. Washington, D. C.: Transportation Research Board, 1988.
|
| [10] |
MONIGL J. A New Approach of Evaluation for Road Network Planning in Hungary[M]. Budapest: Transport and Highway Laboratory, 1984.
|
| [11] |
宗跃光, 陈眉舞, 杨伟, 等. 基于复杂网络理论的城市交通网络结构特征[J]. 吉林大学学报:工学, 2009, 39(4): 910-915. ZONG Yue-guang, CHEN Mei-wu, YANG Wei, et al. Structure Characteristic of Urban Composite Traffic Network Based on Complex Network Theory[J]. Journal of Jilin University:Engineering and Technology Edition, 2009, 39(4): 910-915. |
| [12] |
LI X, CHEN G R. A Local-world Evolving Network Model[J]. Physica A:Statistical Mechanics and Its Applications, 2003, 328(1/2): 274-286. |
| [13] |
WU J J, GAO Z Y, SUN H J. Effects of the Cascading Failures on Scale-free Traffic Networks[J]. Physica A:Statistical Mechanics and Its Applications, 2007, 378(2): 505-511. |
| [14] |
赵月, 杜文, 陈爽. 复杂网络理论在城市交通网络分析中的应用[J]. 城市交通, 2009, 7(1): 57-65. ZHAO Yue, DU Wen, CHEN Shuang. Application of Complex Network Theory to Urban Transportation Network Analysis[J]. Urban Transport of China, 2009, 7(1): 57-65. |
| [15] |
王肖宇.基于层次分析法的京沈清文化遗产廊道构建[D].西安: 西安建筑科技大学, 2009. WANG Xiao-yu. Creation of Beijing-Shenyang Qing (Dynasty) Cultural Heritage Corridor Based on Analytic Hierarchy Process[D]. Xi'an: Xi'an University of Architecture and Technology, 2009. |
| [16] |
李聪颖, 马荣国, 王玉萍, 等. 城市慢行交通网络特性与结构分析[J]. 交通运输工程学报, 2011, 11(2): 72-78. LI Cong-ying, MA Rong-guo, WANG Yu-ping, et al. Characteristics and Structure Analysis of Urban Slow Mode Traffic Network[J]. Journal of Traffic and Transportation Engineering, 2011, 11(2): 72-78. |
| [17] |
蔡祺祥, 翟胡萍, 王炜, 等. 基于层次分析法的多因素模糊综合评价方法在专利转化中的应用[J]. 南京理工大学学报, 2018, 42(4): 497-502. CAI Qi-xiang, ZHAI Hu-ping, WANG Wei, et al. Application of Multi-factor Fuzzy Comprehensive Evaluation Method Based on Analytic Hierarchy Process in Patent Transformation[J]. Journal of Nanjing University of Science and Technology, 2018, 42(4): 497-502. |
| [18] |
张桂欣, 孙柏涛. 基于模糊层次分析的建筑物单体震害预测方法研究[J]. 工程力学, 2018, 35(12): 185-193, 202. ZHANG Gui-xin, SUN Bai-tao. Seismic Damage Prediction for a Single Building Based on a Fuzzy Analytical Hierarchy Approach[J]. Engineering Mechanics, 2018, 35(12): 185-193, 202. |
| [19] |
潘银, 邵振峰, 程涛, 等. 利用深度学习模型进行城市内涝影响分析[J]. 武汉大学学报:信息科学版, 2019, 44(1): 132-138. PAN Yin, SHAO Zhen-feng, CHENG Tao, et al. Analysis of Urban Waterlogging Influence Based on Deep Learning Model[J]. Geomatics and Information Science of Wuhan University, 2019, 44(1): 132-138. |
| [20] |
柳伍生, 周向栋, 贺剑, 等. 基于多需求响应的定制公交绿色线网优化[J]. 公路交通科技, 2018, 35(3): 132-142. LIU Wu-sheng, ZHOU Xiang-dong, HE Jian, et al. Optimization of Green Customized Public Transport Network Based on Multiple Demand Response[J]. Journal of Highway and Transportation Research and Development, 2018, 35(3): 132-142. |
 2019, Vol. 36
2019, Vol. 36
