扩展功能
文章信息
- 吕伟, 李志红, 赵彩虹, 刘丹, 姜昭宇
- LÜ Wei, LI Zhi-hong, ZHAO Cai-hong, LIU Dan, JIANG Zhao-yu
- 城市公交车停靠时间特征的观测试验与实证研究
- Observation Experiment and Empirical Study on Parking Time Characteristics of City Buses
- 公路交通科技, 2019, 36(11): 90-96
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(11): 90-96
- 10.3969/j.issn.1002-0268.2019.11.012
-
文章历史
- 收稿日期: 2018-11-02
公交车停靠行为会导致停靠区域路段车流汇聚, 形成瓶颈效应, 同时也会影响公交服务水平和公交运营效率。研究公交车停靠行为, 揭示公交车停靠时间的特征规律, 对评估公交车循环运行时间、制定效率提升措施, 具有重要现实意义。
针对公交车停靠的行为, 当前国内外学者们关键的一个焦点问题是对公交车停靠时间影响因素的分析。由于公交车靠站停留时间会受到上下车人数、乘客行为、天气状况、公交车型、拥挤度等多重因素影响, 现有的研究大多采用实证分析的方法来揭示影响公交车停靠时间的因素及其之间的相互关系:Kraft等人[1]通过对个体乘客上下车时间的分析发现其与车门数量和宽度、公交踏步的级数和高度、公交售票方式、车内拥挤状况、乘客携带行李情况、公交车内通道宽度、公交车座位构造等诸多因素有关; Rajbhandari等人[2]对公交车站点延误的研究表明公交乘客的平均上下车时间是公交车运行效率的主要影响因素; Alejandro[3]从公交车不同的收费系统、公交车地板和乘客年龄3个方面分析了它们对公交车总停靠时间的影响; 吴叶等人[4]总结了公交车开门到关门这一段时间影响公交车停靠时间的关键因素包括:上车人数、下车人数、公交车型、上下客方式、售票方式、车内拥挤度、站点受干扰程度及上下车乘客本身的特性等; 王剑梅[5]通过实地观测和调查的方法, 对相同线路不同时间采集的乘客上下车及公交车型数据进行分析, 分析了影响公交乘客上下车时间的主、客观因素; 郭四玲等人[6]指出公交车停靠与上下车的乘客数量、其他车辆干扰、道路通畅情况、公交车启动性能以及司机的反应等多重因素有关, 并通过对两处公交车站的实地观测发现, 停靠时间分布类似正态分布但不符合正态分布; 吴鼎新等人[7]从公交站台类型、时段影响以及乘客上下车人数3个方面, 对公交车在站停靠时间进行了统计分析, 并建立了上下车时间和上下车人数间的回归模型; Richard等人[8]研究指出公交车在站点停靠的时间延误取决于乘客上下车的时间延误, 且乘客上下车的时间延误符合负二项分布; Jaiswal等人[9]研究发现公交车在大型公交站的停靠时间与在站内候车的乘客数量呈正相关的关系; Ceder等人[10]针对公交车对停靠对相邻车道的阻断, 提出了一种基于调度的解决方案。此外, 也有学者采用模型模拟的方法探讨了公交车停靠行为或停靠站对道路交通流的影响[11-18]。
综上所述, 现有研究运用实证或模型的方法分析了公交车停靠的时间及其对交通流的影响, 发现并总结出上下车人数和上下车时间是影响公交车停靠时间的重要因素, 但是并未能深入揭示停靠时间与二者间的量化相关关系, 因而无法评估预测公交车的停靠时间。鉴于此, 本研究拟通过实证分析和统计方法, 继续探讨公交车停靠时间的特征规律, 构建具有统计意义的公交车停靠时间模型, 并给出相关建议以提高公交车运行效率。
1 公交车乘客上下车观测试验 1.1 试验对象选取本文期望对公交车停靠时间的特征规律进行深入分析, 必须采用实证的方法获得公交车停靠时间数据, 因此, 需要选取合适的公交站点对公交车乘客上下车过程进行观测。考虑到试验的便捷性、数据的丰富性和易得性, 在选取公交站点作为观测对象时, 考虑如下原则:
(1) 观测点分布在不同的城市干道上, 且间距尽量不太靠近, 具有代表性;
(2) 观测站点应该具有宽广的视野, 便于观测乘客个体的上下车过程;
(3) 观测站点停靠的公交车数量较多, 观测效率较高;
(4) 观测站点应该位于通勤的主要线路, 乘客流量较大;
基于上述原则, 选取武汉市洪山区的5个公交站点作为试验对象, 各观测站点的信息和位置分布分别如表 1所示。
| 编号 | 站名 | 车站信息 | 停靠线路 |
| 1 | 书城路文治街站 | 站长约10 m, 宽约2 m, 直线式, 与非机动共用车道, 客流量中等。 | 625, 797, 817, 908 |
| 2 | 书城路出版城站 | 站长约10 m, 宽约2 m, 直线式, 无非机动车道, 非机动车占用车道, 客流量较大。 | 625, 797, 817, 908 |
| 3 | 武珞路地铁宝通寺站 | 站长约10 m, 宽约2 m, 港湾式, 非机动车道与人行道共用, 部分非机动车占用车道, 客流量中等。 | 401, 510, 518, 538, 583, 596, 702, 703, 715, 723, 728, 804, 811 |
| 4 | 珞喻路广埠屯站 | 站长约5 m, 宽约2m, 直线式, 独立双车道, 社会车辆与公交车共用, 客流量较大。 | 510, 518, 538, 59, 703, 715, 728, 804, 905 |
| 5 | BRT雄楚大道出版城站 | 站长约100 m, 宽约10 m, 直线式, 5个泊位, 专用车道, 无社会车辆干扰, 客流量较大。 | BRT1, 556, 723, 632, 811, 804, 777, 625, 15 |
1.2 试验方案
为了精确提取上下车乘客的数量、乘客的上下车时间、公交车的停靠时间等时间数据, 进而分析公交车停靠时间的特征规律, 本研究设计的试验方案如下:
步骤1:定义观测变量。定义公交车停靠时间为公交车停靠后从打开车门到关闭车门的时间, 排除不同车辆启停性能对停靠时间的影响; 乘客上车时间为个体乘客单脚离地到双脚上车的时间, 乘客下车时间为个体乘客单脚下车到双脚着陆的时间; 上下车乘客数量为公交车停靠时间内上下车的总人数; 上车总时间为第一个上车乘客单脚离地至最后一个上车乘客双脚上车之间的总时间; 下车总时间为第一个下车乘客单脚下车至最后一个下车乘客双脚着陆之间的总时间。
步骤2:开展实地观测。选定周一至周五的工作日上午7—9点和下午5—7点两个时段在观测站点对每一辆独立停靠站点的公交车的停靠和乘客上下车过程进行视频摄录, 对多辆公交车同时停靠的情况, 为排除其停靠时间的相互影响, 只选取最前面一辆公交车作为观测样本。同时, 为保证观测数据的丰富性和统计意义, 在每个站点观测的公交车数量不少于40辆, 各站点的观测试验场景如图 1所示, 观测车辆及上下车乘客统计信息如表 2所示。

|
| 图 1 各站点观测试验场景 Fig. 1 Experiment scene of each observation stop |
| |
| 观测点编号 | 1 | 2 | 3 | 4 | 5 |
| 车辆数/辆 | 43 | 42 | 44 | 43 | 44 |
| 上车总人数/人 | 49 | 73 | 58 | 99 | 82 |
| 下车总人数/人 | 112 | 135 | 112 | 144 | 150 |
| 上下车总人数/人 | 161 | 208 | 170 | 243 | 232 |
步骤3:设计数据采集表, 从视频资料中提取观测变量信息。设计表 3所示的数据采集表, 对每个观测站点, 按每辆停靠公交车上下车乘客的先后顺序, 依次从视频帧序列中提取每辆公交车的停靠时间和每个乘客的上下车时间, 并计算求出乘客上车总时间、下车总时间等观测变量, 填入数据采集表中, 用于后续分析。
| 车编号 | 停靠时间/s | 乘客上车时间/s | 上车总时间/s | 乘客下车时间/s | 下车总时间/s |
| 1 | 1 | 1 | |||
| 2 | 2 | ||||
| ⋮ | ⋮ | ||||
| ⋮ | ⋮ | ⋮ | |||
| N | 1 | 1 | |||
| 2 | 2 | ||||
| ⋮ | ⋮ | ||||
2 公交车停靠和乘客上下车时间特征分析
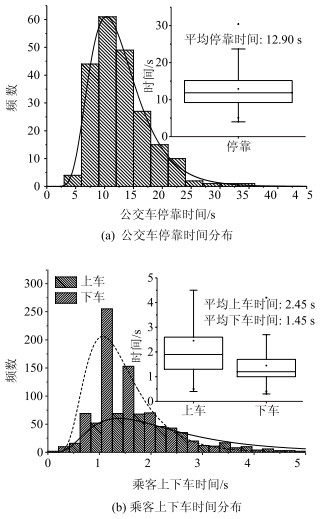
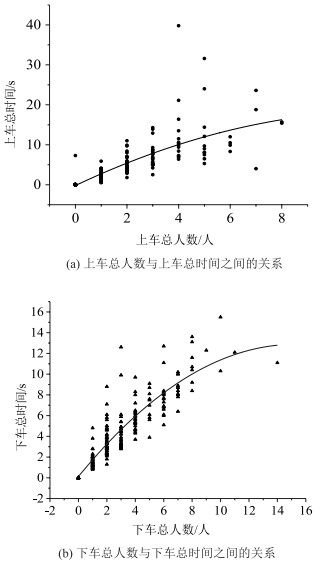
如图 2所示, 对5个观测站点的216辆停靠公交车停车时间、361名乘客上车时间、653名乘客下车时间进行统计分析发现:公交车停靠时间分布区间为4~60.2 s, 平均停靠时间为12.9 s, 呈对数正态分布; 乘客上车时间分布区间为0.4~25.1 s, 平均上车时间为2.45 s; 乘客下车时间分布区间为0.3~10.4 s, 平均下车时间为1.45 s; 乘客上车和下车的时间均呈对数正态分布, 但上车时间要明显大于下车时间。进一步分析, 乘客上下车总时间同上下车乘客数量之间关系, 如图 3所示, 可以看出, 乘客的上下车总时间和上下车乘客数量之间呈正相关关系, 特别是下车总时间同乘客数量的正相关关系更显著, 通过拟合, 可以得到乘客上下车总时间和上下车乘客数量之间呈如下量化关系:
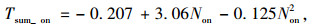
|
(1) |
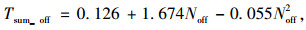
|
(2) |
|
| 图 2 公交车停靠时间分布与乘客上下车时间分布 Fig. 2 Distributions of bus parking time and passengers' boarding & alighting time |
| |
|
| 图 3 乘客上、下车总时间与上、下车乘客总人数之间的关系 Fig. 3 Relationships between total boarding & alighting time and passenger number |
| |
式中, Tsum_on, Tsum_off分别表示乘客上车总时间和乘客下车总时间; Non, Noff分别表示上车、下车乘客人数。
乘客上车的总时间与地面站台上等待乘客数量、上车秩序等因素有关, 乘客下车总时间也与车内乘客拥挤程度、下车乘客初始位置等因素有关, 由于这些因素复杂多变, 难以在实证中进行合理量化, 故本文只探讨可以观察中获得可信数据的上下车总人数、上下车总时间, 进而建立信度较高的量化关系。
3 公交车停靠时间关系因素及模型基于上文统计分析结果, 可以推断公交车的停靠时间可能会受上下车乘客数量、乘客上下车时间、乘客上下车总时间等关系因素影响, 下面对这3个因素进行深入分析。
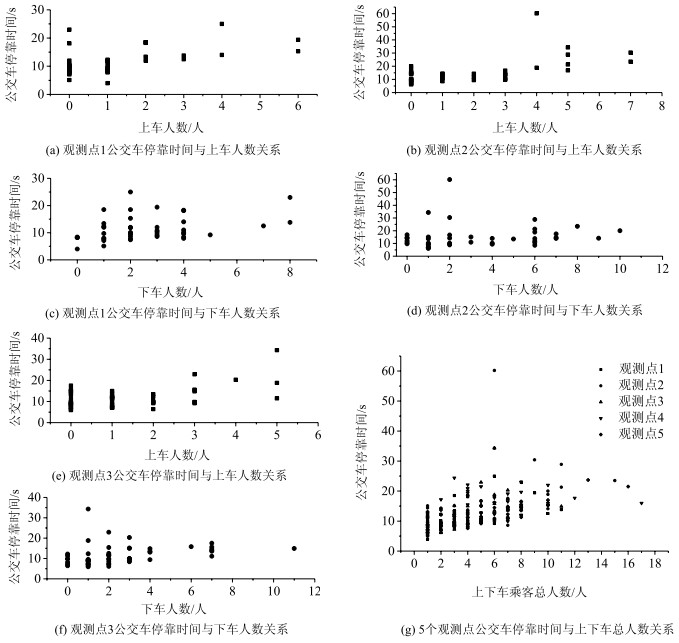
首先, 分析上下车乘客数量与公交车停靠时间的关系, 如图 4所示, 图(a)~图(f)分别为观测点1、观测点2和观测点3的公交车停靠时间与上、下车乘客数量之间的关系, 图(g)为5个观测点的公交车停靠时间与上下车乘客总数量之间的关系, 从图中可以看出, 公交车停靠时间与单一的上车乘客数量或下车乘客数量没有呈现明显的正相关关系, 与上下车乘客总数量呈较弱的正相关关系, 因此, 上下车乘客数量不是影响公交车停靠时间的关键因素。
|
| 图 4 公交车停靠时间与上、下车乘客数量之间的关系 Fig. 4 Relationships between bus parking time and boarding & alighting passenger number |
| |
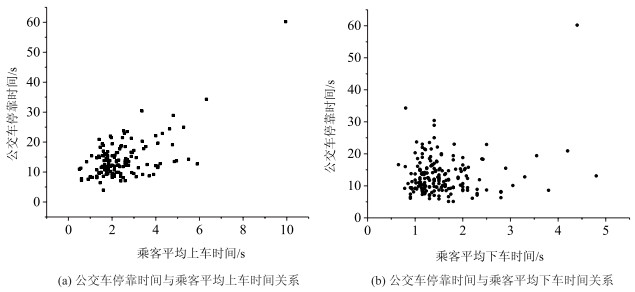
然后, 分析乘客上下车时间与公交车停靠时间的关系, 根据图 5和相关性分析, 乘客上车的平均时间与公交车停靠时间呈显著(p-value=1.11×10-15)的正相关关系, 皮尔逊相关系数为0.607, 而乘客下车的平均时间与公交车停靠时间之间则无显著(p-value=0.206 2)的相关关系, 皮尔逊相关系数仅为0.168, 由此可见, 乘客的上车时间对公交车停靠时间可能存在主要影响, 但下车时间不是影响公交车停靠时间的关键因素。
|
| 图 5 公交车停靠时间与乘客上、下车平均时间之间的关系 Fig. 5 Relationships between bus parking time and passengers' average boarding & alighting time |
| |
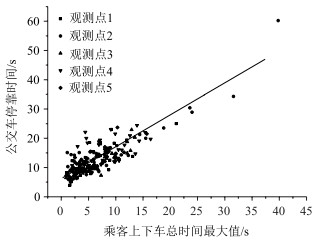
进一步分析乘客上下车总时间与停靠时间之间的关系, 考虑到乘客上下车的过程存在同步发生的情况, 上车总时间或下车总时间均无法独立反映对公交车停靠的滞留效应, 在没有其他在站车辆影响和不考虑车辆动力因素的情况下, 公交车停靠时间可能会由上下车过程中耗时较长的过程决定, 为验证这一假设, 提取每辆公交车停靠过程中乘客上车和下车总时间最长的时间变量作为影响变量, 相关性分析得到二者之间的皮尔逊相关系数为0.85, p-value=0, 呈显著的强正相关关系, 如图 6所示, 作线性拟合, 可以得到如下量化关系:
|
| 图 6 公交车停靠时间与乘客上下车总时间最大值之间的关系 Fig. 6 Relationship between bus parking time and passengers' maximum total boarding & alighting time |
| |
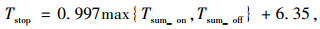
|
(3) |
式中, Tstop为公交车停靠时间; max{Tsum_on, Tsum_off}表示取乘客上、下车总时间的最大值。
4 结论通过对不同公交站点的公交车停靠过程及乘客上下车过程的观测试验, 本文在对公交车停靠时间、乘客上下车时间、乘客数量等数据统计分析的基础上, 深入研究了影响公交车停靠的关键因素, 结果表明, 在没有其他停靠公交车的影响下, 公交车停靠具有如下特征:
(1) 公交车的停靠时间和乘客的上下车时间均呈对数正态分布, 但上车时间要明显大于下车时间。
(2) 乘客上下车总时间与上下车乘客数量之间呈正相关关系, 且下车总时间与下车乘客数量之间的正相关关系更显著。
(3) 上、下车乘客数量及乘客下车总时间不是影响公交车停靠时间的关键因素, 公交车停靠时间由乘客上、下车过程中耗时较长的过程决定, 与乘客上、下车总时间最大值呈显著的强正相关关系。
(4) 利用本研究所构建的上下车人数和上下车总时间、上下车总时间和停靠时间之间的量化关系, 结合公交线路上各站点早晚通勤高峰期的上下车人数统计信息, 可以辅助公交集团公司评估早晚高峰期的公交车辆运行时间, 进而合理安排循环车次。
| [1] |
KRAFT W H, BERGEN T F. Evaluation of Passenger Service Times for Street Transit Systems[M]. Washington, D. C: Transportation Research Board, 1974.
|
| [2] |
RAJBHANDARI R, CHIEN S I, DANIEL J. Estimation of Bus Dwell Times with Automatic Passenger Counter Information[J]. Transportation Research Record, 2003, 1841: 120-127. |
| [3] |
TIRACHINI A. Bus Dwell Time:the Effect of Different Fare Collection Systems, Bus Floor Level and Age of Passengers[J]. Transportmetrica A:Transport Science, 2013, 9(1): 28-49. |
| [4] |
吴叶, 徐大刚. 公交停靠站停靠时间特征分析[J]. 交通与运输, 2007, 3(2): 78-80. WU Ye, XU Da-gang. The Analysis of Berthing Time Characteristics at the Bus Stop[J]. Traffic & Transportation, 2007, 3(2): 78-80. |
| [5] |
王剑梅.城市公交车上下车效率研究[D].西安: 长安大学, 2015. WANG Jian-mei. Research on Efficiency of Getting on and off City Bus[D]. Xi'an: Chang'an University, 2015. |
| [6] |
郭四玲, 韦艳芳, 时伟, 等. 公交车停靠时间的统计分析[J]. 广西师范大学学报:自然科学版, 2006, 24(2): 5-9. GUO Si-ling, WEI Yan-fang, SHI Wei, et al. Statistical Analysis of Buses' Stopping Time[J]. Journal of Guangxi Normal University:Natural Science Edition, 2006, 24(2): 5-9. |
| [7] |
吴鼎新, 张丽媛. 淮安市公交车在站停靠时间特性分析[J]. 物流工程与管理, 2018, 40(1): 111-114. WU Ding-xin, ZHANG Li-yuan. Analysis of Time Characteristics of Bus Stop in Huaian City[J]. Logistics Engineering and Management, 2018, 40(1): 111-114. |
| [8] |
GUENTHNER R P, SINHA K C. Modeling Bus Delays due to Passenger's Boardings and Alightings[J]. Transportation Research Record, 1983, 915: 7-13. |
| [9] |
JAISWAL S, BUNKER J M, FERREIRA L. Operating Characteristics and Performance of a Busway Transit Station[C]//30th Australasian Transport Research Fourm. Melbourne: Australasian Centre for the Governance and Management of Urban Transport, 2007: 1-12.
|
| [10] |
CEDER A, ISRAEL G. Efficient Bus Operational Parking Model[J]. Transportation Research Record, 2009, 2111: 42-49. |
| [11] |
胡建荣, 成华. 公交车停靠对交通流的影响[J]. 城市道桥与防洪, 2007, 24(8): 23-24, 202. HU Jian-rong, CHENG Hua. Influence of Public Transit Bus Stopping on Traffic Flow[J]. Urban Roads Bridges & Flood Control, 2007, 24(8): 23-24, 202. |
| [12] |
姬浩, 吕美, 苏兵. 公交车停靠行为对城市道路通行能力影响研究[J]. 中国安全科学学报, 2015, 25(1): 128-132. JI Hao, LÜ Mei, SU Bing. Effects of Bus Stopping Behavior on Urban Two-lane-road Capacity[J]. China Safety Science Journal, 2015, 25(1): 128-132. |
| [13] |
李庆定, 董力耘, 戴世强. 公交车停靠诱发交通瓶颈的元胞自动机模拟[J]. 物理学报, 2009, 58(11): 7584-7590. LI Qing-ding, DONG Li-yun, DAI Shi-qiang. Investigation on Traffic Bottleneck Induce by Bus Stopping with a Two-lane Cellular Automaton Model[J]. Acta Physica Sinica, 2009, 58(11): 7584-7590. |
| [14] |
HUANG Z, GUO X, ZHANG C, et al. Modeling the Effects of Bus Stops on Bicycle Traffic Flow by Cellular Automata[J]. Journal of Advanced Transportation, 2018(2018): 1-8. |
| [15] |
ZHENG P, WANG W, GE H. The Influence of Bus Stop on Traffic Flow with Velocity-difference-separation Model[J]. International Journal of Modern Physics C, 2016, 27(11): 1650135. |
| [16] |
YANG X B, HUAN M, GAO Z Y. Car Delay Model near Bus Stops with Mixed Traffic Flow[J]. Journal of Applied Mathematics, 2013(2013): 1-6. |
| [17] |
TANG T Q, SHI Y F, HUANG H J, et al. A New Macro Model for Traffic Flow on a Highway with Bus Stop[J]. Communications in Theoretical Physics, 2011, 55(6): 1113-1118. |
| [18] |
JIA B, LI X G, JIANG, et al. The Influence of Bus Stop on the Dynamics of Traffic Flow[J]. Acta Physica Sinica, 2009, 58(10): 6845-6851. |
 2019, Vol. 36
2019, Vol. 36
