扩展功能
文章信息
- 孙锋, 焦方通, 马晓龙, 张倩, 赵菲
- SUN Feng, JIAO Fang-tong, MA Xiao-long, ZHANG Qian, ZHAO Fei
- 交叉口逆向可变车道与信号配时协同优化方法
- A Collaborative Optimization Method for Reversible Lanes and Signal Timing at Intersection
- 公路交通科技, 2019, 36(11): 83-89, 96
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(11): 83-89, 96
- 10.3969/j.issn.1002-0268.2019.11.011
-
文章历史
- 收稿日期: 2018-06-11
2. 青岛海信网络科技有限公司, 山东 青岛 266071;
3. 山东东泰工程咨询有限公司, 山东 淄博 255000
2. Qingdao Hisense TransTech Co., Ltd., Qingdao Shandong 266071, China;
3. Shandong Dongtai Engineering Consulting Co., Ltd., Zibo Shandong 255000, China
在城市路网中, 阶段性流向供需失衡容易引发部分流向短时过饱和, 从而引发严重的区域拥堵[1]。针对此类问题, 交叉口逆向可变车道等变向交通管理方法在我国各大城市被逐步采用, 交叉口逆向可变车道[2-3]一般设置在出口道内侧车道, 兼备了进口左转导向车道和出口车道的功能, 能够缓解交通高峰期中交叉口的左转过饱和拥堵, 同时具有工程投资小、经济效益强等优点, 因此得到了快速推广, 并在前期取得了显著的效果。但是, 随着城市交通压力的进一步增大, 逆向可变车道的效益正在逐步减弱, 主要原因是缺少与交叉口信号控制的协同优化, 未实现交叉口的整体管控效益最大化。为此, 有必要针对设置逆向可变车道的交叉口运行特征进行系统深入的研究, 提出一种逆向可变车道与信号控制的协同优化方法, 以充分发挥多种管理模式的效益。
变向交通组织是美国、欧洲等发达国家最早在桥梁、隧道和高速公路上使用[4-5], 而随着城市路网中流向性供需失衡加剧, 变向交通组织开始逐步被应用于城市道路。为了支撑变向交通组织的有效实施, 国内外学术界在该领域开展了大量的研究, 总体上可以分为两类:一是基于历史数据从系统角度研究变向交通组织的必要性和方案, 如Hausknecht等[6]构建了一个整数线性规划模型, 实现了可变车道的优化设计; 张好智[7]、张鹏[8]使用双层规划方法分别建立了变向交通组织的优化模型, 从系统角度研究了可变车道分配和信号配时对城市交通网络的影响; Wang等[9]则以通行能力最大为目标, 构建了可变车道的双层优化模型; 二是从设施和算法角度研究变向交通组织的实现方法, 如宫晓燕等[10]对潮汐交通中可变通道的通行方向切换算法进行了研究; 李丽丽等[11]提出了基于线圈检测器数据的可变车道控制方法; Li等[12]对主干道潮汐车道的信号控制实现方法进行了系统性研究; 赵靖等[13]从安全角度对交叉口动态车道功能划分的实施方法进行了研究; 上述研究成果对于以人工和定时段管理为主的变向交通组织起到了有力的支撑作用。而随着该领域应用需求的不断增加, 研究者开始对变向组织和信号控制进行协同优化研究, 如曾滢和杨晓光等[14]将交通流理论与信控方法相结合, 在交叉口层面构建了一种车道属性和信号控制的组合优化模型; Zhao等[15]将可变车道和禁左、信号控制等管理措施进行了组合优化, 实现了交叉口时空资源的最优配置。可以看出, 上述研究成果对于提升交通管理水平起到了积极推动作用, 但是目前关于过饱和状态下逆向可变车道与信号控制协同优化的研究却较少涉及。
1 研究思路基于上述分析, 本研究以设置逆向可变车道的交叉口为研究对象, 分析逆向可变车道设置后交叉口通行能力及运行状态的变化, 结合交叉口供需关系提出信号控制参数的计算模型, 并基于效率和安全目标, 构建了逆向可变车道动态开启与信号参数的协同优化模型, 最后通过实例验证模型的有效性, 研究对象如图 1所示。

|
| 图 1 设置逆向可变车道的交叉口 Fig. 1 Intersection with reversible lanes |
| |
2 逆向可变车道设置理论分析
本研究以某一四路交叉口高峰时段运行过程为例, 对逆向可变车道实施前后交叉口运行指标的变化进行研究。
2.1 通行能力当设置逆向可变车道后, 交叉口的通行能力势必增加, 但意外事故发生概率也随之提高[16-17], 一旦有车辆在左转相位绿灯结束后滞留在逆向可变车道内, 那么将会与下一相位直行车辆发生冲突。因此, 为了最大限度减少车辆发生意外的可能性, 必须结合道路条件增设合理的车道安全清空时间。常规情况下, 左转车道组的通行能力通过式(1)计算, 当逆向可变车道设置后, 通行能力通过式(2)计算。
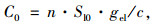
|
(1) |

|
(2) |
式中, C0为常规左转车道组通行能力; C1为设置有逆向可变车道的进口道左转流向通行能力; Sl0为左转车道在理想条件下的基本饱和流率; c为交叉口信号周期时长; gel为左转相位的有效绿灯时长; tlc为逆向可变车道清空时间; n为进口道内左转车道的总数量。
将变量α={0, 1}设定为逆向可变车道的控制变量, α=0表示不开启, α=1表示开启。
因此, 设置逆向可变车道的进口道左转通行能力计算如下:
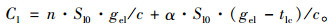
|
(3) |
将式(3)进行转换, 求得左转饱和流率如式(4):
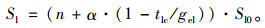
|
(4) |
由于通行能力发生变化, 导致进口道左转供需关系及状态发生变化, 分析如图 2所示。从图中可以看出, 左转需求从tA时刻开始超过其通行能力, 此时处于过饱和状态, 直到tD时刻才缓解; 而当设置逆向可变车道后, 根据实时检测流量确定开启时刻为tO→tC, 过饱和状态将大幅缩短至tE时刻, 相应的阴影部分面积也明显减小, 即二次排队的车辆数明显减少。

|
| 图 2 左转车流供需关系 Fig. 2 Supply and demand of left-turn traffic flow |
| |
2.3 优化目标
根据上述理论分析, 通过设置逆向可变车道能够在一定程度上提升交叉口的运行效率, 但为了减少安全隐患, 应该尽量缩短逆向可变车道开启的时间。因此, 将运行效率提升和安全隐患最小作为逆向可变车道与信号控制协同优化的共同目标。
(1) 效率指标:平均延误、停车次数和最大排队长度;
(2) 安全指标:交叉口逆向可变车道开启时间最短。
3 信号配时优化模型信号配时参数是决定逆向可变车道安全和效率的关键, 本部分基于安全和效率目标, 提出交叉口部分左转过饱和状态下, 信号周期、有效绿灯、提前启亮以及清空时间的计算方法。
3.1 基于环结构相位相序设计以常规四路交叉口为例, 在左转过饱和严重的南进口设置逆向可变车道。在绿灯启亮前, 左转车辆必须提前进入逆向可变车道, 这样才能确保其效能充分发挥。因此, 在同一个进口道的相序设计中, 必须先放左转再放直行, 而逆向可变车道控制的信号则作为相位3和6的跟随相位, 其相位相序设计如图 3所示。

|
| 图 3 相位相序设计 Fig. 3 Phase sequence design |
| |
3.2 信号周期
本研究的思路是通过增加左转车道组的通行能力以缓解交叉口的左转过饱和状态。因此, 当交叉口进口道设置逆向可变车道后, 仅是左转车道组的饱和流量发生了变化, 故仍然采用传统的信号周期计算公式, 只是在计算左转车道组的绿信比时, 首先考虑逆向可变车道是否开启, 而开启后的饱和流量通过式(4)计算得到。在环结构配时模式下, 交叉口的流量比之和[18]通过式(5)计算:

|
(5) |
式中, Y为流量比之和; i为环编号; j为信号蔽障编号; Y'ij为信号蔽障j内环i中的流量比之和; q为交通流量; S为设计饱和流量, 开启逆向可变车道的左转饱和流量通过公式(4)计算。
周期计算采用韦伯斯特公式, 如下:

|
(6) |
式中, c为最佳周期时间; L为每个相位转换所经历的损失时间之和。
3.3 有效绿灯时长每个相位的绿信比和有效绿灯时间按照等饱和度原则进行分配, 先对蔽障中的有效绿灯时间进行计算, 然后计算各相位的有效绿灯时间, 即将蔽障中的绿灯时间分配给环的各个相位。计算方法如式(7)和(8)所示。

|
(7) |
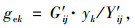
|
(8) |
式中, G'ij为蔽障j中环i的有效绿灯时间之和; gek为相位k的有效绿灯时间; yk为相位k的流量与饱和流率之比。
3.4 逆向可变车道的清空及提前启亮时间逆向可变车道的安全清空时间必须确保驶入的每一辆车都能够在下一个相位绿灯启亮前驶出交叉口; 因此, 依据车辆行驶特征, 提出逆向可变车道安全清空时间的计算模型如下:
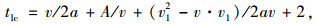
|
(9) |
式中, A为逆向可变车道长度; v1为左转车驶入逆向可变车道时刻的初速度; a为启动加速度; v为交叉口内左转车的稳定行驶车速。
根据实际调查, 交叉口的逆向可变车道长度都与进口道渠化段长度相等, 一般取值为40~60 m, 绿灯末尾驶入车辆的初始速度v1为30 km/h, 小汽车启动加速度为2.5 m/s2。将上述变量代入式(9), 可得:逆向可变车道长度为40, 50, 60 m时, 对应的安全清空时间分别为6, 7, 8 s。
为了充分发挥逆向可变车道的功能, 左转车辆必须提前进入车道等待, 当绿灯启亮后, 左转车辆才能以饱和流量驶离交叉口, 因此, 在信号配时参数中需要设置绿灯提前启亮时间, 如图 3所示。同时, 为了确保逆向可变车道内行驶车辆的安全性, 绿灯提前启亮时间取值如下:
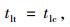
|
(10) |
式中tlt为交叉口逆向可变车道动态控制信号的绿灯提前启亮时间。
4 优化模型 4.1 车辆运行指标计算根据美国HCM2010, 交叉口内车道组的车均延误可由以下公式计算得到:
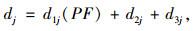
|
(11) |
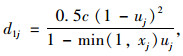
|
(12) |
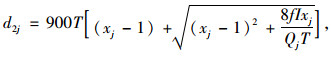
|
(13) |
式中, dj为车均延误; d1j为均衡控制延误; PF为校正系数; d2j为增量延误; d3j为初始排队延误; uj为绿信比; xj为饱和度; T为分析期持续时间; Qj为通行能力; f为控制类型校正系数; I为上游分流或供给校正系数。
根据进口道中各车道组的车均延误, 得到交叉口的车辆总延误为:
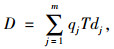
|
(14) |
式中, D为所有车辆延误之和; m为车道组的总数量; qj为车道组j的流量。
当交叉口处于过饱和状态时[19-20], 各项效率指标的计算公式如下:
(1) 每周期剩余车辆数
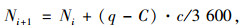
|
(15) |
式中, Ni+1为第i+1周期的剩余车辆数; Ni为第i周期的剩余车辆数。
(2) 过饱和延误
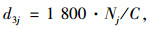
|
(16) |
式中Nj为第j条车道组的剩余车辆数。
(3) 排队长度
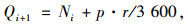
|
(17) |
式中, Qi+1为第i+1周期的排队车辆数; p为车辆平均到达率; r为红灯时间。
(4) 停车率
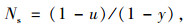
|
(18) |
式中Ns为停车率。
4.2 约束条件在信号配时过程中, 各参数之间存在较强的约束条件, 分述如下:
(1) 有效绿灯不应小于最小绿灯, 即:
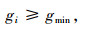
|
(19) |
式中, gi为有效绿灯; gmin为最小绿灯。
(2) 信号周期时长应满足临界的上、下限间的取值范围, 即:
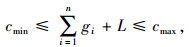
|
(20) |
式中, cmin为最小周期时长; cmax为最大周期时长。
(3) 对于紧邻逆向可变车道相位的上一个直行相位来说, 其有效绿灯时间不应小于逆向可变车道的提前启亮时间, 即:
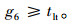
|
(21) |
(4) 为了保证逆向可变车道的使用率, 该相位的有效绿灯时间不能小于清空时间, 即:
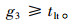
|
(22) |
考虑到车均延误、排队长度和停车次数具有较为显著的正相关性, 因此, 分别选择逆向可变车道开启时长和车均延误作为模型构建的安全控制和效率指标, 模型构建如下:
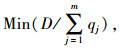
|
(23) |
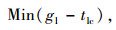
|
(24) |
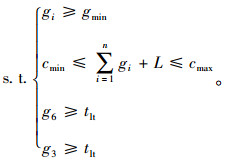
|
(25) |
上式可由MATLAB优化算法对多目标优化问题进行求解, 设定γ为优化求解的终止参数。
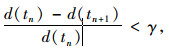
|
(26) |
式中, d(tn), d(tn+1)为第tn和tn+1周期内的车均延误。
经过多次优化迭代后, 每增加一个周期的延误减少率低于γ时, 将其对应的方案作为最优解。
5 实例验证以某市中心城区世纪路与共青团路交叉口为例, 对其逆向可变车道的设置及智能控制方案进行系统设计和验证。
5.1 交通调查通过对交叉口进行详细交通调查, 获取其渠化状况如图 4所示, 高峰时段不同进口及流向的流量如表 1所示。
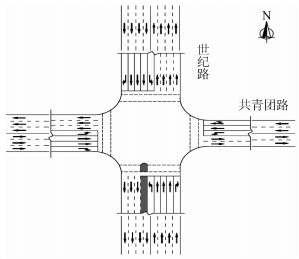
|
| 图 4 世纪路-共青团路交叉口渠化 Fig. 4 Channeling of intersection of Shiji Road and Gongqingtuan Road |
| |
| 进口 | 流向 | 车道数 | 流量/(pcu·h-1) |
| 东进口 | 左转 | 1 | 192 |
| 直行 | 2 | 346 | |
| 右转 | 1 | 253 | |
| 西进口 | 左转 | 1 | 165 |
| 直行 | 2 | 360 | |
| 右转 | 1 | 213 | |
| 南进口 | 左转 | 1 | 350 |
| 直行 | 3 | 1 406 | |
| 右转 | 1 | 170 | |
| 北进口 | 左转 | 1 | 277 |
| 直行 | 3 | 1 172 | |
| 右转 | 1 | 170 |
为了展示逆向可变车道实时控制效果, 在优化过程中其他方向车流按照小时流量输入, 而南进口左转方向则按照周期流量进行输入, 并对逆向可变车道和信号参数进行实时优化, 其高峰时段连续25个周期的实时流量如图 5所示。
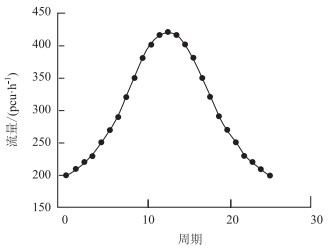
|
| 图 5 高峰时段南进口左转流量变化趋势图 Fig. 5 Change trend of left-turn volume of south approach during peak hour |
| |
5.2 逆向可变车道控制及配时方案优化
将调查数据导入本研究构建的优化模型, 通过循环迭代选取2组近似最优解, 分别将其编号为1和2, 对比分析如表 2所示。
| 编号 | 周期序号 | α | 阶段1 | 阶段2 | 阶段3 | 阶段4 | 阶段5 | 阶段6 | 周期 |
| — |  |
 |
 |
 |
 |
 |
— | ||
| 优化方案1 | T1 | 0 | 20 | 10 | 13 | 16 | 13 | 49 | 133 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| T11 | 1 | 24 | 14 | 13 | 21 | 13 | 57 | 154 | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| T17 | 0 | 23 | 12 | 13 | 24 | 14 | 56 | 154 | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| T25 | 0 | 20 | 10 | 13 | 16 | 13 | 49 | 133 | |
| 优化方案2 | T1 | 0 | 20 | 11 | 13 | 16 | 14 | 47 | 133 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| T9 | 1 | 24 | 14 | 13 | 21 | 13 | 57 | 154 | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| T18 | 0 | 23 | 13 | 13 | 24 | 13 | 56 | 154 | |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | |
| T25 | 0 | 20 | 12 | 12 | 15 | 13 | 49 | 133 |
5.3 效果评价
分别对2组优化方案控制下的车辆运行效率进行测算, 结果如表 3所示。从表中可以看出, 设置逆向可变车道后, 交叉口车均延误下降12.10%、左转最大排队长度下降45.74%、二次停车数量下降97.98%;与方案1相比, 优化方案2的运行指标提升幅度小于2%, 但开启总时长却增加了50%, 意外事故的发生概率将大幅增加。因此, 将γ取值确定为0.6%, 并将方案1作为最终优化方案。
| 效率评价指标 | 现状 | 优化方案1 | 优化方案2 | ||
| 数值 | 提升率/% | 数值 | 提升率/% | ||
| 交叉口平均停车次数 | 0.800 9 | 0.796 6 | -0.54 | 0.794 9 | -0.75 |
| 交叉口车均延误/s | 51.47 | 45.24 | -12.10 | 44.41 | -13.70 |
| 左转平均停车次数 | 0.98 | 0.96 | -2.50 | 0.94 | -3.71 |
| 每周期二次停车数 | 7.14 | 0.14 | -97.98 | 0.00 | -100 |
| 左转最大排队长度/pcu | 17.60 | 9.55 | -45.74 | 9.44 | -46.37 |
| 逆向车道连续开启周期 | 0 | 6 | — | 9 | — |
6 结论
本研究在解析设置逆向可变车道交叉口车流运行特征的基础上, 基于效率和安全目标构建了逆向可变车道与信号控制协同优化模型, 并确定了控制参数的约束条件。实例分析表明, 通过本研究模型设计的优化方案, 能够在保障安全性最大的前提下使得交叉口延误、排队长度、二次停车数明显下降, 有效缓解了由于高峰时段左转过饱和引发的交叉口拥堵, 可以为城市交叉口逆向可变车道的智能化管控提供指导与借鉴。需要说明的是, 本研究仅对单交叉口的逆向可变车道控制进行了研究, 而关于相邻交叉口的信号协调将是作者下一步研究的重点内容。
| [1] |
WU J, LIU P, TIAN Z Z, et al. Operational Analysis of the Contraflow Left-turn Lane Design at Signalized Intersections in China[J]. Transportation Research Part C:Emerging Technologies, 2016, 69: 228-241. |
| [2] |
ZHAO J, MA W, LIU Y, et al. Integrated Design and Operation of Urban Arterials with Reversible Lanes[J]. Transportmetrica B:Transport Dynamics, 2014, 2(2): 130-150. |
| [3] |
KRAUSE C, KRONPRASET N, BARED J, et al. Operational Advantages of Dynamic Reversible Left-lane Control of Existing Signalized Diamond Interchanges[J]. Journal of Transportation Engineering, 2014, 141(5): 04014091. |
| [4] |
WALECZEK H, GEISTEFELDT J, CINDRICMIDDENDORF D, et al. Traffic Flow at a Freeway Work Zone with Reversible Median Lane[J]. Transportation Research Procedia, 2016, 15: 257-266. |
| [5] |
DEY S, MA J M, ADEN Y. Reversible Lane Operation for Arterial Roadways:The Washington, D.C.:USA Experience[J]. ITE Journal, 2011, 81(5): 1-26. |
| [6] |
HAUSKNECHT M, AU T C, STONE P, et al. Dynamic Lane Reversal in Traffic Management[C]//2011 14th International IEEE Conference on Intelligent Transportation Systems. Washington, D.C.: IEEE, 2011: 1929-1934.
|
| [7] |
张好智, 高自友. 可变车道的道路交通网络设计优化方法[J]. 中国管理科学, 2007, 15(2): 86-91. ZHANG Hao-zhi, GAO Zi-you. Optimization Approach for Traffic Road Network Design Problem[J]. Chinese Journal of Management Science, 2007, 15(2): 86-91. |
| [8] |
张鹏, 李文权, 常玉林. 可变车道的城市路网备用容量模型[J]. 西南交通大学学报, 2010, 45(2): 255-260. ZHANG Peng, LI Wen-quan, CHANG Yu-lin. Reserve Capacity Model for Urban Road Network with Variable Lanes[J]. Journal of Southwest Jiaotong University, 2010, 45(2): 255-260. |
| [9] |
WANG J, DENG W. Optimizing Capacity of Signalized Road Network with Reversible Lanes[J]. Transport, 2018, 33(1): 1-11. |
| [10] |
宫晓燕, 康胜. "潮汐式"交通中可变通道的通行方向切换算法的研究与应用[J]. 交通运输系统工程与信息, 2006, 6(6): 33-40. GONG Xiao-yan, KANG Sheng. Study and Application of Traffic Direction Changing Algorithm for Urban Tide Traffic Situation[J]. Journal of Transportation Systems Engineering and Information Technology, 2006, 6(6): 33-40. |
| [11] |
李丽丽, 曲昭伟, 陈永恒, 等. 可变车道的控制方法[J]. 吉林大学学报:工学版, 2009, 39(增1): 98-103. LI Li-li, QU Zhao-wei, CHEN Yong-heng, et al. Control Strategy of Variable Lane[J]. Journal of Jilin University:Engineering and Technology Edition, 2009, 39(S1): 98-103. |
| [12] |
LI X, CHEN J, WANG H. Study on Flow Direction Changing Method of Reversible Lanes on Urban Arterial Roadways in China[J]. Procedia-social and Behavioral Sciences, 2013, 96: 807-816. |
| [13] |
赵靖, 周溪召. 交叉口可变车道最佳车道功能及信号转变方法[J]. 上海理工大学学报, 2016, 38(4): 380-386. ZHAO Jing, ZHOU Xi-zhao. Optimal Switching Method for Lane Assignment and Signal Control for Variable Lanes at Intersections[J]. Journal of University of Shanghai for Science and Technology, 2016, 38(4): 380-386. |
| [14] |
曾滢, 杨晓光, 马莹莹. 交叉口动态车道功能与信号控制协同问题研究[J]. 同济大学学报:自然科学版, 2009, 37(7): 903-908. ZENG Ying, YANG Xiao-guang, MA Ying-ying. Study on Synergy Problem of Dynamic Lane-use Assignment and Signal Control at Intersections[J]. Journal of Tongji University:Natural Science Edition, 2009, 37(7): 903-908. |
| [15] |
ZHAO J, MA W, LIU Y, et al. Integrated Design and Operation of Urban Arterials with Reversible Lanes[J]. Transportmetrica B:Transport Dynamics, 2014, 2(2): 130-150. |
| [16] |
CAO Y, ZUO Z, XU H. The Analysis of Traffic Conflict Characteristic at Temporary Reversible Lane[J]. Periodica Polytechnica Transportation Engineering, 2014, 42(1): 73-76. |
| [17] |
ZHAO J, MA W, ZHANG H, et al. Increasing the Capacity of Signalized Intersections with Dynamic Use of Exit Lanes for Left-turn Traffic[J]. Transportation Research Record, 2013, 2355: 49-59. |
| [18] |
常云涛, 王奕彤. 连续流交叉口信号配时优化模型[J]. 公路交通科技, 2018, 35(4): 93-101. CHANG Yun-tao, WANG Yi-tong. An Optimal Timing Model for Continuous Flow Intersection[J]. Journal of Highway and Transportation Research and Development, 2018, 35(4): 93-101. |
| [19] |
MA D F, WANG D H, SUN F, et al. Method of Spillover Identification in Urban Street Networks Using Loop Detector Outputs[J]. Journal of Central South University of Technology:English Edition, 2013, 20(2): 572-578. |
| [20] |
卢凯, 徐建闽, 郑淑鉴, 等. 交通信号协调控制方案过渡优化算法[J]. 交通运输工程学报, 2012, 12(6): 97-103. LU Kai, XU Jian-min, ZHENG Shu-jian, et al. Optimization Algorithm of Coordinated Control Scheme Transition of Traffic Signal[J]. Journal of Traffic and Transportation Engineering, 2012, 12(6): 97-103. |
 2019, Vol. 36
2019, Vol. 36
