扩展功能
文章信息
- 窦慧丽, 马万经, 王国华
- DOU Hui-li, MA Wan-jing, WANG Guo-hua
- 基于公交优先的单点交叉口车道信号协同配置模型
- An Integrated Lane-marking and Signal Timing Model for Isolated Intersection Based on Transit Priority
- 公路交通科技, 2019, 36(11): 75-82
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(11): 75-82
- 10.3969/j.issn.1002-0268.2019.11.010
-
文章历史
- 收稿日期: 2018-11-26
2. 同济大学 交通运输工程学院, 上海 201804;
3. 浙江省交通规划设计研究院有限公司, 浙江 杭州 310030
2. School of Transportation Engineering, Tongji University, Shanghai 201804, China;
3. Zhejiang Traffic Planning, Design and Research Institute Co., Ltd., Hangzhou Zhejiang 310030, China
随着车辆保有量的增加, 城市交通拥堵问题日渐严重。相关管理部门和研究机构均提出发展优质服务水平的公共交通系统来吸引乘客选用公交服务, 以达到分流小汽车交通、减缓拥堵的目的。为加快公交出行时间, 提高出行可靠性, 增加服务吸引力, Currie等提出了公交信号优先和设计公交车专用道的典型策略[1-4]。公交专用道的设置成本低见效快, 一度被认为是提升公交服务质量的主要策略。但是公交专用道的路权排他性, 限制了其他类型车辆的通行能力, 加剧了交叉口的拥堵水平。信号优先是实现公交优先级的另一种策略, 包括被动优先[5-7], 主动优先[8-9]和实时优先[10]。这些信号优先策略, 均以路面车道设计为输入条件进行信号设置。但是信号设置和车道功能设计均会影响交叉口通行能力, 二者的联合优化比单独设置更能有效提高通行能力[11]。尤其是对于有专用车道的交叉口, 单独进行信号设置, 对于复杂路口, 很难确定一组最优的交通信号。例如, 在十字交叉口, 某方向上一个车道标记为公交专用道, 则该方向其他车辆通行能力减小, 车道饱和度增加, 需要设置更长的绿灯时间来放行交通量, 这又会导致专用车道上公交车的延误和滞留[12]。因此, 孤立的信号和车道设计不能得到在优先权下的交叉口优化方案[13]。
Lam和Wong等[14-15]对车道功能和信号设置的同时优化做了相关研究, 建立了相应模型和算法。然而, 这类模型没有考虑公交优先问题。公交专用道的考虑使得模型中车道饱和率, 信号相位, 延误计算, 通过能力等都将从单模式转化为多模式情形; 曾滢等针对大城市的潮汐现象, 对可变车道功能与实时信号控制做了协同研究, 但模型仅针对单一车道动态功能与信号设计的协同[16-17]; Ma[18]等建立了考虑交叉口时空资源组合的被动优先模型, 通过设置权重将多目标转化为单目标问题, 以延误最小建立了协同设置模型, 然而模型优化效果取决于权重取值的合理性。
本研究在此基础上, 综合考虑公交车和私家车两种车型在能力占用、承载人数和输送功能等方面的不同, 建立协同设置模型, 改变已有研究以通过车辆数最大为目标的做法, 建立以通过总乘客数的备用能力为目标, 以交叉口公交专用道、普通车道设置、信号周期和相位时长等为变量的线性规划模型, 并以实际交叉口为例采用matlab软件进行了算例分析, 最后给出了结论。
1 符号定义定义模型有关符号如下:
δijk为0, 1变量, 如路段i上的车道k允许驶向路段j, 则取值为1, 否则为0;bijk为0, 1变量, 路段i上的车道k为公交专用道, 若允许驶向路段j, 则取值为1, 否则为0;Bij为0, 1变量, 若路段i到路段j包含公交专用道, 则取值为1, 否则为0;qijk为车道k上驶向路段j的小汽车数量; qijkb为车道k上驶向路段j的公交车数量; θij, φij为从路段i到路段j走向上的绿灯开始时间及绿信比; λik, γik为车道k上的绿灯开始时间及绿信比; σij, lm为一组互不相容的车辆运动(i, j)和(l, m)的相序, 若(l, m)的绿灯开始时间紧邻(i, j)的相位, 则取值为1, 否则为0;C, Cmax, Cmin为信号周期长, 最大及最小周期时长; e为附加有效绿灯时间, 等于实际绿灯时间与有效绿灯时间之差; gij为i到j方向上最小绿灯持续时间; Ns为路段总数; Ov, Ob为小汽车和公交车容量; Qij1v, Qij2v为i, j方向上总交通量和总出行人数Qij1b, Qij2b为i, j方向上公交车总出行量和承载人数; Qijb, Qijv为i, j方向上公交车及小汽车的需求量; sik为车道k的饱和流量; smax, smaxb为普通车道和公交专用道上饱和度的上限值; xik, xikb为普通车道和公交专用道上的流量比率; αij为i, j方向上出口道数量; αi, βi为路段i上进口道和出口道的数量; rij, lm为两组运动间的最小全红时间; ε为公交车和小汽车间的转换系数; μ, μb为总流量及公交车备用能力系数; ψ为互不相容的车辆运动集合。
2 优化模型约束条件 2.1 车道功能约束车道功能分配上主要受到以下5个约束:
(1) 每条车道至少包含一条行驶功能, 包括小汽车和公交车的转弯或直行:
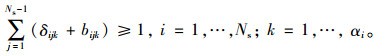
|
(1) |
(2) 考虑到安全性, 在转弯方向上, 不考虑车道汇入的情况, 此时, 路段i上分配的出口道数量应不大于所有其他方向上分配的出口道数量之和:
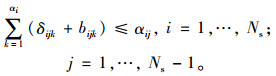
|
(2) |
(3) 公交专用道约束:如果车道k设定为公交专用道, 则不允许小汽车通行:
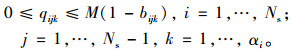
|
(3) |
(4) 路权约束:若δijk=0, 则i, j方向车道k上流量为0:
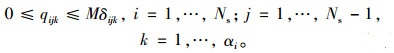
|
(4) |
(5) 为避免同一车道两相邻车道的冲突, 对任意两相邻车道k和k+1而言, 如果车道k+1允许i, j方向行驶, 则车道k不允许向路段j, j+1, …, Ns-1方向行驶(对车道和路段按顺时针方向进行编号):
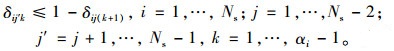
|
(5) |
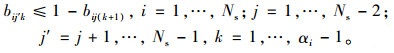
|
(6) |
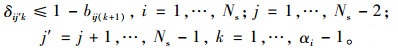
|
(7) |
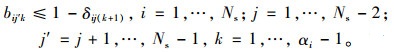
|
(8) |
(1) 普通车道的饱和度约束:为保证交叉口车辆顺畅通行, 每个车道的饱和度应不大于最大可接受饱和度:
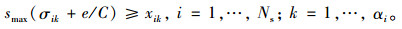
|
(9) |
(2) 公交专用道的饱和度约束:为保证公交优先权, 每条公交专用道的饱和度应不大于相同OD上普通车道的饱和度:
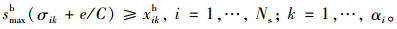
|
(10) |
其中普通车道及公交专用道流量占有率xik, xikb分别计算如下:
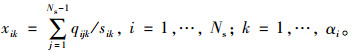
|
(11) |
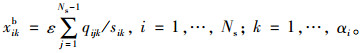
|
(12) |
对所有进口车道而言, 具备相同功能标识的两相邻车道上流量比例应相同:
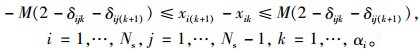
|
(13) |
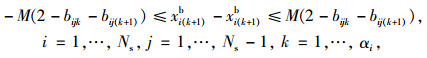
|
(14) |
式(13), (14)中, M为一无穷大数。
2.3 信号配时约束(1) 根据文献[12]给出的模型, 对于信号周期, 绿灯开始时间, 相序, 绿灯时长, 全红时间等变量的约束条件表述如下:
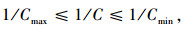
|
(15) |
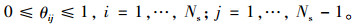
|
(16) |
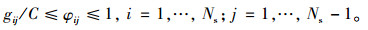
|
(17) |
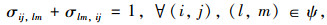
|
(18) |
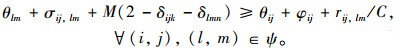
|
(19) |
(2) 车道信号配时:若车道k上包含多个运动方向, 则每一个被设定的运动方向j满足如下约束:
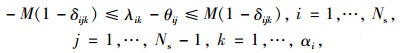
|
(20) |
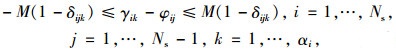
|
(21) |
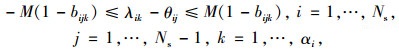
|
(22) |
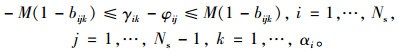
|
(23) |
交叉口公交专用道的设计目标是采用路权优先使得输送人数最大化。因此, 本研究以所有通过车辆所承载的乘客最大化作为车道功能划分与信号配时协同优化的目标函数。交叉口备用通过能力通常用来衡量单点信号控制交叉口设计, 因此在本研究模型中以μ作为优化乘子, 即在车道能力约束, 最佳信号配时条件下, 交叉口可容纳乘客数的最大乘子, 即优化模型转化为求解最大乘子μ, 考虑到公交专用道与普通车道在流量分配, 车道功能及承载乘客数等上的区别, 引入公交客运量乘子μb, 建立目标函数如下:
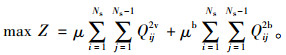
|
(24) |
从式(1)~式(24)可看出, 模型中决策变量:车道功能设置变量包括δijk, bijk, Bij, 均为0, 1变量; 交叉口信号配时变量包括qijk, qijkb, θij, φij, λik, γik, σij, lm, μ, μb。所建立模型为线性混合整数规划模型。同时根据流量守恒定律, Qij1v, Qij2v, Qij1b, Qij2b, qijk, qijkb满足如下等式关系:
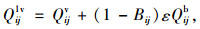
|
(25) |
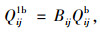
|
(26) |
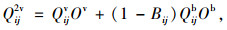
|
(27) |
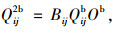
|
(28) |
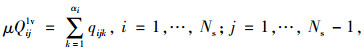
|
(29) |
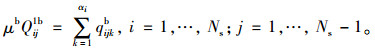
|
(30) |
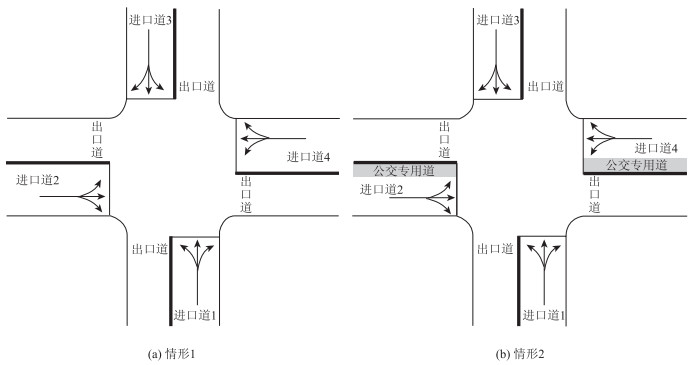
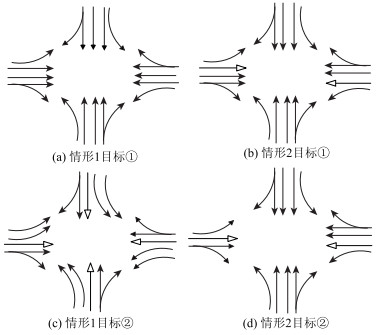
为验证模型和算法有效性, 以图 1所示两个十字交叉口为例, 分别以(1)通过车辆数最大, (2)通过人数最多为优化目标, 计算车道布置及最优信号配时。图 1中交叉口路段标号按逆时针方向依次排序。每条路段上进口道和出口道数均为4, 其中情形1下不预设专用道, 情形2下路段2和路段4上最左边一条车道被设置为公交专用道。
|
| 图 1 十字交叉口 Fig. 1 Cross intersections |
| |
算例其他参数如下:信号周期时长最大值和最小值分别取为60 s, 120 s, 最小绿灯时间设为5 s, 全红时间设为4 s。每条车道的饱和流量为1 800 veh/h。普通车道和专用车道饱和流率设为0.9。小汽车和公交车容量分别为3人和40人, 各方向上出行需求如表 1所示, 表 1中括号外数值表示小汽车流量, 括号内数值为公交车流量, 单位为pcu/h。
| 目标起点 | 目标终点 | |||
| 进口道1 | 进口道2 | 进口道3 | 进口道4 | |
| 进口道1 | — | 172 | 550(50) | 52 |
| 进口道2 | 170 | — | 183 | 675(100) |
| 进口道3 | 656(40) | 171 | — | 152 |
| 进口道4 | 168 | 63(105) | 105/ | — |
4.1 结果分析
用MATLAB编程计算, 结果如表 2, 图 3, 图 4所示。图 2给出了目标①和目标②下的最优车道功能设置, 图 3给出了两种目标下最优的信号配时方案, 表 2给出了两种情形下的优化结果, 包括信号周期时长, 最大备用能力系数及小汽车和公交车的最大输送能力。从表 2可看到, 目标①的优化结果在情形1下提高了44%, 在情形2下, 提高了22%。然而, 目标②的优化结果在情形1和情形2下分别降低了8.7%和10.8%。可看到以最大交叉口通过人数为目标更能体现公交优先的功能。特别地, 在情形2下, 由于交叉口进口道预先设置了专用车道, 目标1的优化结果也能显著提高旅客通过能力。该结果表明以旅客通过能力最大为目标的优化模型不仅优化了公交专用道设置参数Bij, 同时优化了车道功能设置δijk和信号配时方案。
| 交叉口 类型 |
模型 目标 |
备用 能力μ |
备用 能力μb |
周期 时长 |
目标 ①计算值 |
目标 ②计算值 |
| 情形1 | 目标① | 1.42 | 1.42 | 120 | 36.59 | 6 064 |
| 目标② | 0.76 | 3.00 | 120 | 52.70 | 4 582 | |
| 情形2 | 目标① | 1.32 | 2.48 | 120 | 40.73 | 6 118 |
| 目标② | 1.00 | 3.94 | 120 | 51.99 | 5 485 |
|
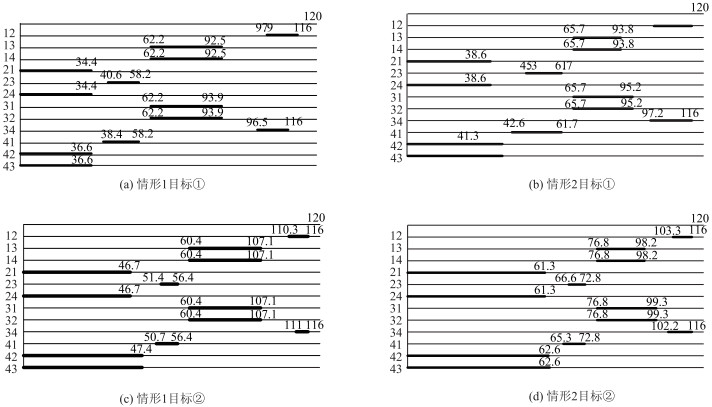
| 图 3 交叉口信号配时 Fig. 3 Signal timing for intersection |
| |
|
| 图 4 通过乘客数和车辆数 Fig. 4 Numbers of passing passengers and vehicles |
| |
|
| 图 2 车道功能设置 Fig. 2 Lane function settings |
| |
比较图 2(a)和图 2(c)可以看到, 在情形1, 不预设公交专用道条件下, 目标②的结果在每条路段上均设置了1条公交专用出口道, 且两方向上左转车道均增加1条, 直行车道相应均减少1条。然而比较图 2(b)和图 2(d)可以看到, 在情形2, 预设公交专用道条件下, 目标②的结果对专用车道的设置与目标①相同。在预设专用车道的方向上, 左转车道增设1条, 直行车道减少1条, 而在被交道路方向上, 车道设置保持不变。出现该结果的原因在于在预设专用车道方向上, 增加了同相位绿灯时间, 因此直行车道数的减少依然提高了旅客通行能力。
图 3给出了两种情形下目标①和目标②的配时方案。粗线条表示绿灯时间, 细线条表示黄灯时间和红灯时间。可看到所有情形下的信号周期时长均取为120 s, 但每个相位的绿灯分配时间不同。对比图 3(a), 3(b)和图 3(c), 3(d)可发现, 目标②在公交需要量大的方向上分配绿灯时间更长, 以保障更大的通过能力和最小的总延误。
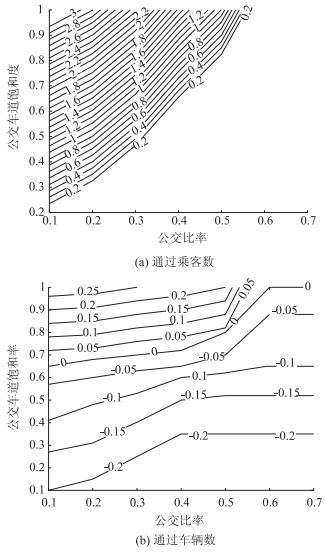
4.2 灵敏度分析图 4给出了公交专用道饱和率smaxb及公交车比率xikb对通行能力的影响。为方便呈现比较结果, 定义PCr=(PC2-PC1)/PC1, VCr=(VC2-VC1)/VC1。其中PCi, VCi分别为目标i下通过的总乘客数和总车辆数。保持其他参数不变, 分别绘制PCr, VCr随smaxb, xikb变化的等值线如图 4所示。可看到图 4(a)中, 等值线均大于0, 表明任何参数取值下目标①可通过更多乘客数。此结论与表 2中结果一致。表中曲线表明公交比例越低, 公交专用道饱和度越高, PCr值越大, 即能通过更多乘客数。特别地, 当公交比例取0.1, 饱和度为0.9时, 目标①下通过乘客数是目标2的3倍以上。此时, 公交需求量为50辆/h, 符合交叉口实际情况。同时注意到, 图 5(a)的右下角区域无等值线, 此时等值线值为0, 表明该区域内对应高公交比例和低饱和率, 此时目标①和目标②下通过乘客数相等。
|
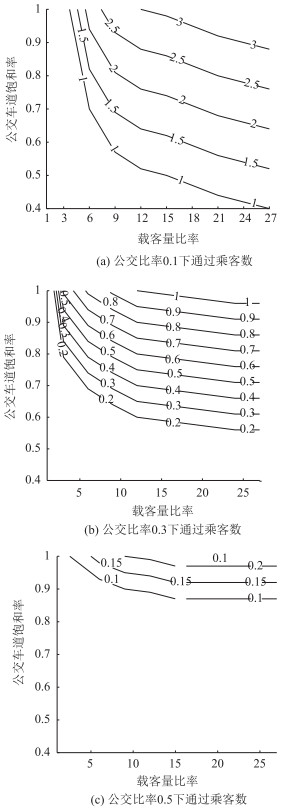
| 图 5 不同公交比率下的通过乘客数 Fig. 5 Numbers of passing passengers with different bus ratios |
| |
图 4(b)给出了通过车辆数的比较。可看到与公交比例相比, VCr对饱和度的灵敏度更高。图形中等值线可能取正也可能取负。表明目标①下总通过车辆数可能小于也可能大于目标②的结果。(如表 2中VC1>VC2)
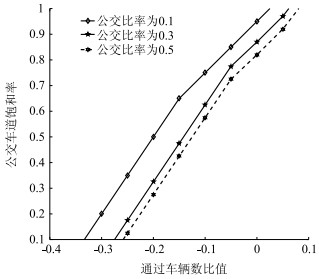
图 5~图 6分别给出了目标①下公交比例取值0.1, 0.3及0.5时, 公交专用道饱和率及公交车, 小汽车载客量比例Or=Ob/Ov对乘客通过能力的影响。从图 5可看到随着载客量比例的增加, 等值线值可达到3(在公交比例取0.1的图 5(a)中), 此公交车比例符合实际情况, 由此可见, 当公交载客量大时, 采用目标①来优化车道功能和信号配时, 能显著提高乘客通过能力。相反, 公交载客比例对车辆通过能力则无大影响。从图 6可看到公交专用道饱和率对VCr影响显著。同时, 增函数曲线也进一步证实了, 目标①模型下, 通过增加公交专用道的通过能力能显著提高车辆通过能力。图 4~图 5中参数的设置可根据实际公交需求和车道饱和率进行调整。同时其结果也为在单点交叉口公交被动优先下, 是否采用乘客通过能力最大来优化车道功能和信号配时提供了依据。
|
| 图 6 车道饱和率灵敏度分析 Fig. 6 Sensitivity analysis of lane saturation |
| |
5 结论
本研究以通过总乘客数的备用能力最大为目标, 建立了以交叉口公交专用道、普通车道设置、信号周期、相位时长等为变量的单点交叉口车道与信号协同设计的线性规划模型。计算结果显示, 在公交小汽车流量比例、荷载人数、车道饱和度等变量定值情况下, 以交叉口通过总乘客数为优化目标, 能保障交叉口获得更大的乘客和车辆通过能力。灵敏度分析发现, 公交比例越低, 公交专用道饱和度越高, 通过乘客数越大; 当公交载客量大时, 采用通过乘客数为目标来优化车道功能和信号配时, 能显著提高乘客通过能力, 公交载客比例对车辆通过能力则无显著影响。研究结果为在单点交叉口公交被动优先下, 是否采用乘客通过能力最大来优化车道功能和信号配时提供了依据。
本研究模型仅考虑了公交车和小汽车两种车型, 当交叉口流量为多种出行需求的混合交通时, 模型将更复杂同时更贴近实际。且目标函数中仅考虑了通过能力, 没有考虑乘客和车辆延误。下一步的工作中将以通过能力和总延误建立多目标模型, 同时考虑交叉口混合交通流的情形, 并对专用道的车道选择优化以及多车道设置专用道的可能性进行验证。
| [1] |
FALBEL S, RODRIGUEZ P, LEVINSON H, et al. Bus Rapid Transit Plans in New York's Capital District[J]. Journal of Public Transportation, 2006, 9(3): 23-50. |
| [2] |
VIEGAS J, LU B. The Intermittent Bus Lane Signals Setting within an Area[J]. Transportation Research Part C:Emerging Technologies, 2004, 12(6): 453-469. |
| [3] |
FUHS C, OBENBERGER J T. Development of High-occupancy Vehicle Facilities:Review of National Trends[J]. Transportation Research Record, 2002, 1781: 1-9. |
| [4] |
SKABARDONIS A. Control Strategies for Transit Priority[J]. Transportation Research Record, 2000, 1727: 20-26. |
| [5] |
别一鸣, 王殿海, 魏强, 等. 考虑饱和度约束的单点主被动有限公交优先策略[J]. 吉林大学学报:工学版, 2011, 41(5): 1222-1227. BIE Yi-ming, WANG Dian-hai, WEI Qiang, et al. Conditional Active and Passive Bus Signal Priority Strategies Considering Saturation Degree Restriction at an Isolated Junction[J]. Journal of Jilin University:Engineering and Technology Edition, 2011, 41(5): 1222-1227. |
| [6] |
李凤, 王殿海, 杨希锐. 单点公交被动优先下信号配时方法研究[J]. 交通信息与安全, 2009, 27(3): 48-52. LI Feng, WANG Dian-hai, YANG Xi-rui. Signal Timing Method for Transit Passive Priority at an Isolated Intersection[J]. Computer and Communications, 2009, 27(3): 48-52. |
| [7] |
林永杰, 杨险峰, 邹难, 等. 城市交通干道上被动式公交信号优先控制[J]. 东北大学学报:自然科学版, 2013, 34(9): 1227-1230. LIN Yong-jie, YANG Xian-feng, ZOU Nan, et al. New Passive Transit Signal Priority Control Strategy for the Bus Vehicles at Urban Arteries[J]. Journal of Northeastern University:Natural Science Edition, 2013, 34(9): 1227-1230. |
| [8] |
谭真, 梅振宇, 黄志义, 等. 协调控制下主动信号优先策略的最佳周期模型[J]. 公路交通科技, 2012, 29(7): 104-110. TAN Zhen, MEI Zhen-yu, HUANG Zhi-yi, et al. Optimal Cycle Model Based on Active Transit Signal Priority Strategies with Artery Coordination[J]. Journal of Highway and Transportation Research and Development, 2012, 29(7): 104-110. |
| [9] |
汪健, 胡娟娟, 李凤. 两交叉口间主动式公交信号优先协调控制配时优化方法[J]. 武汉理工大学学报:交通科学与工程版, 2013, 37(4): 703-712. WANG Jian, HU Juan-juan, LI Feng. A Active Coordinated Control timing Optimization Algorithm of Transit Signal Priority[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2013, 37(4): 703-712. |
| [10] |
曲大义, 蔡国良, 陈秀峰, 等. 公交优先实时在线单点控制策略研究[J]. 公路交通科技, 2011, 28(4): 112-117. QU Da-yi, CAI Guo-liang, CHEN Xiu-feng, et al. Real-time Online Single Point Control Strategy for Transit Priority[J]. Journal of Highway and Transportation Research and Development, 2011, 28(4): 112-117. |
| [11] |
MA W J, LIU Y, YANG X G.Dynamic Programming Model for Optimal Bus Signal Priority Control with Multiple Requests[C/CD]//90th Annual Meeting of the Transportation Research Board.Washington, D. C.: TRB, 2011.
|
| [12] |
马万经, 杨晓光. 基于动态规划的公交信号优先多申请排序模型[J]. 清华大学学报:自然科学版, 2009, 49(12): 1939-1943. MA Wan-jing, YANG Xiao-guang. Serve Sequence Optimization of Multiple Bus Signal Priority Requests Based on Dynamic Programming[J]. Journal of Tsinghua University:Science and Technology Edition, 2009, 49(12): 1939-1943. |
| [13] |
胡兴华, 隆冰, 朱晓宁. 考虑绿时损失均衡的公交优先交叉口配时优化[J]. 公路交通科技, 2016, 32(2): 96-104. HU Xing-hua, LONG Bing, ZHU Xiao-ning. Timing Optimization for Bus Priority Signalized Intersection Considering Green Loss Equilibrium[J]. Journal of Highway and Transportation Research and Development, 2016, 32(2): 96-104. |
| [14] |
LAM W H K, POON A C K, MUNG G K S. Integrated Model for Lane-use and Signal-phase Designs[J]. Journal of Transportation Engineering, 1997, 123(2): 114-122. |
| [15] |
WONG C K, HEYDECKER B G. Optimal Allocation of Turns to Lanes at an Isolated Signal-controlled Junction[J]. Transportation Research Part B:Methodological, 2011, 45(4): 667-681. |
| [16] |
曾滢, 杨晓光, 马莹莹. 交叉口动态车道功能与信号控制协同问题研究[J]. 同济大学学报:自然科学版, 2009, 37(7): 903-908. ZENG Ying, YANG Xiao-guang, MA Ying-ying. Study on Synergy Problem of Dynamic Lane-use Assignment and Signal Control at Intersections[J]. Journal of Tongji University:Natural Science Edition, 2009, 37(7): 903-908. |
| [17] |
丁靖, 周红媚, 姚荣涵. 交叉口可变导向车道与信号配时协同优化模型[J]. 交通运输研究, 2015, 1(3): 7-13. DING Jing, ZHOU Hong-mei, YAO Rong-han. A Simultaneous Optimization Model of Variable Approach Lane and Signal Timing at Intersection[J]. Transport Research, 2015, 1(3): 7-13. |
| [18] |
MA W, YANG X, LIU Y. Development and Evaluation of a Coordinated and Conditional Bus Priority Approach[J]. Transportation Research Record, 2010, 2145: 49-58. |
 2019, Vol. 36
2019, Vol. 36
