扩展功能
文章信息
- 杨永清, 程楚云, 张勇, 蒲黔辉
- YANG Yong-qing, CHENG Chu-yun, ZHANG Yong, PU Qian-hui
- 车辆荷载对正交异性钢桥面疲劳细节应力影响研究
- Study on Influence of Vehicle Loads on Fatigue Detail Stress of Orthotropic Steel Bridge Deck
- 公路交通科技, 2019, 36(11): 50-58
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(11): 50-58
- 10.3969/j.issn.1002-0268.2019.11.007
-
文章历史
- 收稿日期: 2018-07-09
正交异性钢桥面板具有自重轻、承载能力高、适用性广的特点,是现代桥梁工程的标志性创新成就。但公路钢桥正交异性桥面板结构构造复杂、细节种类多样,在各个板件的交叉焊接部位存在集中应力和损伤应力,导致结构极易发生疲劳损伤[1],国内外已有许多钢桥发现了此类病害[5-6]。疲劳开裂严重影响结构的行车舒适性和服役周期,显著增加桥梁的运营和维护成本,已成为阻碍正交异性结构桥梁性能设计和可持续发展的控制性难题[7]。在移动车辆荷载作用下,正交异性钢桥面板疲劳细节的应力影响线具有长度较短、循环次数多[8]等特点,极易发生疲劳损坏。因此,正交异性钢桥面板的疲劳计算必须以板件的真实受力情况为基础,其疲劳寿命的评估需要分析焊接细节周围的应力分布规律及焊趾应力集中效应。
在正交异性桥面板的局部应力分析方面,国内外学者进行了大量研究。童乐为[9]对一个角钢纵肋的大型钢桥面板模型进行有限元分析,探究了钢桥面板各个部位的应力分布状况。吴冲等[10]通过有限元计算分析,研究了横隔板间距对正交异性钢桥面板疲劳应力幅的影响规律。唐亮等[11]通过ANSYS有限元模型对正交异性钢桥面板横隔板弧形开孔周围的应力分布情况进行了分析。郑凯锋等[12]通过有限元模型,分析了正交异性钢桥面板横隔板的不同开孔与纵肋连接焊缝端部的受力特性。顾萍[13]采用有限元方法模拟钢桥面板应力特性,确定了各典型疲劳裂纹最不利位置,在横梁与纵肋连接处,其主应力较大且应力集中效应明显,极易产生疲劳裂纹。高立强[14]采用有限单元法分析了横梁腹板切口形状对横梁腹板与纵肋连接部位及横梁腹板切口边缘疲劳性能的影响规律。Yamada等[15]研究了荷载加载模式和应力集中对正交异性钢桥面板裂纹形状的影响。Ye等[16]考察了不同载荷情况下结构应力随单元尺寸的变化规律,发现在结构应力测试中,结构应力对单元尺寸和单元类型不敏感。在我国《公路钢结构桥梁设计规范》(JTG D64—2015)[17]中也规定在评估钢桥面板的疲劳损伤时只需考虑局部应力影响,即横桥向多车道效应系数为1。可见目前研究中尚未考虑移动荷载不同空间位置对公路钢桥正交异性桥面板构造细节应力状况的影响。
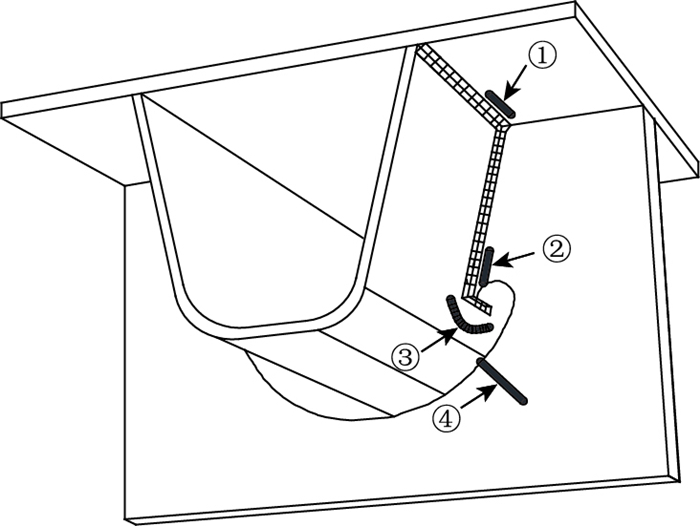
相关研究发现[7],正交异性钢桥面板典型疲劳易损部位主要是纵向加劲肋与横隔板交叉焊接连接(含开孔)、纵向加劲肋与顶板焊接连接、横隔板与顶板焊接连接等部位,如图 1所示。其中发生在纵向加劲肋和横隔板交叉焊缝及开孔部位的疲劳开裂的几率最大(图 1中②③④),占疲劳裂纹总数的38.2%,该部位是正交异性钢桥面板中应力集中程度最为明显、构造最为复杂及焊接初始缺陷风险较高的部位。由于公路桥梁横向尺寸比较大,在移动荷载作用下,即使同一类构造细节,不同横向位置的受力状态也会有较大差异。分析发现,最外侧车道处的钢桥面疲劳敏感部位应力幅更大,故更易发生疲劳破坏。因此,通过建立重庆中渡长江大桥ANSYS有限元模型,选取边车道轮载作用位置的桥面板构造细节作为目标验算构造,并绘制疲劳易损部位应力影响线,分析移动荷载不同空间位置对细节应力状态的影响,最后通过应力等效建立足尺模型试验对等效疲劳敏感点应力进行疲劳试验验证。
|
| 图 1 典型裂纹及应力点 Fig. 1 Typical cracks and stress points |
| |
1 钢桥面板整体分析 1.1 工程概况
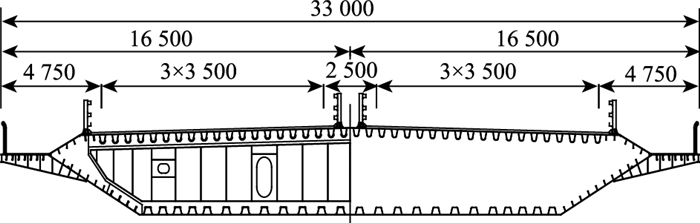
重庆中渡长江大桥是一座双向6车道通行的双塔悬索公路桥,桥跨布置为(50+600+65) m,主梁为高3.0 m、宽33 m的无腹板式钢箱梁。梁顶、底板均采用U型和I型加劲肋结合的正交异性板结构。其中,顶板厚度为16 mm,肋高均为280 mm,厚度为8 mm;横隔板分别采用实腹式和空腹式两种构造形式,厚度均为12 mm,纵向间距为3 m,标准横断面图如图 2所示。
|
| 图 2 无腹板式钢箱梁标准横断面(单位:mm) Fig. 2 Standard cross-section of steel box girder without web (unit: mm) |
| |
1.2 无腹板式钢箱梁有限元模型
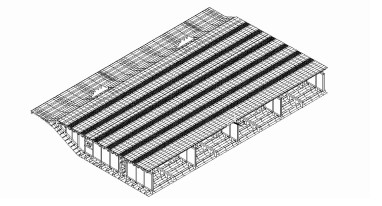
为了准确模拟移动荷载对正交异性钢桥面板各个构造细节的影响,本研究对于全桥模型与局部模型边界条件采用子模型技术衔接,将各工况作用下整体模型中切割边界节点的位移插值到局部模型边界节点上[13]。局部模型为结构模型,共包含两个节段,8个节间,总长25 m。三维精细化有限元模型如图 3所示。有限元模型中的所有板件采用shell63单元模拟,由于主要分析活载作用下的结构受力行为,有限元模型在吊索位置进行约束,以模拟悬索桥吊索的约束作用,在边界上施加了通过全桥有限元Midas模型提取的相应边界力并进行细部受力分析。
|
| 图 3 梁段的三维有限元分析模型 Fig. 3 Three-dimensional FEA model of girder segment |
| |
目前我国还没有公路桥梁疲劳荷载的相关规定,出于安全考虑,车辆荷载加载参考《公路桥涵设计通用规范》(JTG D60—2015)中的技术指标,中后轮胎着地面积为(0.6×0.2)m2,两轮位之间横向距离1.8 m。重庆中渡桥沥青混凝土铺装层的厚度为55 mm,考虑桥面铺装对车辆荷载的分散作用,轮载按照45°方向扩展到桥面板上,扩展后的面积为(0.71×0.31)m2。
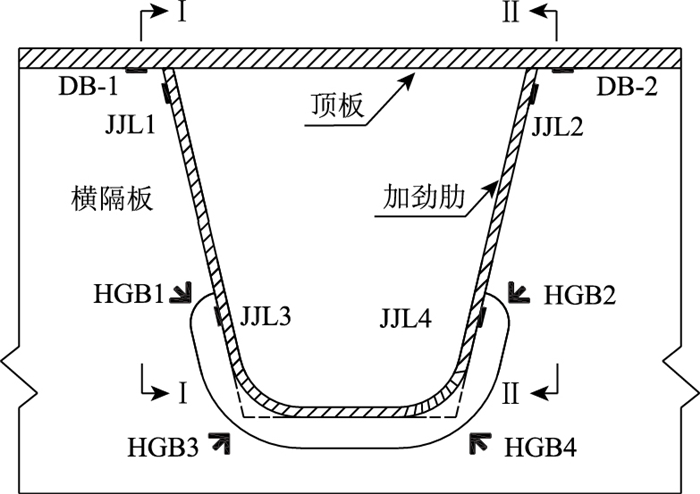
2 有限元细部构造分析结果在研究正交异性钢桥面板疲劳性能之前,首先对正交异性钢桥面板各个疲劳敏感点(如图 4所示)的影响线进行分析,然后将标准车辆按照影响线加载,获得各个点的应力和应力幅情况,最后根据应力的分布特性进行试验模型的设计和疲劳试验。
|
| 图 4 应力考察点布置图 Fig. 4 Arrangement of stress inspection points |
| |
按正交异性板分析理论将结构划分为第1体系、第2体系与第3体系,其中钢箱梁整体参与全桥受力和变形为第1体系,钢箱梁桥面局部(含加劲肋、横隔板和顶板)承受车辆荷载为第2体系,第3体系则将顶板视为支撑在加劲肋和横隔板的连续板。第2体系与第3体系均体现了正交异性板的局部应力效应。经分析可知,第2、第3体系下的活载效应对正交异性桥面板构造细节疲劳应力幅的影响占主导地位,而第1体系下该效应的影响相对较小,因此在绘制影响线时,仅考虑单位荷载。
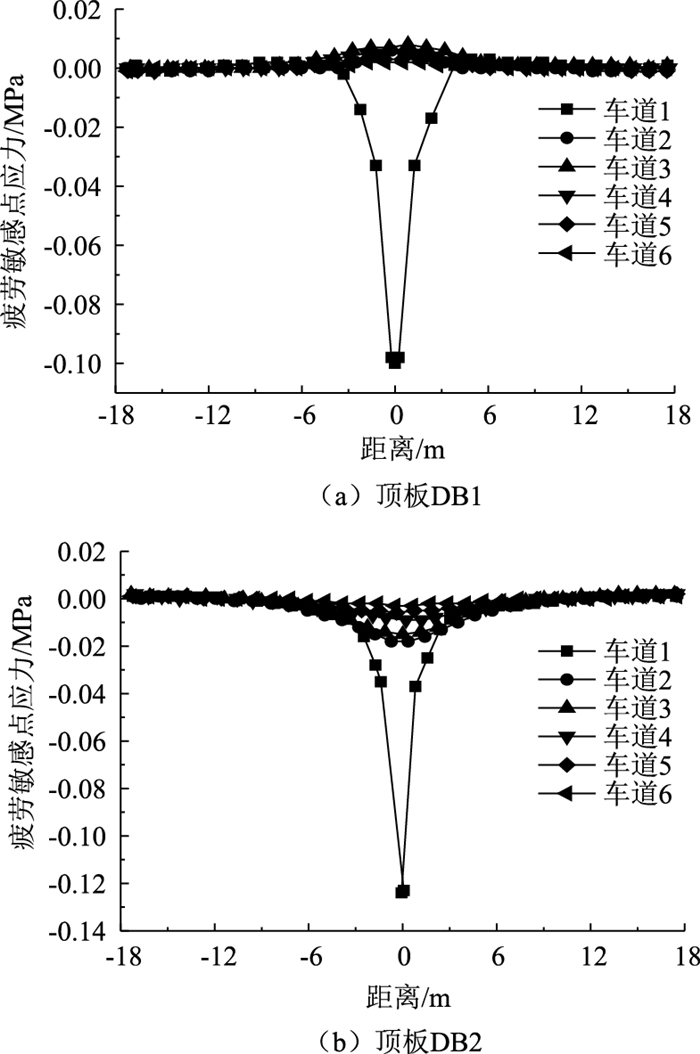
2.1 顶板-加劲肋连接处疲劳敏感点的应力特点顶板处于横桥向和纵桥向的双向正应力状态,且纵桥向正应力远小于横桥向的应力[18],在此只关注顶板的横向应力分布状况。单位轮载作用在不同车道时,顶板底面考察点DB1和DB2横向应力纵向影响线如图 5所示,横坐标为单位轮载距中间横隔板(如图 3所示)的纵向距离。
|
| 图 5 顶板考察点应力影响线 Fig. 5 Stress influence lines of stress inspection points on roof |
| |
由图 5可知,顶板与加劲肋腹板焊接构造细节的纵向影响线长度约为20 m,可近似取为7Ld(Ld为横隔板间距,本研究为3 m),其纵向影响线有效长度Le为2Ld,该值大于规范中标准车辆的最小轴距,且小于最大轴距,表明顺桥向多车效应和同一车辆各轴作用的耦合效应对于顶板焊接构造细节的影响较小。顶板DB2考察点在车辆活载作用下,不同车道的应力幅值差距较大,顶板DB2相对顶板DB1的差值更大,因此,计算该点疲劳应力时可忽略横桥向多车辆荷载耦合效应的影响。当单位轮载作用在车道1时,顶板DB1和顶板DB2的应力梯度较大,顶板DB2出现最大应力,表明桥面板局部支撑作用产生的面外弯曲对顶面与加劲肋连接焊缝处的疲劳应力影响显著。顶板DB2在车辆单位轮载作用下顶板承受较大压应力,在钢桥面板全焊结构中,由于焊接残余应力的存在,该细节仍可能出现疲劳损伤[18]。
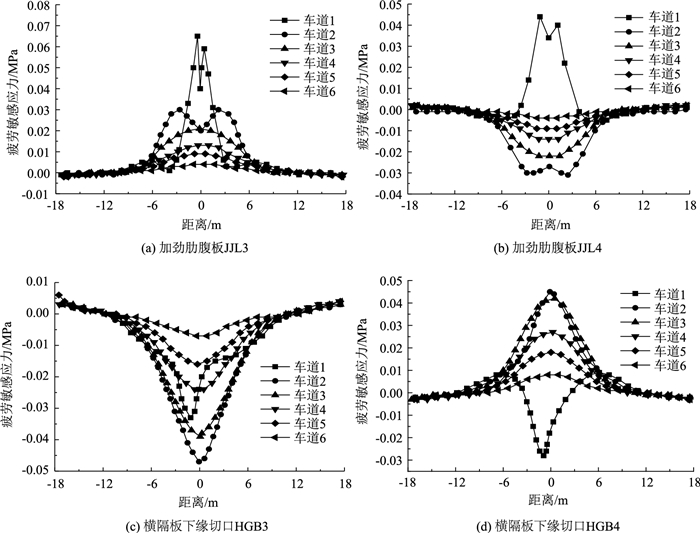
2.2 加劲肋-横隔板连接处和横隔板切口边缘处疲劳敏感点应力特点相关研究表明[18],轮载作用将导致横隔板的剪力发生突变,对加劲肋与横隔板连接处应力产生明显影响,通过单位荷载位置变化模拟车辆的行驶,绘制加劲肋腹板与横隔板焊接处JJL3和JJL4疲劳敏感点的横向应力沿纵桥向影响线。在正交异性钢桥面板发生的开裂中发现,横隔板下边缘处切口更易因拉应力过大产生疲劳损伤[19],遂绘制横隔板下缘切口细节底面关注点HGB3和HGB4横向应力沿纵桥向影响线,如图 6所示,横坐标均为移动荷载距中间横隔板HGB2的纵向距离。
|
| 图 6 疲劳敏感点应力影响线 Fig. 6 Stress influence lines of fatigue sensitive points |
| |
结果表明,(1)加劲肋腹板与横隔板焊接和横隔板下缘切口的构造细节纵向影响线长度约为24,25 m,其纵向影响线有效长度Le为5Ld,加劲肋腹板影响线有效长度较长,表明顺桥向多车效应和前后轴重耦合效应对于这两构造细节的应力影响较大。(2)当移动荷载作用在不同车道时,应力梯度较大且应力幅值差距较小,说明横向多车道荷载交叉作用对这两区域应力影响较大,因此,在进行静力分析与疲劳验算时,应考虑横向多车道效应的影响。(3)移动荷载作用于车道1的两个横隔板中间位置时,加劲肋关注点JJL3和JJL4产生的应力最大,表明加劲肋与横隔板连接焊缝端部应力受加劲肋面内弯曲应力影响明显。(4)横隔板关注点受到横隔板空腹梁工作模式的影响,当车辆荷载位于车道2和车道3时,横隔板HGB4关注点拉应力最大。
2.4 疲劳评估通过对《重庆江津中渡长江大桥工程可行性研究阶段交通需求分析研究报告》中实际交通荷载信息的统计分析,获取了原始荷载谱和等效标准车荷载谱,采用Monte-Carlo方法模拟交通荷载,结合上文中所得到的焊接构造细节应力纵向影响线进行加载,得到各个疲劳敏感点的应力时程曲线。最后运用雨流计数法计算各个疲劳易损细节的应力频值谱,并结合Palmgren-Miner疲劳损伤累计理论式(1),确定疲劳易损部位200万次的等效应力幅,如表 1所示。
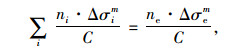
|
(1) |
| 构造细节 | 应力位置与类型 | 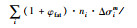 [次·(MPa)3]
[次·(MPa)3] |
2×106次等效疲劳应力幅/MPa | 疲劳等级Eurocode3/MPa | |
| 顶板与横隔板焊接处 | DB-1 | 焊趾处垂直焊缝应力 | 2.618 83×1011 | 50.78 | 90 |
| DB-2 | 2.889 1×1011 | 52.47 | |||
| 加劲肋与横隔板焊接处 | JJL-3 | 绕焊趾处主拉应力 | 5.326 88×1011 | 64.34 | 125 |
| JJL-4 | 5.058 31×1011 | 63.24 | |||
| 横隔板切口边缘 | HGB-3 | 切口边缘最大主拉应力 | 1.469 21×1012 | 90.23 | 125 |
| HGB-4 | 2.441 85×1012 | 106.88 | |||
| 注:φfat为冲击系数,取值为1.4。 | |||||
式中,Δσi为原始荷载应力幅;ni为疲劳应力幅为Δσi时荷载的作用次数;Δσe为等效荷载的应力循环幅度;ne为等效荷载的疲劳循环次数;m为S-N曲线斜率的负倒数,对于焊接结构按照欧洲规范Eurocode3取为3;C为与疲劳等级相关的常数。
由表 1可见,正交异性钢桥面板的应力水平较低,其中横隔板切口边缘主拉应力最大,横隔板与顶板、加劲肋处的应力较小,且都小于欧洲规范Eurocode3中对相应构造细节200万次的疲劳强度限值,表明该正交异性钢桥面板的疲劳性能满足设计要求。加劲肋与横隔板焊接疲劳敏感点JJL-3和JJL-4绕焊趾处的主拉应力小于Eurocode3中变幅疲劳截止值,即此处永久不会发生疲劳破坏,而横隔板切口边缘疲劳易损部位HGB-4的主拉应力最接近Eurocode3中的200万次疲劳强度限值。
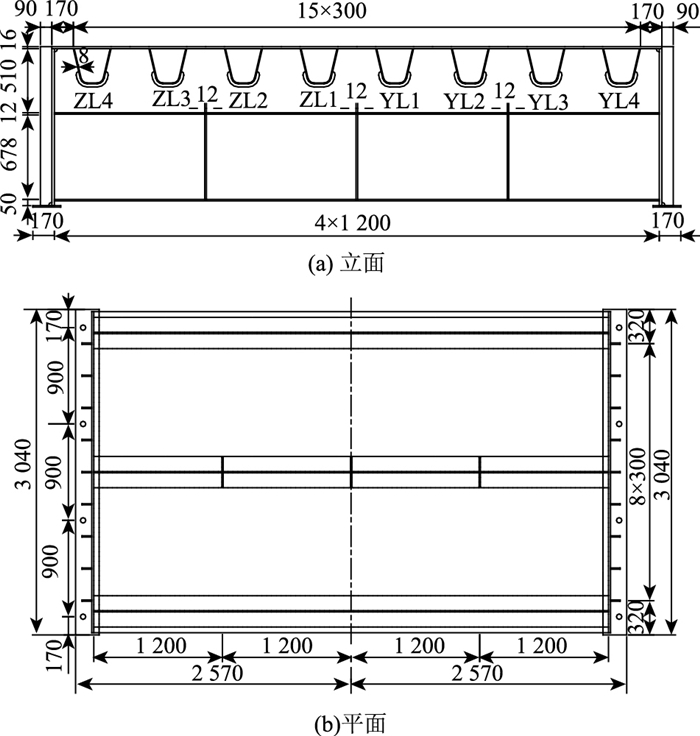
3 正交异性桥面疲劳细节试验验证 3.1 疲劳试验模型概况及模型应力等效分析为探究重庆中渡桥正交异性钢桥面的疲劳性能,根据其正交异性桥面板参数,考虑试验场地与设备、加载和测试简便性、加工制造等疲劳模型试验设计因素,模型试验方案最终采用足尺节段模型。该试验模型的尺寸(长×宽×高)为(3.04 m×5.14 m×1.278 m),在纵向上设置3个横隔板,包括2个高为0.51 m的边横隔板和1个高为1.2 m的中横隔板,其中边横隔板与中横隔板的间距为1.3 m,在横向上设置8条U形加劲肋。U形加劲肋形状和间距、横隔板开口形式及各个板件的厚度等均与实桥相同。模型采用与原桥相同的材料、焊接工艺与加工方法,模型构造及尺寸如图 7所示。
|
| 图 7 模型构造及尺寸(单位:mm) Fig. 7 Structure and dimensions of model(unit: mm) |
| |
在进行结构的疲劳试验前,首先保证试验模型与实际结构等效,即保证原结构疲劳敏感位置的应力分布和应力水平与试验模型一致,误差越小越能确保试验模型反映原桥结构的受力特性。将原桥有限元模型3车道加载的应力与试验有限元模型的应力状态进行对比,表 2列出试验模型YL1加劲肋处疲劳敏感点与原桥节段模型17#加劲肋疲劳敏感点的等效情况,两个模型等效情况较好,相对差值基本保持在10%以内。
| 位置 | 测点号 | 主应力水平 | 主应力方向 | |||||||
| 原桥主应力/MPa | 模型主应力/MPa | 绝对差值/MPa | 相对差值/% | 原桥主应力方向/(°) | 模型主应力方向/(°) | 绝对差值/(°) | 相对差值/% | |||
| 顶板 | 1 | -30.9 | -29 | 1.9 | -6.15 | 25.4 | 26.3 | 0.9 | 3.54 | |
| 2 | 14.4 | 13.6 | -0.8 | -5.56 | 44.4 | 34.7 | -9.7 | -21.85 | ||
| 加劲肋 | 1 | 20.9 | 24.5 | 3.6 | 17.22 | 85 | 83.4 | -1.6 | -1.88 | |
| 2 | -34.4 | -36.1 | -1.7 | 4.94 | 98.7 | 96.9 | -1.8 | -1.82 | ||
| 3 | 40.1 | 39.9 | -0.2 | -0.50 | 79.7 | 85.6 | 5.9 | 7.40 | ||
| 4 | -72.3 | -66.9 | 5.4 | -7.47 | 89.5 | 90.9 | 1.4 | 1.56 | ||
| 横隔板 | 1 | 29.4 | 29.2 | -0.2 | -0.68 | 19.2 | 17.5 | -1.7 | -8.85 | |
| 2 | -31.8 | -26.6 | 5.2 | -16.35 | 3.7 | 4.2 | 0.5 | 13.51 | ||
| 3 | -119.9 | -128.4 | -8.5 | 7.09 | 46.7 | 46.9 | 0.2 | 0.43 | ||
| 4 | 96.1 | 104.3 | 8.2 | 8.53 | 44.4 | 39.7 | -4.7 | -10.59 | ||
3.2 疲劳试验模型应力测点布置与加载方案
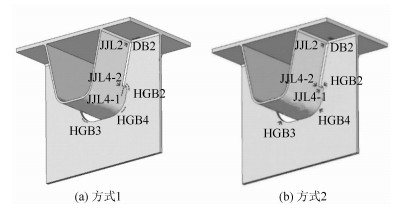
有限元分析结果表明,模型弯剪耦合段加劲肋与横隔板连接部位、横隔板开孔边缘应力集中部位具有较高的疲劳应力,加劲肋与顶板连接部位的局部应力也较高。因此,疲劳试验过程中应重点监测这些疲劳敏感部位的疲劳应力。疲劳易损构造处的应变测点布置采用两种方案,如图 8所示。其中加劲肋疲劳敏测点YL1和YL3的应变片布置采用两种方式,在顶板、横隔板及加劲肋JJL3-1和JJL4-1处布置连续单向应变测片,应变片间距5 mm,以此考察焊趾周围应力梯度的变化情况。在顶板DB处横向应变片的排列为DB1-1~DB1-4和DB2-1~DB2-4,其他位置布置应变花,布置方式见图 8(a),其余加劲肋各个疲劳敏测点均采用应变花的布置方式,见图 8(b)。
|
| 图 8 测点布置 Fig. 8 Arrangement of measuring points |
| |
为模拟公路正交异性钢桥面板顶板、加劲肋腹板、横隔板开口等疲劳敏感部位的应力状态,经过多次有限元计算分析确保关注位置受力与原桥情况一致。遂采用纵向关于中间横隔板对称的分载梁加载形式,横向上分载梁位于ZL1和YL1正上方,加载方案见图 9。

|
| 图 9 试验加载方案(单位:mm) Fig. 9 Loading scheme for test (unit: mm) |
| |
通过Palmgren-Miner损伤累积准则,确定本次试验荷载循环次数500万次,加载荷载幅为ΔP=800 kN,其中荷载上限Pmax=850 kN, 下限Pmin=50 kN,加载频率为1.5 Hz。试验过程中当荷载循环次数达到20万次的整数倍时停机进行静载试验,用动态应变仪对正交异性桥面板各测点应力进行监测,160万次以后,每次停机时都对试验模型的疲劳敏感细节进行一次超声波探伤。
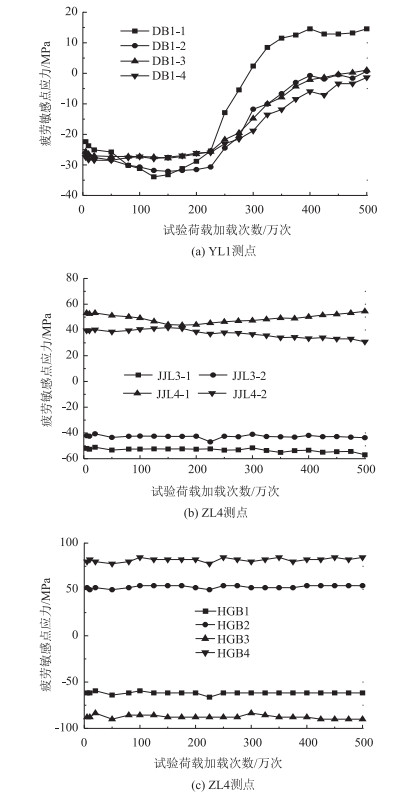
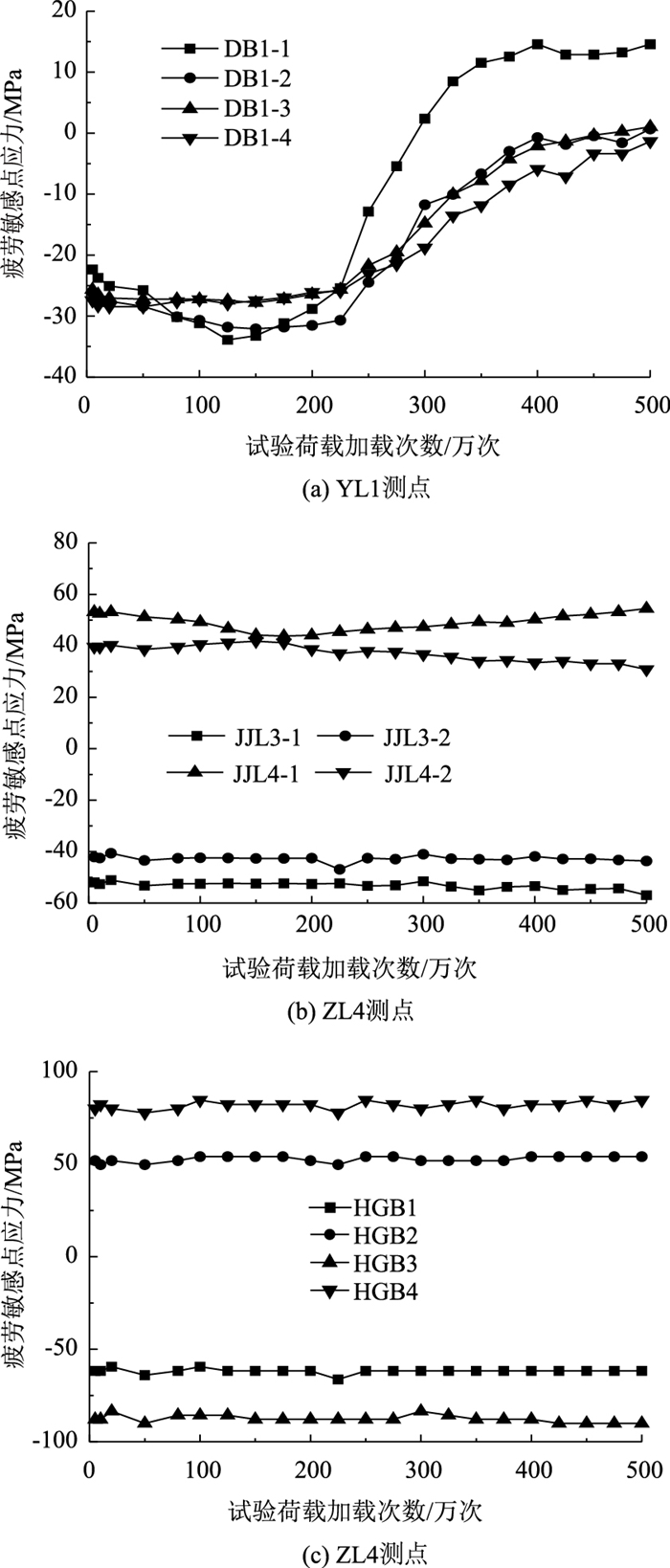
4 型疲劳试验结果与分析疲劳试验过程中,通过动态应变仪对主要部位的测点应力进行了检测。顶板位置DB2测点和加劲肋腹板JJL3, JJL4测点及横隔板测点的应力变化情况如图 10所示。图 11反映了疲劳试验过程中疲劳裂纹随加载次数增加的变化情况。
|
| 图 10 主应力-循环次数关系曲线 Fig. 10 Principal stress vs. loading cycles |
| |
|
| 图 11 疲劳裂缝长度与荷载循环次数的关系 Fig. 11 Relationship between fatigue crack length and loading cycles |
| |
由图 10(a)顶板处应力变化规律可知, (1)在前225万次加载中,各疲劳敏感部位测点的应力量值基本保持不变,且越靠近焊趾压应力数值越大,说明距焊缝越近应力集中现象越明显。(2)加载到225万次以后,YL1焊趾处出现了长度约为8 mm的表面微裂纹,并发生应力重分布,测点处压应力值均逐渐减小,个别测点甚至出现拉应力。(3)试验加载到400万次以后,YL1各测点的应力状态趋于平稳,应力波动较小,表明此处裂纹附近区域应力完全释放和重分配。疲劳试验结束后,对模型切割发现,顶板裂缝长度为130 mm,裂缝贯穿整个桥面板,裂缝长度发展如图 11所示。(4)实测应力值和有限元模型计算值均表明YL1处DB1-1~DB1-4疲劳敏感点处于受压状态,但由于焊接残余应力的存在,导致此焊接细节发生了疲劳破坏。因此,焊接残余应力也会使焊接结构的高压应力循环区产生疲劳开裂。
通过对加劲肋腹板测点和横隔板HGB4测点应力研究发现:(1)在疲劳试验过程中ZY4横隔板切口应力数值基本保持不变,测点JJL4-1与JJL4-2应力发生微小变化,如图 10(b)、(c)所示,表明在疲劳荷载循环加载过程中,该疲劳细节的力学行为未发生明显改变,一直处于弹性状态;(2)在疲劳试验完成后进行了全面探伤,该处未检测到裂纹,表明该疲劳细节具有较高的疲劳抗力。
5 结论本研究通过有限元分析,讨论了移动荷载在不同空间位置布置情况下,正交异性桥面板3种典型构造细节(顶板焊接构造、加劲肋腹板焊接构造及横隔板切口构造)的应力特性,然后模拟交通荷载得到各个疲劳敏感点的应力时程曲线,最后根据Palmgren-Miner疲劳损伤累计理论设计了疲劳模型试验,得出以下结论:
(1) 在多车道正交异性钢桥面板中,车辆轮载作用于边车道时,由于整体弯剪和局部支撑的共同作用致使桥面板受力更为不利。横截面较大的疲劳试验模型能真切反映在实桥最不利受力情况下移动荷载的横向位置对结构疲劳性能的影响。
(2) 顶板与加劲肋焊接处疲劳敏感点DB1和DB2横向应力影响线的纵向有效长度最小,为2个横隔板间距(6 m),而加劲肋腹板JJL3和JJL4及横隔板切口下边缘疲劳敏感点HGB3和HGB4的纵桥向有效长度Le为5个横隔板间距(15 m)。表明顺桥向多车效应和前后轴重的耦合效应对加劲肋腹板焊接构造及横隔板切口构造的应力状态影响较大,而对顶板焊接构造细节的影响较小。
(3) 从影响线分析可知,加劲肋腹板JJL3和JJL4及横隔板HGB3和HGB4的应力影响线在不同车道间的差距较小,表明加劲肋腹板与横隔板焊接构造处及横隔板切口下边缘的应力受横桥向多车道荷载耦合效应影响较大。而顶板处疲劳敏感点DB1和DB2的应力影响线在横桥向不同车道间数值差距较大,表明边车道顶板构造细节的应力受横桥向多车道耦合效应影响较小,进行该处受力计算时可忽略该效应的影响。
(4) 在疲劳试验中,顶板与加劲肋焊接处DB1应力在疲劳荷载施加到225万次时发生突变,若以侧点应力发生突变为疲劳失效判据,则此处焊接细节发生疲劳破坏。加劲肋腹板处和横隔板切口下边缘疲劳易损部位在疲劳试验结束后没发现肉眼可见裂纹,但加劲肋腹板处测点JJL4在疲劳荷载施加到150万次时,应力发生微小波动。
(5) 高压应力幅值区的焊缝处随着荷载加载次数的增加也会萌生疲劳裂纹,在疲劳裂纹扩展前期,其增长速度较慢,但是随着裂纹长度的增加,其速度也会加快,最终将导致焊缝过早发生疲劳损坏,因此残余应力对焊接构造细节的疲劳性能影响必须重视。
| [1] |
唐亮, 黄李骥, 刘高, 等. 正交异性钢桥面板足尺模型疲劳试验[J]. 土木工程学报, 2014, 47(3): 112-122. TANG Liang, HUANG Li-ji, LIU Gao. Fatigue Experimental Study of a Full-scale Steel Orthotropic Deck Model[J]. China Civil Engineering Journal, 2014, 47(3): 112-122. |
| [2] |
张清华, 崔闯, 卜一之, 等. 正交异性钢桥面板足尺节段疲劳模型试验研究[J]. 土木工程学报, 2015, 48(4): 72-83. ZHANG Qing-hua, CUI Chuang, BU Yi-zhi, et al. Experimental Study on Fatigue Features of Orthotropic Bridge Deck through Full-scale Segment Models[J]. China Civil Engineering Journal, 2015, 48(4): 72-83. |
| [3] |
袁周致远, 吉伯海, 杨沐野, 等. 正交异性钢桥面板顶板竖向加劲肋焊接接头疲劳性能试验研究[J]. 土木工程学报, 2015, 49(2): 69-76. YUANZHOU Zhi-yuan, JI Bo-hai, YANG Mu-ye, et al. Study on Fatigue Performance of Welded Joints for Out-of-plane Gusset in Orthotropic Steel Bridge Decks[J]. China Civil Engineering Journal, 2015, 49(2): 69-76. |
| [4] |
曾志斌. 正交异性钢桥面板典型疲劳裂纹分类及其原因分析[J]. 钢结构, 2011, 26(2): 9-15, 26. ZENG Zhi-bin. Classification and Reasons of Typical Fatigue Cracks in Orthotropic Steel Deck[J]. Steel Construction, 2011, 26(2): 9-15, 26. |
| [5] |
DE JONG F B P. Overview Fatigue Phenomenon in Orthotropic Bridge Decks in the Netherlands[C]//2004 Orthotropic Bridge Conference. Sacramento, USA: ASCE, 2004: 25-27.
|
| [6] |
WOLCHUK R. Lessons From Weld Cracks in Orthotropic Decks on Three European Bridges[J]. Journal of Structural Engineering, 1990, 116(1): 75-84. |
| [7] |
张清华, 卜一之, 李乔. 正交异性钢桥面板疲劳问题的研究进展[J]. 中国公路学报, 2017, 30(3): 14-30. ZHANG Qing-hua, BU Yi-zhi, LI Qiao. Review on Fatigue Problems of Orthotropic Steel Bridge Deck[J]. China Journal of Highway and Transport, 2017, 30(3): 14-30. |
| [8] |
王春生, 付炳宁, 张芹, 等. 正交异性钢桥面板足尺疲劳试验[J]. 中国公路学报, 2013, 26(2): 69-76. WANG Chun-sheng, FU Bing-ning, ZHANG Qin, et al. Fatigue Test on Full-scale Orthotropic Steel Bridge Deck[J]. China Journal of Highway and Transport, 2013, 26(2): 69-76. |
| [9] |
童乐为, 沈祖炎. 正交异性钢桥面板静力试验和有限元分析[J]. 同济大学学报:自然科学版, 1997, 25(6): 617-622. TONG Le-wei, CHEN Zu-yan. Static Test and Finite Element Analysis of Orthotropic Steel Bridge Decks[J]. Journal of Tongji University:Natural Science Edition, 1997, 25(6): 617-622. |
| [10] |
丁文俊, 吴冲, 赵秋. 横隔板间距对钢桥面板疲劳应力幅的影响[J]. 公路交通技术, 2011, 27(4): 59-62. DING Wen-jun, WU Chong, ZHAO Qiu. Influences of Space between Diaphragms on Fatigue Stress Amplitude of Steel Bridge Decks[J]. Technology of Highway and Transport, 2011, 27(4): 59-62. |
| [11] |
唐亮, 黄李骥, 刘高. 正交异性钢桥面板横梁弧形切口周边应力分析[J]. 公路交通科技, 2011, 28(6): 83-90. TANG Liang, HUANG Li-ji, LIU Gao. FEA of Stress along Cope Hole Edge of Crossbeam in Orthotropic Steel Deck[J]. Journal of Highway and Transportation Research and Development, 2011, 28(6): 83-90. |
| [12] |
吴臻旺, 郑凯锋, 税彦斌, 等. 钢箱梁正交异性桥面板球扁钢纵肋球头朝向和横隔板空孔的优化[J]. 公路交通科技, 2011, 28(9): 112-118. WU Zhen-wang, ZHENG Kai-feng, SHUI Yan-bin, et al. Optimization of Bulb Direction and Diaphragm Cutout of Bulb Flat Ribs in Steel Orthotropic Deck of Box Girder[J]. Journal of Highway and Transportation Research and Development, 2011, 28(9): 112-118. |
| [13] |
顾萍, 周聪. 铁路正交异性钢桥面板典型疲劳裂纹寿命估算[J]. 铁道学报, 2012, 34(1): 97-102. GU Ping, ZHOU Cong. Estimation of Fatigue Life of Typical Fatigue Cracks of Orthotropic Steel Decks of Railway Bridges[J]. Journal of the China Railway Society, 2012, 34(1): 97-102. |
| [14] |
高立强. 横梁腹板切口形状对正交异性钢桥面板疲劳性能的影响研究[J]. 铁道标准设计, 2014(12): 67-71. GAO Li-qiang. Influence of Crossbeam Web Cutout Shape on Fatigue Performance of Steel Orthotropic Deck[J]. Journal of Railway Standard Design, 2014(12): 67-71. |
| [15] |
BAIK B, YAMADA K, ISHIKAWA T. Fatigue Crack Propagation Analysis for Welded Joint Subjected to Bending[J]. International Journal of Fatigue, 2011, 33(5): 746-758. |
| [16] |
YE X W, YI T H, WEN C, et al. Reliability-based Assessment of Steel Bridge Deck Using a Mesh-insensitive Structural Stress Method[J]. Smart Structures and Systems, 2015, 16(2): 367-382. |
| [17] |
JTG D64-2015, 公路钢结构桥梁设计规范[S]. JTG D64-2015, Specifications for Design of Highway Steel Bridge[S]. |
| [18] |
吕彭民, 李大涛. 正交异性钢桥面板顶板疲劳性能研究[J]. 中国公路学报, 2014, 27(2): 84-89, 97. LÜ Peng-min, LI Da-tao. Fatigue Research on Bridge Deck-plate of Orthotropic Steel Bridge Deck[J]. China Journal of Highway and Transport, 2014, 27(2): 84-89, 97. |
| [19] |
唐亮, 黄李骥, 王秀伟, 等. 钢桥面板U肋-横隔板连接接头应力分析[J]. 公路交通科技, 2014, 31(5): 93-101. TANG Liang, HUANG Li-ji, WANG Xiu-wei, et al. Analysis of Stress in U-rib-diaphragm Joints of Steel Deck[J]. Journal of Highway and Transportation Research and Development, 2014, 31(5): 93-101. |
 2019, Vol. 36
2019, Vol. 36
