扩展功能
文章信息
- 侯炜, 贺拴海, 吴礼杰, 闫磊
- HOU Wei, HE Shuan-hai, WU Li-jie, YAN Lei
- 基于失效模式的双联塔非对称PC斜拉桥弹塑性极限承载力分析
- Analysis on Elasto-plastic Ultimate Bearing Capacity of United Twin-pylon Asymmetrical PC Cable-stayed Bridge Based on Failure Mode
- 公路交通科技, 2019, 36(11): 40-49
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(11): 40-49
- 10.3969/j.issn.1002-0268.2019.11.006
-
文章历史
- 收稿日期: 2018-05-25
2. 西安科源市政工程咨询有限公司, 陕西 西安 710068
2. Xi'an Keyuan Municipal Engineering and Consulting Co., Ltd., Xi'an Shaanxi 710068, China
通过增加桥梁结构宽度及跨度来满足与日俱增的交通量,一种造型新颖的桥梁结构形式——双幅桥面斜拉桥应运而生[1]。双幅桥面斜拉桥的桥塔可以采用单塔和双塔两种形式。双塔主要为分离和联塔两种形式。前者本质上为两座完全相同且独立的斜拉桥,而后者结构新颖,可减少占用横向空间,由于双塔共同受力,能够增大横向抗弯惯矩,在双幅主梁不增加横向联系的条件下,提高结构的横向抗弯扭刚度和稳定性。双联塔分幅4索面斜拉桥[2]在国内外均较罕见,已建成的主要有1995年的美国Fred Hartman桥、2000年的青岛丹山特大桥、2004年的澳门西湾大桥、2011年的广州李家沙大桥及2015年的宁波甬江特大桥。
为了保障桥梁结构正常运营,必须了解结构在不同荷载作用下的破坏形式和安全储备,即对结构进行极限承载力分析[3]。对于结构极限承载力的研究内容非常广泛,研究方法也较为成熟,主要有平衡法[4-5]、能量法[6]、数值解法[7]。其中,有限元法[8-9]作为最具代表性的数值计算方法广泛应用于结构分析中。调查研究发现,大型复杂结构主要采用梁单元或板壳单元进行有限元分析,较少采用三维弹塑性实体有限元进行结构极限承载力分析,即便采用也主要集中在简单结构的分析中,如简支梁桥[[10-14],这是因为采用三维弹塑性实体有限元进行几何、材料非线性的大型复杂结构极限承载力分析时,计算难以收敛。
现行规范中,所采用的汽车荷载是简化等效后的,能够便捷地用于理论研究和设计计算。但是对于桥梁结构的实际运营,却不能给出实际车队的重量及布置形式,对指导桥梁结构安全合理地运营存在一定缺陷。因此,本研究基于弹塑性有限位移理论,采用三维弹塑性实体有限元分析方法,选择合理的材料本构、强度准则、加载方式及收敛条件,考虑公路-Ⅰ级和汽-超20级设计荷载作用下,从理论分析及实际运营指导两方面对某在建双联塔非对称预应力混凝土斜拉桥5个最不利荷载工况下成桥状况的极限承载能力进行分析,并根据上述两种设计荷载作用下结构的破坏模式指导实际车辆在该类结构上的合理运营,为同类桥梁的安全运营管理提供科学依据。
1 理论分析对斜拉桥极限承载力进行计算,首先要考虑几何非线性及材料非线性[15],并采用逐级增大荷载方式分析结构的变形和受力,然后通过计算结构的收敛情况来判断结构某部分发生破坏的情况,最终得到结构破坏时的最大承受荷载,即极限承载力。
1.1 几何非线性根据参照构形不同,进行结构几何非线性极限承载力的分析方法分为总体拉格朗日列式法和更新拉格朗日列式法,后者适用于结构的大应变分析和弹塑性分析,其增量平衡方程[16]为:

|
(1) |
式中,K0t和Kst分别为以t时刻结构为参考的结构弹性刚度矩阵和结构初应力刚度矩阵;δ为节点位移列阵;F为节点荷载列阵。
有限元法进行结构非线性分析中,式(1)即为最终控制方程。其解法很多,其中,混合法综合了荷载增量法和迭代法的优点,可有效地控制计算累积误差,加快收敛速度,得到广泛应用。
1.2 材料非线性在弹塑性増量理论中,小变形假设仍然成立。因此,无需变动弹性范围内的应力-应变几何运动方程和平衡方程,仅需要调整塑性区范围内的材料本构模型矩阵。当材料应力处于弹性极限和比例极限之间时,需要用塑性材料的本构关系矩阵Dep替代原来的弹性系数矩阵De,则可得到基于弹塑性理论的有限元平衡方程[16]:

|
(2) |
式中,
混凝土的破坏准则[17]是建立在试验基础上的。鉴于国内外大量的试验研究,已提出众多参数不同的混凝土破坏准则。其中,Ottosen 4参数强度准则适用于混凝土并得到国际学者广泛应用,其表达式为:
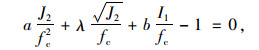
|
(3) |
式中,a和b为确定子午线形状的常数;J2为应力偏量第2不变量;I1为静水压应力;fc为混凝土轴心抗压强度;λ为确定偏平面破坏图形的函数,其表达式为:
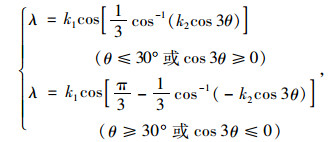
|
(4) |
式中,θ为相似角;k1和k2分别为尺寸系数和型式系数,决定偏平面包络线的大小和形状,均与材料单轴抗拉、抗压强度相关,见表 1。
| ft/fc | a | b | k1 | k2 |
| 0.08 | 1.807 2 | 4.096 1 | 14.486 4 | 0.991 2 |
| 0.10 | 1.275 3 | 3.196 1 | 11.736 2 | 0.980 3 |
| 0.12 | 0.921 6 | 2.596 7 | 9.911 1 | 0.964 8 |
| 注:ft和fc分别为混凝土的单轴抗拉、单轴抗压强度。 | ||||
经过计算分析得到结构控制截面的内力和应力,利用材料力学得到结构某点处的主应力,即可按Ottosen强度准则计算混凝土破坏强度值, 并判断该点的混凝土是否破坏。
1.4 钢材强度准则有限元模型中的钢材采用Von Mises屈服准则[18],表达式为:
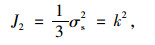
|
(4) |
式中,σs为单向拉伸屈服极限; k为常数。
该准则表明当某点应力偏量的第2不变量达到一定值时,该点开始进入塑性状态。
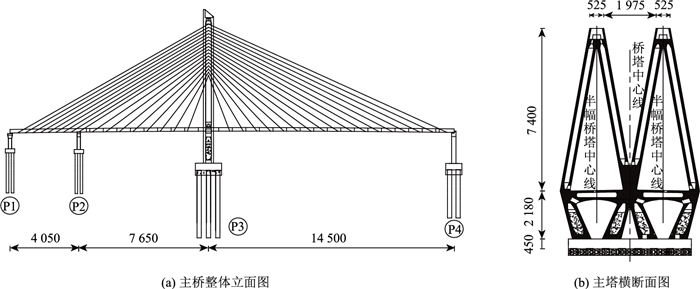
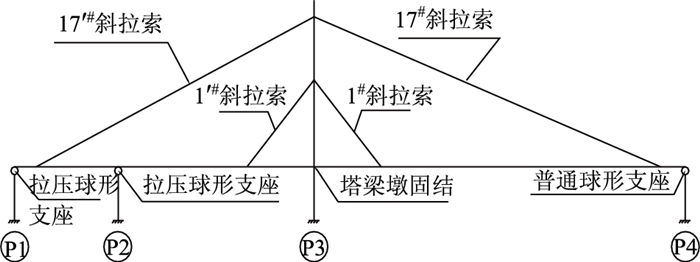
2 有限元分析模型 2.1 背景工程以某在建双联塔分幅4索面斜拉桥为研究对象,桥梁总长262 m,主桥结构采用塔墩梁固结的双联塔非对称PC斜拉桥,其主跨为145 m,边跨为(40.5+76.5) m。主梁断面为双幅分离式Π型截面,内、外侧梁肋采用不等高设计,梁肋底部齐平,高度分别为2.65, 2.20 m,采用C55混凝土。主塔为双菱形联体结构,高95.80 m,采用C50混凝土材料。斜拉索采用空间4索面扇形布置,在P1墩与P2墩之间由于主梁配重需要,采用箱型截面,设计荷载为公路-Ⅰ级,其结构示意图如图 1所示。主桥结构的P1墩和P2墩墩顶支座均采用拉压支座,P4墩墩顶为仅受压支座,边界条件如图 2所示。
|
| 图 1 主桥结构示意图(单位:cm) Fig. 1 Schematic diagram of main bridge structure(unit:cm) |
| |
|
| 图 2 主桥结构边界条件示意图 Fig. 2 Schematic diagram of boundary condition of main bridge structure |
| |
2.2 基本原则与规定
根据Abaqus[19]的特有功能和结构特点,依据下列基本原则与规定进行计算分析:
(1) 假设索梁、索塔及预应力锚固区、支座等不先发生局部破坏,以此研究结构主梁、主塔、斜拉索的控制截面的抗弯极限承载力。
(2) 不考虑混凝土收缩、徐变、温度和支座变位的影响,计算荷载为:结构自重、二期恒载、预应力荷载、斜拉索索力、汽车荷载和人群荷载。
(3) 以荷载-位移曲线(λ-Δ曲线)作为结构破坏的判断依据,同时查看对应位置处的材料应力状态。计算结果以挠度竖直向下为正,应力以拉为正。
(4) 采用力加载的方式进行模型加载,采用2.5%的位移收敛精度,在结构接近破坏时将其精度放宽到5%,以此加快收敛。
(5) 为了观察混凝土截面断裂发展过程,通过定义后续破坏应力为开裂区应变函数来考虑开裂后混凝土的软化现象。
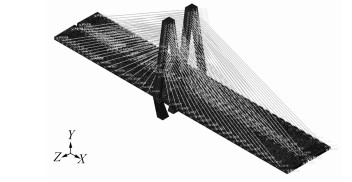
2.3 仿真模型建立为了确定主桥成桥结构的安全系数和极限承载能力,利用Abaqus有限元软件建立三维实体弹塑性模型,其中主梁、主塔均采用C3D8R(线性六面体减缩积分单元),以结构锚固点建立有限元参考点,在主梁、主塔连接处采用Compling约束,主塔底部采用全部固结,拉压支座采用MPC约束(拉压杆单元端部与支座面处主梁单元区域内节点进行耦合)以防止局部应力集中。钢束预应力和斜拉索初张力均采用降温法施加[16]。其主桥结构三维实体模型如图 3所示。
|
| 图 3 三维实体单元有限元模型 Fig. 3 Three-dimensional solid element finite element model |
| |
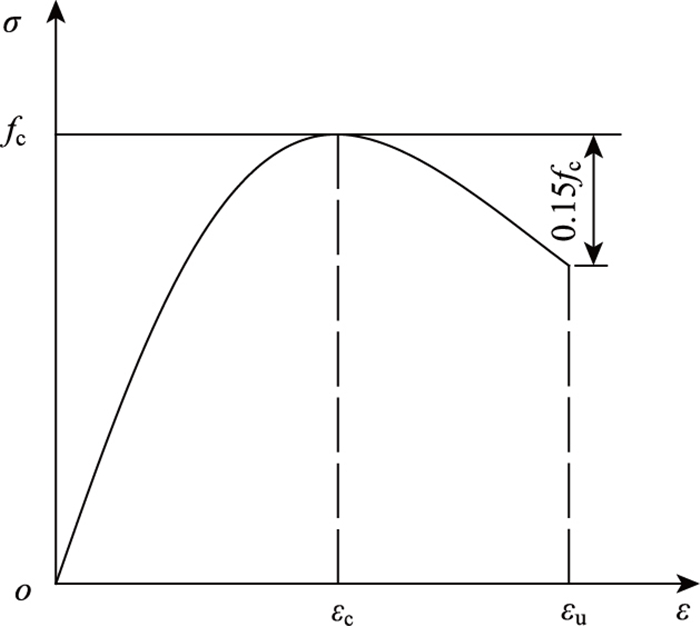
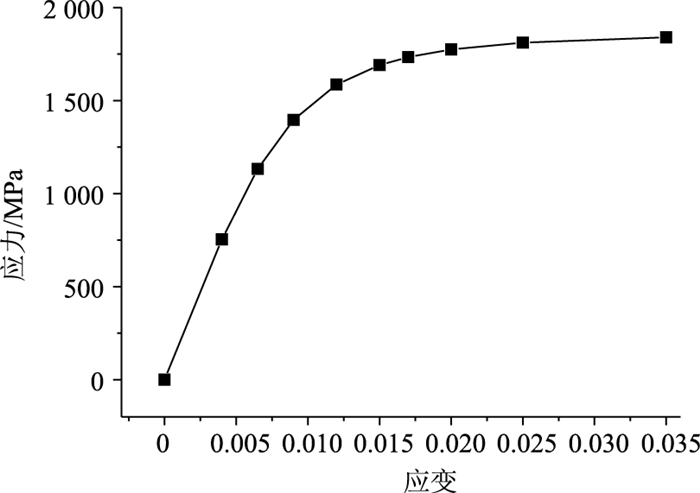
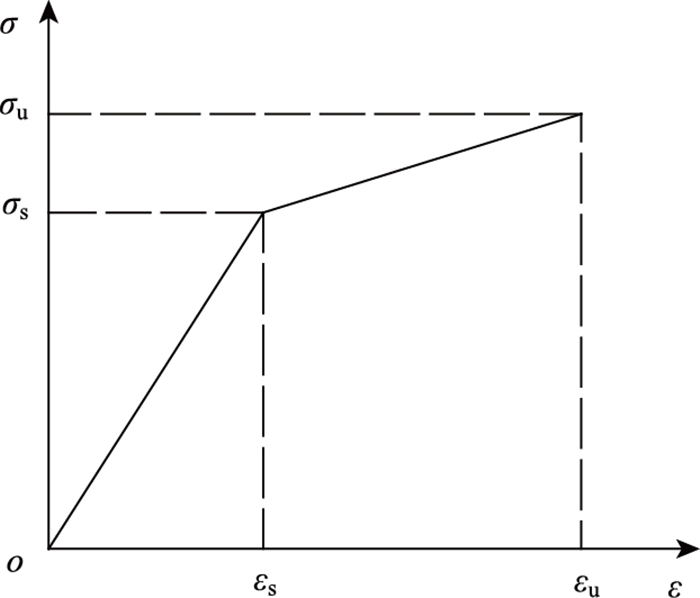
混凝土本构关系采用Hongestad模型[12],上升段为抛物线,下降段为直线,如图 4所示。预应力钢绞线的本构模型[14]如图 5所示。斜拉索采用弹延性本构模型[18], 并取双线性本构模型模拟钢丝应力应变关系,如图 6所示。几何非线性分析已考虑梁柱效应、大位移效应和斜拉索垂度效应等。
|
| 图 4 混凝土受压本构模型 Fig. 4 Concrete compression constitutive model 注:εc和εu分别为混凝土的峰值压应变和极限压应变。 |
| |
|
| 图 5 预应力钢绞线本构模型 Fig. 5 Prestressed steel strand constitutive model |
| |
|
| 图 6 斜拉索本构模型 Fig. 6 Cable constitutive model 注:σs和σu分别为斜拉索的屈服拉应力和极限拉应力,εs和εu分别为对应的峰值拉应变和极限拉应变。 |
| |
3 设计荷载与布载工况分析
桥梁运营状态下,所受活荷载的种类较多,为计算便捷,主要考虑车辆荷载和人群荷载RQ并进行组合分析,其中车辆荷载由均布荷载qk及集中荷载Pk确定。由于桥梁为左右双幅,各有4条车道及1条人行道。因此,考虑4车道横向折减的荷载:
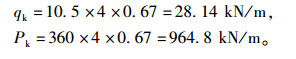
|
双车道荷载:

|
桥梁位于市郊,因此人群荷载应相应提高,人群荷载:
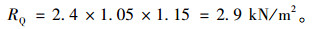
|
根据上述计算结果,结构活荷载按4车道荷载+人群荷载进行布载。
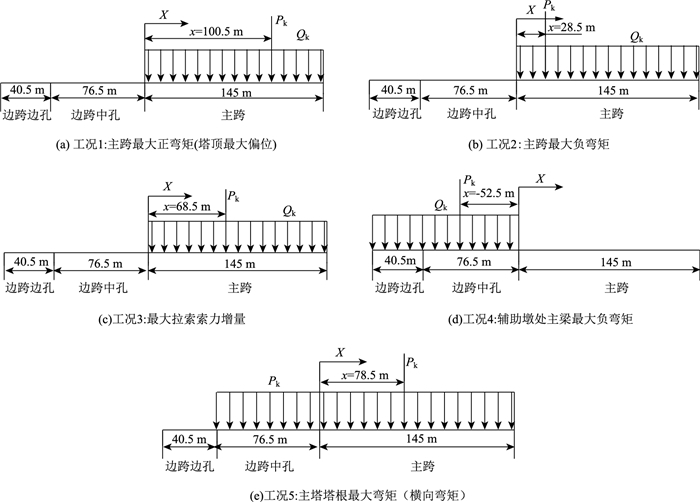
根据斜拉桥各计算控制内力和位移影响线,得出5个最不利布载工况方案。设定塔根处位置为x=0,x轴表示桥梁纵向位置,则主跨为正值,边跨为负值。具体布载工况如表 2和图 7所示。《公路桥涵设计通用规范》(JTG D60—2015)所采用的设计活载,能够方便地进行理论分析和设计计算,但对于实际车辆合理运营的指导不够便捷。因此本研究结合新旧规范的设计活载,从理论分析和实际应用两方面进行结构极限承载能力研究,对比计算结果,指导结构运营管理。汽车-超20级荷载布置方法:将重车后轴布置于公路-Ⅰ级荷载Pk处,其余车辆按规范间距进行布置。
| 工况 | 控制内力 | 荷载组合 | 布载方式 | Pk加载位置/m |
| 1 | 主跨最大正弯矩 | 恒载+1×人群荷载+4×车道荷载(折减) | 双幅主跨满载 | x=100.5 |
| 2 | 主跨最大负弯矩 | x=28.5 | ||
| 3 | 索力最大增量 | 双幅边跨满载 | x=68.5 | |
| 4 | 辅助墩处主梁最大负弯矩 | x=-52.5 | ||
| 5 | 主塔塔根最大弯矩 | 双主跨+边跨中孔满载 | x=76.5 |
|
| 图 7 工况加载布置图 Fig. 7 Loading layout of each working condition |
| |
4 结果分析
由于恒、活载分布形式不同,需分别考虑结构在设计恒、活载作用下各构件控制截面的内力,因此两种荷载无法直接叠加计算。近似取某荷载组合下控制截面活载效应与恒载效应的比值K=P1/Pd(Pd为成桥结构恒载,P1为结构设计活载)。经计算分析及综合考虑,取平均值K=0.123,则结构极限安全系数表达式为[20]:

|
(5) |
式中λ为相应工况荷载增量因子。
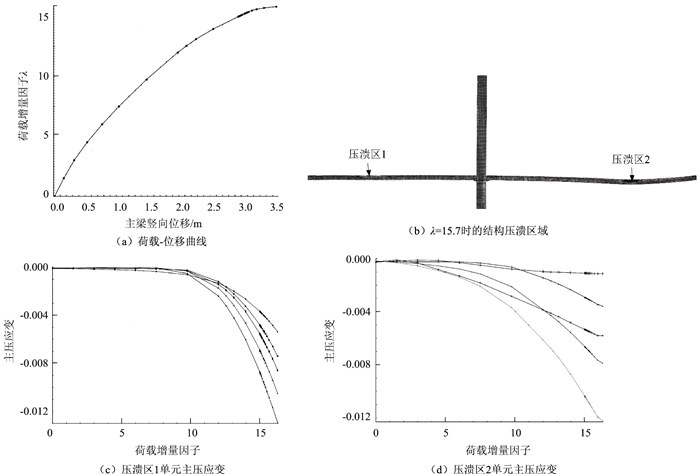
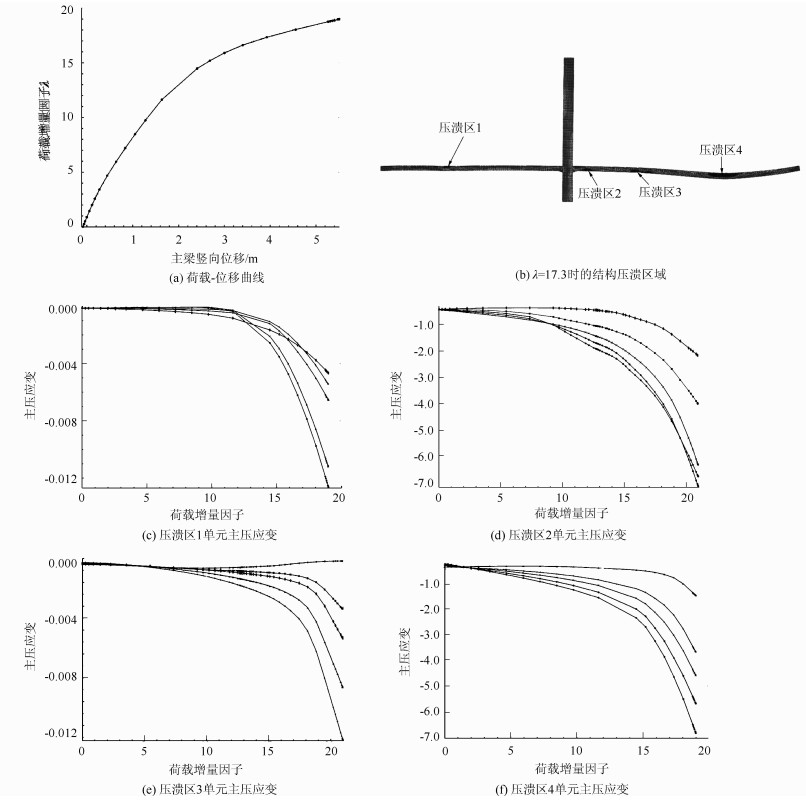
通过计算分析给出各工况下横隔板底缘中点的荷载-位移曲线(λ-Δ曲线)和主压应变曲线。当荷载增量因子λ变化时,不同主梁区域均会出现混凝土压溃破坏,但压溃程度及范围各不相同。因此,在每个区域沿竖向截面分别选取5个单元进行分析计算。以工况1为例,分别给出公路-Ⅰ级和汽车-超20级荷载作用下的荷载-位移曲线(λ-Δ曲线)、结构压溃区域图及主压应变曲线,如图 8和图 9所示。两种设计荷载作用下,区域竖向压溃范围随对应荷载增量因子λ的变化情况如表 3、表 4所示。
|
| 图 8 压溃区荷载位移、主压应变曲线(公路-Ⅰ级:工况1) Fig. 8 Curves of load displacement and main compressive strain in crushing zone(Highway-I load:working condition 1) |
| |
|
| 图 9 压溃区荷载位移、主压应变曲线图(汽车-超20级:工况1) Fig. 9 Curves of load displacement and main compressive strain in crushing zone(Vehicle-Super 20 load:working condition 1) |
| |
| 工况 | 压溃区 | 截面竖向压溃范围 | |||||
| 编号 | 截面位置x/m | 压溃临界 | 1/5高度 | 2/5高度 | 3/5高度 | ||
| 1(λ=15.7) | 1 | -76.5 | 11.5(上缘) | 12.7 | 13.3 | 14.0 | |
| 2 | 100.5 | 7.3(上缘) | 9.5 | 11.1 | 11.5 | ||
| 2(λ=16.0) | 1 | 12.0 | 10.2(上缘) | 12.6 | 13.1 | 14.4 | |
| 2 | 100.5 | 12.1(上缘) | 13.3 | 14.2 | 15.4 | ||
| 3(λ=15.9) | 1 | 68.5 | 10.0(上缘) | 12.4 | 13.7 | 15.9 | |
| 4(λ=17.1) | 1 | -76.5 | 9.3(下缘) | 11.8 | 13.2 | 13.7 | |
| 2 | -52.5 | 8.2(上缘) | 10.3 | 10.7 | 15.3 | ||
| 5(λ=15.9) | 1 | 76.5 | 9.5(上缘) | 12.0 | 13.1 | 15.9 | |
| 工况 | 压溃区 | 截面竖向压溃范围 | |||||
| 编号 | 截面位置x/m | 压溃临界 | 1/5高度 | 2/5高度 | 3/5高度 | ||
| 1(λ=17.3) | 1 | -76.5 | 13.7(上缘) | 15.2 | 15.6 | 16.9 | |
| 2 | 12.0 | 13.0(下缘) | 14.2 | 15.8 | 16.2 | ||
| 3 | 42.0 | 15.7(下缘) | 16.2 | 16.4 | 17.0 | ||
| 4 | 100.5 | 9.2(上缘) | 12.0 | 14.0 | 16.1 | ||
| 2(λ=21.0) | 1 | -76.5 | 14.3(上缘) | 15.5 | 15.9 | 16.7 | |
| 2 | 12.0 | 10.6(下缘) | 13.8 | 14.7 | 15.7 | ||
| 3 | 28.0 | 15.3(上缘) | 18.5 | 19.5 | 21.0 | ||
| 4 | 133.0 | 11.5(上缘) | 15.5 | 16.3 | 19.5 | ||
| 3(λ=18.5) | 1 | -76.5 | 12.5(上缘) | 13.5 | 13.9 | 14.5 | |
| 2 | 12.0 | 12.6(下缘) | 15.2 | 15.8 | 17.5 | ||
| 3 | 26.0 | 16.3(下缘) | 17.2 | 17.4 | 17.8 | ||
| 4 | 68.5 | 13.1(上缘) | 14.9 | 16.0 | 18.0 | ||
| 4(λ=18.0) | 1 | -76.5 | 11.8(下缘) | 13.6 | 14.9 | 17.9 | |
| 2 | -52.5 | 8.8(上缘) | 12.2 | 12.7 | — | ||
| 5(λ=19.0) | 1 | -76.5 | 12.2(上缘) | 13.5 | 13.9 | 14.8 | |
| 2 | 12.0 | 14.2(下缘) | 16.8 | 17.0 | 17.3 | ||
| 3 | 34.0 | 16.7(下缘) | 17.1 | 17.3 | 17.6 | ||
| 4 | 76.5 | 12.0(上缘) | 14.7 | 16.1 | 18.7 | ||
以工况1的形式对结构进行公路-Ⅰ级布载。当λ=7.3时,集中荷载作用处的主梁梁肋截面混凝土发生压溃;当λ=11.5时,已有2个主梁梁肋截面的混凝土发生压溃;当λ=14.0时,已有2个主梁区域竖向截面3/5高度的混凝土压溃。此时,斜拉索最大拉应力为1 563 MPa,其抗拉极限强度为1 770 MPa,安全储备仅为13%。位于主梁12#隔板底缘的预应力钢束,拉应力值为1 794 MPa,已接近极限抗拉强度值。随着λ继续增大,当λ=15.7时,结构达到极限承载状态,主梁在x=100.5 m处出现最大竖向位移3.45 m(向下),主塔最大纵向位移为0.55 m(向主跨方向)。此时,工况1下的结构极限安全系数为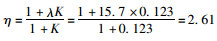
在不同荷载工况下,主塔混凝土的主压应变均未超过其极限应变,且塔顶位移曲线基本呈线性分布,说明主塔结构刚度较大,稳定性较好。
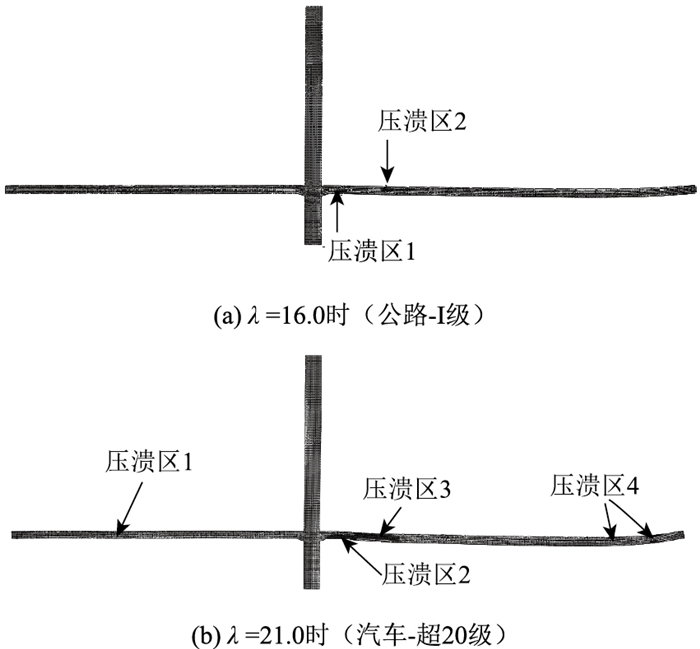
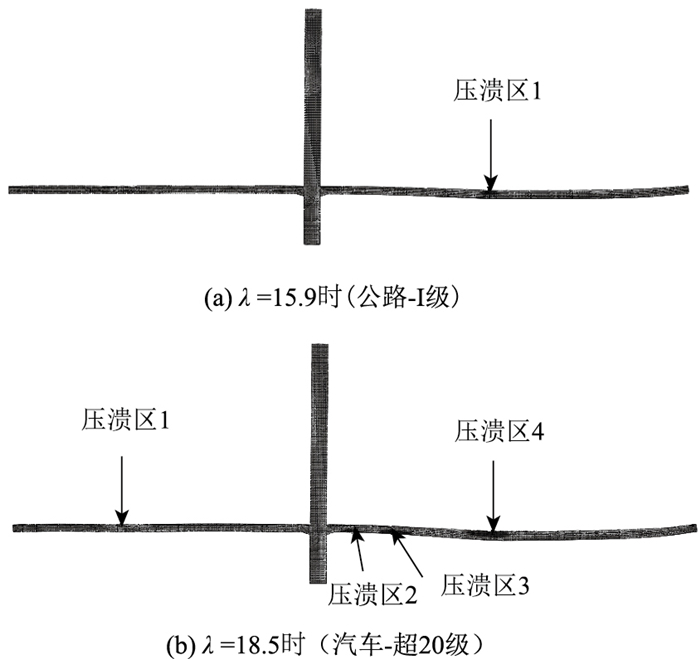
由于篇幅有限,其他4种工况与工况1类似,仅给出工况2~工况5的区域压溃图,如图 10~图 13所示。
|
| 图 10 结构压溃区域(工况2) Fig. 10 Structural collapse zone (working condition 2) |
| |
|
| 图 11 结构压溃区域图(工况3) Fig. 11 Structural collapse zone(working condition 3) |
| |
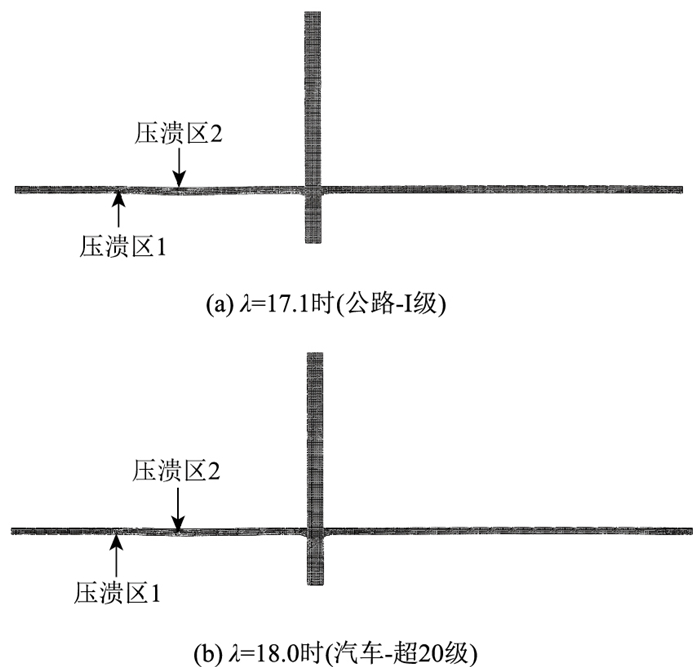
|
| 图 12 结构压溃区域图(工况4) Fig. 12 Structural collapse zone(working condition 4) |
| |
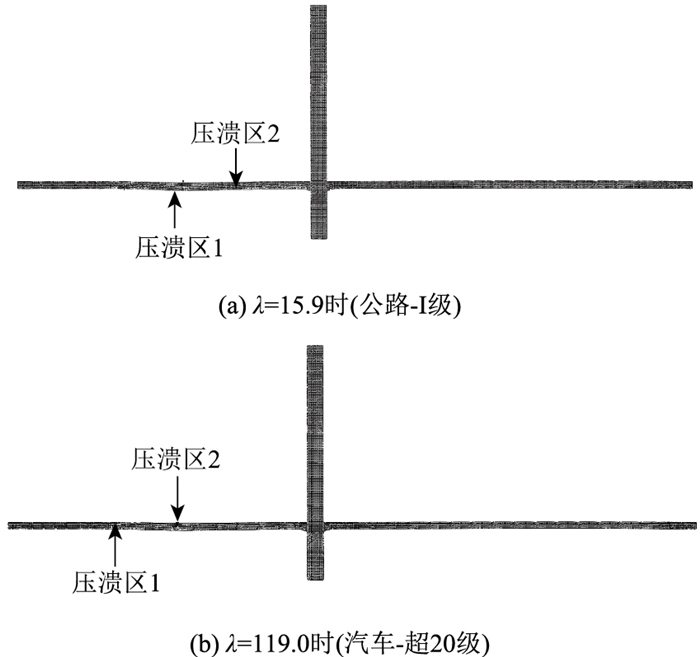
|
| 图 13 结构压溃区域图(工况5) Fig. 13 Structural collapse zone(working condition 5) |
| |
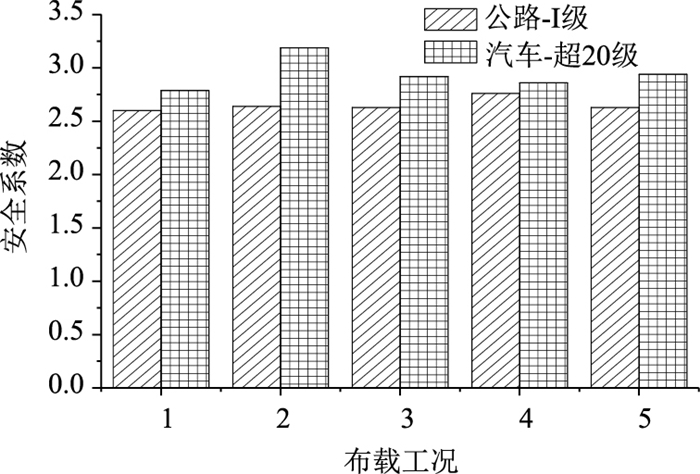
两种设计荷载作用下,5种最不利布载工况对应的结构安全系数、结构最大位移对比如图 14~图 16所示。
|
| 图 14 安全系数对比 Fig. 14 Comparison of safety factors |
| |
|
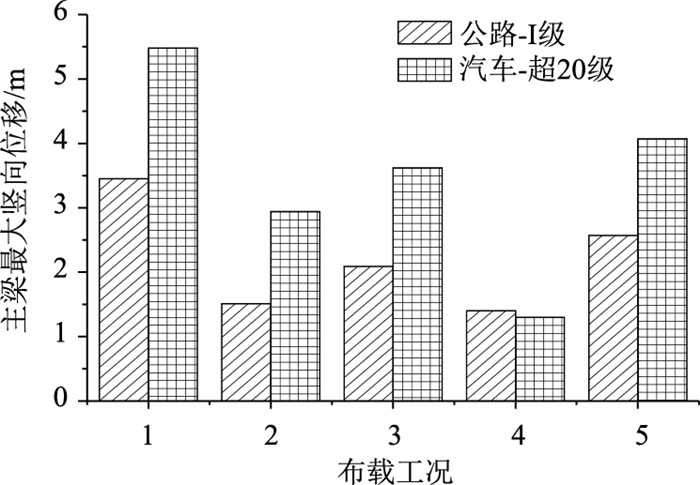
| 图 15 主梁最大挠度对比 Fig. 15 Comparison of maximum deflections of main beam |
| |
|
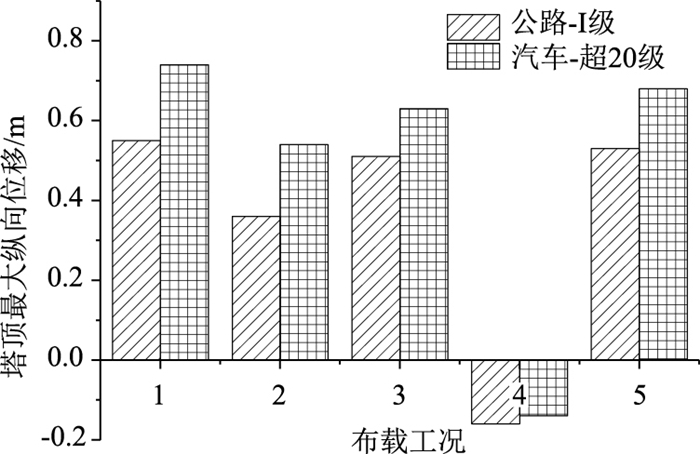
| 图 16 塔顶最大位移对比 Fig. 16 Comparison of maximum displacements at top of pylon |
| |
公路-Ⅰ级荷载作用下,当λ=15.7, 16.0, 15.9, 17.1, 15.9时,对应结构的5种工况已进入极限承载状态,主梁最大竖向位移为1.51~2.57 m,塔顶最大纵向位移为-0.16~0.53 m;汽车-超20级荷载作用下,当λ=17.3,21.0,18.5,18.0,19.0时,对应结构的5种工况已进入极限承载状态,主梁最大竖向位移1.30~5.48 m,塔顶最大纵向位移为-0.14~0.74 m。对于公路-Ⅰ级及汽车-超20级设计荷载作用下的5种最不利荷载工况,后者的结构极限安全系数均大于前者的,且两者的结构极限安全系数均大于2.6,说明结构具有良好的承载能力。
两种设计荷载工况1(主跨最大正弯矩)下的结构极限安全系数均为最小,其值分别为2.61和2.79,说明结构在这两种设计荷载作用下,最不利控制断面均为主跨最大正弯矩断面。
5 结论双联体独塔预应力混凝土斜拉桥是斜拉桥中的一种独特桥型,继承了独塔斜拉桥的经济性、利于施工等优点。主塔横桥向的双幅连体构造,增加了主塔乃至整个主桥的横向刚度,加之斜拉桥的景观价值,这种桥型也日益受到青睐。对于这种桥型的极限承载能力分析具有非常重要的意义。
(1) 本研究基于斜拉桥极限承载力的极值点失稳理论,建立了考虑公路-Ⅰ级设计荷载作用的Abaqus三维实体成桥弹塑性模型,根据结构计算控制内力和位移影响线,得出了5种最不利布载工况,并计算分析了各工况下主桥成桥结构的极限承载能力,得出各工况下结构极限安全系数均大于2.6,具有良好的承载能力。
(2) 根据荷载增量因子计算得到公路-Ⅰ级和汽车-超20级荷载作用下5种最不利工况的结构极限安全系数,后者均大于前者,其差值在3.6%~17.2%。在两种设计荷载作用下,结构在工况1(主跨最大正弯矩)下的结构极限安全系数最小,说明主桥结构最先达到极限承载状态的位置为主跨最大正弯矩断面。
(3) 由于汽车-超20级荷载作用下的结构极限安全系数大于公路-Ⅰ级荷载作用下的,因此在桥梁运营阶段,按汽车-超20级的车辆布置形式进行实际车辆的运行管理控制是偏安全的。根据汽车-超20级荷载的布置方法,将重车后轴布置于公路-Ⅰ级荷载Pk处,其余车辆按规范间距布置。
(4) 本研究针对双联体独塔非对称PC斜拉桥进行了极限承载力的研究,利用不同设计荷载作用下的荷载增量因子计算结构极限安全系数,其分析结果对更好地保障结构的设计承载能力和结构的安全设计水平有积极作用。
| [1] |
《中国公路学报》编辑部. 中国桥梁工程学术研究综述·2014[J]. 中国公路学报, 2014, 27(5): 1-96. Editorial Department of China Journal of Highway and Transport. Review on China's Bridge Engineering Research:2014[J]. China Journal of Highway and Transport, 2014, 27(5): 1-96. |
| [2] |
刘兆丰.大跨度联塔分幅斜拉桥结构行为与联塔结构模型试验研究[D].成都: 西南交通大学, 2009. LIU Zhao-feng. Study on Structural Behaviors of Cable-stayed Bridge with United Twin-pylons and Separate Twin-decks and Model Test on United Twin-pylons[D]. Chengdu: Southwest Jiaotong University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10613-2010115756.htm |
| [3] |
刘刚.空间扭背索组合梁斜拉桥极限承载力分析[D].西安: 长安大学, 2010. LIU Gang. Analysis on Ultimate Bearing Capacity of Cable-stayed Bridge with Spatial Torsion Backed Composite Beam[D]. Xi'an: Chang'an University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-11941-2010220891.htm |
| [4] |
周凌远.斜拉桥非线性理论及极限承载力研究[D].成都: 西南交通大学, 2007. ZHOU Lin-yuan. Research on Nonlinear Theory and Load Bearing Capacity of Cable-stayed Bridges[D]. Chengdu: Southwest Jiaotong University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10613-2007118173.htm |
| [5] |
吴光宇.大跨PC桥梁非线性行为的分析理论及其极限承载力计算研究[D].杭州: 浙江大学, 2006. WU Guang-yu. Study on Nonlinear Behavior Analysis Theory and Ultimate Bearing Capacity Calculation of Long-span Pre-stressed Concrete Bridge[D]. Hangzhou: Zhejiang University, 2006. http://cdmd.cnki.com.cn/article/cdmd-10335-2007015466.htm |
| [6] |
贺拴海, 刘志文, 宋一凡. 斜拉桥的极限承载力分析[J]. 中国公路学报, 2000, 13(3): 53-58. HE Shuan-hai, LIU Zhi-wen, SONG Yi-fan. Analysis for Ultimate Load Capacity of Cable-stayed Bridges[J]. China Journal of Highway and Transport, 2000, 13(3): 53-58. |
| [7] |
何红丽, 黄侨, 郑一峰.部分斜拉桥极限承载力的理论研究与数值分析[C]//中国公路学会2005年学术年会论文集.北京: 中国公路学会, 2005: 262-267. HE Hong-li, HUANG Qiao, ZHENG Yi-feng. Theoretical and Numerical Analysis of Ultimate Bearing Capacity of a Partial Cable-stayed Bridge[C]//Proceedings of 2005 Academic Annual Meeting of CHTS. Beijing: CHTS, 2005: 262-267. |
| [8] |
杨鸥, 李惠, 欧进萍. 钢筋混凝土斜拉桥寿命期内整体极限承载力分析[J]. 土木工程学报, 2012, 45(3): 116-126. YANG Ou, LI Hui, OU Jin-ping. Life-cycle Evolution of the Ultimate Load Carrying Capacity of RC Cable-stayed Bridges[J]. China Civil Engineering Journal, 2012, 45(3): 116-126. |
| [9] |
REN W X, LIN Y Q, PENG X L. Field Load Tests and Numerical Analysis of Qinzhou Cable-stayed Bridge[J]. Journal of Bridge Engineering, 2007, 12(2): 261-270. |
| [10] |
高向玲, 张业树, 李杰. 基于ABAQUS梁单元的钢筋混凝土框架结构数值模拟[J]. 结构工程师, 2013, 29(6): 19-26. GAO Xiang-ling, ZHANG Ye-shu, LI Jie. Numerical Simulation of a RC Frame Based on ABAQUS Beam Elements[J]. Structural Engineers, 2013, 29(6): 19-26. |
| [11] |
MEHRABI A B. In-service Evaluation of Cable-stayed Bridges, Overview of Available Methods and Findings[J]. Journal of Bridge Engineering, 2006, 11(6): 716-724. |
| [12] |
邓凌宇.双联塔非对称PC斜拉桥施工控制与分析[D].西安: 长安大学, 2015. DENG Ling-yu. Construction Control and Analysis of Twin-tower Asymmetric PC Cable-stayed Bridge[D]. Xi'an: Chang'an University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10710-1016790763.htm |
| [13] |
戴显荣. 双塔联体分幅斜拉桥塔结构极限承载力试验研究[J]. 公路, 2009(10): 55-59. DAI Xian-rong. Experimental Study on Ultimate Bearing Capacity of Cable-stayed Bridge with Sub Span in Twin Tower[J]. Highway, 2009(10): 55-59. |
| [14] |
徐金勇, 颜全胜. 大跨度混合梁斜拉桥弹塑性极限承载力分析[J]. 桥梁建设, 2012, 42(5): 44-50. XU Jin-yong, YAN Quan-sheng. Analysis of Elasto-plastic Ultimate Load Bearing Capacity of Long Span Hybrid Girder Cable-stayed Bridge[J]. Bridge Construction, 2012, 42(5): 44-50. |
| [15] |
胡世翔, 黄侨, 刘义河. 矮塔斜拉桥抗弯极限承载力数值计算及验证[J]. 华南理工大学学报:自然科学版, 2016, 44(8): 114-122. HU Shi-xiang, HUANG Qiao, LIU Yi-he. Validation and Numerical Calculation of Ultimate Bending Bearing Capacity of Extra-dosed Bridges[J]. Journal of South China University of Technology:Natural Science Edition, 2016, 44(8): 114-122. |
| [16] |
贺拴海. 桥梁结构理论与计算方法[M]. 北京: 人民交通出版社, 2003. HE Shuan-hai. Structure Theory and Calculation Method of Bridge[M]. Beijing: China Communications Press, 2003. |
| [17] |
易建国, 陈小琪. 混凝土强度准则在桥梁结构中应用的探讨[J]. 同济大学学报, 1999, 27(2): 160-164. YI Jian-guo, CHEN Xiao-qi. Concrete Strength Criterion with Its Application in Bridge Structure[J]. Journal of Tongji University, 1999, 27(2): 160-164. |
| [18] |
李海青, 杨万里, 高璇. 预应力混凝土薄壁高墩刚构桥梁极限承载力分析[J]. 中国公路学报, 2013, 26(6): 128-134. LI Hai-qing, YANG Wan-li, GAO Xuan. Analysis of Ultimate Bearing Capacity of Pre-stressed Concrete Frame Bridge with High Piers[J]. China Journal of Highway and Transport, 2013, 26(6): 128-134. |
| [19] |
石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M]. 北京: 机械工业出版社, 2013. SHI Yi-ping, ZHOU Yu-rong. Example Explanation of ABAQUS Finite Element Analysis[M]. Beijing: China Machine Press, 2013. |
| [20] |
吴礼杰.双联体独塔预应力混凝土斜拉桥极限承载力分析[D].西安: 长安大学, 2015. WU Li-jie. Study on Ultimate Load Bearing Capacity of Prestressed Concrete Cable-stayed Bridge with Double Couplet of Single Tower[D]. Xi'an: Chang'an University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10710-1015803180.htm |
 2019, Vol. 36
2019, Vol. 36
