扩展功能
文章信息
- 张成良, 刘维正, 曾奕珺
- ZHANG Cheng-liang, LIU Wei-zheng, ZENG Yi-jun
- 基于尖点突变理论的路基下伏溶洞顶板稳定性分析
- Analysis on Stability of Karst Cave Roof under Subgrade Based on Cusp Catastrophe Theory
- 公路交通科技, 2019, 36(11): 24-32
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(11): 24-32
- 10.3969/j.issn.1002-0268.2019.11.004
-
文章历史
- 收稿日期: 2018-07-11
2. 中南大学 土木工程学院, 湖南 长沙 410075
2. School of Civil Engineering, Central South University, Changsha Hunan 410075, China
我国西南地区岩溶发育强烈,大规模建设的高速公路不可避免地要穿越众多的岩溶区,而岩溶区是否满足工程需求,关键取决于荷载作用下溶洞顶板的稳定性。沿线下伏溶洞顶板失稳引发路基塌陷,是公路岩溶路基修建和运营过程中的常见病害。因此,正确、有效地进行路基下伏溶洞顶板结构稳定性分析与评价,对合理选取岩溶路基工程处治措施具有重要意义。
根据影响溶洞顶板稳定性主要因素(溶洞跨度、顶板厚度、岩体强度和产状、裂隙与充填状况、外部荷载、地下水等)的分析,岩溶顶板的稳定性评价经历了从定性到半定量、定量的过程。定性分析由于依靠经验对顶板稳定性进行评价,导致结果具有较大的主观性和区域性。半定量方法为目前工程中较为实用的方法,主要包括顶板厚跨比法[1]、结构力学近似法(抗弯和抗剪的顶板安全厚度验算)[2]、坍塌填塞法[2]、破裂拱分析法和荷载传递线交汇法[3],但该类方法不能全面反映不同地质模式下顶板的受力变形及破坏情况。定量分析主要通过数值分析方法[4-6]、系统理论和模糊数学方法[7-8]对顶板稳定性进行评价和分级,或构建区划稳定与不稳定状态的边界曲线。然而顶板失稳破坏具有不连续和不规则的突发特点,前述方法均不能考虑,影响了结果的可靠性。
为描述加载过程中能量集聚导致突发失稳的力学行为,突变理论作为研究参数连续变化导致系统状态突变的一种学说,近年来在岩体系统失稳领域应用较为广泛。例如:赵明华等[9]建立了岩溶区桩端溶洞顶板安全厚度确定的突变模型。何忠明等[10]基于尖点突变理论,以位移为判据分析了顶板厚度与极限填筑高度之间的关系。赵延林等[11]、黄昌富等[12]、徐恒等[13]将突变理论应用于采空区顶板失稳的力学机制分析,对顶板的安全系数与安全厚度进行了确定。S. Qin等[14]建立了滑坡的尖点突变模型,对边坡失稳机制及滑坡的全过程进行了合理解释。李亚生等[15]、华成亚等[16]分别建立了以位移和塑性应变能为判据的尖点突变模型,得到了不同状态下边坡的安全稳定系数。由此可见,突变理论为溶洞、采空区顶板结构稳定性评价提供了一种新的定量研究方法,但对于溶洞顶板结构采用何种突变失稳判据还未形成统一认识。此外,溶洞稳定性主要集中于顶板安全厚度的分析,而对路基填筑过程中不同影响因素下溶洞顶板的极限承载力与稳定性评价的研究不多。
鉴于此,本研究以新建桂柳高速公路沿线岩溶路基工程为背景,采用FLAC3D软件模拟路堤填筑过程中下伏溶洞顶板结构的应力应变响应,基于尖点突变理论构建稳定性判定的数学模型,对比分析溶洞顶板失稳的位移、塑性区体积、塑性应变能3种突变判据的合理性与适用性,确定评判溶洞顶板稳定性的定量方法。分析顶板厚度、溶洞跨度、顶板上覆土层厚度、岩石强度参数对岩溶顶板极限承载力的影响,给出不同安全储备系数下路基填高与厚跨比之间的关系,以便为工程的设计与施工提供科学合理的决策依据。
1 路堤填筑下伏溶洞顶板失稳的突变理论分析 1.1 顶板失稳判定的突变模型突变系统中包括状态变量和控制变量。状态变量表征系统的行为状态,控制变量表示对系统状态产生影响的因素。只包含1个状态变量的突变模型根据其控制变量的个数可分为4种,分别是:折叠突变、尖点突变、燕尾突变、蝴蝶突变。当突变模型中控制变量较少时,所建立的函数多项式拟合结果不够精确,如折叠突变模型;而当模型中控制变量较多时,其系统势函数的分叉集计算又太过繁琐,如燕尾突变、蝴蝶突变。综合考虑上述因素,本研究采用尖点突变模型,既满足了精度要求,又不会导致计算量过大。
为了分析溶洞顶板失稳过程中状态变量的变化,建立状态变量与每级路堤荷载之间的函数关系,一般认为状态变量D在逐渐失稳过程中的变化是连续的。因此可以用连续函数D-f(h)来表示状态变量在逐渐失稳过程中的变化,将连续函数展开成泰勒级数四次项式,如式(1)所示:
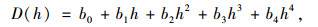
|
(1) |
式中,b0~b4为拟合系数;h为路堤填筑高度。
令h=m-n,n=b3/4b4,可将式(1)转化为突变模型的一般形式:
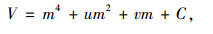
|
(2) |
式中,
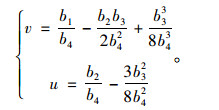
|
(3) |
由式(3)可通过式(4)得到交叉集Δ:
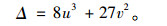
|
(4) |
当Δ大于0时,系统未发生突变;当Δ=0时,系统处于临界状态;当Δ<0时,系统失稳。
1.2 顶板失稳突变判据在顶板稳定性分析中,可以将一些能够明显表征顶板失稳的特征量作为突变模型中的状态变量对其进行分析,例如顶板测点位移、塑性区体积、塑性区应变能等。
1.2.1 位移突变判据在数值计算中,用测点的位移判断围岩稳定状况非常形象直观。因为岩土体失稳的极限状态与岩土体结构上部分测点位移的变化量及变化速率有关,当岩土体结构在发生失稳的同时,某些测点的位移变化量及变化速率会突然急剧增大。因此可以考虑以溶洞顶板模型边缘节点位移为状态变量来建立判别顶板失稳的势函数。
1.2.2 塑性区贯通突变判据塑性区贯通是指在岩土体结构分析的过程中,屈服区扩展、连接,最后形成一个连通的屈服区域,使结构丧失承载能力。在岩土体结构即将失稳破坏的过程中,由于进入塑性区的单元体越来越多,使失稳部位产生塑性区贯通,塑性区体积增量会急剧增大,因此可以采用塑性区体积作为建立判别岩土体结构失稳势函数的状态变量。
1.2.3 塑性区应变能突变判据岩土体的破坏过程是某些应力较大部分的岩体或土体单元应力达到屈服强度首先进入屈服阶段,随着应力不断增大,塑性区不断延展,最终导致整个岩土体结构失稳。当荷载超过岩土体的极限承受能力时,该结构将逐渐进入濒临破坏的状态并伴随着应变能耗散的过程。在失稳过程中,塑性区应变能会逐渐增大并且一直持续到发生突变。因此可以用塑性区应变能作为建立顶板失稳势函数的状态变量。在数值计算的过程中,塑性区应变能可以按照式(5)计算:
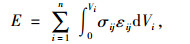
|
(5) |
式中,σij和εij分别为网格单元i对应的应力张量和应变张量;Vi为单元i的体积。将计算结束后每个进入塑性区的单元的应变能进行累加就能得到整个岩土体结构的总塑性区应变能。
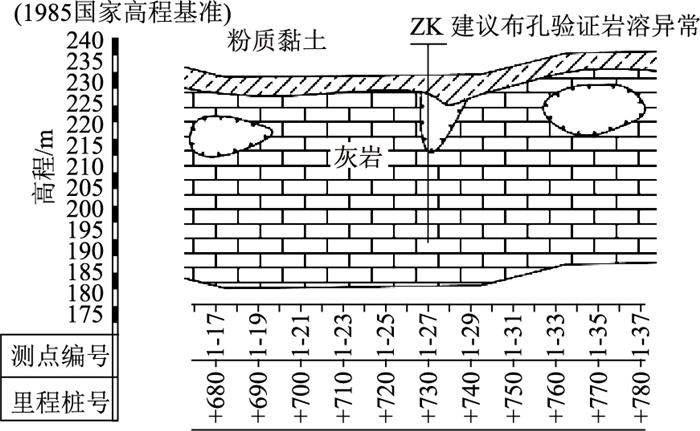
2 工程实例分析 2.1 工程概况广西桂柳高速公路第1标段内地下岩溶较为发育,沿线下伏隐蔽性溶洞较多,对路基稳定影响较大。根据工程地质详细勘察结果可知,该区段内沿设计线路上覆覆盖层主要以粉质黏土层为主,下伏基岩主要为泥盆系灰岩、白云质灰岩。溶洞多沿水平发育,形成水平溶洞。沿线碳酸盐岩分布地带的岩溶泉、地下暗河较为发育,多处于向斜构造收敛部位、断裂构造附近及与碎屑岩相接触部位,溶洞开口方向多与线路行车方向斜交。该区段典型工程地质断面如图 1所示。
|
| 图 1 典型溶洞地质断面 Fig. 1 Typical cave geological section |
| |
2.2 数值模型建立
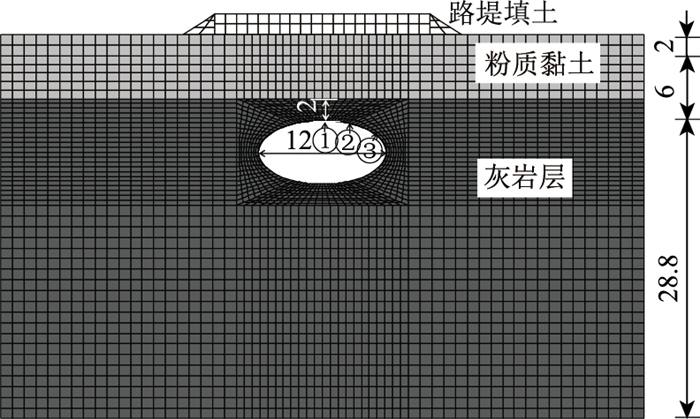
假设溶洞位于线路正下方,且洞口开口方向与行车方向平行,洞跨12 m,洞高6 m,埋深8 m,溶洞为椭圆形。采用FLAC3D软件建立下伏溶洞的数值计算模型,如图 2所示,行车方向取1 m长,上覆粉质黏土及坡积土层厚度取6 m,溶洞顶板厚度取2 m。上覆土层及距溶洞较远处岩层采用六面块体单元建模,溶洞及周围岩体采用柱形隧道外围渐变放射网格单元划分,上覆土层及基岩层均采用摩尔库伦(Mohr-Coulomb)屈服准则进行弹塑性数值分析,整个模型长×宽×高为60 m×1 m×36.8 m,整个模型共划分了8 628个单元、13 146个节点。在计算前首先使模型达到初始地应力平衡状态,并在初始平衡后定义null单元使溶洞形成,再次计算至地应力平衡。模型地层参数如表 1所示。
|
| 图 2 FLAC3D溶洞计算模型(单位:m) Fig. 2 FLAC3D-based cave calculation model (unit:m) 注:图中①②③分别为顶板跨中、距跨中1/6跨度、距跨中1/3跨度。 |
| |
| 岩土体地层 | 重度/(kN·m-3) | 泊松比 | 弹性模量/MPa | 黏聚力/kPa | 内摩擦角/(°) |
| 路堤填土 | 18.4 | 0.30 | 15.6 | 9.5 | 20 |
| 粉质黏土 | 19.5 | 0.30 | 16.4 | 30.0 | 13 |
| 泥盆系灰岩 | 27.0 | 0.25 | 1.0×104 | 70.0 | 40 |
2.3 计算结果对比分析
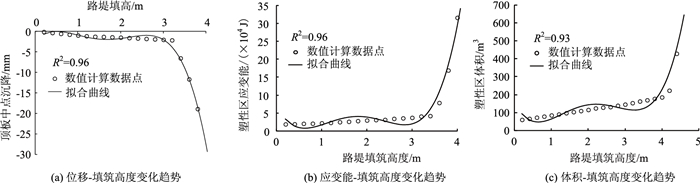
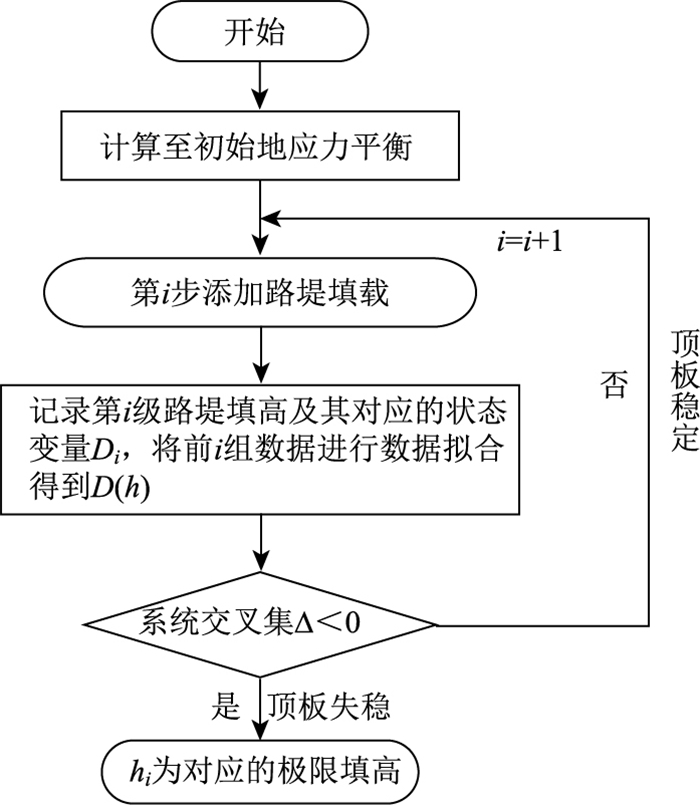
计算中逐级添加竖向应力,每级荷载的增加量相当于路基高度增加0.2 m,采用均布荷载的形式。在每级荷载添加后计算至收敛,记录每级填筑高度hi对应的顶板稳定性状态变量数据Di。然后通过对每级路堤填高hi及其对应状态变量数据值进行数据拟合(如图 3所示),得到Di关于路堤填筑高度hi的泰勒级数四次项式,最后通过式(3)计算出系统分叉集Δ的值。具体判定流程如图 4所示。
|
| 图 3 Di-hi泰勒公式拟合曲线 Fig. 3 Di-hi Taylor formula fitting curves |
| |
|
| 图 4 失稳判定流程图 Fig. 4 Flowchart of instability judgement |
| |
本研究分别采用顶板位移突变判据、塑性区应变能突变判据、塑性区体积突变判据3种不同的顶板稳定性判据进行对比分析。拟合曲线的决定系数分别为R2=0.96,R2=0.96,R2=0.93,表明拟合效果良好。3种判据计算得到的系统交叉集Δ的变化如表 2所示。
| 路堤填高/m | 系统交叉集Δ | ||
| 位移判据 | 塑性区应变能判据 | 塑性区体积判据 | |
| 2.0 | 215.3 | 770.5 | 3 854.2 |
| 2.2 | 275.7 | 396.6 | 19 262.3 |
| 2.4 | 579.2 | 337.8 | 3 547.9 |
| 2.6 | 1 908.0 | 31 634.6 | 75 014.9 |
| 2.8 | 13 044.6 | 13 191.4 | 279 354.9 |
| 3.0 | 857 141.9 | 34 101.6 | 28 401.7 |
| 3.2 | 1 810 333.0 | 3 361.8 | 15 990.9 |
| 3.4 | -68.3 | 12 159.4 | 36 652.7 |
| 3.6 | -77.8 | -6.2 | 96 903.2 |
| 3.8 | -82.1 | -89.6 | 358 116.2 |
| 4.0 | — | -115.3 | 6 764.4 |
| 4.2 | — | — | -107.1 |
| 4.4 | — | — | -284.8 |
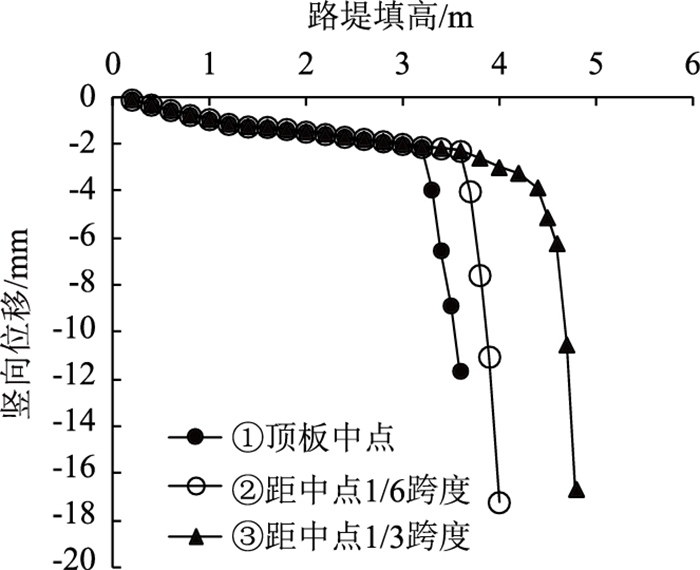
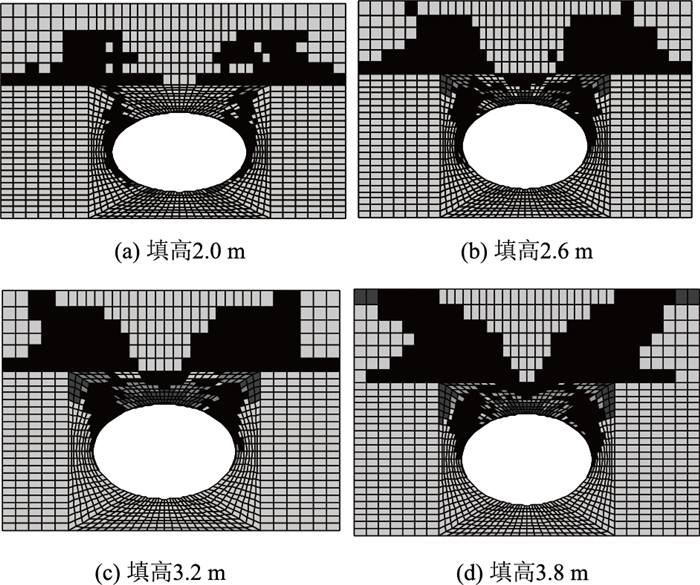
从表 2可以看出,无论采用位移、塑性区体积或塑性区应变能作为突变判据,系统交叉集Δ首先都随着路堤填高增大剧增,当系统发生突变时,Δ值由正变负,但负值绝对值相对于突变前正值极小,之后随着填高增大,Δ逐渐减小,减幅较平缓。采用位移突变判据的极限填筑高度为3.2 m、塑性区应变能突变判据的极限填筑高度为3.4 m、塑性区体积突变判据的极限填筑高度为4 m。然而计算过程中塑性区在填高达到3.2 m后就已经开始贯通(见图 5),并且此时顶板下方测点向下的位移也急剧增长(见图 6),说明顶板已经失稳,因此采用塑性区体积作为突变判据明显不合理。
|
| 图 5 塑性区分布 Fig. 5 Distribution of plastic zones |
| |
|
| 图 6 竖向位移分布云图(单位:m) Fig. 6 Nephograms of vertical displacement distribution (unit: m) |
| |
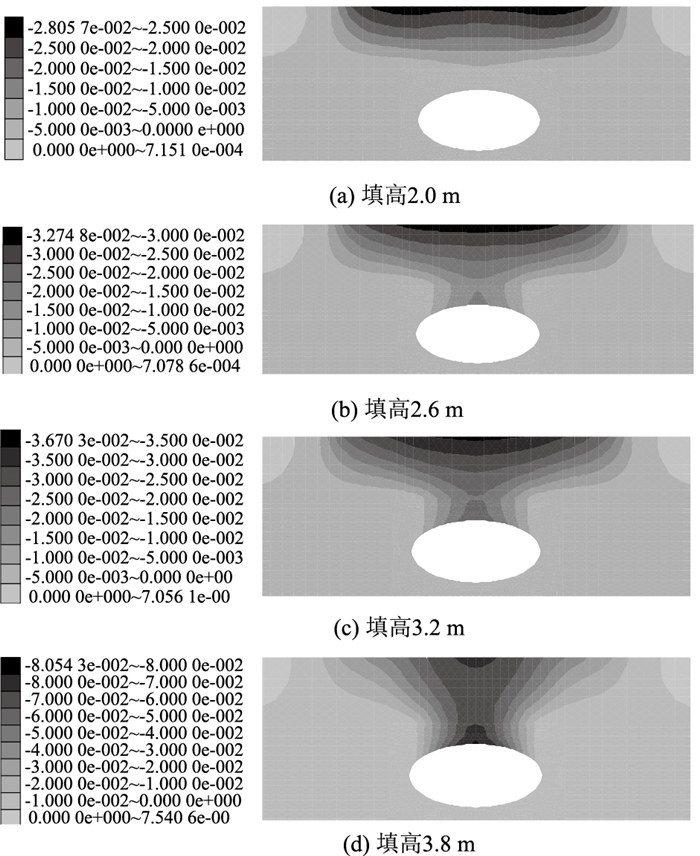
综上所述,采用位移突变判据在岩土体发生失稳的过程中通常无法确定其最先失稳部位。本研究通过对比顶板中点及中点旁两个测点(3个测点的位置见图 2)的失稳过程(见图 7),发现岩层顶板上测点并不是同时达到失稳状态,这与文献[17]得到的结论一致,因此采用位移突变判据时选取不同测点进行稳定性分析可能出现发生失稳时的路堤填高不一致的情况。相比之下,塑性区应变能受局部材料的强度和结构影响较小,能反映结构整体稳定的特点,应变能这一指标包括体变能和形变能,同时考虑了应力和变形两方面对于顶板稳定性的影响(由式(5)可知),并且塑性区单元同时包括剪切屈服和拉伸屈服单元(见图 5),即分别考虑了抗剪失稳和抗弯失稳两种主要的顶板失稳情况,因此采用塑性区应变能作为判定顶板失稳的状态变量更为合理。
|
| 图 7 顶板测点竖向位移随路堤填高变化曲线 Fig. 7 Curves of vertical displacement varying with subgrade filling height at measuring point on roof |
| |
3 顶板稳定性影响因素分析
广西桂柳高速公路第1标段岩溶发育路段所包括的溶洞所处地质条件繁杂,涉及不同厚跨比、上覆土层以及不同岩层特性。根据影响顶板稳定性的3个主要因素:厚跨比、上覆土层厚度、岩层物理力学参数,采用尖点突变理论并应用塑性应变能突变判据进行稳定性数值计算分析,通过改变3个因素的取值研究其对顶板极限承载力的影响(极限承载力按照填土天然重度乘以路堤填高来计算),进而有效地指导实际工程的设计施工。
3.1 溶洞厚跨比根据常见溶洞厚跨比的取值范围,在分别使顶板厚度和洞跨度不变的情况下设计了5种工况,同时考虑1,2,3,4 m这4种不同顶板厚度和8,10,12 m这3种不同溶洞跨度,计算每种工况下的极限承载力,从而得到极限承载力随厚跨比的变化规律。
不同厚跨比工况的计算方案如表 3所示,得到的计算结果如图 8所示。
| 厚跨比 | 顶板厚 | 洞跨 | ||||||
| 1 m | 2 m | 3 m | 4 m | 8 m | 10 m | 12 m | ||
| 溶洞跨度/m | 顶板厚度/m | |||||||
| 0.2 | 5.0 | 10.0 | 15.0 | 20.0 | 1.6 | 2.0 | 2.4 | |
| 0.4 | 2.5 | 5.0 | 7.5 | 10.0 | 3.2 | 4.0 | 4.8 | |
| 0.6 | 1.6 | 3.3 | 5.0 | 6.7 | 4.8 | 6.0 | 7.2 | |
| 0.8 | 1.3 | 2.5 | 3.8 | 5.0 | 6.4 | 8.0 | 9.6 | |
| 1.0 | 1.0 | 2.0 | 3.0 | 4.0 | 8.0 | 10.0 | 12.0 | |

|
| 图 8 极限承载力随厚跨比变化曲线 Fig. 8 Curves of ultimate bearing capacity varying with thickness-span ratio |
| |
由图 8可知,随着溶洞顶板厚跨比的增大,顶板极限承载力逐渐增大。在厚跨比小于0.4且顶板厚度大于2 m或厚跨比小于0.4且洞跨大于10 m的情况下,路堤极限承载力均小于100 kPa。
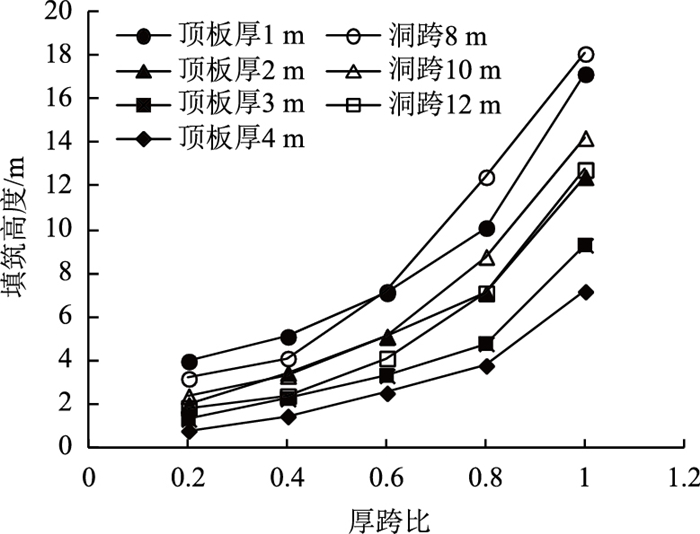
图 9为安全系数1.5时填筑高度随厚跨比变化曲线。
|
| 图 9 安全系数1.5时填筑高度随厚跨比变化曲线 Fig. 9 Curves of filling height varying with thickness-span ratio when security coefficient is 1.5 |
| |
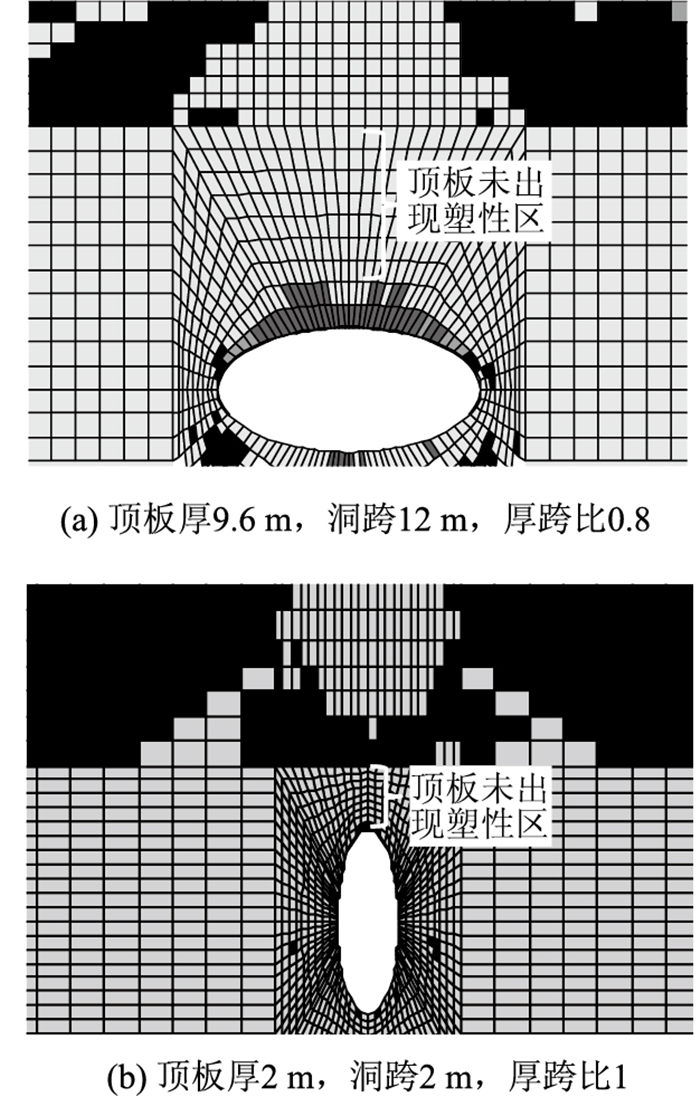
可以看出,顶板厚度小于2 m,洞跨小于10 m且厚跨比不小于0.6时才能保证5 m填筑高度。对于厚跨比较小的溶洞,主要表现为顶板下边缘拉伸屈服,随着荷载的增大,顶板上边缘处首先进入塑性区并逐渐向下延伸直至顶板岩层全部屈服。对于厚跨比较大的溶洞,主要表现为拉剪屈服,塑性区首先出现在路基两侧,然后向上延伸至覆土层贯通,最后才延伸至顶板岩层,导致顶板整体剪切破坏。在计算过程中值得注意的是,当顶板厚跨比在0.8以上时,随着荷载的增加,塑性区逐渐贯通上覆土层,而顶板岩层只有溶洞上方岩层少许单元拉伸屈服或溶洞两侧少许岩体剪切屈服(见图 10,上覆土层几乎塑性区贯通,岩层顶板却几乎没有塑性区),因此在厚跨比较大的情况下,可以对上覆土层进行注浆处理或强夯压实,以防上覆土层先于岩层顶板失稳破坏。
|
| 图 10 上覆土层先于顶板岩层进入塑性区 Fig. 10 Overlying soil entered into plastic zone before karst cave roof |
| |
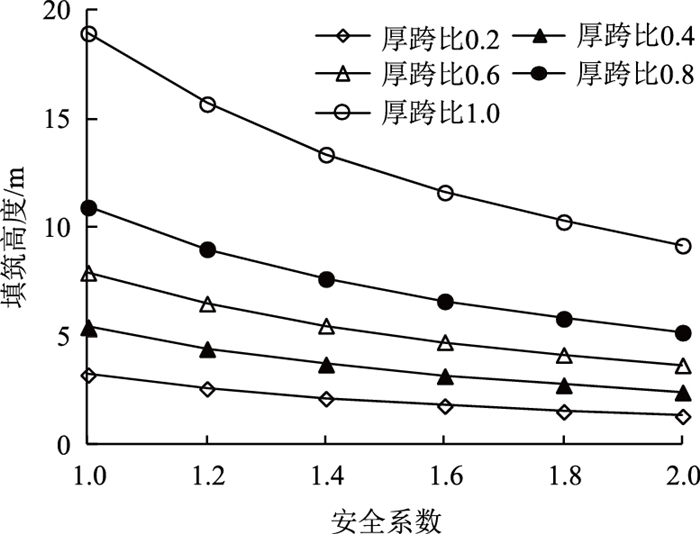
采用公路-Ⅰ级车道荷载均布荷载标准值作为活载,不同厚跨比下填筑高度随所取安全系数的变化曲线如图 11所示,填筑高度按式(6)计算:
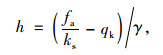
|
(6) |
|
| 图 11 顶板填筑高度随安全系数的变化曲线 Fig. 11 Curves of roof filling height varying with security coefficient |
| |
式中,fa为顶板极限承载力;ks为安全系数;qk为可变荷载,取10.5 kPa[18];γ为填土天然重度(取值见表 1)。
可以看出,路基填筑高度与安全系数成反比。当厚跨比超过0.6时,对于任意安全系数的取值(1.0~2.0),填筑填高均超过5 m,顶板安全储备较高。当厚跨比处于0.2至0.6之间时,安全系数取值需要小于1.4才能使顶板所能承受的填筑高度保持在5 m左右。
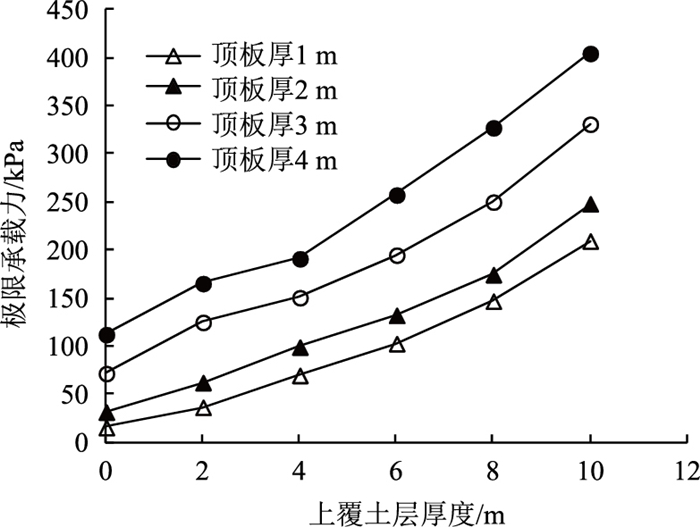
3.2 溶洞上覆土层厚度为分析溶洞上覆土层厚度对溶洞顶板极限填高的影响,在原始模型基础上改变上覆土层厚度,洞跨保持12 m不变,上覆土层厚分别取0,2,4,6,8,10 m(上覆土层为0 m即为岩质顶板模式[19]),并分析1,2,3,4 m这4种不同顶板厚度情况下上覆土厚变化对顶板稳定性的影响,计算结果如图 12所示。
|
| 图 12 极限承载力随上覆土层厚度变化曲线 Fig. 12 Curves of ultimate bearing capacity varying with overlying soil thickness |
| |
可以看出,上覆土层厚度越大,极限承载力越高,当上覆土层厚度在4 m以下且顶板厚度小于2 m时,顶板极限承载力不超过100 kPa,顶板安全储备较低,当上覆土层厚为0时(即荷载直接作用在岩层顶板),顶板厚度3 m的极限承载力仍小于100 kPa,且无覆土相比于有覆土时顶板极限承载力下降较明显,这是因为荷载直接作用在岩层顶板上,失去了覆土层缓冲作用,无法产生应力吸收效应,整体结构脆性更大。因此覆土层越厚,对线路施工越安全。
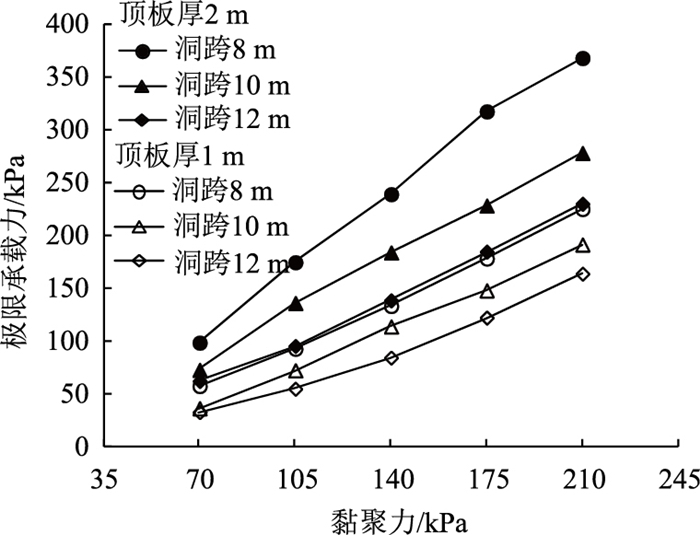
3.3 溶洞岩石强度参数 3.3.1 黏聚力影响分析根据常见强风化灰岩黏聚力取值范围,将黏聚力值依次取为70,105,140,175,210 kPa,内摩擦角值保持40°不变,并在每种工况内计算不同顶板厚度及洞跨情况下的极限承载力,顶板厚1 m和2 m,洞跨8,10,12 m,计算结果如图 13所示。
|
| 图 13 极限承载力随黏聚力变化曲线 Fig. 13 Curves of ultimate bearing capacity varying with cohesion |
| |
3.3.2 内摩擦角影响分析
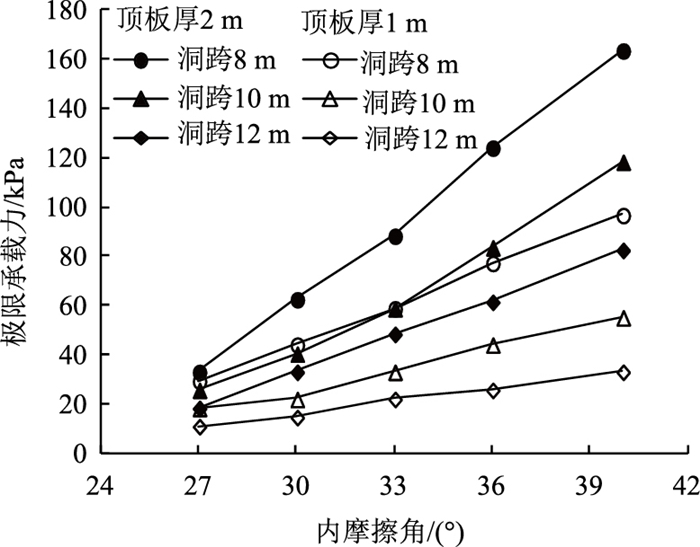
根据常见强风化灰岩内摩擦角取值范围,将内摩擦角值依次取为27°,30°,33°,36°,40°,黏聚力保持70 kPa不变,每种工况内计算不同顶板厚度和洞跨情况下的极限承载力。顶板厚取1 m和2 m,洞跨取8,10,12 m,计算结果如图 14所示。
|
| 图 14 极限承载力随内摩擦角变化曲线 Fig. 14 Curves of ultimate bearing capacity varying with internal friction angle |
| |
随着顶板黏聚力值、内摩擦角值的不断增加,路堤极限承载力近似呈线性增长趋势,并且极限承载力的增长速率随顶板厚度的增大和洞跨减小而增大。如图 13和图 14所示,当顶板厚度为2 m、洞跨为8 m时,黏聚力从70 kPa增至210 kPa的过程中极限承载力增大270 kPa,内摩擦角从27°增至40°过程中极限承载力增大130 kPa。当顶板厚度1 m、洞跨8 m时,黏聚力由70 kPa增至210 kPa,极限承载力增大168 kPa,内摩擦角从27°增至40°的过程中极限承载力增大67 kPa,因此极限承载力增长速率随顶板厚度成正比。当顶板厚度为2 m、洞跨为10 m时,黏聚力从70 kPa增至210 kPa,极限承载力增大205 kPa,内摩擦角从27°增至40°,极限承载力增大93 kPa,因此极限承载力增长速率随溶洞跨度成反比。
4 结论(1) 相对于竖向位移和塑性区体积,塑性应变能综合考虑了拉、压、剪切屈服导致的体变能和形变能,体现了应力和应变共同对结构稳定性的影响,且为单一数值,可作为采用突变理论分析顶板稳定性时的失稳判据和破坏准则。
(2) 溶洞顶板极限承载力随厚跨比增大呈非线性增加。相同厚跨比下,溶洞跨度越小或顶板厚度越小,承载力越高。对于厚跨比超过0.8且尺寸较小的溶洞,上覆土层先于岩层顶板发生屈服破坏,并给出了不同安全储备系数下路堤填高与厚跨比之间的关系。
(3) 溶洞顶板极限承载力随上覆土层厚度减小而降低。当厚度减小至零时,由于上覆土层应力吸收效应缺失,承载力急剧降低,且随顶板厚度的增大,上覆土层厚度对溶洞顶板极限承载力的影响增加。
(4) 溶洞顶板极限承载力随黏聚力和内摩擦角的增加呈线性增大,顶板厚度越大、洞跨越小,岩溶顶板极限承载力线性增加的速率越大。
| [1] |
SWIFT G, REDDISH D. Stability Problems Associated with an Abandoned Ironstone Mine[J]. Bulletin of Engineering Geology and the Environment, 2002, 61(3): 227-239. |
| [2] |
常士骠, 张苏民. 工程地质手册[M]. 4版. 北京: 中国建筑工业出版社, 2007. CHANG Shi-biao, ZHANG Su-min. Engineering Geology Manual[M]. 4th ed. Beijing: China Architecture and Building Press, 2007. |
| [3] |
NOMIKOS P P, SOFIANOS A I, TSOUTRELLS C E. Structural Response of Vertically Multi-jointed Roof Rock Beams[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(1): 79-94. |
| [4] |
曹文贵, 程晔, 赵明华. 公路路基岩溶顶板安全厚度确定的数值流形方法研究[J]. 岩土工程学报, 2005, 27(6): 621-625. CAO Wen-gui, CHEN Ye, ZHAO Ming-hua. Studies on Numerical Manifold Method for Determination of Safe Thickness of Karst Roof in Roadbed[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(6): 621-625. |
| [5] |
HATZOR Y H, WAINSHTEIN I, MAZOR D B. Stability of Shallow Karstic Caverns in Blocky Rock Masses[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(8): 1289-1303. |
| [6] |
YACINE A, RIDHA M M, LAID H M, et al. Karst Sinkholes Stability Assessment in Cheria Area, NE Algeria[J]. Geotechnical and Geological Engineering, 2014, 32(2): 363-374. |
| [7] |
吴明鑫, 李伍平. 溶洞地基稳定性模糊综合评价法综述[J]. 长春工程学院学报:自然科学版, 2012, 13(1): 39-42. WU Ming-xin, LI Wu-ping. Fuzzy Synthetic Evaluation on the Stability of the Foundation to Karst Cave[J]. Journal of Changchun Institute of Technology:Social Science Edition, 2012, 13(1): 39-42. |
| [8] |
康虔, 王新民, 蒲浩, 等. 基于变权-未确知测度理论的岩溶路基稳定性分析[J]. 东北大学学报:自然科学版, 2016, 37(3): 435-439. KANG Qian, WANG Xin-min, PU Hao, et al. Analysis of Subgrade Stability in Karst Area Based on Variable Weight Theory-uncertainty Measurement Method[J]. Journal of Northeastern University:Natural Science Edition, 2016, 37(3): 435-439. |
| [9] |
赵明华, 蒋冲, 曹文贵. 岩溶区桩端溶洞顶板安全厚度确定的突变模型[J]. 四川大学学报:自然科学版, 2007, 39((增1): 149-152. ZHAO Ming-hua, JIANG Chong, CAO Wen-gui. Catastrophe Model of Rock-socked Pile Load Cave Roof Safe Thickness in Karst Region[J]. Journal of Sichuan University:Engineering Science Edition, 2007, 39(S1): 149-152. |
| [10] |
何忠明, 刘森峙, 胡庆国, 等. 基于尖点突变理论的路堤填筑下伏溶洞顶板稳定性研究[J]. 中南大学学报:自然科学版, 2016, 47(7): 2456-2462. HE Zhong-ming, LIU Seng-zhi, HU Qing-guo, et al. Stability of Karst Cave Roof during Embankment Filling Based on Cusp Catastrophe Theory[J]. Journal of Central South University:Science and Technology Edition, 2016, 47(7): 2456-2462. |
| [11] |
赵延林, 吴启红, 王卫军, 等. 基于突变理论的采空区重叠顶板稳定性强度折减法及应用[J]. 岩石力学与工程学报, 2010, 29(7): 1424-1434. ZHAO Yan-lin, WU Qi-hong, WANG Wei-jun, et al. Strength Reduction Method to Study Stability of Goaf Overlapping Roof Based on Catastrophe Theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(7): 1412-1513. |
| [12] |
黄昌富, 田书广, 吴顺川, 等. 基于突变理论和广义H-B强度准则的采空区顶板稳定性分析[J]. 煤炭学报, 2016, 41(增2): 330-337. HUANG Chang-fu, TIAN Shu-guang, WU Shun-chuan, et al. Stability Analysis of Goaf Roof Based on Catastrophe Theory and Generalized H-B Failure Criterion[J]. Journal of China Coal Society, 2016, 41(S2): 330-337. |
| [13] |
徐恒, 王贻明, 吴爱祥, 等. 基于尖点突变理论的充填体下采空区安全顶板厚度计算模型[J]. 岩石力学与工程学报, 2017, 36(3): 579-586. XU Heng, WANG Yi-ming, WU Ai-xiang, et al. A Computational Model of Safe Thickness of Roof under Filling Body Based on Cusp Catastrophe Theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(3): 579-586. |
| [14] |
QIN S, JIAO J J, WANG S. A Cusp Catastrophe Model of Instability of Slip-buckling Slope[J]. Rock Mechanics and Rock Engineering, 2001, 34(2): 119-134. |
| [15] |
李亚生, 周翠英, 张惠明. 基于位移突变判据的强度折减法边坡稳定分析[J]. 人民黄河, 2012, 34(2): 146-148. LI Ya-sheng, ZHOU Cui-ying, ZHANG Hui-ming. Stability Analysis of Slope by Using Strength Reduction FEM Based on the Criterion of Uncontrolled Displacement at Three Characteristic Nodes[J]. Yellow River, 2012, 34(2): 146-148. |
| [16] |
华成亚, 赵旭, 刘子剑, 等. 塑性应变能判据在三维边坡稳定性分析中的应用[J]. 工业建筑, 2016, 46(4): 93-97. HUA Cheng-ya, ZHAO Xu, LIU Zi-jian, et al. The Plastic Strain Energy Criterion in Analysis of Three-dimensional Slope Stability[J]. Industrial Construction, 2016, 46(4): 93-97. |
| [17] |
郑东健, 雷霆. 基于突变理论的高拱坝失稳判据研究[J]. 岩土工程学报, 2011, 33(1): 23-27. ZHENG Dong-jian, LEI Ting. Instability Criteria for High Arch Dams Using Catastrophe Theory[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 23-27. |
| [18] |
JTG D60-2015, 公路桥涵设计通用规范[S]. JTG D60-2015, General Specifications for Design of Highway Bridges and Culverts[S]. |
| [19] |
周斌.岩溶地基中不同模式的岩溶顶板的稳定性分析及应用研究[D].广州: 华南理工大学, 2016. ZHOU Bin. Stability Analysis and Application Research of Karst Roof in Different Patterns of Karst Foundation[D]. Guangahou: South China University of Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10561-1016771363.htm |
 2019, Vol. 36
2019, Vol. 36
