扩展功能
文章信息
- 李军, 贾顺平
- LI Jun, JIA Shun-ping
- 道路客运提前购票行为模型
- A Model for Advance Ticketing Behaviors of Road Passenger Transport
- 公路交通科技, 2019, 36(10): 144-151
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(10): 144-151
- 10.3969/j.issn.1002-0268.2019.10.019
-
文章历史
- 收稿日期: 2018-10-09
2. 中国交通通信信息中心, 北京 100011
2. China Transport Telecommunications & Information Center, Beijing 100011, China
随着道路客运与互联网的深度融合以及客运联网售票系统的建设,线上售票等多元化售票方式迅速发展。道路客运逐渐形成了站内窗口、代售点、网站、手机APP、自助售票机等多渠道售票格局。道路客运售票渠道的变化改变甚至重构了旅客购票行为和模式,一个明显的变化是站内排队、随到随买的旅客比例减少,站外提前购票比例逐渐增大,特别是随着网站、移动端APP等线上售票方式的普及,旅客足不出户便可购票,使旅客更倾向于提前购票,节假日期间尤为明显。据第三方调查数据显示,2018年春运期间部分线路的提前预售率高达63%。
旅客提前购票行为在交通运输学术界和产业界受到较多关注。在民航方面,旅客提前购票行为是航空公司制定收益管理策略的关键依据。航空公司根据旅客购票时间区分其对票价的敏感程度和支付意愿,并提高座位分配的效率,通过设置提前购票折扣,可以诱导价格敏感的旅客提前购票,并诱导价格不敏感但时间敏感的旅客延迟购票[1]。在铁路方面,有关学者[2-4]对铁路旅客的购票时间选择问题进行了研究,基于线上订票数据,利用多项Logit(Multinomial Logit,MNL)模型、潜分类模型、混合Logit模型等研究方法,定量分析了票价、出发日期、工作日对购票提前时间的影响,并将时间选择模型和需求函数纳入收入优化问题,此类问题大多以交通行为问卷调查数据为基础进行研究[5]。与民航、铁路相比,道路客运行业鲜有旅客提前购票行为的相关研究。道路客运作为城际出行的重要交通方式,2017年完成营业性客运量145.68亿人,占全国交通运输营业性客运量的78.8%,覆盖了绝大部分的客运出行群体,然而,对这一庞大群体购票行为的研究几乎是空白;另一方面,道路客运线上售票的发展,生成了大量的售票记录数据,为进行旅客购票行为分析提供了基础和条件。综合来看,研究并明晰旅客预购票行为,对道路客运优化营销策略、科学调配运力、动态定价等均具有重要意义。因此,开展道路旅客提前购票行为研究十分必要,且具有可行性。
本研究基于道路客运联网售票信息系统数据,选择长途和短途典型线路,定量分析旅客提前购票、取票主要时间点分布特征;在比较行为分析方法适用性的基础上,基于随机效用理论构建旅客提前购票行为连续选择Logit模型;利用联网售票数据进行实证分析,并设计不同场景评估票价调整对旅客预购票行为的影响,揭示旅客提前购票行为规律,为道路客运企业运力配置和科学调度提供依据。
1 提前购票问题与行为特征 1.1 问题描述在道路客运多渠道购票环境下,道路旅客提前购票通常可分为2种类型:一是站外提前购票,乘车当天站内取票;二是乘车当天提前到站购票,随到随购。旅客购票过程中主要时间点包括站外提前购票时间、站内取票时间、提前进站购票时间、检票时间等,如图 1所示。假设站外提前购票时间为T1、乘车当天站内取票时间为T2、乘车当天站内购票时间为T3、检票乘车时间为Tc。对于站外提前购票,提前购票时间可分为提前购买时间(T2-T1)和取票后候车时间(Tc-T2)2段;对于乘车当天站内购票,购买和取票同时发生,没有单独取票环节,提前购票时间(Tc-T3)可等同于候车时间。

|
| 图 1 旅客购票过程时间点 Fig. 1 Time points of passengers' ticketing process |
| |
无论是站外购买站内取票还是乘车当天提前站内购票,T2和T3与到站时间息息相关。虽然如此,2类购票旅客表现出不同的到站时间选择行为和倾向,即T2会早于或晚于T3,但(Tc-T2)和(Tc-T3)均可视为旅客在站内候车时间。因此,道路旅客提前购票行为可归结为2个时间选择问题:一是旅客站外提前购票时间;二是旅客乘车当天提前到站候车时间。在旅客候车时间方面已有较多研究[6-7],但对于旅客提前购票时间分布特征、影响因素及票价调整策略等尚缺乏相关研究,本研究即针对此问题展开。本研究所指提前购票行为是道路旅客利用线上渠道选择站外购票提前天数行为,不包含出行当天在站内或利用线上渠道购票的情况,也就是说(Tc-T1)≥1d。
1.2 行为特征道路客运联网售票系统的建设和运营积累了大量的售票记录和运营调度数据,售票记录中包含售票时间、站内取票时间、检票时间等时间信息,据此可以计算站外购票提前天数、当天购票提前时间、当天提前取票时间等。同时,售票记录中包含旅客个人属性、出行特征等,运营调度数据中包含有发车频率、实载率等运营信息,这些数据为分析旅客提前购票行为提供了条件和基础。
本研究基于道路客运联网售票数据,选择北京—林东、北京—滦南2条线路作为实例,分析旅客提前购票行为特征。2条线路的长度分别为700 km和230 km,全年按月份统计的客流量如图 2所示,可知客流量在2月(春节)、7~8月(暑假)3个月份客流量较高,11月份客流量最小。

|
| 图 2 研究线路每月旅客发送量 Fig. 2 Passenger transport volumes of research routes per month |
| |
旅客提前购票时间定义为出发日期与客票购买日期之间的天数,图 3为2条线路旅客提前购票天数的分布情况,原点坐标表示当天购买客票的旅客数量。由图 3可知,近60%的旅客是出行当天购票。图 4进一步描述了出行当天购票的旅客提前站内购票时间,以及站外购票旅客提前站内取票时间的分布。北京—滦南线路在检票前15~105 min站内购票的旅客占比为75%,时间较为分散且旅客数量波动性较大;相比较而言,此线路站外购票的旅客提前站内取票的时间则较为集中,提前10~60 min的旅客占比为72%。北京—林东线路在检票前20~80 min站内购票的旅客占比为73%,时间较为集中,提前45 min购票的旅客最为集中,占比为11%;一个有趣的现象是,该线路站外购票的旅客,提前站内取票的时间较为分散,检票前30~130 min的旅客占比为78%。

|
| 图 3 研究线路预购曲线 Fig. 3 Advance purchase curves of research lines |
| |

|
| 图 4 站内提前购票与取票时间分布 Fig. 4 Time distribution of advance ticket purchase and pick-up in station |
| |
2 模型方法 2.1 方法适用性
基于随机效用理论的离散选择类模型是交通行为分析的支柱,此类模型广泛应用于出行方式等离散选择行为分析中[8]。尽管如此,与交通出行相关的诸多决策和选择行为中,其本质上非离散而是连续的[9-10],比如住宅位置选择和出行目的地选择可以被视为二维连续变量,提前购买时间、出发时刻等也是连续变量。在此类分析中,虽然可以通过设置区间边界将这些连续选择离散化处理,但往往存在明显的限制和不足:一是基于不同的研究目的,人为设定区间边界,如果研究目的和边界改变,则模型校准和应用中可能会出现不同的结果;二是行为分析模型应用通常需要点预测,而离散模型仅提供区间预测;三是从旅客的角度,2个相邻的时间点可以作为同一购票时间选择,然而离散化处理经常会导致这2个时间点分布于2个区间。尽管一些研究仍利用离散选择模型分析订票、购票提前时间等连续行为问题[3],但将连续变量离散化处理难以描述决策行为的连续过程,另一方面,不同的离散区间设置还会导致不同和不稳定的计算结果[11]。因此,在提前购票时间等连续选择环境行为分析问题中,将时间变量进行连续处理更为合理和可取[12-13]。作为MNL模型的发展,连续Logit模型提供了连续选择情境下的行为分析方法,并首先应用于位置选择问题的分析[14-15],有研究利用三角函数来分析航空旅客的偏好[16],在基于活动模型的框架中,对于出发时刻、到达时刻等与时间相关的分析也利用了此类模型[17-18]。
2.2 模型构建道路旅客提前购票时间决策是一个典型的连续选择行为问题,因此本研究基于连续Logit理论方法,构建旅客提前购票决策行为模型。假设道路客票的预售期为T(自开始售票至发车的天数),与离散选择模型类似,连续Logit模型也有一个备选方案选择集,所不同的是,离散选择模型的选择集是一个个离散的选择方案,比如时间选择集tk(k=1,2, …,K),而对于连续选择模型而言,选择集是一个区间,假设为[0,T]。假设旅客n在预售期第t天(t∈[0, T])购买了j班次的1张客票,其效用函数Unj(t)由固定项Vnj(t)和随机项εnj(t)2部分组成:
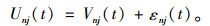
|
(1) |
从式(1)中可以看出,由于时间是一个连续变量,作为时间的函数,效用函数中包含的变量也应该是连续的。在旅客提前购票行为中,影响效用函数固定项Vnj(t)的变量可以分为2类:第1类是随购票时间变化的变量,比如票价[19];第2类是不随购票时间变化的变量,比如性别、年龄、发车频率等。第1类变量可以直接引入效用函数中,第2类变量通过购票时间的三角函数与其的相互作用来引入。效用函数表示为:

|
(2) |

|
(3) |
式中,Xnj为不随时间变化的向量,包括旅客n的年龄、性别等社会经济属性以及班次j的发车频率、实载率等运营特征;fnj(t)为旅客n购买班次j的票价;α和β为参数向量;D(t)为预售期T内正弦函数和余弦函数的集合;L为特征变量的个数。
连续选择模型的选择概率函数如式(4)所示。本研究采用GAUSS软件包对模型进行估计[20]。

|
(4) |
本研究基于道路客运联网售票和运营调度数据,选择15条200 km左右的短途线路和15条800 km左右的长途线路进行实证分析。基于2类线路售票数据,利用构建的提前购票行为连续Logit模型,分析旅客的提前购票决策行为及影响因素。旅客性别、年龄、出行时间以及班次发车频率、实载率等作为影响变量,同时,道路客运票价在1个预售期内一般保持不变,但为了后续的分析,将票价作为1个变量引入效用函数中。变量选取与定义如表 1所示。
| 变量名称 | 变量 | 变量定义与描述 |
| 性别 | Xgen | M:男性为1,否则为0 |
| F:女性为1,否则为0 | ||
| 年龄 | Xage | A1:25岁及以下为1,否则为0 |
| A2:26~45岁为1,否则为0 | ||
| A3:46~65岁为1,否则为0 | ||
| A4:66岁及以上为1,否则为0 | ||
| 发车频率 | Xfr | F1:1天1班为1,否则为0 |
| F2:1天2班~5班为1,否则为0 | ||
| F3:1天5班以上为1,否则为0 | ||
| 出行时间 | Xdt | H:节假日出行为1,否则为0 |
| 实载率 | Xlr | L1:小于30%为1,否则为0 |
| L2:30%~60%为1,否则为0 | ||
| L3:大于60%为1,否则为0 |
3.1 模型估计与行为分析
使用GAUSS软件,利用极大似然法对模型参数进行估计,结果如表 2所示。从标定结果来看,大部分选择的解释变量都具有良好的显著性。
| 变量 | 短途线路(200 km) | 长途线路(800 km) | ||||
| 系数 | 95%置信区间 | 系数 | 95%置信区间 | |||
| Xage | sin(2πt/30) | 0.058 6 | (-0.007 6, 0.125 9) | 0.073 5 | (0.034 8, 0.117 6) | |
| sin(4πt/30) | 0.061 7 | (-0.021 8, 0.142 9) | 0.076 1 | (0.030 2, 0.128 1) | ||
| sin(6πt/30) | 0.011 7 | (-0.043 9, 0.067 6) | 0.019 5 | (-0.012 7, 0.056 9) | ||
| sin(8πt/30) | 0.017 6 | (-0.003 8, 0.037 6) | 0.013 8 | (0.001 2, 0.027 8) | ||
| cos(2πt/30) | -0.212 6 | (-0.363 9, -0.071) | -0.202 2 | (-0.312 8, -0.045 6) | ||
| cos(4πt/30) | -0.125 2 | (-0.208 1, -0.046) | -0.103 6 | (-0.167 8, -0.049 3) | ||
| cos(6πt/30) | -0.065 7 | (-0.105 7, -0.029 1) | -0.043 2 | (-0.069 8, -0.019 7) | ||
| cos(8πt/30) | -0.026 8 | (-0.049, -0.008 8) | -0.013 5 | (-0.026 7, -0.003 3) | ||
| Xgen | sin(2πt/30) | 0.717 2 | (0.152 2,1.362 1) | 0.758 9 | (0.314 6,1.206 1) | |
| sin(4πt/30) | 0.699 1 | (0.208 3,1.186 6) | 0.734 6 | (0.570 3,1.006 6) | ||
| cos(2πt/30) | -0.156 8 | (-1.279 6,0.978 3) | -0.317 8 | (-0.746 1,0.128 3) | ||
| cos(4πt/30) | 0.239 2 | (-0.218 6,0.756 1) | 0.147 9 | (-0.207 1,0.498 1) | ||
| Xfr | sin(2πt/30) | -3.101 6 | (-4.817 7,-1.465 5) | -2.449 1 | (-3.012,-1.805 8) | |
| sin(4πt/30) | -2.343 | (-4.179 9,-0.436 1) | -1.520 8 | (-2.061 7,-1.004 7) | ||
| sin(6πt/30) | -0.763 9 | (-2.002 9,-0.526 3) | -0.413 9 | (-1.053 8,0.237 6) | ||
| cos(2πt/30) | -0.341 2 | (-4.946,3.497 8) | -1.812 5 | (-2.365 8,-1.325) | ||
| cos(4πt/30) | -0.813 3 | (-3.700 2,1.550 6) | -1.534 3 | (-1.983 2,-1.004 7) | ||
| cos(6πt/30) | -0.629 1 | (-1.929 7,0.652 8) | -0.767 | (-1.183 5,-0.312 8) | ||
| Xdt | sin(2πt/30) | -0.161 7 | (-0.670 5,0.349 1) | -0.110 5 | (-0.465 9,0.217 9) | |
| cos(2πt/30) | 0.331 | (-0.710 8,1.318 7) | 0.178 2 | (-0.178 2,0.567 8) | ||
| Xlr | sin(2πt/30) | 0.034 1 | (-0.012 9,0.076 3) | 0.028 7 | (-0.007 7,0.071) | |
| sin(4πt/30) | -0.036 5 | (-0.097,0.018 6) | -0.027 5 | (-0.079,0.022) | ||
| sin(6πt/30) | -0.006 3 | (-0.032 8,0.028 9) | -0.008 2 | (-0.031 8,0.018 2) | ||
| cos(2πt/30) | 0.063 3 | (-0.038 9,0.159 9) | 0.067 1 | (-0.020 9,0.153 9) | ||
| cos(4πt/30) | -0.002 9 | (-0.067 9,0.049 8) | 0.005 1 | (-0.052 1,0.055 8) | ||
| cos(6πt/30) | -0.058 9 | (-0.079 3,-0.028 9) | -0.040 6 | (-0.070 1,-0.019 9) | ||
从预售期内不同乘车线路的不同性别旅客来看,同一距离线路类型的预购函数基本相同,表明性别对提前购票时间的影响很小。在出发前10 d内,预购函数发生了变化,长距离线路的预测值要高于短距离线路的预测值,意味着长距离线路的旅客提前购票的概率更大。由不同节假日旅客的预购函数来看,假日出行的旅客往往会提前购票,相比之下,大部分旅客仍偏好于临近出发日购票,这与道路旅客的出行目的主要以非公务出行为主有关。由不同年龄旅客的预购曲线可以看出,长距离线路的预购曲线较为平坦,尤其在出发前,短距离线路的预购曲线陡峭,表明长距离出行旅客往往提前购票,而短途旅客往往当天购票。不同年龄在长距离和短距离出行中提前购票行为有所区别,年龄较大者在长途出行中提前购票的概率较大,而短途出行恰恰相反。分析不同发车频率的预购曲线,发车频率较低的线路提前预购的比例较大,发车频率较高的线路预购比例较低,而在出发当天急剧增加。不同实载率对提前购票时间的影响较为明显,实载率大于60%的线路比实载率小于30%的线路提前20 d购票的比例增加了5%,实载率较高的长途线路提前购票的概率更高。不同年龄的提前购票时间密度函数曲线如图 5所示,直观地描述了年龄对旅客提前购票行为的影响。

|
| 图 5 年龄对概率密度影响 Fig. 5 Influence of age on probability density |
| |
3.2 票价调整对预购票行为的影响
目前,我国道路客运市场的票制票价机制较为简单,提前购票的票价与当日站内购票的票价基本一致,未能刺激旅客提前购票的积极性。总体来看,道路旅客提前购票比例较低,80%以上的旅客选择在出发前3 d购买客票,而且近60%的旅客选择当天购票。为增大道路客票预售率,提高旅客进站持票率,道路客运服务商应提供客票折扣、优惠等促销措施,鼓励旅客提前购票。为评估票价调整对旅客提前购票行为的影响,设计了3个票价调整场景,分别假设票价上涨20%、下降20%、下降35%。在3种场景下,旅客提前购票时间的概率密度如图 6所示,展示了价格对道路旅客提前购票时间决策的影响。当票价上涨20%时,旅客在出发前3 d以上购票的概率降低了9.67%,表明旅客倾向于延迟购买;当票价下降20%时,旅客提前3 d购票的概率从39.21%增加到43.27%;当票价下降35%时,旅客提前3 d购票的概率从39.21%增加到51.06%。

|
| 图 6 不同定价场景下旅客提前购票时间分布 Fig. 6 Distribution of passengers' advance ticketing time in different pricing scenarios |
| |
4 结论
本研究围绕道路旅客提前购票时间选择问题,基于道路客运联网售票数据,深入研究了道路旅客提前购票行为的决策机制及时间选择影响因素,得出以下主要结论:
(1) 将旅客提前购票分为提前站外购票出行当天站内取票、出行当天提前进站购票2种类型,通过购票、取票、检票等不同时间点的关系分析,明晰了提前购票行为的时间内在机制及需要重点研究的问题。基于道路客运联网售票数据,分析了旅客站外提前购票天数和提前进站购票、取票的时间分布规律,发现近60%的旅客当天站内购票。与站外提前购票旅客相比,当天站内购票旅客的进站时间平均提前约45 min。
(2) 分析了提前购票时间选择和基于随机效用的行为分析理论方法二者之间的适用性,构建了道路旅客提前购票行为连续Logit模型。基于道路客运联网售票数据,进行了实证应用,揭示了旅客提前购票时间与旅客特性、运营特征等因素之间的关系,发现旅客性别、年龄,发车频率、节假日、实载率等因素对旅客提前购票时间均有影响。长途和短途2类不同线路旅客的提前购票行为有所差异,总体而言,长距离出行的旅客比短距离出行的旅客提前3 d购票的概率高28%,实载率大于60%的线路提前20 d购票的比例增加5%。经实证分析,该模型是分析旅客提前购票行为的有效方法。
(3) 评估了票价变动对提前购票行为的影响,票价上涨20%、下降20%、下降35%时,旅客提前3 d以上购票的概率分别降低9.67%、提高3.6%、提高11.85%。研究结论有助于道路客运服务主体了解旅客提前购票时间的决策机制,为道路客运动态定价、运力科学调配以及定制化服务运营提供参考和依据。
本研究以北京地区为例进行道路旅客提前购票行为的研究,虽然得出了一些研究结论,但由于道路客运行业的地区差异性和复杂性,本研究结论并不完全适用于其他地区,在研究分析其他地区道路旅客的提前购票行为时,应根据区域差异进行修正。另外,利用道路客运联网售票数据进行研究,未能包含收入、职业等旅客个人社会经济属性变量,可能会使本研究的结论产生一定的偏差。下一步,将信息化系统数据与交通行为意向调查数据结合,进行提前购票行为的建模和分析,也是一个值得研究的方向。旅客提前购票行为是一个较新的研究领域,希望本研究能起到抛砖引玉的作用,引起更多研究者对该领域的关注,以丰富交通出行行为和出行心理学研究内容。
| [1] |
LI T T, XIE J X, LU S M, et al. Duopoly Game of Callable Products in Airline Revenue Management[J]. European Journal of Operational Research, 2016, 254(3): 925-934. |
| [2] |
刘帆洨, 彭其渊, 梁宏斌, 等. 基于PCA-聚类分析的高铁旅客购票行为特性研究[J]. 交通运输系统工程与信息, 2017, 17(6): 126-132. LIU Fan-xiao, PENG Qi-yuan, LIANG Hong-bin, et al. High-speed Railway Passenger Ticketing Behavior Characteristics Based on PCA and Clustering[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(6): 126-132. |
| [3] |
HETRAKUL P, CIRILLO C. Accommodating Taste Heterogeneity in Railway Passenger Choice Models Based on Internet Booking Data[J]. Journal of Choice Modelling, 2013, 6: 1-16. |
| [4] |
HETRAKUL P, CIRILLO C. A Latent Class Choice Based Model System for Railway Optimal Pricing and Seat Allocation[J]. Transportation Research Part E:Logistics and Transportation Review, 2014, 61: 68-83. |
| [5] |
赵鹏, 李云峰, 李博. 基于时段偏好的高铁旅客车次选择行为研究[J]. 北京交通大学学报, 2017, 41(6): 49-54. ZHAO Peng, LI Yun-feng, LI Bo. Study on the Train Choice Behavior for High-speed Railway Passengers Considering the Departure Time Preference[J]. Journal of Beijing Jiaotong University, 2017, 41(6): 49-54. |
| [6] |
吕慎, 田锋, 莫一魁. 轨道交通枢纽地铁换乘接运公交乘客平均候车时间研究[J]. 公路交通科技, 2014, 31(12): 92-97. LÜ Shen, TIAN Feng, MO Yi-kui. Average Waiting Time of Passengers Transferring from Subway to Feeder Bus at Rail Transit Hub[J]. Journal of Highway and Transportation Research and Development, 2014, 31(12): 92-97. |
| [7] |
马卫武, 刘小燕, 李立清, 等. 铁路客运站旅客候车时间研究[J]. 铁道学报, 2009, 31(5): 104-107. MA Wei-wu, LIU Xiao-yan, LI Li-qing, et al. Research of Waiting Time of Passengers at Railway Stations[J]. Journal of the China Railway Society, 2009, 31(5): 104-107. |
| [8] |
BEN-AKIVA M, MCFADDEN D, TRAIN K, et al. Hybrid Choice Models:Progress and Challenges[J]. Marketing Letters, 2002, 13(3): 163-175. |
| [9] |
LEMP J D, KOCKELMAN K M, DAMIEN P. The Continuous Cross-nested Logit Model:Formulation and Application for Departure Time Choice[J]. Transportation Research Part B:Methodological, 2010, 44(5): 646-661. |
| [10] |
李军, 贾顺平, 钱剑培, 等. 习惯影响下城际出行方式选择意向形成机理[J]. 交通运输系统工程与信息, 2018, 18(2): 7-12, 39. LI Jun, JIA Shun-ping, QIAN Jian-pei, et al. Intention Formation Mechanism in the Intercity Travel Mode Choice Influenced by the Habit[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(2): 7-12, 39. |
| [11] |
CHIOU Y C, LIU C H. Advance Purchase Behaviors of Air Tickets[J]. Journal of Air Transport Management, 2016, 57: 62-69. |
| [12] |
BHAT C R, STEED J L. A Continuous-time Model of Departure Time Choice for Urban Shopping Trips[J]. Transportation Research Part B:Methodological, 2002, 36(3): 207-224. |
| [13] |
BEN-AKIVA M, ABOU-ZEID M. Methodological Issues in Modelling Time-of-travel Preferences[J]. Transportmetrica A:Transport Science, 2013, 9(9): 846-859. |
| [14] |
BEN-AKIVA M, LITINAS N, TSUNOKAWA K. Continuous Spatial Choice:The Continuous Logit Model and Distributions of Trips and Urban Densities[J]. Transportation Research Part A:General, 1985, 19(2): 119-154. |
| [15] |
WREDE M. Urban Land Use, Sorting, and Population Density:A Continuous Logit Model[J]. Transportation Research Part B:Methodological, 2017, 101: 283-294. |
| [16] |
KOPPELMAN F S, COLDREN G M, PARKER R A. Schedule Delay Impacts on Air-travel Itinerary Demand[J]. Transportation Research Part B:Methodological, 2008, 42: 263-273. |
| [17] |
YAGI S, MOHAMMADIAN A. An Activity-based Microsimulation Model of Travel Demand in the Jakarta Metropolitan Area[J]. Journal of Choice Modelling, 2010, 3(1): 32-57. |
| [18] |
POPURI Y, BEN-AKIVA M, PROUSSALOGLOU K. Time-of-day Modeling in a Tour-based Context:Tel Aviv Experience[J]. Transportation Research Record, 2008, 2076: 88-96. |
| [19] |
李晓伟, 王炜, 杨敏, 等. 多因素作用下旅客多模式交通出行时间节省价值测算与应用[J]. 公路交通科技, 2018, 35(3): 86-93. LI Xiao-wei, WANG Wei, YANG Min, et al. Calculation and Application of Saving Value of Travel Time for Traveler Regional Multimode Transport under Multidimensional Factors Influence[J]. Journal of Highway and Transportation Research and Development, 2018, 35(3): 86-93. |
| [20] |
WEN C H, CHEN P H. Passenger Booking Timing for Low-cost Airlines:A Continuous Logit Approach[J]. Journal of Air Transport Management, 2017, 64: 91-99. |
 2019, Vol. 36
2019, Vol. 36
