扩展功能
文章信息
- 李义罡, 焦朋朋, 乔伟栋
- LI Yi-gang, JIAO Peng-peng, QIAO Wei-dong
- 基于改进粒子群优化BP神经网络的弯道转向行为预测
- Prediction of Steering Behaviors on Curves Based on BP Neural Network Optimized by Modified PSO
- 公路交通科技, 2019, 36(10): 128-136
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(10): 128-136
- 10.3969/j.issn.1002-0268.2019.10.017
-
文章历史
- 收稿日期: 2017-11-06
道路安全问题是一个由人、车、路等多个因素相互作用而产生的复杂系统问题,在诸多变量中,人的因素最为复杂多变。美国印地安纳大学在一项对交通事故长达5 a的综合研究中表明:驾驶人的认知延误或错误判断等原因,引起的交通事故占全部调查事故的57.1%[1]。因此对驾驶人在行车过程中的反应进行研究有着极大的现实意义。
根据相关研究数据,在驾驶人行车过程中,视觉系统为驾驶人提供的交通信息数比例占80 %,是获取外界信息最重要的途径[2]。正因为驾驶人对外界信息的获取与感知大部分依赖于视觉,视觉行为会对其驾驶行为特别是转向行为等产生极大的影响。据我国2010年交通事故统计年报显示,弯道事故数量占我国道路交通事故总量的10.5%,且由于弯道易发生严重交通事故,弯道驾驶的安全性也就显得愈发重要,对驾驶人的弯道转向能力也提出更高要求。因此,研究基于驾驶人视觉特性的弯道处转向行为预测,对完善道路风险评估理论,提高道路交通安全具有重要意义。
目前,针对驾驶人行为判断与预测问题,国内外专家学者进行了广泛研究。Lee等[3]运用驾驶模拟器开发了基于隐马尔科夫模型(HMM)的驾驶行为识别模型,并运用该模型对驾驶员不同类型的变道行为进行模拟和识别;Salvucci等[4]运用“模型追踪”的方法,构建了一个针对变道行为的驾驶员意图识别和行为预测的模型;Yang等[5]针对车辆抗侧风稳定性,和车辆纵向碰撞,建立了相应的驾驶员模型;冀秉魁[6]通过辨识城市交通环境下的驾驶意图,利用隐马尔科夫算法搭建了驾驶行为预测模型;Wahab等[7]基于加速踏板和制动踏板的压力,运用“小脑模型(CMAC)”来对驾驶员在不同驾驶环境下的行为进行建模;Francesco等[8]以感知操作速度的曲线作为表现形式,通过驾驶模拟器试验来测试司机的速度行为水平曲线;赵晓华等[9]利用驾驶模拟试验, 探索急弯处不同警告标志位置对驾驶行为的影响机理;Moon等[10]分析了驾驶员典型驾驶操作行为(跟车距离把握、接近前车减速、车辆启停加速,正常和强烈制动)的特性,然后把这些驾驶特性考虑到自适应巡航系统控制策略之中;Cole等[11]利用驾驶模拟器从测试对象对转向控制器的使用中获得数据,从而获得最优的线性机制操作和车速。
从国内外研究现状来看,现有对驾驶人行为的研究主要集中在车辆变道与意图识别上,对驾驶人弯道驾驶行为所做的针对性分析还不够,且没有将驾驶人的视觉特性与驾驶人行为进行关联性分析,从驾驶人自身反应过程中发现交通事故的原因与隐患。因此为了提高公路安全服务水平,有必要对驾驶人视觉特性进行研究,进而找出其与弯道转向行为、驾驶人安全驾驶行为之间的关系,以便为道路几何设计提供理论依据,增加道路、车辆设计与驾驶人之间的匹配性。
1 试验设计与数据采集 1.1 试验设备(1) FORUM8驾驶模拟系统
该驾驶模拟系统设备由仿真车辆、控制台区、视景系统、计算机系统等硬件系统及相应软件系统构成,系统具有与某汽车公司真车相同的驾驶区设备和布局。通过对某些组件进行数字化及功能改造,能够捕获用户的输入动作,并对用户的输入及其他相关信息进行虚拟仿真计算;仿真结果对应的信息将通过视景显示系统、声音仿真系统及信号输出系统等反馈给用户,为驾驶员营造较为真实的驾驶环境。
(2) 头戴式眼动仪
选用的眼动仪为某德国公司生产的头戴式眼动仪,相较于固定式眼动仪,头戴式眼动仪使用更加灵活。该眼动仪具有以下适合本试验研究的特点:
① 高速记录双眼数据,数据采集频率为:200 Hz;
② 数据准确度较高,注视位置平均误差小于0.5°;
③ 操作反馈及时高效,最高延迟小于3 ms;
④ 配套的数据处理软件能方便地处理试验数据。
1.2 路段设计及驾驶规则通过UC-win/Road软件搭建虚拟驾驶场景,设计道路为双向四车道,等级为一级公路,全长1.5 km,设计车速为80 km/h。考虑到驾驶人在模拟驾驶试验初始和结束阶段的加减速驾驶过程,拟选取道路的中间1 km作为研究和观察路段。为对比研究在不同弯道半径下的弯道转向行为,设计道路包含了3种半径不同的弯道,半径分别为300,500 m和1 200 m。为避免其他车辆对驾驶人造成影响,干扰数据可靠性,试验路段没有设计其他车辆行驶。整个模拟驾驶试验过程要求驾驶人在中间车道行驶,可以按照平时驾驶习惯对车速和车辆位置进行调整。试验路段和路况分别如图 1和图 2所示。

|
| 图 1 试验路段示意图 Fig. 1 Schematic diagram of experiment road |
| |

|
| 图 2 试验路况示意图 Fig. 2 Schematic diagram of experiment road condition |
| |
1.3 被试者选择
考虑到中青年驾驶人生理特性最为稳定,本次试验对象选取50名年龄在23~35岁间的中青年(其中28名男性,22名女性)。所有驾驶人均具有3年以上驾龄,且视觉机能正常,无生理缺陷和重、特大事故经历。为保证被试者在测试中精神状态良好,要求其在试验前一天保证正常睡眠;并且从试验开始前1 h不能饮用茶、酒、咖啡等刺激饮品,以减少身体心理因素对试验准确性的影响。此外,在正式试验前,被试者将进行10 min左右的练习,以熟悉模拟器操作和掌握试验整体流程。
1.4 数据采集启动并校准试验设备后,进入设定场景行驶。在试验过程中,确保软件时间与采集仪器时间同步,眼动仪始终自动记录相关参数,共获取有效数据46组。为保证试验数据的准确性与可靠性,需对异常数据进行剔除。常用的异常数据剔除方法有拉依达准则法、肖维勒准则法、狄克逊准则法以及罗马诺夫斯基准则法等[12]。经过对比分析,针对本次试验眼动仪采样频率较高,采集数据量较大的特点,使用拉依达准则对异常数据进行剔除。
2 各特性参数分析研究驾驶人视觉特性与弯道转向行为,需建立和定义相关描述指标,以便对其进行定性、定量描述。通过查阅视觉生理学、视觉认知心理学、人机工程学等书籍及相关国内外研究资料[13-16],选定瞳孔面积变化率、扫视速度和扫视幅度3个指标作为对驾驶人视觉特性的研究对象;为更好地反映驾驶人弯道转向行为的安全性,选定方向盘旋转率与车辆侧向加速度作为对驾驶人弯道转向行为的研究对象;为反映取得视觉特性与驾驶行为时的车辆状态,选取平均车速与车辆侧向偏移量作为车辆行驶状态的判断依据。
2.1 车辆行驶状态平均车速是最基本的车辆行驶状态指标,它可以最直观地反映出车辆在不同半径弯道下的行驶状态。侧向偏移量是评价车辆行驶状态的另一重要指标,它指车辆在行驶车道中心的位置偏移,模拟驾驶软件对侧向偏移量的记录有正负之分,正值代表车辆行驶向左偏移,负值代表车辆行驶向右偏移。各半半径下驾驶人在曲线路段行车时,平均车速和侧向偏移量数据如表 1所示。
| 曲线半径R/m | 平均车速/(km·h-1) | 侧向偏移/m |
| 300 | 57.00 | -0.28 |
| 500 | 60.27 | 0.69 |
| 1 200 | 64.21 | -1.55 |
因侧向偏移量的数值有正负之分,本文选用侧向偏移量的标准差来评价匝道圆曲线半径对于车辆行驶状态的影响。采用单因素方差分析法(ANOVA)研究弯道半径对进入弯道路段车辆的速度和侧向偏移量标准差的影响。结果显示弯道半径对进入弯道车辆的车速有显著影响(F=6.83,P < 0.05), 弯道半径同样对侧向偏移量的标准差有显著影响(F=5.99,P < 0.05)。
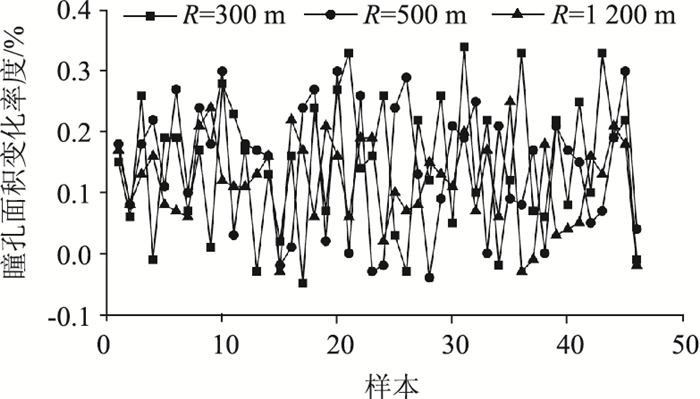
2.2 瞳孔面积变化率驾驶人的瞳孔变化除与光线强弱及物体距离远近有关之外,还与知觉、记忆、思维、语言加工、动机、情绪等诸多高级心理活动相联系[17]。由于瞳孔面积变化率可以衡量驾驶人紧张程度,因此将其选择为评价驾驶人弯道操作能力的视觉特性指标。对有效数据中46名被试驾驶人的平均瞳孔面积变化率进行统计,统计结果如图 3所示。
|
| 图 3 弯道路段驾驶人瞳孔面积变化率 Fig. 3 Pupil area change rate of driver on curve |
| |
观察图 3可以发现:弯道路段的驾驶人平均瞳孔面积变化率多集中在5%~30%的范围内;比较3个半径下的驾驶人瞳孔面积变化率情况,发现随着弯道半径的增大,驾驶人瞳孔面积变化率呈现逐渐缩小的趋势。用Pearson检验法分析驾驶瞳孔面积变化率与转弯半径间的关系,发现两者存在显著的线性关系,且为负相关(F=-0.175,P=0.040)。造成这一现象的主要原因是:半径较小时,弯道环境相对复杂,驾驶难度较大,驾驶人易产生较大驾驶负荷与心理压力,随着弯道半径的增加,驾驶难度也随之降低,驾驶人的驾驶负荷与心理压力变小,因此瞳孔面积变化率呈现随弯道半径增大快速下降的态势。
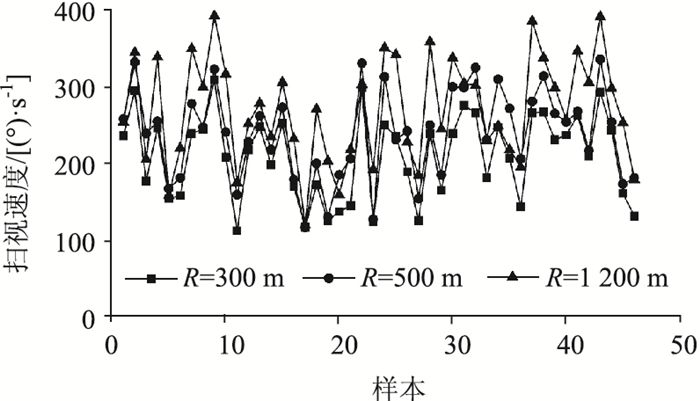
2.3 扫视速度扫视的过程是眼球大幅度运动的过程,扫视速度即每一次扫视的距离(角度)与扫视持续时间的比值。扫视速度能够说明前一次注视过程中信息加工的速度及被试者寻找下一个目标的速度。对有效数据中46名被试驾驶人的平均扫视速度进行统计,统计结果如图 4所示。
|
| 图 4 弯道路段驾驶人扫视速度 Fig. 4 Saccadic velocity of driver on curve |
| |
观察图 4可以发现,驾驶人的平均扫视速度分布范围较广,多集中在每秒150°~300°的范围内。比较3个半径下的驾驶人扫视速度情况,可以看出随着弯道半径的增大,驾驶人扫视速度呈现逐渐增大的趋势。采用Pearson检验法分析扫视速度与转弯半径间的关系,发现两者存在显著的线性关系,且两者呈正相关(F=0.222,P=0.039)。这一情况出现的主要原因是:大曲率半径弯道环境下驾驶难度较小,驾驶人驾驶负荷与心理压力也较小,整个驾驶过程的眼睛变化较为敏捷,驾驶人有能力获取更多的道路信息。
2.4 扫视幅度扫视幅度是衡量驾驶人视觉特性的又一重要指标,扫视幅度即在人眼完成一次注视点转移过程中,人眼视线经过的范围,通常表现为视线经过的角度。目前的研究结论普遍认为:人眼扫视幅度可以作为注视深度的衡量指标,即对驾驶人而言,驾驶人扫视幅度可直接体现其在驾驶过程中所获得的信息量。对有效数据中46名被试驾驶人的平均扫视幅度进行统计,统计结果如图 5所示。

|
| 图 5 弯道路段驾驶人扫视幅度 Fig. 5 Saccadic amplitude of driver on curve |
| |
从图 5可以发现,被试驾驶人的平均扫视幅度不均匀地分布在2°~10°之间。比较3个半径下的驾驶人扫视幅度情况,可以看出随着弯道半径的增大,驾驶人扫视幅度呈现逐渐减小的趋势。采用Pearson检验法分析扫视幅度与转弯半径间的关系,发现两者存在显著的线性关系,且两者呈正相关(F=0.234,P=0.038)。造成这一现象的主要原因是:随着弯道曲线半径的减小,驾驶难度逐渐增大,驾驶人主动选择减小扫视幅度以快速获取足够的道路信息。
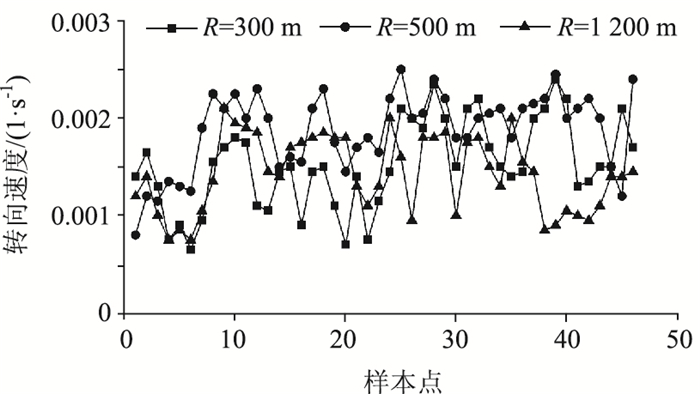
2.5 方向盘旋转率方向盘旋转率是对方向盘转向速度的描述,指的是方向盘每秒的转动比例。驾驶人在整个转向过程中的转弯稳定度与方向盘旋转率直接相关,因而方向盘旋转率也常被用来评价驾驶人弯道转向行为的安全性。对有效数据中46名被试驾驶人的平均方向盘旋转率进行统计,统计结果如图 6所示。
|
| 图 6 弯道路段驾驶人方向盘旋转率 Fig. 6 Steering velocity of driver on curve |
| |
从图 6可以发现,不同驾驶人的平均方向盘旋转率分布较为广泛。比较3个半径下的方向盘旋转率,可以看出随着弯道半径的增大,驾驶人每秒转动方向盘的幅度呈递减的态势。采用Pearson检验法分析方向盘旋转率与转弯半径间的关系,发现两者存在显著的线性关系,且两者呈负相关(F=-0.296,P=0.024)。
2.6 侧向加速度在平曲线路段上,车辆最常发生的事故为侧翻事故,而这类事故多是车辆的侧向稳定性较差造成的。因此,为反映车辆在不同半径圆曲线路段行驶时侧向稳定性,选取车辆侧向加速度作为侧向稳定性的表现指标,其具体数值可由模拟驾驶软件输出的瞬时车辆切向速度和行驶路段的圆曲线半径计算得到,具体计算公式如下:
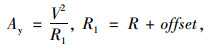
|
(1) |
式中,Ay为车辆侧向加速度;V为车辆切向速度;R1为圆曲线半径;R为匝道圆曲线半径;offset为车道偏移车道中心线的偏移量,左偏为正,右偏为负。
对有效数据中46名被试驾驶人的平均侧向加速度进行统计,统计结果如图 7所示。

|
| 图 7 弯道路段车辆侧向加速度 Fig. 7 Lateral acceleration of vehicle on curve |
| |
从图 7可以发现,不同驾驶人间的侧向加速度变化不明显,但驾驶人在不同半径下的侧向加速度差别较大,且随半径的增大,侧向加速度呈递减态势。用Pearson检验法分析侧向加速度与转弯半径间的关系,发现两者存在显著的线性关系,且两者呈负相关(F=-0.992,P=0.00)。
3 改进PSO优化BP神经网络预测算法现阶段关于驾驶人驾驶行为预测算法主要分为隐马尔科夫算法和神经元网络算法两种。其中,隐马尔科夫算法简单易行,在分析真实系统的时候表现出了巨大的价值,但此种方法受限于自身假设的过于简化,导致一个状态只依赖与其相关联的其他状态,难以保证预测的状态序列总体最优。相较而言,神经元网络算法具有更强的非线性拟合能力及自学习能力,能够更高效地实现多因子模型的建立[18]。因此本研究将借助已有的测试数据,使用反映非线性映射关系的BP神经网络方法,量化驾驶人视觉特性对弯道转向行为特性指标的影响,预测驾驶人弯道转向行为,进而较为直观地表现出其内在关系。
3.1 BP神经网络预测模型BP神经网络模型共有3层,输入层为驾驶人视觉特性,隐藏层有5个神经元,输出层为驾驶人弯道转向行为。输入层与隐藏层之间的连接权值为wjk,隐藏层与输出层之间的连接权值为wkr。在输入层输入样本,经隐含层激励作用,在输出层导出输出结果。检验输出结果是否符合模型误差要求,若输出结果误差大于期望误差,则采取反向传播修正的方法,对网络进行反复训练,最终使输出结果误差在模型的误差要求范围以内。
3.2 粒子群优化算法粒子群算法是由美国电器工程师Russell Eherhart和社会心理学家James Kenned提出的一种经典的群智能算法。其基本思想是:问题的候选解都是空间中的一个粒子的位置。每个粒子的适应度值都由一个优化函数决定,每个粒子的飞行方向与距离都由其速度决定。在求解过程中,粒子根据自身的最优解和当前最优粒子的最优解进行搜索,直至满足要求为止。
假设在一个M维空间中,有n个粒子组成种群X=(X1,X2, …, Xn)。其中每个粒子代表一个m维向量,粒子的位置p与速度v按式(2)进行更新:
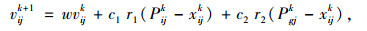
|
(2) |
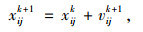
|
(3) |
式中,k代表当前迭代次数;w为惯性权重;j为维度;c1与c2是学习因子;r1,r2为随机数,迭代时需满足各项约束条件。
基本的PSO算法虽然具有算法简单、搜索速度快、搜索效率高、适用于实值型处理等优点,但其搜索过程受惯性权重w的影响极大。当惯性权重较大时,粒子的收敛速度较快但收敛精度不高;而当惯性权重较小时,粒子的收敛精度较高但收敛速度慢。这一问题的存在使得基本PSO算法在面对小样本训练中,难以帮助BP网络降低预测误差。因此,为了提高预测精度,使其能在小样本训练中发挥作用,本文将对PSO算法的惯性权重取值进行如下改进:
(1) 采用动态惯性权值
惯性权重取值的过大或过小只是网络训练精度不高的表象,而究其本质是在基本的PSO算法中,粒子对自身和全局环境认知分配不均。因此需采用可实时调整的动态惯性取值来获得更好的寻优结果。目前较为通用的做法是采用线性递减权值,即:
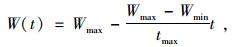
|
(4) |
式中,t为当前的迭代次数;Wmax是最大惯性权值;Wmin是最小惯性权值;tmax是最多迭代次数。
通过以上公式,可以在迭代初期取得较大的惯性权值,使得粒子在初期侧重于自身认知;在迭代末期,惯性权值随迭代过程不断减小,粒子侧重于全局认知,从而保证粒子对自身认知能力和全局认知能力的动态分配。
3.3 引入自适应方法采用动态惯性权值虽然能在一定程度上调整惯性权值,提高粒子的搜索效率与精度,但也存在一个弊端, 即在通过公式(4)来确定惯性权重变化的过程中,惯性权重的值都会越来越小, 且过程不可逆,易使粒子丧失自适应性。因此需引入比较公式来动态判别粒子状态并相应地调节权重取值。在粒子适应度值具有较大差异时适当减小惯性权重值,在粒子适应度值趋于一致时适当增加惯性权重值。
综合以上两个改进措施,得到惯性权重W如下表示:
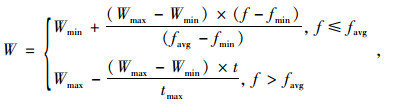
|
(5) |
式中,Wmax和Wmin分别为最大和最小惯性权值;favg和fmin分别为当前所有粒子的平均适应值和最小适应值;t和tmax分别为当前和最大迭代次数。
通过式(5)方法来对PSO算法的惯性权值进行设置,当粒子适应度的值小于平均适应度的值时,惯性权重较小,粒子具有较强的局部搜索能力,便于寻找最优解;当粒子适应度的值大于平均适应度的值时,惯性权重较大,粒子具有较强的全局搜索能力,可以更加快速地向最优解区域靠近。
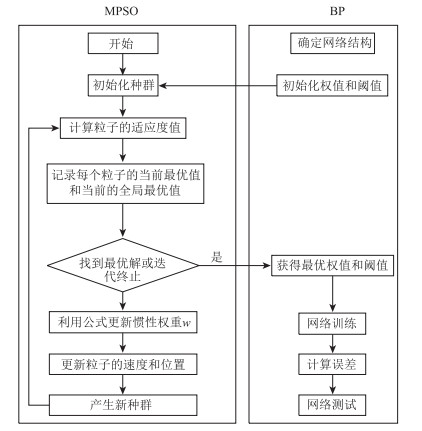
3.4 基于改进PSO的BP算法基于改进PSO的BP算法的核心思路为:通过改进的PSO算法来获取BP神经网络方法所需的权值和阈值。在训练过程中,选取BP神经网络的误差来作为改进PSO算法(MPSO)的适应值,迭代的终止条件由事先确定的最大迭代次数与误差范围共同决定。选取驾驶人瞳孔面积变化率、扫视速度、扫视幅度3个典型的视觉特征指标,构建如图 8所示的MPSO-BP算法。
|
| 图 8 MPSO-BP算法流程图 Fig. 8 Flowchart of MPSO-BP algorithm |
| |
如图 8所示,该算法由两部分构成,一部分是图中左侧的MPSO部分,另一部分是图中右侧所示的BP网络训练部分。对于MPSO部分,设置种群规模n=30,最大迭代次数K=100,粒子位置和速度区间分别为[-5, 5]和[-1, 1],加速因子c1=c2=2,r1,r2为0到1之间的随机数,惯性权值W按上文中给出的取值公式进行取值和变化调整;对于BP部分,算法共3层,输入向量为驾驶人视觉特性X=(X1,X2,X3)T,隐藏层有5个神经元,输出层为驾驶人弯道转向行为,训练次数取100,学习率取0.01,其他取值均取常规值。
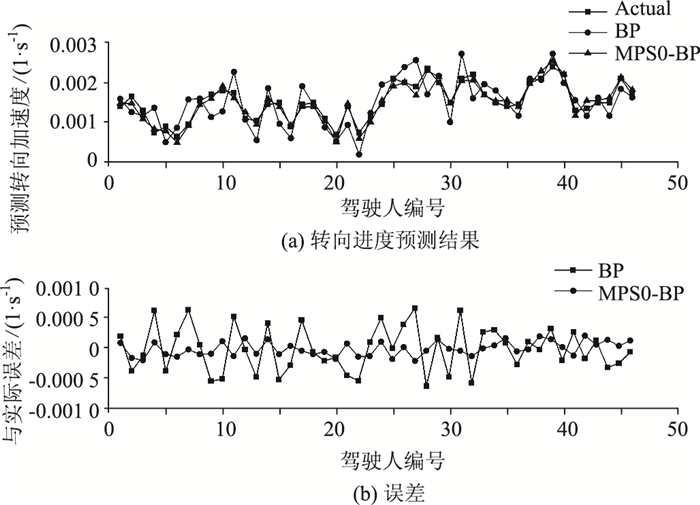
为了验证MPSO-BP算法对预测驾驶人弯道转向行为有效性,同时采用BP模型和运用MPSO-BP算法的模型完成驾驶人弯道转向行为的预测。对于BP模型,其参数设置与本研究方法的BP部分相同。采用经过全部训练集数据(46组)训练后的2种方法对驾驶人弯道转向行为测试数据进行预测,运用Matlab R2012b,编程实现MPSO-BP驾驶人弯道转向行为算法。考虑到视觉特性、驾驶人弯道转向行为均与弯道半径存在显著的线性相关关系,为证明预测方法的适用性,在300,500 m和1 200 m共3个转弯半径下分别进行预测。获得各方法的预测结果及误差如图 9~图 14所示。
|
| 图 9 转向速度预测结果及误差(300 m转弯半径) Fig. 9 Prediction result and errors of steering velocity (300 m radius) |
| |
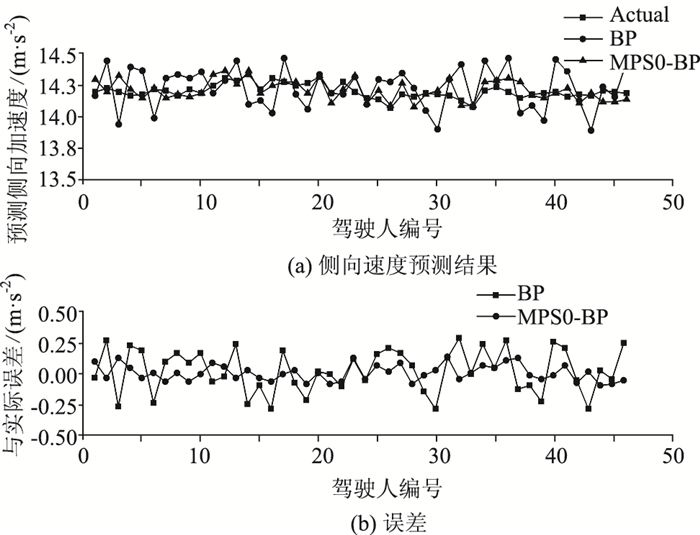
|
| 图 10 侧向加速度预测结果及误差(300 m转弯半径) Fig. 10 Prediction result and errors of lateral acceleration (300 m radius) |
| |
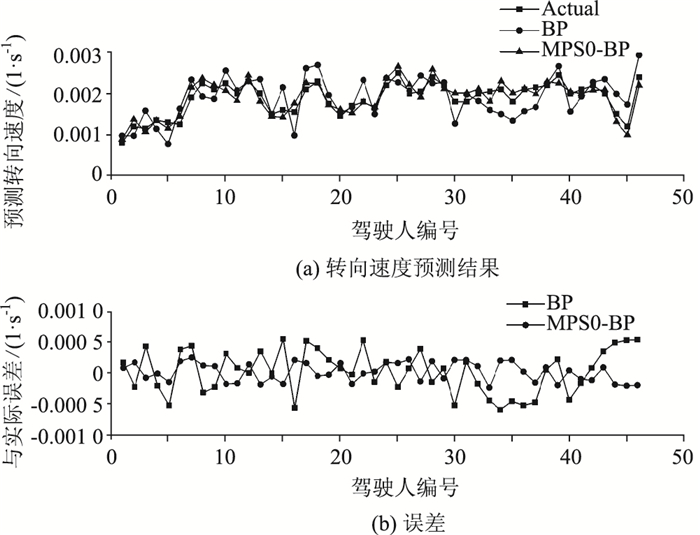
|
| 图 11 转向速度预测结果及误差(500 m转弯半径) Fig. 11 Prediction result and errors of steering velocity (500 m radius) |
| |
|
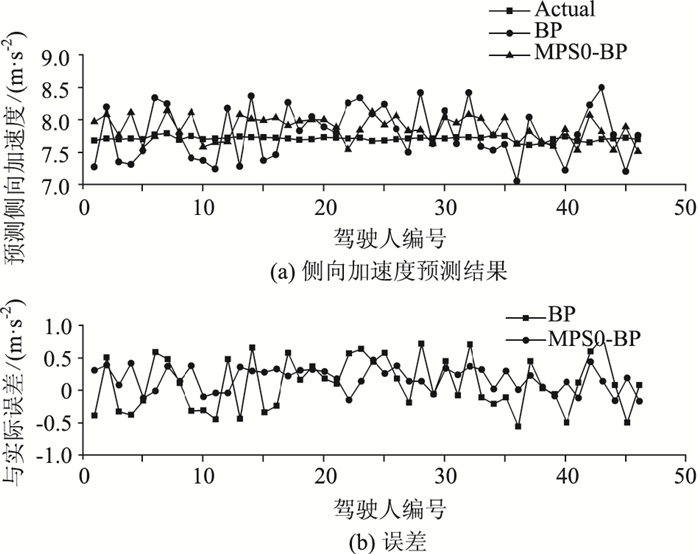
| 图 12 侧向加速度预测结果及误差(500 m转弯半径) Fig. 12 Prediction result and errors of lateral acceleration (500 m radius) |
| |
|
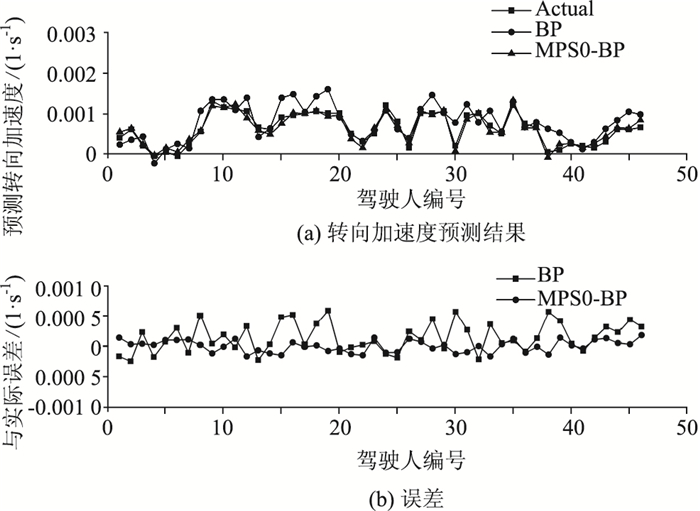
| 图 13 转向速度预测结果及误差(1 200 m转弯半径) Fig. 13 Prediction result and errors of steering velocity (1 200 m radius) |
| |
|
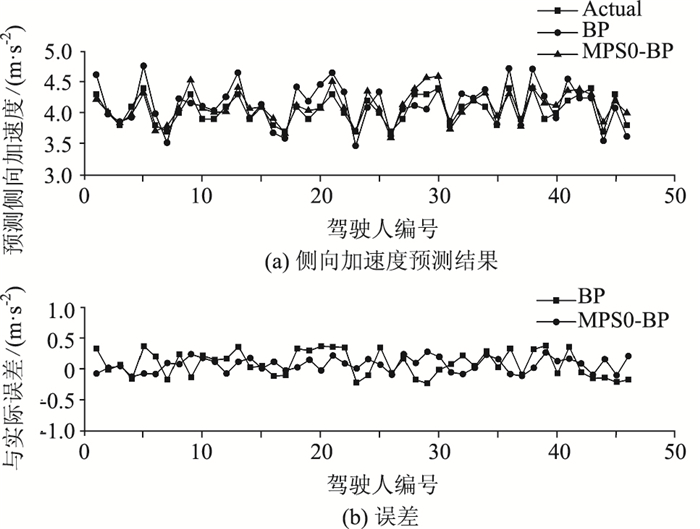
| 图 14 侧向加速度预测结果及误差(1 200 m转弯半径) Fig. 14 Prediction result and errors of lateral acceleration (1 200 m radius) |
| |
从图 9~图 14中可以看出,两种模型的预测结果都在真实结果的一定范围内浮动,反映出两者都可以在一定程度上反映驾驶人在转向速度和侧向加速度上的特点,证明了使用BP神经网络预测驾驶人弯道驾驶行为的可行性。但相比较而言,MPSO-BP模型在各转弯半径下的预测结果与驾驶人实际弯道驾驶行为的偏差均更小,模型预测精度更高,这主要是因为MPSO-BP的算法较好地解决了PSO中因粒子快速趋同效应而导致的误差较大问题,因而使得预测结果更加贴合真实情况。MPSO-BP算法在300 m, 500 m和1 200 m 3个半径下的预测结果表明:运用MPSO-BP算法可以在不同半径的水平上预测驾驶人弯道转向行为,预测模型具有较好的普适性。然而上述预测仍有进一步改进的空间,因现实道路中有道路状况差异、其他车辆干扰等因素影响,作为模型神经网络部分输入变量的驾驶人视觉特性指标还有进一步丰富的空间,还应进行多次反复的试验并进行比对研究。
4 结论本文借助模拟驾驶仿真平台,设计了包括3种半径长度的曲线路段仿真试验场景,并对比不同场景下驾驶人视觉特性和弯道转向行为的差异,对样本影响因子相关性作了说明。研究发现:驾驶人弯道的视觉特性指标与弯道半径间存在显著的线性关系,驾驶人瞳孔面积变化率与弯道半径呈负相关而驾驶人扫视速度和扫视幅度与弯道半径呈正相关,即半径越大,驾驶人的压力越小,获得的道路信息也越多。从驾驶人弯道转向行为的角度看,随着弯道半径的增加,方向盘旋转率和侧向加速度都有变小的趋势,反映出驾驶人对车辆的掌控程度有所上升,驾驶的安全性有显著提高。此外,本文还使用基于改进PSO的BP神经网络建立了以驾驶人视觉特性为输入变量的弯道转向行为预测模型,以期通过分析驾驶者弯道视觉特性与弯道转向行为间的关系,预测驾驶人弯道转向行为。为解决运用BP神经网络在预测驾驶人弯道转向行为中存在的易陷入局部极小值的问题并进一步提高收敛速度,在PSO算法中引入动态惯性权值和自适应方法,提出了一种基于改进PSO算法优化BP神经网络的驾驶人弯道转向行为预测方法,并与BP模型进行了比较。结果表明:所提出的方法能够较好地解决预测模型的局部极小缺陷,极大地提高模型的收敛速度。利用MPSO-BP模型可准确预测驾驶人弯道转向行为,所得结果可作为对弯道驾驶人行为的预判和引导的依据。后续研究将采用机器学习方法针对城市区域不同道路条件(如立交、坡道、交叉口等)建立驾驶人转向行为预测模型,寻求更有效的模型设计方法,提高对驾驶人转向行为的预测精度。
| [1] |
李作敏. 交通工程学[M]. 2版. 北京: 人民交通出版社, 2000., 2000: 200. LI Zuo-min. Traffic Engineering[M]. 2ed ed. Beijing: China Communications Press, 2000. |
| [2] |
赵炳强. 驾驶员动态视觉特征及其影响[J]. 公路交通科技, 1998, 15. ZHAO Bing-qiang. Driver's Dynamic Visual Characters and Its Effects[J]. Journal of Highway and Transportation Research and Development, 1998, 15(S1): 102-104. |
| [3] |
LEE D, KOGA T, KOZAKI M, et al. A Research to Effective Signboard Cognition during Driving Situation by Using Driving Simulator[C]//The Transportation and Logistics Conference. New York: [s.n.], 2015: 343-346.
|
| [4] |
SALVUCCI D D. Distraction Beyond the Driver: Predicting the Effects of In-vehicle Interaction on Surrounding Traffic[C]//Proceedings of the SIGCHI Conference on Human Factors in Computing System. New York: ACM, 2013: 3131-3134.
|
| [5] |
YANG H H. Driver Models to Emulate Human Anomalous Behaviors Leading to Vehicle Lateral and Longitudinal Accidents[D]. Ann Arbor: University of Michigan, 2010.
|
| [6] |
冀秉魁.基于驾驶员视觉特性的驾驶行为预测方法研究[D].长春: 吉林大学, 2014. JI Bing-kui. Research on Driving Behavior Prediction Method Based on Driver's Visual Characteristics[D].Changchun: Jilin University, 2014. |
| [7] |
ABDUL W, WEN T G, KAMARUDDIN N. Understanding Driver Behavior Using Multi-dimensional CMAC[C]//20076th International Conference on Information, Communications & Signal Processing. Singapore: IEEE, 2008: 1-5.
|
| [8] |
BELLA F. Driver Perception Hypothesis:Driving Simulator Study[J]. Transportation Research Part F:Traffic Psychology, 2014, 24: 183-196. |
| [9] |
赵晓华, 关伟, 黄利华, 等. 急弯处警告标志位置对驾驶行为的影响研究[J]. 公路交通科技, 2014, 31(9): 101-107. ZHAO Xiao-hua, GUAN Wei, HUAN Li-hua, et al. Research on Influence of Warning Sign Position in Sharp Curve on Driving Behavior[J]. Journal of Highway and Transportation Research and Development, 2014, 31(9): 101-107. |
| [10] |
MOON S, YI K. Human Driving Data-based Design of a Vehicle Adaptive Cruise Control Algorithm[J]. Vehicle System Dynamics, 2008, 46(8): 661-690. |
| [11] |
ODHAMS A M C, COLE D J. Identification of the Steering Control Behavior of Five Test Subjects Following a Randomly Curving Path in a Driving Simulator[J]. International Journal of Vehicle Autonomous Systems, 2014, 12(1): 44-64. |
| [12] |
张璇, 程敏熙, 肖凤平. 利用Origin对数据异常值的剔除方法进行比较[J]. 试验科学与技术, 2012, 10(1): 74-76. ZHANG Xuan, CHENG Min-xi, XIAO Feng-ping. Origin Used in Comparison the Methods of Eliminating the Excrescent Data[J]. Experiment Science and Technology, 2012, 10(1): 74-76. |
| [13] |
陈亮, 熊坚, 郭凤香, 等. 基于视觉及认知的驾驶模拟器图像标定方法[J]. 中国公路学报, 2017, 30(1): 129-135. CHEN Liang, XIONG Jian, GUO Feng-xiang, et al. Image Calibration Method of Driving Simulator Based on Vision and Cognition[J]. China Journal of Highway and Transport, 2017, 30(1): 129-135. |
| [14] |
郭忠印. 道路安全工程[M]. 北京: 人民交通出版社, 2012. GUO Zhong-yin. Road Safety Engineering[M]. Beijing: China Communications Press, 2012. |
| [15] |
吕杰锋, 陈建新, 徐进波. 人机工程学[M]. 北京: 清华大学出版社, 2009. LÜ Jie-feng, CHEN Jian-xin, XU Jin-bo. Ergonomics[M]. Beijing: Tsinghua University Press, 2009. |
| [16] |
QI Wei-wei, PEI Yu-long, SONG Mo, et al. Pattern Analysis of Driver's "Pressure-state-response" in Traffic Congestion[J]. Discrete Dynamics in Nature and Society, 2013, 2013(6): 1-11. |
| [17] |
李勇, 阴国恩, 陈燕丽. 阅读中疲劳、心理负荷因素对瞳孔大小的调节作用[J]. 心理与行为研究, 2004, 2(3): 545-548. LI Yong, YIN Guo-en, CHEN Yan-li. the Regulating Effect of Fatigue and Mental Load on Pupil Size in Text Reading[J]. Studies of Psychology and Behavior, 2004, 2(3): 545-548. |
| [18] |
李松, 刘力军, 解永乐. 遗传算法优化BP神经网络的短时交通流混沌预测[J]. 控制与决策, 2011, 26(10): 1581-1585. LI Song, LIU Li-jun, XIE Yong-le. Chaotic Prediction for Short-term Traffic Flow of Optimized BP Neural Network Based on Genetic Algorithm[J]. Control and Decision, 2011, 26(10): 1581-1585. |
 2019, Vol. 36
2019, Vol. 36
