扩展功能
文章信息
- 李建强
- LI Jian-qiang
- 竞争条件下公共交通最优出行方式选择
- Selection of Optimal Travel Mode of Public Transport under Competitive Condition
- 公路交通科技, 2019, 36(10): 121-127
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(10): 121-127
- 10.3969/j.issn.1002-0268.2019.10.016
-
文章历史
- 收稿日期: 2018-05-16
随着交通方式的多样化,城市内常常存在多种交通方式共线运行的局面。对于两种或以上交通方式共线运行的线路区间可以看作是多种交通方式的竞争运行,在这种竞争条件下出行者的出行方式选择是首先需要考虑的问题。轨道交通因为其速度快、可靠性、舒适性等优点成为城市居民出行者首选的交通出行方式。但是部分出行者忽略了乘坐轨道交通会引发进站安检等额外出行成本,导致其出行效率降低。除此之外,轨道交通站点的能级大小相对固定,难以满足日趋增长的客流需求[1],因此站点内的拥堵和安全问题日益显著,造成公交系统整体运行效率下降[2]。针对该问题,若能有效地引导出行者的交通方式选择,使各交通出行方式的分担比率达到最优,则可以提高公交系统的协调程度和交通资源的配置优化。
多种交通方式并存下的出行方式选择可以归结为竞争条件下的出行方式选择问题[3]。针对此类问题,永贵[4]研究了地铁和驾车两种方式在不同的收费策略下的选择问题;慈玉生[5]运用Lotka-Volterra模型描述了公共交通和私人交通的矛盾演化问题;刘贤腾[6]提出了“生态位”概念,指出各种出行方式的“生态位”存在重叠的竞争关系,上述研究主要针对私人和公共交通的竞争关系分析,但并非所有出行者都拥有私人交通工具,故上述研究并不具有普遍适用性。而对于交通工具可获得性较强的公共交通间的竞争关系研究有:张杰林[7]选取出行时耗和费用为建模的主变量,将其作为效用函数,研究轨道交通和常规公交在共线情况下的竞争关系;马超群[8]将广义费用函数代替效用函数,利用Logit模型,探求二者的客流分担率问题;Kuan[9]等在客流竞争的基础上,利用启发式的遗传算法和蚁群优化解决衔接公交的设计问题以实现二者的互补。Ahmadreza Faghih-Imani[10]等通过对纽约市的数据调查,分析纽约市出租车和自行车共享系统(BSS)在出行时间方面的竞争情况,认为在交通拥堵区域使用BBS系统更加节省时间成本;Giulio Erberto Cantarella[11]等采用多层前馈网络模型对交通出行方式进行选择和预测;Daniel A. RodrÍguez[12]等将物理环境等条件也列为对出行者方式选择的影响因素之一。但目前成果均从宏观角度进行分析,就个体角度而言,研究尚不充分,且涉及的交通方式较为单一,难以满足目前多种交通方式并存的复杂情况。随着新型交通方式的普及,个体出行方式的选择问题趋于复杂化,影响个体交通方式选择的因素众多,其中一个很重要的影响因素是出行距离,即出行距离不同时,交通出行方式的选择意愿具有明显差异[6, 13-16]。
针对现有研究的不足和相关需求,本研究引入经济学概念—规模效应,从个体角度出发,以出行距离为已知变量,个体出行成本为研究对象,通过假设出行者为理性人(理性人总是以最小的代价获取最大的利益),综合考虑各种交通出行方式的固定出行成本和可变出行成本,分析平均出行总成本和出行距离之间的关系,以确定不同出行距离下出行者的最优出行方式,通过给予出行者有效的交通出行方式选择引导,对竞争条件下各交通方式的客流量进行优化,从而实现各种交通资源的合理配置,以此提高整体的运营效率。
1 出行成本的规模效应分析规模效应现象是指生产规模扩大使经济效益提高的现象[17]。由于生产成本等于固定成本和可变成本之和,扩大生产规模使可变成本同比例增加,而固定成本相对保持不变,最终将导致单位成本下降,经济效益提高。按照经济学概念,若以出行距离为产出量,以广义费用为成本,则平均出行成本可以表示为:
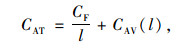
|
(1) |
式中,CAT为平均出行成本,表示出行效益,平均出行成本越低,出行效益越高;CF为固定出行成本,是指因出行行为产生的一系列必需的程序型行为(例如:地铁进出站等,统称“出行程序”)所引发的广义费用,取值与交通出行方式有关,出行方式一旦确定,固定出行成本随之确定;l为出行距离;CF/l为单位化的固定出行成本,即平均固定出行成本,从形式上看其是反比例函数,在(0, +∞)为减函数,这表示随着出行距离的增加,平均固定出行成本呈现不断降低的趋势;CAV(l)为平均可变出行成本,表示出行者在行程中产生的单位广义费用,其取值不仅与出行方式有关,也与出行距离有关(表现在出行距离较远时,由于旅途过长导致的出行者心理和生理耐受能力下降,使得广义费用增加)。
式(1)整体描述了在不同出行距离下平均出行成本的变化规律。由于不同交通出行方式的出行特征相异,其规模效应对应的出行距离也各不相同,因此本研究针对不同的出行方式,以出行距离为已知变量,通过分析比选各种交通出行方式在不同出行距离下的平均出行成本,选取成本最低的出行方式,以优化出行方式选择。
针对竞争条件的具体情况,有以下基本假设:一是假设在出行中各种交通出行方式均可一次到达,无需换乘,即假设各种公共交通出行方式处于共线情况下;二是忽略个体的差异性,从整体客观角度进行分析。
2 出行活动的影响因素分析居民出行方式以轨道交通、常规公交、私家车、摩托车、电动自行车、自行车和步行为主[18-19]。本研究以交通工具的可获得性为筛选条件,最终选定轨道交通、常规公交、共享单车(公共自行车)等常用公共交通和步行共4类出行方式为研究对象。
2.1 人体活动疲劳积累由于交通出行的影响因素众多,其中出行过程中运动性疲劳和心理疲劳积累带来的人体抗阻能力下降现象不可忽略。且在出行活动中人体能量消耗规律较为复杂[20],人体活动持续时间与负荷(即人体抗阻能力)之间为反比例关系,而出行时间与出行距离为正比例关系[21]。为满足客观事实且尽量简化运算,本研究引入疲劳惩罚系数μ,以修正出行者因人体抗阻能力下降导致出行效率降低的误差。惩罚原则为:当疲劳影响因素为0时,疲劳惩罚系数μ为1,即不惩罚;当疲劳影响因素持续作用时,疲劳惩罚系数μ按出行方式的不同以不同的速率正比例增加。综上所述,可根据产生疲劳的不同,将交通出行方式分为两类,其一是运动性出行方式,包括步行和共享单车,特点是可引发明显的运动性疲劳,对疲劳惩罚系数的影响指标为出行距离l,表达式为:μ=1+l/lmax;其二是静态出行方式,包括常规公交和轨道交通,特点是无明显运动性疲劳,心理疲劳为主要影响原因,对疲劳惩罚系数的影响指标为行程总时间T,表达式为:μ=1+T/lmax。
2.2 交通控制和站点停靠时间延误交通控制和(常规公交和轨道交通)站点停靠的时间延误具有相同的特点,即延误时间为出行距离的分段函数,但若假设单个交叉口(站点)延误的时间相同,则可看作交叉口(站点)数量和出行距离之间为线性变化,因此,本研究对全国主要大型城市进行道路交叉口(常规公交和轨道交通站点)数量和出行距离的分层抽样测量分析,并利用Origin 9.0软件对数据进行线性拟合,拟合结果如表 1所示。
| 影响因素 | 斜率a | 截距b | 可决系数R2 |
| 交叉口个数 | 0.438 9 | -0.061 9 | 0.993 3 |
| 轨道交通站点个数 | 1.078 5 | 0.090 5 | 0.997 6 |
| 常规公交站点个数 | 0.633 4 | -0.053 0 | 0.997 2 |
由于出行距离l的数据存在误差,因此本研究选择交叉口(站点)数量为拟合方向。从表 1可以看出,出行距离与3种影响因素的数量变化均存在线性关系(3者线性拟合的可决系数R2均接近于1),其中斜率a表示相邻交叉口(站点)之间距离。b表示测量起点距离编号为0的交叉口(站点)的距离,在实际应用中应该舍掉该值,即认为编号为0的交叉口(站点)的出行距离l为0 km。因此二者之间的关系可以表示为l=aN,即N=l/a,若假设单个交通控制和站点停靠的时间延误为常数Ta(可通过数据调查取平均值得到),则交通控制延误和站点延误总成本时间可以表示为:
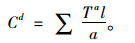
|
(2) |
由于步行不需要交通工具的参与,因此步行成本只包含可变出行成本,其成本构成是步行时耗和由交通控制导致的额外时耗,其成本函数为:
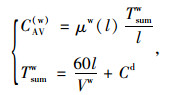
|
(3) |
式中,CAV(w)为步行条件下的平均可变出行成本,单位为min/km;μw为步行的疲劳惩罚系数,与步行距离有关;Tsumw为步行总时间;Vw为步行速度;60为单位换算值;Cd为交通控制的交叉口延误和站点延误时耗。
3.2 共享单车共享单车(公共自行车)由于车辆获取容易和骑行方便灵活而成为出行者在短距离出行中的重要选择,其出行成本包括寻找车辆等的固定出行成本和骑行过程中的可变出行成本,成本函数具体可以表示为:
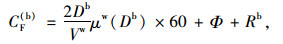
|
(4) |
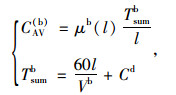
|
(5) |
式中,CF(b)为共享单车的固定出行成本;2Db/Vw为起讫点两端到共享单车接驳点(即共享单车电子围栏或公共自行车桩)的时耗;Db为单侧接驳距离之和,由文献[22]可知公共自行车网点的步行吸引范围为0.19 km,假设出行者距离起讫点呈均匀分布,因此起讫点两端的接驳距离可取为吸引范围的1/2,若有调查数据结果,应当按照实际调查数据取值;μw(Db)为接驳距离的步行惩罚系数;Φ为使用智能手机定位车辆和开锁等其他时耗;Rb为使用共享单车的经济费用,通过市场调查可得经济费用为2元/h,根据当地的人均时薪换算成时间费用进行统一计算; CAV(b)为使用共享单车的平均可变出行成本;μb(l)为共享单车方式的耐受阻力系数;Tsumb为骑行总时间,包括骑行时间和交通控制延误时间;Vb为骑行速度;Cd意义同上。
3.3 常规公交常规公交作为城市最常见的公共交通出行方式,具有站点覆盖率高、线路灵活等优势,常规公交出行成本包括出行程序的固定出行成本和行车期间的可变出行成本,成本函数量化为:
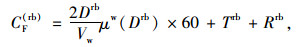
|
(6) |
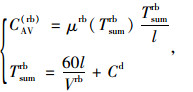
|
(7) |
式中,CF(rb)为常规公交的固定出行成本;Drb为出行起讫点单侧到公交接驳站点的距离,以5 min的步行距离作为公交的最远站点服务半径,假设出行者距离起讫点呈均匀分布,因此起讫点两端的接驳距离可取为吸引范围的1/2;μw(Drb)为接驳距离的步行惩罚系数;Trb为候车时间;Rrb为经济费用,即公交的票价。CAV(rb)为常规公交的可变出行成本;μrb为常规公交的耐受阻力系数;Tsumrb为乘车期间的总时间;Vrb为公交的行驶速度,一般取15 km/h;Cd意义同上。
3.4 轨道交通轨道交通的出行成本分为固定出行成本和可变出行成本,固定出行成本包括出行起讫点两端接驳时间、进出时间、购票时间、安检时间、过检票机时间和候车时间,成本函数量化为:
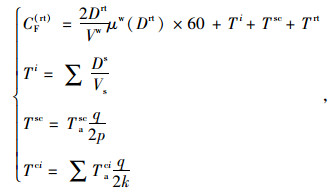
|
(8) |
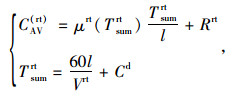
|
(9) |
式中,CF(rt)为轨道交通的固定出行成本;Drt为出行起讫点到轨道交通接驳点两端的距离,采用轨道交通站点服务半径作为最远接驳距离,假设出行者距离起讫点呈均匀分布,因此起讫点两端的接驳距离可取为吸引范围的1/2;μw(Drt)为接驳距离的步行惩罚系数;Ti为进出站的时间;Ds为进出站的不同路面情况距离,分为自动扶梯路面、楼梯和平面3类,由于轨道交通站点的站房具有类似的结构,因此进出站取值相同;Vs为对应的行进速度;Tsc为安检所需的时间;Tasc为一个人安检所需时间,可通过调查平均值求得;q为进站的客流量,具体可通过调查求得;p为安检机的台数;Tci为进出站过检票机的时间;Taci为个人过检票机的时间;k为进出站口检票机的数量;Trt为候车时间,取为发车间隔的一半。CAV(rt)为轨道交通的可变出行成本;Rrt为轨道交通的平均单位公里票价,其他指标量化方法与常规公交类似。
4 最优出行方式确定 4.1 单一出行方式(包含步行的接驳):单一出行方式包括步行和以步行方式(此处步行不看作独立的)进行接驳的其他一种出行方式的情况,其选择目标函数可以表示为:
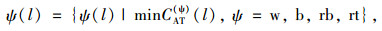
|
(10) |
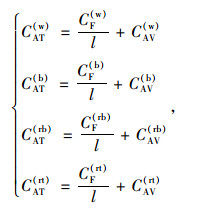
|
(11) |
式中,ψ为出行方式的种类,w,b,rb,rt分别为步行、共享单车、常规公交、轨道交通方式,进行对式(11)的求解可以得到不同出行距离下平均出行成本最低的交通出行方式,其结果应为若干个距离区间,在区间内对应的平均出行成本最低方式即为最优出行方式,下面通过实例进行详细说明。
4.2 多种类组合联运出行方式费用说明:对于给定出行距离l,根据式(11):单一最优出行方式的平均出行成本为:
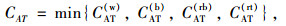
|
(12) |
而多种类组合联运出行方式的平均出行成本为
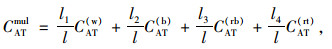
|
(13) |
其中,
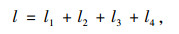
|
(14) |
由此可得,
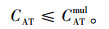
|
(15) |
在多种出行方式共线竞争的情况下,由于出行距离不变,在一次出行中引入新的交通方式(除步行外),会造成固定出行成本总量的增加,对其中的每种出行方式而言,其集聚距离减少,规模效应难以体现;步行虽然没有固定成本,但由于步行距离分担了出行距离,导致其他出行方式的集聚距离变少,规模效应减弱。综上所述,多种类组合联运出行方式其平均出行成本高于单一出行方式的平均出行成本。
5 实例分析本研究以成都市某轨道交通枢纽周边区域为例进行说明。该交通枢纽位于城市西北片区,距离市中心14 km。枢纽区域内包含了地铁、常规公交、共享单车等城市交通出行方式。为了确定区域内在不同出行距离下的最优出行方式,合理配置交通资源,按照上述出行成本指标进行相关数据的调查并进行计算,对于出行者可忍受步行距离等指标采用问卷调查的方法,将距离分为不同的区间,调查每个区间的人数分布情况,调查结果以人数比例为权重进行加和,在调查中,调查人数为202人,有效问卷186份。计算结果如表 2所示。
| 指标 | 步行/km | 共享单车/km | 常规公交/min | 地铁/min |
| 可忍受距离/时间 | 1.65 | 3.50 | 23.20 | 28.9 |
根据表 2可得各种交通出行方式的疲劳惩罚系数,同时根据调查结果输入其他参数为:Φ=2 min;Trb=4 min;Rrb=2元;Ti=8 min;Tasc=10 s; q=206人;p=2台;Taci=3 s;k=10台;Trt=4 min,同时,通过调查可得:常规公交站点吸引范围为500 m,轨道交通站点吸引范围取800 m,最终经过计算,得到每种出行方式的出行成本如表 3所示。
| 出行方式 | 固定出行成本 CF/min |
平均可变出行 成本CAV/min |
平均总成本/min |
| 步行 | 0 | 9.78l+19.56 | 9.78l+19.56 |
| 共享单车 | 8.17 | 6.02l+12.06 | 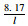 +6.02l+12.06 +6.02l+12.06 |
| 常规公交 | 18.14 | 1.27l+18.45 | 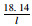 +1.27l+18.45 +1.27l+18.45 |
| 轨道交通 | 32.6 | 0.09l+19.88 | 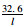 +0.09l+19.88 +0.09l+19.88 |
由表 3可知,步行、共享单车、常规公交、轨道交通等出行方式的固定出行成本依次增加,实际表示其出行行为中的程序性活动愈加繁琐。从平均可变出行成本角度分析,其形式均为距离l的一次式,其中比例系数表示在行程中疲劳产生的速率,常数项表示速度、交叉口和站点时间延误等固定指标(轨道交通还包含了票价)。各出行方式的平均总成本变化曲线如图 1所示。
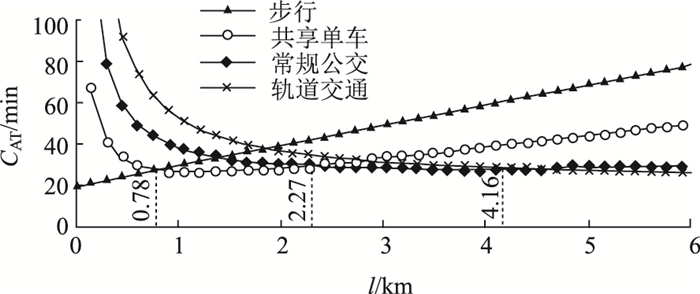
|
| 图 1 各出行方式的平均出行成本曲线 Fig. 1 Average travel cost curve of each travel mode |
| |
从图 1可以看出,除步行外,各出行方式的平均出行成本均呈现先下降、后上升的趋势(由于图的大小限制,常规公交和轨道交通的上升区域并不明显),故存在出行效益最高的出行距离点,这是由于固定出行成本和疲劳因素的客观存在导致的。并且由表 2可知,各出行方式的固定出行成本值和疲劳产生速率大体为负相关,因此各出行方式的平均成本曲线一定存在交点,从而形成4个出行距离区间(图 1),即为各出行方式的最优距离区间(由于区间边界两种出行方式成本相等,故本研究均给出闭区间),如表 4所示。
| 出行方式 | 最优区间/km |
| 步行 | (0, 0.78] |
| 共享单车 | [0.78, 2.27] |
| 常规公交 | [2.27, 4.16] |
| 轨道交通 | [4.16, +∞) |
最优距离区间内各出行方式在区间内其成本取得最低值。值得一提的是,区间[2.27, 4.16]虽然为常规公交的最优距离区间,但轨道交通的平均总出行成本值与其相差较小,难以使出行方式选择有较大的差别,因此可根据常规公交的特点进行一些优化,提高竞争力,例如降低发车间隔、使用舒适度较高的车型等;同时尽量减少常规公交与轨道交通的共线情况,以充分发挥常规公交的线路灵活等优势,并控制线路长度,定位于客流在地块和轨道交通站点间的接驳,从而减少资源的浪费,实现二者间的互补。
6 结论本研究引入固定出行成本和可变出行成本等概念对竞争条件下不同出行距离的交通出行方式选择问题进行了探讨,提出了出行成本在出行距离增加的情况下具有与生产成本类似的规模效应,并通过对步行、共享单车、常规公交和轨道交通4类常用出行方式的成本进行量化分析,确定了各种出行方式的最优出行区间,为交通资源的合理配置提供了理论依据。主要结论为:
(1) 按照出行距离递增,其最优出行方式依次为步行、共享单车、常规公交、轨道交通。
(1) 步行、共享单车、常规公交和轨道交通的固定出行成本依次递增,其意义是出行行为中的程序性活动愈加繁琐。
(2) 在竞争条件下,各出行方式的出行效益最高点不一致,共享单车、常规公交和轨道交通随出行距离依次升高(步行无效益最高点)。
(3) 常规公交在其最优区间内,成本值与轨道交通相差较小,难以让出行选择有实质性的差别。
由于目前研究对人体疲劳衰减数学过程的了解知之甚少,故本研究在出行成本量化中的疲劳惩罚系数由调查问卷所得,带有一定的主观色彩;本研究笼统地将经济费用统筹考虑,没有详细分析个体的金钱观等主观因素,在实际操作中可对时耗和经济费用单独列开,仅为出行者提供一个建议参考值,以达到更好的引导行为。
| [1] |
吴娇蓉, 陈小鸿. 轨道网络形成期轨道交通客流培育与聚集策略研究[J]. 武汉理工大学学报:交通科学与工程版, 2009, 33(2): 211-214. WU Jiao-rong, CHEN Xiao-hong. Research on the Passenger Cultivation and Gather Strategy in the Railway Network Form Period[J]. Journal of Wuhan University of Technology:Traffic Science and Engineering Edition, 2009, 33(2): 211-214. |
| [2] |
冷彪, 赵文远. 基于客流数据的区域出行特征聚类[J]. 计算机研究与发展, 2014, 51(12): 2653-2662. LENG Biao, ZHAO Wen-yuan. Region Ridership Characteristic Clustering Using Passenger Flow Data[J]. Journal of Computer Research and Development, 2014, 51(12): 2653-2662. |
| [3] |
过秀成, 王炜, 吕慎. 基于合作竞争类OD的轨道客流预测方法研究[J]. 公路交通科技, 2000, 17(4): 57-59, 63. GUO Xiu-cheng, WANG Wei, LÜ Shen. Study on URT's Forecast Model on Cooperant and Competitive OD Matrix[J]. Journal of Highway and Transportation Research and Development, 2000, 17(4): 57-59, 63. |
| [4] |
永贵, 黄海军. 竞争交通系统中异质性用户的出行方式选择[J]. 系统工程理论与实践, 2016, 36(9): 2320-2327. YONG Gui, HUANG Hai-jun. Modal Split in a Competitive System of Transit and Highway with Heterogeneous Users[J]. Systems Engineering-Theory And Practice, 2016, 36(9): 2320-2327. |
| [5] |
慈玉生, 赵家发, 吴丽娜. 基于Lotka-Volterra的城市客运走廊机动化交通方式竞争模型[J]. 交通运输系统工程与信息, 2017, 17(3): 39-45, 52. CI Yu-sheng, ZHAO Jia-fa, WU Li-na. Lotka-Volterra-based Competition Mode of Transportation in Urban Passenger Corridor[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(3): 39-45, 52. |
| [6] |
刘贤腾. 城市交通方式竞争态势及来自生态学的理论启示[J]. 城市规划学刊, 2012(5): 66-75. LIU Xian-teng. An Analysis on the Competitive Tension of Travel Modes and the Heuristic Thoughts from Ecology[J]. Urban Planning Forum, 2012(5): 66-75. |
| [7] |
张杰林, 李铁柱. 基于竞争模型的轨道交通与常规公交共线分析[J]. 交通信息与安全, 2014, 32(4): 108-112, 118. ZHANG Jie-lin, LI Tie-zhu. Urban Rail Transit and Bus Collinear Analysis Based on Competition Model[J]. Journal of Transport Information and Safety, 2014, 32(4): 108-112, 118. |
| [8] |
马超群, 王玉萍, 陈宽民. 城市轨道交通与常规公交之竞争模型[J]. 交通运输系统工程与信息, 2007, 7(3): 140-143. MA Chao-qun, WANG Yu-ping, CHEN Kuan-min. Competition Model between Urban Rail and Bus Transit[J]. Journal of Transportation Systems Engineering and Information Technology, 2007, 7(3): 140-143. |
| [9] |
KUAN S N, ONG H L, NG K M. Solving the Feeder Bus Network Design Problem by Genetic Algorithms and Ant Colony Optimization[J]. Advances in Engineering Software, 2006, 37(6): 351-359. |
| [10] |
FAGHIH-IMANI A, ANOWAR S, MILLER E J, et al. Hail a Cab or Ride a Bike? A Travel Time Comparison of Taxi and Bicycle-sharing Systems in New York City[J]. Transportation Research Part A Policy & Practice, 2017, 101: 11-21. |
| [11] |
CANTARELLA G E, DE LUCA S. Multilayer Feedforward Networks for Transportation Mode Choice Analysis:An Analysis and a Comparison with Random Utility Models[J]. Transportation Research Part C:Emerging Technologies, 2005, 13(2): 121-155. |
| [12] |
RODRIGUEZ D A, JOO J. The Relationship between Non-motorized Mode Choice and the Local Physical Environment[J]. Transportation Research Part D:Transport & Environment, 2004, 9(2): 151-173. |
| [13] |
张昱, 刘学敏, 张红. 城市慢行交通发展的困境与思路[J]. 城市发展研究, 2014, 21(6): 113-116. ZHANG Yu, LIU Xue-min, ZHANG Hong. Dilemmas and Strategies for the Development of Urban Non-notorized Travel[J]. Urban Development Studies, 2014, 21(6): 113-116. |
| [14] |
郝忠娜, 何玉宏. "新地铁时代"常规公交的扬长避短与创新优化[J]. 上海城市管理, 2013, 22(2): 59-62. HAO Zhong-na, HE Yu-hong. Pros and Cons of Regular Traffic and Transportation and Innovative Improvement in New Metro Age[J]. Shanghai Urban Management, 2013, 22(2): 59-62. |
| [15] |
陈鹏, 张璋, 胡啸峰, 等. 影响城市轨道交通安检速度的乘客特征分析[J]. 城市轨道交通研究, 2016, 19(5): 5-9. CHEN Peng, ZHANG Zhang, HU Xiao-feng, et al. Analysis of Passenger Behaviors Impacting on Subway Station Security Test[J]. Urban Mass Transit, 2016, 19(5): 5-9. |
| [16] |
孙连娇, 戢晓峰, 陈方. 欠发达地区中长距离出行方式选择行为机理研究[J]. 公路交通科技, 2019, 36(1): 131-137. SUN Lian-jiao, JI Xiao-feng, CHEN Fang. Study on Travel Mode Choice Mechanism of Middle and Long Distance in Underdeveloped Areas[J]. Highway Traffic Science And Technology, 2019, 36(1): 131-137. |
| [17] |
张方, 陈凯. 运输成本、规模效应与区域经济差距:以辽宁省为例[J]. 东北大学学报:自然科学版, 2018, 39(2): 293-296. ZHANG Fang, CHEN Kai. Transportation Cost, Scale Effect and Regional Economic Disparity:Taking Liaoning as an Example[J]. Journal of Northeastern University:Natural Science Edition, 2018, 39(2): 293-296. |
| [18] |
赵林, 吴海俊, 姜恒, 等. 迁安市居民出行调查与交通特性分析[J]. 道路交通与安全, 2014, 14(5): 39-43. ZHAO Lin, WU Hai-jun, JIANG Heng, et al. Research on the Travel Survey of Residents and Characteristics in Qian'an[J]. Road Traffic & Safety, 2014, 14(5): 39-43. |
| [19] |
蒋梦帆, 朱查松, 刘健枭.共享单车影响下的居民出行行为研究——以厦门市思明区为例[C]//2017中国城市规划年会.北京: 中国建筑工业出版社, 2017: 15. JIANG Meng-fan, ZHU Zha-song, LIU Jian-xiao. Study on Residents' Travel Behaviors under Influence of Shared Bicycle: A Case Study of Siming District, Xiamen City[C]//Annual Conference of 2017 China Urban Planning. Beijing: China Architecture & Building Press, 2017: 15. |
| [20] |
KOLBL R, HELBING D. Energy Laws in Human Travel Behaviour[J]. New Journal of Physics, 2003, 5(48): 1-4812. |
| [21] |
蔡启明. 人体体力极限负荷试验研究[J]. 系统工程学报, 1995, 10(3): 75-81. CAI Qi-ming. Study on Testing the Limit Load of the Humanbody's Physical Strength[J]. Journal of Systems Engineering, 1995, 10(3): 75-81. |
| [22] |
舒诗楠, 边扬, 荣建. 基于发生吸引源分布特征的公共自行车网点规模优化模型[J]. 北京工业大学学报, 2018, 44(1): 159-162. SHU Shi-nan, BIAN Yang, RONG Jian. Station Scale Optimization Model of Public Bicycle System Based on Distribution of Generated and Attractive Points[J]. Journal of Beijing University of Technology, 2018, 44(1): 159-162. |
 2019, Vol. 36
2019, Vol. 36
