扩展功能
文章信息
- 胡立伟, 杨锦青, 何越人, 孟玲, 罗振武
- HU Li-wei, YANG Jin-qing, HE Yue-ren, MENG Ling, LUO Zhen-wu
- 基于改进BP神经网络的城市交通拥塞环境下车辆运行风险识别研究
- Study on Vehicle Operational Risk Identification in Urban Traffic Congestion Based on Improved BP Neural Network
- 公路交通科技, 2019, 36(10): 105-113
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(10): 105-113
- 10.3969/j.issn.1002-0268.2019.10.014
-
文章历史
- 收稿日期: 2018-04-11
拥塞环境给驾驶员的驾驶行为和身心健康造成很大的压力,严重影响道路的交通安全和运行效率。驾驶员为获得自身期望的驾驶条件,车辆在拥塞环境下不良换道频次和不良速度变化会有所增加。Gurupackiam和Jones[1]研究发现大量的驾驶员在道路拥挤条件下往往会接受较自由流环境下小的间隙,但换道持续时间在交通流状态下没有明显的差异。胡立伟[2]等利用自组织理论建立了交通拥塞自疏散模型,对于研究提高道路运行效率具有一定参考意义。Singh和Li[3]针对换道行为的时间差异性,借助马尔科夫链过程来分析车辆换道行为,Sayer[4]设计了车辆换道警示系统,以避免换道过程中交通事故的发生。Hennessy等[5]对交通拥塞与驾驶人心理的关系进行研究,指出交通拥塞时驾驶人需要承受更大的心理压力。道路交通拥堵容易引起攻击性驾驶行为或路怒驾行为,不同道路交通流状态下,这种影响有所差异[6]。王崇伦[7]运用车辆运动学理论,根据驾驶人在不同交通状态下不同的驾驶特性,构建了椭圆最小安全距离换道模型。唐秋生[8]在BP神经网络的基础上建立了交通事故模型并进行了仿真。刘梦涵等[9]建立了基于Logistic回归的道路交通拥堵强度评价模型。丁恒[10]等利用MFD特性提出了一种宏观交通网络拥堵区边界最优控制模型,该方法能有效解决交通拥塞环境下的区域交通控制难题。臧金蕊、宋国华[11]通过交通流理论建立了交通事件下快速路拥堵蔓延消散的时空范围模型。王曦[12]以速度作为关键指标,建立了基于高斯混合分布的交通拥堵综合评价模型。孙超[13]提出了一种新的城市路网交通状态评价方法,并确定了状态临界值。李泽钧[14]等基于区域交通运行指数,构建了区域拥堵评价模型,并确定了预警分级标准。郭仁拥[15]对拥堵收费问题进行了细致的研究。胡立伟[16]对公路交通工程设施的基本信息量分析方法进行了研究。刘有军等[17]研究了不同路网形态城市交通拥堵特性。
目前对交通拥塞的研究多是集中在拥塞程度、拥塞强度、拥塞时间、拥塞范围以及传播特性、拥堵收费、路径优化、拥塞治理等方面的研究,缺少对城市交通拥塞环境下车辆运行风险的研究。在拥塞形成和消散阶段车辆的不良换道、速度变化较常规情况具有犹豫(踌躇)、冒险、攻击性等特点,对行车安全构成很高的风险,存在许多安全隐患。因此,本研究从拥塞形成和拥塞消散过程中车辆运行风险入手,采用主成分分析法筛选、识别出对车辆运行风险影响显著的风险因子,利用专家调查法对车辆运行风险等级进行打分,再结合BP神经网络计算出风险值,建立城市交通拥塞环境下车辆运行风险识别评估模型。
1 城市道路拥塞环境下车辆运行风险分析由于长时间在拥塞环境下行车以及驾驶员之间竞争博弈,驾驶人生理、心理都较为疲惫,容易产生焦虑、烦躁等不良情绪。强制换道、不良加减速等行为的增加给车辆运行带来很高的风险,是车辆运行潜在的安全隐患。其次在拥塞形成和消散过程中驾驶人面对大量复杂变化的交通信息,在路径决策上容易发生错误,这也是车辆在拥塞环境下的运行风险。
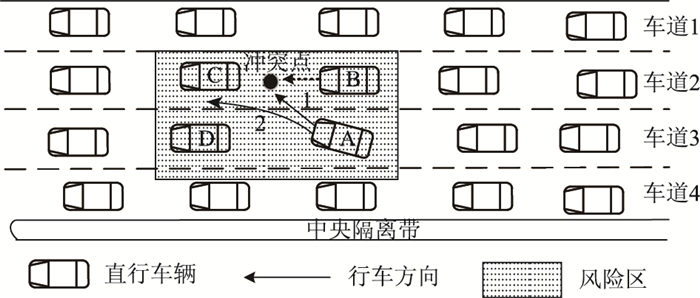
1.1 拥塞形成阶段车辆运行风险分析在拥塞形成阶段见图 1,A车根据前方拥塞发生车道,为争夺优先发车权,获取更大的行车空间,可能采取第1种强制换道模式直接斜插换道至车道2,在换道过程中,速度变化不当极易与B车发生侧碰、刮擦,与B车产生很严重的交通冲突。在觉察到A车换道意图后,B车为了不降低自身的行车条件,极有可能加速至A车与B车交叉点来阻止A车换道。即使A车换道成功,在本就拥塞的道路环境下,强行加塞又会给B车造成很大的心理负担,存在重大的交通安全隐患。
|
| 图 1 拥塞形成阶段车辆运行风险分析 Fig. 1 Vehicle operation risk analysis during congestion formation |
| |
随着拥塞的加剧,B与C之间的距离进一步缩小,在不具备换道条件的情况下A车为满足自身驾驶期望会伺机采取换道,慢慢向车道2靠近,不断挤压B车的行车空间,给行车双方都造成巨大的压力。交通拥塞下的换道行为具有冒险性,在拥塞形成整个阶段车辆运行风险都很高。
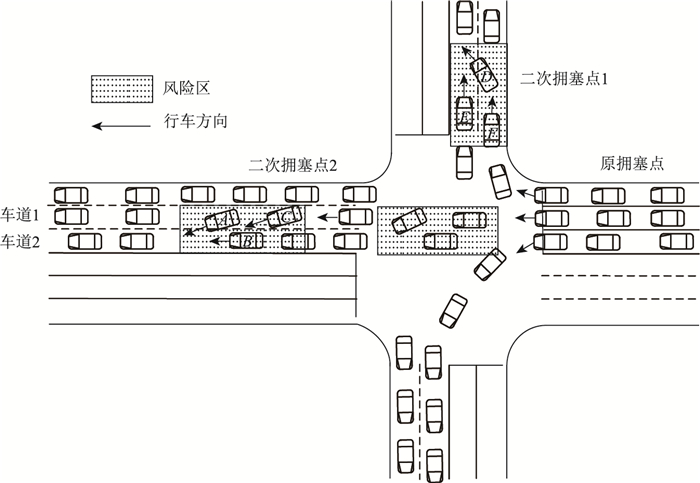
1.2 拥塞消散阶段车辆运行风险分析拥塞消散阶段如图 2所示,在某一交叉口拥挤车流由原拥塞点开始分流疏散,由于在原拥塞点处等待了较长时间,驾驶员容易产生烦躁、焦虑等不良情绪,进而采取许多不规范的驾驶行为,A车为满足自身的驾驶条件,可能会抢道至车道2,对于在拥塞环境下运行的车流,多是处在跟驰状态。由研究可知,在跟车过程中,后车驾驶行为容易受前车影响。假设C车跟随A车换道,在拥塞消散的整个行车过程中车辆的运行秩序较为混乱,A车、D车车速和不良车道变化以及C车路径选择错误等都对行车安全构成了很高的风险,且极易引发消散过程中的两次拥塞,产生二次拥塞点1和二次拥塞点2,更有可能将拥塞延伸至交叉口内造成交通锁死。
|
| 图 2 拥塞消散阶段车辆运行风险分析 Fig. 2 Vehicle operation risk analysis during congestion dissipation |
| |
2 风险识别模型构建 2.1 影响指标体系
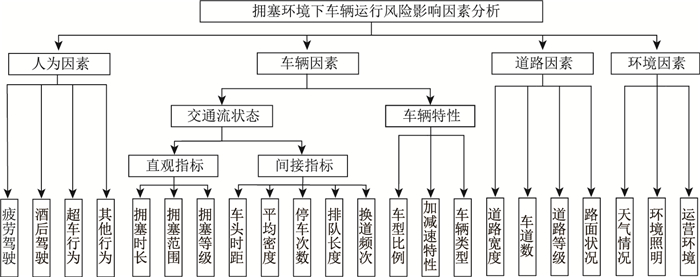
拥塞环境下影响车辆运行风险的因素包括人为因素、车辆因素、道路因素和环境因素等,如图 3所示。这些因素数量较多,分析复杂,需要筛选关键因素。一般人为因素为主观风险因素,属于局部性风险,相对而言车、路、环境因素更加客观。本研究主要对客观的全局性风险因素进行研究,且重点研究拥塞环境给车辆运行造成的风险,因此选择了直观反映拥塞的3个维度;拥塞时长、拥塞范围、拥塞等级。对于拥塞等级的划分参考我国《城市交通运行状况评价规范》(GBT33171—2016)[18],将其划分为5级,具体如表 1所示。以此为依据,定义主干路上平均行程车速≤20 km/h时为拥塞。
|
| 图 3 拥塞环境下车辆运行风险影响指标体系 Fig. 3 Vehicle operation risk influence index system in congested environment |
| |
| 运行状况等级 | 畅通 | 基本畅通 | 轻度拥堵 | 中度拥堵 | 重度拥堵 |
| 平均行程速度 Vs与自由流行程速度 Vf关系 | Vs>Vf×70% | Vf×50%≤Vs ≤Vf×70% |
Vf×40%≤Vs ≤Vf×50% |
Vf×30%≤Vs ≤Vf×40% |
Vf×30%≤Vs ≤Vf×30% |
| 城市交通运行指数 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) |
| 严重拥堵里程比例 | [0,4%) | [4%,8%) | [8%,11%) | [11%,14%) | ≥14% |
| 行程时间比 | [1,1.3) | [1.3,1.6) | [1.6,1.9) | [1.9,2.2) | ≥2.2 |
| 延误时间比 | [0,0.3) | [0.3,0.5) | [0.5,0.6) | [0.6,0.7) | [0.7,1) |
间接指标中换道频次是指行车方向单位时间内所有车辆换道次数总和。在拥塞环境下为争夺优先发车权, 不良换道次数会增加,致使行车风险增高。其次为研究拥塞特征下的车辆运行风险,平均密度、车头时距、停车次数以及排队长度是反映车辆运行状态的重要参数, 也要作为影响因子列入模型的研究。对于道路因素和环境因素, 笔者主要研究城市主干路, 道路宽度、车道数以及道路等级较为固定,环境照明情况较好。据事故统计表明,在不良天气和路面状况下行车事故发生率是正常情况下的2~3倍,故选取对行车安全影响较大的路面状况和天气情况作为对车辆运行风险模型的研究。选取的关键因素指标分析如表 2所示。对于本次研究数据来源主要取自对某市城市主干路与交叉口的数据调查,调查时段主要是工作日上午7:00—9:00,调查方式采用视频录像,在数据采集完毕后进行归纳整理共采集200组数据,其中170组数据作为模型训练使用,30组数据用作模型测试。
| 关键风险因数 | 说明 | |
| 车辆特性 | 车型比例 | 行车方向中大客车(公交、大巴等)与小客车的比例 |
| 直观指标 | 拥塞时长/min | 行车方向拥塞持续时间 |
| 拥塞范围/km | 行车方向前方最远拥塞扩散距离 | |
| 拥塞等级 | 划分为畅通、基本畅通、轻度拥堵、中度拥堵、重度拥堵五级 | |
| 间接指标 | 车头时距/(s·pcu-1) | 行车方向车流的平均车头时距 |
| 平均密度/(pcu·h-1) | 行车方向所有车道的密度平均值 | |
| 停车次数/(次·min-1) | 行车方向单位时间内每辆车的平均停车次数 | |
| 排队长度/km | 道路堵塞时车辆排队长度 | |
| 换道频次/(次·min-1) | 行车方向单位时间内所有车辆换道次数总和 | |
| 道路因素 | 路面状况 | 将路面状况分为干燥、潮湿、积水3种状况 |
| 环境因素 | 天气情况 | 将气候分为晴天、雨天、大风3种天气 |
2.2 模型构建 2.2.1 模型基础
BP神经网络是一种基于误差反向传播的多层向前神经网络[19]。其主要计算公式见式(1):
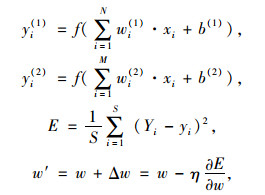
|
(1) |
BP神经网络学习时,令输入层节点为xi,输出层节点为yi,其中, f为激活函数;wi(1)为输入层节点与输出层节点之间的连接权值;wi(2)为隐含层节点与输出层节点之间的连接权值;b(1)是隐含层各神经元的阀值;b(2)是输出层各神经元的阀值;Yi为数据中的实际值;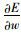
标准的BP神经网络迭代次数较高,需要对模型进行改进优化,且初选的影响因子存在或多或少的相关性,用主成分分析可以有效避免这种缺陷。主成分分析可以将许多相关性很高的变量转换为不相关的变量,通过分析选出比原始数量个数少,能解释大部分资料中变量的几个新变量,通过对指标进行降维以减少模型的复杂程度[13],主成分向量系数公式见式(2)。
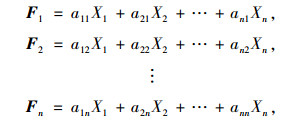
|
(2) |
式中,Fn是第n个主成分;a是各主成分因子的相关系数;X是处理后的样本数据。
2.2.2 BP网络层数设计由2.1节可知, 本研究初定了换道频次、停车次数、排队长度、车头时距、车型比例、平均密度、天气情况、路面状况、拥塞时长、拥塞范围、拥塞等级11个影响因子作为对车辆运行风险模型的研究,因此输入层的神经元个数初定为11个。
输出层节点数为期望输出的车辆运行风险等级,通过专家打分法将车辆运行风险等级划分为低风险,中等风险,高风险,极高风险4级。其对应得分如表 3,因此输出层节点数初定为4个。
| 风险等级 | 低风险(y1) | 中等风险(y2) | 高风险(y3) | 极高风险(y4) |
| 专家打分 | y1≤0.2 | 0.2y2≤0.4 | 0.4y3≤0.6 | y4≥0.6 |
对于隐藏层的神经元数目,由于没有统一的标准,主要通过以下的经验公式(3)和(4)式来确定神经元数目:
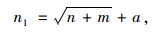
|
(3) |
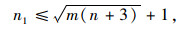
|
(4) |
式中,n1为隐含层神经元数,n为输入层的神经元数,m为输出层神经元数;a为常数,取值[1,10]。通过计算,初定隐含层节点数为6,8,10。后期再根据训练情况和样本数据进行确定。
2.2.3 模型训练检验对于神经网络模型,要先通过大量样本数据的训练学习才能应用于模型的评估,使用MATLAB仿真软件对模型进行训练调整。将在某市内采集的样本数据归一化处理后代入模型,训练其中170组用做训练,30组用作验证误差,将预测值与目标值作比较,直到期望误差达到10-4。
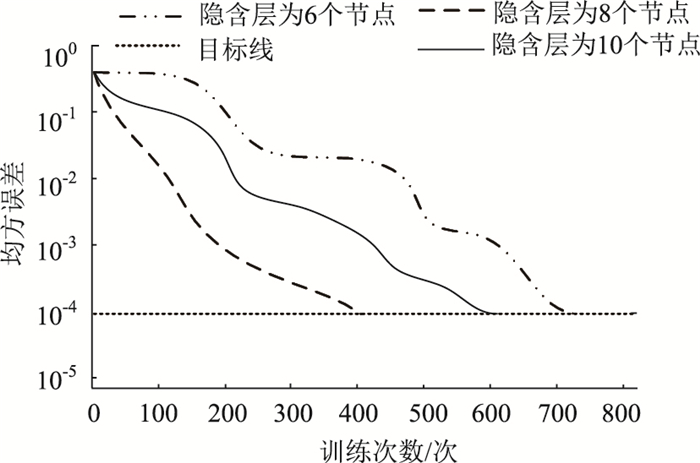
参数设置完毕将标准化后的样本数据带入模型进行训练,将隐含层节点数为6,8,10时的训练曲线进行整合,得出训练误差曲线如图 4所示。
|
| 图 4 BP神经网络训练结果 Fig. 4 BP neural network training result |
| |
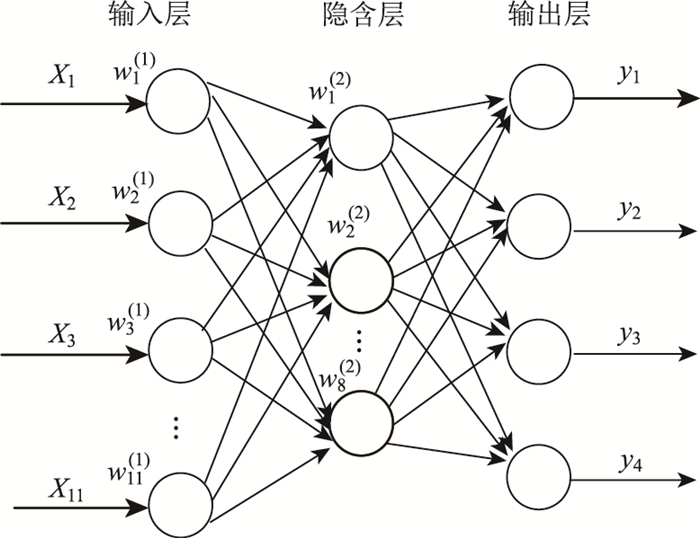
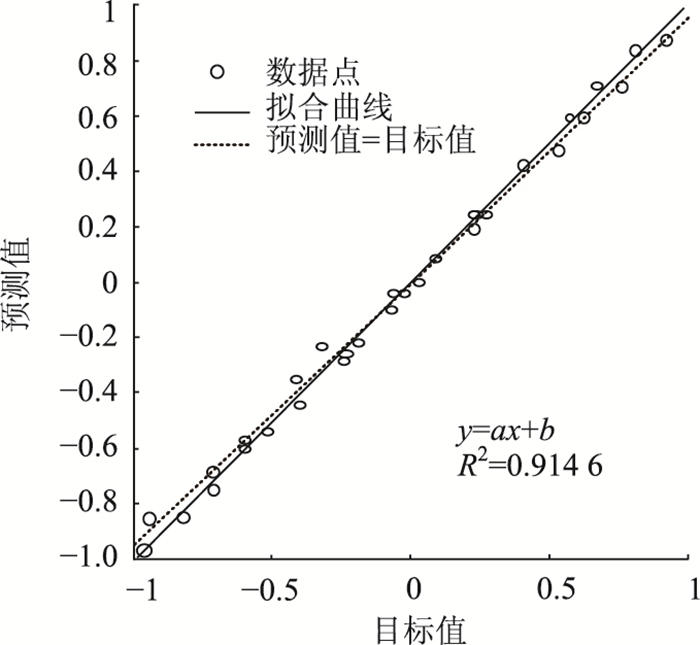
由图 4可知,当隐含层神经元数为10时,神经网络训练次数为609次;隐含层节点数为8时,训练次数为407次;收敛速度最快;当隐含层数为6时,收敛速度最慢,训练次数为724次。因此选择收敛速度最快的模型作为风险评估模型,即隐藏层节点数为8时的模型。此时车辆运行风险识别模型如图 5所示(BP神经网络模型结构为输入层节点数为11、隐含层节点为8,输出层节点数为4)。再对模型进行拟合优度检验得R2=91.46%,神经网络回归如图 6所示。
|
| 图 5 神经网络模型结构 Fig. 5 Neural network model structure |
| |
|
| 图 6 神经网络回归 Fig. 6 Neural network regression |
| |
2.2.4 模型改进
通过使用SPSS软件对样本数据进行主成分分析,将各主成分结果进行排序处理得到各新影响变量的贡献率以及特征值如表 4所示,其中贡献率是指各主成分方差在总方差中所占的比例,累积贡献率是多个主成分的方差在总方差中所占的比例。
| 影响变量 | 贡献率 | 累积贡献率 | 特征值 |
| 1 | 58.807 | 58.807 | 9.821 |
| 2 | 46.659 | 50.101 | 5.283 |
| 3 | 25.672 | 59.901 | 2.927 |
| 4 | 8.981 | 88.428 | 1.856 |
| 5 | 5.907 | 90.501 | 1.361 |
| 6 | 2.551 | 92.893 | 0.785 |
| 7 | 1.179 | 96.437 | 0.562 |
| 8 | 0.961 | 98.383 | 0.452 |
| 9 | 0.832 | 98.281 | 0.322 |
| 10 | 0.377 | 99.527 | 0.109 |
| 11 | 0.062 | 100.000 | 0.008 |
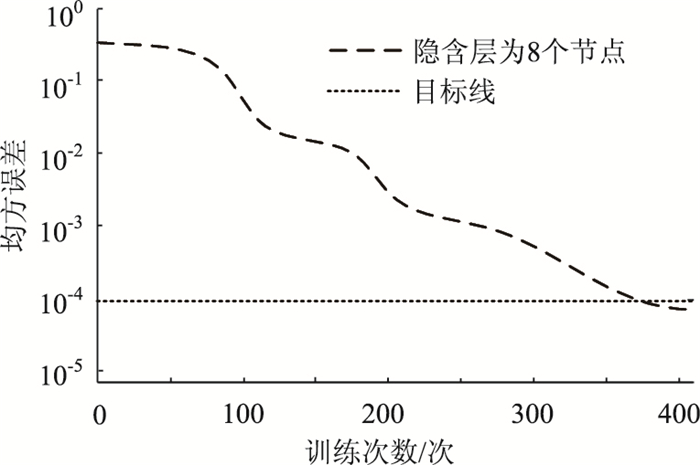
由表 4可知经过主成分分析,前5项新变量的贡献率较大,累积贡献率已经超过90%,特征值相对于其他主成分的特征值也高出很多,因此选定前5项作为主成分。通过主成分降维处理将11个指标数据降至具有代表性的5个主成分,大大简化了模型复杂程度,将经过主成分分析后的数据代入神经网络系统进行训练,得到训练误差曲线如图 7(隐含层节点数为8),由图可知经过主成分降维后样本数据的收敛速度更快,训练次数减至371次。
|
| 图 7 优化后BP训练结果 Fig. 7 Optimized BP training result |
| |
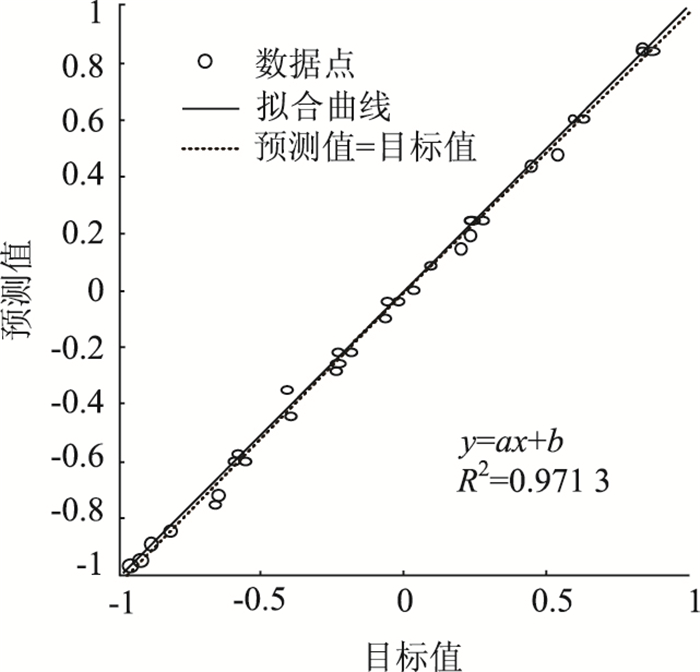
由于在表 3中通过专家打分的形式将风险等级进行数字量化,可将输入层的神经元个数简化为1个综合评价单元,模型输出分数越高表明风险越大。经过改进的神经元结构包括5个输入层节点、8个隐藏层节点、1个输出层节点,优化后的模型结构如图 8所示。网络学习结束将输出值与期望值进行拟合得出其适应度如图 9,预测值与目标值间的拟合度达到97.13%,表明改进后的模型预测精度更高。

|
| 图 8 改进后车辆运行风险识别模型 Fig. 8 Improved vehicle operating risk identification model |
| |
|
| 图 9 改进神经网络回归 Fig. 9 Improved neural network regression |
| |
2.2.5 对比分析
改进后的BP神经网络较标准的BP神经网络模型结构更加简洁,隐含层节点数不变,输入层和输出层节点数分别减少了6个和3个。训练次数由407次降至358次,收敛速度加快,性能更好。对模型进行拟合优度检验对比精度提高了5.67%。对比分析结果如表 5。
| 项目 | 标准 BP神经 网络 |
改进后 BP神经 网络 |
| 模型结构(输入/隐含/输出) | 11+8+4 | 5+8+1 |
| 训练次数、性能/次 | 407 | 371 |
| 拟合优度/% | 91.46 | 97.13 |
3 应用分析
利用上述主成分分析与BP神经网络相结合的改进模型,并且基于本研究所选取的指标体系,对昆明市城市道路拥塞环境下的车辆运行风险进行评估,首先邀请行业内的10名专家对各指标进行综合评估打分得表 6。其次运用SPSS软件对样本数据进行主成分分析得到主成分向量系数表 7。
| 指标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | — |
| 评分 | 0.461 | 0.176 | 0.208 | 0.184 | 0.282 | 0.292 | 0.265 | 0.332 | 0.342 | 0.237 | 0.322 | — |
| 主成分向量系数 | F1 | F2 | F3 | F4 | F5 | 平均值 |
| X1(换道频次) | 0.372 | 0.583 | 0.368 | 0.445 | 0.363 | 0.426 |
| X2(停车次数) | 0.172 | 0.242 | 0.196 | -0.221 | 0.289 | 0.224 |
| X3(排队长度) | 0.128 | 0.261 | -0.103 | -0.228 | 0.129 | 0.170 |
| X4(车头时距) | 0.162 | 0.064 | -0.073 | 0.108 | -0.137 | 0.109 |
| X5(车型比例) | -0.281 | -0.296 | 0.318 | 0.312 | 0.381 | 0.318 |
| X6(平均密度) | -0.286 | 0.391 | 0.291 | -0.267 | 0.312 | 0.309 |
| X7(路面状况) | 0.161 | 0.279 | -0.104 | -0.121 | 0.182 | 0.169 |
| X8(天气情况) | 0.258 | 0.470 | 0.361 | 0.376 | -0.231 | 0.339 |
| X9(拥塞时长) | 0.506 | -0.341 | 0.412 | 0.289 | 0.362 | 0.382 |
| X10(拥塞范围) | 0.282 | 0.251 | 0.303 | -0.106 | 0.261 | 0.241 |
| X11(拥塞等级) | -0.292 | 0.315 | 0.302 | 0.326 | -0.280 | 0.303 |
该表计算公式如式(5),其中F为主成分得分,X为归一化处理后的样本数据。
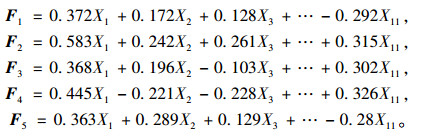
|
(5) |
将标准化后的样本数据代入主成分公式(5)进行计算得到各主成分得分表 8。最后将表 8中的主成分得分值代入优化后的BP神经网络模型得到最终的风险评价值为0.483。
| 主成分1 | 主成分2 | 主成分3 | 主成分4 | 主成分5 |
| 0.513 | -0.261 | 0.326 | -0.065 | 0.148 |
对结果进行分析,可得到如下结论:
(1) 模型输出的风险评价值为0.483对比表 3风险等级量化表可知在0.4和0.6之间,表明昆明市城市道路拥塞环境下的车辆运行处在高风险状态。
(2) 由表 7可知,拥塞环境下影响车辆运行风险的关键因素主要为换道频次、拥塞时长、天气情况、车型比例、平均密度、拥塞等级。6个影响因子的主成分荷载系数平均值均在0.3以上,相对其他因子要高,其中换道频次主成分系数平均值为0.426,在11个风险因子中最高。这表明换道频次是导致车辆运行风险的最重要因数,换道越频繁风险越高,在拥塞形成和消散过程中,驾驶员为获得自身期望的驾驶条件,强制换道,不良加减速的频次会增加,研究车辆与其他车辆存在着一种竞争的博弈关系,换道频次在各种风险因数中权重最高。
由主成分向量系数表可知X9的荷载系数平均值为0.382,排在第2位。主成分向量F1的X9荷载系数为0.506,在F1的荷载系数中最高,表明X9是影响主成分F1的最主要因数,即拥塞时长对拥塞环境下的车辆运行风险影响较大,且拥塞时间越长风险越大,这是因为随着拥塞时间的增长,驾驶员开始产生烦躁不安的心情,进而采取许多不规则的驾驶行为使车辆运行风险增高。天气情况也是影响车辆运行风险的重要因素,特别是雨天和大风天气相对晴天风险要高。车型比例主成分系数平均值为0.318,研究得出大客车的比例越高风险越大,由于大客车和小客车所占的时空资源不一样,大客车在机动性和驾驶操作上较小客车要困难许多,且大客车过多会给小客车司机造成压力,容易在交叉口节点造成拥塞和安全风险,所以其主成分向量系数表各荷载系数相对而言较高。对于拥塞等级来说,随着拥塞等级的上升,车辆运行风险先是增高,这主要是为争夺优先发车权,抢夺停车位而导致车辆运行风险的上升,随着拥塞的加重,车辆间距减少车流运行呈现跟驰状态,速度较低,车辆运行的安全风险降低,但后方驾驶人在获悉实时交通路况后可能对路径进行重新选择,又会增加路径决策错误的风险。车流密度与拥塞等级是相关的,其作用机理与拥塞等级相似。
(3) 车头时距、停车次数、排队长度、路面状况拥塞范围各主成分荷载系数均不是很高,表明对风险的影响相对较小。车头时距的主成分系数平均值最小为0.109,这是因为车头时距的大小是不受车速影响的,而与驾驶员的行为特性等有关,一般情况较为稳定,对车辆运行风险影响较小。对于路面状况,拥塞环境下车辆运行速度较正常情况下要低,路面的附着系数变化对行车的影响不大。对于拥塞范围,5个主成分系数相对拥塞时长和拥塞程度要低,经过调查驾驶人通过导航地图获得的实时路况对拥塞时长, 以及拥塞程度关注度高于拥塞范围,其对车辆运行风险的影响弱于两者。
4 结论(1) 首先对城市道路交通拥塞环境下的车辆运行风险进行了细致的分析,将其分解为拥塞形成阶段和拥塞消散阶段的车辆运行风险。
(2) 选取换道频次、停车次数、排队长度、车头时距、车型比例、平均密度、路面状况、天气情况、拥塞时长、拥塞范围、拥塞等级等11个影响因素作为模型自变量。对标准的BP神经网络模型进行改进,运用SPSS软件进行主成分分析将11个影响因子降维为5个主成分,通过MATALAB仿真软件对模型进行训练,得出换道频次、车型比例、平均密度、拥塞时长、拥塞等级和天气情况的主成分向量系数较其他指标要高,表明换道频次、车型比例、平均密度、拥塞时长、拥塞范围以及天气情况对车辆运行风险影响较为显著,其中换道频次在主成分荷载系数中平均值最大为0.426,表明换道频次对车辆运行风险影响最大。而车头时距、停车次数、排队长度、路面状况、拥塞范围的影响不显著。对模型进行拟合,其拟合优度判定系数达97.13%较标准模型要高出5.67%,模型预测精度较高,可为城市道路发生交通拥塞时规避车辆运行风险和拥塞治理提供参考。
(3) 虽已识别出拥塞环境下的车辆运行风险因子以及各风险因子的贡献率,但选取的自变量之间存在或多或少的相关性,虽通过主成分分析降低相关度,但下一步需对各自变量间对风险的耦合作用以及解耦技术(风险控制技术)进行更深入的研究。
| [1] |
GURUPACKIAM S, JONES S L. Empirical Study of Lane Changing in urban Streets under Varying Traffic Conditions[J]. Procedia-Social and Behavioral Sciences, 2011, 16(6): 259-269. |
| [2] |
胡立伟, 祁首铭, 孙亚南, 等. 基于自组织理论的道路交通拥塞自疏散模型研究[J]. 交通运输系统工程与信息, 2015, 15(2): 135-141. HU Li-wei, QI Shou-ming, SUN Ya-nan, et al. Research on Road Traffic Congestion Self-evacuation Model Based on Self-organization Theory[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(2): 135-141. |
| [3] |
SINGH K, LI B. Estimation of Traffic Densities for Multilane Roadways Using a Markov Model Approach[J]. IEEE Transactions on Industrial Electronics, 2012, 59(11): 4369-4376. |
| [4] |
National Highway Traffic Safety Administration. Integrated Vehicle Based-Safety Systems Light:Vehicle Field Operational Test, Key Findings Report[J]. Annals of Emergency Medicine, 2011, 58(2): 205-206. |
| [5] |
HENNESSY D A, WIESENTHAL D L. Relationship between Traffic Congestion, Driver Stress and Direct versus Indirect Coping Behaviors[J]. Ergonomics, 1997, 40(3): 348-361. |
| [6] |
MCLINTON S S, DOLLARD M F. Work Stress and Driving Anger in Japan[J]. Accident Analysis & Prevention, 2010, 42(1): 174-181. |
| [7] |
王崇伦, 李振龙, 陈阳舟, 等. 考虑换道约束空间的车辆换道模型研究[J]. 公路交通科技, 2012, 29(1): 121-126. WANG Chong-lun, LI Zhen-long, CHEN Yang-zhou, et al. Research on Lane-changing Models Considering Restricted Space[J]. Journal of Highway and Transportation Research and Development, 2012, 29(1): 121-126. |
| [8] |
唐秋生, 杜营营. 基于BP神经网络的交通事故预测模型及仿真[J]. 交通信息与安全, 2011, 29(1): 68-70. TANG Qiu-sheng, DU Ying-ying. A Model of Traffic Accident Forecast Based on BP Neural Network[J]. Journal of Transport Information and Safety, 2011, 29(1): 68-70. |
| [9] |
刘梦涵, 于雷, 张雪莲, 等. 基于累计的Logistic回归道路交通拥堵强度评价模型[J]. 北京交通大学学报, 2008, 32(6): 53-56. LIU Meng-han, YU Lei, ZHANG Xue-lian, et al. Cumulative Logistic Regression-based Measurement Models of Road Traffic Congestion Intensity[J]. Journal of Beijing Jiaotong University, 2008, 32(6): 53-56. |
| [10] |
丁恒, 郑小燕, 张雨, 等. 宏观交通网络拥堵区边界最优控制[J]. 中国公路学报, 2017, 30(1): 111-120. DING Heng, ZHNEG Xiao-yan, ZHAMG Yu, et al. Optimal Control for Traffic Congested Area Boundary in Macroscopic Traffic Network[J]. China Journal of Highway and Transport, 2017, 30(1): 111-120. |
| [11] |
臧金蕊, 宋国华, 万涛, 等. 交通事件下快速路拥堵蔓延消散时空范围模型[J]. 交通运输系统工程与信息, 2017, 17(5): 179-185. ZANG Jin-rui, SONG Guo-hua, WAN Tao, et al. A Temporal and Spatial Model of Congestion Propagation and Dissipation on Expressway Caused by Traffic Incidents[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(5): 179-185. |
| [12] |
王曦, 祝付玲. 基于高斯混合分布的交通拥堵评价模型[J]. 公路交通科技, 2011, 28(2): 127-132. WANG Xi, ZHU Fu-ling. Evaluation Model of Traffic Congestion Based on Gaussian Mixture Distribution[J]. Journal of Highway and Transportation Research and Development, 2011, 28(2): 127-132. |
| [13] |
孙超, 王波, 张云龙, 等. 基于一种交通状态系数的城市路网交通状态评价研究[J]. 公路交通科技, 2011, 28(5): 113-120. SUN Chao, WANG Bo, ZHANG Yun-long, et al. Research on Urban Traffic Network State Evaluation Based on a Traffic Network State Coefficient[J]. Journal of Highway and Transportation Research and Development, 2011, 28(5): 113-120. |
| [14] |
李泽钧, 邸小建, 翁剑成, 等. 基于拥堵时空特征的区域分类与评价方法研究[J]. 公路交通科技, 2019, 36(2): 121-127. LI Ze-jun, DI Xiao-jian, WENG Jian-cheng, et al. Regional Classification and Evaluation Method Based on Congestion Temporal-spatial Characteristics[J]. Journal of Highway and Transportation Research and Development, 2019, 36(2): 121-127. |
| [15] |
郭仁拥, 黄海军. 道路收费和通行能力的联合最优控制理论模型[J]. 交通运输系统工程与信息, 2007, 6(12): 61-66. GUO Ren-yong, HUANG Hai-jun. A Joint Optimization Model of Road Tolls and Capacities Using the Optimal Control Theory[J]. Journal of Transportation Systems Engineering and Information Technology, 2007, 6(12): 61-66. |
| [16] |
胡立伟, 祁首铭. 公路交通工程设施基本信息量分析方法[J]. 昆明理工大学学报:自然科学版, 2014, 39(5): 35-41. HU Li-wei, QI Shou-ming. Analysis Methods of Basic Information Quantity of Traffic Engineering Facilities[J]. Journal of Kunming University of Science and Technology, 2014, 39(5): 35-41. |
| [17] |
刘友军, 田聪. 不同路网形态下城市交通拥堵特性分析[J]. 中国公路学报, 2013, 26(1): 163-169. LIU You-jun, TIAN Cong. Analysis of Dynamic Characteristics of Urban Traffic Congestion Based on Specificity of Network Configuration[J]. China Journal of Highway and Transport, 2013, 26(1): 163-169. |
| [18] |
GBT33171-2016, 城市交通运行状况评价规范[S]. GBT33171-2016, Specification for Urban Traffic Performance Evaluation[S]. |
| [19] |
张德慧, 张德育, 刘清云, 等. 基于粒子群算法的BP神经网络学习优化技术[J]. 计算机工程与设计, 2015, 36(5): 1321-1326. ZHANG De-hui, ZHANG De-yu, LIU Qing-yun, et al. BP Neural Network Optimized by Improved PSO[J]. Computer Engineering and Design, 2015, 36(5): 1321-1326. |
 2019, Vol. 36
2019, Vol. 36
