扩展功能
文章信息
- 凌同华, 杨宇, 张胜
- LING Tong-hua, YANG Yu, ZHANG Sheng
- 锚杆缺陷模拟试验及其超声波检测信号特征的EMD分析
- Simulation Experiment on Rock Bolt Defect and EMD Analysis on Features of Its Ultrasonic Testing Signals
- 公路交通科技, 2019, 36(10): 91-97
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(10): 91-97
- 10.3969/j.issn.1002-0268.2019.10.012
-
文章历史
- 收稿日期: 2019-05-31
2. 湖南城市学院 土木工程学院, 湖南 益阳 413000
2. School of Civil Engineering, Hunan City University, Yiyang Hunan 413000, China
岩土锚固技术经济有效, 在隧道、边坡、水利等工程中被广泛应用, 其施工工程隐蔽, 潜在缺陷会造成工程事故和重大经济损失[1-3]。传统锚杆拉拔试验属于破坏性检测, 会对试验锚杆和结构体造成破坏。近年来, 许多学者应用超声波法对锚杆进行无损检测[4-6]。基于应力波反射原理, 介质成分差异和裂纹等缺陷都会使超声波的传播受到影响, 通过提取信号特征, 可以实现内部缺陷的检测[7-8]。超声波法具有灵敏度高、安全性能好等优点, 随着检测技术的发展, 其可靠性越来越高, 已在土木工程领域有广泛应用[9-10]。
超声波法解决了锚杆动测技术只能对锚杆有效长度和缺陷作定性评价, 检测受限于锚固质量等问题[11-13]。付文光[14]通过对比国内外锚杆试验的不同, 提出应增加锚杆探究性试验。何忠明等[15]认为锚杆的长度、倾角等参数会影响边坡的稳定性。许明等[16]通过动测法测定锚杆振动响应, 应用小波方法进行信号处理, 取得了良好的效果, 但精度有限。李义等[17]通过激发应力波检测锚杆质量, 得出底部反射受限于锚固长度的结论。张世平等[18]应用快速傅里叶变换(FFT), 研究锚杆中超声导波的传播规律, 但FFT方法本身存在一定误差, 且不能有尺度的变化。传统分析方法仍无法准确确定锚杆长度和缺陷位置, 只能对这些参数作定性评价, 需采用更先进且与之匹配的现代信号分析技术。
本研究通过试验模型中内置钢筋来模拟锚杆, 应用超声检测系统对其进行测试, 基于EMD方法对超声波检测信号进行质量的缺陷识别和能量分布特征的分析, 从而揭示超声波在锚杆中的传播规律和特性。
1 锚杆超声波检测试验 1.1 试验仪器概况本次试验采用的Pocket-UT超声检测系统是世界著名无损检测公司美国物理声学公司推出的世界首款基于PDA技术的掌上超声系统, 见图 1。相较目前市场上其他同类产品, 该系统具有以下特点:

|
| 图 1 Pocket-UT超声检测系统 Fig. 1 Pocket-UT ultrasonic testing system |
| |
(1) 手掌式/口袋型:重量不到1 kg; (2)方便使用:可实现一手持机, 另一手操作传感器; (3)触屏操作:包括参数设置和出图, 方便高效。
1.2 试验模型的设计和制作本次试验通过在沙槽中埋设钢筋来模拟锚杆, 主要进行锚杆体材料的质量缺陷检测。分别设置完整光圆钢筋、截断光圆钢筋、完整螺纹钢筋和截断螺纹钢筋4种。完整光圆钢筋、截断光圆钢筋均有3种不同型号的直径, 分别为16, 20 mm和22 mm。完整螺纹钢筋和截断螺纹钢筋的直径均为22 mm。每根钢筋的长度为50 cm, 其中截断钢筋由两根25 cm长的完整钢筋拼接而成, 具体的示意图见图 2。

|
| 图 2 试验模型的示意图(单位:mm) Fig. 2 Schematic diagram of experimental model(unit:mm) ①-完整螺纹钢筋; ②-截断螺纹钢筋; ③-完整光圆钢筋; ④-截断光圆钢筋; ⑤-水平线; ⑥-刻度线; ⑦-沙槽 |
| |
1.3 试验及结果分析
为了保证每根锚杆埋置深度的准确性, 在沙槽表面拉设基准线, 螺纹钢筋的埋设见图 3(左侧图(a)为完整螺纹钢筋, 右侧图(b)为截断螺纹钢筋, 其中截断位置在25 cm处)。测试中超声波成像方法为A型, 脉冲形状为全检波形, 采样率为50 MHz, 声速校准为5.535 3 mm/us, 探头直径20 mm。在探头与锚杆端头之间涂匀耦合剂, 以减少超声波信号的损失。为保证检测信号的准确性, 对每一根锚杆应以测得两次以上重复性较好的数据为准。

|
| 图 3 螺纹钢筋的埋设 Fig. 3 Embedment of thread rebar |
| |
实测原始超声波检测信号见图 4。从图 4可以看出, 无论锚杆直径大于、等于还是小于探头直径, 光圆锚杆或者螺纹锚杆, 应用超声波法都可以确定锚杆长度以及断裂位置。
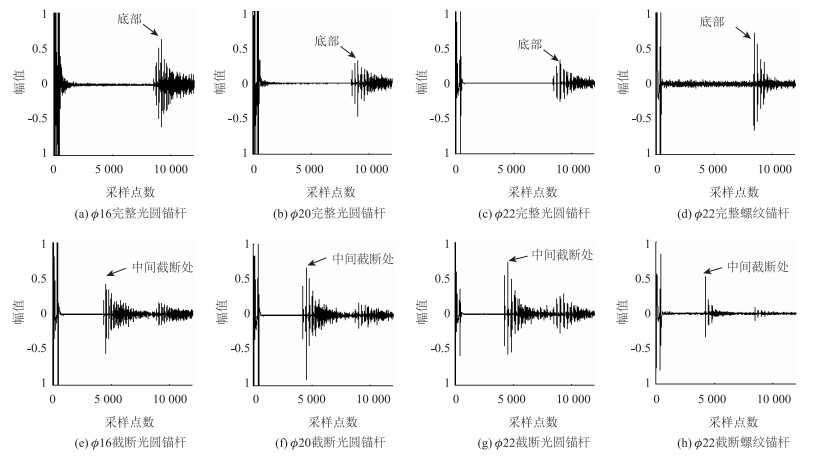
|
| 图 4 原始超声波检测信号的时程曲线 Fig. 4 Time-history curves of original ultrasonic testing signals |
| |
2 EMD方法
实测超声波检测信号由于衰减、散射、突变等情况, 属于典型的非平稳信号, 其分析方法也由原来的时域分析, 发展到频域分析以及时频域分析。时频域分析方法主要有短时傅里叶变换、小波(包)变换等[19]。然而, 短时傅里叶变换只具有单一分辨率分析功能, 小波(包)变换用不同的小波基, 分析同一信号会产生不同的结果。针对非平稳信号的特点, 黄锷教授提出了希尔伯特-黄变换[20]。它由EMD方法和Hilbert变换两部分组成。其核心为EMD方法, 是一种更具适应性的时频局部化方法。它没有固定的基函数, 是自适应的。
2.1 EMD方法的原理EMD方法能根据信号本身的局部特征属性进行自适应分解, 得到一系列具有不同特征时间尺度的"固有模态函数"(Intrinsic Mode Function, IMF), 频率成分随分解阶数的增加而降低。另一方面, EMD方法得到的IMF分量数量较少, 特别适用于非平稳信号的分析[21]。
原始信号x(t)经过EMD分解, 得到n个IMF分量和残余函数, 即
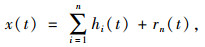
|
(1) |
式中, hi(t)(i=1, 2, …, n)为各阶IMF分量; rn(t)为残余函数。
2.2 超声波检测信号能量的表征超声波检测信号经EMD分解后的各IMF分量分别代表了一组特征尺度下的平稳信号, 各平稳信号能量的变化就表征了超声波检测信号的特征情况[22]。应用EMD方法提取超声波检测信号能量特征的过程如下:
(1) 信号EMD分解, 求取各IMF分量;
(2) 求各IMF分量的总能量:
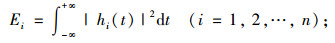
|
(2) |
(3) 以能量为元素构造特征向量T:
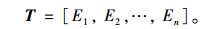
|
(3) |
当能量较大时, Ei(i=1, 2, …, n)通常为较大数值, 为方便数据分析, 对T进行归一化处理得到T':
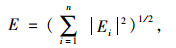
|
(4) |
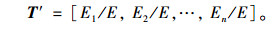
|
(5) |
EMD方法在将非平稳、非线性信号进行平稳化、线性化处理的同时, 保留了原始数据的固有特性, 使得信号的特征信息在不同的分辨率下显示出来。该方法没有固定的基函数, 分解过程更为简单和高效, 分解得到的每一个IMF分量都包含了不同的特征尺度信息, 可以用来表征原始信号的特征信息。
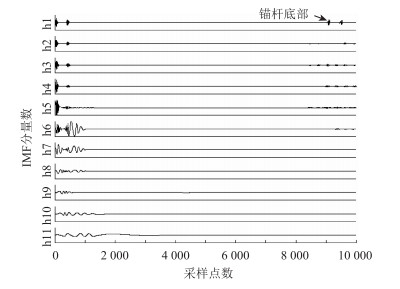
由于原始数据的信号特征主要集中于高频段, 在Matlab语言平台上, 对直径22 mm的完整光圆锚杆和截断光圆锚杆超声波检测信号进行EMD分解, 选取前11阶IMF分量作为进一步的研究对象(频率成分由高到低的顺序排列), 结果分别见图 5和图 6。对其进行分析, 结论如下:
|
| 图 5 完整锚杆的EMD分解结果 Fig. 5 EMD result of intact rock bolt |
| |
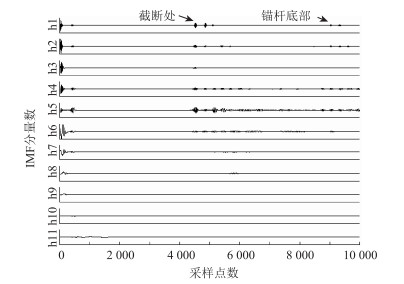
|
| 图 6 截断锚杆的EMD分解结果 Fig. 6 EMD result of truncated rock bolt |
| |
(1) 前5个IMF分量包含了锚杆长度和缺陷位置的主要信息; 从第6个IMF分量起, 锚杆缺陷及底部的特征信息不为明显。
(2) 锚杆底部位置为采用点数、采样间隔和声速的乘积, 本试验中采样间隔0.02 μs, 声速5.535 3 mm/μs, 锚杆底部的突变位置在采样点903 3处, 从而可以得知锚杆底部位于距试验模型表面50 cm处, 与实际相符; 从图 6还可以看出, 锚杆缺陷位置位于距试验模型表面25 cm处。
(3) 为了验证应用EMD方法识别锚杆质量
缺陷的可靠性, 需要了解奇异信号主要集中的时间和频率范围。因此, 有必要对超声波检测信号进行能量分布特征分析。
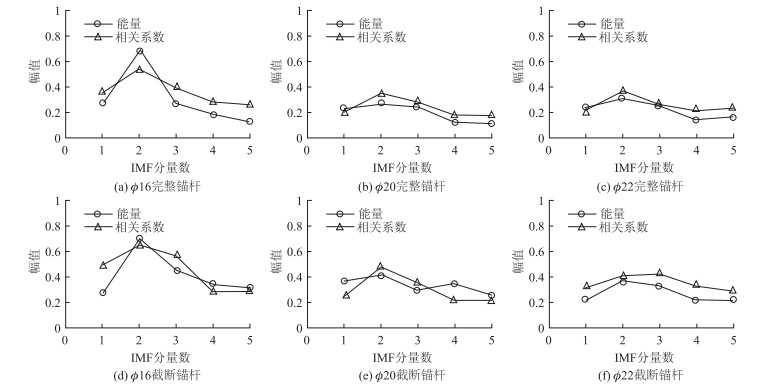
3.2 超声波检测信号的能量分布特征 3.2.1 锚杆直径对能量分布特征的影响为研究不同直径锚杆对超声波检测信号能量分布特征的影响, 选取直径16, 20 mm和22 mm的光圆完整锚杆和光圆截断锚杆, 按式(2)~式(5)分别提取前5阶IMF分量的特征向量T'。数字信号处理中, 常用相关系数来反映两个信号的相关程度, 计算原始超声波信号与各IMF分量的相关系数, 结果见表 1。以各IMF分量为横坐标, 以相关系数和能量特征向量T'为纵坐标, 将数值绘制成曲线, 结果见图 7。对其进行分析, 结论如下:
| IMF | ϕ16锚杆 | ϕ20锚杆 | ϕ22锚杆 | |||||
| 完整 | 截断 | 完整 | 截断 | 完整 | 截断 | |||
| 1 | 0.354 | 0.488 | 0.207 | 0.260 | 0.218 | 0.328 | ||
| 2 | 0.542 | 0.654 | 0.350 | 0.478 | 0.374 | 0.420 | ||
| 3 | 0.397 | 0.569 | 0.285 | 0.363 | 0.259 | 0.426 | ||
| 4 | 0.279 | 0.293 | 0.179 | 0.226 | 0.217 | 0.339 | ||
| 5 | 0.259 | 0.298 | 0.177 | 0.228 | 0.228 | 0.301 | ||
|
| 图 7 不同锚杆直径各IMF分量的相关系数与能量分布 Fig. 7 Correlation coefficients and energy distribution of IMF components of with different rock bolt diameters |
| |
(1) 超声波检测信号经EMD分解后, 各IMF分量的相关系数曲线与能量分布曲线的走势基本一致, 相关程度较高, 绝大部分IMF分量相关系数间于0.3~0.7之间, 属于强相关或中等程度相关。由此表明, EMD方法能根据超声波检测信号本身特性进行自适应分解, 分解得到的各IMF分量具有一定的物理意义, 可以用来识别超声波奇异信号, 且较为准确。
(2) 超声波检测信号各IMF分量的能量分布的变异系数分别为57.51%, 10.47%, 13.64%, 43.74%, 17.29%, 24.99%, 表明各IMF分量的能量分布不均匀。但当锚杆直径小于探头直径时, 各IMF分量的能量分布的变异系数更大。
(3) 超声波检测信号前3阶IMF分量的能量占该信号总能量的比例分别为79.97%, 75.56%, 74.38%, 70.26%, 68.76%和68.84%, 表明超声波检测信号的能量主要集中在前3阶高频IMF分量内; 应用EMD方法提取高频信号, 并据此识别锚杆缺陷和底部位置是可行的。
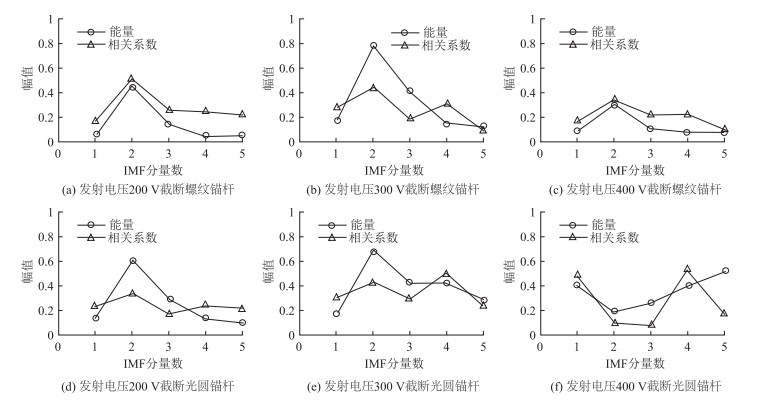
3.2.2 发射功率对能量分布特征的影响为研究发射功率对超声波检测信号能量分布的影响, 分别设置200, 300, 400 V发射电压对直径22 mm的截断螺纹锚杆和截断光圆锚杆进行检测, 提取其特征向量, 如图 8所示。对其进行分析, 结论如下:
|
| 图 8 不同发射电压各IMF分量的相关系数与能量分布 Fig. 8 Correlation coefficients and energy distribution of IMF components with different emission voltages |
| |
(1) 超声波检测信号经EMD分解后, 各IMF分量能量分布的变异系数分别为85.81%, 67.17%, 73.98%, 67.72%, 59.28%和38.91%, 表明各IMF分量的能量分布不均匀; 超声波检测信号前3阶IMF分量的能量占该信号总能量的比例分别为87.80%, 83.56%, 64.64%, 81.57%, 75.22%和7.81%, 表明超声波检测信号的能量主要集中在前3阶IMF分量内。
(2) 发射功率的改变对超声波检测信号能量分布影响不明显; 但发射功率过大时, 对于截断光圆锚杆, 由超声效应所致, 超声波检测信号的能量分布不稳定。
综上可知, 锚杆超声波检测信号经EMD分解后, 得到的各IMF分量的能量分布不会随锚杆直径、发射功率等外界因素的变化而改变, 可以用来定量表征原始信号的物理特性和识别锚杆缺陷。相较于小波分析等时频分析方法, EMD方法能够根据信号本身固有的特性进行自适应地分解, 且不需要预设固定的基函数, 具有准确和高效的特点。
4 结论(1) 应用超声波法检测不同直径的锚杆并进行了EMD分析, 前3阶IMF分量包含了锚杆长度及缺陷位置的主要信息, 可以定量表征原始信号的物理特性; 各IMF分量的能量占该信号总能量的比例变异性较大, 且分布不均。
(2) 发射功率等外界因素的改变对超声波信号经EMD分解得到的各IMF分量的能量分布影响较小; 但发射功率过大时, 由超声效应所致, 超声波检测信号的能量分布不稳定, 不利于识别锚杆缺陷。
(3) EMD方法能够根据信号本身固有的特性进行自适应地分解, 一定程度上揭示了超声波在被检测对象介质中的传播机理和能量分布特征, 为实现锚杆质量缺陷的精准识别奠定了基础。
| [1] |
郭小龙, 谭忠盛, 李磊, 等. 早强锚杆在高地应力层状软岩隧道中的应用研究[J]. 土木工程学报, 2017, 50(增1): 59-64. GUO Xiao-long, TAN Zhong-sheng, LI Lei, et al. Application of Early Strength Bolt in High Geostress Layered Soft Rock Tunnel[J]. China Civil Engineering Journal, 2017, 50(S1): 59-64. |
| [2] |
张期树, 徐则民, 夏香波, 等. 差异化锚长组合支护方式对边坡稳定性影响的数值分析[J]. 公路交通科技, 2017, 34(3): 26-37. ZHANG Qi-shu, XU Ze-min, XIA Xiang-bo, et al. Numerical Analysis on Influence of Support Pattern of Variation Bolt Length Combination on Slope Stability[J]. Journal of Highway and Transportation Research and Development, 2017, 34(3): 26-37. |
| [3] |
朱宏伟, 项琴. 锚杆支护边坡动力响应规律及锚固参数影响[J]. 公路交通科技, 2011, 28(7): 30-34, 99. ZHU Hong-wei, XIANG Qin. Dynamic Response of Anchored Slopes and Influence of Anchoring Parameters[J]. Journal of Highway and Transportation Research and Development, 2011, 28(7): 30-34, 99. |
| [4] |
何文, 王成, 石文芳, 等. 锚杆锚固质量的超声导波检测技术研究[J]. 北京理工大学学报, 2017, 37(6): 567-572, 578. HE Wen, WANG Cheng, SHI Wen-fang, et al. Evaluation of Anchorage Quality of Rock Bolts Using Ultrasoinc Guided Wave[J]. Transactions of Beijing Institute of Technology, 2017, 37(6): 567-572, 578. |
| [5] |
邓东平, 李亮, 赵炼恒. 2种应力波信号增强方式在预应力锚杆(索)锚固质量检测中的适用性研究[J]. 中南大学学报:自然科学版, 2016, 47(3): 936-945. DENG Dong-ping, LI Liang, ZHAO Lian-heng. Applicability of Two Stress Wave Signal Enhancement Modes in Anchorage Quality Testing of Pre-stressed Anchor (Cable)[J]. Journal of Central South University:Science and Technology Edition, 2016, 47(3): 936-945. |
| [6] |
佚名. 超声波检测研究及应用进展[M]. 北京: 中国原子能出版社, 2014. Anon. Progress in Research and Application of Ultrasonic Testing[M]. Beijing: China Atomic Energy Press, 2014. |
| [7] |
HWANG Y I, KIM H J, SONG S J, et al. Improving the Ultrasonic Imaging of Hydrogen-induced Cracking Using Focused Ultrasound[J]. Journal of Mechanical Science & Technology, 2017, 31(8): 3803-3809. |
| [8] |
吉伯海, 袁周致远, 傅中秋, 等. 钢箱梁疲劳裂纹特征超声波检测方法试验研究[J]. 中南大学学报:自然科学版, 2016, 47(6): 2023-2029. JI Bo-hai, YUANZHOU Zhi-yuan, FU Zhong-qiu, et al. Fatigue Crack Features in Steel Box Girder by Ultrasonic Testing[J]. Journal of Central South University:Science and Technology Edition, 2016, 47(6): 2023-2029. |
| [9] |
SCHNEIDER N, BÖDECKER J, BERGER C, et al. Frequency Effect and Influence of Testing Technique on the Fatigue Behaviour of Quenched and Tempered Steel and Aluminium Alloy[J]. International Journal of Fatigue, 2016, 93: 224-231. |
| [10] |
ZIMA B, RUCKA M. Non-destructive Inspection of Ground Anchors Using Guided Wave Propagation[J]. International Journal of Rock Mechanics & Mining Sciences, 2017, 94: 90-102. |
| [11] |
SALEEM M. Evaluating the Pull-out Load Capacity of Steel Bolt Using Schmidt Hammer and Ultrasonic Pulse Velocity Test[J]. Structural Engineering and Mechanics, 2018, 65(5): 601-609. |
| [12] |
陈建功, 胡俊强, 张永兴. 基于完整锚杆动测技术的围岩质量识别研究[J]. 岩土力学, 2009, 30(6): 1799-1804. CHEN Jian-gong, HU Jun-qiang, ZHANG Yong-xing. Identification of Surrounding Rock Quality Based on Dynamic Testing Technology of Integrated Anchor[J]. Rock and Soil Mechanics, 2009, 30(6): 1799-1804. |
| [13] |
孙冰, 曾晟, 丁德馨, 等. 低应变动测桩及锚杆中波的传播规律差异研究[J]. 岩土力学, 2011, 32(4): 1143-1148. SUN Bing, ZENG Sheng, DING De-xin, et al. Research on Transmit Rules of Stress Wave with Low Strain in Dynamic Test Pile and Anchorage Bolt[J]. Rock and Soil Mechanics, 2011, 32(4): 1143-1148. |
| [14] |
付文光. 国内外锚杆试验类型简介[J]. 岩土工程学报, 2014, 36(增2): 191-197. FU Wen-guang. Brief Introduction to Worldwide Test Types of Anchorage[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(s2): 191-197. |
| [15] |
何忠明, 林杭. 节理岩体边坡稳定性的锚杆支护影响分析[J]. 公路交通科技, 2010, 27(11): 8-12, 19. HE Zhong-ming, LIN Hang. Influence of Bolt Reinforcement on Stability of Rock Jointed Slope[J]. Journal of Highway and Transportation Research and Development, 2010, 27(11): 8-12, 19. |
| [16] |
许明, 张永兴, 阴可. 某隧道锚杆完整性的无损检测方法[J]. 土木工程学报, 2004, 37(5): 78-80, 100. XU Ming, ZHANG Yong-xing, YIN Ke. Study on Nondestructive Detection of Bolts' Integrality in a Tunnel[J]. China Civil Engineering Journal, 2004, 37(5): 78-80, 100. |
| [17] |
李义, 张昌锁, 王成. 锚杆锚固质量无损检测几个关键问题的研究[J]. 岩石力学与工程学报, 2008, 27(1): 108-116. LI Yi, ZHANG Chang-suo, WANG Cheng. Study on Several Key Issues in Nondestructive Detection of Bolt Bonding Integrity[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(1): 108-116. |
| [18] |
张世平, 张昌锁, 白云龙, 等. 注浆锚杆完整性检测方法研究[J]. 岩土力学, 2011, 32(11): 3368-3372. ZHANG Shi-ping, ZHANG Chang-suo, BAI Yun-long, et al. Research on Method for Detecting Integrity of Grouted Rock Bolts[J]. Rock and Soil Mechanics, 2011, 32(11): 3368-3372. |
| [19] |
胡广书. 现代信号处理教程[M]. 北京: 清华大学出版社, 2015. HU Guang-shu. Modern Signal Processing Course[M]. Beijing: Tsinghua University Press, 2015. |
| [20] |
SHEN S S P, SHU T, Huang N E, et al. HHT Analysis of The Nonlinear and Non-stationary Annual Cycle of Daily Surface Air Temperature Data[M]//Hilbert-Huang Transform and Its Applications. Singapore: World Scientific Publishing Co., 2005: 187-209.
|
| [21] |
HUANG N E, SHEN Z, LONG S R, et al. The Empirical Mode Decomposition and The Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J]. Proceedings of the Royal Society of London. Series A:Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. |
| [22] |
凌同华, 张胜, 李升冉. 地质雷达隧道超前地质预报检测信号的HHT分析法[J]. 岩石力学与工程学报, 2012, 31(7): 1422-1428. LING Tong-hua, ZHANG Sheng, LI Sheng-ran. Hilbert-Huang Transform Method for Detection Signal of Tunnel Geological Prediction Using Ground Penetrating Radar[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(7): 1422-1428. |
 2019, Vol. 36
2019, Vol. 36
