公路交通科技  2019, Vol. 36 Issue (10): 83−90

扩展功能

文章信息

胡刚, 费鸿禄, 包士杰, 杨智广
HU Gang, FEI Hong-lu, BAO Shi-jie, YANG Zhi-guang
爆破荷载作用下隧道初次衬砌结构的动力响应
Dynamic Response of Tunnel Primary Lining Structure under Blasting Load
公路交通科技, 2019, 36(10): 83-90
Journal of Highway and Transportation Research and Denelopment, 2019, 36(10): 83-90
10.3969/j.issn.1002-0268.2019.10.011

文章历史

收稿日期: 2018-03-21
引用本文 0
胡刚, 费鸿禄, 包士杰, 杨智广. 爆破荷载作用下隧道初次衬砌结构的动力响应[J]. 公路交通科技, 2019, 36(10): 83-90.
HU Gang, FEI Hong-lu, BAO Shi-jie, YANG Zhi-guang. Dynamic Response of Tunnel Primary Lining Structure under Blasting Load[J]. Journal of Highway and Transportation Research and Denelopment, 2019, 36(10): 83-90.
爆破荷载作用下隧道初次衬砌结构的动力响应
胡刚 , 费鸿禄 , 包士杰 , 杨智广     
辽宁工程技术大学 爆破技术研究院, 辽宁 阜新 123000
收稿日期: 2018-03-21
作者简介: 胡刚(1990-), 男, 辽宁阜新人, 博士研究生.
摘要: 为了研究隧道初次衬砌结构在爆破荷载作用下的动力响应，采用现场试验和数值模拟相结合的方法，应用TC-4850测振仪获得3个测点8次监测试验的质点振动速度峰值数据，依据最小二乘法拟合得出质点振动速度峰值传播规律的萨道夫斯基公式；采用LS-DYNA数值模拟软件，定义材料参数及其状态方程，在依据质点振动速度峰值传播规律可靠性分析验证数值模型合理性的基础上，建立隧道初次衬砌结构仿真模型，考虑初次衬砌强度的变化，分析隧道结构关键位置（拱脚、拱腰、拱肩、拱顶）处应力及位移的变化规律。研究结果表明：隧道初次衬砌结构X方向拱脚和拱顶处应力峰值明显大于其余关键位置，Y方向应力峰值出现在拱脚位置，为118 100 Pa，Z方向应力峰值同样出现在拱脚处，为239 100 Pa，且Z方向应力峰值明显大于X和Y方向；隧道初次衬砌结构位移峰值出现在拱腰位置，为0.361 cm，且Z方向位移峰值出现时间明显早于X和Y方向；在C30的基础上，增加C25和C35初次衬砌强度等级，随着初次衬砌强度的递增，应力呈正相关关系，位移呈负相关关系。
关键词: 隧道工程     动力响应     数值模拟     初次衬砌     爆破    
Dynamic Response of Tunnel Primary Lining Structure under Blasting Load
HU Gang, FEI Hong-lu, BAO Shi-jie, YANG Zhi-guang    
Institute of Blasting Technique, Liaoning Technical University, Fuxin Liaoning 123000, China
Abstract: To research the dynamic response of tunnel primary lining structure under blasting loads, the peak data of mass point vibration velocity at 3 measuring points are obtained from 8 monitoring tests using TC-4850 vibrometer by combing field test with numerical simulation. The Sadaovsk formula for the peak propagation rule of the mass point vibration velocity is fitted by least square method. The material parameters and state equation are defined by applying numerical simulation software LS-DYNA. Based on the of the rationality of the numerical model which is verified by the reliability analysis of the peak propagation rule of the mass point vibration velocity, the simulation model of tunnel primary lining structure is established. Considering the strength of the primary lining, the variation rules of the stress and displacement at key positions(arch foot, haunch, spandrel, vault) of the tunnel structure are analysed. The research result indicates that (1) The peak stresses of the tunnel primary lining structure on the arch foot and vault in X direction are obviously greater than those of other key positions. The peak stresses in Y and Z directions are 118 100 Pa and 239 100 Pa respectively which appear at arch foot position, and the peak stress in Z direction is larger than those in X and Y directions. (2)The peak displacement of the tunnel primary lining structure is 0.361 cm at haunch, which is 0.361 cm, and the peak displacement in Z direction appears earlier than those in X and Y directions. (3) The primary lining strength grades of C25 and C35 are increased in addition to C30. With the increase of primary lining strength, the stress is positively correlated while the displacement is negatively correlated.
Key words: tunnel engineering     dynamic response     numerical simulation     primary lining     blasting    
0 引言

施工条件的复杂和建设标准的提高, 使得我国隧道工程的发展[1]在设计理论、工程实践等方面遇到了诸多难题。"重二衬, 轻初支"的错误理念[2]又使得我国隧道工程难以在纵观全局的基础上确定出安全可靠且经济合理的方案。

关于隧道初次衬砌结构的问题[3-5], 国内外学者进行了大量研究[6-9]。李晓红等[10]针对软岩有无初期支护的隧道围岩位移进行了黏弹性解析分析; 李鹏飞等[11-12]采用数值模拟软件分析了隧道初期支护的力学特性; 高杰[13]研究了正常和缓慢铁路列车行驶动载作用下隧道初期支护的应力和位移响应; 朱永全等[14]系统地介绍了初期支护极限位移的确定方法; 仇文革等[15]通过室内相似模型试验对深埋硬岩隧道初期支护的劣化过程进行了模拟。但爆破载荷作用下初次衬砌结构的动力响应却少有分析。

本研究依托钻爆法掘进的某隧道, 采用现场监测和数值模拟相结合的手段, 分析初次衬砌结构关键位置处3方向质点振速、应力和位移的响应规律。

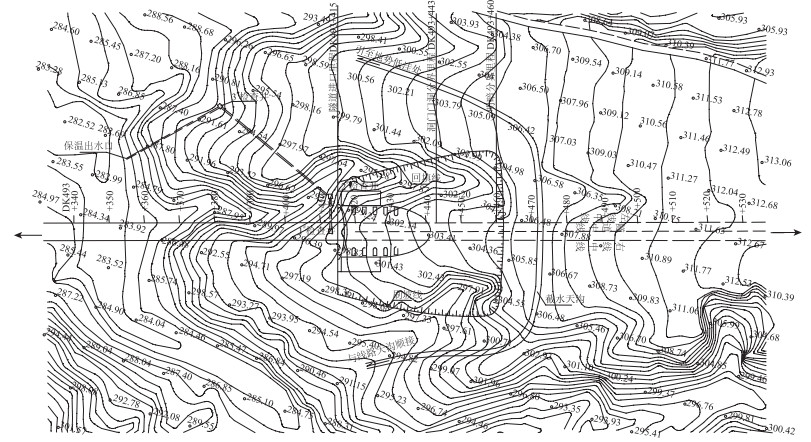
1 工程背景

京沈高速铁路某隧道位于辽宁省阜新市境内, 全长8 888 m。在隧道范围内, 西南方向比东北方向地势低, 设计位置如图 1所示, 所在位置海拔高程大于280 m, 小于490 m, 最大埋深为217.56 m。

图 1 隧道设计位置图 Fig. 1 Designed tunnel location

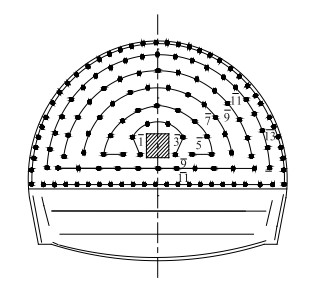
该隧道围岩等级为Ⅲ级, 宽度为12.6 m, 高度为10.1 m, 采用2级台阶法进行爆破开挖, 初次喷射混凝土12 cm厚, 型号为C30等级; 爆破掘进参数为:钻孔直径为42 mm, 钻孔深度为3~4 m, 并考虑10%~15%的超深, 炮孔布置如图 2所示; 爆破施工采用药卷直径为32 mm的2号岩石乳化炸药, 1~13段的毫秒导爆管雷管。

图 2 炮孔布置图 Fig. 2 Layout of blasting holes

2 现场监测试验

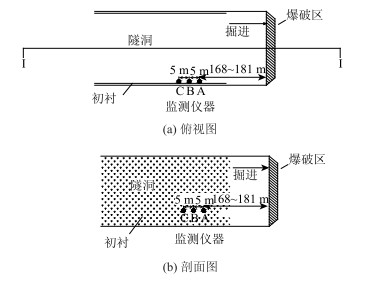
测振仪在隧道拱脚, 即仰拱顶部位置布置; X方向为隧道轴向, Y方向为隧道径向, Z方向为隧道埋深方向; 共进行8组试验, 每组采用3台仪器, 与掌子面相距168~191 m, 且两台仪器相距5 m, 具体如图 3所示。所得试验数据如表 1所示。

图 3 测点布置 Fig. 3 Layout of measuring points

表 1 监测试验数据 Tab. 1 Data of monitoring test
组别 仪器编号 爆心距/m 总药量/kg 单段最大药量/kg 质点振动速度峰值/(cm·s-1)
X方向 Y方向 Z方向
1 A 172.0 288.0 59.0 0.778 0.604 0.662
B 177.0 0.588 0.459 0.588
C 182.0 0.479 0.402 0.510
2 A 175.0 288.0 59.0 0.659 0.463 0.621
B 180.0 0.535 0.429 0.585
C 185.0 0.438 0.367 0.446
3 A 178.0 288.0 59.0 0.551 0.460 0.589
B 183.0 0.438 0.378 0.467
C 188.0 0.393 0.306 0.361
4 A 181.0 288.0 59.0 0.535 0.424 0.585
B 186.0 0.431 0.355 0.427
C 191.0 0.277 0.293 0.283
5 A 168.0 240.0 56.0 0.967 0.519 0.643
B 173.0 0.937 0.459 0.564
C 178.0 0.478 0.455 0.415
6 A 172.0 240.0 56.0 0.964 0.459 0.614
B 177.0 0.505 0.455 0.529
C 182.0 0.297 0.344 0.305
7 A 176.0 240.0 56.0 0.505 0.455 0.539
B 181.0 0.328 0.395 0.361
C 186.0 0.216 0.246 0.279
8 A 180.0 240.0 56.0 0.458 0.395 0.409
B 185.0 0.274 0.339 0.284
C 190.0 0.168 0.157 0.222
表选项

基于最小二乘法, 应用origin9.0拟合萨道夫斯基公式:

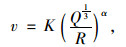
(1)

式中, v为爆破质点振动速度峰值; Q为单段最大药量; R为爆心距; K, α为相关系数。

从而得出质点振动速度峰值的传播规律[16]:

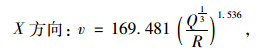
(2)
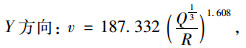
(3)
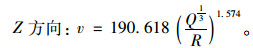
(4)
3 隧道初次衬砌结构动力响应的数值模拟分析 3.1 数值模型

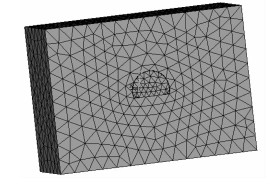
按照隧道掘进的断面尺寸进行实际比例建模, 仅分析掏槽爆破振动且不考虑仰拱结构的影响; 在满足隧道结构5~10倍范围计算区域的基础上, 为了缩短计算时间, 将三维模型尺寸设置为宽×高×厚=70 m×50 m×30 m; 围岩和空气结构模型网格划分采用自由方式, 网格尺寸分别为5 m和2 m, 初次衬砌和炸药结构模型采用扫掠方式, 具体如图 4所示; LS-DYNA数值模型采用ALE算法, 且在模型底面及侧面施加无反射边界条件。

图 4 网格划分 Fig. 4 Meshing

3.2 材料参数及状态方程

炸药材料采用HIGH-EXPLOSIVE-BURN且定义JWL状态方程; 空气为NULL且定义LINER-POLYNOMIAL状态方程; 初次衬砌材料采用SOIL-AND-FOAM模型; 围岩材料为ELASTIC模型, 材料参数见表 2。

表 2 材料参数 Tab. 2 Material parameters
材料 名称 数值 名称 数值 名称 数值
炸药 密度/(g·cm-3) 1.24 爆速/(m·s-1) 3 200 PCJ压力/Pa 1×1010
A 1×109 B 4.19×1010 R1 10
R2 3.6 ω 0.038 E0 7×109
空气 密度/(g·cm-3) 1.29×10-3 材料内能/Pa 2.5×105 相对体积 1.0
初次衬砌 密度/(g·cm-3) 2.3 剪切模量/MPa 1.3×104 体积模量/MPa 1.7×104
塑性屈服函数常数A0/MPa 1.69×102
围岩 密度/(g·cm-3) 2.4 弹性模量/MPa 1.3×104 泊松比 0.27
注:A, B, R1, R2, w, E0均为JWL状态方程中的参数。
表选项

3.3 动力响应分析 3.3.1 可靠性分析

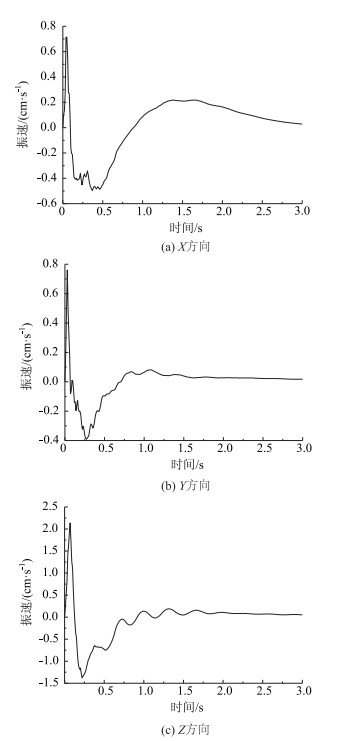
按照上述模型、材料以及隧道掘进单段最大药量进行数值计算, 得到距离掌子面10 m, 即node2768位置处X, Y, Z方向的振速时程曲线, 如图 5所示。

图 5 node2768振速时程曲线 Fig. 5 Curves of vibration velocity vs. time of 2768 node

根据图 5可以得到node2768处X, Y, Z方向质点振动速度峰值分别为0.714, 0.762 m/s和2.14 m/s; 根据式(2)~式(4)可以得到X, Y, Z方向质点振动速度峰值为0.339 5, 0.348 1 m/s和0.366 9 m/s; 由于模型材料均质、现场工况复杂、监测仪器误差等因素造成数值计算与现场监测所得质点振动速度峰值存在差别, 但是误差较小, 仍能说明数值计算结果具有较高的可靠性。

3.3.2 应力结果分析

为了探究隧道初次衬砌结构的应力变化规律, 选取拱脚(elem10473)、拱腰(elem10369)、拱肩(elem10330)、拱顶(elem10278)关键位置处的应力峰值[17-18], 如表 3所示。

表 3 应力峰值 Tab. 3 Stress peak values
关键位置 X方向应力/Pa Y方向应力/Pa Z方向应力/Pa
拱脚 163 300 118 100 239 100
拱腰 12 900 65 800 61 900
拱肩 29 700 60 800 71 500
拱顶 169 400 29 100 154 200
表选项

隧道初次衬砌结构拱脚和拱顶位置处X方向应力峰值几乎相同, 且远大于拱腰与拱肩位置处应力峰值; Y, Z方向应力峰值均出现在拱脚位置处。结合表 3可知:采用钻爆法进行隧道施工时, 隧道初次衬砌结构拱脚位置处应力峰值偏大。

纵向分析表 3可知:隧道初次衬砌结构Z方向的应力峰值在拱脚和拱肩处大于X和Y方向的应力峰值, 在拱腰和拱顶处应力峰值相差不大, 同时说明垂直方向所受应力最大。

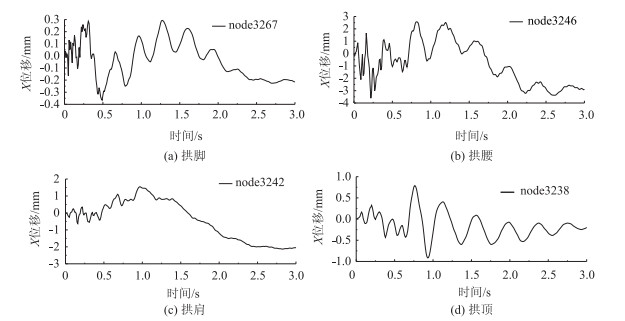
3.3.3 位移结果分析

隧道初次衬砌结构掌子面关键位置处3方向的位移时程曲线[19-20]如图 6~8所示。

图 6 X方向位移时程曲线 Fig. 6 Curves of displacement vs. time in X direction

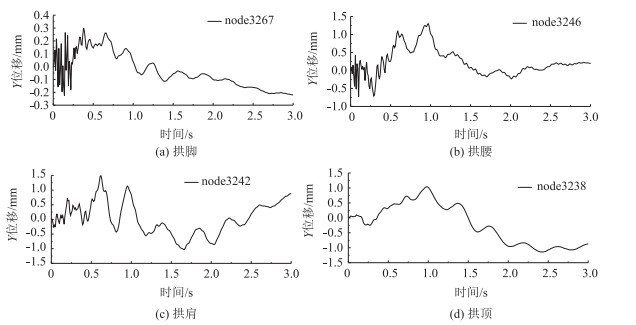
图 7 Y方向位移时程曲线 Fig. 7 Curves of displacement vs. time in Y direction

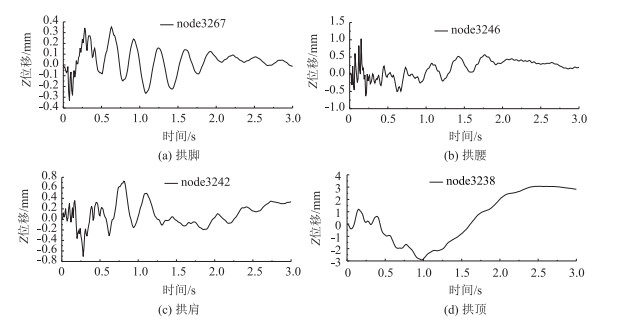
图 8 Z方向位移时程曲线 Fig. 8 Curves of displacement vs. time in Z direction

X方向位移峰值出现在拱腰位置处, 为0.361 cm; 通过图 6(a)~(d)可以发现:任意关键位置处, 隧道初次衬砌结构X方向位移峰值对应时刻均大于1.0 s。

隧道初次衬砌结构拱腰、拱肩和拱顶位置处Y方向位移峰值相差不大, 但均大于拱脚处位移峰值。通过图 7(a)~(d)可以发现:除个别点外, 隧道初次衬砌结构Y方向位移峰值对应时刻的规律与X方向相同。

Z方向位移峰值出现在拱顶位置处, 为0.307 cm; 通过图 8(a)~(d)可以发现:Z方向位移峰值对应时刻均出现在0.5 s左右。

3.3.4 初次衬砌强度改变的对比分析

在初次衬砌强度等级C30的基础上, 增加C25和C35类别, 在LS-DYNA数值模型k文件中, 改变材料参数, 计算隧道初次衬砌结构不同强度等级下3方向关键位置处的应力和位移数值结果。

(1) 应力结果对比分析

C25和C35强度下, 隧道初次衬砌结构3方向关键位置处应力峰值见表 4。

表 4 C25和C35强度下应力峰值 Tab. 4 Peak stresses under strength grades of C25 and C35
关键位置 C25强度初次衬砌结构应力/Pa C35强度初次衬砌结构应力/Pa
X方向 Y方向 Z方向 X方向 Y方向 Z方向
拱脚 142 700 109 400 210 700 170 200 119 900 239 800
拱腰 11 700 61 100 59 300 14 600 68 600 73 200
拱肩 27 600 56 600 65 400 37 300 70 300 77 500
拱顶 153 200 21 900 146 800 184 300 34 800 168 500
表选项

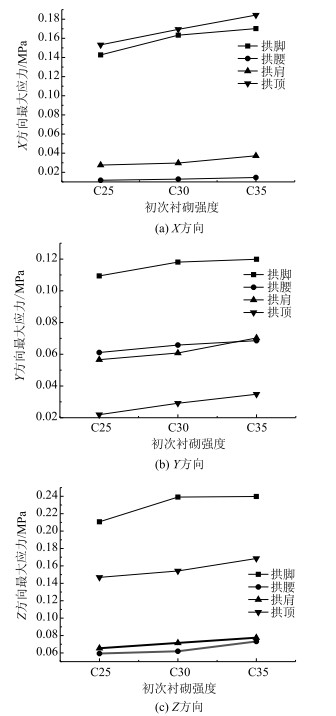
根据表 3和表 4可以得出初次衬砌强度为C25, C30和C35时X, Y, Z方向关键位置处应力峰值变化规律, 如图 9所示。

图 9 应力峰值变化规律曲线 Fig. 9 Curves of variation rule of peak stress

当隧道初次衬砌强度等级由C25增加至C35时, X方向应力峰值呈现递增趋势, 但变化幅度不大; Y方向应力峰值同样呈现递增趋势, 初次衬砌强度由C30变化至C35时, Y方向变化幅度相对较大; Z方向初次衬砌强度由C25变化至C30时, 变化幅度相对较大。

(2) 位移结果对比分析

隧道初次衬砌结构在C25和C35强度等级下3方向关键位置处位移峰值见表 5。

表 5 C25和C35强度下位移峰值表 Tab. 5 Peak displacements under strength grades of C25 and C35
关键位置 C25强度初次衬砌结构位移/cm C35强度初次衬砌结构位移/cm
X方向 Y方向 Z方向 X方向 Y方向 Z方向
拱脚 0.045 0.096 0.043 0.033 0.027 0.033
拱腰 0.363 0.165 0.105 0.352 0.123 0.101
拱肩 0.245 0.165 0.087 0.211 0.142 0.071
拱顶 0.127 0.129 0.321 0.091 0.107 0.304
表选项

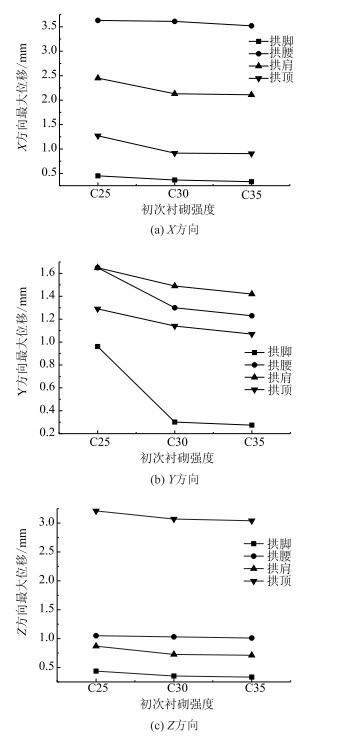
根据表 5和图 6~8可以得出初次衬砌强度为C25, C30和C35时X, Y, Z方向关键位置处位移峰值变化规律, 如图 10所示。

图 10 位移峰值变化规律曲线 Fig. 10 Curves of variation rule of peak stress

当隧道初次衬砌强度等级由C25增加至C35时, X, Y, Z方向位移峰值均呈现递减趋势, 但X和Z方向变化幅度较小; 初次衬砌强度由C25变化至C30时, Y方向变化幅度较大。

4 结论

(1) 隧道初次衬砌结构应力峰值出现在拱脚位置处, 为239 100 Pa, 且Z方向应力峰值明显大于X和Y方向。

(2) 隧道初次衬砌结构位移峰值出现在拱腰位置处, 为0.361 cm, 且Z方向位移峰值出现时间明显早于X和Y方向。

(3) 随着隧道初次衬砌强度的递增, 应力呈正相关关系, 位移呈负相关关系。适当增加拱腰处衬砌强度, 降低拱脚处衬砌强度, 可以确保隧道初次衬砌结构的经济安全。

参考文献
[1]
王梦恕. 中国铁路、隧道与地下空间的发展概况[J]. 隧道建设, 2010, 30(4): 351-364.
WANG Meng-shu. An Overview of Development of Railways, Tunnels and Underground Works in China[J]. Tunnel Construction, 2010, 30(4): 351-364.
[2]
李鹏飞, 田四明, 赵勇, 等. 高地应力软弱围岩隧道初期支护受力特性的现场监测研究[J]. 岩石力学与工程学报, 2013, 32(增2): 3509-3519.
LI Peng-fei, TIAN Si-ming, ZHAO Yong, et al. In-situ Monitoring Study of Mechanical Characteristics of Primary Lining in Weak Rock Tunnel with High Grostress[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3509-3519.
[3]
李兴华, 龙源, 纪冲, 等. 爆破地震波作用下既有圆形隧道衬砌动应力集中系数分析[J]. 岩土力学, 2013, 34(8): 2218-2224.
LI Xing-hua, LONG Yuan, JI Chong, et al. Analysis of Dynamic Stress Concentration Factor for Existing Circular Tunnel Lining under Blasting Seismic Wave[J]. Rock and Soil Mechanics, 2013, 34(8): 2218-2224.
[4]
张永兴, 杨超, 黄达, 等. 山岭隧道初期支护安全性综合评判方法[J]. 重庆大学学报:自然科学版, 2012, 35(8): 11-16.
ZHANG Yong-xing, YANG Chao, HUANG Da, et al. Analysis of Comprehensive Evaluation Method on Safety of Mountain Tunnel Initial Support[J]. Journal of Chongqing University:Natural Science Edition, 2012, 35(8): 11-16.
[5]
易长平, 卢文波, 张建华, 等. 爆破振动作用下城门洞形衬砌的临界振速研究[J]. 岩土力学, 2008, 29(8): 2203-2208.
YI Chang-ping, LU Wen-bo, ZHANG Jian-hua, et al. Study on Critical Failure Vibration Velocity of Arch with Vertical Wall Lining Subjected to Blasting Vibration[J]. Rock and Soil Mechanics, 2008, 29(8): 2203-2208.
[6]
李磊, 谭忠盛, 喻渝, 等. 成兰铁路千枚岩隧道初期支护形式试验研究[J]. 土木工程学报, 2017, 50(增1): 19-24.
LI Lei, TAN Zhong-sheng, YU Yu, et al. Experimental Study on Primary Lining form of Tunnels in Phyllite on Chengdu-Lanzhou Railway[J]. China Civil Engineering Journal, 2017, 50(S1): 19-24.
[7]
曹峰, 凌同华, 刘家澍, 等. 分岔隧道浅埋连拱段的爆破振动效应分析[J]. 公路交通科技, 2018, 35(2): 86-94.
CAO Feng, LING Tong-hua, LIU Jia-shu, et al. Analysis on Blasting Vibration Effect of Shallow Multi-arch Section of Bifurcated Tunnel[J]. Journal of Highway and Transportation Research and Development, 2018, 35(2): 86-94.
[8]
赵秀绍, 庄锦彬, 徐长节, 等. 浅覆大跨度小净距隧道中岩墙及初支力学特性研究[J]. 公路交通科技, 2015, 32(12): 100-107.
ZHAO Xiu-shao, ZHUANG Jin-bin, XU Chang-jie, et al. Study of Mechanical Properties of Middle Rock Wall and Preliminary Lining of Shallow Buried Large Span Tunnel with Small Clear Distance[J]. Journal of Highway and Transportation Research and Development, 2015, 32(12): 100-107.
[9]
QIAN F, ZHANG D, LOUIS W, et al. Study of Contact Pressure between Primary Lining and Secondary Lining for Tunnels of Passenger Dedicated Lines[J]. Chinese Journal of Rock Mechanics & Engineering, 2011, 30: 3377-3385.
[10]
李晓红, 李登新, 靳晓光, 等. 初期支护对软岩隧道围岩稳定性和位移影响分析[J]. 岩土力学, 2005, 26(8): 1207-1210.
LI Xiao-hong, LI Deng-xin, JIN Xiao-guang, et al. Discussion on Influence of Initial Support to Stability and Deformation of Surrounding Rock Mass in Soft Rock Tunnel[J]. Rock and Soil Mechanics, 2005, 26(8): 1207-1210.
[11]
扈世民, 张顶立, 李鹏飞, 等. 大断面黄土隧道初期支护适应性研究[J]. 岩土力学, 2011, 32(增2): 660-665.
HU Shi-min, ZHANG Ding-li, LI Peng-fei, et al. Analysis of Initial Support Adaptability of the Large-section Loess Tunnel[J]. Rock and Soil Mechanics, 2011, 32(S2): 660-665.
[12]
周烨, 李鹏飞, 张翾. 大断面黄土隧道初期支护合理施作时机[J]. 北京交通大学学报, 2012, 36(1): 41-47.
ZHOU Ye, LI Peng-fei, ZHANG Xuan. Study on Construction Time of Initial Support in Loess Tunnel of Large Sections[J]. Journal of Beijing Jiaotong University, 2012, 36(1): 41-47.
[13]
高杰. 三孔小净距隧洞下穿既有铁路列车振动荷载动力响应研究[J]. 石家庄铁道大学学报:自然科学版, 2016, 29(2): 39-44.
GAO Jie. Dynamic Response of Three Pipes Small Spacing Tunnels under Train-induced Dynamic Load[J]. Journal of Shijiazhuang Tiedao University:Natural Science Edition, 2016, 29(2): 39-44.
[14]
朱永全, 张素敏, 景诗庭. 铁路隧道初期支护极限位移的意义及确定[J]. 岩石力学与工程学报, 2005, 24(9): 1594-1598.
ZHU Yong-quan, ZHANG Su-min, JING Shi-ting. Concept and Determination of Limit Displacements of Primary Support System of Railway Tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(9): 1594-1598.
[15]
仇文革, 冯冀蒙, 陈雪峰, 等. 深埋硬岩隧道初期支护劣化过程衬砌力学特性试验研究[J]. 岩石力学与工程学报, 2013, 32(1): 72-77.
QIU Wen-ge, FENG Ji-meng, CHEN Xue-feng, et al. Model Testing Research on Lining Mechanical Variation with Deterioration Process of Primary Support in Deep Hard Rock Tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(1): 72-77.
[16]
李洪涛, 卢文波, 舒大强, 等. P波作用下衬砌混凝土的爆破安全振动速度研究[J]. 爆炸与冲击, 2007, 27(1): 34-39.
LI Hong-tao, LU Wen-bo, SHU Da-qiang, et al. Study on the Safety Velocity for Concrete Lining under P Wave Loading[J]. Explosion and Shock Waves, 2007, 27(1): 34-39.
[17]
饶增.隧道钻爆施工对初期支护的影响及控制标准的研究[D].北京: 北京交通大学, 2010.
RAO Zeng. Study of Impacts and Control Standard of Drilling and Blasting Method on Primary Support of Tunnel[D]. Beijing: Beijing Jiaotong University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10004-2010120547.htm
[18]
贾磊, 解咏平, 李慎奎. 爆破振动对邻近隧道衬砌安全的数值模拟分析[J]. 振动与冲击, 2015, 34(11): 173-177, 211.
JIA Lei, XIE Yong-ping, LI Shen-kui. Numerical Simulation for Impact of Blasting Vibration on Nearby Tunnel Lining Safety[J]. Journal of Vibration and Shock, 2015, 34(11): 173-177, 211.
[19]
朱正国, 孙明路, 朱永全, 等. 超小净距隧道爆破振动现场监测及动力响应分析研究[J]. 岩土力学, 2012, 33(12): 3747-3752, 3759.
ZHU Zheng-guo, SUN Ming-lu, ZHU Yong-quan, et al. Field Monitoring on Blasting Vibration and Dynamic Response of Ultra-small Spacing Tunnels[J]. Rock and Soil Mechanics, 2012, 33(12): 3747-3752, 3759.
[20]
周嘉宾, 张小旺, 侯腾飞. 浅埋偏压隧道洞口段初期支护变形分析与控制[J]. 地下空间与工程学报, 2012, 8(增1): 1411-1417.
ZHOU Jia-bin, ZHANG Xiao-wang, HOU Teng-fei. Analysis and Control of Primary Support Deformation for the Entrance of a Shallow Tunnel under Unsymmetrical Pressure[J]. Chinese Journal of Underground Space and Engineering, 2012, 8(S1): 1411-1417.