扩展功能
文章信息
- 刘辉, 章国鹏, 王羿童, 江欣国
- LIU Hui, ZHANG Guo-peng, WANG Yi-tong, JIANG Xin-guo
- 无控制交叉口交通安全影响因素分析
- Analysis on Factors Affecting Traffic Safety at Uncontrolled Intersection
- 公路交通科技, 2019, 36(9): 110-116
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(9): 110-116
- 10.3969/j.issn.1002-0268.2019.09.015
-
文章历史
- 收稿日期: 2018-04-09
无控制交叉口未规定各行驶方向车辆的路权,也缺少行人与非机动车过街信号,故机动车、非机动车、行人之间也存在较大的干扰。因此,无控制交叉口相比于信号交叉口存在着更多潜在的交通冲突,发生交通事故的风险也更高。根据交通调查数据[1],40%的交通事故发生在交叉口内,其中28%发生在无控制交叉口。由此可见,无控制交叉口的安全形势严峻。
学者们在无控制交叉口的安全研究方面已做了大量工作。关于无控制交叉口安全影响因素的分析方法主要包括两类:(1)一类是基于交通事故统计的直接分析方法,对无控制交叉口实际发生的交通事故伤亡数据进行分析,甄别对于交叉口安全具有较为严重影响的因素,包括摩托车辆[2]、行人的交通过失、大型货车数量、照明条件和限速条件[3]等。但是基于交通事故统计的直接分析方法在应用上存在着“样本获取难度大、研究周期时间长和对事故预防的指导性差”等缺陷[4]。(2)另一类则是基于交通冲突技术的间接分析方法,以冲突量和冲突严重程度为指标以衡量无控制交叉口的安全性,并针对此类指标进行影响因素分析。既有间接分析研究发现,视距障碍[5]、行人的过街等待时间、行人过街等待区域设置[6]、驾驶员的性格因素[7]等对无控制交叉口的安全运营具有显著影响。与此同时,冲突风险程度模型[8]、车流当量期望冲突量模型[9]、交通冲突预测模型[10]等一系列无控制交叉口交通冲突影响评价模型的建立也使得此类方法得到了进一步的完善。此外,基于GIS系统的无控制交叉口的参数提取系统[11]和基于视频识别技术的冲突检测方法[12]等技术手段也使得此类方法“数据精度偏低、人力消耗较大”的缺陷得到了一定的改善。
目前,对于无控制交叉口安全性研究的方法与技术已经臻于完善,但是现存研究未考虑车道等级、是否渠化等因素,所使用的影响因素还相对比较片面,也缺少综合考虑主支路交通量、车道等级、是否渠化、车道宽度和冲突车辆类型等因素的全局安全性研究,因此有必要进一步对无控制交叉口的安全影响因素进行全面分析。
本研究采用间接安全评价方法——交通冲突技术分析无控制交叉口。首先,以后侵入时间作为冲突严重程度的定量指标,将冲突严重程度分为潜在、一般、严重冲突这3个有序等级。然后,采用广义有序logit模型全面鉴别对冲突严重程度具有显著影响的车、路和环境等相关因素。最后,通过边际效应计算反映各种影响因素对交通冲突严重程度等级的影响作用程度。
1 研究方法 1.1 交通冲突技术交通冲突技术在交通安全领域被广泛采用,如研究无控制交叉口的碰撞潜力[13]、电动自行车交通冲突模型[14]等。此外,冲突数据具有采集时间短、样本量大和能够永久保存等优点,因此,本文采用交通冲突技术作为交通安全评价方法。
目前,国内外基于交通冲突技术的研究大多采用避撞时间(time to collision,TTC)和后侵入时间(post-encroachment time,PET)作为交通冲突严重程度的定量判定指标。TTC是假设冲突者双方不采取任何保护措施,持续保持原有速度和行驶方向,两车发生碰撞的预期时间;而PET则是指第1辆车离开潜在碰撞点与第2辆车到达潜在碰撞点的时间差[15]。TTC数据的收集比较困难,相比之下,PET数据只需确定车辆冲突位置且无需测量速度。因此,采用PET作为冲突严重程度判定的定量指标。
采用交通冲突技术分析前,还需解决两个问题:(1)PET最大临界值。研究发现,PET大于5 s的比例较小[16],且5 s也被作为判定交叉口能见度的临界时间[17]。故本研究以5 s作为PET的最大临界值。(2)冲突严重程度的划分方法。参考有关文献[18]的方法,根据PET累积频率分布曲线的拐点,把交通冲突分成潜在、一般、严重3个等级。
1.2 广义有序logit模型本研究把冲突严重程度分为3个等级,且3个等级之间有明显的顺序关系,为有序多分类离散变量,可采用有序响应模型进行建模。有序响应模型在交通安全领域已有广泛的应用,比如用于公交车事故严重程度[19]、驾驶员伤害严重程度[20]、自行车车辆冲突的性别差异[15]等。该模型能挖掘并预测出危险因素对冲突严重程度的影响,其中有序logit模型表达式如下:
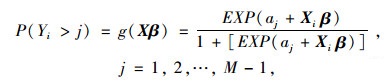
|
(1) |
式中,P(*)为某冲突严重程度等级出现的概率;Yi为第i个冲突严重程度等级;j为冲突严重程度等级;X为自变量组成的向量;β为X的系数;αj为第j个等级的常数项。
有序logit模型自变量系数β在各有序等级中始终固定,这一限制导致无法探究自变量对不同冲突严重程度等级的影响。因此,本研究采用其改进模型——广义有序logit模型,优势在于其自变量系数βj对于不同冲突严重程度等级可以不同。模型具体表达式如下:
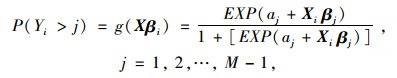
|
(2) |
或者:
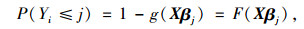
|
(3) |
式中,βj为第j等级的自变量系数向量;F(*)为标准logistics累计分布函数。
广义有序logit模型冲突严重程度Yi发生概率的计算方程组如下:
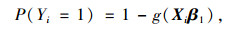
|
(4) |
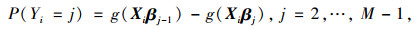
|
(5) |
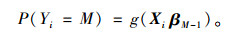
|
(6) |
为了进一步探究各种显著影响因素对冲突严重程度等级影响的大小和趋势,本研究还将计算其边际效应值。边际效应是指在其他变量固定不变时,该变量取值变化一个单位对因变量取值所产生的影响。计算方法如下:
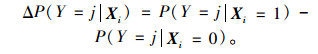
|
(7) |
选取了成都市7个存在较大安全隐患且不受其他道路设施干扰的十字形无控制平面交叉口进行交通冲突数据采集。各无控制交叉口特性见表 1。
| 特征 | 交叉口 | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 主路左转车道数 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 是否渠化 | 无 | 有 | 有 | 无 | 有 | 有 | 有 |
| 中央隔离 | 无 | 绿化带 | 隔离栏 | 无 | 无 | 无 | 无 |
| 主路路段机非隔离 | 无 | 有 | 有 | 无 | 无 | 无 | 无 |
| 交叉口机非隔离 | 无 | 有 | 无 | 无 | 无 | 无 | 无 |
| 主路车道数 | 2 | 2 | 2 | 1 | 2 | 2 | 2 |
| 次路车道数 | 1 | 1 | 1 | 1 | 1 | 2 | 1 |
| 主路车道宽度/m | 3.00 | 3.50 | 3.00 | 3.00 | 3.00 | 3.50 | 3.50 |
| 次路车道宽度/m | 3.00 | 3.25 | 2.75 | 2.75 | 3.00 | 3.50 | 3.00 |
| 主路对向停车线距离/m | 30 | 40 | 37 | 37 | 32 | 70 | 55 |
| 次路对向停车线距离/m | 32 | 60 | 40 | 37 | 28 | 70 | 55 |
| 主路限制标志的速度/(km·h-1) | 30 | 30 | 40 | 20 | 30 | 40 | 30 |
| 次路限制标志的速度/(km·h-1) | 20 | 30 | 20 | 20 | 20 | 30 | 20 |
| 注:主路为车流量较大方向的道路 | |||||||
为保证数据的一致性,本研究选择在天气晴朗的工作日的早晚高峰时段(08:00—09:00及17:30—18:30),通过现场俯视拍摄无控制交叉口来采集数据。当两车存在冲突点或区域且发生明显的减速或改变轨迹的行为时,则视为交通冲突发生。因此,在提取某个冲突数据时,首先确定冲突发生的具体位置,然后分别确定前车尾部离开冲突位置的时刻t1和后车前端到达冲突点的时刻t1,t2-t1,即为PET值。调查共获得1 034组冲突数据。
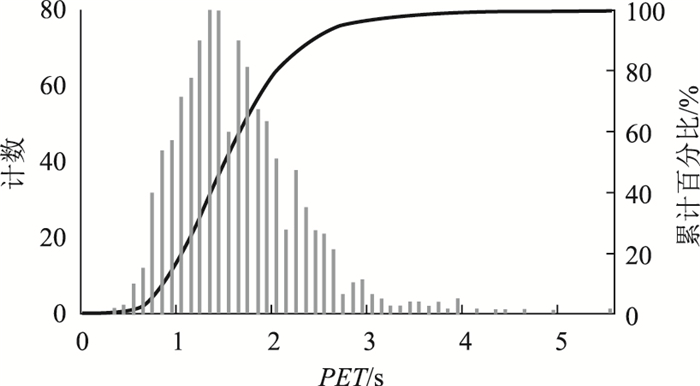
2.2 变量定义调查得到的冲突数据中PET值最大为5.5 s,最小值为0.3 s,均值为1.6 s,其频数及累计百分比分布如图 1所示。
|
| 图 1 交通冲突PET分布 Fig. 1 Distribution of PET values of traffic conflict |
| |
本文采用5 s作为PET最大临界值,取累计百分比曲线的第一个拐点对应的PET值作为严重冲突的临界点,约为1.0 s;然后将剩余的冲突数据平均分成两层,对应的临界点作为一般冲突和潜在冲突的PET临界值,约1.6 s。得表 2中划分结果。
| 冲突严重程度 | 等级 | PET范围/s | 样本量/% |
| 潜在冲突 | 1 | PET>1.6 | 455(44.0) |
| 一般冲突 | 2 | 1.0<PET≤1.6 | 402(38.9) |
| 严重冲突 | 3 | PET≤1.0 | 177(17.1) |
此外,还收集了无控制交叉口关于车、路和环境等方面的信息,变量定义见表 3。
| 变量 | 变量描述 |
| 冲突类型 | 1—分流冲突;2—合流冲突;3—直角冲突;4—追尾冲突 |
| 二次冲突 | 0—否,1—是 |
| 前车类型 | 0—大、中型车;1—小型车 |
| 前车进入车道等级 | 0—次路;1—主路(车流量较大的方向) |
| 前车接收车道等级 | 0—次路;1—主路 |
| 后车类型 | 0—大、中型车;1—小型车 |
| 后车进入车道等级 | 0—次路;1—主路 |
| 后车接收车道等级 | 0—次路;1—主路 |
| 是否停车 | 0—停车;1—减速 |
| 是否改变轨迹 | 0—未改变轨迹;1—改变轨迹 |
| 冲突过程中交叉口内大型车辆数 | 发生冲突时,交叉口内的大型车辆 |
| 主路交叉口大型车辆流量 | 一小时通过交叉口的大型车辆数目 |
| 次路交叉口大型车辆流量 | 一小时通过交叉口的大型车辆数目 |
| 交叉口交通流量 | 0—交通流量不大于262;1—交通流量小于262,pcu/h |
| 主路交叉口车流量 | 一小时的车辆数目 |
| 次路交叉口车流量 | 一小时的车辆数目 |
| 主路左转车道数 | 主路设置的左转车道的数量 |
| 是否渠化 | 0—未渠化;1—渠化 |
| 中央隔离 | 0—无隔离;1—隔离栏;2—绿化带 |
| 主路路段机非隔离 | 0—无隔离;1—有隔离 |
| 交叉口机非隔离 | 0—无隔离;1—有隔离 |
| 主路车道数目 | 车流量较大方向的车道数 |
| 次路车道数目 | 车流量较小方向的车道数 |
| 主路车道宽度/m | 机动车道宽度 |
| 次路车道宽度/m | 机动车道宽度 |
| 主路限制标志的速度/(km·h-1) | 限速标志上的速度 |
| 次路限制标志的速度/(km·h-1) | 限速标志上的速度 |
3 分析与讨论 3.1 自变量的相关性分析
在利用回归模型对冲突数据分析前,需对变量进行多重共线性检验。论文利用相关性分析检验多重共线性,将分流冲突、合流冲突、直角冲突、追尾冲突、后车接收车道等级、是否停车、冲突过程中交叉口内大型车辆数、主路交叉口车流量、次路交叉口车流量和是否渠化等10个变量依次用Var1~Var10表示,采用Stata 14.0计算变量间的Pearson相关系数,计算得到自变量的简单相关系数矩阵,如表 4所示。
| Var1 | Var2 | Var3 | Var4 | Var5 | Var6 | Var7 | Var8 | Var9 | Var10 | |
| Var1 | 1.000 | |||||||||
| Var2 | -0.129* | 1.000 | ||||||||
| Var3 | -0.443* | -0.712* | 1.000 | |||||||
| Var4 | -0.061 | -0.098 | -0.337* | 1.000 | ||||||
| Var5 | 0.026 | 0.142* | -0.139* | 0.013 | 1.000 | |||||
| Var6 | 0.155* | 0.158* | -0.254* | 0.074 | 0.070 | 1.000 | ||||
| Var7 | 0.020 | -0.040 | 0.000 | 0.047 | 0.061 | -0.162* | 1.000 | |||
| Var8 | -0.035 | -0.014 | 0.056 | -0.054 | 0.054 | -0.019 | -0.031 | 1.000 | ||
| Var9 | -0.074 | 0.040 | -0.002 | 0.025 | -0.057 | -0.044 | -0.058 | -0.054 | 1.000 | |
| Var10 | 0.005 | -0.077 | 0.112* | -0.113* | 0.083 | 0.140* | 0.023 | 0.573* | -0.117* | 1.000 |
| *在0.05水平(双侧)上显著相关。 | ||||||||||
由表 4可知,合流冲突和直角冲突之间的简单相关系数为-0.712,其他的简单相关系数均小于0.5,可初步判断不存在共线性问题。
3.2 广义有序logit模型回归冲突严重程度被分成潜在、一般和严重冲突3个等级,该变量属于有序多分类变量。选取“冲突严重程度等级”作为因变量,把表 3中的所有变量都作为模型的潜在解释变量,利用广义有序logit模型探索潜在解释变量与冲突严重程度等级间的关系。运用Stata 14.0统计分析软件对冲突数据进行广义有序logit模型回归,显著性水平取0.05。得到结果见表 5。
| 冲突严重程度 | 参数估计 | 标准差 | p值 | |
| α1 | 截距 | -2.786 | 0.510 | <0.001 |
| β1 | 冲突类型 | |||
| 分流冲突 | 1.091 | 0.422 | 0.010 | |
| 合流冲突 | 1.411 | 0.382 | <0.001 | |
| 直角冲突 | 1.911 | 0.364 | <0.001 | |
| 追尾冲突 | 0 | |||
| 后车接收车道等级 | -0.176 | 0.135 | 0.193 | |
| 是否停车 | 0.871 | 0.159 | <0.001 | |
| 冲突过程中交叉口内大型车辆数 | -0.217 | 0.106 | 0.041 | |
| 主路交叉口车流量 | 0.002 | 0.000 | <0.001 | |
| 次路交叉口车流量 | 0.001 | 0.000 | 0.010 | |
| 是否渠化 | -1.218 | 0.196 | <0.001 | |
| α2 | 截距 | -5.877 | 1.182 | <0.001 |
| β2 | 冲突类型 | |||
| 分流冲突 | 1.607 | 1.106 | 0.146 | |
| 合流冲突 | 2.120 | 1.041 | 0.042 | |
| 直角冲突 | 2.909 | 1.027 | 0.005 | |
| 追尾冲突 | 0 | |||
| 后车接收车道等级 | -0.344 | 0.175 | 0.050 | |
| 是否停车 | 1.109 | 0.225 | <0.001 | |
| 冲突过程中交叉口内大型车辆数 | -0.270 | 0.241 | 0.262 | |
| 主路交叉口车流量 | 0.002 | 0.001 | 0.013 | |
| 次路交叉口车流量 | 0.002 | 0.001 | 0.016 | |
| 是否渠化 | -1.176 | 0.266 | <0.001 | |
根据回归结果,冲突类型、后车接收车道等级、是否停车、冲突过程中交叉口内大型车辆数、主路交叉口车流量、次路交叉口车流量、是否渠化等变量与交通冲突严重程度显著相关。并且,回归结果还反映了在广义有序logit模型中同一变量对不同冲突严重程度等级的影响存在差异,其中后车接收车道等级显著影响潜在冲突发生的概率,但对一般冲突发生的概率无显著影响;而冲突过程中交叉口内大型车辆数对一般冲突发生具有显著影响,却不影响潜在冲突发生的概率。
3.3 边际效应及结果分析边际效应反映了某一变量改变一个单位对冲突严重程度等级产生的影响。模型回归得到的显著影响变量对冲突严重程度等级的边际效应影响见表 6。
| 变量 | 潜在冲突 | 一般冲突 | 严重冲突 | |
| 冲突类型 | 分流冲突 | -0.237 | -0.057 | 0.294 |
| 合流冲突 | -0.303 | -0.082 | 0.385 | |
| 直角冲突 | -0.443 | 0.186 | 0.256 | |
| 追尾冲突 | 0 | 0 | 0 | |
| 后车接收车道等级 | 0.043 | -0.001 | -0.042 | |
| 是否停车 | -0.214 | 0.010 | 0.115 | |
| 冲突过程中交叉口内大型车辆数 | 0.053 | -0.021 | -0.033 | |
| 主路交叉口车流量 | -0.000 4 | 0.000 2 | 0.000 2 | |
| 次路交叉口车流量 | -0.000 3 | 0.000 1 | 0.000 2 | |
| 是否渠化 | 0.277 | -0.104 | -0.173 | |
由边际效应计算结果可知,发生分流、合流和直角冲突时,其严重冲突发生概率分别提高29.4%, 38.5%和25.6%,且直角冲突中一般冲突的发生概率提高18.6%。同时,在采集到的冲突数据中发现,分流、合流和直角冲突这3类冲突发生的几率大于95%[9],其中直角冲突占比为70.9%。由此可见,直角冲突的发生概率和严重程度均最高,这说明了无控制交叉口事故预防的重点在于减少直角冲突。
然而,当后车接收车道在主路时,其冲突严重程度较低。分析冲突数据发现,在后车接收车道为次路的冲突中,冲突类型为合流和直角冲突的严重冲突比例高于均值6.6%和3.7%。主要原因是由于在无控制交叉口内,直行及转弯等多股车流在接收车道处汇合,由于次路车道数目较主路少且较窄,驾驶员为争夺路权而加速行驶,相互争抢,此时极易发生严重的合流冲突。因此,在次路接收车辆较多的无控制交叉口,驾驶员应更加谨慎驾驶。
车辆经过无控制交叉口是否停车也会显著影响冲突严重程度。相比于停车让行,冲突车辆未停车将使得严重的发生概率提高11.5%。若车辆进入交叉口前停车等待以选择合理间隙通过,即使通过时发生冲突,因车辆速度较小,其冲突严重程度较低[21]。因此,对于交通冲突严重的交叉口,驾驶员应耐心停车等待以选择合理通过间隙。
交叉口内的大型车辆数与冲突严重程度呈负相关。因为当冲突过程中交叉口内的大型车辆较多时,容易遮挡附近车辆视线,使得驾驶员更加谨慎[22];此外,大型车辆体积较大且速度较慢,容易阻挡各方车流的行车视距,导致其他车辆减速甚至停车等待,从而间接降低了冲突严重程度。
交叉口车流量也是冲突严重程度的影响因素之一。交叉口每增加一辆机动车,其严重冲突发生概率提高0.02%。主要原因是机动车流量增大,车辆间隙减小,使得不同方向上的车流相互干扰更为严重,驾驶员为节省时间容易在较小间隙冒险通过交叉口,导致冲突的数量及严重程度均增加,使得交叉口趋于不安全[23]。因此,经过车流量大的无控制交叉口时,驾驶员应耐心等待以选择合理通过间隙。
由边际效应计算结果还发现,交叉口是否渠化会显著影响冲突严重程度,渠化交叉口严重和一般冲突的发生概率比非渠化交叉口分别降低17.3%和10.4%。合理的渠化设计能规范各方向机动车流行驶路径,减少交叉口内的冲突点,降低冲突发生的可能性。因此,针对有条件的无控制交叉口,可以考虑对其进出口道进行合理的渠化设计。
4 结论(1) 采用了交通冲突技术交通安全评价方法,选取交通冲突中的PET值作为冲突严重程度的定量指标,利用了广义有序logit模型探究车、路和环境等因素对无控制交叉口交通安全的影响作用。
(2) 分析结果表明在无控制交叉口内,直角冲突最为严重;后车未停车、交叉口车流量增大、交叉口未渠化等,将加剧冲突严重程度。
(3) 为提高无控制交叉口安全性,可对其进行合理的渠化设计;在经过无控制交叉口时,驾驶员应主动减速甚至停车等待,以选择合理的通过间隙。
需要说明的是,本研究采用的交通冲突技术属于间接安全评价方法,而交通事故能更直接地反映出交通安全状况,未来关于无控制交叉口的安全研究,可以在完善交通事故记录的基础上,开展其交通事故特征分析,研究事故类型分布和事故严重程度等问题。
| [1] |
WU Z, YANG J, HUANG L. Study on the Collision Avoidance Strategy at Unsignalized Intersection Based on PreScan Simulation[J]. Procedia-Social and Behavioral Sciences, 2013, 96: 1315-1321. |
| [2] |
STRAUSS J, MIRANDA-MORENO L F, MORENCY P. Multimodal Injury Risk Analysis of Road Users at Signalized and Non-signalized Intersections[J]. Accident Analysis & Prevention, 2014, 71(10): 201-209. |
| [3] |
HALEEM K, ALLURI P, GAN A. Analyzing Pedestrian Crash Injury Severity at Signalized and Non-signalized Locations[J]. Accident Analysis & Prevention, 2015, 81: 14-23. |
| [4] |
周伟, 罗石贵. 路段交通事故多发点的冲突判定方法[J]. 中国公路学报, 2000, 13(1): 81-86. ZHOU Wei, LUO Shi-gui. Traffic Conflict Identification of Road Accident Blackspots[J]. China Journal of Highway and Transport, 2000, 13(1): 81-86. |
| [5] |
LAURESHYN A, DE C T, KARLSSON C, et al. In Search of the Severity Dimension of Traffic Events:Extended Delta-V as a Traffic Conflict Indicator[J]. Accident Analysis & Prevention, 2017, 98: 46-56. |
| [6] |
ALMODFER R, XIONG S, FANG Z, et al. Quantitative Analysis of Lane-based Pedestrian-vehicle Conflict at a Non-signalized Marked Crosswalk[J]. Transportation Research Part F:Traffic Psychology & Behaviour, 2015, 42: 468-478. |
| [7] |
张邻, 黄选伟, 吴伟明. 无信号交叉口交通冲突分析[J]. 重庆交通大学学报:自然科学版, 2015, 34(3): 105-111. ZHANG Lin, HUANG Xuan-wei, WU Wei-ming. Analysis of Traffic Conflict in Non-signalized Intersection[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2015, 34(3): 105-111. |
| [8] |
YIN W, ZOU Q, LÜ C, et al. A Quantitative Model of Conflict Risk Degree at Non-signalized Intersections[J]. Procedia Engineering, 2016, 137: 171-179. |
| [9] |
袁黎, 刘汉龙. 基于车流当量期望冲突量无信号交叉口安全风险分析研究[J]. 武汉理工大学学报:交通科学与工程版, 2014(4): 757-762. YUAN Li, LIU Han-long. Research on Risk of Un-signalized Intersection Based on Expected Traffic Conflict Unit[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2014(4): 757-762. |
| [10] |
项乔君, 卢川, 吴群, 等. 无信号控制平面交叉口交通冲突预测模型研究[J]. 公路交通科技, 2009, 26(5): 132-135. XIANG Qiao-jun, LU Chuan, WU Qun, et al. Research on Traffic Conflict Prediction Model of Unsignalized Highway Intersection[J]. Journal of Highway and Transportation Research and Development, 2009, 26(5): 132-135. |
| [11] |
SIMANDL J, GRAETTINGER A J, SMITH R K, et al. Utilizing GIS to Develop a Non-signalized Intersection Data Inventory for Safety Analysis[J]. International Journal of Engineering Research & Applications, 2015, 5(4): 50-60. |
| [12] |
刘淼淼, 鲁光泉, 王云鹏, 等. 交叉口交通冲突严重程度量化方法[J]. 交通运输工程学报, 2012, 12(3): 120-126. LIU Miao-miao, LU Guang-quan, WANG Yun-peng, et al. Quantitative Method of Traffic Conflict Severity at Intersection[J]. Journal of Traffic and Transportation Engineering, 2012, 12(3): 120-126. |
| [13] |
IBITOYE B A, ABDULWAHAB R, BAMIDELE A. Evaluation of Collision Potential at Four-legged Unsignalized Intersection Using Traffic Conflict Technique[J]. European Journal of Engineering Research and Science, 2017, 2(3): 1-4. |
| [14] |
张开冉, 邱谦谦. 平面交叉口电动自行车交通冲突模型研究[J]. 安全与环境学报, 2017, 17(2): 422-425. ZHANG Kai-ran, QIU Qian-qian. Innovative Traffic Jam-dissolving Model for the Motor-bicycles in the Cross-road Sections[J]. Journal of Safety and Environment, 2017, 17(2): 422-425. |
| [15] |
STIPANCIC J, ZANGENEHPOUR S, MIRANDA-MORENO L, et al. Investigating the Gender Differences on Bicycle-vehicle Conflicts at Urban Intersections Using an Ordered Logit Methodology[J]. Accident Analysis & Prevention, 2016, 97: 19-27. |
| [16] |
ZHENG L, ISMAIL K, MENG X. Investigating the Heterogeneity of Post Encroachment Time Thresholds Determined by Peak over Threshold Approach[J]. Transportation Research Record, 2016, 2601: 17-23. |
| [17] |
AASHTO. A Policy on Geometric Design of Highways and Streets, 1994[M]. Washington, D. C.: American Association of State Highway and Transportation Official, 2001.
|
| [18] |
JIANG X, ZHANG G, WEI B, et al. Safety Evaluation of Signalized Intersections with Left-turn Waiting Area in China[J]. Accident Analysis & Prevention, 2015, 95(Pt B): 461-469. |
| [19] |
KAPLAN S, PRATO C G. Risk Factors Associated with Bus Accident Severity in the United States:A Generalized Ordered Logit Model[J]. Journal of Safety Research, 2012, 43(3): 171-180. |
| [20] |
CHEN C, ZHANG G, HUANG H, et al. Examining Driver Injury Severity Outcomes in Rural Non-interstate Roadway Crashes Using a Hierarchical Ordered Logit Model[J]. Accident Analysis & Prevention, 2016, 96: 79-87. |
| [21] |
王玉全, 邢芳, 郭伟伟. 信号交叉口混合交通冲突研究[J]. 中国安全科学学报, 2016, 26(6): 47-51. WANG Yu-quan, XING Fang, GUO Wei-wei. Research on Mixed Traffic Conflict at Signalized Intersection[J]. China Safety Science Journal, 2016, 26(6): 47-51. |
| [22] |
JIANG X, ZHANG G, ZHOU Y, et al. Safety Assessment of Signalized Intersections with Through-movement Waiting Area in China[J]. Safety Science, 2017, 95: 28-37. |
| [23] |
RAO V T, RENGARAJU V R. Probabilistic Model for Conflicts at Urban Uncontrolled Intersection[J]. Journal of Transportation Engineering, 1997, 123(1): 81-84. |
 2019, Vol. 36
2019, Vol. 36
