扩展功能
文章信息
- 孟嘉铭, 林南南, 史宏飞
- MENG Jia-ming, LIN Nan-nan, SHI Hong-fei
- 基于鲁棒优化的公交实时到站信息优化
- Optimization of Bus Real-time Arrival Information Based on Robust Optimization
- 公路交通科技, 2019, 36(9): 103-109
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(9): 103-109
- 10.3969/j.issn.1002-0268.2019.09.014
-
文章历史
- 收稿日期: 2018-08-23
2. 上海工程技术大学 轨道交通学院, 上海 201620;
3. 北控水务集团有限公司, 北京 100102
2. School of Urban Rail Transportation, Shanghai University of Engineering Science, Shanghai 201620, China;
3. Beijing Enterprises Water Group Limited, Beijing 100102, China
由于城市人口众多,城市居民工作出行的半径越来越大,同时城市化加大了对公交系统的依赖性。公交系统将成为一个城市能否良性运转的重要标志之一,其中包括政府管理部门、公交公司、城市居民、广告主、智能交通等将通过实时公交连接起来[1]。为出行者提供准确及时的信息服务,将能吸引更多出行者使用公共交通,从而加速促进公共交通的发展。换言之,实时公交APP改善了公交出行的体验,加强了人们对公交出行的选择意愿,继而提升了公交出行的选择率。而实时公交APP提供的实时信息是否准确,尤其是在车辆运行延误的情况下,将最直观地影响乘客感知[2]。
实时到站信息是公交实时信息中的一项重要指标,不可靠的到站信息容易误导乘客。例如乘客按照公交实时信息提供的到站时间进站等候,但是公交车却提前到达并离开,此时乘客不得不继续等待下一辆公交车或者换乘其他出行方案;如果公交车发生延误,此时乘客对延误的忍耐力远低于其不知道到站时间(即正常等待时)的忍耐力,而且会对公交实时信息的精确度产生质疑。因此,十分有必要对公交实时信息的到站信息进行优化。
1 文献综述早在20世纪70年代左右,国外的学者就对公交车到站时间的预测开展了一系列研究,但那时绝大多数的城市公交系统处于“定点发车,两头卡点”的人工调节模式[3],缺少对运营公交车的通讯与监控,导致了行车间隔不固定,经常导致公交车间隔时间过长、“串车”等现象出现,严重影响了公交车到站时间的预测,以至于专家设置的预测方法、预测模型只能通过对比历史规律来获取数据[4-5],所以预测的结果与预期具有较大差别,并且发现一旦道路或公交车上出现特殊状况,预测方法与预测模型便不能发挥应有的作用,所以学者们开始研究更贴近实际应用的预测模型。进入21世纪后,随着计算机网络信息技术、GPS、GIS还有硬件的快速发展与应用,公交车GPS系统开始出现,不仅能把公交车的的实时数据传输到公交公司,将实时的公交车到站信息传达给乘客,而且将数据提供给研究交通系统的人员进行更深一步的试验与研究,建立了越来越优秀的预测方法与模型,在此基础上深入公交到站时间预测的研究,提高预测准确度。目前,国内外关于公交到站时间预测的模型一般分为两种,分别是基于统计学的预测模型和基于分析的预测模型。前者通过历史规律来预测未来的公交车到站时间,后者考虑影响公交车到站时间的各种因素而建立对应的预测模型。已有研究使用的模型主要有:使用历史数据的模型[6-8]、利用回归理论的模型[9]、卡尔曼滤波(Kalman Filter)模型[10]、人工神经网络模型(ANN)[11-12]、基于支持向量机(SVM)的预测模型[12-15]等。此外,还有其他预测方法,比如k-NN分类法(k-NN Classifier)[16]、萤火虫群优化方法(Glowworm Swarm Optimization,GSO)[17]、多源数据法(Meta-model Approach)[18]、元模型(Meta-model Approach)[19]、实时数据(Real-time Data)[20],以及混合法(Hybrid Method)[21]。以上研究方法中,有些需要对模型做出特定的假设条件,有些完全依靠研究者的研究经验和知识水平对数据进行预处理以选择控制变量,同时模型的预测精度也有待提高。
因此,本研究通过鲁棒线性优化,考虑突发客流等需求不确定条件下,在现有的公交实时到站时间预测中增加运行延误信息,以最大节省乘客的出行时间成本为目标,建立优化模型,给乘客提供辅助信息来调整其出行计划及行为,降低不准确的公交实时到站时间预测对乘客的影响。
2 鲁棒优化模型建立考虑一条有n(n≥3)个公交站点的公交线路,如图 1所示。
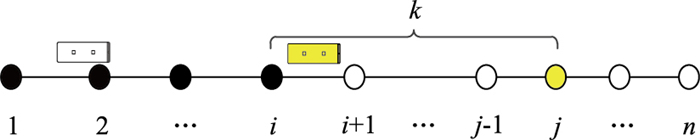
|
| 图 1 研究公交线路示意图 Fig. 1 Schematic diagram of study bus line |
| |
在图 1中,站点j是乘客目前候车站点,灰色的公交车是距离站点j最近的公交车。通过公交实时信息,乘客可以在终端(比如手机公交APP)查看到最近的公交车已离开站i,距离站点j还有k站的距离,预测运行时间是Tij,运行时间估计误差为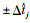
图 2表示的是客流量和时间之间的关系,包括乘客集散和公交车进出站,即在没有公交实时信息的情况下,在站点j乘客数量和时间的关系,其中λ0j为乘客到达率;μ为乘客平均上车速率;Q为乘客数量;t为时间。已有研究中,表明即使发车频率高如5 min一班,也会有乘客根据或者说受到公交到站信息提供的影响选择合理时间到站候车,呈现出离信息提供给定的公交到离站时间越近,到达站点的乘客越多的特征,乘客的到达率服从混合分布[22-23]。本研究为了保证所建鲁棒优化模型的线性特征,假设乘客在某时间段内均匀到达。
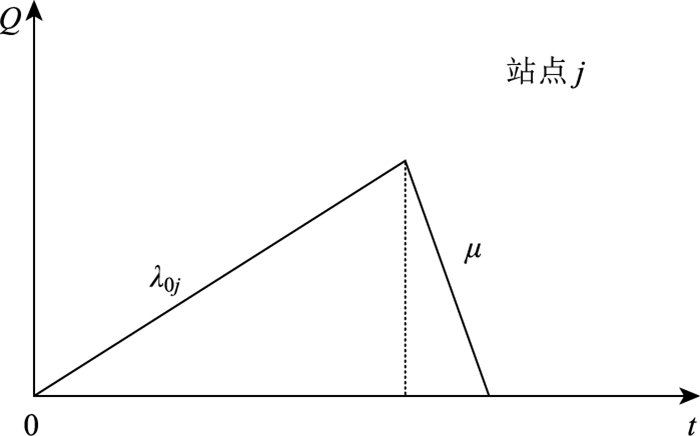
|
| 图 2 没有公交实时信息时站点客流量和时间的关系示意图 Fig. 2 Schematic diagram of relationship between passenger flow and time at bus station without real-time bus information |
| |
在获知公交实时信息的情况下,尤其是公交车目前所在位置、预计到站时间等,乘客的出行行为会发生变化。部分乘客可能根据时间安排选择去做其他事情而不是枯燥的到公交站点候车。此时,站点j乘客数量和时间之间的关系变成如图 3所示,其中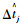
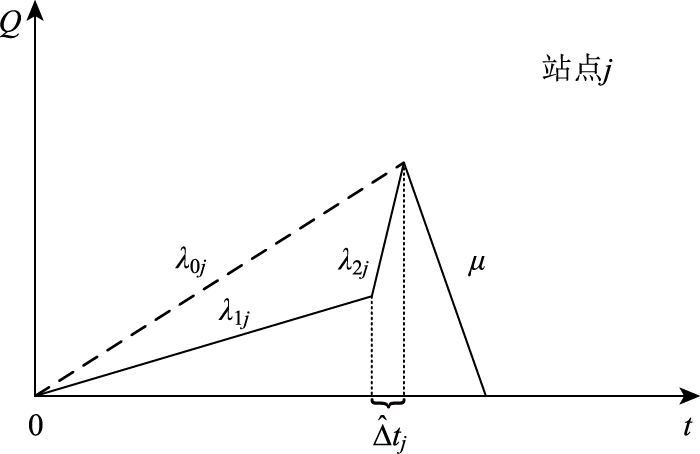
|
| 图 3 有公交实时信息时站点客流量和时间的关系示意图 Fig. 3 Schematic diagram of relationship between passenger flow and time at bus station with real-time bus information |
| |
通过公交延误传播理论,可以得知,如果公交车在到达站点i时发生了Δti的延误,那么在离开时会有更大的延误Δt′i,如图 4所示。
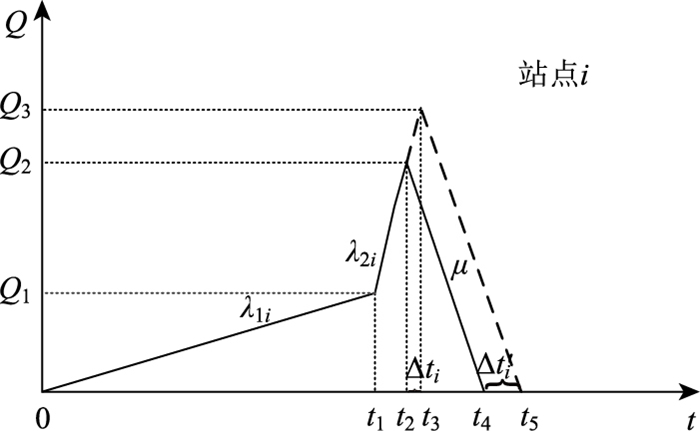
|
| 图 4 公交延误传播理论示意图 Fig. 4 Schematic diagram of bus delay propagation theory |
| |
其中,t1为根据公交实时信息调整候车行为的乘客实际准备进站时间;t2为公交车计划进站时间;t3为公交车实际进站时间;t4为公交车计划离站时间;t5为公交车实际离站时间;Q1,Q2,Q3分别为对应时刻站点的乘客数量;λ1i为0~t1时间段站点i乘客的平均到达率;λ2i为t1~t2时间段站点i乘客的平均到达率。根据图 4,可以得到:
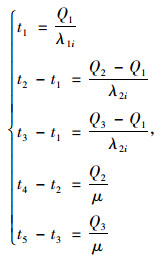
|
(1) |
因此,
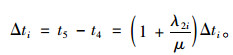
|
(2) |
另外,如果公交车发生延误,驾驶员会采取一定的措施去尽可能的降低延误,比如调整车速,该行为被称为驾驶员恢复行为。由于驾驶员恢复行为的存在,公交车从站点i到达下一站点i+1的延误会降低至αΔt′i,其中α为驾驶员恢复系数。则,
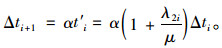
|
(3) |
以此类推,可以得到公交车到达站点j时的延误Δtj,站点j与站点i之间有k个站点的距离。其中λ2s为t1~t2时间段站点s乘客的平均到达率, 则有,
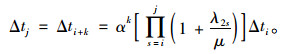
|
(4) |
所以当有公交实时信息,同时公交运行发生延误时站点j乘客数量和时间的关系就变成了如图 5所示。
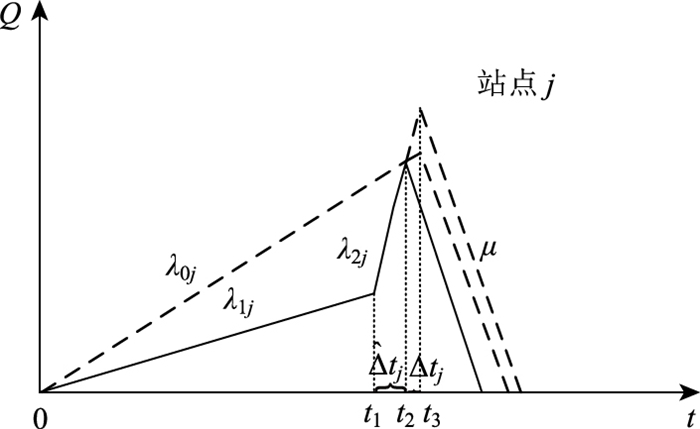
|
| 图 5 有公交实时信息且公交发生延误时客流量与时间的关系示意图 Fig. 5 Schematic diagram of relationship between passenger flow and time with real-time bus information and delay |
| |
令Cj为乘客在站点j受公交实时信息影响节省的时间成本;c0为没有公交实时信息时乘客的候车时间成本系数;c1为有公交实时信息时乘客在时间段(0, t1)内的候车时间成本系数;c2为有公交实时信息时乘客在时间段(t1, t3)内的候车时间成本系数。因此可以得到Cj的表达式如下所示。
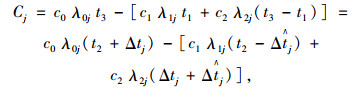
|
(5) |
式中,t2的值即为公交车的发车间隔,t2=h,那么有,
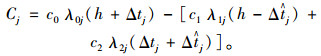
|
(6) |
与图 4表示的一样,可以看出Cj的值随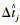
在实际生活中,经常会发生突发客流,尤其是在高峰时段,如下班高峰或者学生放学等,以至于一辆公交车无法将全部乘客带走。对于被滞留在站点的乘客而言,他们不得不继续等待下一辆公交车。此时他们每人的候车成本平均增加了h,乘客总的节省时间成本下降了(Q0·h),其中Q0是被滞留在站点的乘客数量,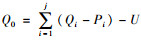
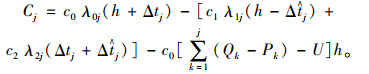
|
(7) |
以最大化研究公交线路所有站点乘客节省的时间成本为目标,建立以下优化模型。
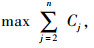
|
(8) |
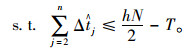
|
在式(7)中,h和Δtj(α, λ)为已知的;c和λ为随机变量;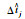

|
(9) |
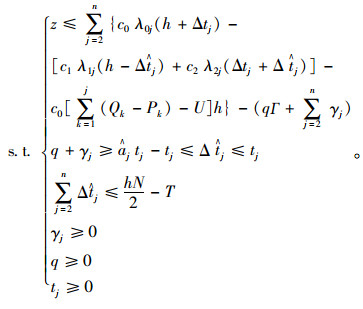
|
(10) |
本研究通过拥挤度、交通堵塞、噪音、环境、候车时间和服务等6个指标,对上海已提供公交实时信息服务的各公交线路进行比较。通过各指标调查结果的对比,最终选择一条评分较高的市内公交49路和一条评分较低的市域公交北安线分别对模型进行验证。
目前两路公交线路分别设置20和36个公交站点,包括首末站;运营公交车辆数分别为30辆和20辆;最大载客量均为86人次/车;晚高峰时段发车间隔分别为5 min和10 min。
首先对模型中各变量值的设定进行说明。关于驾驶员行为恢复系数α,Chen等(2005)应用美国东北部一家公交公司的AVL数据和时刻表信息获得了某公交线路上驾驶员恢复系数分布。他们的研究结果显示在大部分运行路段,驾驶员恢复系数平均值主要分布在-0.5~0.5之间[26]。在本研究中假设驾驶员恢复系数是非负数,也就是说,驾驶员总是在努力追赶运行延误。因此,可以假设驾驶员恢复系数α随机分布在区间[0,0.5]上。根据式(4),可以通过收集到的AVL数据计算得到Δtj的值。另外,根据客流调查结果,假设乘客平均上车速率μ为15人/min。
因为建模时考虑突发客流等情况,将乘客需求设定为不确定因素,因此模型中的不确定变量为乘客到达率λ1j和λ2j。定义不确定变量λ1j随机分布在区间[0, λj ]上,不确定变量λ2j随机分布在区间[λj, λj-max]上,其中λj是平均值,λj-max是最大值。λ1j和λ2j是不相关的独立变量。
关于c0,c1和c2值的设定,提出了3种假设情况:Case1,Case2和Case3。这3种情况分别考虑了3种不同的乘客思想状态,同时也反映了公交实时信息的应用普及程度。Case1假设所有乘客对公交实时信息的态度是一样的;Case2假设使用公交实时信息的乘客比不使用公交实时信息的乘客等待时间成本更高;Case3比Case2设定了更高的等待时间成本。求解结果及对应的曲线图分别如表 1和表 2所示。
| No.49 | Case 1 c0=c1=c2=1 |
Case 2 c0=1, c1=0.5, c2=2 |
Case 3 c0=1, c1=0.3, c2=3 |
|||||
| 站点j | 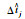 |
Cj | 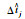 |
Cj | 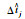 |
Cj | ||
| 1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| 2 | 0.03 | 0.93 | 0.03 | 0.93 | 0.02 | 0.93 | ||
| 3 | 0.15 | 0.78 | 0.14 | 0.79 | 0.12 | 0.80 | ||
| 4 | 0.96 | 5.05 | 0.86 | 5.24 | 0.78 | 5.41 | ||
| 5 | 1.76 | 7.78 | 1.58 | 8.27 | 1.43 | 8.71 | ||
| 6 | 1.29 | -0.74 | 1.16 | 0.75 | 1.04 | 1.05 | ||
| 7 | 1.97 | 2.45 | 1.77 | 2.88 | 1.60 | 3.27 | ||
| 8 | 2.38 | 2.35 | 2.14 | 2.92 | 1.93 | 3.43 | ||
| 9 | 1.99 | 2.43 | 1.79 | 2.87 | 1.61 | 3.27 | ||
| 10 | 2.82 | 2.95 | 2.54 | 3.62 | 2.28 | 4.23 | ||
| 11 | 2.79 | 2.22 | 2.51 | 2.67 | 2.26 | 3.07 | ||
| 12 | 3.44 | 0.52 | 3.10 | 1.41 | 2.79 | 2.22 | ||
| 13 | 1.94 | 1.67 | 1.75 | 1.87 | 1.57 | 2.04 | ||
| 14 | 2.77 | -2.58 | 2.49 | -0.86 | 2.24 | 0.82 | ||
| 15 | 1.52 | -0.66 | 1.37 | -0.51 | 1.23 | -0.38 | ||
| 16 | 1.98 | -0.22 | 1.78 | 0.29 | 1.60 | 0.75 | ||
| 17 | 1.81 | 3.83 | 1.63 | 4.05 | 1.47 | 4.24 | ||
| 18 | 1.51 | 0.04 | 1.36 | 1.55 | 1.22 | 0.91 | ||
| 19 | 0.93 | 0.81 | 0.84 | 0.83 | 0.75 | 0.85 | ||
| 20 | 0.48 | 0.00 | 0.43 | 0.00 | 0.39 | 0.00 | ||
| 总节省成本∑Cj | — | 29.59 | — | 39.58 | — | 45.63 | ||
| 北安线 | Case 1 c0=c1=c2=1 |
Case 2 c0=1, c1=0.5, c2=2 |
Case 3 c0=1, c1=0.3, c2 =3 |
|||||
| 站点j | 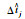 |
Cj | 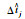 |
Cj | 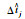 |
Cj | ||
| 1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| 2 | 0.14 | 0.96 | 0.13 | 0.96 | 0.12 | 0.96 | ||
| 3 | 0.26 | 0.92 | 0.23 | 0.92 | 0.21 | 0.93 | ||
| 4 | 0.52 | 0.62 | 0.47 | 0.64 | 0.42 | 0.66 | ||
| 5 | 1.39 | 1.43 | 1.25 | 1.47 | 1.12 | 1.51 | ||
| 6 | 1.22 | 2.12 | 1.10 | 2.18 | 0.99 | 2.23 | ||
| 7 | 2.14 | 5.50 | 1.93 | 5.65 | 1.74 | 5.79 | ||
| 8 | 2.50 | 0.22 | 2.25 | 0.27 | 2.03 | 0.32 | ||
| 9 | 2.13 | 3.15 | 1.92 | 3.23 | 1.73 | 3.31 | ||
| 10 | 2.66 | 0.17 | 2.40 | 0.22 | 2.16 | 0.27 | ||
| 11 | 3.10 | 4.87 | 2.79 | 5.15 | 2.51 | 5.40 | ||
| 12 | 3.59 | -0.99 | 3.23 | 0.54 | 2.91 | 0.77 | ||
| 13 | 3.50 | 4.46 | 3.15 | 4.78 | 2.84 | 5.06 | ||
| 14 | 4.28 | 4.24 | 3.86 | 4.67 | 3.47 | 5.05 | ||
| 15 | 4.28 | -1.23 | 3.85 | 0.37 | 3.46 | 0.49 | ||
| 16 | 4.19 | -0.64 | 3.77 | -0.26 | 3.40 | 0.08 | ||
| 17 | 4.93 | 3.01 | 4.44 | 3.46 | 3.99 | 3.86 | ||
| 18 | 5.02 | 0.87 | 4.52 | 1.27 | 4.07 | 1.63 | ||
| 19 | 5.14 | 1.23 | 4.63 | 1.70 | 4.16 | 2.11 | ||
| 20 | 5.33 | 1.02 | 4.80 | 1.50 | 4.32 | 1.93 | ||
| 21 | 5.81 | -0.74 | 5.22 | -0.16 | 4.70 | 0.36 | ||
| 22 | 5.91 | 0.75 | 5.32 | 1.58 | 4.79 | 2.32 | ||
| 23 | 6.20 | 0.42 | 5.58 | 1.04 | 5.02 | 1.60 | ||
| 24 | 6.77 | -3.45 | 6.09 | 0.01 | 5.48 | 0.56 | ||
| 25 | 7.09 | -2.17 | 6.38 | -1.39 | 5.74 | -0.68 | ||
| 26 | 7.01 | -1.17 | 6.31 | -0.61 | 5.68 | -0.10 | ||
| 27 | 6.16 | 0.48 | 5.54 | 1.09 | 4.99 | 1.65 | ||
| 28 | 5.10 | 1.27 | 4.59 | 1.73 | 4.13 | 2.15 | ||
| 29 | 4.89 | 1.00 | 4.40 | 1.53 | 3.96 | 2.02 | ||
| 30 | 4.42 | 0.92 | 3.98 | 1.23 | 3.58 | 1.51 | ||
| 31 | 4.34 | -0.48 | 3.90 | 0.69 | 3.51 | 0.93 | ||
| 32 | 4.01 | 0.70 | 3.61 | 0.94 | 3.25 | 1.16 | ||
| 33 | 3.36 | 0.58 | 3.02 | 0.74 | 2.72 | 0.89 | ||
| 34 | 3.14 | -0.64 | 2.83 | -0.55 | 2.54 | -0.46 | ||
| 35 | 2.99 | 0.70 | 2.69 | 0.73 | 2.42 | 0.76 | ||
| 36 | 2.89 | 0.00 | 2.60 | 0.00 | 2.34 | 0.00 | ||
| 总节省成本∑Cj | — | 31.18 | — | 38.71 | — | 42.34 | ||
4 结果分析与讨论
通过对模型进行案例验证,可以得出以下结论:
(1) 对同一条公交线路而言,不同的等待时间成本系数导致结果发生明显的变化。从Case1到Case3,到站时间预测误差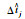
(2) 在表 2和表3中,可以发现Cj的值出现了一些负值, 这是正常的。这些负数反映了该模型的弊端,说明其存在一定的风险成本。如果公交车比公交实时信息提供的到站时间提前进站,而此时部分乘客并未到达站点,对这部分乘客而言,不得不在站点等候下一辆公交车,其等待时间成本是增加的。这就是本章所建立模型存在的风险成本。
(3) 比较两路公交车的模型求解结果,可以发现,与49路公交相比,北安线的运行延误估计值更大,更不稳定,同时其风险成本也较大。这说明对于服务水平较差的公交线路而言,模型应用产生的风险成本更大。模型在服务水平较好的公交线路上应用效果会更好。就该模型而言,这主要是由于市内公交和市域公交服务区域的不同导致的。49路公交车主要在市内中心区域运行,乘客出行多为通勤,客流相对较为稳定。虽然市内交通较为拥堵,但是公交实时信息在预测到站时间时,可根据历史同时段道路情况对其进行预测。而北安线服务上海多个区,途径大型购物中心、各种商品市场、建材市场、多个工厂以及长途大巴集散点等,乘客出行目的较为复杂多变,突发客流情况较多,造成了客流的不稳定性。
5 结论本研究基于鲁棒优化的方法,提出了一种新的公交实时到站信息优化方法。不同于已往研究通过建立模型寻找更精确的到站时间预测方法,本研究在已有的公交实时到站信息中,考虑客流情况的不确定性,以及乘客对公交实时信息的不同态度,同时考虑驾驶员在行驶过程中的恢复行为,建立数学模型,增加一项对已有实时到站时间的误差估计。最后通过案例验证了模型的有效性。通过本研究提出的公交实时到站信息优化方法,可以使现有的公交实时信息内容更为完善、精确,降低不准确的实时信息带给乘客的负面影响,从而帮助乘客更好的利用公交实时信息规划出行方案。
| [1] |
华雪东, 阳建强, 王炜, 等. 基于数据融合的公交到站时间组合预测模型[J]. 公路交通科技, 2019, 36(2): 112-120. HUA Xue-dong, YANG Jian-qiang, WANG Wei, et al. Hybrid Bus Arrival Time Prediction Models Based on Data Fusion[J]. Journal of Highway and Transportation Research and Development, 2019, 36(2): 112-120. |
| [2] |
何民, 李沐轩, 税文兵, 等. 可靠性和舒适性对响应式定制公交线路设计的影响[J]. 公路交通科技, 2019, 36(5): 145-151. HE Min, LI Mu-xuan, SHUI Wen-bing, et al. Influence of Reliability and Comfort on Responsive Custom Bus Route Design[J]. Journal of Highway and Transportation Research and Development, 2019, 36(5): 145-151. |
| [3] |
陈国俊, 杨晓光, 刘好德, 等. 基于动态百分位行程时间的公交到站时间预测模型[J]. 公路交通科技, 2009, 26(增1): 102-106, 123. CHEN Guo-jun, YANG Xiao-guang, LIU Hao-de, et al. Prediction Model of Bus Arrival Time Based on Dynamic Percentile Link Travel Time[J]. Journal of Highway and Transportation Research and Development, 2009, 26(S1): 102-106, 123. |
| [4] |
CEDER A, WILSON N H M. Bus Network Design[J]. Transportation Research Part B:Methodological, 1986, 20(4): 331-344. |
| [5] |
CEDER A. Bus Frequency Determination Using Passenger Count Data[J]. Transportation Research Part A:General, 1984, 18(5/6): 439-453. |
| [6] |
CHEN M, LIU X, XIA J, et al. A Dynamic Bus-arrival Time Prediction Model based on APC Data[J]. Computer-Aided Civil and Infrastructure Engineering, 2004, 19(5): 364-376. |
| [7] |
FAGAN D, MEIER R. Intelligent Time of Arrival Estimation[C]//2011 IEEE Forum on Integrated and Sustainable Transportation System (FISTS). Vienna, Austria: IEEE, 2011: 60-66.
|
| [8] |
GONG J, LIU M, ZHANG S. Hybrid Dynamic Prediction Model of Bus Arrival Time based on Weighted of Historical and Real-time GPS Data[C]//2013 25th Chinese Control and Decision Conference (CCDC), Guiyang: IEEE, 2013: 972-976.
|
| [9] |
CHIEN S I J, KUCHIPUDI C M. Dynamic Travel Time Prediction with Real-time and Historic Data[J]. Journal of Transportation Engineering, 2003, 129(6): 608-616. |
| [10] |
CHUNG E H, SHALABY A. Expected Time of Arrival Model for School Bus Transit Using Real-time Global Positioning System-based Automatic Vehicle Location Data[J]. Journal of Intelligent Transportation Systems, 2007, 11(4): 157-167. |
| [11] |
CHIEN S I J, DING Y, WEI C. Dynamic Bus Arrival Time Prediction with Artificial Neural Networks[J]. Journal of Transportation Engineering, 2002, 128(5): 429-438. |
| [12] |
LIU J, YU X, XU Z, et al. A Cloud-based Taxi Trace Mining Framework for Smart City[J]. Software:Practice and Experience, 2017, 47(8): 1081-1094. |
| [13] |
YU B, LAM W H K, TAM M L. Bus Arrival Time Prediction at Bus Stop with Multiple Routes[J]. Transportation Research Part C:Emerging Technologies, 2011, 19(6): 1157-1170. |
| [14] |
YU B, WU S, YAO B, et al. Dynamic Vehicle Dispatching at a Transfer Station in Public Transportation System[J]. Journal of Transportation Engineering, 2011, 138(2): 191-201. |
| [15] |
YU B, YANG Z Z, WANG J. Bus Travel-time Prediction Based on Bus Speed[J]. Proceedings of the Institution of Civil Engineers-transport, 2010, 163(1): 3-7. |
| [16] |
KUMAR B A, JAIRAM R, ARKATKAR S S, et al. Real Time Bus Travel Time Prediction using k-NN Classifier[J]. Transportation Letters, 2017, 11(7): 1-11. |
| [17] |
ZHOU P, ZHENG Y, LI M. How Long to Wait? Predicting Bus Arrival Time with Mobile Phone Based Participatory Sensing[J]. IEEE Transactions on Mobile Computing, 2014, 13(6): 1228-1241. |
| [18] |
ZHOU Y, YAO L, CHEN Y, et al. Bus Arrival Time Calculation Model Based on Smart Card Data[J]. Transportation Research Part C:Emerging Technologies, 2017, 74: 81-96. |
| [19] |
O'SULLIVAN A, PEREIRA F C, ZHAO J, et al. Uncertainty in Bus Arrival Time Predictions:Treating Heteroscedasticity with a Metamodel Approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(11): 3286-3296. |
| [20] |
BERREBI S J, WATKINS K E, LAVAL J A. A Real-time Bus Dispatching Policy to Minimize Passenger Wait on a High Frequency Route[J]. Transportation Research Part B:Methodological, 2015, 81: 377-389. |
| [21] |
CATS O, LOUTOS G. Evaluating the Added-value of Online Bus Arrival Prediction Schemes[J]. Transportation Research Part A:Policy and Practice, 2016, 86: 35-55. |
| [22] |
LUETHI M, WEIDMANN U A, NASH A. Passenger Arrival Rates at Public Transport Stations[C]//Transportation Research Board 86th Annual Meeting (TRB 2007), Zurich: Institute for Transport Planning and Systems, 2007.
|
| [23] |
INGVARDSON J B, NIELSEN O A, RAVEAU S, et al. Passenger Arrival and Waiting Time Distributions Dependent on Train Service Frequency and Station Characteristics:A Smart Card Data Analysis[J]. Transportation Research Part C:Emerging Technologies, 2018, 90: 292-306. |
| [24] |
BERTSIMAS D, SIM M. The Price of Robustness[J]. Operations Research, 2004, 52(1): 35-53. |
| [25] |
BEN-TAL A, NEMIROVSKI A. Robust Solutions of Linear Programming Problems Contaminated with Uncertain Data[J]. Mathematical Programming, 2000, 88(3): 411-424. |
| [26] |
CHEN M, LIU X, XIA J. Dynamic Prediction Method with Schedule Recovery Impact for Bus Arrival Time[J]. Transportation Research Record, 2005, 1923: 208-217. |
 2019, Vol. 36
2019, Vol. 36
