扩展功能
文章信息
- 刘磊, 唐克双, 董可然
- LIU Lei, TANG Ke-shuang, DONG Ke-ran
- 基于决策树模型的信号控制交叉口交通状态估计
- Estimation of Traffic State at Signalized Intersection Based on Decision Tree Model
- 公路交通科技, 2019, 36(9): 93-102
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(9): 93-102
- 10.3969/j.issn.1002-0268.2019.09.013
-
文章历史
- 收稿日期: 2018-03-15
城市道路信号控制交叉口的交通状态估计是交通管控和信息服务的重要基础。近年来,随着机动车保有量提高,交通需求与供给的矛盾日益尖锐,交通拥堵已成为我国大多数城市发展面临的重大难题。随着我国交通信息化发展,各类检测技术与设备已被广泛应用于城市道路交通状态估计与预测。常用的检测器类别可以分为定点检测器与移动检测器[1]。其中,定点检测器主要包括感应线圈、地磁、微波雷达等,可以以一定的时间间隔(通常为20~60 s)上传断面流量、速度、占有率等数据;移动检测主要包括出租车浮动车、自动车辆识别(AVI)设备、车载或手机导航等,可以记录车辆轨迹、路径等信息。国内外学者针对基于定点和移动检测器数据对城市道路交通状态估计进行了大量研究,为我国各大城市交通信息化、智能化发展建设提供了大量的算法支撑。
而我国大部分中小城市普遍存在浮动车渗透率不足(通常小于5%)、采样频率低(通常为1/60 s)的问题,难以实际应用于城市道路交通状态估计;AVI布设密度有限且受到车辆捕获率与匹配率的影响,交通状态估计可靠性较差;车载导航数据一般需要政府向高德、百度等运营商购买,经济成本高。交通信息采集与服务主要依赖于布设在交叉口上游路段的低频定点检测器数据(通常为1/60 s)。
我国工程实践应用中,信号控制交叉口(下文简称“信控交叉口”)主要有以下3种典型定点检测器布设方案:(1)进口道检测器,布设于路段下游停车线位置,由于距离交叉口较近,受交叉口信号控制影响较大,工程实践中主要用于交叉口信号配时参数优化而很少应用于交通状态估计;(2)出口道检测器,布设于路段上游靠近出口道位置,主要用于交叉口车辆溢出检测与信号控制,且覆盖率较低,难以应用于交通状态估计;(3)路中检测器,检测器布设在路段中间位置,主要用于路段交通参数的检测。相比之下,路中定点检测器具有覆盖率高,受交叉口信号控制影响较小、稳定可靠的特点,在实际工程应用中经常用于城市道路交通状态估计。
然而,传统的基于路中检测器的交通状态估计方法大部分通过检测获取的断面速度按照一定的阈值范围直接对应交通状态,而未考虑下游信号控制交叉口周期、绿信比等因素的影响,同时没有充分利用检测所采集的流量、占有率数据。针对上述问题,本研究基于我国大部分中小城市交通数据采集条件和交通状态发布时间间隔(5 min)的需求,提出了一种基于分类决策树的信控交叉口交通状态估计方法。
1 研究综述基于定点检测器的信控交叉口交通状态估计方法主要可分为两种:一种是基于交通波理论,通过分析检测数据反映的微观交通特征,实现最大排队长度、二次排队等交通状态评价指标的估计。另一种方法是基于数理统计,通过建立检测数据与拥堵状态之间的函数关系进而实现交通状态的估计。
基于交通流理论进行交通状态估计的典型方法包括到达-驶离累计曲线、排队论、交通波理论、CTM(Cell Transmission Model)模型等。Skabardonis等[2-3]。基于交通波理论,以30 s间隔统计线圈数据,建立交叉口排队长度估计模型。Liu[4-6]基于交通波理论,结合信号配时数据,建立了最大排队长度估计模型,但该方法要求基于事件的秒级定点检测器数据并且需要精确的交叉口信号配时。江龙晖[7]应用CTM传输模型,通过建立路段和节点模型,设计了城市道路基本交通参数和排队长度参数的估计方法,该方法计算简单、所需标定参数较少,但是边界条件难以确定,并且CTM模型在计算过程中采用线性递推方式,而实际的城市道路交通系统是非线性的,所以CTM模型应用于城市道路交通参数估计中存在一定误差。
基于数理统计估计交通状态的典型方法有单截面算法、双截面算法、突变理论和模糊聚类等。基于单截面检测数据判断交通状态的代表算法有McMaster算法、神经网络算法[8]、非参数回归模型等。具有代表性的双截面算法主要有:加州算法、波动分析算法、贝叶斯算法、神经网络算法。这些算法的主要思想是基于大量历史数据建立交通状态与检测器参数的对应关系,通过模式识别来判断交通状态,常用于偶发性交通拥堵的判别。而模糊聚类方法在城市交通状态估计中应用最为广泛。该方法针对交通状态的模糊性,通过建立交通流参数与交通顺畅程度的隶属函数,实现交通状态的推理[2]。但缺少评价算法效果的实时值,难以完成有效评价[9]。
近年来,城市交通状态估计取得了进一步发展,主要分为两大类:第1类是基于新型数据源或融合其他数据源进行算法的开发;第2类是在定点检测器数据源基础之上,开发更加先进有效的算法,深层挖掘检测器数据中蕴含的交通信息,从而实现交通状态估计。
第一类方法中,钱蕾[10]利用GPS浮动车数据,基于改进K-Means聚类方法,实现路段行程速度估计;郭义荣[11]等通过视频数据,以行程速度为出发点,根据相同等级道路设定统一速度阈值,实现交通状态判别;Cai[12]融合线圈数据与轨迹数据,分析车辆排队形成和消散波关键点,基于交通波理论进行交叉口交通状态估计;王春娥[13]开发了一种基于移动检测器、固定检测器以及人工报告等多数据源决策级融合的自动拥挤估计算法,该方法将多种方式获得的交通状态估计结果进行融合,进而得出交通状态最终结果。第2类方法中,唐克双[14]等基于低频定点检测器,提出了基于线性拟合的交通状态分界线建立方法;李爱杰[15]等利用低频定点检测器采集的时间占有率、流量、速度之间的函数关系对长排队进行识别,进而基于交通波理论,通过关键点判别求取周期最大排队长度;Hsun-Jung Cho等[16]利用双截面定点检测数据估计交通波波速与上游车辆到达率,进而基于交通波理论计算信号交叉口排队长度;曲昭伟[17]等基于路网的下游和上游线圈检测器组的5 min集计数据,由路段和交叉口状态估计模型建立了区域交通状态的综合估计模型,并分析路网整体指标P与路网车辆平均速度的关系以确定P与交通状态的关系,并用仿真数据进行了验证。
综上所述,城市交通状态估计的研究中,既往研究主要存在以下几点局限:(1)基于交通波的方法需要高精度定点检测数据以及精确匹配的交叉口信号配时,我国中小城市数据检测环境很难满足要求。(2)数理统计方法通过模式识别来判断交通状态,但是往往忽略交叉口信号配时参数的影响,使得在实际应用中算法可移植性较差。(3)基于多源数据融合或多截面定点检测器的方法对数据源要求较高,实际应用中存在经济成本、数据精度以及采样频率的限制。上述原因导致已有研究算法很难完全适应我国中小城市交通信息采集与服务的技术现状,开发基于路中检测器数据的交通状态估计算法具有重要的实际应用价值。
2 建模思路 2.1 基本思想针对我国中小城市干道交通检测数据条件:道路中各车道布设定点检测器(地磁、线圈、微波雷达等),通常以1 min的频率上传集计的流量、占有率、瞬时速度数据,路段下游与信控交叉口相连,基于路中检测器大量历史数据与交叉口离线信号配时数据,利用数据挖掘(分类决策树)方法,开发一种城市道路交通状态估计方法。
2.2 方法流程该算法主要包含以下4个步骤:
步骤1:数据提取
选取干道交叉口及特定车道(本研究以直行车道为例),提取路中检测器数据(流量q、速度v、占有率O)、相应时段信号配时数据(周期C、绿信比λ)、路段真实交通状态数据(基于对应集计时间段内路段平均行程车速进行状态划分为3种状态,状态0为阻塞,状态1为拥挤,状态2为畅通)。
步骤2:数据处理与分析
对步骤1中获得检测器数据集计处理(通常为5 min),分析各特征变量与交通状态之间的相关性分析,筛选出与交通状态相关性强的变量作为特征变量。
步骤3:决策树训练
以步骤2中的数据训练决策树,得出交通检测数据与路段交通状态之间的对应关系,获得交通状态分类规则。
步骤4:交通状态估计
提取实时路中检测器数据与交叉口信号配时数据,根据上述方法,进行实时交通状态估计。在实际应用中,随着历史数据不断增加,可以动态更新历史数据库,实现交通状态的滚动预测,提高交通状态估计准确率。
2.3 分类决策树算法原理在决策树算法中,CART(Classification and Regression Tree)算法是一种十分有效的非参数分类和回归方法。该方法是由Breiman等[18]在1984年提出,采用二分递归分割技术,将当前样本集划分为两个子样本集。
假设包含n个样本的训练样本集S={(vi, ci), i=1, 2, …, n},其中:特征向量V=(a1, a2, …, am)且aj(j=1, 2, …, m)为特征属性,Vi为训练样本集中第i个样本的特征向量;ci为该样本的类别标签。CART的训练过程就是构造二叉树的过程,算法流程如下:
(1) 创建初始根节点Root,包含所有训练样本。
(2) 对特征向量V中每一个特征属性aj,选取基尼系数(Gini Index)最小的点作为根节点的分裂属性。基尼系数定义如下:
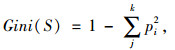
|
(1) |
式中,S为未被分组前的训练样本数据集;k为类别变量的个数;pi为在S中类别i的概率。
Gini系数越小,样本的纯度就越高,划分效果也越好。若S根据属性F被划分为S1和S2,那么此时给定划分的Gini系数为:
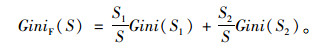
|
(2) |
根据以上两个公式,将样本数据集分为两组后与原Gini系数相比,减少量为:
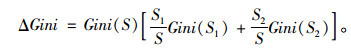
|
(3) |
Gini系数减少量表明样本数据集分组后,变量取值总的异质性减少,即分组后样本类别变量趋向相同类别值,纯度增加。
(3) 对根节点的分裂属性对应的两个样本子集S1和S2,采用步骤(1)相同的方法迭代计算,保证决策树的每个节点均取Gini系数减少量最大的特征变量。
(4) 为防止决策树过拟合,对生成决策树进行剪枝,使用独立于训练样本集的测试样本集对子树的分类错误计算,找出分类错误最小的子树作为最理想的二叉决策树。
3 数据采集与模型建立由于决策树模型需要大量样本作为训练数据,而现实环境中,与交叉口相关的环境变量组合(周期、绿信比)较为单一,且上游路段的流量变化有限,短期内难以获得所需样本量,而在仿真中,能够设置不同的环境变量组合和上游路段的输入值,有效地解决了研究数据获取的局限性,极大地提高了研究效率,因此本研究基于仿真环境进行方法研究,并用实证数据进行模型验证。
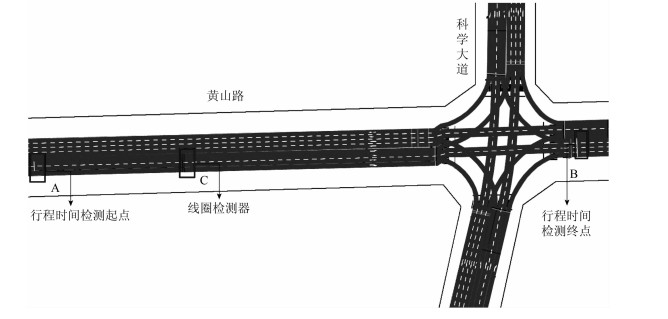
3.1 仿真场景设置选取安徽省合肥市黄山路-科学大道交叉口西进口道为研究对象,如图 1所示,该路段为城市主干道,符合本研究基本场景。基于VISSIM微观仿真软件建立模型,以路段中间直行车道作为研究区域,在交叉口上游C处布设路中检测器;同时在该进口道上游A处与下游出口道B处布设行程时间检测器,检测车头通过该区域的平均行程时间。
|
| 图 1 仿真模型设置与标定 Fig. 1 Setting and calibration of simulation model |
| |
通过调整交叉口信号周期和绿信比数据,其中周期取值为60,90,120,150,180 s;绿信比分别为0.2,0.3,0.33,0.36,0.39,0.42,0.5,0.6;共计40种组合,这些组合基本涵盖了我国中小城市信控交叉口信号配时方案。为了模拟交通流波动性特点以及涵盖不同交通状态数据,仿真模型以15 min间隔输入流量,流量范围为每车道300~1 000 pcu/h,每种组合的流量输入保持一致。每种组合仿真时长为8 000 min,即1 600个5 min间隔,共得到64 000个样本。
3.2 数据采集与处理对于上述40组仿真试验中的每一种组合,提取路中检测器与相对应的行程时间检测器的5 min集计数据,包括路中检测器的流量(veh/5 min), 速度(km/h)、占有时间(s/5 min)以及5 min的研究路段车辆平均行程时间(s)。对该数据进一步处理为5 min流量q(veh/5 min)、实际占有率O(%)、对应区间(图 2中检测器A, B之间)行程速度v(km/h)以及对应交通状态,其中交通状态由区间平均行程速度决定,速度阈值临界点为:阻塞(v≤15 km/h),拥挤(15 km/h < v < 25 km/h),畅通(25 km/h≤v),对应行程速度阈值,将学习数据分为3类。仿真数据记录如表 1所示。
|
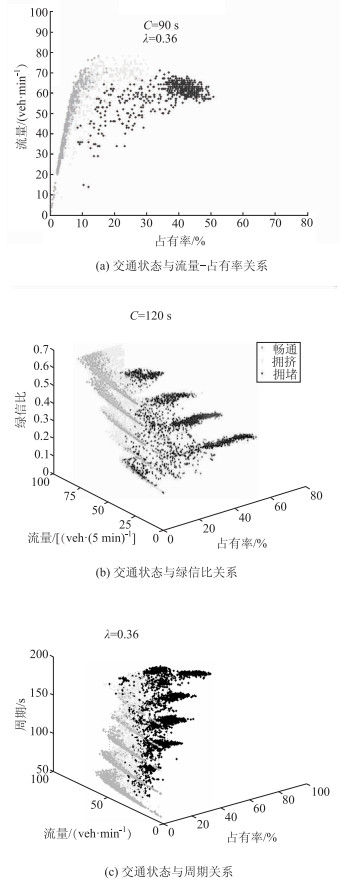
| 图 2 交通状态与各因素的关系 Fig. 2 Relationships between traffic state and each factor |
| |
| 编号 | q/[veh·(5 min)-1] | v/(km·h-1) | O/% | 周期C/s | 绿信比λ | 交通状态 |
| 1 | 110 | 5 | 12.87 | 90 | 0.33 | 0(阻塞) |
| 2 | 80 | 17 | 8.66 | 120 | 0.36 | 1(拥挤) |
| | | | | | | |
| 64 000 | 30 | 55 | 5.24 | 180 | 0.6 | 2(畅通) |
3.3 检测器数据、信号配时数据与交通状态关系分析
为避免引入与交通状态无关的特征变量,下面分析各特征变量与交通状态之间的相关性。通过图 2(a)可见,随着占有率增加,流量逐渐增加,当占有率较小时候,交通运行畅通,此时车辆为自由运行状态;随着占有率继续增大,流量不在继续增大,此时车辆行程速度下降,交通开始出现拥挤;当占有率超过某一阈值时,流量开始下降,车辆运行速度下降,此时交通阻塞,其流量-速度-占有率关系基本符合Greenshields宏观交通流三参数模型(即:速度随着占有率增加线性减小,流量与占有率呈现抛物线关系,流量与速度呈现抛物线关系)。通过图 2(b)可见,在交叉口相同周期和流量输入的情况下,当交叉口绿信比较小时,交通运行阻塞,当绿信比大时,交通运行更畅通。由图 2(c)可见,当交叉口绿信比相同,且流量输入相同情况下,周期越长,交叉口阻塞越严重。
各变量与行程速度之间的方差分析如表 2所示,由表可见,检测器参数和交叉口信号配时参数与行程速度之间的相关性比较显著(P=0 < 0.05)。其结论与图 2得出结论一致。通过上述分析可见,检测器数据和信号配时数据与交通状态之间确实存在着某种对应关系,因此,通过某种方法建立交通状态与这些参数之间的关系具有合理性与必要性。
| 影响因素 | 平方和 | 自由度df | 均方 | F检验值 | 显著性(sig) |
| 周期 | 662 878.43 | 4 | 165 719.61 | 2 397.10 | 0.000 |
| 绿信比 | 1 694 982.02 | 7 | 242 140.29 | 4 567.98 | 0.000 |
| 流量 | 1 051 728.07 | 3 | 350 576.02 | 5 559.73 | 0.000 |
| 占有率 | 3 031 021.87 | 3 | 1 010 340.62 | 31 447.46 | 0.000 |
| 检测器速度 | 1 394 750.78 | 3 | 464 916.93 | 8 058.01 | 0.000 |
本研究中,流量、速度、占有率等特征变量都是连续变量,在决策树建模过程中,为了简化数据结构,提高决策树对样本的聚类能力,将流量、检测器速度、占有率数据离散化处理。其中流量根据饱和度阈值分为4类,检测器占有率和速度使用K-均值聚类的方法划分为4类。K-均值聚类结果如表 3所示,由表可见,3个变量通过K-均值聚类后,各组间均值存在明显差异(Sig < 0.05),进一步验证了各变量聚类分析的有效性。各变量与名义变量的替换结果如表 4所示。
| 变量 | 聚类 | 误差 | F检验值 | sig | |||
| 均方 | 自由度df | 均方 | 自由度df | ||||
| v | 1 223 438.07 | 3 | 8.39 | 31 993 | 145 772.71 | 0.00 | |
| O | 3 340 044.64 | 3 | 15.54 | 31 996 | 214 939.40 | 0.00 | |
| V | 911 048.71 | 2 | 7.03 | 31 997 | 129 539.11 | 0.00 | |
| 注:v为检测器速度;O为占有率;V为路段平均车速。 | |||||||
| 变量名称 | 名义变量取值 | 对应实际变量取值范围 | 划分依据 |
| 流量 | 0 | 0~0.60 | 饱和度 |
| 1 | 0.60~0.80 | ||
| 2 | 0.80~1.00 | ||
| 3 | > 1.0 | ||
| 占有率 | 0 | 0~13.47 | K-均值聚类 |
| 1 | 13.47~29.89 | ||
| 2 | 29.89~46.66 | ||
| 3 | > 46.66 | ||
| 检测器速度 | 0 | 0~22.48 | K-均值聚类 |
| 1 | 22.48~33.38 | ||
| 2 | 33.38~43.31 | ||
| 3 | > 43.31 |
4 决策树结果分析 4.1 生成决策树
该分类方法中,通过对样本标记,得到17 914个畅通样本,23 252个拥挤样本以及22 834个阻塞样本,基于上文所述分类方法(CART),使用85%的样本训练决策树,15%的样本评估模型。
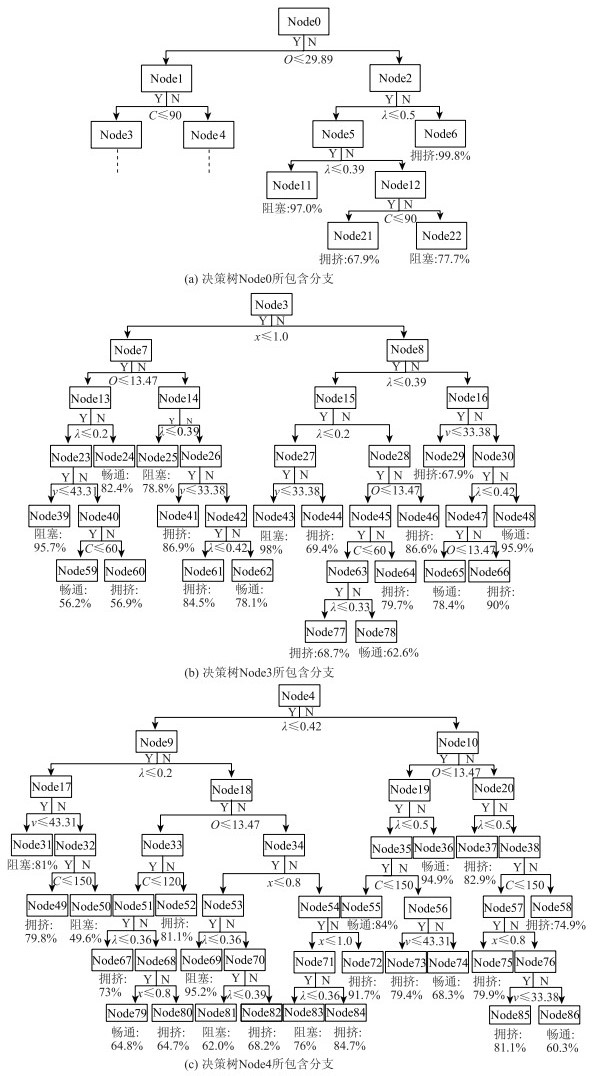
生成树如图 3所示,生成的分类决策树共包含87个节点,其中终端节点44个,即有44条分类规则。每个节点对应着该节点分裂的特征标签以及特征标签判断条件,每个终端节点对应着该条路径判断的分类结果以及判断得出该结果的精确度。总结以下几个代表性的交通状态分类规则:
|
| 图 3 畅通/拥挤/阻塞分类树 Fig. 3 Classification tree for smooth/congestion/jam 注:图中,流量以饱和度x代表;v代表速度;O代表占有率;C代表周期(单位:s);λ代表绿信比;Node代表决策树节点编号。 |
| |
(1) 当O>29.89,C>90,且0.39 < λ≤0.5,此时对应的交通状况最可能是阻塞,概率为77.7%;(2)当13.47 < O≤29.89,x≤1,v>33.38,C≤90,且λ>0.42,此时对应的交通状况最可能是畅通,概率为78.1%;(3)当13.47 < O≤29.89,0.8 < x≤1,C>90,且0.36 < λ < 0.42,此时对应的交通状况最可能是拥挤,概率为84.7%;(4)当O≤13.47,C>90,且λ>0.5,此时对应的交通状况最可能是畅通,概率为94.9%。
4.2 模型分析决策树分类结果如表 5所示。
| 已观测 | 已预测 | ||||
| 阻塞 | 拥挤 | 畅通 | 正确百分比/% | ||
| 训练集 | 阻塞 | 17 722 | 1 396 | 244 | 91.53 |
| 拥挤 | 1 561 | 15 188 | 2 982 | 76.98 | |
| 畅通 | 65 | 2 229 | 12 979 | 84.98 | |
| 总体百分比/% | 35.59 | 34.60 | 29.81 | 84.41 | |
| 检验集 | 阻塞 | 3 177 | 263 | 32 | 91.50 |
| 拥挤 | 255 | 2 699 | 567 | 76.65 | |
| 畅通 | 7 | 410 | 2 224 | 84.21 | |
| 总体百分比/% | 35.70 | 35.00 | 29.30 | 84.08 | |
由表 5可见,当交通状态为阻塞时,估计精度最高,正确百分比达到91.5%以上;当交通状态为畅通时候,估计精度接近总体估计精度,但是当交通状态为拥挤时,估计准确率最低,为77%左右,分析原因为拥挤交通状态介于畅通状态与阻塞状态之间,由于交通状态固有的模糊特性,因此处于临界位置的样本数据分类偏差比较大。但是模型总体精度也能达到84%以上,可以基本满足估计误差要求,并且,检验数据的精度趋势与训练数据的精度趋势相同,可见CART算法用于该分类情况较为合适。
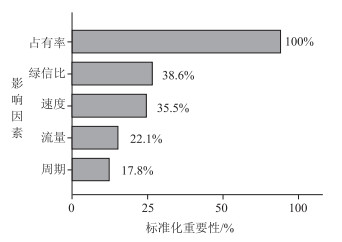
此外,不同的特征标签对输出结果的影响水平不同,BREIMAN等[18]于1984年提出在决策树中对变量重要性进行检测的一种方法,变量重要性是该输入变量在所有节点基尼系数的平均减少。通过标准化处理后,各影响因素的重要性如图 4所示。
|
| 图 4 各因素重要性 Fig. 4 Importance of each factor |
| |
该图表明定点检测器的占有率数据对模型的影响程度最大,信号周期和检测器流量数据对模型影响水平比较小。因此在应用决策树判断交通状态的过程中,必须保证检测器采集的数据精度,尤其是占有率数据精度,才能确保模型输出结果更加接近实际交通状态。
4.3 实证分析本研究实证数据来源于青岛市福州南路3个路段4 d早高峰微波检测器数据和视频数据。本研究中使用George2.0软件提取车辆路段行程时间。将交叉口视频数据导入软件后,预先画出车辆到达标记线和车辆驶离标记线,其中到达标记线在上游交叉口进口道处,驶离标记线位于下游交叉口进口道。通过记录车辆经过标记线时刻标记车辆到达和驶离该路段的时刻,两时刻之差为单个车辆在该路段的行程时间。
通过视频数据,在每个集计时间段(5 min),随机提取5~10辆车的路段行程时间,然后计算出路段平均速度,共得到107组集计路段行程速度数据如表 6所示。根据前文所述速度阈值法判别此刻路段真实交通状态,其中交通状态为阻塞、畅通、拥挤的样本量分别为38,37和32。将对应路段检测器数据以及交叉口信号配时数(周期、绿信比)放入上文训练好的决策树中,通过决策树规则判断,最终得出此路段当前时间段模型判别的交通状态。
| 路段名称 | 路段长度/m | 交叉口信号配时 | 采集车辆数/veh | 采集样本数/组 | |
| 周期/s | 绿信比 | ||||
| 福州南路(漳浦路—漳州二路) | 160 | 175 | 0.8 | 492 | 52 |
| 福州南路(漳州二路—香港中路) | 218 | 175 | 0.31 | 401 | 41 |
| 福州南路(漳州二路—漳浦路) | 160 | 175 | 0.83 | 105 | 14 |
通过对比视频数据获得的真实交通状态与决策树模型获得的估计状态,计算决策树估计精度,结果如表 7所示。
| 实际交通状态 | 总样本 | 预测交通状态 | 样本 | 预测正确率/% | 总精度/% | 严重错误率/% |
| 阻塞 | 38 | 阻塞 | 24 | 63.15 | 75.70 | 0.00 |
| 拥挤 | 14 | |||||
| 畅通 | 0 | |||||
| 拥挤 | 37 | 阻塞 | 3 | 89.19 | ||
| 拥挤 | 33 | |||||
| 畅通 | 1 | |||||
| 畅通 | 32 | 阻塞 | 0 | 75.00 | ||
| 拥挤 | 8 | |||||
| 畅通 | 24 |
实证结果表明:
(1) 当交通状态为阻塞时,模型估计精度为63.15%,精度较低。总结原因可能为阻塞与拥挤状态之间的速度阈值偏大,人为将拥挤状态误判为阻塞状态;同时仿真环境过于理想,而实际环境中影响交通流的因素多,因此交通流的波动大,得到的流密速数据结果偏小,导致决策树将阻塞状态误判为拥挤状态。
(2) 当实际交通状态为拥挤或畅通时,模型估计精度在75%以上,能够基本满足中小城市交通状态估计精度。
同时,本研究中使用微波检测器,微波雷达检测器在车型单一、车速均匀、交通顺畅的路段上有较高检测精度,而当在交通拥堵情况下常因车辆间的遮挡、开普勒效应的影响,造成检测精度的下降;测量的速度、占有率不如仿真中的精度高。
此外,通过视频数据采集车辆行程时间过程中,每个集计时间段所能采集的车辆行程时间数据有限,随机性比较大,不能准确地反映整个路段车辆的平均行程时间,导致在路段真实交通状态估计时出现误差。
本算法与唐克双[14]算法(下文称为算法1)数据源、仿真模型以及实证环境基本保持一致,两种算法结果比较结果如表 8所示。由表可见,两种算法总体估计精度几乎相同,但是本算法严重错误率为0,相较于算法1,本算法得出的交通状态结果偏差更小,结果更可靠。虽然两种算法都适用于我国中小城市只有低频定点检测器的数据条件,但是本算法以其模型简单、结果可靠等优势,具有很好的应用价值。
| 模型精度/% | |||||
| 畅通 | 拥挤 | 阻塞 | 总精度 | 严重错误率 | |
| 算法1 | 75.00 | 80.00 | 69.23 | 75.00 | 2.08 |
| 本算法 | 75.00 | 89.19 | 63.15 | 75.70 | 0.00 |
5 结论
针对我国中小城市道路交通检测数据条件,以城市道路交叉口间断流为研究对象,以VISSIM仿真软件为工具建立微观仿真模型,基于分类决策树建立了信控交叉口交通状态估计模型,主要结论如下:
(1) 通过采集的流量、占有率、速度数据与离线信号配时参数,建立了适用于我国中小城市信控交叉口常用配时方案的交通状态分类规则。
(2) 利用CART决策树所建交通状态估计模型结果表明,对畅通、拥挤、阻塞3种交通状态的判断准确率总体达到84%以上。实证结果显示,模型总体精度为75.70%,CART决策树模型可以较准确地判断交通状态,预测精度能够基本满足中小城市交通状态估计需求。
(3) 不同因素对交通状态的影响程度不同,由大到小依次为:占有率、绿信比、检测器速度、流量、信号周期,因此在使用模型时要确保占有率精度。
同时,本研究也存在一些不足之处,仿真环境没有充分考虑实际路段检测器误差,实证数据精度低于仿真模型。此外,未来将研究定点检测器与其他数据源(例如,轨迹数据或电警卡口数据等)的融合算法,进一步提高交通状态估计模型精度与稳定性。
| [1] |
唐克双, 孙剑. 基于多源数据融合的城市道路交通控制与管理[M]. 上海: 同济大学出版社, 2015. TANG Ke-shuang, SUN Jian. Urban Traffic Control and Management Based on Fusion of Multi-source Data[M]. Shanghai: Tongji University Press, 2015. |
| [2] |
SKABARDONIS A, GEROLIMINIS N. Real-time Monitoring and Control on Signalized Arterials[J]. Journal of Intelligent Transportation Systems, 2008, 12(2): 64-74. |
| [3] |
SKABARDONIS A, GEROLIMINIS N. Real-time Estimation of Travel Times on Signalized Arterials[C]//16th International Symposium on Transportation and Traffic Theory. College Park: University of Maryland, 2005: 387-406.
|
| [4] |
WU X, LIU H X. A Shockwave Profile Model for Traffic Flow on Congested Urban Arterials[J]. Transportation Research Part B:Methodological, 2011, 45(10): 1768-1786. |
| [5] |
WU X, LIU H X, GETTMAN D. Identification of Oversaturated Intersections Using High-resolution Traffic Signal Data[J]. Transportation Research Part C:Emerging Technologies, 2010, 18(4): 626-638. |
| [6] |
LIU H X, WU X, MA W, et al. Real-time Queue Length Estimation for Congested Signalized Intersections[J]. Transportation Research Part C:Emerging Technologies, 2009, 17(4): 412-427. |
| [7] |
江龙晖.城市道路交通状态判别及拥挤扩散范围估计方法研究[D].吉林: 吉林大学, 2007. JIANG Long-hui. Study on Methods of Traffic State Identification and Congestion Propagation Estimation for Urban Road[D]. Jilin: Jilin University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10183-2007096023.htm |
| [8] |
巫威眺, 靳文舟, 林培群. 基于BP神经网络的道路交通状态判别方法研究[J]. 交通信息与安全, 2011, 29(4): 71-74, 79. WU Wei-tiao, JIN Wen-zhou, LIN Pei-qun. The Method of Traffic State Identification Based on BP Neural Network[J]. Journal of Transportation Information and Safety, 2011, 29(4): 71-74, 79. |
| [9] |
姜桂艳, 郭海锋, 吴超腾. 基于感应线圈数据的城市道路交通状态判别方法[J]. 吉林大学学报:工学版, 2008(增1): 37-42. JIANG Gui-yan, GUO Hai-feng, WU Chao-teng. Identification Method of Urban Road Traffic Conditions Based on Inductive Coil Data[J]. Journal of Jilin University:Engineering and Technology Edition, 2008(S1): 37-42. |
| [10] |
钱蕾, 韩印, 姚佼. 基于改进K-Means算法的交叉口影响路段行程速度估计[J]. 公路交通科技, 2017, 34(12): 115-122. QIAN Lei, HAN Yin, YAO Jiao. Estimation of Travel Speed on Intersection Influenced Link Based on Improved K-means Algorithm[J]. Journal of Highway and Transportation Research and Development, 2017, 34(12): 115-122. |
| [11] |
郭义荣, 董宝田, 吴蕾. 基于速度的交通状态识别及动态评价研究[J]. 公路交通科技, 2012, 29(增1): 26-31. GUO Yi-rong, DONG Bao-tian, WU Lei. Traffic State Recognition and Dynamic Evaluation Based on Velocity[J]. Journal of Highway and Transportation Research and Development, 2012, 29(S1): 26-31. |
| [12] |
CAI Q, WANG Z, ZHENG L, et al. Shock Wave Approach for Estimating Queue Length at Signalized Intersections by Fusing Data from Point and Mobile Sensors[J]. Transportation Research Record, 2014, 2422: 79-87. |
| [13] |
王春娥.基于数据融合的城市道路交通状态判别算法研究[D].吉林: 吉林大学, 2008. WANG Chun-e. Estimation Algorithm of Urban Road Traffic State Based on Data Fusion[D].Jilin: Jinlin University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10183-2008062428.htm |
| [14] |
唐克双, 徐天祥, 董可然, 等. 基于低频定点检测数据的交叉口交通状态估计[J]. 同济大学学报:自然科学版, 2017, 45(5): 705-713, 720. TANG Ke-shuang, XU Tian-xiang, DONG Ke-ran, et al. Traffic State Estimation Based on Low Frequency Detection Data at Intersections[J]. Journal of Tongji University:Natural Science Edition, 2017, 45(5): 705-713, 720. |
| [15] |
李爱杰, 唐克双, 董可然. 基于单截面低频检测数据的信号交叉口排队长度估计[J]. 交通信息与安全, 2018, 36(1): 57-64, 95. LI Ai-jie, TANG Ke-shuang, DONG Ke-ran. Estimation of Queuing Length at Signalized Intersections Using Low-frequency Point Detector Data[J]. Journal of Transport Information and Safety, 2018, 36(1): 57-64, 95. |
| [16] |
CHO H J, TSENG M T, HWANG M C. Using Detection of Vehicular Presence to Estimate Shockwave Speed and Upstream Traffics for A Signalized Intersection[J]. Applied Mathematics & Computation, 2014, 232(6): 1151-1165. |
| [17] |
曲昭伟, 魏强, 别一鸣, 等. 基于固定检测器的区域交通状态判别方法[J]. 中南大学学报:自然科学版, 2013, 44(1): 403-410. QU Zhao-wei, WEI Qiang, BIE Yi-ming, et al. Method for Traffic State Identification Based on Fixed Detector[J]. Journal of Central South University:Science and Technology Edition, 2013, 44(1): 403-410. |
| [18] |
BREIMAN L, FRIEDMAN J, STONE C J, et al. Classification and Regression Trees[M]. Boca Raton: CRC Press, 1984.
|
 2019, Vol. 36
2019, Vol. 36
