扩展功能
文章信息
- 姚荣涵, 张文松, 龙梦, 孙立
- YAO Rong-han, ZHANG Wen-song, LONG Meng, SUN Li
- 基于车队离散的信号交叉口交通需求估算方法
- A Traffic Demand Estimation Method for Signalized Intersections Based on Platoon Dispersion
- 公路交通科技, 2019, 36(9): 83-92, 116
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(9): 83-92, 116
- 10.3969/j.issn.1002-0268.2019.09.012
-
文章历史
- 收稿日期: 2018-04-10
随着社会经济的快速发展,机动车保有量不断增加致使城市交通拥堵日益严峻。交叉口信号配时优化是缓解城市交通拥堵的一种有效途径。作为信号配时优化的基础,交通需求数据准确与否决定信号配时方案是否可靠。
近年来,国内外许多学者致力于交通需求估算研究。研究人员基于改进的四阶段法预测了城市路网的年交通需求或者日交通需求[1-3]。但以上研究通常需要大规模的交通调查来获取起讫点交通需求数据,耗费大量的人力物力[4-5]。与起讫点交通需求数据相比,路段交通流量数据更容易获取,因此利用路段交通流量数据进行交通需求估算的研究得到了发展[6-8]。年交通需求或者日交通需求可用于道路规划和道路等级确定,但并不适用于信号配时优化。为了使路网交通流高效运行,信号配时优化需要考虑一日内交通需求的时变特性。与年交通需求或者日交通需求相比,小时交通需求能够反映这种时变特性,因此在信号配时优化中尤为重要。结合手机定位数据和ArcGIS软件可以获得城市路网的小时交通需求,但其仅能展示城市不同区域间交通需求的差异,无法对每条道路的交通需求的时变特性进行深入研究[9]。文献[10-11]利用道路检测器数据分别估算了车道组和城市路网的交通需求,且其估算结果的时间尺度小于1 h,更为细致地反映了交通需求的时变特性。
上述研究从路网层面探讨交通需求的估算与预测,大多不考虑信号配时对道路阻抗的影响。在设计信号配时方案时,大多将进口道实测车流量作为其交通需求[12-13]。如果交通流处于拥挤状态,进口道实测车流量不能反映其真实的交通需求。此时,还原真实的交通需求对信号配时设计具有重要意义。针对干道交通系统,何龙[14]根据流量守恒定律由起讫点交通需求估算了每个交叉口每个机动车相位的高峰小时流量,但忽略了车队从上游驶向下游过程中发生的离散现象。同时,现有研究很少讨论进口道实测车流量与真实交通需求的差异,及其对交通流运行所带来的影响。鉴于此,针对干线信号控制系统,本研究基于车队离散提出一种车道组交通需求估算方法,并分析该方法对信号配时优化及交通流运行的影响。
1 交通需求分析通常,交通需求具有较强的时变特性。就信号控制而言,为有效满足高峰期交通需求,准确掌握其时变规律尤为重要[15]。对于干线信号控制系统,下游进口道的交通需求取决于上游进口道的交通需求。这里进口道交通需求是指其到达车流量。实践中,在系统中设置检测断面以获取进口道到达车流量。如果检测断面设置在停止线上游较远位置,因为车队离散现象,所得到达车流量的变化曲线与实际交通需求的变化曲线并不吻合;如果检测断面设置在停止线附近,因信号控制车辆排队长度往往会超过检测断面,此时所得到达车流量实质上是驶离车流量,因而很难反映真实的交通需求。
以图 1为例,分析上、下游断面驶离车流量和到达车流量的关系。各进口道渠化方式如图 1所示,DUD为上、下游交叉口西进口的停止线间距,DDU为上、下游交叉口东进口的停止线间距,假设DUD=DDU,将其简称为交叉口间距。这里将检测断面设在停止线处,各检测断面到达-驶离车流量的关系如下:
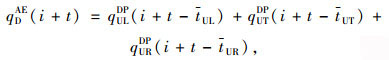
|
(1) |
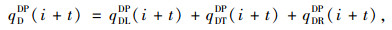
|
(2) |
|
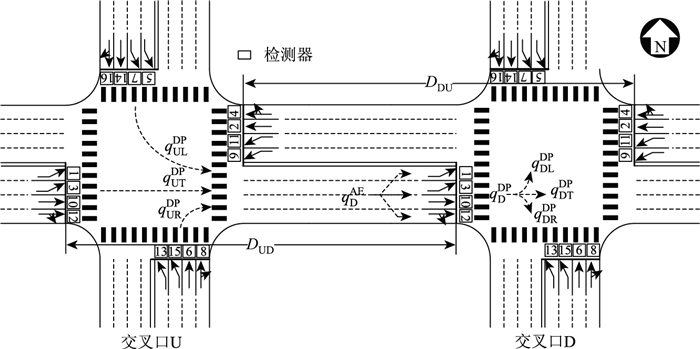
| 图 1 交叉口示意图 Fig. 1 Layout of intersection |
| |
式中, qDAE(i+t)为时间间隔[i, i+t)内下游交叉口西进口的到达车流量;qULDP(i+t-tUL),qUTDP(i+t-tUT)和qURDP(i+t-tUR)分别为时间间隔[i-tUL, i+t-tUL),[i-tUT, i+t-tUT)和[i-tUR, i+t-tUR)内上游交叉口北进口左转、西进口直行和南进口右转的驶离车流量;qDDP(i+t)为时间间隔[i, i+t)内下游交叉口西进口的驶离车流量;qDLDP(i+t),qDTDP(i+t)和qDRDP(i+t)分别为时间间隔[i, i+t)内下游交叉口西进口左转、直行和右转的驶离车流量;tUL,tUT和tUR分别为上游交叉口北进口左转、西进口直行和南进口右转三股车流由上游停止线至下游停止线的平均行程时间。
由式(1)可见,下游交叉口西进口的交通需求依赖于上游交叉口北进口左转、西进口直行和南进口右转的交通需求。根据相关文献[16],上游交叉口北进口左转、西进口直行和南进口右转三股车流在驶向下游交叉口的过程中,由于车辆行驶速度差异致使车队离散现象发生。为设计有效的信号配时方案,需要准确估计车道组的交通需求。由于车队离散现象普遍存在,因此估算车道组交通需求时不可忽视该现象。
2 交通需求估算模型 2.1 车队离散特性不考虑图 1中的下游交叉口,利用VISSIM软件建立仿真路网。针对上游交叉口,采用四相位信号控制方案。信号周期时长为120 s,相位相序为东西直行、东西左转、南北直行和南北左转,这4个相位的显示绿灯时长分别为35,20,25和20 s,各相位的全红时间和黄灯时间分别为2 s和3 s。这里所有右转车流均不受单独的信号控制。
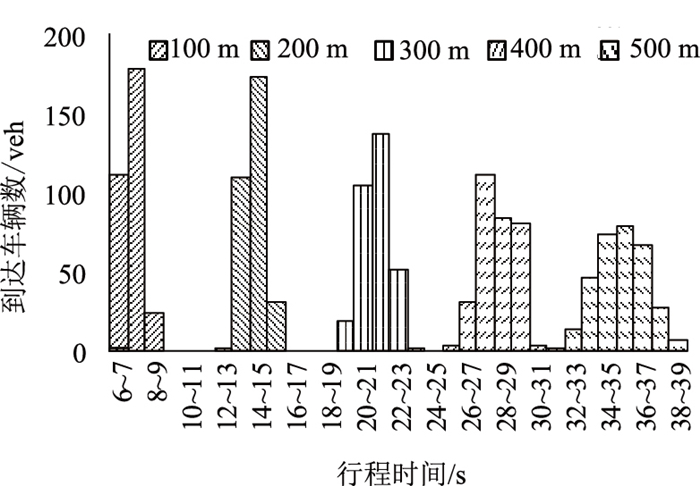
为描述不同断面的流量图式,以上游交叉口西进口的直行车流为例,以1 s为统计间隔,使用行程时间检测器获取车辆行程时间和到达车辆数。设西进口停止线处为起始检测断面,终止检测断面分别位于停止线下游100,200,300,400 m和500 m处。选取960~2 160 s为数据统计时段,图 2展示了这5个断面的流量图式。由该图可以看出,车队从上游驶向下游的过程中,通过下游断面的持续时间逐渐拉长,到达车辆数的峰值逐渐下降,即发生了车队离散现象。
|
| 图 2 流量图式 Fig. 2 Pattern of traffic volumes |
| |
1969年,Robertson提出描述车队离散现象的几何分布模型[16],其具体表达式为
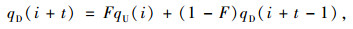
|
(3) |
式中,F=1/(1+αt);qD(i+t)和qD(i+t-1)分别为时段i+t和i+t-1内下游断面到达车流量;qU(i)为时段i内上游断面驶离车流量;t为上、下游断面之间车辆平均行驶时间的0.80倍;F为车队离散系数;α为修正系数。
研究表明,Robertson模型应用范围广,适合描述短距离的行驶时间分布[17]。因此,采用该模型提出交通需求估算方法。
2.2 数学模型建立考虑车流转向因素,对式(3)进行修正,可得交通需求估算模型,即
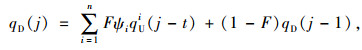
|
(4) |
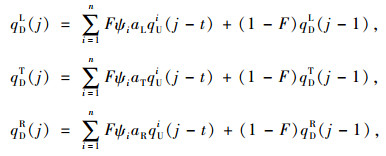
|
(5) |
式中, qD(j)和qD(j-1)分别为时段j和j-1内下游交叉口停止线处的到达车流量;ψi为判断上游交叉口车流i是否对下游交叉口车流有贡献的标识符,如果是ψi=1,否则ψi=0;qUi(j-t)为时段j-t内上游交叉口车流i的驶离车流量;qDL(j),qDT(j)和qDR(j)分别为时段j内下游交叉口停止线处左转、直行和右转的到达车流量;qDL(j-1),qDT(j-1)和qDR(j-1)分别为时段j-1内下游交叉口停止线处左转、直行和右转的到达车流量;aL,aT和aR分别为下游交叉口停止线处左转、直行和右转的比例;n为时段j-t内驶离上游交叉口的车流数。
使用交通需求估算模型时,首先需要标定车队离散系数。在标定车队离散系数时,需获取各进口道的历史车流量数据。车队离散系数标定之后,还需采集各进口道的驶离车流量数据。根据标定的车队离散系数和采集的驶离车流量数据,利用交通需求估算模型可得到每条进口道的估算车流量。若采集的驶离车流量为实时统计数据,可得到实时估算车流量,否则为历史估算车流量。
为验证交通需求估算的必要性,使用不同的交通需求估计值优化交叉口信号配时方案。这里采用估算车流量和实测车流量分别作为交通需求估计值,对于每条车道组,估算车流量是指由式(5)计算得到的交通需求,实测车流量是指在停止线处测得的交通需求。为获取最优的信号配时方案,采用文献[18]给出的优化模型,其表达式为
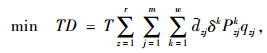
|
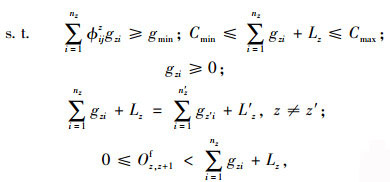
|
(6) |
式中,TD为车辆延误;T为分析期;r为交叉口数;m为车道组数;w为机动车类型数;dzj为交叉口z车道组j的车均延误;δk为k类机动车的换算系数;Pzjk为交叉口z车道组j上k类机动车比例;qzj为交叉口z车道组j的需求流率;nz和nz′分别为交叉口z和z′的相位数;ϕijz为判断交叉口z车道组j是否在相位i内通行的标识符,如果是,ϕijz=1,否则,ϕijz=0;gzi和gz′i分别为交叉口z和z′相位i的有效绿灯时间;gmin为最小有效绿灯时间;Cmin为最小周期时长;Lz和Lz′分别为交叉口z和z′的总损失时间;Cmax为最大周期时长;Oz, z+1f为交叉口z+1相对于z的相位差。
3 实例与仿真验证为验证交通需求估算模型的准确性及交通需求估算的必要性,首先采用实际路段车流量数据进行交通需求估算,验证交通需求估算模型在实际应用中的准确性;然后利用VISSIM软件建立仿真模型,考虑3种交通需求水平和3种交叉口间距,获取每种方案下的车流量数据,进一步获得每种方案下的估算和预设车流量,并对比实测、估算和预设车流量;最后利用实测和估算车流量分别进行配时方案优化,验证交通需求估算的必要性。
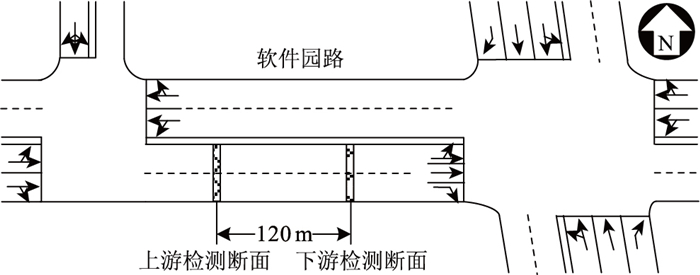
3.1 需求估算的实例分析为获取实际路段车流量数据,选取大连市软件园路进行实地调查,选取的具体路段位于大连东软信息学院东2门与软件园路交叉口和数码路与软件园路交叉口之间,上游检测断面位于大连东软信息学院东2门与软件园路交叉口东出口下游80 m处,调查时间为2018年9月,调查时段为7:00—8:30。如图 3所示,该路段为双向四车道,上、下游检测断面的间距为120 m,下游检测断面距交叉口较远,故交通信号对其车流影响较小。我国现行公路工程技术标准中将车型分成小汽车、中型车、大型车、拖挂车,其换算系数分别为1,1.5,2和3[19]。这里将拖挂车归入大型车,则车辆类型分为小汽车、中型车和大型车3种,其换算系数分别为1,1.5和2.5,进而得到该时段内上、下游检测断面当量小汽车车流量数据。经过统计,调查时段内共通过2 100辆车,其中小汽车1 961辆、中型车46辆、大型车93辆。
|
| 图 3 调查路段示意图 Fig. 3 Schematic diagram of surveyed road section |
| |
为估算下游检测断面的交通需求,需要标定车队离散系数,标定车队离散系数大多是标定式(3)中的修正系数α,其值范围一般为0.10~0.35[20]。利用7:00—8:00的车流量数据进行车队离散系数标定。以1 min为间隔估算下游检测断面到达车流量,以0.01为间隔从0.10取到0.35,为寻求最佳修正系数α,以最小化下游检测断面估算车流量与实测车流量的平均相对误差的绝对值为目标,利用MATLAB软件编程实现。求得该路段最佳修正系数α为0.11。
为了检验α标定值是否合适,引入卡方值,其计算公式为
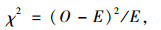
|
(7) |
式中, χ2为卡方值;O为估算车辆数;E为检测车辆数。
对该路段的车流量数据进行卡方检验,因其卡方值69.78小于卡方临界值77.93,这说明该路段的α标定值合适。同时,经过计算标定时下游检测断面估算车流量与实测车流量的平均相对误差的绝对值为15.05%,这一误差较小也说明α标定值合适。
采用修正系数α的标定值0.11,利用8:00—8:30车流量数据进行到达车流量估计,验证交通需求估算模型的准确性。以1 min为间隔估算下游检测断面到达车流量,经计算下游检测断面估算车流量与实测车流量的平均相对误差的绝对值为10.33%,该误差较小说明交通需求估算模型在实际应用中具有较高准确性。
3.2 需求估算的仿真验证为考虑车队离散的更多影响因素,利用VISSIM软件建立仿真模型。如图 1所示路网,各交叉口每条进口道均渠化两条左转专用车道、一条直行车道和一条直右车道。为分析交通需求估算结果的影响因素,考虑交叉口间距和交通需求,分别设置3种水平。上、下游交叉口分别记为交叉口A和B,交叉口间距取为200, 400 m和600 m,交通需求加载表 1所示的低(L)、中(M)和高(H)3种水平,表 1中数据均为假定所得。每个交叉口均采用四相位信号控制方案,相位1~4分别为东西直行、东西左转、南北直行和南北左转,各相位全红时间和黄灯时间分别为2 s和3 s。
| 方案 | 转向 | 小时流量/(veh·h-1) | |||
| 西进口 | 北进口 | 东进口 | 南进口 | ||
| A-L | 左转 | 381 | 437 | 299 | 421 |
| A-L | 直行 | 423 | 393 | 598 | 421 |
| A-L | 右转 | 42 | 44 | 99 | 94 |
| A-M | 左转 | 433 | 537 | 499 | 468 |
| A-M | 直行 | 1 044 | 483 | 997 | 468 |
| A-M | 右转 | 15 | 54 | 166 | 104 |
| A-H | 左转 | 466 | 659 | 570 | 614 |
| A-H | 直行 | 1 126 | 592 | 1 139 | 614 |
| A-H | 右转 | 17 | 66 | 190 | 137 |
| B-L | 左转 | 286 | 374 | 437 | 426 |
| B-L | 直行 | 572 | 374 | 486 | 383 |
| B-L | 右转 | 96 | 84 | 49 | 42 |
| B-M | 左转 | 506 | 452 | 409 | 575 |
| B-M | 直行 | 1 011 | 452 | 987 | 518 |
| B-M | 右转 | 168 | 100 | 14 | 57 |
| B-H | 左转 | 577 | 582 | 465 | 649 |
| B-H | 直行 | 1153 | 582 | 1 121 | 584 |
| B-H | 右转 | 192 | 129 | 16 | 65 |
假设相位1~4的显示绿灯时长分别为35,20,25 s和20 s,并对两个交叉口进行单向协调,协调方向由西向东,当交叉口间距为200,400 m和600 m时,相位差分别采用15,29 s和43 s,称此方案为现状方案。
在仿真模型中,交通流组成选择100%的小汽车,仿真时长取4 500 s,仿真次数为5。选择Wiedemann 74模型来描述车辆跟驰行为,根据文献[21]将左转、直行和右转车道的饱和流率分别取为1 810, 1 850 pcu/h和1 810 pcu/h,VISSIM模型中通过调整车道对应的安全距离的附加部分和倍数部分两个参数来模拟所给定的饱和流率。依据VISSIM用户手册,左转、直行和右转车道对应的安全距离的附加部分为2.45,2.40和2.45,其倍数部分为3.45,3.40和3.45。为每股车流设置上、下游检测断面以获取车流量,上游检测断面设置在每条路段的起点,下游检测断面设置在进口道停止线处,数据采集时段取900~4 500 s,统计间隔设为5 s。
现状方案下,选取960~4 440 s共计29个周期为统计时段,统计上游车流量到达下游交叉口时在绿灯期间通过的比例。上、下游交叉口间距为600, 400 m和200 m时,低水平交通需求下A东进口到达车辆分别有58.82%,70.89%和87.27%在绿灯期间通过,B西进口到达车辆分别有89.18%,88.48%和83.97%在绿灯期间通过;中水平交通需求下A东进口到达车辆分别有46.05%,63.54%和18.21%在绿灯期间通过,B西进口到达车辆分别有89.21%,92.15%和3.33%在绿灯期间通过;高水平交通需求下A东进口到达车辆分别有0.00%,2.47%和0.00%在绿灯期间通过,B西进口到达车辆分别有10.54%,13.78%和0.06%在绿灯期间通过。相比于A东进口,进行协调的B西进口到达车辆在绿灯期间通过比例更高;相比于中、低交通需求水平,高水平交通需求时下游交叉口到达车辆在绿灯期间通过比例更低,大多车辆都需排队等待后才能通过。可以看出,低水平交通需求时,下游交叉口的处理能力较好;中水平交通需求时,下游交叉口的处理能力尚可接受;高水平交通需求时,因加载车流量过大,下游交叉口处理能力较差。
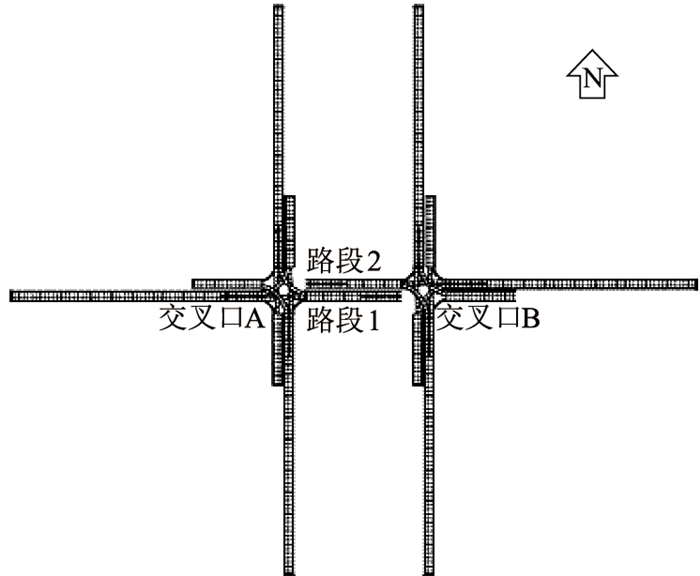
为估算交通需求,首先需进行车队离散系数标定。车队离散模型描述连续流运动规律,不考虑交通信号对车流造成的周期性干扰。为模拟连续流,在仿真模型中通过删除连接器来消除下游交通信号对车流的干扰。图 4为车队离散系数标定的仿真模型,以行驶在路段1和2上的车流为例,删除路段1和2与其下游路段之间的连接器。
|
| 图 4 车队离散系数标定的仿真模型 Fig. 4 Simulation model for calibrating platoon dispersion coefficients |
| |
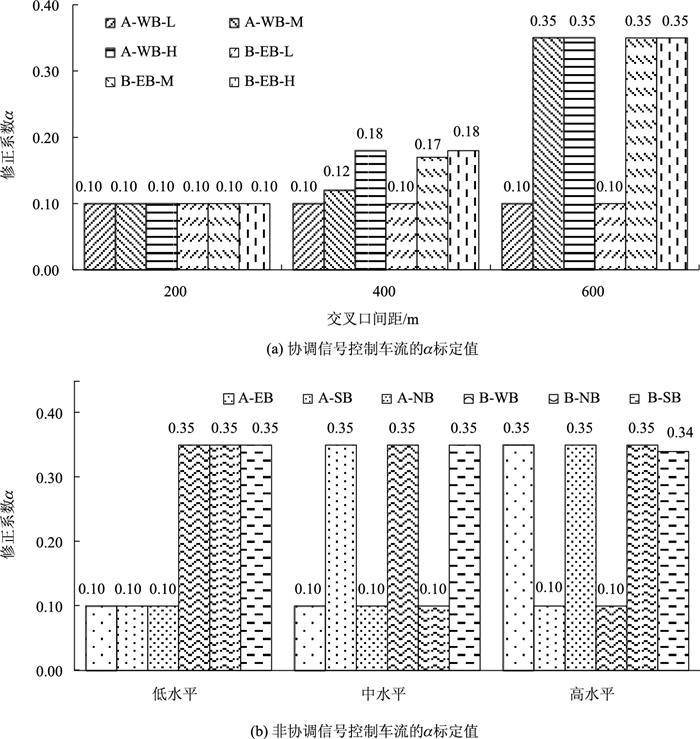
图 5给出了不同交叉口间距和交通需求水平下每股车流的α标定值,这里EB,SB,WB和NB分别代表西进口、北进口、东进口和南进口[15]。A东进口和B西进口的车流为协调信号控制的车流,其余进口的车流均为非协调信号控制的车流。从图 5(a)可以看出,在相同的交通需求水平下,随着交叉口间距增加,同一路段上α标定值逐渐增加;针对相同的交叉口间距,随着交通需求水平提高,同一路段上α标定值逐渐增加。这说明随着交叉口间距的增加和交通需求水平的提高,车队的离散程度越来越高。从图 5(b)可以看出,针对相同的交通需求水平和行驶路段长度,α标定值对于不同路段取决于其具体的车辆产生规律,这说明车辆产生规律对车队离散程度有显著影响。
|
| 图 5 α标定值 Fig. 5 Calibrated α values |
| |
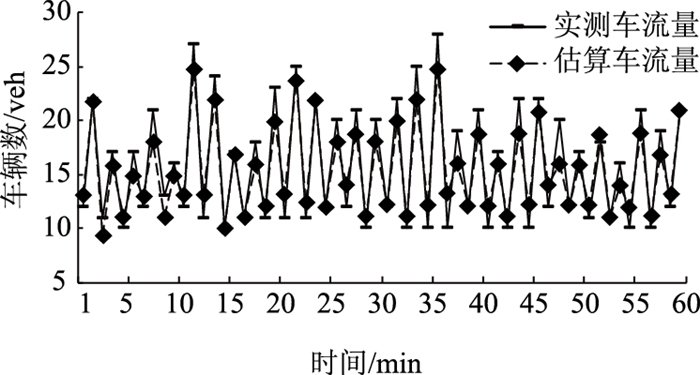
考虑不同的交叉口间距和交通需求水平,对车流量数据进行卡方检验,共计72次,其中最大的卡方值为14.11。因为卡方值都小于卡方临界值77.93,所以α标定值均合适。此外,当交通需求处于低水平,上、下游交叉口间距为200 m时,即方案200-L下B西进口估算车流量与实测车流量的平均相对误差的绝对值最大,其值为12.85%,这也说明α标定值都合适。图 6中给出了标定时方案200-L下B西进口的估算车流量和实测车流量。
|
| 图 6 方案200-L下B西进口估算车流量和实测车流量 Fig. 6 Estimated and measured volumes of westbound approach of intersection B under scheme 200-L |
| |
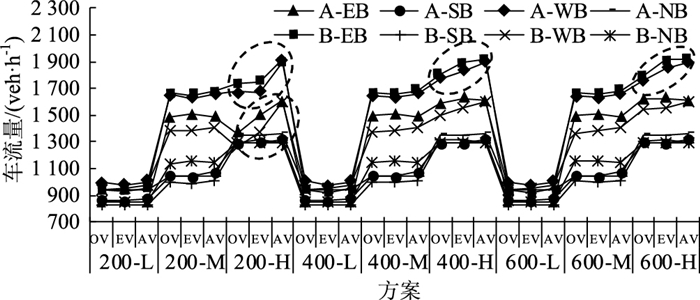
为获得仿真模型各进口道每分钟的实时估算车流量,需以1 min为间隔采集实时的驶离车流量数据。针对不同交叉口间距和交通需求水平,图 7对比了每个进口道的实测车流量OV、估算车流量EV和预设车流量AV。预设车流量是根据流量守恒定律由起讫点对和车流转向比例推算得到。
|
| 图 7 实测车流量、估算车流量和预设车流量对比 Fig. 7 Comparison of measured, estimated and assumed volumes |
| |
从图 7中可以看出,当交通需求处于中、低水平,实测车流量与估算车流量都接近于预设车流量;当交通需求处于高水平,方案200-H下A和B东、西进口以及方案400-H和600-H下A东进口和B西进口的实测车流量均小于预设车流量(如图中虚线圈所示),这几种情况中除方案200-H下A东进口和B西进口外估算车流量相比于实测车流量更接近预设车流量,其他情况下实测车流量、估算车流量与预设车流量都接近。当整体交通需求处于高水平时,图中所示虚线圈说明进口道实测车流量可能远远小于预设车流量,即此时停车线处所测得的驶离车流量难以反映车道组的真实交通需求,其原因在于发生了交通拥堵;相比之下,所建模型估算的到达车流量能更好地反映车道组的真实交通需求。
实际上,实测车流量和估算车流量都具有很强的时变特性,这种时变特性可以由变异系数来表征。变异系数通过消除测量尺度和量纲的影响来反映样本数据的波动性[22],其表达式为
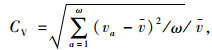
|
(8) |
式中,CV为变异系数;va为指定时间间隔内第a股车流的交通量;ω为指定时间间隔的个数;v-为指定时间间隔内ω股车流的平均交通量。
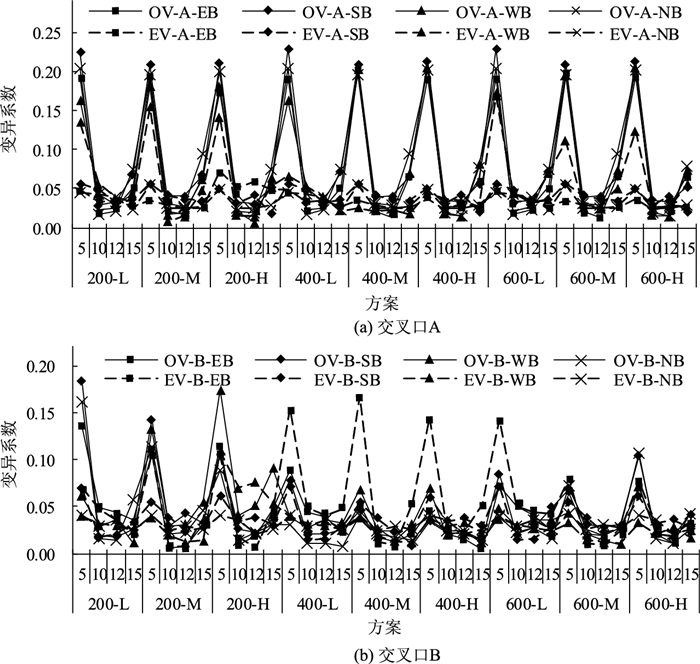
这里,时间间隔分别取5,10,12 min和15 min。针对不同的需求水平和时间间隔,图 8展示了每条进口道实测车流量和估算车流量的变异系数。该图显示,实测车流量和估算车流量的变异系数大多差异很大;对于实测车流量与估算车流量,多数情况下时间间隔为5 min时其变异系数最大,时间间隔为15 min时居中,时间间隔取10 min或12 min时最小。考虑到交通需求的稳定性和波动性[15],后续进行信号配时优化时选择15 min的时间间隔。
|
| 图 8 实测车流量和估算车流量的变异系数 Fig. 8 Variation coefficients of measured and estimated volumes |
| |
3.3 需求估算的必要性检验
为检验交通需求估算的必要性,分别采用仿真模型中的实测车流量和估算车流量作为到达车流量(即交通需求估计值),利用式(6)获得两种信号配时方案,分别记为优化方案Ⅰ和Ⅱ。优化过程中,最小有效绿灯时间取10 s、最小周期时长取60 s、最大周期时长取180 s、黄灯时间取3 s、全红时间取2 s、前损失时间取2 s、后补偿时间取2 s。针对不同的交通需求水平和交叉口间距,表 2列出了优化方案Ⅰ和Ⅱ的信号配时参数。表中,OP1和OP2分别代表优化方案Ⅰ和Ⅱ。该表显示,优化方案Ⅰ不同于优化方案Ⅱ。这说明交通需求数据的准确性会影响信号配时方案的优化。
| 方案 | 交叉口 | 周期时长/s | 绿灯时间/s | 相位差/s | |||
| 相位1 | 相位2 | 相位3 | 相位4 | ||||
| OP1-200-L | A/B | 60 | 12/12 | 8/9 | 9/9 | 11/10 | 0/0 |
| OP1-200-M | A/B | 65 | 19/18 | 8/8 | 8/9 | 10/10 | 0/59 |
| OP1-200-H | A/B | 87 | 24/25 | 12/12 | 15/15 | 16/15 | 0/62 |
| OP1-400-L | A/B | 60 | 12/12 | 8/9 | 10/9 | 10/10 | 0/0 |
| OP1-400-M | A/B | 67 | 20/19 | 8/9 | 9/9 | 10/10 | 0/8 |
| OP1-400-H | A/B | 104 | 32/31 | 16/16 | 18/18 | 18/19 | 0/0 |
| OP1-600-L | A/B | 60 | 12/12 | 8/10 | 10/9 | 10/9 | 0/0 |
| OP1-600-M | A/B | 67 | 20/18 | 9/9 | 9/9 | 9/11 | 0/0 |
| OP1-600-H | A/B | 105 | 33/31 | 15/16 | 18/17 | 19/21 | 0/0 |
| OP2-200-L | A/B | 60 | 12/10 | 9/9 | 10/12 | 9/9 | 0/0 |
| OP2-200-M | A/B | 64 | 19/17 | 8/8 | 8/9 | 9/10 | 0/59 |
| OP2-200-H | A/B | 83 | 25/24 | 11/11 | 13/13 | 14/14 | 0/34 |
| OP2-400-L | A/B | 60 | 12/13 | 8/9 | 9/9 | 11/9 | 0/0 |
| OP2-400-M | A/B | 64 | 19/17 | 8/8 | 8/9 | 9/10 | 0/38 |
| OP2-400-H | A/B | 93 | 29/29 | 13/14 | 15/14 | 16/16 | 0/0 |
| OP2-600-L | A/B | 60 | 13/13 | 8/9 | 9/9 | 10/9 | 0/0 |
| OP2-600-M | A/B | 65 | 19/17 | 9/8 | 8/9 | 9/11 | 0/42 |
| OP2-600-H | A/B | 97 | 30/30 | 14/15 | 16/15 | 17/17 | 0/0 |
对于前述仿真模型,信号配时方案依次采用现状方案CP、优化方案Ⅰ和Ⅱ,使用路网性能评价工具获得每种方案对应的车均延误、停车次数和行驶速度,如表 3所示,其中所列数据是5次仿真结果的平均值。
| 方案 | 停车次数 | 行驶速度/(km·h-1) | 车均延误/(s·veh-1) |
| CP-200-L | 1.00 | 23.03 | 50.55 |
| CP-400-L | 1.04 | 23.51 | 54.61 |
| CP-600-L | 1.07 | 24.70 | 55.26 |
| OP1-200-L | 1.00 | 29.05 | 32.15 |
| OP1-400-L | 1.06 | 29.35 | 35.22 |
| OP1-600-L | 1.10 | 30.99 | 34.36 |
| OP2-200-L | 1.01 | 28.74 | 32.92 |
| OP2-400-L | 1.05 | 29.46 | 34.91 |
| OP2-600-L | 1.11 | 30.93 | 34.52 |
| CP-200-M | 1.50 | 17.96 | 78.70 |
| CP-400-M | 1.17 | 22.29 | 63.29 |
| CP-600-M | 1.21 | 23.79 | 63.64 |
| OP1-200-M | 1.41 | 22.87 | 53.04 |
| OP1-400-M | 1.30 | 25.63 | 49.15 |
| OP1-600-M | 1.34 | 27.15 | 49.49 |
| OP2-200-M | 1.39 | 23.31 | 51.26 |
| OP2-400-M | 1.34 | 26.12 | 47.60 |
| OP2-600-M | 1.34 | 27.12 | 49.74 |
| CP-200-H | 3.15 | 9.87 | 168.65 |
| CP-400-H | 2.40 | 13.98 | 127.51 |
| CP-600-H | 2.51 | 14.95 | 131.25 |
| OP1-200-H | 3.19 | 11.52 | 142.76 |
| OP1-400-H | 1.78 | 18.48 | 87.42 |
| OP1-600-H | 1.75 | 19.77 | 87.85 |
| OP2-200-H | 2.25 | 14.99 | 102.58 |
| OP2-400-H | 1.57 | 19.91 | 76.20 |
| OP2-600-H | 1.61 | 20.98 | 79.19 |
从表 3可以看出,中、低交通需求水平下各方案对应的车均延误较低,各交叉口性能较好;在高水平交通需求下,现状方案和优化方案Ⅰ对应的车均延误较大,交叉口性能较差,相比之下优化方案Ⅱ对应的车均延误较小,交叉口性能有所提升。与现状方案相比,优化方案使车均延误下降15.35%~40.24%、行驶速度提高14.00%~51.87%,这说明所采用的信号配时优化方法有效。
为评价交通需求估算的必要性,引入优化方案Ⅰ与Ⅱ对应的车均延误的相对误差,即
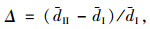
|
(9) |
式中, Δ为车均延误的相对误差;dⅠ和dⅡ分别为优化方案Ⅰ与Ⅱ对应的车均延误。
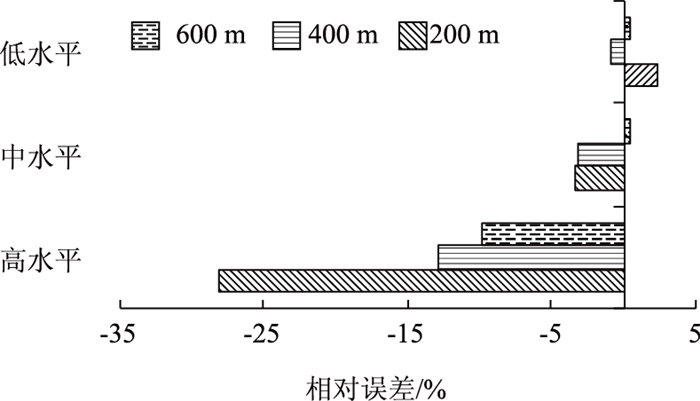
图 9给出了不同交通需求水平下优化方案Ⅰ和Ⅱ对应的车均延误的相对误差。优化方案Ⅰ和Ⅱ分别基于实测车流量和估算车流量计算得到。与实测车流量所得优化方案Ⅰ相比,当交通需求处于高水平时,估算车流量所得优化方案Ⅱ使车均延误下降9.85%~28.15%;当交通需求处于中水平时,估算车流量所得优化方案Ⅱ使车均延误下降3.15%~3.36%或增加0.51%;当交通需求处于低水平时,估算车流量所得优化方案Ⅱ使车均延误下降0.87%或增加0.46%~2.37%。由此可见,在高水平交通需求下,采用实测与估算车流量得到的优化方案对应的车均延误存在明显差异;而在中、低水平交通需求下,二者并无太大差异。这说明对于信号配时设计应该进行交通需求估算。特别是,当交通流处于拥挤状态时,这种估算显得尤为必要。
|
| 图 9 优化方案Ⅰ和Ⅱ所得车均延误的相对误差 Fig. 9 Relative errors of average delay between optimized scheme Ⅰ and optimized scheme Ⅱ |
| |
4 结论
以上、下游交叉口为例,分析了下游交叉口到达车流量与上游交叉口驶离车流量之间的关系。利用VISSIM仿真模型获得了车队在上、下游断面的流量图式,并分析了车队离散特性,进而建立了车道组交通需求估算模型。以大连市软件园路为例,使用实地调查数据验证了交通需求估算模型在实际应用中的准确性。以两交叉口系统为例,考虑交叉口间距和交通需求分别设3种水平,并为信号配时设置现状方案。通过仿真试验,对比了实测车流量、估算车流量和预设车流量的差异,并使用变异系数分析了实测车流量和估算车流量的波动性。采用已有信号配时优化方法,利用实测车流量和估算车流量获得了两种优化配时方案。针对现状和优化配时方案,利用VISSIM软件模拟了交通流运行状况,得到了停车次数、行驶速度和车均延误等性能指标。结果显示,当其他条件相同时,α标定值对不同路段取决于其具体的车辆产生规律,对同一路段随着交叉口间距和交通需求水平的增加而增加;在高水平交通需求下,相比实测车流量,估算车流量能更好地反映车道组的真实交通需求;根据变异系数,存在合适的时间间隔能使所得交通需求的波动性最小;获得真实的车道组交通需求对于信号配时设计及交叉口运行非常重要,尤其发生交通拥堵时。研究成果表明,当交通需求水平较高时,交通流处于拥挤状态,进口道检测的车流量很难反映真实的交通需求,此时需进行交通需求估算;当交通需求水平较低时,交通流处于非拥挤状态,进口道检测的车流量尽管不能较好地反映真实的交通需求,但与其预设值比较接近,可以用于信号配时优化。对于干线道路系统,建议采用所提出的模型估算车道组交通需求来进行信号配时优化。
| [1] |
喻翔, 毛敏, 刘建兵. 城市交通需求预测组合模型的研究[J]. 西南交通大学学报, 2003, 38(1): 75-79. YU Xiang, MAO Min, LIU Jian-bing. Study on Combined Models of Demand Forecasting for Urban Traffic[J]. Journal of Southwest Jiaotong University, 2003, 38(1): 75-79. |
| [2] |
陈艳艳, 史建港. 震后交通需求预测的修正四阶段法[J]. 公路交通科技, 2004, 21(8): 78-81. CHEN Yan-yan, SHI Jian-gang. Application of Revised Four-stage Method in Urban Transport Plan for Emergency Response[J]. Journal of Highway and Transportation Research and Development, 2004, 21(8): 78-81. |
| [3] |
涂圣文, 过秀成, 张小辉. 城市结点对外交通需求分析方法[J]. 交通运输系统工程与信息, 2014, 14(2): 13-18. TU Sheng-wen, GUO Xiu-cheng, ZHANG Xiao-hui. Analysis Method of External Traffic Demand in City Area[J]. Journal of Transportation System Engineering and Information Technology, 2014, 14(2): 13-18. |
| [4] |
牛虎. 四阶段法交通需求预测的局限与非集计模型的发展[J]. 交通标准化, 2007(12): 73-76. NIU Hu. Limits of Four-step Traffic Demand Forecast Model and Development of Disaggregate Model[J]. Communications Standardization, 2007(12): 73-76. |
| [5] |
王凤群, 王晓原, 苏跃江. 基于非集计模型的交通需求预测方法[J]. 山东理工大学学报:自然科学版, 2009, 23(2): 7-12, 16. WANG Feng-qun, WANG Xiao-yuan, SU Yue-jiang. Forecast Method of Traffic Demand Based on Disaggregate Model[J]. Journal of Shandong University of Technology:Natural Science Edition, 2009, 23(2): 7-12, 16. |
| [6] |
TAMIN O Z, WILLUMSEN L G. Transport Demand Model Estimation from Traffic Counts[J]. Transportation, 1989, 16(1): 3-26. |
| [7] |
ZHOU X, QIN X, MAHMASSANI H. Dynamic Origin-destination Demand Estimation with Multiday Link Traffic Counts for Planning Applications[J]. Transportation Research Record, 2003, 1831: 30-38. |
| [8] |
马俊来, 王炜, 李文权, 等. OD矩阵推算技术在高速公路影响区交通需求预测中的应用[J]. 公路交通科技, 2004, 21(6): 88-92. MA Jun-lai, WANG Wei, LI Wen-quan, et al. Application of OD Matrix Estimation in Traffic Demand Forecasting of Expressway's Influencing Area[J]. Journal of Highway and Transportation Research and Development, 2004, 21(6): 88-92. |
| [9] |
李追日.基于手机定位数据的城市道路交通需求推估及分析[D].深圳: 深圳大学, 2016. LI Zhui-ri. Estimation and Analysis of Urban Road Traffic Demand Based on Mobile Phone Positioning Data[D]. Shenzhen: Shenzhen University, 2016. |
| [10] |
MA D, LUO X, LI W, et al. Traffic Demands Estimation for Lane Groups at Signal-controlled Intersections Using Travel Times from Video-imaging Detectors[J]. IET Intelligent Transport Systems, 2017, 11(4): 222-229. |
| [11] |
POHLMANN T, FRIEDRICH B. A Combined Method to Forecast and Estimate Traffic Demand in Urban Networks[J]. Transportation Research Part C:Emerging Technologies, 2013, 31(2): 131-144. |
| [12] |
罗格P R, 艾琳娜S P, 威廉姆R M. 交通工程[M]. 北京: 机械工业出版社, 2008. ROGER P R, ELENA S P, WILLIAM R M. Traffic Engineering[M]. Beijing: China Machine Press, 2008. |
| [13] |
URBANIK T, TANAKA A, LOZNER B, et al. Signal Timing Manual, NCHRP 812[R].2nd ed. Washington, D.C.: Federal Highway Administration, 2015.
|
| [14] |
何龙.面向双向绿波的干道协调控制方法研究[D].大连: 大连理工大学, 2015. HE Long. Coordinated Control Method Research of Main Road for Bidirectional Green Wave[D]. Dalian: School of Transportation and Logistics, Dalian University of Technology, 2015. |
| [15] |
National Research Council. Highway Capacity Manual (HCM)2000[M]. Washington, D.C.: Transportation Research Board, 2000.
|
| [16] |
全永燊. 城市交通控制[M]. 北京: 人民交通出版社, 1989. QUAN Yong-shen. Urban Traffic Control[M]. Beijing: China Communications Press, 1989. |
| [17] |
王殿海, 汪志涛. 车队离散模型研究[J]. 交通运输工程学报, 2001, 1(1): 68-71. WANG Dian-hai, WANG Zhi-tao. Study on Platoon Dispersion Model[J]. Journal of Traffic and Transportation Engineering, 2001, 1(1): 68-71. |
| [18] |
YAO R, GUO W, ZHOU H. Integrative Design of Left-turn Lane Space and Signal Coordination for Two Adjacent Intersections[J]. Canadian Journal of Civil Engineering, 2017, 44(4): 274-285. |
| [19] |
曲大义, 杨建, 陈秀锋, 等. 动态车辆换算系数的交通流特性分析方法[J]. 公路交通科技, 2012, 29(4): 132-136. QU Da-yi, YANG Jian, CHEN Xiu-feng, et al. Method of Dynamic Vehicle Conversion Factors Based on Traffic Flow Characteristic Analysis[J]. Journal of Highway and Transportation Research and Development, 2012, 29(4): 132-136. |
| [20] |
全永燊, 郭继孚, 郑猛, 等. 我国城市道路车流离散规律初探[J]. 北京规划建设, 2001(1): 32-35. QUAN Yong-shen, GUO Ji-fu, ZHENG Meng, et al. A Preliminary Study on Dispersion Rule of Urban Road Traffic Flow in China[J]. Beijing City Planning&Construction Review, 2001(1): 32-35. |
| [21] |
AKCELIK R. Traffic Signals: Capacity and Timing Analysis, ARR 123[R]. Vermont South: Australian Road Research Board, 1981.
|
| [22] |
蒋冲, 李芬, 高艳妮, 等. 1956-2012年三江源区河流流量变化及成因[J]. 环境科学研究, 2017, 30(1): 30-39. JIANG Chong, LI Fen, GAO Yan-ni, et al. Streamflow Variation in the Three-river Headwaters Region during 1956-2012[J]. Research of Environmental Science, 2017, 30(1): 30-39. |
 2019, Vol. 36
2019, Vol. 36
