扩展功能
文章信息
- 沈锐利, 王文弟, 王路, 白伦华
- SHEN Rui-li, WANG Wen-di, WANG Lu, BAI Lun-hua
- 基于可靠度理论的悬索桥预应力锚固系统时变计算方法研究
- Study on Time-variant Calculation Method of Prestressed Anchor System of Suspension Bridge Based on Reliability Theory
- 公路交通科技, 2019, 36(9): 57-64
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(9): 57-64
- 10.3969/j.issn.1002-0268.2019.09.009
-
文章历史
- 收稿日期: 2017-09-04
2. 中铁大桥(南京)桥隧诊治有限公司, 江苏 南京 210032;
3. 华南理工大学 土木与交通学院, 广东 广州 510641
2. China Railway Major Bridge(Nanjing) Bridge and Tunnel Inspect & Retrofit Co., Ltd., Nanjing Jiansu 210032, China;
3. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou Guandong 510641, China
悬索桥主缆锚固系统是连接主缆索股与锚碇、将索股荷载传递至锚碇的重要结构,其在长期荷载作用下的可靠度水平直接关系到全桥的运营安全性与耐久性。目前,锚固系统主要有型钢框架和预应力两种形式[1]。型钢框架锚固系统较为传统,早期大量采用;预应力锚固系统由于具有用钢量少、施工难度低、调节索长方便、可吸收索股偏载等优点,近20~30年也得以较多应用。
国内的悬索桥预应力锚固系统主要采用高强预应力钢绞线,早期使用预应力管道内灌注砂浆的防腐形式,如厦门海沧大桥、江阴长江大桥、润扬长江大桥等,这种形式存在注浆不密实导致防腐能力不可靠,以及钢束、夹片由于砂浆黏结固化无法更换等问题。武汉阳逻长江大桥首次采用了无黏结锚固系统,即采用预应力钢绞线喷涂环氧树脂、预应力管道及锚头防护罩内灌注油脂等防腐方式,预应力钢绞线设计可更换。其后,贵州坝陵河大桥、舟山西侯门大桥、矮寨大桥、泰州长江公路大桥等也均采用了这种锚固系统。
由于预应力锚固系统的预应力筋使用应力高、腐蚀敏感性强,工程应用中对其耐久性总存在疑虑。且油脂有一定的寿命期,在酸性或碱性条件下会水解,产物最终分解成水、二氧化碳等。在一些悬索桥的养护过程中发现,锚头打开后有出水的现象。李海[2]、陈晓军[3]等认为,传统的型钢框架锚固系统钢构件使用应力较低,且锚固系统整体被混凝土浇筑、密封性好,从全寿命的角度考虑,型钢框架锚固系统的耐久性更好;苏强等[4]则认为,随着无黏结预应力锚固系统技术的提出及防腐措施的不断改进,其耐久性将完全可以满足工程寿命要求。然而,由于缺乏针对预应力锚固系统时变可靠性的研究,导致对该问题的认识缺乏量化基础。鉴于此,考虑到影响腐蚀的因素较多,实际不确定性较大,本研究基于可靠度理论,建立腐蚀作用下预应力锚固系统的时变可靠性计算方法,并利用可靠度指标对预应力锚固系统安全性进行评价,以期为工程实践研究提供有益参考。
1 预应力钢绞线腐蚀时变模型 1.1 截面损伤模型根据法拉第腐蚀定律,1 μA/cm2的腐蚀电流密度每年导致的钢筋截面腐蚀深度为11.6 μm[5],即
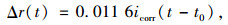
|
(1) |
式中,t0为腐蚀开始年份;icorr为腐蚀电流密度;Δr(t)为t年的钢筋半径减少量。
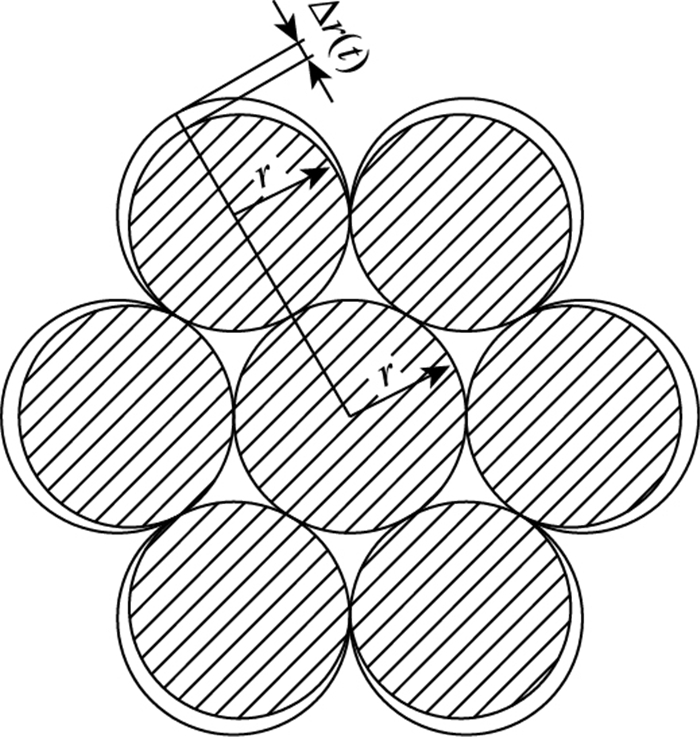
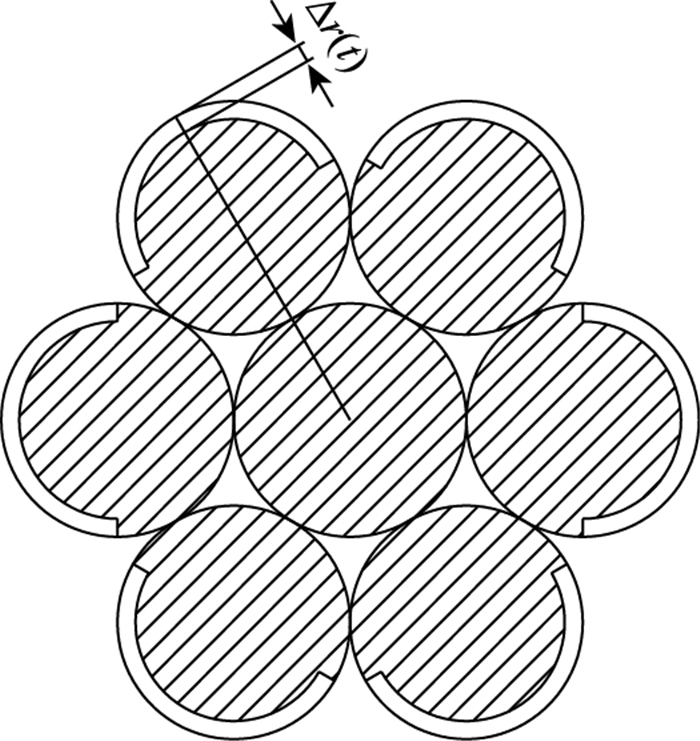
对钢绞线应用上述腐蚀模型[6],如图 1所示,钢绞线由中心钢丝和外层缠绕钢丝组成,只有外层暴露部分发生腐蚀,假定各处腐蚀电流密度一致,则腐蚀面积可近似按图 2计算,由此可得到预应力钢绞线在t时刻的剩余面积为:
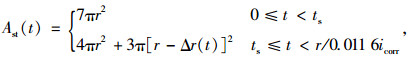
|
(2) |
|
| 图 1 损伤模型 Fig. 1 Damage model |
| |
|
| 图 2 简化模型 Fig. 2 Simplified model |
| |
式中ts为腐蚀开始的年份。
由式(2)可进一步得到钢绞线质量锈蚀率ρw:
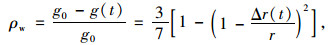
|
(3) |
式中,g0为腐蚀前的质量;g(t)为腐蚀t年后的重量;r为钢绞线中钢丝的半径。
将式(1)代入式(3),考虑模型与实际的误差,引入不确定系数进行修正:
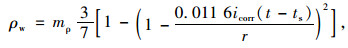
|
(4) |
式中,mρ为损伤模型的不确定性系数,为正态分布随机变量,均值=1.0,标准差=0.02。
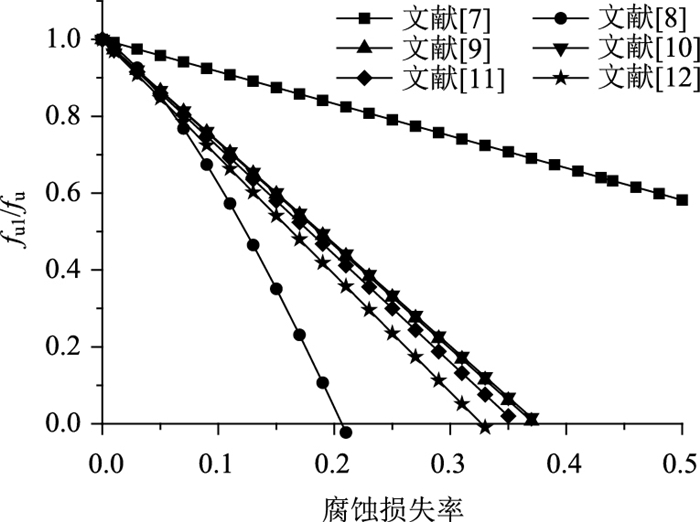
1.2 力学性能时变模型 1.2.1 名义极限强度时变模型腐蚀损失会引起钢绞线名义极限强度的降低,综合对比既有试验研究以确定合理的时变模型:文献[7]通过试验得知名义极限强度与整根钢绞线的平均锈蚀率相关性不明显,而与单根钢丝的最大截面损失率有较好的线性关系;文献[8]通过试验发现随着锈蚀率增加,钢绞线塑性变差,极限伸长率降低,并对钢绞线极限强度与锈蚀率关系进行曲线拟合;文献[9]分别对钢绞线和单根钢丝进行了锈蚀试验,并分别拟合了单根钢丝与钢绞线对质量锈蚀率的关系曲线;文献[10]通过试验发现,腐蚀后的钢绞线钢丝断裂是间断发生的,当腐蚀率较大时,钢丝断裂发生在屈服之前;文献[11-12]对钢绞线进行了加速腐蚀试验,分别提出了锈蚀钢绞线的力学性能时变模型及本构模型。为便于对比,将上述各文献所建立的钢绞线名义极限强度退化曲线绘于图 3中。
|
| 图 3 名义极限强度退化曲线 Fig. 3 Nominal ultimate strength degradation curves |
| |
从图 3中可以看出,文献[7]由于采用的是单丝最大锈蚀率,同样锈蚀率下名义极限强度偏高,模型不便应用;文献[8]试验中钢绞线的最大腐蚀率未超过10.4%,样本范围较窄,故将拟合曲线延伸时可能与实际有偏差,可以看到当腐蚀率为20%时极限强度降为0,偏于保守;文献[9-12]试验拟合的曲线比较接近,而文献[11]中拟合曲线的相关性最好,故本研究以文献[11]的模型为基础,并引入不确定性系数进行修正:
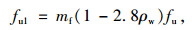
|
(5) |
式中,fu1为锈蚀钢绞线的极限强度;fu为未锈蚀钢绞线的极限强度;mf为强度模型的不确定性系数,服从正态分布,均值=1.0,标准差=0.1。
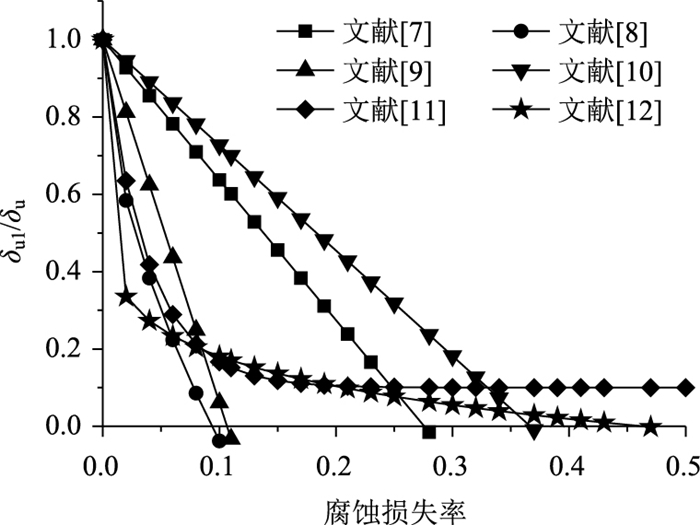
1.2.2 极限伸长率时变模型腐蚀钢绞线的塑性会下降,极限伸长率降低。根据既有文献提出的模型绘出极限伸长率退化曲线,如图 4所示。
|
| 图 4 极限伸长率退化曲线 Fig. 4 Ultimate elongation percentage degradation curves |
| |
从图 4可见,文献[7, 10]模型的极限延伸率退化速度较慢,文献[8, 11]模型腐蚀率为5%以下时极限伸长率退化速度相近。当腐蚀率在10%时左右时,文献[8-9]模型的极限伸长率退化为0,偏于保守。当腐蚀率在10%~20%时文献[11-12]模型的极限伸长率相近。综合考虑采用文献[11]的模型,并引入不确定系数进行修正:
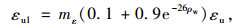
|
(6) |
式中,εu1为锈蚀钢绞线的极限伸长率;ε1为未锈蚀钢绞线的极限伸长率;mε为伸长率模型的不确定系数,服从正态分布,均值=1.0,标准差=0.1。
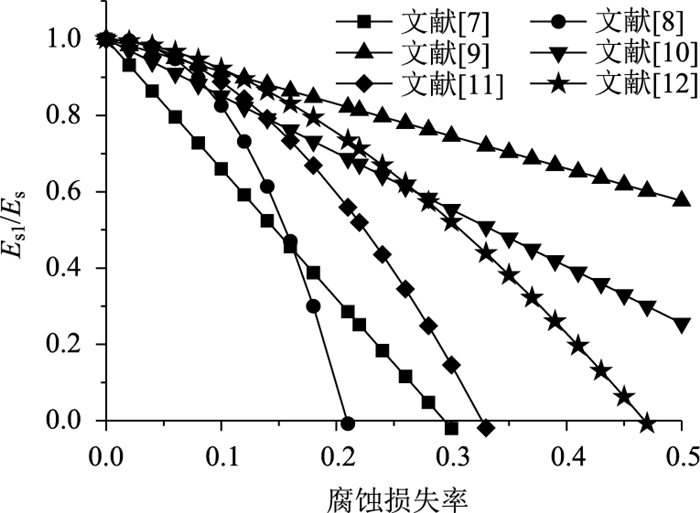
1.2.3 名义弹性模量时变模型不同文献的试验研究均表明腐蚀后钢绞线的弹性模量会降低。当腐蚀率较低时,钢丝间挤压紧密,对钢绞线整体性能影响较小;随着腐蚀率增大,钢丝截面损伤,表面形成蚀坑,钢丝间共同作用能力降低,导致钢绞线整体刚度迅速下降。李富民13]的试验结果也证明了这一点。根据既有文献提出的模型绘出名义弹性模量退化曲线,如图 5所示。
|
| 图 5 名义弹性模量退化曲线 Fig. 5 Nominal elasticity modulus degradation curves |
| |
本研究采用文献[11]的弹性模量退化模型,并引入不确定系数进行修正:
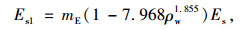
|
(7) |
式中,Es1为锈蚀钢绞线的弹性模量;Es为未锈蚀纲绞线的弹性模量;mE为弹性模量模型的不确定系数,服从正态分布,均值=1.0,标准差=0.1。
2 预应力锚固系统时变计算方法本研究以某公路悬索桥为例,对预应力锚固系统时变可靠性的计算方法进行阐述。该桥主跨1 196 m,主缆由169束索股组成,每股91根ϕ5.2 mm镀锌高强钢丝。锚固系统采用公称直径15.2 mm,抗拉强度为1 860 MPa低松弛钢绞线。不失一般性地,以最低处的1#索股所对应的锚固钢束为例,建立其时变抗力模型,计算其时变可靠度。锚固系统的构造示意如图 6所示,每个孔道内的预应力钢束由12根高强钢绞线组成。

|
| 图 6 预应力锚固系统构造 Fig. 6 Structure of prestressed anchor system |
| |
2.1 锚固系统承载力极限状态
预应力锚固系统由张拉在前后锚面之间的预应力钢束和连接件组成,主缆索股通过连接件与锚固系统相连,将力传递给锚体。《公路悬索桥设计规范》中规定,锚固钢束的预张力不小于1.2倍的主缆索股力。锚固钢束的承载力满足:

|
(8) |
式中,γ0为结构重要性系数;σd为锚固钢束应力设计值;fd为锚固钢束强度设计值。
悬索桥主缆是其主要承力构件,主缆索股在桥梁运营的全寿命期间不可放松或卸载[14]。因此与之对应的锚固系统不可退出工作,故锚固系统预应力钢束在运营阶段应当满足下式的安全性要求:
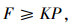
|
(9) |
式中,F为有效锚固力;P为运营阶段的最大索股力;K为持久状况安全系数,一般为1.2~1.5。
2.2 锚固钢束的时变抗力定义两种锚固系统的失效模式:(1)由于腐蚀导致预应力钢束的极限强度降低至使用应力;(2)由于腐蚀导致预应力钢束的极限伸长率降低至初始伸长率。其中,预应力钢束的实际内力为锚固张力和索股传递拉力中的较大值,初始伸长率根据锚固张拉控制应力计算。
根据上述分析,当腐蚀预应力钢束退化的极限强度fu(t)或极限延伸率εu(t)满足以下任一条件时,预应力钢束即失去锚固能力:
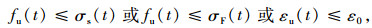
|
(10) |
式中,σs(t)为荷载效应产生的应力;σF(t)为锚固张力产生的应力;ε0为初始伸长率。
腐蚀预应力钢束的极限强度和极限延伸率分别可由式(5)、式(6)得到,不考虑锚体的变形,则腐蚀后的预应力钢束的伸长率与初始伸长率相同,即:
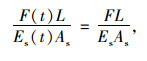
|
(11) |
式中,F, F(t)分别为腐蚀前与腐蚀t年后预应力钢束的锚固力;Es,Es(t)分别为腐蚀前与腐蚀t年后预应力钢束的弹性模量;L为预应力钢束锚固后初始长度;As为钢束截面积。
简化变形式(11)可得到:
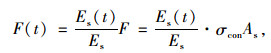
|
(12) |
式中,σcon为张拉控制应力,根据设计资料为0.7fpk;fpk为钢绞线标准强度。
将腐蚀预应力筋弹性模量退化模型式(7)代入式(12),得到锚固力退化函数:
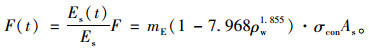
|
(13) |
预应力钢束的失效模式是由式(10)中3个失效模式串联而成的系统,任一失效模式发生即导致预应力钢束失去抗力,退出工作。
将式(10)第1个失效模式作为功能函数,另外两个失效模式作为产生随机数的条件,采用Monte-Carlo方法模拟锚固钢束抗力分布。采用伪随机数法生成同一时刻腐蚀钢绞线样本,其参数包括极限强度、极限伸长率与弹性模量,腐蚀开始时间取0年。将满足式(10)后2个条件钢绞线样本剔除(视为失去抗力),则锚固钢束的抗力为剩余的预应力钢绞线极限强度之和。生成不同时刻的样本则得到不同时刻锚固钢束抗力的分布。表 1为各随机变量参数的分布类型。
采用上述方法得到不同时刻锚固钢束的抗力分布情况如图 7所示,可以看到随时间变化分布的形式有所不同。对不同时刻的抗力分别进行拟合并进行优度检验,当腐蚀时间在70 a以内,抗力服从极值Ⅰ型极小值分布,超过70 a后,服从正态分布。表 2给出了部分时刻的分布参数拟合结果。
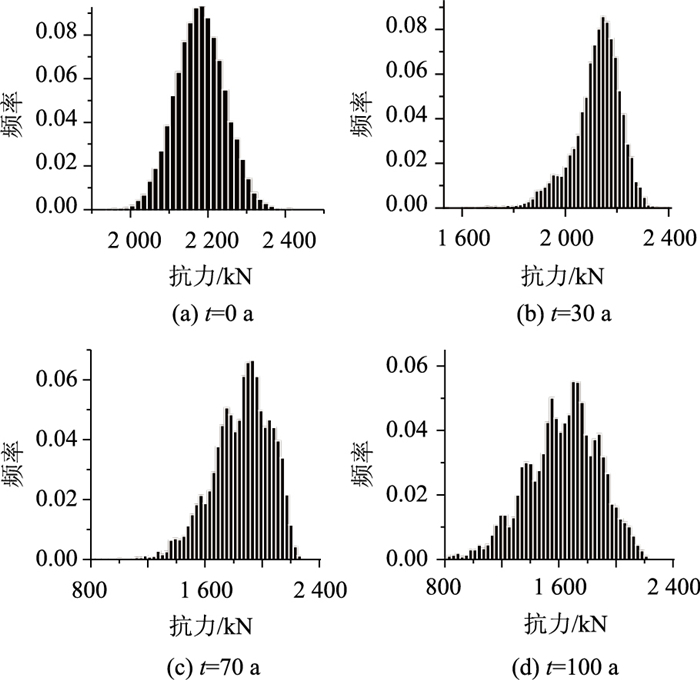
|
| 图 7 锚固钢束抗力分布 Fig. 7 Distribution of resistances of anchor strands |
| |
| t/a | 分布类型 | 分布参数 | |
| 0 | 极值Ⅰ型极小值分布 | u=3 161.84 | α=100.55 |
| 5 | u=3 115.96 | α=103.12 | |
| 10 | u=3 070.18 | α=108.29 | |
| 15 | u=3 023.59 | α=116.10 | |
| 20 | u=2 976.41 | α=126.02 | |
| 25 | u=2 927.66 | α=138.32 | |
| 30 | u=2 876.68 | α=152.65 | |
| 35 | u=2 824.30 | α=168.08 | |
| 40 | u=2 771.41 | α=183.33 | |
| 45 | u=2 716.28 | α=198.90 | |
| 50 | u=2 660.65 | α=214.78 | |
| 55 | u=2 604.49 | α=229.47 | |
| 60 | u=2 547.42 | α=243.04 | |
| 65 | u=2 490.36 | α=256.95 | |
| 70 | u=2 434.39 | α=268.98 | |
| 75 | 正态分布 | μ=2 225.68 | σ=313.44 |
| 80 | μ=2 165.25 | σ=321.98 | |
| 85 | μ=2 104.91 | σ=330.31 | |
| 90 | μ=2 045.28 | σ=337.96 | |
| 95 | μ=1 987.79 | σ=344.54 | |
| 100 | μ=1 931.00 | σ=350.35 | |
2.3 锚固钢束的荷载效应 2.3.1 锚固钢束的恒载效应
锚跨索股恒载力的随机性一方面是由于施工监控中锚跨张力调整时实际张拉力与索股设计拉力之间会有偏差,另一方面索力测试过程中也会带来误差。锚跨张力调整完后索股力通常是用索力加速度计采集振动信号,利用频谱法计算索股张力,由于索股边界条件和计算长度的不确定性,利用简化模型计算出的索股力与真实值会有偏差。
根据以往大跨度悬索桥的施工监控数据总结,成桥阶段锚跨索股力服从正态分布,变异系数介于0.03~0.05之间。本桥1#索股的成桥锚跨张力设计值为SG=1 137 kN,变异系数取0.04。
2.3.2 锚固钢束的活载效应文献[19]根据车辆荷载实测数据计算了不同跨径混凝土梁桥的荷载效应,建立车辆荷载效应概率模型。本研究采用随机车流模拟车辆活载,利用有限元模型计算活载效应并进行统计分析。首先建立悬索桥包括锚跨索股单元的有限元模型,计算锚跨张力的活载影响线;采用文献[20]的统计数据,包括车重及车距信息,利用MATLAB平台编制随机车流模拟程序,然后模拟计算活载效应的分布,具体步骤为:
(1) 运行程序生成n条随机车流数据,n为车道数,每条随机车流数据的样本数量能够反映车重的分布。
(2) 利用影响线加载计算锚跨张力活载效应,每条车道同时对应1条随机车流数据。将随机车流荷载沿桥跨方向移动,每移动固定的长度计算1次活载效应。当所有车道的随机车流全部通过影响线后,记录荷载效应的最大值,作为1天的最大值。
(3) 重复步骤(1),(2)可以得到每天的荷载效应最大值数据。当得到的N天(N足够大)的荷载效应最大值数据后进行统计分析和分布拟合,即得到荷载效应的日最大值分布,用日最大值分布代表年最大值分布。
根据上述方法,生成5 000条随机车流数据进行影响线加载,得到1#索股活载效应最大值分布,如图 8所示。
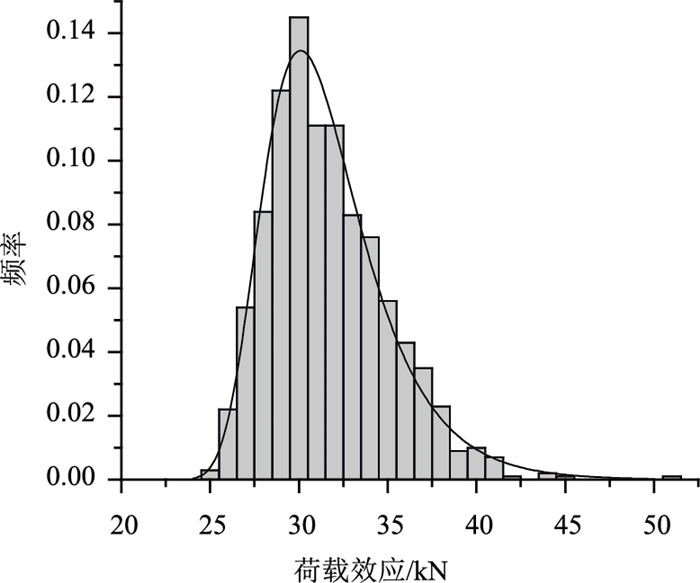
|
| 图 8 锚跨索股活载效应分布 Fig. 8 Distribution of live load effect on anchor cable strands |
| |
对其进行分布拟合并经K-S检验,结果表明索股活载效应年最大值SQτ服从极值Ⅰ型极大值分布。SQτ的累积分布函数为:
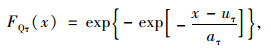
|
(14) |
式中,FQτ(x)为SQτ的累积分布函数,uτ=30.14 kN,aτ=2.74 kN。SQτ的0.05上分位点=30.86 kN。
索股活载效应在设计基准期100年内的最大值SQT的分布可根据极值统计学原理得到:
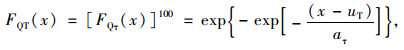
|
(15) |
式中,FQT(x)为SQT的累积分布函数;aT=aτ=2.74 kN,uT=uτ+aτln100=42.76 kN。SQT的0.05上分位点=50.91 kN。
若取用《公路桥涵通用设计规范》中的车道荷载设计值进行计算,得到1#索股的活载效应为91.50 kN。可以看到对于大跨度桥梁,由于其影响线较长,活载效应主要取决于车重及车辆数,而规范中的车道荷载考虑了轴重分布尾部的重车对中小跨度桥梁活载效应的影响,因此按照规范中的设计车道荷载计算结果要偏保守。
2.4 锚固系统时变可靠度锚固钢束的失效功能函数可表示为:
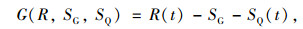
|
(16) |
式中,SG为锚固钢束恒载效应;SQ(t)为活载效应;t为服役时间。
采用离散综合法[21]计算1#锚固钢束的时变可靠度指标,将功能函数转变为:
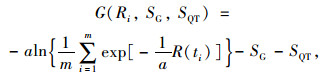
|
(17) |
式中,SQT为服役基准期T内活载效应最大值;a为活载效应最大值分布的比例参数;R(ti)为第i个时段中点的抗力。
采用腐蚀电流密度表征腐蚀状态,腐蚀电流密度0.10,0.25,0.50 μA/cm2分别为轻微腐蚀、中等腐蚀、严重腐蚀[22]。取腐蚀电流密度均值分别为0.15,0.25,0.35,0.45,0.55 μA/cm2,标准差均为0.1 μA/cm2,不同腐蚀电流密度下的钢绞线腐蚀速率如图 9所示。
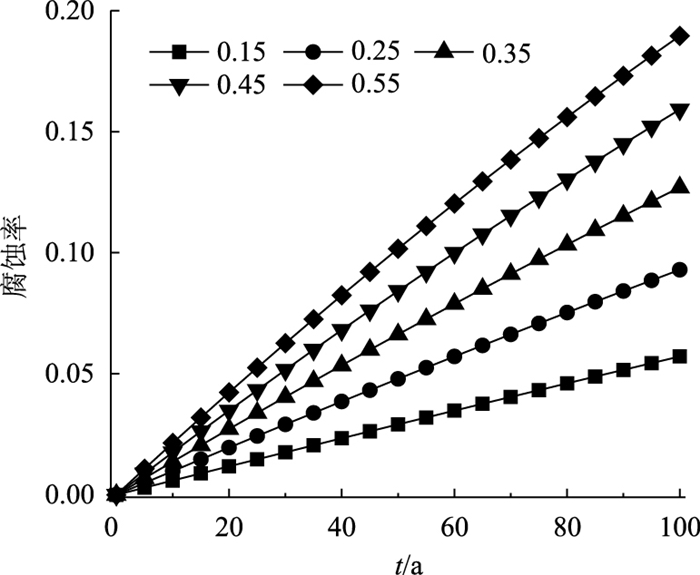
|
| 图 9 不同腐蚀电流密度下钢绞线的腐蚀速率 Fig. 9 Corrosion rates of strands with different corrosion current densities |
| |
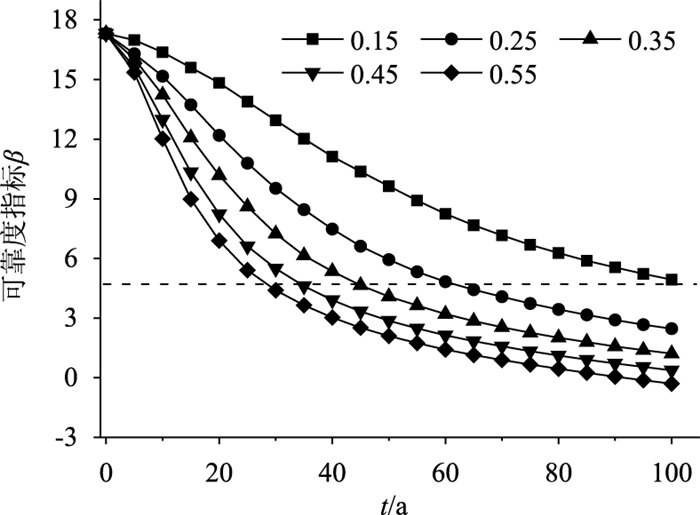
计算不同腐蚀电流密度下锚固钢束的时变可靠度指标,结果如图 10所示。
|
| 图 10 锚固系统时变可靠度指标 Fig. 10 Time-variant reliability indicators of anchor system |
| |
由于预应力锚固系统设计为可更换,按《公路工程结构可靠度设计统一标准》,目标可靠度指标可取4.7。从图 10中可以看出,当腐蚀电流密度为0.15 μA/cm2时,在设计基准期100 a内锚固钢束能够满足目标可靠度指标;当腐蚀电流密度为0.25,0.35,0.45,0.55 μA/cm2时,锚固钢束的可靠度指标降低至目标值的时间分别为60,45,35,28 a,随着腐蚀电流密度的增加,锚固钢束的可靠度指标降低速度也加快。因此,在实桥的设计、施工及运营期养护中均应对锚固系统的防腐问题给予关注。
3 结论本研究在既有试验研究基础上,提出了腐蚀预应力钢绞线的力学性能时变模型,进而建立了预应力锚固系统抗力的时变模型。通过对预应力锚固系统的可靠度分析得出以下结论:
(1) 锚固系统的可靠度受预应力筋腐蚀的影响明显,随着预应力筋的腐蚀率增大,锚固系统的可靠度指标会迅速降低。
(2) 腐蚀电流密度增大,锚固系统可靠度指标降低的速率也将增大,这在腐蚀开始的早期尤其明显,锚固系统的可靠服役年限将缩短。
(3) 当腐蚀电流密度在0.15 μA/cm2以下时,可以认为预应力锚固系统能够在设计基准期内可靠地服役。
本研究根据腐蚀电流密度计算钢绞线腐蚀速率是基于均匀腐蚀的假设,若考虑到蚀坑的产生模型将更加复杂。预应力筋的腐蚀对悬索桥预应力锚固系统的可靠度的影响非常大,因此有必要对悬索桥锚固系统的实际工作情况进行调查研究,结合电化学检测方法,测试锚索的腐蚀电流密度等参数,从而在本研究计算方法的基础上研究锚固系统的可靠度量化评价,这是本研究主要研究目的的体现,也可作为下一阶段研究工作的出发点。
| [1] |
孟凡超. 悬索桥[M]. 北京: 人民交通出版社, 2011. MENG Fan-chao. Suspension Bridge[M]. Beijing: China Communications Press, 2011. |
| [2] |
李海, 鲜亮, 姚志安. 国内大跨径悬索桥锚碇锚固系统比较研究[J]. 公路工程, 2011, 36(6): 97-101. LI Hai, XIAN Liang, YAO Zhi-an. The Compare and Investigation of Anchor System for Anchorage of Domestic Long-Span Suspension Bridge[J]. Highway Engineering, 2011, 36(6): 97-101. |
| [3] |
陈晓军. 大跨径悬索桥锚碇锚固系统的比较[J]. 交通世界, 2012, 19(8): 203-205. CHEN Xiao-jun. Comparison of Anchor Systems Used in Long-span Suspension Bridges[J]. Transpo World, 2012, 19(8): 203-205. |
| [4] |
苏强, 王强, 曾诚, 等. 悬索桥主缆预应力锚固系统设计探讨[J]. 预应力技术, 2014, 16(5): 19-21, 30. SU Qiang, WANG Qiang, ZENG Cheng, et al. Discussion about Design of Prestressed Strand Anchor System of Suspension Bridges[J]. Prestress Technology, 2014, 16(5): 19-21, 30. |
| [5] |
VAL D V, MELCHERS R E. Reliability of Deteriorating RC Slab Bridges[J]. Journal of Structural Engineering, 1997, 123(12): 1638-1644. |
| [6] |
彭建新, 邵旭东, 张建仁. 考虑气候变化的受碳化腐蚀先张预应力混凝土梁时变可靠性评估[J]. 长沙理工大学学报:自然科学版, 2010, 7(2): 33-42. PENG Jian-xin, SHAO Xu-dong, ZHANG Jian-ren. Time-dependent Reliability of Pretensioned Prestressed Concrete Bridge Girders Subject to Carbonation-induced Corrosion Considering Climate Change[J]. Journal of Changsha University of Science and Technology:Natural Science Edition, 2010, 7(2): 33-42. |
| [7] |
郑亚明, 欧阳平, 安琳. 锈蚀钢绞线力学性能的试验研究[J]. 现代交通技术, 2005, 2(6): 33-36. ZHENG Ya-ming, OUYANG Ping, AN Lin. Study on the Test of Mechanical Properties of Corroded Steel Bar Embedded in Concrete[J]. Modern Transportation Technology, 2005, 2(6): 33-36. |
| [8] |
罗小勇, 李政. 无黏结预应力钢绞线锈蚀后力学性能研究[J]. 铁道学报, 2008, 30(2): 108-112. LUO Xiao-yong, LI Zheng. Mechanical Performance of Corroded Unbonded Prestressed Steel Stranded Wires[J]. Journal of the China Railway Society, 2008, 30(2): 108-112. |
| [9] |
曾严红, 顾祥林, 张伟平, 等. 锈蚀预应力筋力学性能研究[J]. 建筑材料学报, 2010, 13(2): 169-174, 209. ZENG Yan-hong, GU Xiang-lin, ZHANG Wei-ping, et al. Study on Mechanical Properties of Corroded Prestressed Tendons[J]. Journal of Building Materials, 2010, 13(2): 169-174, 209. |
| [10] |
毛燕红, 宋全伟. 腐蚀钢绞线受拉性能退化规律及模型[J]. 四川建材, 2014, 40(6): 45-47. MAO Yan-hong, SONG Quan-wei. Degradation Rule and Models of Tensile Behavior of Corroded Steel Strands[J]. Sichuan Building Materials, 2014, 40(6): 45-47. |
| [11] |
吴雪峰.锈蚀钢绞线力学性能和黏结性能研究[D].长沙: 中南大学, 2014. WU Xue-feng. Research on Mechanical Properties and Bonding Performance of Corroded Prestressing Steel Strand[D]. Changsha: Central South University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10533-1014408077.htm |
| [12] |
余芳.钢绞线腐蚀后的部分预应力混凝土梁受力性能研究[D].大连: 大连理工大学, 2013. YU Fang. Study on Mechanical Performance of Partial Prestressed Concrete Beam with Corroded Strand[D]. Dalian: Dalian University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10141-1014154693.htm |
| [13] |
李富民.氯盐环境钢绞线预应力混凝土结构的腐蚀效应[D].徐州: 中国矿业大学, 2008. LI Fu-min. Corrosion Effect of Steel Strands on Prestressed Concrete Structures under Chloride Environment[D]. Xuzhou: China University of Mining and Technology, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10290-2008196402.htm |
| [14] |
彭元诚. 悬索桥可更换式无黏结预应力钢绞线锚固系统[J]. 桥梁建设, 2010, 40(6): 25-28. PENG Yuan-chen. Replaceable Anchoring System of Unbonded Prestressing Strand for Anchorage Block of Suspension Bridge[J]. Bridge Construction, 2010, 40(6): 25-28. |
| [15] |
AL-HARTHY A, FRANGOPOL D. Reliability Assessment of Prestressed Concrete Beams[J]. Journal of Structural Engineering, 1994, 120(1): 180-199. |
| [16] |
李欣, 武岳, 沈世钊. 钢拉杆与钢绞线的抗力分项系数研究[J]. 土木工程学报, 2008, 41(9): 8-13. LI Xin, WU Yue, SHEN Shi-zhao. Resistance Partial Factors for High Strength Steel Rods and Spiral Strands[J]. China Civil Engineering Journal, 2008, 41(9): 8-13. |
| [17] |
GB/T 5224-2014, 预应力混凝土用钢绞线[S]. GB/T 5224-2014, Steel Strand for Prestressed Concrete[S]. |
| [18] |
彭建新, 邵旭东. 混凝土桥梁结构性能退化可靠性评估及全寿命设计方法[M]. 北京: 人民交通出版社, 2014. PENG Jian-xin, SHAO Xu-dong. Reliability Assessment of Concrete Bridges with Deteriorating Performance and Life Cycle Design Method[M]. Beijing: China Communications Press, 2014. |
| [19] |
杨晓艳, 贡金鑫, 冯岷, 等. 公路桥梁车辆荷载效应概率模型及可靠度分析[J]. 公路交通科技, 2012, 29(10): 59-65. YANG Xiao-yan, GONG Jin-xin, FENG Min, et al. Analysis on Probabilistic Model of Vehicle Load Effect on Highway Bridge and Its Reliability[J]. Journal of Highway and Transportation Research and Development, 2012, 29(10): 59-65. |
| [20] |
安振源.基于实桥车辆调查的在役桥梁可靠度研究[D].西安: 长安大学, 2010. AN Zhen-yuan. Research on Reliability of Existing Bridges Based on Traffic Investigation[D]. Xi'an: Chang'an University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-11941-2010221425.htm |
| [21] |
贡金鑫.钢筋混凝土结构基于可靠度的耐久性分析[D].大连: 大连理工大学, 1999. GONG Jin-xin. Reliability Based Durability Analysis of Reinforced Concrete Structures[D]. Dalian: Dalian University of Technology, 1999. http://cdmd.cnki.com.cn/Article/CDMD-10141-2005107454.htm |
| [22] |
王崧全.矿用钢丝在腐蚀环境中应力与腐蚀的交互作用研究[D].徐州: 中国矿业大学, 2014. WANG Song-quan. Study on Interaction of Stress and Corrosion of Mine Steel Wire in Corrosive Environment[D]. Xuzhou: China University of Mining and Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10290-1014073985.htm |
 2019, Vol. 36
2019, Vol. 36
