扩展功能
文章信息
- 商明菊, 胡尧, 周江娥
- SHANG Ming-ju, HU Yao, ZHOU Jiang-e
- 基于改进递归小波变换的交通流异常点与变点检测算法
- An Algorithm for Detecting Outlier and Change Point of Traffic Flow Based on Improved Recursive Wavelet Transform
- 公路交通科技, 2019, 36(8): 133-143
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(8): 133-143
- 10.3969/j.issn.1002-0268.2019.08.017
-
文章历史
- 收稿日期: 2018-04-10
2. 贵州省公共大数据重点实验室, 贵州 贵阳 550025
2. Guizhou Provincial Key Laboratory of Public Big Data, Guiyang Guizhou 550025, China
道路交通拥堵问题在各大城市普遍存在,针对交通流状态的研究也备受学者关注。突发性交通事件和交通运行中的不稳定状态是引发交通拥挤和瘫痪等不安全状况的主要原因[1],常表现为交通流突变,即出现异常点或变点。交通流异常点是在一定观测周期内,交通流状态与长期出现的交通流水平相偏离之点。这种交通流异常点呈现出来的状态,通常与短时交通拥挤、检测设备故障等有关。交通流变点则是指交通流模型中的某个或某些参数起突然变化之点[2]。交通流变点发生后,模型参数将发生质的变化:如早、晚高峰常发性交通繁忙造成的交通流波动,这种波动随着交通需求的减少可逐渐消退;而如非高峰期突发性交通事故造成的交通流一段时期内的波动,则急需交通管理部门的干预。交通流变点在发生初期,易被误认为是交通流异常点。若能对交通流状态进行及时界定,如融合多源交通数据对交通事件进行自动检测[3],则异常事件更易被及时处理。因此,对交通流状态进行实时监控与预警,短时间内检测并区分异常点与变点,是非常必要的。
利用在线变点检测方法对实时数据进行异常监控,是当前研究的一个热点,如手机用户的行为监控[4]、营销广告的在线推送[5]等。交通领域,Xiao等[6]通过计算交通流量变化率,在分析实时流量序列变化趋势的同时检测异常点,以达到对流量状态进行监控的目的。过程控制领域,Wu等[7]采用分段线性模型对噪声信号进行逼近,利用精确的Bayesian推理,在线检测变点。推荐系统领域,Zhang等[8]研究稀疏时间序列变点的在线检测问题,利用辅助时序快速、准确地识别变点。算法改进方面,李拂晓等[9]对在线检测随机系数自回归模型的变均值点方法进行了改进,通过引入一个窗宽参数来缩短检测的延迟时间。然而交通数据海量,上述文献提及的变点检测方法计算复杂度均较高,难以用于实际。
小波变换是分析微观异常的有效工具。异常点检测方面,李志敏等[10]结合最小二乘法,利用小波变换的多分辨分析特点对交通流异常数据进行检测,实例分析表明该方法应用于智能交通控制领域的可行性与有效性,但检测不及时。变点检测方面,Alarcon-aquino等[11]基于最大重叠离散小波变换和Bayesian分析,通过比较两窗口方差是否相等来实现变点的在线检测,但该方法检测延迟大且统计量难以满足在线检测要求。离散小波变换存在平移敏感性、方向性差、无相位信息的应用缺陷;复小波变换优于实小波之处在于,除能提供幅度、相位等简单信息外,还能提供多种复合信息,且可克服前述应用缺陷[12]。1996年,Chaari等[13]就提出了基于复小波的递归小波变换,该变换的正向递推仅依赖于历史数据,能够满足实时性需求;而反向递推却需要未来数据,实时性受限。在此基础上,张传利等[14]探究出一种只由单方向递推组成的小波变换,即改进递归小波变换(Improved Recursive Wavelet Transform,IRWT)算法,它只采用历史数据,计算速度更快,更能满足实时性需求。此小波变换的系数中,尺度和频率之间有着明确的关系;小波变换系数幅值稳定,能更准确地反映对应信号频率的幅值[15]。随后,Rahmati等[16]证实了IRWT响应时间快且计算复杂度小,周德新等[17]将IRWT应用于飞行发动机数据异常类型的实时判定。
针对异常点与变点同时检测的必要性,苏卫星等[18]提出了一种基于递归小波分析有效分数向量的时间序列异常点与变点检测算法。该算法克服了传统变点检测算法延迟大、检测统计量数值无限增大的不足,实时性强,能够满足在线检测要求,但文中未涉及异常点与变点的位置估计问题。鉴于此,本研究基于前述幅值快速衰减、计算速度更快的改进递归小波变换标准化有效分数向量,提出一种能够实时监控与预警,短时间内检测并区分交通流异常点与变点的快速检测算法。仿真试验验证了算法的有效性;贵阳市交通流量实测数据的监控分析说明了算法的实用性。
1 异常点与变点检测算法 1.1 基于IRWT的变点检测理论基于有效分数向量(Efficient Score Vector,ESV)的变点检测算法由Gombay[19]提出,该算法通过检测时序数据所服从分布的参数变化来检测变点。设待测时序{xt}独立同分布,密度函数为f(x; θ, η),其中θ∈Rd(d≥1)表示分布中“感兴趣”的参数,η∈Rq(q≥0)表示分布中“不感兴趣”的冗余参数。将变点检测算法转换为如下假设检验问题:

|
(1) |
式中,τ为变点,θ0与θA分别为变点发生前、后参数θ的取值。若f(x; θ, η)属于指数分布族,有:
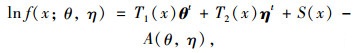
|
(2) |
式中, T1(x), T2(x), S(x), A(θ, η)均为已知函数,θt与ηt表示列向量。记ξ=(θ, η),时序长度为k的ESV表达式为:
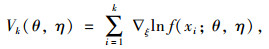
|
(3) |
因η为冗余参数,则有:
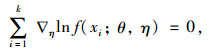
|
(4) |
若η估计值为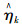
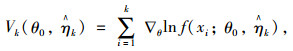
|
(5) |
将式(5)标准化,构造统计量:
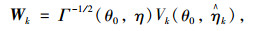
|
(6) |
式中,Γ(θ, η)=I11-I12I22-1I21,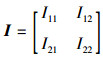
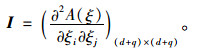
|
(7) |
当H0为真时,统计量Wk具有零均值且近似于布朗过程W(k);而变点发生后,近似不存在,得到无穷数据变点双边检测算法[19]。检测原则即随着k的增加,如果出现:

|
(8) |
则判定k附近有变点发生,式中α为显著性水平向量。C2*(α)中各分量的计算,如下式:
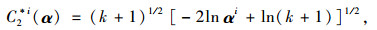
|
(9) |
式中i=1, …, d。
对交通流时序{yt}而言,其分布通常未知。引入基于模型的残差分析思想,利用时间序列鲁棒建模得到如下自回归AR(p)模型:
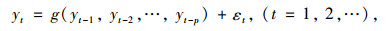
|
(10) |
式中εt~N(μ, σ2)。
若某时刻τ出现变点,则τ后交通流将不再符合上述AR(p)模型。如果仍采用该模型对后续观测值进行拟合,则会出现较大的拟合残差,从而可看成服从Gaussian分布的拟合残差εt的方差σ2发生了变化[18]。交通流变点检测即转换为如下方差变点检验问题:
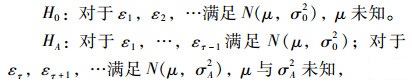
|
(11) |
将此检验问题代入式(6)求解,得如下统计量:
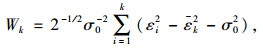
|
(12) |
式中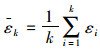
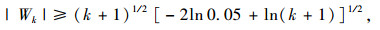
|
(13) |
则k为变点τ。
如前所述,统计量Wk在式(11)H0条件下均值为0,若发生异常,其值增大。为满足快速检测的需要,引入改进递归小波变换算法[14],其小波母函数φ(t)为:

|
(14) |
式中,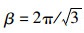

|
(15) |
式中φ是φ的共轭复数。该小波系数表示kT时刻采样信号频率f时,信号成分波形与此位置上对应小波的相似程度。对式(15)进行Z变换,得到快速递推算法如下[15]:
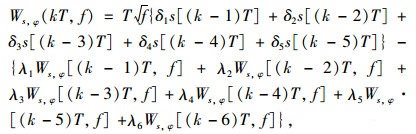
|
(16) |
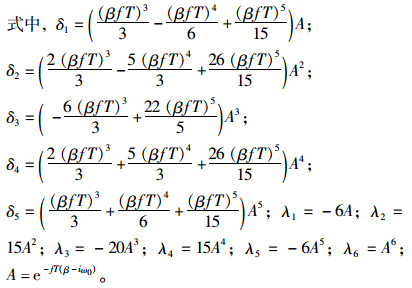
|
由式(16)可知,在所关心的频率范围内选择适当频率,利用各序列值与式(15)计算出的6个初始小波系数,就可实现残差时序标准化ESV的改进递归小波变换。
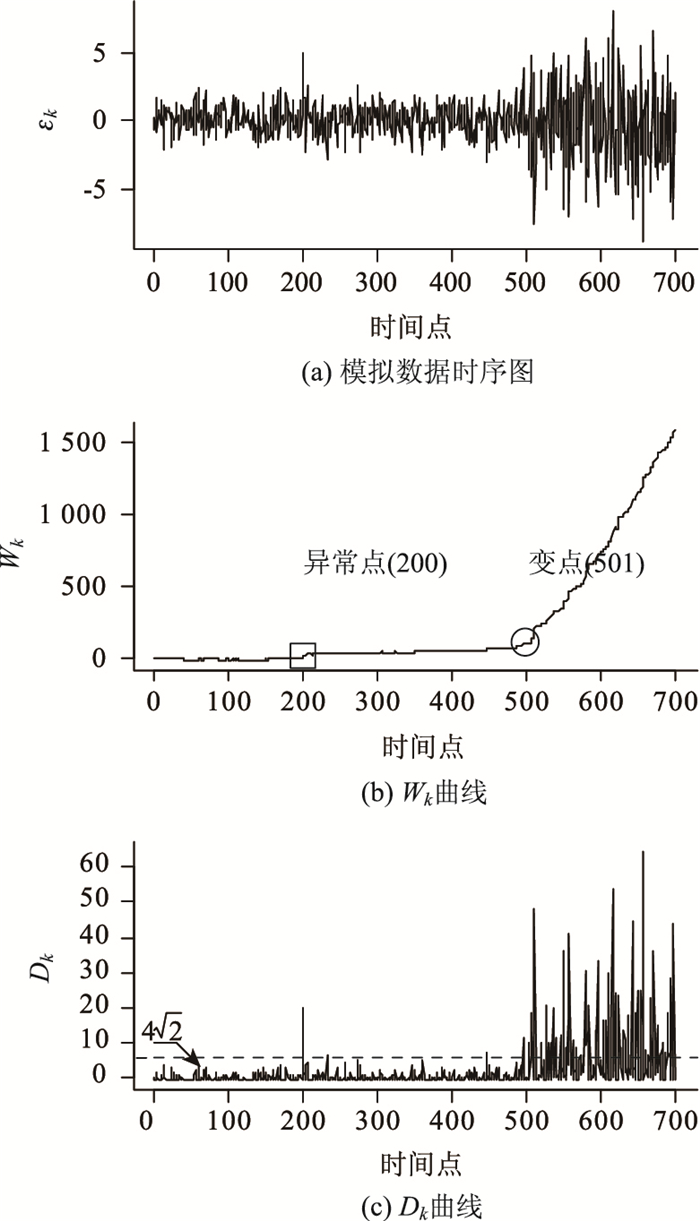
1.2 异常点与变点检测算法框架以一组700步零均值白噪声数据来模拟残差序列{εt},自501步起序列的方差由1突变为3,并在200步加入异常值5,时序图见图 1(a)。由图 1(b)可知,异常点发生后,Wk曲线出现一定骤变后又趋于平稳;而变点发生后,Wk曲线出现突变且呈正比例增大趋势。
|
| 图 1 模拟数据时序图与统计量曲线 Fig. 1 Time series diagram of simulated data and curves of statistics |
| |
将统计量Wk一阶差分值记为Dk,表达式如下:
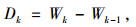
|
(17) |
根据3-Sigma原则,若残差序列发生异常,则|εi-μ|>3σ。假设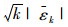
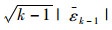
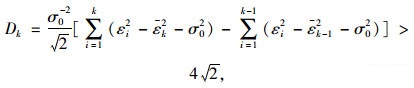
|
(18) |
因此,设定统计量Dk阈值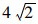
复小波变换的简单信息包括实部WTR、虚部WTI、幅度WTM与相位WTPH。在异常点检测中,WTM可描述异常点的强度;而WTPH常用来分析异常点的位置[12],它既能反映待测信号在主要频率成分的相位突变,又能避免次要频率成分的干扰[21]。结合复小波变换的实部、虚部构建复合信息WTMPH3,它能综合评价信号与小波变换的匹配程度,其效果优于简单的判据WTM[22]。计算公式如下:
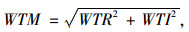
|
(19) |
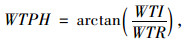
|
(20) |
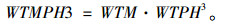
|
(21) |
不同的小波变换频率具有不同的信号分辨特性。小波变换的低频系数常表征数据变化的平稳态势和整体趋势,而高频系数常表征数据变化的突变态势和局部特征。因此,高频系数更利于提取变点发生后Wk曲线的趋势特征。进而,考虑结合复数谱方差[23]实现特征频率的选取。
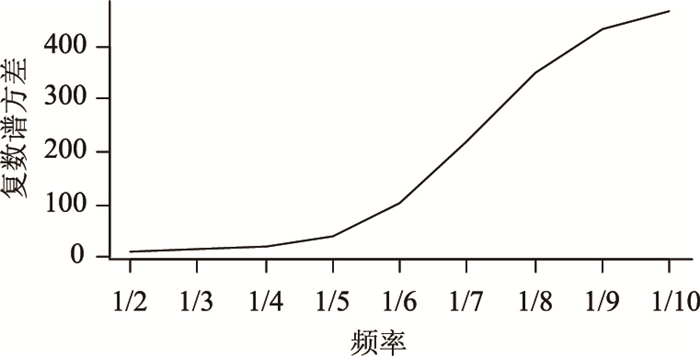
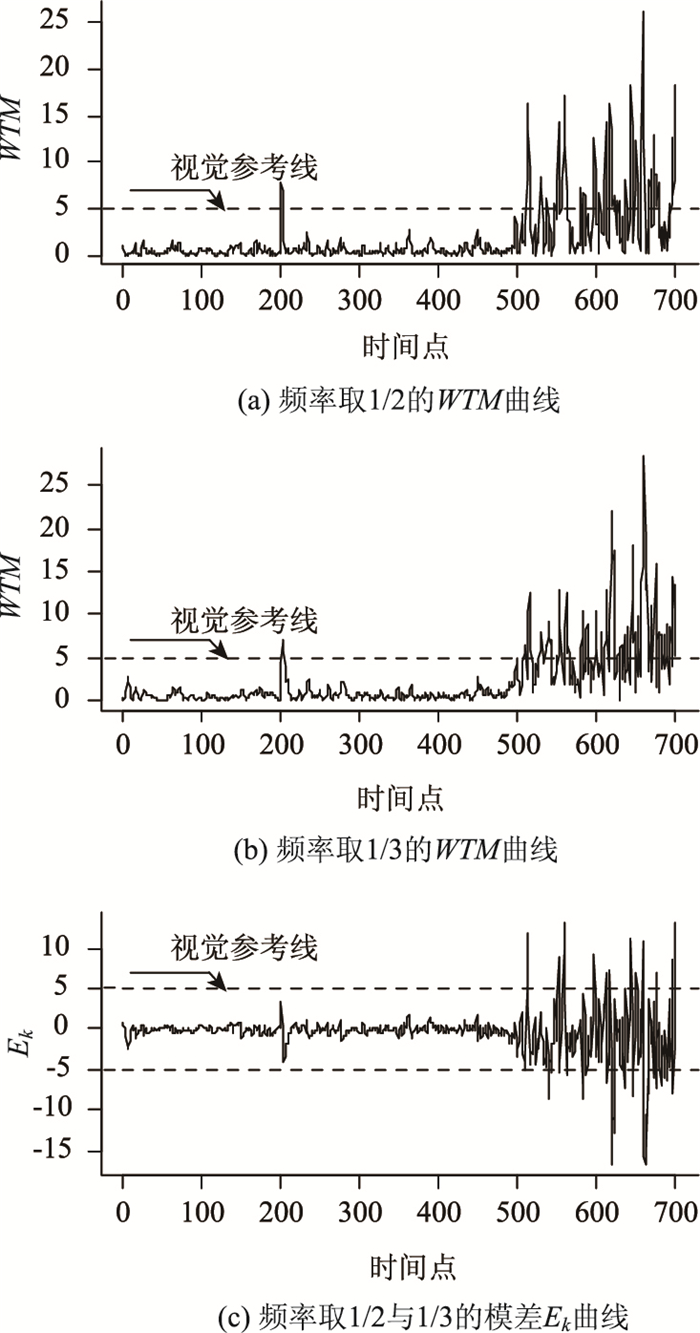
为确保实际交通流数据的检测精度,采样周期T取1。对Wk曲线(图 1(b))进行多频小波分析。由多频复数谱方差图(图 2)可知,频率取1/2方差最小,取1/3次之。进而对Wk分别进行频率取1/2和1/3的改进递归小波变换,相应的WTM曲线(视觉参考线5)分别如图 3(a)~(b)所示。从WTM曲线看到,无论是异常点还是变点,幅度均出现极大值现象;不同的是,变点发生后极大值现象更频繁。
|
| 图 2 复数谱方差曲线 Fig. 2 Curve of complex number spectrum variance |
| |
|
| 图 3 模拟数据检测结果(1) Fig. 3 Detection result of simulated data (1) |
| |
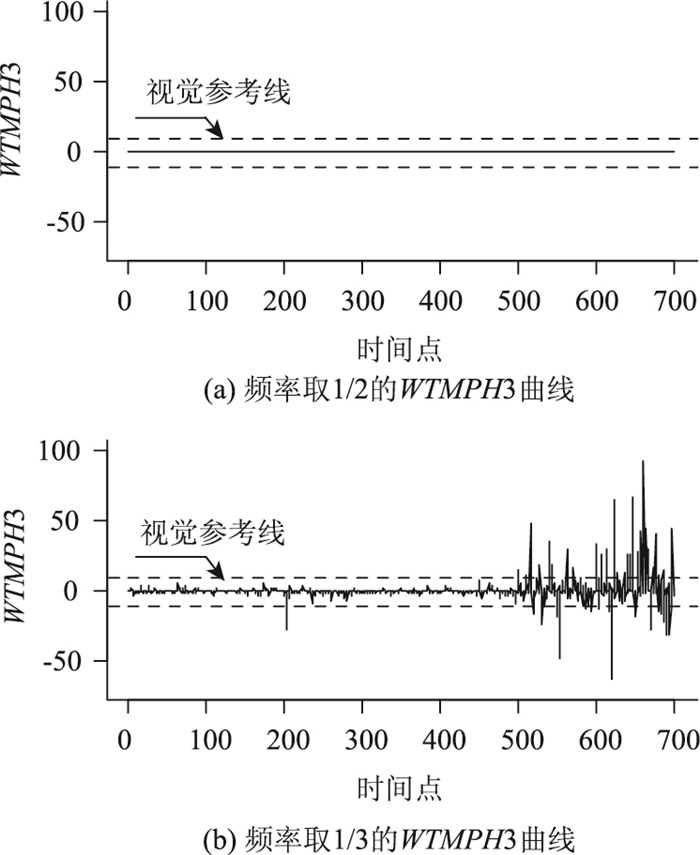
将上述两频率变换系数的幅度作差得模差Ek,绘制模差曲线如图 3(c)(视觉参考线5与-5)所示。图 4为频率分别取1/2与1/3的WTMPH3曲线(视觉参考线10与-10),由图可知,频率取1/2的WTMPH3曲线近似为一条直线;而频率取1/3的WTMPH3曲线对异常值的可视化判别效果较优,能较好地反映异常点与变点附近幅值和相位的突变现象,且变换幅度大于WTM曲线。这与小波变换的幅值、相位紧密相关,Wk经频率取1/2的小波变换后相位绝对值过小(图 5(b)),致使WTMPH3近似为0。虽然模差Ek曲线中异常点处幅度出现相互削弱现象,但就抗干扰能力与可视化判别效果而言,WTM与Ek均不如频率取1/3的WTMPH3,故可将其视为预警辅助决策参考,以区分真、假异常点。
|
| 图 4 模拟数据检测结果(2) Fig. 4 Detection result of simulated data (2) |
| |
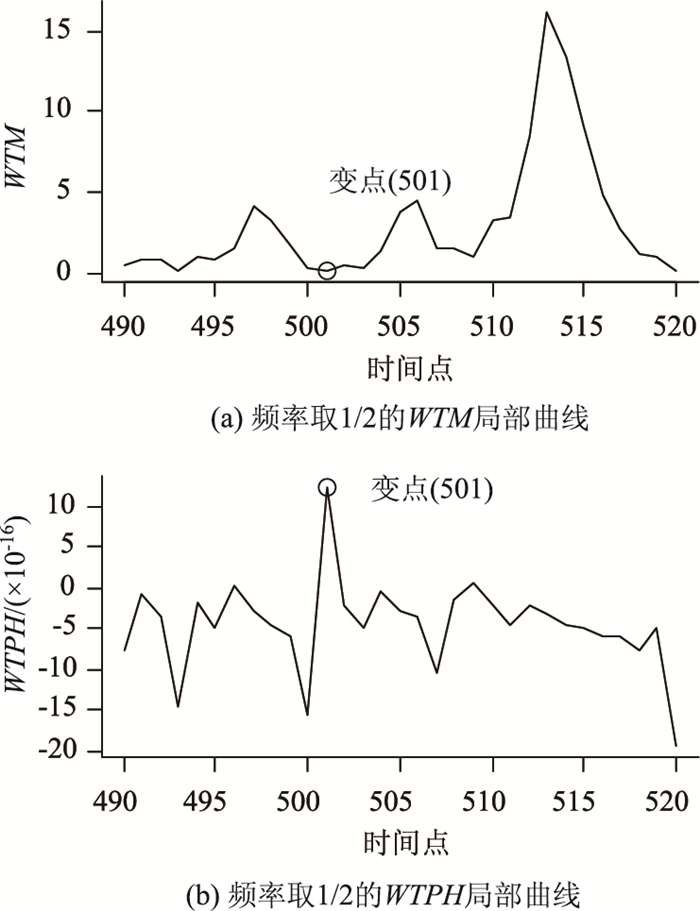
|
| 图 5 频率取1/2的小波变换信息 Fig. 5 Wavelet transform information with frequency of 1/2 |
| |
变点处,实际也可看作一次异常信号的发生。图 5是频率取1/2时变点邻域的WTM曲线与WTPH曲线,由图可知,幅度的极大值现象为局部信息,故可利用Dk预警并在局部窗口内搜索相位最大值处,以定位变点。因此,选择适当的频率与搜索长度,便可对变点位置进行估计。
综上,可得到一种基于改进递归小波变换(IRWT)的交通流异常点与变点快速检测算法,对交通流进行实时监控与预警。算法具体步骤如下:
Step 1:对交通流时序建立AR(p)模型,得到实时残差序列{εt},在线计算统计量Wk与Dk,并对Wk进行改进递归小波变换。
Step 2:当统计量Dk超过阈值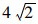
Step 3:选定搜索长度h,在τ1邻域[τ1, τ1+2h]内,结合WTMPH3曲线的辅助预警信息,将出现3种可视化情况。第1种,邻域内WTMPH3曲线未出现极小值现象时,认为该邻域内不存在异常点,此预警点实为虚报; 第2种,邻域内WTMPH3曲线仅出现1次极小值现象时,认为该邻域内存在异常点,其位置估计即为τ1; 第3种,邻域内WTMPH3曲线出现多次极值现象时,认为τ1邻域内存在变点, 即刻搜索[τ1-h-1, τ1+h]内幅度最大值处(记为m),接着搜索[m-2h-1, m]内相位最大值处(记为τ′1),将τ′1作为变点的位置估计。
Step 4:对预警点τ1进行判定,若为Step 3第3种情况,则自变点时刻起重建AR(p)模型,返回Step 1进行新一轮检测。若为Step 3前两种情况,说明变点未发生,则后续预警点继续参照Step 3进行检测,将τ2按τ1判定方式处理。若τ2邻域仍为Step 3前两种情况,则τ3继续按τ1判定方式处理,后续预警点如此循环按序检测。
1.3 算法特征参数的选择前述算法检测步骤中,邻域的搜索窗口长度与h的选择直接相关。记第1类错误概率(β1)为未变异的观测值落入估计变异区域的概率,记第2类错误概率(β2)为已变异的观测值落入估计未变异区域的概率,两类错误概率反映了真实变点与估计变点之间的差异[24]。为研究算法的收敛性,以犯这两类错误概率作为评价变点检测算法的性能指标。如前,原始序列长度700,真实变点501,则若τ < 501,β1=(501-τ)/500,β2=0;若τ≥501,β1=0,β2=(τ-501)/200。对检测算法进行多次模拟,计算犯第1类错误概率均值(β1)与犯第2类错误概率均值(β2),以对变点检测算法性能进行评价。
为探究参数对算法性能的影响,模拟800步零均值的残差序列,自401步起序列的方差由1突变为3,并在200步加入异常值5。若τ < 401,β1=(401-τ)/400,β2=0;若τ≥401,β1=0,β2=(τ-401)/400。对检测算法进行5 000次模拟仿真,研究9种不同小波变换频率与10种不同搜索长度对算法性能的影响。因多次高频预警后必有变点发生,故将400步后前4次预警的检测结果取平均记为β1,β2,模拟结果见表 1。表 1中“平均”指在相同小波变换频率下,10种不同h搜索检出的变点犯两类错误的平均概率均值。
| 频率f | 错误类型 | h=6 | h=7 | h=8 | h=9 | h=10 | h=11 | h=12 | h=13 | h=14 | h=15 | 平均 | 平均(β1+β2) |
| 1/2 | β1 | 0.289 7 | 0.401 5 | 0.524 9 | 0.647 3 | 0.784 9 | 0.915 9 | 1.062 9 | 1.190 8 | 1.328 0 | 1.488 8 | 0.863 5 | 1.816 1 |
| β2 | 1.130 1 | 1.057 2 | 0.993 1 | 0.956 2 | 0.922 2 | 0.914 0 | 0.895 0 | 0.888 7 | 0.883 3 | 0.886 6 | 0.952 6 | ||
| 1/3 | β1 | 0.204 4 | 0.307 3 | 0.412 7 | 0.526 8 | 0.644 2 | 0.768 2 | 0.883 1 | 1.001 9 | 1.135 2 | 1.255 7 | 0.713 9 | 1.865 8 |
| β2 | 1.352 5 | 1.257 7 | 1.189 9 | 1.155 5 | 1.123 2 | 1.104 9 | 1.087 1 | 1.087 6 | 1.079 1 | 1.081 7 | 1.151 9 | ||
| 1/4 | β1 | 0.145 2 | 0.223 2 | 0.318 9 | 0.422 0 | 0.533 0 | 0.658 9 | 0.784 2 | 0.900 4 | 1.044 6 | 1.160 6 | 0.619 1 | 1.845 6 |
| β2 | 1.431 0 | 1.363 4 | 1.305 6 | 1.248 1 | 1.202 6 | 1.175 1 | 1.148 8 | 1.136 7 | 1.126 3 | 1.127 4 | 1.226 5 | ||
| 1/5 | β1 | 0.120 0 | 0.185 9 | 0.267 4 | 0.353 0 | 0.448 8 | 0.578 1 | 0.706 7 | 0.815 3 | 0.950 1 | 1.074 4 | 0.550 0 | 1.888 2 |
| β2 | 1.517 4 | 1.467 9 | 1.408 6 | 1.378 6 | 1.338 8 | 1.290 4 | 1.257 4 | 1.243 6 | 1.241 9 | 1.237 3 | 1.338 2 | ||
| 1/6 | βf1 | 0.097 2 | 0.158 5 | 0.226 9 | 0.300 5 | 0.385 1 | 0.470 3 | 0.582 4 | 0.687 4 | 0.808 3 | 0.934 3 | 0.465 1 | 1.905 4 |
| βf2 | 1.634 3 | 1.546 5 | 1.496 4 | 1.455 6 | 1.430 6 | 1.415 6 | 1.393 6 | 1.367 2 | 1.335 1 | 1.327 9 | 1.440 3 | ||
| 1/7 | βf1 | 0.089 1 | 0.125 2 | 0.183 7 | 0.256 3 | 0.336 0 | 0.425 5 | 0.530 9 | 0.628 3 | 0.733 5 | 0.836 4 | 0.414 5 | 1.954 4 |
| βf2 | 1.685 9 | 1.677 3 | 1.600 9 | 1.541 3 | 1.509 7 | 1.489 9 | 1.472 6 | 1.472 5 | 1.477 3 | 1.471 9 | 1.539 9 | ||
| 1/8 | βf1 | 0.103 9 | 0.128 0 | 0.165 1 | 0.228 3 | 0.299 9 | 0.379 4 | 0.463 9 | 0.556 8 | 0.653 6 | 0.756 3 | 0.373 5 | 2.003 1 |
| βf2 | 1.638 5 | 1.707 4 | 1.730 3 | 1.680 8 | 1.630 8 | 1.598 3 | 1.590 4 | 1.579 8 | 1.568 8 | 1.571 2 | 1.629 6 | ||
| 1/9 | βf1 | 0.107 0 | 0.137 8 | 0.165 4 | 0.209 4 | 0.272 3 | 0.350 4 | 0.443 2 | 0.527 1 | 0.608 1 | 0.693 9 | 0.351 5 | 2.022 0 |
| βf2 | 1.620 5 | 1.651 5 | 1.731 4 | 1.762 4 | 1.729 9 | 1.670 5 | 1.636 5 | 1.638 3 | 1.630 1 | 1.634 6 | 1.670 5 | ||
| 1/10 | βf1 | 0.118 6 | 0.143 4 | 0.174 6 | 0.208 0 | 0.249 0 | 0.308 2 | 0.385 9 | 0.473 1 | 0.571 6 | 0.656 5 | 0.328 9 | 2.040 1 |
| βf2 | 1.619 6 | 1.615 9 | 1.657 9 | 1.745 8 | 1.797 3 | 1.792 5 | 1.755 7 | 1.723 7 | 1.703 7 | 1.700 1 | 1.711 2 |
就交通流实时监控与预警而言,快速有效地检测变点是关键。若要预警及时,则必须控制检测延迟时间,也就是h的选择不易过大。从表 1可知,当h固定时,β1随小波变换频率的减小,多呈递减趋势;相反,β2随小波变换频率的减小,多呈递增趋势。因此,可通过选择特征小波变换频率f与搜索长度h,来控制犯两类错误的概率。较其他8种频率而言,频率取1/2时:犯第1类错误的平均概率均值为0.863 5%,最大;犯第2类错误的平均概率均值为0.952 6%,最小;而犯两类错误的平均概率均值总和为1.816 1%,仍最小。因此,结合复数谱方差信息,模拟判断基于改进递归小波变换进行交通流监控时频率取1/2最佳。
为保证算法的收敛性,下面来研究搜索长度h的选择。频率取1/2时,若选择的h过大,β1增大;而h过小时,β2将增大。综合考虑犯两类错误的概率,将10种不同h下的概率均值与平均概率均值进行比较。当h取10时,犯两类错误的概率均值,均低于平均水平。因此,为保证局部搜索质量,h不易过大或过小,基于模拟结果,本研究h取10。
综上,可采用1.2节检测算法对交通流状态进行实时监控与预警,同时对异常点与变点进行快速检测。在预警点中辨别真实异常点时,以频率取1/3的WTMPH3作为辅助信息为宜。在预警点邻域内搜索相位最大值处以定位变点时,参考频率取1/2的WTM, WTPH小波信息更为准确。
2 仿真试验 2.1 数值验证为验证提出的检测算法有效,利用4组700步零均值白噪声数据模拟由AR(p)模型拟合交通流时序后的残差序列{εt}。自501步起序列方差由σ02突变到σA2, 如表 2所示,并在200步和400步分别加入异常值O1与O2。对这4组数据进行异常点与变点检测,限于篇幅,仅列出部分结果。第4组数据时序如图 6所示,其检测结果见图 7、图 8。
| 组别 | σ02 | σA2 | O1 | O2 |
| 1 | 1 | 3 | 5 | -5 |
| 2 | 3 | 6 | 12 | -12 |
| 3 | 5 | 9 | -20 | -20 |
| 4 | 18 | 33 | 70 | -70 |

|
| 图 6 第4组模拟数据时序图 Fig. 6 Time series diagram of the 4th group of simulated data |
| |
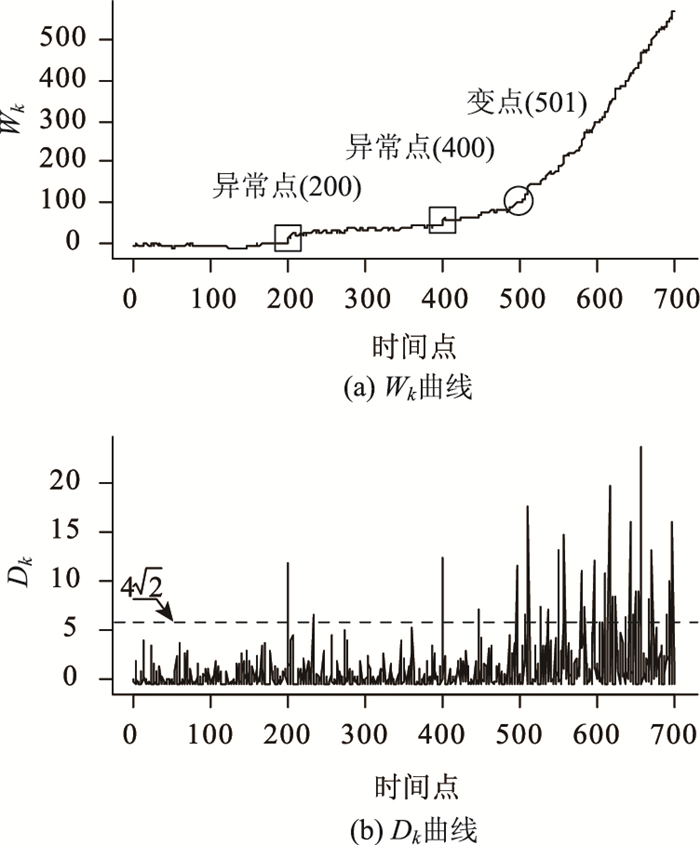
|
| 图 7 第4组模拟数据的检测结果(1) Fig. 7 Detection result of the 4th group of simulated data (1) |
| |

|
| 图 8 第4组模拟数据的检测结果(2) Fig. 8 Detection result of the 4th group of simulated data (2) |
| |
Wk曲线(图 7(a))在第1个异常点处的骤变现象明显,而在第2个异常点处的骤变现象相对较弱,但二者均可通过结合Dk曲线(图 7(b))与频率取1/3的WTMPH3曲线(图 8(b))来识别。同时,Wk曲线在变点发生后仍呈突变上升趋势。小波系数WTM曲线(图 8(a))中幅度极大值现象频繁,难以区分异常点与变点。然而WTMPH3曲线(图 8(b))在异常点与变点附近的不同起伏频率与幅度跳跃现象,能够较好地反映异常点与变点发生后Wk呈现的不同变化趋势。仿真试验再次证明WTMPH3曲线对异常点与变点的识别度优于WTM曲线。
鉴于不同频率变换下的小波信息不同,对4组数据分别进行3种不同频率的小波变换。检测结果(表 3)中列出了前7个预警点及其邻域内对应检出的相位最大值处。由表 3可知,同组数据在不同频率变换下的检测结果有较大差异。以第一组数据为例:同频率下,异常点(预警次序1, 3)由于无变点发生后的正比例增大趋势,导致IRWT定位精度低;不同频率下,特征频率取1/2时的IRWT对Wk曲线变点(预警次序6,7)处的突变现象仍然定位准确。
| 组别 | 预警次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 预警点points | 200 | 232 | 400 | 446 | 495 | 503 | 505 |
| f=1/2 | 195 | 222 | 386 | 429 | 488 | 501 | 501 | |
| f=1/4 | 191 | 231 | 400 | 445 | 481 | 506 | 514 | |
| f=1/8 | 207 | 233 | 400 | 448 | 497 | 497 | 497 | |
| 2 | 预警点points | 200 | 232 | 400 | 446 | 495 | 506 | 507 |
| f=1/2 | 195 | 222 | 386 | 429 | 488 | 501 | 501 | |
| f=1/4 | 191 | 231 | 400 | 445 | 481 | 508 | 508 | |
| f=1/8 | 207 | 226 | 400 | 448 | 497 | 497 | 497 | |
| 3 | 预警点points | 200 | 232 | 400 | 446 | 495 | 506 | 511 |
| f=1/2 | 195 | 222 | 386 | 430 | 488 | 501 | 501 | |
| f=1/4 | 191 | 223 | 394 | 445 | 481 | 514 | 514 | |
| f=1/8 | 207 | 233 | 400 | 448 | 497 | 497 | 511 | |
| 4 | 预警点points | 200 | 232 | 400 | 446 | 495 | 506 | 511 |
| f=1/2 | 195 | 222 | 386 | 429 | 488 | 501 | 501 | |
| f=1/4 | 191 | 223 | 400 | 445 | 481 | 514 | 516 | |
| f=1/8 | 207 | 226 | 407 | 448 | 497 | 497 | 511 |
综上,4组模拟数据的仿真试验可以证明,提出的基于改进递归小波变换的异常点与变点快速检测算法具有一定的有效性。
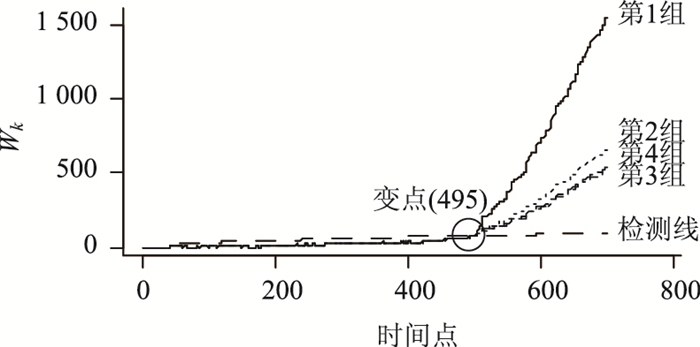
2.2 比较为进一步说明基于IRWT的快速变点检测算法性能优,与传统ESV变点检测算法作对比,显著性水平取0.05。在异常值存在情况下,传统ESV变点检测算法将失效,故将2.1节4组数据异常值去除后再进行比较。基于IRWT的快速变点检测算法均准确检测出变点501,而传统ESV变点检测算法结果均为495(图 9),存在提前“检测出”变点现象。
|
| 图 9 4组模拟数据基于ESV的变点检测结果 Fig. 9 Detection result on 4 groups of simulated data based on ESV |
| |
为客观评价算法的变点检测性能,基于IRWT算法的犯两类错误概率均值β1与β2,由500步后第1个预警点定位检测出的变点计算。对上述4组数据模拟5 000次,检测结果见表 4,表中“漏检率”即未检测出变点的概率。从表 4可知,基于IRWT的快速变点检测算法,其平均漏检率仅为0.01%,远低于传统ESV变点检测算法的7.19%。平均意义下,传统ESV变点检测算法犯两类错误的概率均较高,易出现误报,而基于IRWT的快速变点检测算法犯两类错误的概率均较低。两种算法均存在检测延迟现象,但基于IRWT的快速变点检测算法因兼顾Dk预警频率信息,其检测性能更优,特别在同时快速检测异常点与变点方面更有优势。
| 方法 | ESV | IRWT | ||||
| 组别 | 漏检率 | βf1 | βf2 | 漏检率 | βf1 | βf2 |
| 1 | 0.000 0 | 23.006 0 | 9.883 5 | 0.000 0 | 0.863 8 | 0.850 4 |
| 2 | 5.840 0 | 23.097 7 | 22.178 9 | 0.000 0 | 0.676 6 | 2.365 0 |
| 3 | 12.340 0 | 26.275 5 | 23.831 5 | 0.040 0 | 0.598 7 | 3.777 6 |
| 4 | 10.580 0 | 25.994 0 | 23.544 3 | 0.000 0 | 0.594 3 | 3.515 4 |
| 平均 | 7.190 0 | 24.593 3 | 19.859 5 | 0.010 0 | 0.683 3 | 2.627 1 |
综上,两种方法的模拟对比可以证明,利用改进递归小波变换进行方差变点检测,误检率更低、检测性能更优、操作性较强。
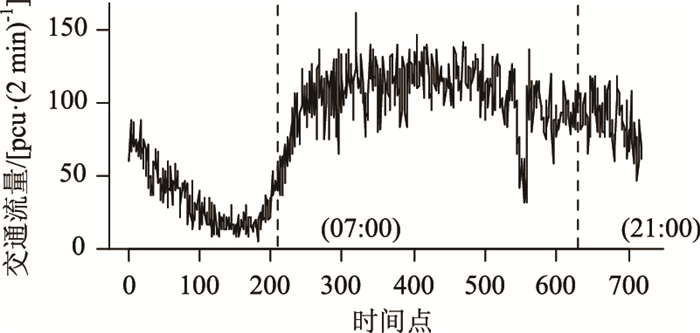
3 实例分析实例数据源于2016年4月17日贵阳市主城区一环线宝山北路某断面的交通流量数据(粒度:2 min),时序如图 10所示,图中两条虚线为贵阳市小客车专段号牌限行时段(07:00—21:00)的起止时间,该时段内交通流量长期居高不下。图中各时刻均采用时间点顺序标记,如时间点1,其对应时段(00:00—00:02),记录时刻为00:00。作为交通流的一个重要参数,交通流量与交通拥堵程度紧密相关。若能对该时段交通流量进行实时有效的监控与预警,便能在一定程度上降低突发性交通异常事件引起交通拥堵的可能性,进而保障交通需求者出行便利。
|
| 图 10 交通流量时序图 Fig. 10 Time series diagram of traffic flow |
| |
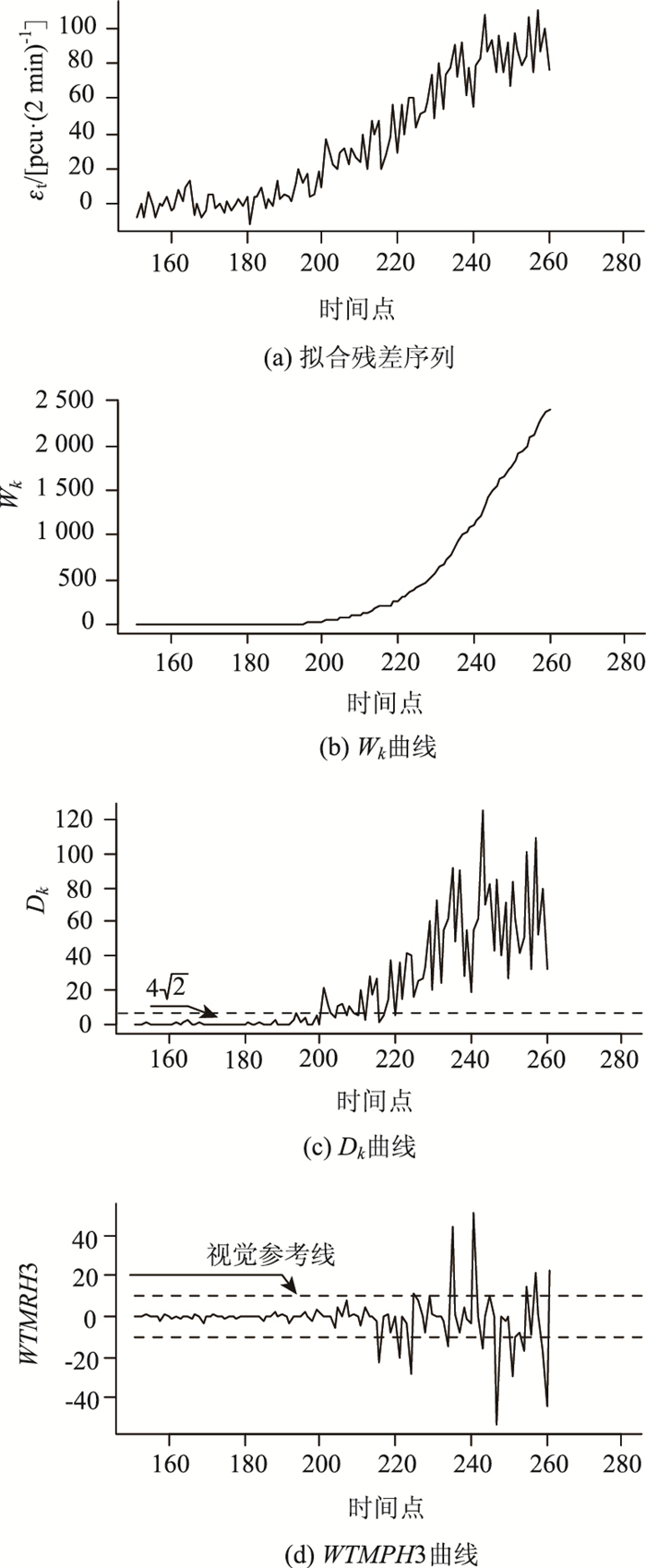
为对限行时段内交通流量进行实时监控,取时刻05:00起20个交通流量序列值,拟合AR(p)模型,运用提出的算法对序列进行异常点与变点检测,各阶段检测结果见表 5。第1阶段(时间点151起)拟合残差时序(图 11(a))对应的Wk曲线、Dk曲线以及WTMPH3曲线分别如图 11(b)~(d)所示。该阶段前4个预警时间点依次为194,201,202,203,分别对应时刻06:26,06:40,06:42,06:44;检测出变点200,对应时刻06:38。检测出变点后,利用自变点起20个交通流量序列值重新建立AR(p)模型,继续检测。第2阶段(时间点200起),检测出变点230,对应时刻07:38。如此,继续更新模型,对后序数据进行检测。
| 阶段 | 模型阶数 | 预警次序 | 1 | 2 | 3 | 4 |
| 1 | 0 | 预警点 | 194 | 201 | 202 | 203 |
| IRWT定位 | 200 | 200 | 200 | 200 | ||
| 2 | 0 | 预警点 | 229 | 231 | 234 | 235 |
| IRWT定位 | 230 | 230 | 230 | 230 | ||
| 3 | 1 | 预警点 | 319 | 544 | 545 | 548 |
| IRWT定位 | 316 | 532 | 550 | 550 | ||
| 4 | 1 | 预警点 | 552 | 553 | 554 | 556 |
| IRWT定位 | 557 | 557 | 557 | 564 |
|
| 图 11 第1阶段检测结果 Fig. 11 Detection result of stage 1 |
| |
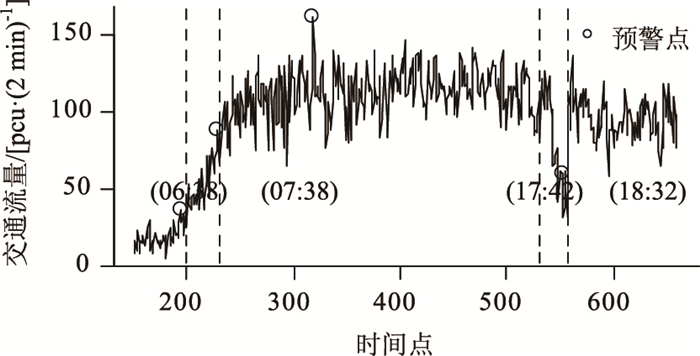
最终,依次检测出变点(图 12虚线标注)06:38,07:38,17:42,18:32,未检测到异常点。图 12中,圆圈标注处为各检测阶段的第一个预警点,不难发现,变点大多出现在交通需求量较大的高峰期。需要注意的是,检测出的变点17:42,18:32,期间交通流量骤减后又徒升。这可能由于交通事故快处快赔,也可能由于高峰期路段下游拥堵所致,具体情况可通过视频监控查实。从图 12也可看到,Dk监控阈值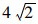
|
| 图 12 交通流量时序检测结果 Fig. 12 Detection result of traffic flow time series |
| |
以上实例分析,证明了提出的交通流异常点与变点快速检测算法具有较强的实用性。此外,为提高交通流监管的科学化水平,可综合考虑行程时间、占有率等交通流参数,在线检测异常点与变点。
4 结论实时交通流数据通常含有异常值,为此本研究提出了基于IRWT的异常点与变点快速检测算法,并将其应用于实际交通流状态的监控与预警。算法通过在线拟合交通流自回归模型,继而对残差序列的方差变点进行检测。仿真试验显示:采用改进递归小波变换标准化有效分数向量Wk,结合Dk与复合信息WTMPH3,可对交通流进行实时监控与预警,并对异常点进行检测;小波变换频率取1/2时,复数谱方差较小,利于提取变点时刻交通流的突变特征;与基于ESV的传统算法相比,提出的算法检测延迟小、收敛性更佳。
本文利用在线异常点与变点检测算法解决交通流实时监控与预警问题,实例分析时仅针对断面交通流监测。若要实现整个路网的监控与预警,可考虑多个断面并行监测。速度、行程时间等交通流参数,能够直观刻画交通流运行状态,构建地理加权回归模型对它们进行路网监控是下一步的研究方向。
| [1] |
苑敬雅, 朱茵. 高速公路交通流分析与安全预警机制研究[J]. 中国安全科学学报, 2016, 26(9): 146-150. YUAN Jing-ya, ZHU Yin. Freeway Traffic Flow Analysis and Fore-warning Research[J]. China Safety Science Journal, 2016, 26(9): 146-150. |
| [2] |
王晓原, 隽志才, 朴基男, 等. 局部比较的变点统计理论及其在交通流突变研究中的应用[J]. 公路交通科技, 2002, 19(6): 112-115. WANG Xiao-yuan, JUAN Zhi-cai, PIAO Ji-nan, et al. A Statistical Theory of Change-point with Local Comparison and Its Application in Studing Traffic Flow Breakdown[J]. Journal of Highway and Transportation Research and Development, 2002, 19(6): 112-115. |
| [3] |
翁剑成, 赵晓娟, 荣建. 基于D-S理论的城市快速路交通事件自动检测算法[J]. 公路交通科技, 2011, 28(12): 112-116, 144. WENG Jian-cheng, ZHAO Xiao-juan, RONG Jian. Urban Expressway Automatic Incident Detection Algorithm Based on D-S Theory[J]. Journal of Highway and Transportation Research and Development, 2011, 28(12): 112-116, 144. |
| [4] |
KHAN N, MCCLEAN S, ZHANG S, et al. Optimal Parameter Exploration for Online Change-point Detection in Activity Monitoring Using Genetic Algorithms[J]. Sensors, 2016, 16(11): 1784. |
| [5] |
APREM A, KRISHNAMURTHY V. Utility Change Point Detection in Online Social Media:A Revealed Preference Framework[J]. IEEE Transactions on Signal Processing, 2017, 65(7): 1869-1880. |
| [6] |
XIAO Q, HE R, YU J, et al. Road Traffic Flow Forewarning and Control Model with the Slope of the Change Rate[J]. Tehnički Vjesnik, 2017, 24(S1): 185-191. |
| [7] |
WU J, CHEN Y, ZHOU S. Online Detection of Steady-state Operation Using a Multiple-change-point Model and Exact Bayesian Inference[J]. ⅡE Transactions, 2016, 48(7): 599-613. |
| [8] |
ZHANG J, WEI Z, YAN Z, et al. Online Change-point Detection in Sparse Time Series with Application to Online Advertising[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2017, 49(6): 1141-1151. |
| [9] |
李拂晓, 田铮, 陈占寿. 随机系数自回归模型变均值点在线监测与应用[J]. 控制理论与应用, 2012, 29(4): 497-502. LI Fu-xiao, TIAN Zheng, CHEN Zhan-shou. Online Monitoring of Mean Change Point in a Random Coefficient Autoregressive Model[J]. Control Theory and Applications, 2012, 29(4): 497-502. |
| [10] |
李志敏, 易良友, 薛平, 等. 基于小波分析的交通流量异常数据检测[J]. 计算机应用研究, 2011, 28(5): 1677-1678. LI Zhi-min, YI Liang-you, XUE Ping, et al. Short-term Traffic Flow Detection Based on Wavelet[J]. Application Research of Computers, 2011, 28(5): 1677-1678. |
| [11] |
ALARCON-AQUINO V, BARRIA J A. Change Detection in Time Series Using the Maximal Overlap Discrete Wavelet Transform[J]. Latin American Applied Research, 2009, 39(2): 145-152. |
| [12] |
张大波, 刘志刚, 张亚军. 复小波研究现状及其在电力系统中的应用进展[J]. 电力系统自动化, 2006, 30(17): 97-104. ZHANG Da-bo, LIU Zhi-gang, ZHANG Ya-jun. Complex Wavelet Transform Review and Its Applications in Power System[J]. Automation of Electric Power Systems, 2006, 30(17): 97-104. |
| [13] |
CHAARI O, MEUNIER M, BROUAYE F. Wavelets:A New Tool for the Resonant Grounded Power Distribution Systems Relaying[J]. IEEE Transactions on Power Delivery, 1996, 11(3): 1301-1308. |
| [14] |
张传利, 黄益庄, 马晓旭, 等. 改进递归小波变换在变压器保护中的应用研究[J]. 电力系统自动化, 1999, 23(17): 20-22, 53. ZHANG Chuan-li, HUANG Yi-zhuang, MA Xiao-xu, et al. Study of Relaying Protection for Transformer Applying IRWT[J]. Automation of Electric Power Systems, 1999, 23(17): 20-22, 53. |
| [15] |
赵成勇, 何明锋. 基于复小波变换相位信息的谐波检测算法[J]. 中国电机工程学报, 2005, 25(1): 38-42. ZHAO Cheng-yong, HE Ming-feng. A Novel Method for Harmonics Measurement Using Phase Information of Complex Wavelet Transform[J]. Proceedings of the CSEE, 2005, 25(1): 38-42. |
| [16] |
RAHMATI A, ADHAMI R, DIMASSI M. Real-time Electrical Variables Estimation Based on Recursive Wavelet Transform[J]. International Journal of Electrical Power and Energy Systems, 2015, 68: 170-179. |
| [17] |
周德新, 刘宸宇, 牛亚月. 关于飞行发动机数据异常实时检测仿真研究[J]. 计算机仿真, 2016, 33(9): 118-122. ZHOU De-xin, LIU Chen-yu, NIU Ya-yue. Simulation Research about Flight Engine Data Anomaly Detection in Real-time[J]. Computer Simulation, 2016, 33(9): 118-122. |
| [18] |
苏卫星, 朱云龙, 刘芳, 等. 时间序列异常点及突变点的检测算法[J]. 计算机研究与发展, 2014, 51(4): 781-788. SU Wei-xing, ZHU Yun-long, LIU Fang, et al. Outliers and Change-points Detection Algorithm for Time Series[J]. Journal of Computer Research and Development, 2014, 51(4): 781-788. |
| [19] |
GOMBAY E. Sequential Change-point Detection and Estimation[J]. Sequential Analysis, 2003, 22(3): 203-222. |
| [20] |
GOMBAY E. Parametric Sequential Tests in the Presence of Nuisance Parameters[J]. Theory of Stochastic Processes, 2002, 8(24): 107-118. |
| [21] |
段建东, 匡军, 周琴, 等. 基于改进递归复小波变换的输电线路边界保护元件算法[J]. 中国电机工程学报, 2010, 30(19): 69-75. DUAN Jian-dong, KUANG Jun, ZHOU Qin, et al. Algorithm of Transmission Line Boundary Protection Unit on the Basis of Improved Recursive Complex Wavelet Transform[J]. Proceedings of the CSEE, 2010, 30(19): 69-75. |
| [22] |
董杰, 张举, 王增平, 等. 利用改进递归小波变换区分电力系统振荡与故障[J]. 继电器, 2002, 30(4): 15-18. DONG Jie, ZHANG Ju, WANG Zeng-ping, et al. Distinguish Fault from Power Swing Based on Improved Recursive Wavelet Transform[J]. Relay, 2002, 30(4): 15-18. |
| [23] |
易克初, 田斌, 付强. 语音信号处理[M]. 北京: 国防工业出版社, 2000. YI Ke-chu, TIAN Bin, FU Qiang. Speech Signal Processing[M]. Beijing: National Defense Industry Press, 2000. |
| [24] |
聂斌, 王超霞, 何耀东. 基于K-S检验的自由分布过程变点识别及其应用[J]. 数学的实践与认识, 2014, 44(6): 7-18. NIE Bin, WANG Chao-xia, HE Yao-dong. Change Point Identification of Distribution-free Process Based on K-S Test and Application[J]. Mathematics in Practice and Theory, 2014, 44(6): 7-18. |
 2019, Vol. 36
2019, Vol. 36
