扩展功能
文章信息
- 陈雨, 汪凡, 陈雨人
- CHEN Yu, WANG Fan, CHEN Yu-ren
- 低等级公路行车速度分布与行车环境协调性分析
- Analysis on Driving Speed Distribution and Driving Environment Coordination on Low-grade Highways
- 公路交通科技, 2019, 36(8): 115-123
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(8): 115-123
- 10.3969/j.issn.1002-0268.2019.08.015
-
文章历史
- 收稿日期: 2019-01-04
由于低等级公路,尤其处于城乡接合部的公路,交通环境复杂,交通监管效果不佳,交通出行工具多元化,小型客车增长快,及驾驶人交通安全意识淡薄等,相对其他道路来说,更容易发生交通事故,安全隐患突出,已成为影响公路交通安全的重要因素。国家主管部门对低等级公路安全保障非常重视,持续进行了多轮安全保障工作,且众多研究者从不同角度和层面进行了深入研究,如Polus等人提出采用运行速度与平均加权速度所围成的相对面积和运行速度标准差这两个速度离散度指标对线形一致性进行分析,分别建立相应的评价标准,并建立双车道公路线形一致性评价指标,用于路段的整体线形一致性分析[1]。吴德华、涂圣文、Mattar-Habib等也建立了类似评价模型和标准[2-6]。陈富坚等[7]针对过弯过程,以车辆的横向滑移失稳作为失效约束,建立道路平曲线的功能函数,根据具体条件选用解析法或蒙特卡洛法计算可靠度指标来评价公路曲线半径设计的可靠性。Richl等[8]采用一次二阶矩法来研究由于中央分隔带和圆曲线造成的视距供给的可靠性来分析道路设施的安全性。Khoury等[9]则采用蒙特卡洛法来计算在超车视距受限情况下带来的安全问题。Pentland和Liu[10]建立了隐马尔科夫模型预测制动和转弯行为来分析汽车和道路设施的安全性。Kuge等[11]采用HMM模型预测变道行为特征,分析行车环境的安全性。然而,驾驶行为随公路条件而变化,仅对驾驶人自身行为的建模和预测缺乏普适性,因此,Oliver和Pentlan[12]建立双隐马尔科夫模型,描述公路线形和出入口条件与变道行为的关系。Pomerleau[13]通过神经网络学习固有公路图像与驾驶人的方向盘转角之间的关系,并进行实时更新和反馈,可预测下一时刻的最佳方向盘转角,进而分析公路行车环境安全性。Inata等[14]建立基于神经网络的个性化辅助驾驶系统,对有无前车的公路环境分别提供跟驰、碰撞和制动距离预判功能,其中涉及到对公路行车环境的安全性分析。Messer建立基于驾驶员负荷的农村双车道公路设计一致性的主观评价模型[15]。Krammes、Wooldridge等分别建立不熟悉路况和熟悉路况的曲线段平均视觉需求模型[16-17]进行安全评价。归纳起来大致有这么两大方面:大部分研究以关注公路线形因素为主,利用运行车速、可能速度、交通事故率与道路几何要素关系等进行研究和应用;另一方面综合考虑驾驶人和车辆因素,利用驾驶人行为、工作负荷等进行评价以及对车辆运行过程中的三轴加速度等进行研究和应用。
上述研究从不同角度对公路行车环境安全性进行了研究和分析,从应用来看,有的效果不是非常理想,甚至还会出现实施一些安全保障或道路条件改善措施后事故发生率不降反升及超速现象越发严重的情况。大部分研究中以公路线形作为主要影响因素进行了安全评估与分析,但对于设计车速并不是很高的低等级公路来说,除了要考虑公路线形以外,周边行车环境及各因素之间的协调性更需要考虑,且行车环境是如何影响驾驶行为及交通安全性的内在因素也需要关注。理想的情况应该是行车环境各要素对驾驶行为产生的影响是均衡的,避免一些因素产生不利于安全的影响,削弱甚至抵消了其他有利于交通安全的因素作用。这种协调性还体现在低等级公路的“供给”与驾驶行为的“需求”一致性方面,低等级公路设施供给能力应尽可能满足驾驶人的行为需求。国家科技支撑计划课题《低等级公路安全防控关键技术研发与集成示范》子课题“低等级公路行车环境与驾驶行为协调性研究”针对上述问题进行了数据采集和深入分析,为解决低等级公路规划设计和安全保障进行了一些探索。
1 驾驶数据采集与行车环境分类 1.1 低成本设备采集数据GARMIN GDR35作为低成本驾驶数据采集设备,搭载GPS模块、三轴加速度传感器模块,能够采集车辆实时位置、速度、三轴加速度信息,采集频率可达30 Hz,平均误差不超过1.3%。前置摄像头能够记录前方道路视觉环境信息,视频格式为avi格式,视频清晰度可达1 080 p,帧率可达30 fps,配备64 G内存卡,连续记录时长可达680 min,足以满足数据采集的完整性与连续性。摄像头安装至汽车挡风玻璃上,以驾驶员视高和视角为基准,尽量模拟驾驶人实际驾驶过程中的视角和视线高度,如图 1所示。在多个特征区域内的低等级公路环境下,采集了超过20位驾驶人(试验车辆包括超过5辆农村公路客运车辆)驾驶行为和行车环境数据。每位驾驶人低等级公路资料采集里程不低于1 000 km,最终得到数据资料超过500 G,视频数据包括驾驶行为数据和行车环境信息,总里程超过20 000 km。驾驶行为与行车环境数据可以通过辅助软件《路视觉环境信息分析计算V1.0》(2016SR210398)自动提取。

|
| 图 1 行车记录仪GARMIN GDR35的安装 Fig. 1 Installation of Drive Recorder GARMIN GDR 35 |
| |
1.2 驾驶人第一视角行车环境分类
驾驶人第一视角行车环境,是指驾驶人在驾驶过程中所观察获取信息的外界环境总和,包括了低等级公路环境、路上其他车辆、交通标志标线及绿化景观等。根据低等级公路协调性研究需求,需要对低等级公路行车环境进行分类和分级。考虑到道路安全研究领域中对道路环境的关注重点,主要从道路线形与路面条件、周边景观绿化、道路附属设施等3大方面来进行分类,具体分为6大类。按照每种类别的基本特征,如平面线形特征、路面平整与否、是否经过村镇、周边视野条件、是否有标志线、是否有路侧护栏等特征,将每类分为2个级别,具体如表 1所列。该分类方式虽然6种道路环境有所重叠,但是考虑到驾驶员的关注点有所不同,可认为各变量之间是相互独立的。
| 道路线形与路面条件 | 周边景观绿化 | 道路附属设施 | |||||
| 平直路段 | 路面平整 | 基本路段 | 空旷通视 | 有标志线 | 无需防护 | ||
| 转弯路段 | 路面破损 | 经过村镇 | 有行道树 | 无标志线 | 防撞护栏 | ||
1.3 试验数据有效性检验与筛选
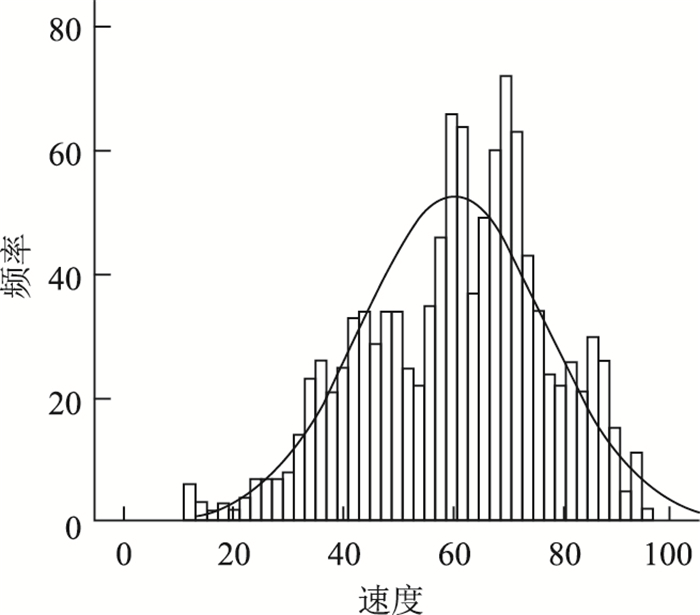
试验数据由20位驾驶人获得,车型包括超过5辆客运中巴,数据量庞大。试验数据不可避免会存在数据无效的情况,因此必须对获取的数据进行有效性检验,从而剔除不合适的样本。由于中巴车与一般小型客车较为类似,可以认为车型对结果的影响不大。主要从两个方面进行筛查,一是只选择自由流情况的数据进行分析研究,驾驶行为一般分为自由、跟驰和变道超车行驶等几种情况,主要考察对象是低等级行车环境协调性,而不是对广义的交通环境进行分析,因此侧重于自由流情况下的驾驶行为特征进行分析,事实上试验路段车辆较少,绝大部分都属于自由流状态;二是甄别驾驶人个体行为特征是否符合规律,寻求驾驶员共性的特征。本文采用对每一个驾驶人在自由流情况下的产生的行车速度分布进行正态分布检验,只有基本符合正态分布的驾驶人对应的数据资料才会被采用,图 2是有效性通过检验的一位驾驶人行车速度分布图。20人中共有17人通过有效性检验,相应的数据资料参与后续的分析。
|
| 图 2 通过有效性检验的驾驶人行车速度分布 Fig. 2 Validated driving speed distribution |
| |
2 低等级公路不同行车环境自由流行车速度分布特征 2.1 自由流行车速度特征描述
研究表明,公路上车辆的行车速度总体上应该服从正态分布,但是由于车辆速度差的不同,车辆速度可能呈现单峰或多峰特征,一般可以采用混合高斯模型对其特征进行描述[18]。由于客观研究对象的多态性,难以采用一个分布对某一复杂客观事物进行描述。高斯混合模型采用多个用高斯概率密度函数,将一个研究对象分解为由若干个基于高斯概率密度函数(正态分布曲线)组成的模型:
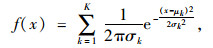
|
式中,f(x)为概率密度函数;x为行驶速度;K为高斯概率密度函数的个数;λk,μk,σk为第k个高斯密度函数的权重、期望值和标准差。
当混合高斯模型中高斯函数的数量为2就成为了双峰模型。双峰模型可以对数据分布有效地拟合,而且不会让模型参数的数量过多,采用双峰模型分析不同行车环境下行驶速度分布及特征情况,此时模型为:

|
将获取的所有驾驶人有效数据资料按照不同行车环境特征进行筛选分类形成数据集Seti,数据集中的行车速度可能为多个高斯分布共同构成,如果试验车辆全部的行驶车速作为总体SetAll,本研究中各个数据集相当于多个不同的高斯分布集Setl,SetJ,SetK…组成。由于不同行车环境的影响,研究中筛选出的数据集Seti相当是由一定比例从Setl,SetJ…中抽样组成,所以对于Seti进行分布参数估计就是一个混合高斯分布的参数估计问题。主要难点在于构成数据集的多个高斯分布的参数变量为隐变量,数据集中每个行车速度来自于哪个分布不可知,需要进行参数估计。目前关于混合分布的拟合方法主要包括RBF(神经网络)、SVM(支持向量机)和EM(Expectation-Maximization)[19]等,其中EM算法常用作对参数隐变量进行估计。该方法采用迭代算法,若参数θ已知,则可采用训练集中数据对最优隐变量ω进行计算;反之,若隐变量ω已知,则可以采用最大似然估计方法对参数θ进行计算。
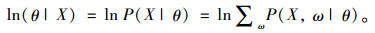
|
由于本研究中高斯分布个数未知,因此假设每个数据集中可能存在两个不同的高斯分布,通过抽样比例,也可以体现出单个高斯分布的情况。两个不同的高斯分布容易进行对比分析和解释,其均值μ1μ2和方差σ1σ2均便于计算。
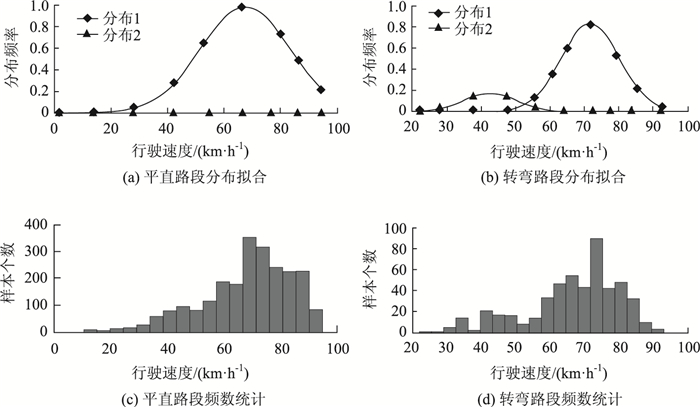
2.3 不同行车环境条件下的行车速度分布特征为了分析不同行车环境条件对驾驶行为的影响,在数据分析处理中,采用控制变量的方式,从海量数据里筛选其他条件相同,只有一个条件变化的样本进行分析。根据上述算法和分类得到的各个行车环境下的行车速度分布图,如图 3~图 8所示。每种分类下都采用混合分布对行驶速度进行了描述。图中横坐标为行驶速度(km/h),纵坐标分别为分布频率和样本个数。分布参数如表 2所列。在分析过程中,对每种环境条件下的速度分布都采用了混合高斯模型进行描述,取高斯函数的数量为2。两个分布都为高斯分布,随着其权重值的不同,代表了在该种环境条件下驾驶员所体现出的两种最为典型的速度特征分布及其所占比例。
|
| 图 3 平直路段与转弯路段 Fig. 3 Straight section and turning section |
| |
|
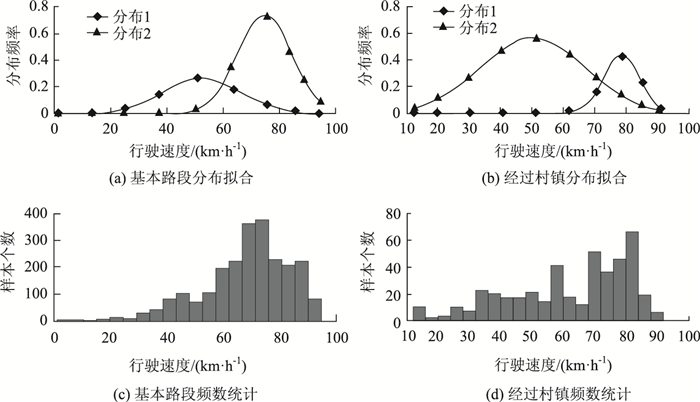
| 图 4 基本路段与经过村镇 Fig. 4 Basic section and through-town section |
| |
|
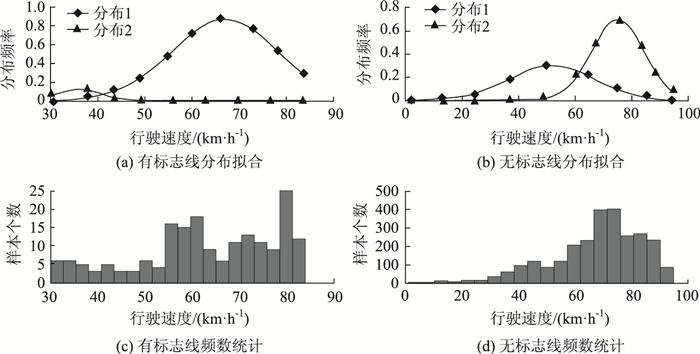
| 图 5 有标志线与无标志线 Fig. 5 Lane mark and no lane mark |
| |
|
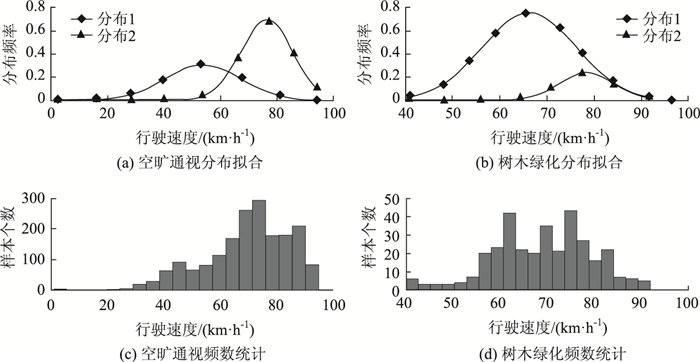
| 图 6 空旷通视与树木绿化 Fig. 6 Open vision and tree greening |
| |
|
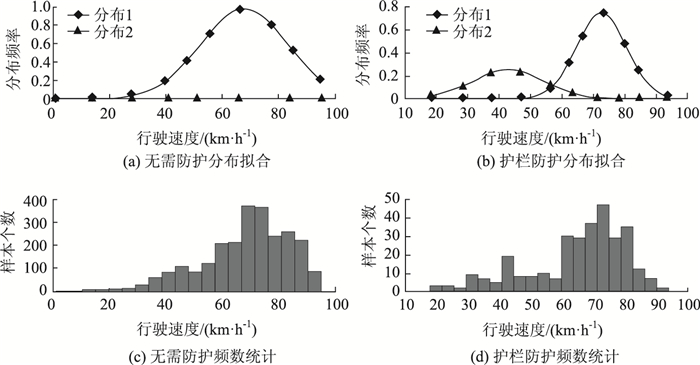
| 图 7 无需防护与护栏防护 Fig. 7 No need for guard and guardrail |
| |
|
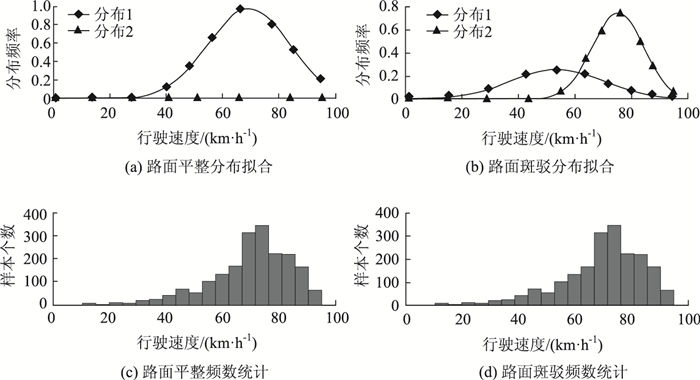
| 图 8 路面平整与路面斑驳 Fig. 8 Smooth pavement and mottled pavement |
| |
| 比例 | 均值 | 方差 | ||||||
| λ1 | λ2 | μ1 | μ2 | σ1 | σ2 | |||
| 平直路段 | 0.977 8 | 0.022 2 | 67.644 4 | 91.000 0 | 15.774 9 | 0.000 0 | ||
| 转弯路段 | 0.829 9 | 0.170 1 | 71.732 8 | 42.729 3 | 8.389 2 | 7.510 4 | ||
| 基本路段 | 0.262 8 | 0.737 2 | 52.365 8 | 74.758 1 | 13.885 8 | 9.535 4 | ||
| 经过村镇 | 0.436 3 | 0.563 7 | 78.645 3 | 50.185 1 | 5.784 8 | 16.647 4 | ||
| 有标志线 | 0.880 9 | 0.119 1 | 66.946 8 | 36.014 5 | 11.142 8 | 4.247 5 | ||
| 无标志线 | 0.301 3 | 0.698 7 | 51.921 9 | 75.266 1 | 15.132 6 | 9.252 8 | ||
| 空旷通视 | 0.304 1 | 0.695 9 | 54.096 2 | 76.655 3 | 13.189 6 | 9.161 9 | ||
| 有行道树 | 0.763 6 | 0.236 4 | 66.203 2 | 78.426 4 | 9.882 0 | 5.713 4 | ||
| 无需防护 | 0.979 5 | 0.020 5 | 67.775 7 | 91.000 0 | 15.340 5 | 0.000 0 | ||
| 护栏防护 | 0.745 6 | 0.254 4 | 72.640 7 | 42.952 3 | 7.994 3 | 11.285 2 | ||
| 路面平整 | 0.024 9 | 0.975 1 | 90.512 5 | 69.111 5 | 0.585 8 | 14.491 7 | ||
| 路面破损 | 0.745 1 | 0.254 9 | 75.105 0 | 53.683 1 | 9.003 7 | 16.378 2 | ||
为了保证采用混合高斯分布对研究对象进行描述具有一定的意义,需要对分布权重的阈值进行确定。根据表 2中的统计结果,在某种道路环境下,两种分布的变异系数在量级上存在差异时,可认为该分布没有存在的必要。所提取出的3个分布比例分别为0.977 8, 0.997 95,0.975 1。不失一般性地,可取0.95分位值作为其阈值,即当混合高斯分布模型其中一个分布的权重大于0.95时,可以认为没有必要采用高斯混合分布,只需要一个单独的高斯分布就可以对研究对象进行描述。在上述几种分类中,“平直路段”、“无需防护”和“路面平整”3种道路环境下,行驶速度的混合模型其中一个分布权重都超过了0.95,且该分布的均值约等于总体均值,说明该道路环境下驾驶行为处于一种比较平稳顺适的行驶状态之中,这3种道路环境对驾驶行为没有显著的不良影响。相反地,在某种道路环境下,两种分布的变异系数相差不超过20%时,可认为存在着明显的双峰分布。所提取出的分布比例为0.436 3, 0.301 3, 0.304 1。不失一般性地,可取0.3分位值作为其阈值, 即当混合高斯分布模型其中一个分布的权重大于0.3时,可认为该情况下存在着两个明显不同的分布。在“经过村镇”、“无标志线”和“空旷通视”3种道路环境下,行驶速度的混合模型中其中一个分布的权重占到了0.3以上,且两个分布的均值相差较大。这说明在以上道路环境中,驾驶员倾向于选择两种不同的驾驶状态。该情况往往会导致车速离散性增大,表明该道路条件对驾驶行为存在着显著的不良影响。分布的方差可认为是该种分布对应的驾驶状态的离散性,离散性越小则驾驶状态越稳定。
在每组道路环境的分类下,“平直路段”与“转弯路段”、“有标志线”与“无标志线”、“无需防护”与“护栏防护”、“路面平整”与“路面斑驳”4组对比较为明显,其特征都为:一种道路条件下驾驶状态较为稳定,另一种道路条件下驾驶状态较为离散。这说明4种道路环境对驾驶行为的影响较为明显,也证明了路侧防护、路面条件、标志标线与线形条件对驾驶安全至关重要。道路安全条件改善应以这4种道路环境条件为重点整治对象,其改善对于驾驶安全的效果较为显著。同时值得注意的是,“护栏防护”条件下,虽然道路环境条件相较“无需防护”有所改善,但其驾驶状态稳定性反而有所下降。这可能是由于护栏防护路段往往在临水临崖、急弯陡坡等路段,其他道路环境条件较为复杂,且护栏的设置本身就暗示着危险道路环境,其设置应根据实际条件因地制宜。而“有标志线”条件下驾驶状态仍存在着一定的离散性,这可能是由于标志标线的设置无法引起驾驶员注意,在设置该道路环境时也应考虑其醒目性与有效性。
在“基本路段”与经过村镇”道路环境分类组别下,都存在着两个较为离散的分布,但经过村镇时总体速度较低,说明驾驶员在经过村镇路段倾向于采用较低的驾驶速度。类似地,在“有行道树”与“空旷通视”道路环境分类下,“有行道树”的环境会使驾驶员采用较低的驾驶速度。
3 低等级公路行车环境协调性分析根据上面对各个环境条件下行车速度分布特征的分析,可以根据分布情况分为3类:(1)“平直路段”、“无需防护”、“路面平整”的情况下驾驶人受行车环境因素影响比较小,只存在一个较为明显的分布。(2)“经过村镇”、“无标志线”和“空旷通视”的情况下驾驶人受到行车环境影响比较大,存在一个较为平缓的低速分布和一个较为集中的高速分布特征,体现了两种不同的驾驶状态,但行车速度从总体上看保持稳定。(3)其余情况下行车速度分布表现得并不稳定,并且无论是行驶速度分布图还是参数表 2中所体现的变化也各不相同,没有一定规律,说明这几种行车环境情况下行车速度不稳定,行车环境相互之间存在不协调的情况。在此基础上总结出各个行车环境条件下两个行车速度分布的比例差、比例较大分布的均值以及两个分布的方差和,得到表 3。在此基础上总结出3种不同的行车速度分布形态特征,列在表 4中。这3种行驶速度分布特征可以作为分析低等级公路行车环境协调性的参考依据。总之,行车速度单峰分布是较理想的。
| 比例差 | 比例较大分布均值 | 方差和 | |
| 平直路段 | 0.955 6 | 67.644 4 | 15.774 9 |
| 无需防护 | 0.959 | 67.775 7 | 15.340 5 |
| 路面平整 | 0.950 2 | 69.111 5 | 15.077 5 |
| 基本路段 | 0.474 4 | 74.758 1 | 23.421 2 |
| 有标志线 | 0.397 4 | 75.266 1 | 24.385 4 |
| 空旷通视 | 0.391 8 | 76.655 3 | 22.351 5 |
| 护栏防护 | 0.491 2 | 72.640 7 | 19.279 5 |
| 路面破损 | 0.490 2 | 75.105 | 25.381 9 |
| 转弯路段 | 0.659 8 | 71.732 8 | 15.899 6 |
| 经过村镇 | 0.127 4 | 50.185 1 | 22.432 2 |
| 无标志线 | 0.761 8 | 66.946 8 | 15.390 3 |
| 有行道树 | 0.527 2 | 66.203 2 | 15.595 4 |
| 行车环境协调性 | 比例差 | 比例较大的分布均值 |
| 好 | 均大于0.95,表现为其中一个行车速度分布占主导地位 | 行车速度分布在67~70之间,接近数据的整体均值 |
| 中 | 在0.39~0.5之间,两个分布的形态稳定 | 行车速度分布在72~76之间,均值相差不大 |
| 差 | 不规律,并不会出现某一分布占主导地位或两个分布之间保持恰当的距离 | 行车速度分布不规律,大多数情况下分布的均值偏低 |
综上所述,低等级公路行车环境组成比较复杂,总体上会导致驾驶人行车速度分布不一致,离散型比较多,但是行车环境各因素对驾驶人行车速度分布的影响并不相同,尤其是不同的组合会产生不同效果的影响,因此就有一个协调问题。所谓协调性好,本质上将就是参与其中的驾驶人行车速度总体容易保持稳定,整个低等级公路系统容易处于一种相对稳定的行车状态,显然此时安全性比较高,发生事故的概率降低,表现在行车速度分布上就是一个比较明确的单峰正态分布。如果行车环境协调差,表明构成行车环境各因素对驾驶人行车速度影响不一致,或者说驾驶人在这种低等级公路系统中行车状态不稳定,行车速度的离散性比较大,整体安全风险提高,发生事故的概率会大大增加,表现在行车速度分布上就会比较凌乱,可能会形成双峰或多峰正态分布,甚至毫无规律可言。此时安全性是较低的,发生事故的概率也较高。
通过试验发现,这种不协调情况普遍存在于农村低等级道路之中,在进行有关安全保障措施时,对这类不协调情况并没有引起足够的重视或者给予专项的评估,这就可能导致采取安全保障措施后,效果不尽理想,甚至加剧了行车速度的离散性,带来更大的安全风险。比如205国道1 845~1 848 km(江山小竿岭)路段,该路段等级为山区二级公路,设计速度40 km/h,2006年12月路面由水泥路面改为沥青路面,在竣工3个月时间内,共发生交通事故16起,其中死亡事故4起,死亡10人,受伤13人。经专家认定,其主要原因是将路面等级提高,但线形指标未变,路面条件诱发车速过快,但几何条件供给不足,从而容易发生交通事故。因此在进行公路安全评价时,除了常规几何指标的一致性筛查以外,行车环境协调性评估分析也应该给予足够的重视,尤其是对于行车环境相对复杂的低等级公路更应如此。
4 结论针对低等级公路行车环境复杂的现状,为了使相关安全保障措施措施更加精准有效,对低等级公路行车环境特征以及驾驶人行为特征进行深入调查和分析研究是必不可少的。本研究在大范围采集低等级公路行车环境特征和驾驶行为数据基础上,对行车环境进行了初步分类,采用高斯混合模型结合EM算法对不同行车环境下的行车速度分布特征进行了深入分析,一定程度上证实了低等级公路行车环境可能存在不协调的情况。
在后续研究中,可从以下几方面进行进一步深化:一是建立较为细化的行车环境拓扑结构分类,使得协调性研究更加细致;二是针对共性特征和个性特征进行分别提炼和研究;三是结合驾驶人共性行为特征,甄别影响协调性的行车环境因素和组合,研究低等级公路行车环境协调性改善技术。这也是低等级公路行车环境协调性研究的根本目的。
通过上述持续有针对性的研究,希望能够从低等级公路行车环境协调性的角度,为扎实提高低等级公路交通运行安全性作出不懈努力。
| [1] |
POLUS A, MATTER-HABIB C. New Consistency Model for Rural Highways and Its Relationship to Safety[J]. Journal of Transportation Engineering, 2004, 130(3): 286-293. |
| [2] |
吴德华, 方守恩. 高速公路线形设计的质量量化评价模型[J]. 同济大学学报:自然科学版, 2005, 33(11): 1469-1473. WU De-hua, FANG Shou-en. Quantity Evaluation Model of Line Design Quality of Freeway[J]. Journal of Tongji University:Natural Science Edition, 2005, 33(11): 1469-1473. |
| [3] |
涂圣文, 过秀成, 何建明. 双车道公路线形一致性评价模型[J]. 交通运输系统工程与信息, 2008, 8(5): 94-100. TU Sheng-wen, GUO Xiu-cheng, HE Jian-ming. Evaluation Model for Alignments Consistency of Two-lane Highways[J]. Journal of Transportation Systems Engineering and Information Technology, 2008, 8(5): 94-100. |
| [4] |
MATTAR-HABIB C, POLUS A, FARAH H. Further Evaluation of the Relationship between Enhanced Consistency Model and Safety of Two-lane Rural Roads in Israel and Germany[J]. European Journal of Transport and Infrastructure Research, 2008, 8(4): 320-332. |
| [5] |
RUSSO F, MAURO R, DELL'ACQUA G. Rural Highway Design Consistency Evaluation Model[J]. Procedia-Social and Behavioral Sciences 53, 2012, 53(3): 953-961. |
| [6] |
DELL'ACQUA G, BUSIELLO M, RUSSO F. Safety Data Analysis to Evaluate Highway Alignment Consistency[J]. Journal of the Transportation Research Board, 2013, 2349: 121-128. |
| [7] |
陈富坚, 郭忠印, 陈富强, 等. 公路平曲线半径的可靠性设计[J]. 哈尔滨工业大学学报, 2012, 44(4): 100-104. CHEN Fu-jian, GUO Zhong-yin, CHEN Fu-qiang, et al. Reliability Design Method for Horizontal Curve Radius of Highway Alignment[J]. Journal of Harbin Institute of Technology, 2012, 44(4): 100-104. |
| [8] |
RICHL L, SAYED T. Evaluating the Safety Risk of Narrow Medians Using Reliability Analysis[J]. Journal of Transportation Engineering, 2006, 132(5): 366-375. |
| [9] |
KHOURY J, HOBEIKA A G. Assessing the Risk in the Design of Passing Sight Distances[J]. Journal of Transportation Engineering, 2007, 133(6): 370-377. |
| [10] |
PENTLAND A, LIU A. Modeling and Prediction of Human Behavior[J]. Neural Computation, 1999, 11(1): 229-242. |
| [11] |
KUGE N, YAMAMURA T, SHIMOYAMA O, et al. A Driver Behavior Recognition Method Based on a Driver Model Framework[C]//Proceedings of the Society of Automotive Engineers World Congress.[S.l.]: SAE, 2000.
|
| [12] |
OLIVER N, PENTLAND A P. Graphical Models for Driver Behavior Recognition in a Smartcar[C]//Proceedings of the IEEE Intelligent Vehicles Symposium 2000. Dearborn, USA: IEEE, 2000: 7-12.
|
| [13] |
POMERLEAU D. Neural Network Vision for Robot Driving[M]. Anon: Handbook of Brain Theory & Neural Networks, 997: 161-181.
|
| [14] |
INATA K, RAKSINCHAROENSAK P, NAGAI M. Driver Behavior Modeling Based on Database of Personal Mobility Driving in Urban Area[C]//2008 International Conference on Control, Automation and Systems. Seoul: IEEE, 2008: 2902-2907.
|
| [15] |
MESSER C J. Methodology for Evaluating Geometric Design Consistency[J]. Transportation Research Record, 1980, 757: 7-14. |
| [16] |
KRAMMES R A, BRACKETT R Q, SHAFER M A, et al. Horizontal Alignment Design Consistency for Rural Two-Lane Highway, FHWA-RD-94-034[R]. Washington, D.C.: Federal Highway Administration, 1995.
|
| [17] |
WOOLDRIDGE M D, BAUER K, GREEN P, et al. Comparison of Driver Visual Demand in Test Track, Simulator, and On-road Environments[C]//Proceedings of the 79th Annual Meeting of the Transportation Research Board. Washington, D.C.: Transportation Research Board, 1999: 1-10.
|
| [18] |
岳佳, 王士同. 高斯混合模型聚类中EM算法及初始化的研究[J]. 微计算机信息, 2006, 22(33): 244-246, 302. YUE Jia, WANG Shi-tong. Algorithm EM and Its Initialization in Gaussian-mixture-model Based Clustering[J]. Microcomputer information, 2006, 22(33): 244-246, 302. |
| [19] |
王继利, 杨兆军, 李国发, 等. 基于改进EM算法的多重威布尔可靠性建模[J]. 吉林大学学报:工学版, 2014, 44(4): 1010-1015. WANG Ji-li, YANG Zhao-jun, LI Guo-fa, et al. Reliability Modeling of Finite Weibull Distribution Based on Improved EM Algorithm[J]. Journal of Jilin University:Engineering and Technology Edition, 2014, 44(4): 1010-1015. |
 2019, Vol. 36
2019, Vol. 36
