扩展功能
文章信息
- 罗浩, 吕海龙, 谢献忠, 汪建群, 郭辉
- LUO Hao, LÜ Hai-long, XIE Xian-zhong, WANG Jian-qun, GUO Hui
- 风浪荷载共同作用下大跨度刚构桥动力响应规律研究
- Study on Dynamic Response Rule of Long-span Rigid Frame Bridge Subjected to Coupled Actions of Wind and Wave Loads
- 公路交通科技, 2019, 36(8): 78-85
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(8): 78-85
- 10.3969/j.issn.1002-0268.2019.08.010
-
文章历史
- 收稿日期: 2018-04-18
2. 中国铁道科学研究院 铁道建筑研究所, 北京 100081
2. Railway Engineering Research Institute, China Academy of Railway Sciences, Beijing 100081, China
在世界经济高速发展的今天,陆路交通的建设已满足不了当代发展的所有运输需求,在此背景下跨海桥梁应运而生。由于所处地理位置的特殊性,跨海桥梁经常受到风浪荷载的作用。随着跨海桥梁的兴建,桥梁所受风浪的动力作用在跨海桥梁设计时越来越受到工程师的重视。对于桥梁受到风浪作用的影响研究目前主要有试验研究和数值模拟方法,由于试验设备与成本要求都非常高[1-5],因此从工程应用的角度考虑,研究风浪作用的数值分析方法具有重要意义。
在研究海洋工程结构的风浪作用时,由于风浪之间存在复杂的耦合关系,如何描述这种关系是研究风浪共同作用的关键。由于直接对风浪场进行模拟非常困难,因此本研究基于风浪反演模型,将风浪的耦合性体现在风、浪各参数之间的相关性上,并引入比较常用的,即SMB风浪经验模型和海洋工程波浪理论[6-15],对各参数之间的耦合关系进行阐述。在此基础上运用数值计算方法,模拟计算对应海况下的风荷载及波浪荷载,通过通用有限元软件ANSYS建立刚构桥的有限元模型,并对其风浪作用下的空间响应进行分析。
1 风浪耦合关系数值分析时,风浪的耦合关系主要体现在风浪参数之间的相关性上,比较常用的风浪模型为风浪经验模型, 即SMB(Sverdrup, Munk and Bretschneider)模型[4]。根据此模型可知,风浪中的海面风速与波高满足如下关系:

|
(1) |
式中,g为重力加速度;Hs为有效波高;U10为10 m高度处的平均风速;fp为海浪谱中的峰值频率。
根据文圣常院士提出的适用于深水和浅水的普遍风浪谱(文氏谱)[5],谱峰频率表示为:
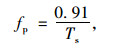
|
(2) |
式中Ts为有效波周期。
由波浪的弥散关系可得,波周期T与波龄β(波速和风速的比值)存在如下关系:
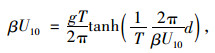
|
(3) |
式中d为水深。
此时风浪中的波高、风速关系改写为式(4):
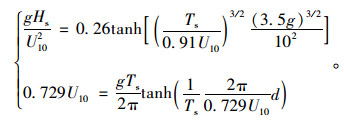
|
(4) |
有相关观测资料和研究证实,波龄作为风浪变化的指标,当风浪处于充分发展阶段时,波龄等于0.7~0.8,波高达到最大。参考相关资料,取波龄β为0.729[6-7]。
2 桥梁空间振动分析模型 2.1 工程概况某跨海湾刚构桥,跨度为(88+160+88) m,主梁为单箱单室截面,跨中及端支座截面梁高5 m,中支座处梁高9.8 m,梁底部曲线采用1.8次抛物线。主墩为双肢薄壁结构,墩柱中心距为8 m。因该桥受潮水的影响,计算时取历史最高水位,距承台底部为13.4 m。根据相关文献,最大波高可取参考值5 m[10-15],对应6级海况。全桥布置图如图 1所示。

|
| 图 1 全桥布置 Fig. 1 Bridge layout |
| |
2.2 桥梁有限元模型
桥梁空间有限元模型中,主梁采用Beam188单元,采用自定义变截面方法建立变截面梁单元模型,桥墩采用Beam188单元建立等截面单元模型,主梁共划分为91个单元,桥墩共划分为60个单元。主梁与墩之间采用刚接形式,桥墩底部采用固结形式,主梁边跨支座设置为滚动支座,有限元模型如图 2所示,振型图如图 3所示。

|
| 图 2 全桥有限元模型 Fig. 2 FE model of bridge |
| |
|
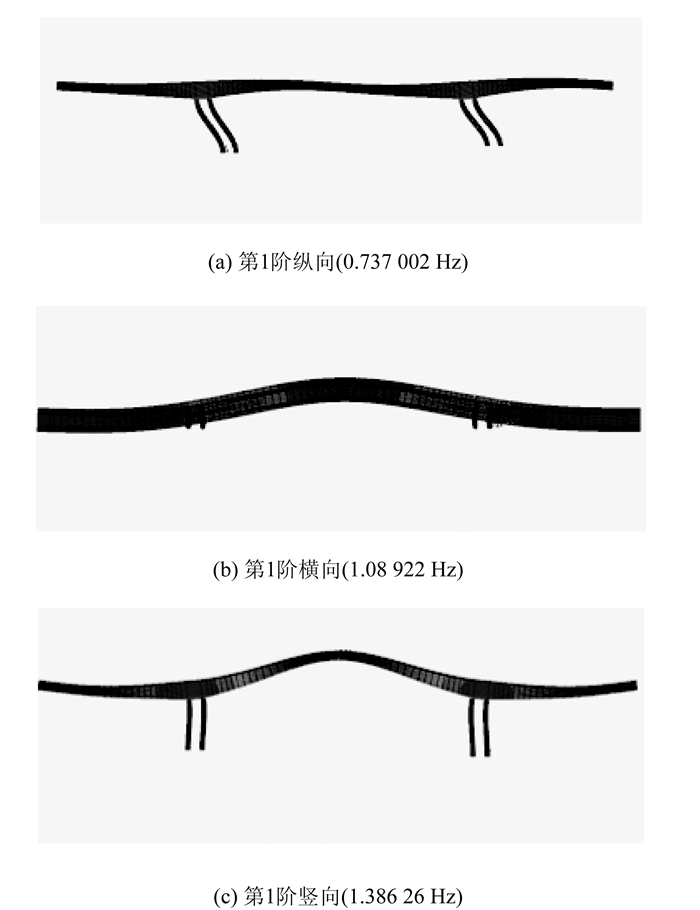
| 图 3 有限元模型振型 Fig. 3 Mode shapes of FE model |
| |
从图 3可以看出,第1阶振型表现为纵向振动,第2阶振型表现为横向弯曲振动,第3阶振型才为竖向弯曲振动,说明结构的纵向弯曲刚度相对较小,因此结构的第1阶振型为整体纵飘,与相关文献的数值分析结论一致[16-18],同时也说明了所建立桥梁结构有限元模型的正确性。
3 风浪荷载的数值模拟国家海洋预报平台根据海面在风的作用下波动的情况对海况进行了分级描述,因此在进行结构风浪荷载作用响应研究时,采用海况对不同计算工况进行描述。本研究以6级海况进行说明。6级海况下,有效波高为4~6 m,风力等级为7级[11],取有效高度为5 m时,由风浪耦合关系确定的有效波周期为8.4 s,10 m高度处的平均风速为16.69 m/s,风速在海况对应风级范围之内。
3.1 风荷载的数值计算根据桥梁风工程理论[12],风荷载主要分为平均风引起的静风荷载和脉动风引起的脉动风荷载。对于不同高度处的平均风速,采用Davenport提出的指数率模型来描述:
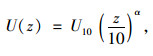
|
(5) |
式中,z为任意一点距地面高度;α为地面粗糙度。
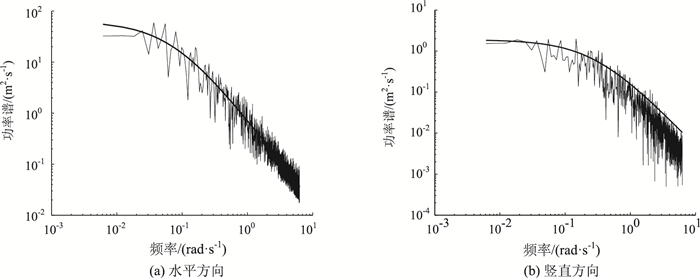
横桥向和竖向脉动风速根据目标功率谱通过谐波叠加法模拟得到,风速谱分别采用Kaimal谱和Panofsky谱[12],相干函数采用Davenport相干函数,对模拟的谱特性和相关性的检验如图 4~图 5所示。
|
| 图 4 模拟风速谱和目标谱比较 Fig. 4 Comparison of simulated wind speed spectrum and target spectrum |
| |
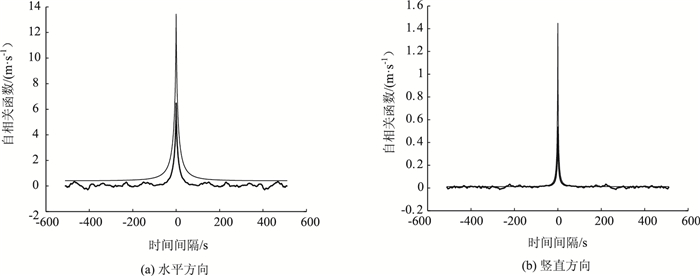
|
| 图 5 相关函数比较 Fig. 5 Comparison of correlation functions |
| |
从图 4~图 5可以看出,模拟风速的谱密度和目标谱密度比较吻合,模拟风速的相关函数与理论值也基本吻合。按照Davenport准定常抖振理论[12],作用在桥梁上的抖振力三分力计算表达式如下:
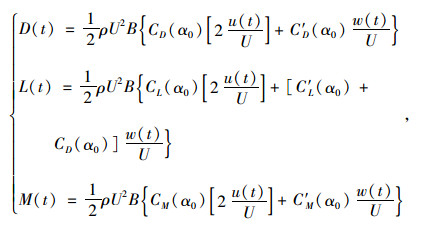
|
(6) |
式中,D(t), L(t), M(t)分别为阻力、升力、扭矩;ρ为空气密度;U为平均风速;B为桥梁宽度;CD(α0), CL(α0), CM(α0)分别为阻力系数、升力系数和扭矩系数;u(t)和w(t)分别为横桥向和竖向脉动风速;C′D (α0), C′L(α0), C′M(α0)分别为阻力系数、升力系数和扭矩系数曲线斜率;α0为平均风攻角。
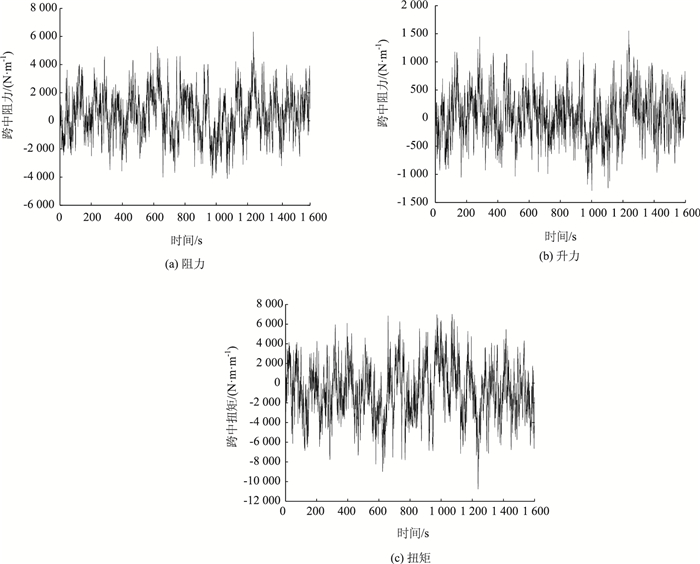
三分力系数及其导数通常按照风洞试验来确定,本研究采用相关文献中的数值分析结果[18],脉动风则采用谐波叠加法进行模拟。模拟得到的脉动风荷载时程曲线如图 6所示。
|
| 图 6 跨中三分力时程曲线 Fig. 6 Time-history curves of three-component force in mid-span |
| |
3.2 波浪荷载的数值计算
实际海浪波形很难统一量化,但在极端海浪状况下,海浪的波形一般比较规则,因此运用数值方法模拟6级海况下的规则波浪场。
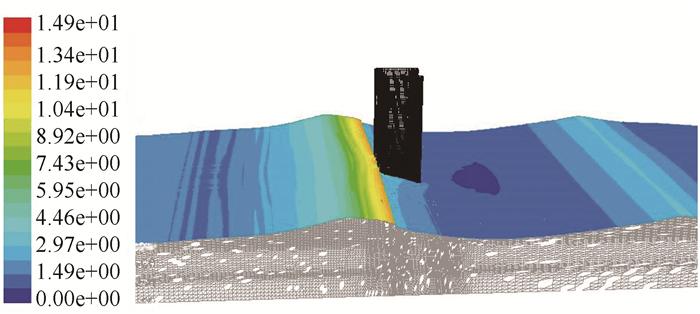
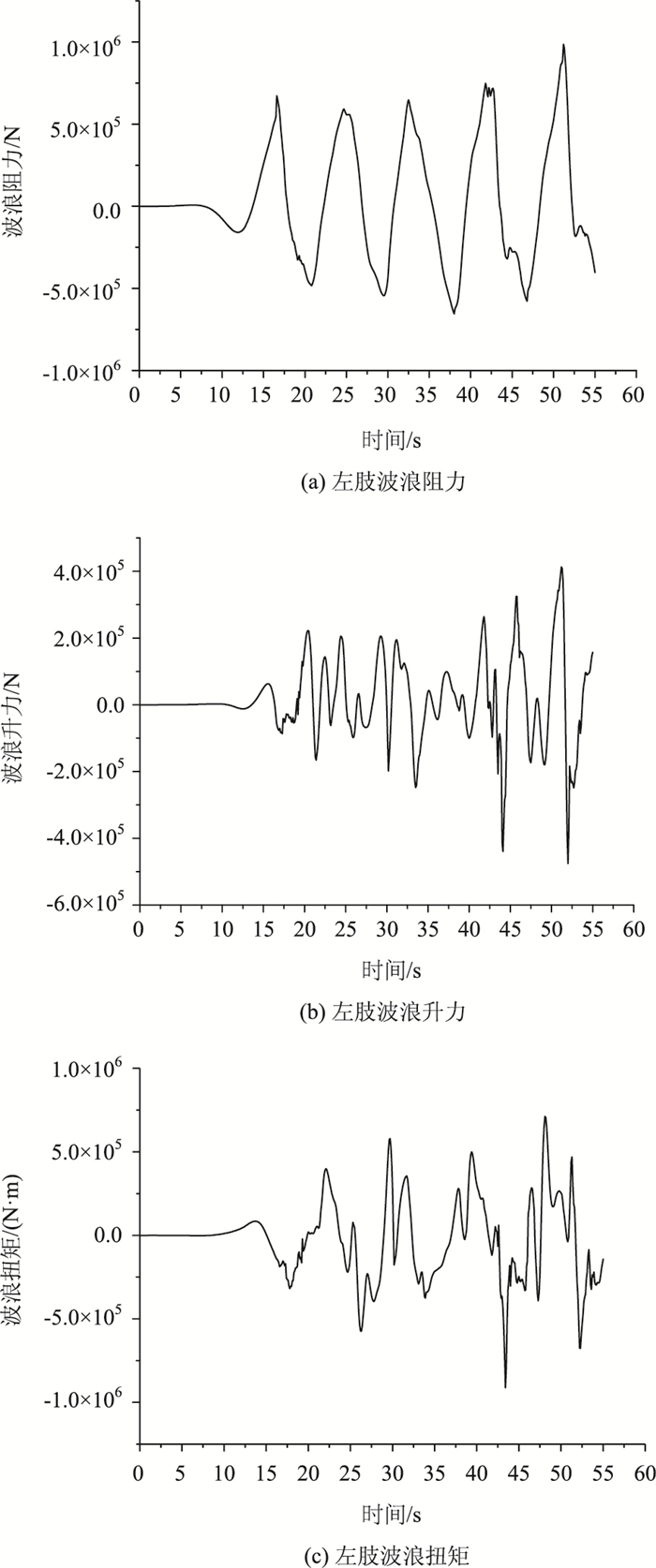
对作用小尺度结构的波浪力,一般采用莫里森方程计算,然而跨海桥梁桥墩的存在一般会对波浪场产生影响,因此主要运用ANSYS CFD软件进行数值求解,采用边界造波方法对波浪场进行模拟[13-15],模拟波高与周期采用风浪耦合关系中的有效波高、有效波周期。模拟得到波浪场速度云图和波浪力时程曲线图,如图 7~图 8所示。
|
| 图 7 波浪场速度云图(t=16.6 s) (单位: m/s) Fig. 7 Nephogram of wave field velocity when t= 16.6 s (unit: m/s) |
| |
|
| 图 8 波浪力时程曲线 Fig. 8 Time-history curves of wave force |
| |
4 风浪荷载作用下空间结构响应
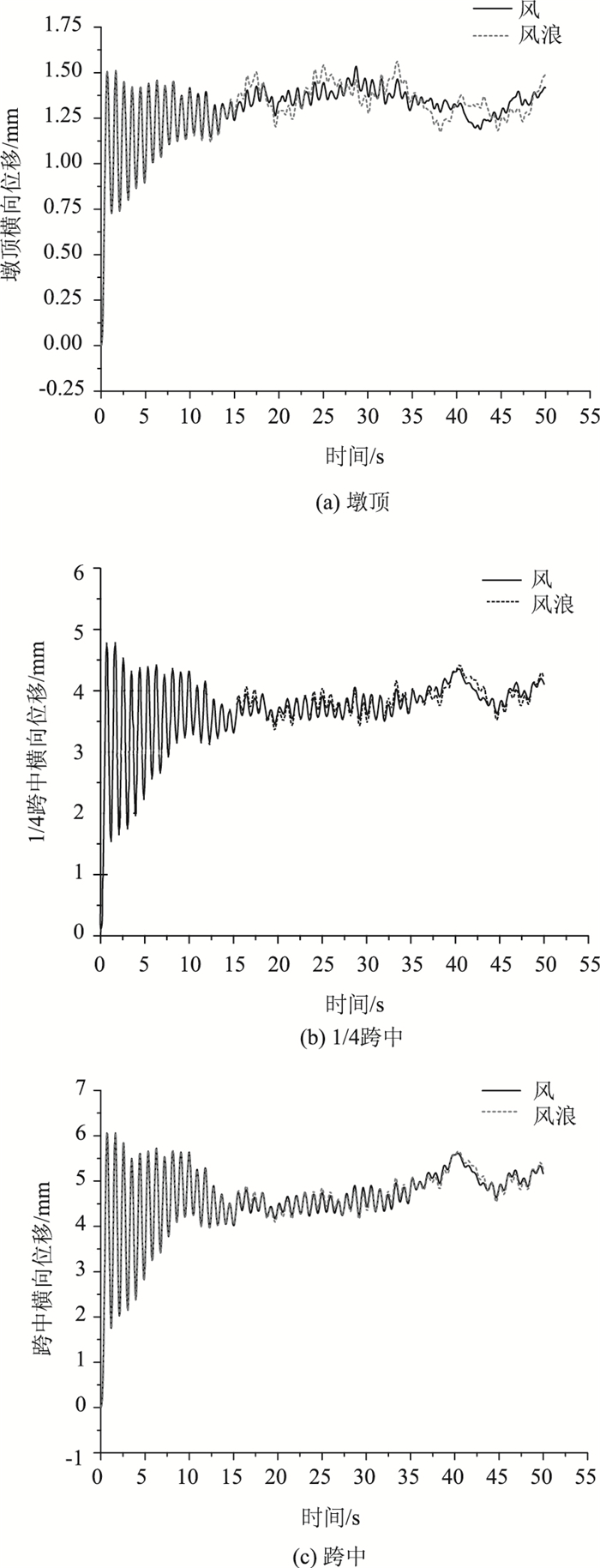
为了便于对比,列出典型位置的响应结果(限于篇幅仅列出部分结果),并对风浪荷载作用时结构的响应规律进行分析。图 9分别为风荷载和风浪荷载作用下,墩顶、1/4跨中和跨中的横向位移时程曲线。
|
| 图 9 横向位移时程曲线 Fig. 9 Time-history curves of transverse displacement |
| |
对图 9趋于平稳后的位移响应进行分析可以看出,与单独风荷载作用相比,在加入了波浪荷载的影响时,墩顶位移局部时刻横向位移增幅最大值为0.1 mm左右,局部时刻幅值相对增加7%左右;1/4跨中局部时刻横向位移增幅最大为0.17 mm,局部时刻幅值相对增加为4%左右;跨中横向位移局部时刻增幅最大值为0.1 mm左右,局部时刻幅值相对增加2%左右。由此表明,虽然墩顶位移响应绝对增幅与跨中横向位移响应的绝对增幅相差不多,但墩顶位移相对增幅比跨中相对振动幅度增幅大很多,波浪对墩顶响应时程曲线的影响也比跨中位移明显。
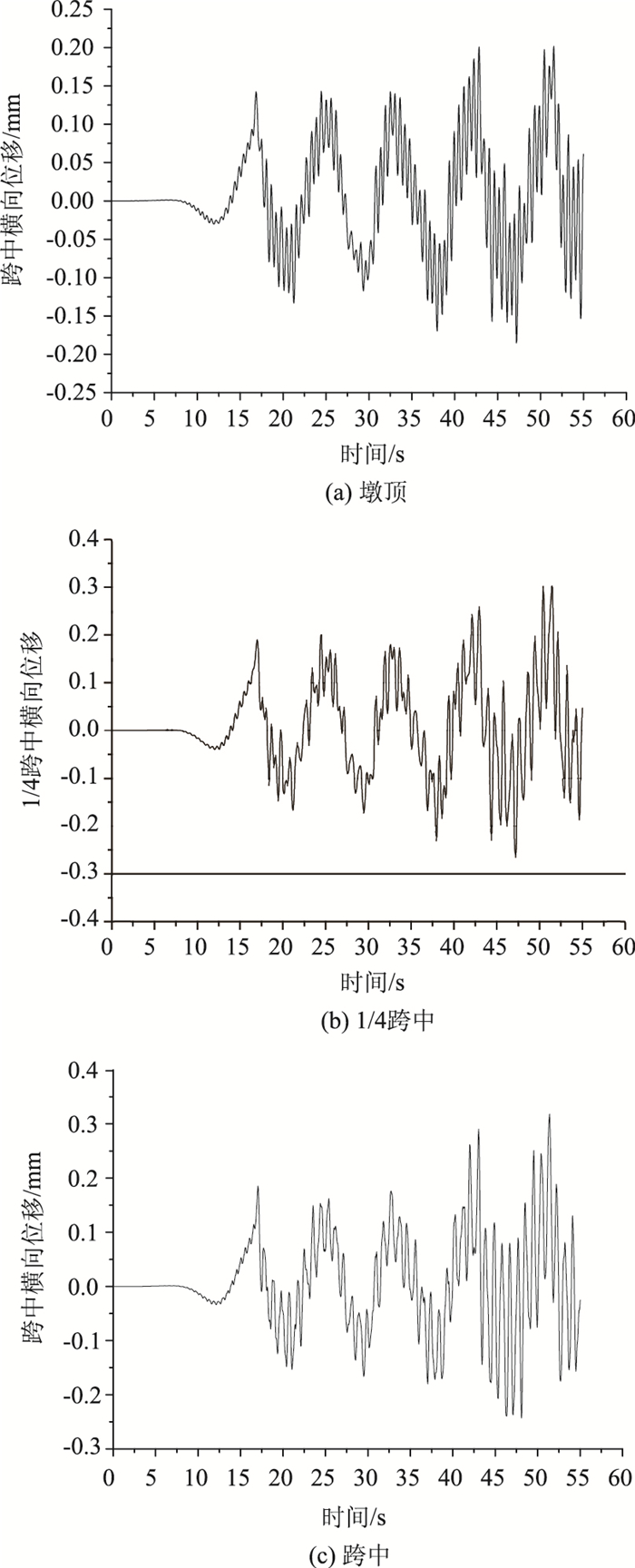
图 10为波浪荷载单独作用时的横向位移时程曲线。
|
| 图 10 波浪荷载单独作用下横向位移时程曲线 Fig. 10 Time-history curves of transverse displacement under wave load alone |
| |
结合图 9~图 10可以看出,波浪荷载单独作用下,墩顶横向位移峰值为0.15~0.2 mm左右,1/4跨中横向位移峰值为0.2~0.3 mm左右,跨中横向位移峰值为0.18~0.3左右;风浪荷载共同作用与风荷载单独作用时相比,墩顶横向位移和跨中横向位移最大增幅均为0.1 mm左右,位移增幅均小于波浪荷载单独作用时的最大位移增幅。由此表明,风浪荷载共同作用并不是风、浪荷载单独作用下响应的简单叠加。
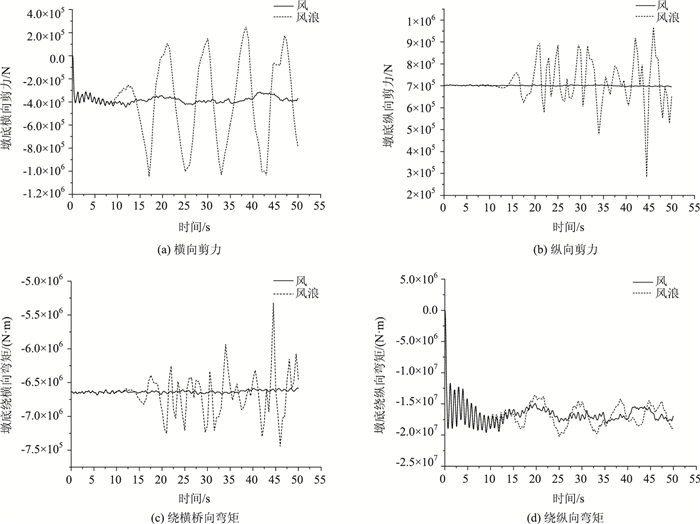
图 11为风荷载和风浪荷载作用下,墩底剪力和弯矩响应的时程曲线。
|
| 图 11 墩底内力时程曲线 Fig. 11 Time-history curves of internal force at pier bottom |
| |
从图 11可以看出,与风荷载单独作用时相比,墩底横向剪力幅值增加了600 kN左右,墩底纵桥向剪力幅值增加了260 kN左右,墩底绕横桥向弯矩增加了500 kN·m左右,墩底绕纵向弯矩增加了2 500 kN·m左右;墩底横向剪力相对增幅为150%左右,墩底纵桥向剪力相对增幅为37%左右,墩底绕横桥向弯矩相对增幅为7%左右,墩底绕纵桥向弯矩相对增幅为14%左右。由此表明,波浪荷载作用对墩底横向剪力、墩底纵向剪力增幅影响很大,对墩底绕横桥向弯矩、墩底绕纵桥向弯矩影响也较大;波浪荷载作用对横向剪力、纵向剪力、横向弯矩与纵向弯矩时程曲线的影响皆很明显,其振动幅度明显增大。
5 结论(1) 从横向位移响应时程曲线可以看出,距离桥墩由远到近的几个典型截面,横向位移绝对增大分别为0.1,0.17,0.1 mm,相对增大幅度分别为2%,4%,7%,虽然位移增大的绝对值不明显,但相对增大幅度却逐渐增大,说明距离桥墩越远,波浪对结构的横向位移响应影响越小。
(2) 与风、浪荷载分别单独作用时的位移响应相比,风浪荷载共同作用并不是风、浪荷载单独作用下响应的简单叠加。风浪荷载共同作用时,整体位移响应均受到风荷载和波浪荷载作用的影响,但对横向位移响应影响较大的主要作用为风荷载作用,但并不意味着可以忽略波浪荷载的作用。
波浪荷载作用对墩底横向剪力、墩底纵向剪力增幅影响很大,而对墩底绕横桥向弯矩和绕纵桥向弯矩的增幅影响也较大。波浪荷载作用对墩底横向剪力、纵向剪力、绕横桥向弯矩与绕纵桥向弯矩时程曲线的影响皆很明显,其振动幅度明显增大,在桥梁设计时应予以重视。
| [1] |
GUO A, LIU J, CHEN W, et al. Experimental Study on the Dynamic Responses of a Freestanding Bridge Tower Subjected to Coupled Actions of Wind and Wave Loads[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 159: 36-47. |
| [2] |
AIJAZ S, ROGERS W E, BABANIN A V. Wave Spectral Response to Sudden Changes in Wind Direction in Finite-depth Waters[J]. Ocean Modelling, 2016, 103: 98-117. |
| [3] |
涂志斌, 黄铭枫, 楼文娟. 风浪耦合作用下桥塔-基础体系的极限荷载效应[J]. 浙江大学学报:工学版, 2016, 50(5): 813-821. TU Zhi-bin, HUANG Ming-feng, LOU Wen-juan. Extreme Load Effects on Bridge Tower-basement System due to Joint Actions of Wind and Wave[J]. Journal of Zhejiang University:Engineering Science Edition, 2016, 50(5): 813-821. |
| [4] |
李伦, 吴雄斌, 徐兴安, 等. 高频地波雷达风速反演经验模型[J]. 武汉大学学报:信息科学版, 2012, 37(9): 1096-1099. LI Lun, WU Xiong-bin, XU Xing-an, et al. An Empirical Model for Wind Speed Inversion by HFSWR[J]. Geomatics and Information Science of Wuhan University, 2012, 37(9): 1096-1099. |
| [5] |
王树青, 梁丙臣. 海洋工程波浪力学[M]. 青岛: 中国海洋大学出版社, 2013. WANG Shu-qing, LIANG Bing-chen. Wave Mechanics of Ocean Engineering[M]. Qingdao: China Ocean University Press, 2013. |
| [6] |
张宪堂, 高康宁. 桥梁上部结构风浪流荷载效应分析与设计方法[M]. 北京: 人民交通出版社, 2013. ZHANG Xian-tang, GAO Kang-ning. Analysis and Design Method of Wind Wave Current Load Effect on Bridge Superstructure[M]. Beijing: China Communications Press, 2013. |
| [7] |
沙文钰, 潘玉萍, 葛苏放, 等. 海面粗糙度方案的适用性研究[J]. 海洋学报, 2012, 34(6): 50-58. SHA Wen-yu, PAN Yu-ping, GE Su-fang, et al. Application Studies on Sea Surface Roughness Parameterization Schemes[J]. Acta Oceanologica Sinica, 2012, 34(6): 50-58. |
| [8] |
杨咏昕, 陈艾荣, 项海帆. 桥梁结构动力特性分析中节点刚性区问题的处理[J]. 土木工程学报, 2001, 34(1): 14-28. YANG Yong-xin, CHEN Ai-rong, XIANG Hai-fan. Problems of Nodal Rigid Zone in Modeling Bridge Structures for Dynamic Analysis[J]. China Civil Engineering Journal, 2001, 34(1): 14-28. |
| [9] |
李权. Ansys在土木工程中的应用[M]. 北京: 人民邮电出版社, 2005. LI Quan. Application of Ansys in Civil Engineering[M]. Beijing: Posts and Telecom Press, 2005. |
| [10] |
JTG/T 60-01-2004, 公路桥梁抗风设计规范[S]. JTG/T 60-01-2004, Wind-resistant Design Specification for Highway Bridges[S]. |
| [11] |
SIMIU E, SCANLAN R H. Wind Effects on Structures[J]. Proceedings of the Institution of Mechanical Engineers, 1978, 185(92): 301-317. |
| [12] |
陈政清. 桥梁风工程[M]. 北京: 人民交通出版社, 2005. CHEN Zheng-qing. Bridge Wind Engineering[M]. Beijing: China Communications Press, 2005. |
| [13] |
张婷.波浪的三维数值模拟及其应用[D].天津: 天津大学, 2009. ZHANG Ting. 3D Numerical Simulation of Wave and Its Application[D]. Tianjin: Tianjin University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10056-2010090758.htm |
| [14] |
中国气象局. 地面气象观测规范[M]. 北京: 气象出版社, 2003. China Meteorological Administration. Specifications for Surface Meteorological Observation[M]. Beijing: China Meteorological Press, 2003. |
| [15] |
李培英, 杜军, 刘乐军, 等. 中国海岸带灾害地质特征及评价[M]. 北京: 海洋出版社, 2007. LI Pei-ying, DU Jun, LIU Le-jun, et al. Geological Characteristics and Assessment of Coastal Hazards in China[M]. Beijing: Maritime Press, 2007. |
| [16] |
PHILIPPE M, BABARIT A, FERRANT P. Modes of Response of an Offshore Wind Turbine with Directional Wind and Waves[J]. Renewable Energy, 2013, 49: 151-155. |
| [17] |
杨昀, 周列茅, 周勇军. 弯桥与高墩[M]. 北京: 人民交通出版社, 2011. YANG Yun, ZHOU Lie-mao, ZHOU Yong-jun. Curved Bridge and High Pier[M]. Beijing: China Communications Press, 2011. |
| [18] |
郭辉.大跨连续刚构桥风荷载数值模拟及空间风致响应研究[D].长沙: 中南大学, 2008. GUO Hui. Research on Numerical Simulation of Wind Load and Space Wind-induced Response of Long-span Continuous Rigid Frame Bridge[D]. Changsha: Central South University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10533-2008166555.htm |
 2019, Vol. 36
2019, Vol. 36
