扩展功能
文章信息
- 张劲泉, 左新黛, 赵尚传, 白冰
- ZHANG Jin-quan, ZUO Xin-dai, ZHAO Shang-chuan, BAI Bing
- 公路钢筋混凝土桥梁正常工作年限计算方法及影响因素分析
- A Method for Calculating Normal Working Life of Highway Reinforced Concrete Bridge and Analysis on Its Influencing Factors
- 公路交通科技, 2019, 36(8): 47-58
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(8): 47-58
- 10.3969/j.issn.1002-0268.2019.08.007
-
文章历史
- 收稿日期: 2019-04-20
如同飞机结构的使用寿命有两个评价指标:一是工作使用寿命(疲劳寿命),二是维护使用寿命(耐久寿命)。公路钢筋混凝土桥梁主要功能是承受车辆反复荷载作用,其正常工作年限也应分两种:抵抗准静态作用的静载年限和抵抗车辆反复作用的工作年限,前者主要是考虑静载和耐久性的维护年限,后者主要是考虑车辆反复荷载作用的工作年限。
目前现行的公路桥梁规范[1]中,对静载下结构设计使用年限做出了相应规定。为了确保该设计年限,《混凝土结构耐久性设计规范》(GB/T 50476—2008)中针对不同环境类别和作用等级进行了相应的耐久性设计规定。而对于车辆反复荷载下的工作年限,规范中并无相应的规定,无法判断是否满足设计年限的要求。
本研究以公路钢筋混凝土桥梁的正常工作年限为研究对象,介绍了该年限的内涵及相关计算理论,提出了一种公路钢筋混凝土桥梁工作年限的计算方法,并应用此方法于典型桥梁的计算,分析跨径、横隔板、配筋率、车辆荷载、S-N曲线方程等因素对工作年限的影响。最终得到了目前通用图设计下T梁桥的工作年限情况和影响因素,可为今后相关标准规范对公路钢筋混凝土桥梁正常工作年限要求提供设计依据或验算支撑。
1 正常工作年限的内涵正常工作年限是指结构正常承受各种设计荷载作用而不用进行结构性大修的时间期限[1]。
分为考虑耐久性的静载年限和考虑车辆反复荷载的工作年限,前者通常指在不同环境类别和作用等级下,承载力和耐久性满足最低可接受目标可靠指标,且变形和裂缝不超过正常使用极限状态和耐久极限状态,在文献[1]中有相应的年限规定(如表 1所示);后者通常指的是结构构件在车辆荷载反复作用下,由于累积损伤引起的疲劳性能不超过稳定发展期(即发生疲劳破坏)。
| 公路等级 | 主体结构 | 可更换部件 | ||||
| 特大桥大桥 | 中桥 | 小桥涵洞 | 斜拉索吊索系杆等 | 栏杆伸缩缝支座等 | ||
| 高速公路/一级公路 | 100 | 100 | 50 | 20 | 15 | |
| 二级公路/三级公路 | 100 | 50 | 30 | |||
| 四级公路 | 100 | 50 | 30 | |||
针对规范尚未提及的工作年限,由于钢筋混凝土梁允许带裂缝工作,跨径相对小,活恒载比相对较大,累积损伤引起的疲劳问题明显,需要判断其车辆荷载下的工作年限是否满足表 1规定的设计使用年限要求。钢筋混凝土梁有两种疲劳破坏模式,一是混凝土疲劳破坏,二是钢筋疲劳破坏。对这种复合材料构件,要摸清哪种材料占疲劳破坏的主导因素。根据文献[2],对公路钢筋混凝土受弯梁在重复荷载作用下,适筋梁的疲劳破坏模式主要为钢筋的疲劳破坏,这个结论也可以从国内外构件疲劳试验中得到验证。由此,我们可以将钢筋混凝土梁的工作年限问题转换为纵向受拉钢筋的疲劳年限问题。
2 计算方法理论 2.1 累积损伤计算针对车辆反复荷载下的工作年限,目前常用的评估方法有基于名义应力、断裂力学和损伤力学的寿命预测法等。对钢筋混凝土构件,以第1种方法应用最广泛,该方法以材料的名义应力为累积损伤指标,通过试验回归和统计分析得到材料的名义应力与作用次数的关系,以此预测构件的工作年限。
由于实际作用桥梁的车辆荷载通常是变幅荷载或随机荷载,在累积损伤计算时通常使用等效等幅应力幅法进行简化,根据损伤度相等原则,推导出等效等幅应力幅Δσe(累积损伤)的计算公式。目前有以下两种常见的累积损伤准则计算方法:
(1) 基于Miner累积损伤准则[3]
每种车辆通过桥梁结构时,实测或计算得到车辆应力历程曲线,控制截面受拉钢筋的应力经历多次循环,可经雨流法分析,得到大小不等的各级应力幅Δσi和其作用次数ni,用Miner线性累积损伤准则,换算为等效等幅应力幅。
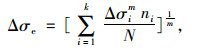
|
(1) |
式中, Δσe为材料在相应的变幅重复应力作用下的等效等幅应力幅; m为疲劳强度指数(S-N曲线的斜率); N为设计寿命期内的次数。
(2) 基于Corten-Dolan累积损伤准则[4]
Corten-Dolan累积损伤准则充分考虑了加载顺序和非线性的影响,较Miner准则计算更精确,等效等幅应力幅表达式为:

|
(2) |
式中, Δσe为将多级变幅或随机荷载等效的等幅重复应力幅;m和k为S-N曲线函数的系数;Nl为在最大交变应力作用下直到破坏的循环数;Mi为第i级荷载水平下对应的弯矩值;Ml为最大交变应力作用下对应的弯矩值; ni为第i级荷载水平下循环作用次数;d为由试验确定的常数,一般由二级变幅疲劳试验得出。由于该方法主要参数需要根据试验结果来确定,在进行寿命计算时比较困难,通常情况下应用Miner累积损伤准则较多。
2.2 累积损伤与作用次数的关系在计算钢筋混凝土梁的工作年限时,最直接的方式是获取累积损伤与作用次数关系,目前以S-N曲线最为普遍。由第1节分析可知,对于适筋梁,S可以取普通钢筋的名义应力,所以钢筋混凝土梁的S-N曲线方程可直接采用纵向受拉钢筋S-N曲线方程。其双对数坐标的表达式一般为:
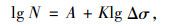
|
(3) |
式中,N为疲劳破坏时的循环次数;A为S-N曲线的截距;K为曲线斜率;Δσ为常幅疲劳试验下的钢筋应力幅。A, K系数的影响因素主要为钢筋种类、连接形式、钢筋弯度及腐蚀程度。
根据国外规范,钢筋混凝土梁采用循环次数为200万次或500万次的应力幅作为常幅疲劳极限。也有试验表明在低应力幅下,有些钢筋混凝土梁构件的循环次数在107和108之间会发生疲劳破坏,所以常采用钢筋疲劳S-N曲线不设截止线,而是在循环次数大于107后将曲线斜率在原有基础上加2。下面列出一些国家规范中规定的钢筋S-N曲线方程:
ECCS[5]欧洲钢结构协会中变形钢筋的S-N曲线方程(97.7%保证率):
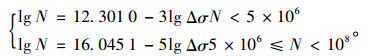
|
(4) |
JSCE代表日本土木工程师学会对变形钢筋的S-N曲线方程[5](97.7%保证率):
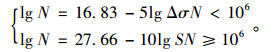
|
(5) |
我国铁路规范[6]对高强钢筋的S-N曲线方程(97.7%保证率):
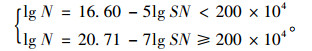
|
(6) |
以上列出的是钢筋S-N曲线,根据文献[7],基于国内较权威的疲劳试验研究成果, 对寿命预测采用如下的钢筋S-N曲线方程, 这些方程均取97.7%的保证率。
(1) 对于跨度10 m及以下的钢筋混凝土梁, 一般不需考虑主筋焊接问题, 可采用式(7)作为疲劳寿命预测计算的S-N曲线:
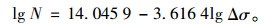
|
(7) |
(2) 对于跨度10 m以上的钢筋混凝土梁, 一般考虑主筋焊接问题, 采用式(8):
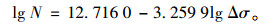
|
(8) |
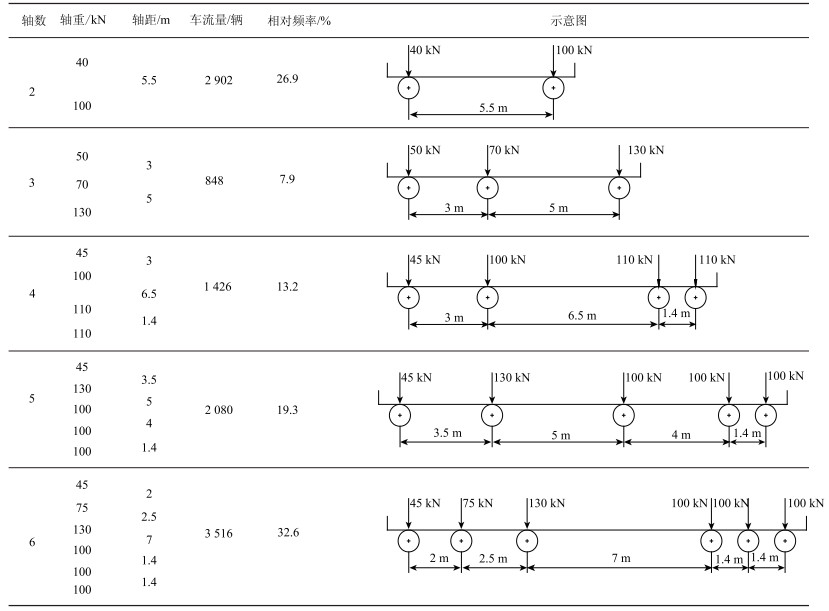
用于工作年限计算的车辆荷载模型,通常采用3种形式[8]:
(1) 车辆荷载频谱,通过公路桥梁交通调查出各种典型车辆的轴重及出现的相对频率;
(2) 标准疲劳车,通过第1种形式简化而来,通过累计损伤等效原则,将荷载谱简化成一种或几种疲劳车来代表;
(3) 静载设计时标准活载中的一辆重车。
很多国家根据本国的交通特点,在规范中制定了相应的标准疲劳车, 见表 2。英国BS5400规范[9]以4A-H为基础制定了一辆虚拟“标准疲劳车”来表示典型车辆荷载谱效应,其为一辆总重320 kN的4轴单车模型;美国AASHTO规范[10]采用3轴325 kN标疲车代表美国道路运营货车对桥梁产生的疲劳损伤;Eurocode1[11]共给出了5种疲劳荷载模型,模型1,2适用于钢桥,模型3,4,5适用于混凝土桥,其中模型3为4轴480 kN标疲车,模型4为5辆车组成的荷载谱。
| 规范名称 | 疲劳荷载谱 | 标准疲劳车 | |
| 总重(kN)和轴数 | 标准疲劳车示意图 | ||
| BS5400 | 建议25种运营车的形式,并分为重载、中载、轻载3种形式 | 320(4轴) |  |
| Eurocode | 采用5种标准货车来反映各典型交通 | 480(4轴) |  |
| AASHTO | 仅提供了一种疲劳车模型进行通用计算 | 325(3轴) |  |
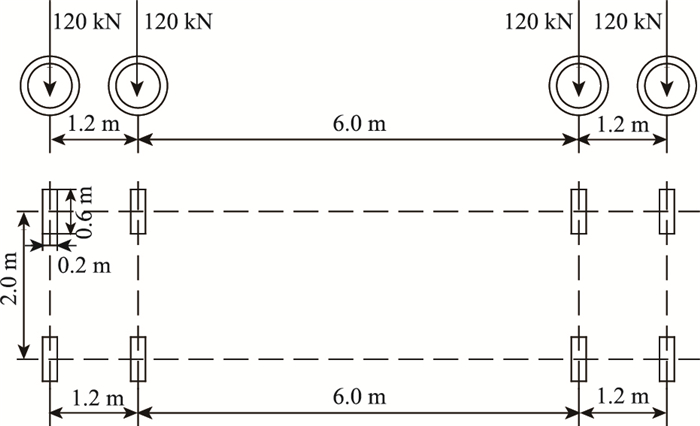
我国公路桥梁的疲劳荷载谱研究起步较晚,文献[1]中提出了3种形式的疲劳车辆荷载:计算模型Ⅰ采用等效的车道荷载,集中荷载为0.7Pk, 均布荷载为0.3qk, Pk和qk按公路1级车道荷载标准取值,模型Ⅰ对应无限寿命设计;计算模型Ⅱ采用双车模型;计算模型Ⅲ采用单车模型(如图 1所示),模型Ⅲ采用了Eurocode1中的模型3,轴重、间距相同。这与公路钢结构桥梁设计规范(JTG D64—2015)中的疲劳车辆荷载完全相同,但文献[1]中未提及荷载作用次数相关规定以及损伤等效系数的计算方法。
目前我国桥梁设计者在选用疲劳车作疲劳设计时, 大部分都是参照国外规范或钢桥规范进行的。由于钢桥的疲劳参数与混凝土桥梁不一致,而国外规定的疲劳车荷载模型是根据其国家的交通特点,直接照搬使用不能真实代表我国公路混凝土桥梁的疲劳车辆特点。国内有部分学者[12-15]认识到这个问题,通过调查个别高速公路或典型桥梁的交通荷载,建立了具有区域特点的荷载谱或标准疲劳车。
3 正常工作年限计算方法在计算工作年限时,一般计算流程为选取车辆荷载模型-累积损伤计算-通过累积损伤与年限的关系得到工作年限,年限计算方法流程如图 2所示,具体步骤如下:
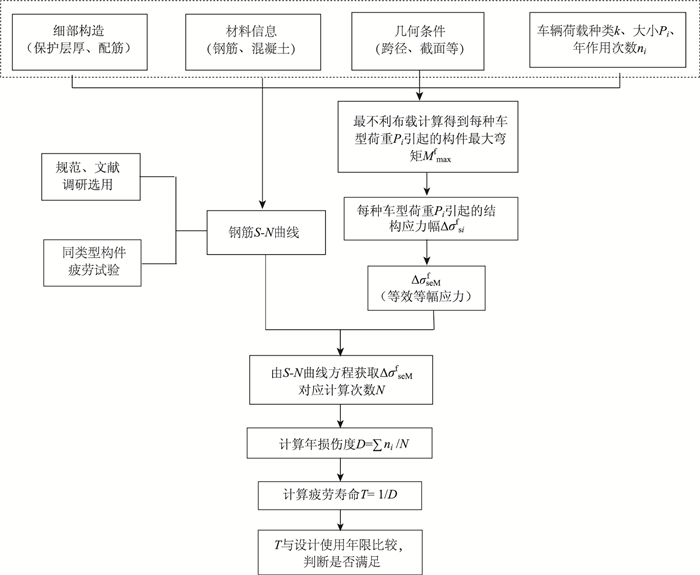
|
| 图 2 正常工作年限计算方法流程 Fig. 2 Flowchart of Calculating normal working life |
| |
(1) 假定构件的材料、细部构造、跨径、截面等设计参数已知,荷载信息可根据桥梁车辆调查,统计出车辆种类k、每类车荷载Pi(轴重及轴距)及其年交通量ni,也可根据桥址环境,直接选用已有的调查荷载。
(2) 通过有限元软件或解析算法进行车辆荷载的纵向最不利布载,即可提取在各个Pi下构件的最大弯矩值Mmaxf和恒载作用下的最小弯矩值Mminf。
(3) 将构件最不利受力截面换算成疲劳验算的换算截面后,即可得到受拉钢筋的应力幅Δσsif。通过基于Miner准则的等效等幅应力幅公式,计算得到等效等幅应力ΔσseMf。
(4) 通过国内外资料选用S-N曲线函数,也可以直接由同类型构件疲劳试验得到更为精确。将ΔσseMf代入S-N曲线函数,得到荷载作用次数的计算值N。
(5) 由各种车辆荷载统计的年均交通总量
以10 m跨钢筋混凝土T梁[16]为例(见图 3),在以文献[17]调查的车辆荷载模型下进行使用年限计算说明。

|
| 图 3 10 m跨径桥梁断面布置示意图(单位:cm) Fig. 3 Layout of section of 10 m span bridge(unit:cm) |
| |
4.1 计算模型
采用Midas建立10 m T梁梁格模型(见图 4),混凝土容重按26 kN/m3取值,计算得到二期恒载重量8.7 kN/m。10 m T梁:钢筋1#、2#ϕ32 mm,3#、4#ϕ28 mm,5#ϕ22 mm,6#ϕ8 mm,均为Ⅱ级纵向钢筋, T梁横截面图见图 5。
|
| 图 4 10 m跨T梁梁格计算模型 Fig. 4 T-beam calculation model of 10 m span |
| |
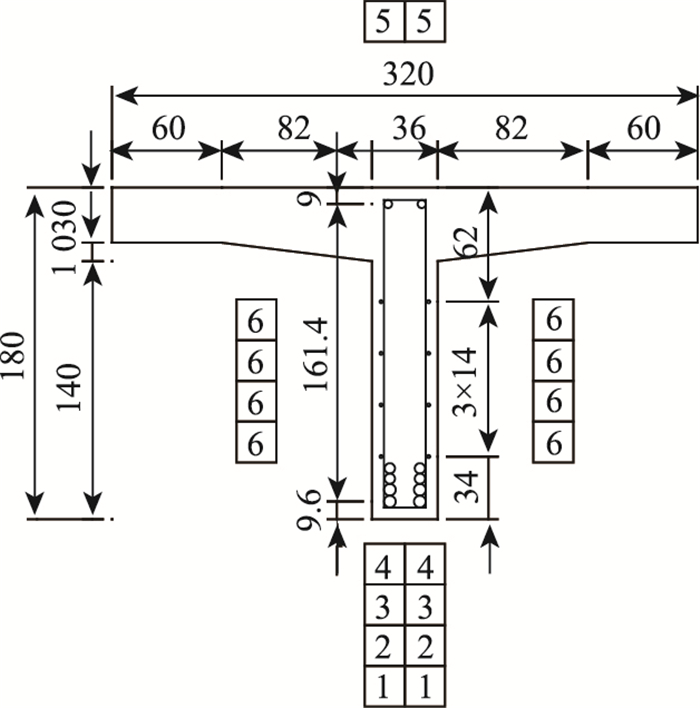
|
| 图 5 10 m跨跨中截面配筋图(单位:cm) Fig. 5 Reinforcement diagram of mid-span section of 10 m span(unit:cm) |
| |
本算例采用的车辆荷载为贵州地区调查的某高速车辆荷载模型[17],荷载形式如表 3~表 4所示。
| 车重范围/t | 1~3 | 3~5 | 5~7 | 7~9 |
| 车辆数/辆 | 1 029 737 | 598 606 | 443 794 | 364 043 |
| 车重范围/t | 15~20 | 20~25 | 25~35 | 35~45 |
| 车辆数/辆 | 447 078 | 310 562 | 365 919 | 176 861 |
4.2 计算过程
(1) 选取车辆荷载模型,提取各典型车辆下最大弯矩Mmaxf
仅考虑30 kN以上车辆,共有6种车辆类型(车重Pi、次数ni),分别进行纵向最不利布载,经计算,对10 m T梁最大弯矩发生在边梁跨中部位, 计算得到如表 5所示的各车辆类型下的最大弯矩。
| 桥梁跨径 | 车型 | 最大弯矩值/(kN·m) | 单车总重/kN |
| 10 m | 恒载 | 252.9 | 0 |
| 客3 | 297.2 | 90.98 | |
| 客4 | 307.0 | 115.0 | |
| 2轴货车 | 358.2 | 151.1 | |
| 3轴货车 | 438.5 | 350.4 | |
| 4轴货车 | 564.4 | 586.8 | |
| 5轴货车 | 450.2 | 509.9 |
(2) 计算各典型车辆下的受拉钢筋应力幅Δσsif
根据混凝土结构设计规范(GB500010—2010),疲劳验算时需换算截面,要求由拉区、压区到中性轴的面积距相等,且假设拉区混凝土由于开裂而完全退出工作,计算得到10 m T梁换算截面的受压区高度x0=163.4 mm、惯性矩I0f=1.91×1010mm4。计算最底层受拉纵向钢筋的应力幅,公式见式(9)~(10):

|
(9) |
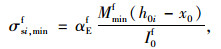
|
(10) |
式中,αEf为钢筋与混凝土弹模比;h0i为最底层的钢筋到截面上缘的距离;x0为受压区高度。
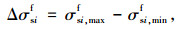
|
(11) |
式中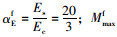
| 典型车辆类型 | 应力幅Δσsif/MPa |
| 客3 | 10.65 |
| 客4 | 13.01 |
| 2轴货车 | 25.32 |
| 3轴货车 | 44.63 |
| 4轴货车 | 74.90 |
| 5轴货车 | 47.44 |
(3) 计算等效等幅应力幅ΔσseMf
基于Miner线性累积损伤准则,换算为几种车辆类型通过桥梁时的等效等幅应力幅ΔσseMf:
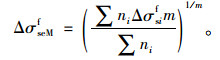
|
(12) |
选用式(8)的S-N曲线方程,m=3.259 9,ni为各车型年车流量实测值(表 4),得到ΔσseMf=34.46 MPa。
(4) 计算工作年限Y
根据选用的S-N曲线,代入ΔσseMf,得到计算车辆作用次数N=506 225 63,∑ni=1 326 222,再根据年损伤度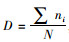
应用上述方法,以钢筋混凝土T梁为研究对象,分析跨径、横隔板、配筋率、车辆荷载、S-N曲线方程的选用这几种因素对其工作年限的影响。
5.1 变化参数(1) 跨径
变化参数:10,13,16,20 m,设计参数均按文献[16]建模。
(2) 横向联系
4种跨径下考虑原设计有横隔板情况和无横隔板情况,其他参数不变。
(3) 配筋率
4种跨径下在原设计配筋率基础上,分别去掉1排、2排纵向受拉钢筋,表 7给出了几种情况受拉钢筋配筋率。
| 路径/m | 10 | 13 | 16 | 20 |
| 少2排 | 1.99% | 2.44% | 2.06% | 2.98% |
| 少1排 | 2.75% | 3.06% | 2.75% | 3.57% |
| 原设计 | 3.51% | 3.68% | 3.44% | 4.17% |
| 注:受拉钢筋配筋率按照混凝土设计规范(GB50010—2010),即按全截面面积扣除受压翼缘面积后的截面面积计算。 | ||||
(4) 车辆荷载
分别考虑以下4种车辆荷载对比计算:
模型1:文献[1]中疲劳车辆荷载模型Ⅲ,为一辆480 kN 4轴标疲车(图 1),暂按寿命期内(30 a)作用次数500万次计。
(5) S-N曲线方程
分别用文献[7]总结的钢筋混凝土构件的S-N曲线方程(式8)、ECCS欧洲钢结构协会对变形钢筋的S-N曲线方程(式4第1个方程)、JSCE日本土木工程师学会(式5第1个方程)、我国铁路规范(式6第1个方程)进行年限计算。
5.2 计算结果(1) 换算截面参数
计算疲劳验算时的换算截面受压区高度x0和惯性矩I0f(表 10)。由于边梁横向分布系数最大,在此仅列出边梁换算截面参数。需要注意,在配筋率变化情况下,x0和I0f也相应变化。
| 桥梁跨径/m | 截面受压区高度/mm | 换算截面惯性矩/(×1010 mm4) |
| 10 | 163.4 | 1.91 |
| 13 | 207.9 | 3.64 |
| 16 | 247.3 | 5.79 |
| 20 | 328.7 | 10.10 |
(2) 等效等幅应力幅
由于篇幅有限,在此仅列出原设计在4种荷载下的等效等幅应力幅,如表 11所示。
| S-N | 荷载 | 等效等幅应力幅ΔσseMf/MPa | |||
| 10 m | 13 m | 16 m | 20 m | ||
| 构件 | 荷载1 | 43.02 | 42.90 | 42.09 | 41.41 |
| 荷载2 | 34.46 | 32.23 | 30.01 | 27.14 | |
| 荷载3 | 47.91 | 45.00 | 42.54 | 37.86 | |
| 荷载4 | 41.15 | 38.63 | 36.74 | 34.47 | |
| 欧洲 | 荷载1 | 43.02 | 42.90 | 42.09 | 41.41 |
| 荷载2 | 33.42 | 31.30 | 29.15 | 26.33 | |
| 荷载3 | 47.17 | 44.39 | 42.01 | 37.40 | |
| 荷载4 | 40.79 | 38.31 | 36.45 | 34.19 | |
| 日本/我国铁路 | 荷载1 | 43.02 | 42.90 | 42.09 | 41.41 |
| 荷载2 | 40.77 | 37.72 | 35.12 | 31.83 | |
| 荷载3 | 52.00 | 48.29 | 45.31 | 40.21 | |
| 荷载4 | 43.10 | 40.31 | 38.25 | 35.93 | |
(3) S-N曲线方程的选用
可以看出,文献[7]中钢筋混凝土构件的S-N曲线方程(式8)与ECCS欧洲钢结构协会的第1个方程系数相近,日本土木工程师学会和我国铁路规范系数相近。
(4) 计算年限
荷载1仅为1辆重车,纵向最不利布载得到的应力幅即为等效等幅应力,荷载作用次数暂按寿命期30年内500万次计,即年均作用次数166 667次。对4种荷载类型下,不同跨径T梁应用不同S-N曲线方程进行工作年限计算,计算结果如表 12所示。
| S-N曲线 | 车型 | 疲劳寿命/a | |||
| 10 m | 13 m | 16 m | 20 m | ||
| 构件 | 荷载1 | 147.4 | 148.8 | 158.4 | 167.0 |
| 荷载2 | 38.2 | 47.5 | 59.9 | 83.2 | |
| 荷载3 | 2.4 | 2.9 | 3.5 | 5.1 | |
| 荷载4 | 7.2 | 8.9 | 10.4 | 12.9 | |
| 欧洲 | 荷载1 | 150.7 | 152.0 | 161.0 | 169.0 |
| 荷载2 | 40.4 | 49.2 | 60.9 | 82.6 | |
| 荷载3 | 2.6 | 3.1 | 3.7 | 5.2 | |
| 荷载4 | 7.5 | 9.0 | 10.5 | 12.7 | |
| 日本 | 荷载1 | 2 753.6 | 2 791.8 | 3 072.7 | 3 332.9 |
| 荷载2 | 452.7 | 667.4 | 954.6 | 1 559.3 | |
| 荷载3 | 24.3 | 35.1 | 48.3 | 87.7 | |
| 荷载4 | 115.6 | 161.5 | 210.0 | 287.1 | |
| 我国铁路 | 荷载1 | 1 621.4 | 1 643.9 | 1 809.3 | 1 962.6 |
| 荷载2 | 266.6 | 393.0 | 562.1 | 918.2 | |
| 荷载3 | 14.3 | 20.7 | 28.4 | 51.6 | |
| 荷载4 | 68.0 | 95.1 | 123.6 | 169.0 | |
5.3 影响因素分析
(1) 跨径的影响
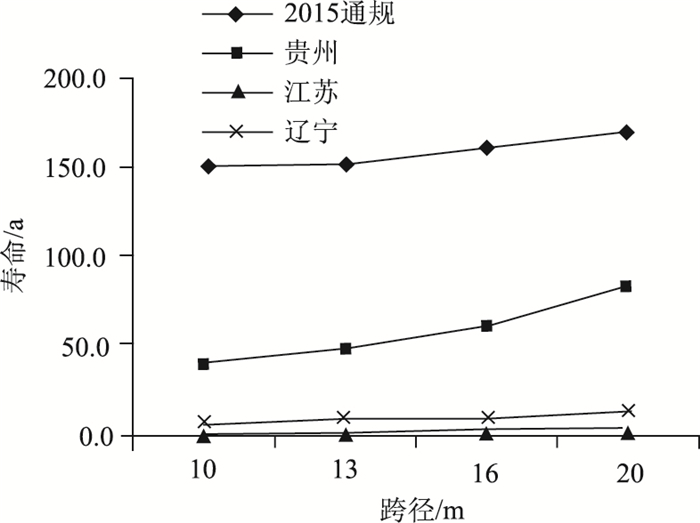
从表 12可看出,随着跨径的增大,T梁桥的工作年限相应增大,增长率随着跨径的增大而变大。以荷载2、欧洲规范S-N曲线为例(图 6),10~13 m之间,跨径每增加1 m,年限增大2.9 a;13~16 m之间,跨径每增加1 m,年限增大3.9 a;16~20 m之间,跨径每增加1 m,年限增大5.4 a。当然,年限随跨径的增长率与荷载、选用的S-N曲线都有关,但总体增长趋势相同。这里需要说明的是,年限与跨径的关系,不能仅仅由跨径单一因素决定,从表 7可知,跨径增大配筋率增大,所以工作年限随跨径的增大与配筋率也有关。
|
| 图 6 不同跨径不同荷载T梁计算年限对比图(欧洲规范) Fig. 6 Comparison of calculation lives of T-beams with different spans and loads (European specification) |
| |
(2) 不同地区荷载的影响
从表 12可以看出,车辆荷载对T梁计算年限影响很大。仍以采用欧洲规范S-N曲线为例,在2015年规范疲劳车辆荷载Ⅲ下,各种跨径T梁的计算年限远大于按高速公路要求的设计使用年限,说明T梁桥设计满足规范中的疲劳车辆荷载作用下的年限要求;在贵州地区典型高速车辆荷载下,仅16 m跨径能满足50 a要求,其余跨径仅满足二级公路设计年限要求;江苏和辽宁的典型高速/桥梁的车辆荷载下,最大计算年限12.7 a,均不满足规范要求。需要说明的是,车辆荷载2,3,4及计算年限仅限于引用文献中的数据,不具有地区普遍性。
为了研究后3种车辆荷载对计算年限的影响,表 13列出了车流量对比图,可以看出,江苏车流年均总量最大、辽宁次之,贵州最小。35~45 t重车,江苏是贵州的20倍,是辽宁的6.5倍。45~55 t重车,江苏是贵州的15倍,是辽宁的1.7倍。55~65 t重车,辽宁是贵州的31倍,是江苏的87倍。由此可知,江苏和辽宁桥梁寿命低,主要是由于35 t以上重车车流量大,对T梁桥工作年限影响很大。
| 车重/t | 贵州 | 江苏 | 辽宁 |
| 9~11 | 309 624 | 0 | 0 |
| 11~14 | 265 995 | 2 610 300 | 1 059 230 |
| 15~20 | 447 078 | 0 | 0 |
| 21~30 | 0 | 0 | 309 520 |
| 35~45 | 176 861 | 3 424 200 | 520 490 |
| 45~55 | 85 381 | 1 283 148 | 759 200 |
| 55~65 | 41 283 | 14 664 | 1 283 340 |
| 年均总量 | 1 326 222 | 7 332 312 | 3 931 780 |
(3) 横隔板的影响
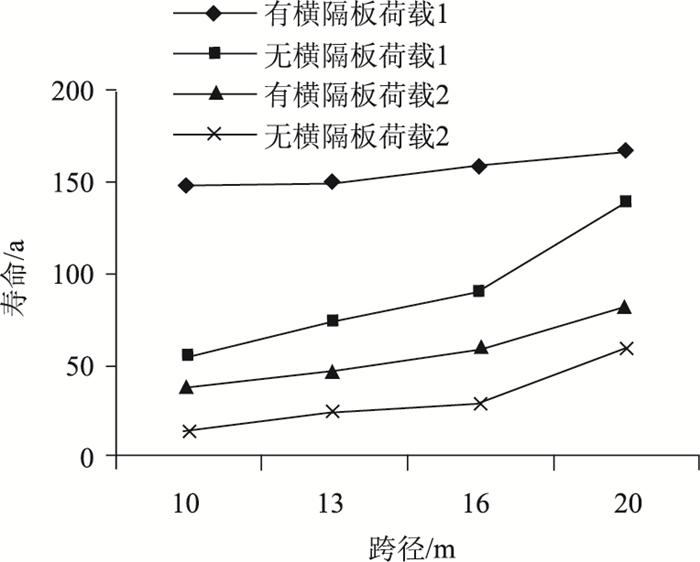
表 14和图 7列出了在规范荷载下和贵州地区荷载下,采用构件的S-N曲线(式8),得到不同跨径T梁桥在有、无横隔板下的计算年限。可以看出,横隔板的设置对T梁桥工作年限影响较大。在规范疲劳荷载下,各种跨径的T梁计算年限仍满足高速公路设计使用年限要求;在贵州地区荷载下,10,13,16,20 m跨径无横隔板工作年限较有横隔板工作年限分别降低了63%,48%,50%,28%,16%,20 m跨径在无横隔板下仍满足二级公路设计使用年限要求,其余跨径不满足年限要求。
| 跨径/m | 10 | 13 | 16 | 20 |
| 有横隔板荷载1 | 147.4 | 148.8 | 158.4 | 167.0 |
| 无横隔板荷载1 | 54.5 | 74.1 | 89.5 | 139.8 |
| 有横隔板荷载2 | 38.2 | 47.5 | 59.9 | 83.2 |
| 无横隔板荷载2 | 14.1 | 24.5 | 30.2 | 59.4 |
|
| 图 7 横隔板对T梁计算年限影响对比 Fig. 7 Comparison of influences of diaphragm on calculated life of T-beam |
| |
(4) 配筋率的影响
前面提到,当配筋率增大到一定程度(如超筋梁),钢筋混凝土梁的破坏形式可能是混凝土的疲劳破坏,就不能用钢筋的S-N曲线进行分析,所以这里没有列出配筋率增大的情况。表 15和图 8列出了贵州地区荷载、采用构件的S-N曲线(式8),不同跨径T梁桥在配筋率减小情况下的计算年限。可以看出,配筋率对T梁年限影响较大,年限随着配筋率的减小而减小。对10 m跨径配筋率减少0.76%,年限分别减少46%,57%;13 m跨径配筋率减少0.62%,年限分别减少38%,46%;16 m跨径配筋率减少0.69%,年限分别减少45%,55%;20 m跨径配筋率减少0.60%,年限分别减少33%,38%。
| 跨径/m | 10 | 13 | 16 | 20 |
| 少2排 | 8.7 | 15.9 | 14.8 | 34.5 |
| 少1排 | 20.4 | 29.4 | 32.9 | 56 |
| 原设计 | 38.2 | 47.5 | 59.9 | 83.2 |

|
| 图 8 不同跨径配筋率对T梁计算年限对比图 Fig. 8 Comparison of calculated lives of T-beams with different spans and reinforcement ratios |
| |
(5) 不同S-N曲线方程对比
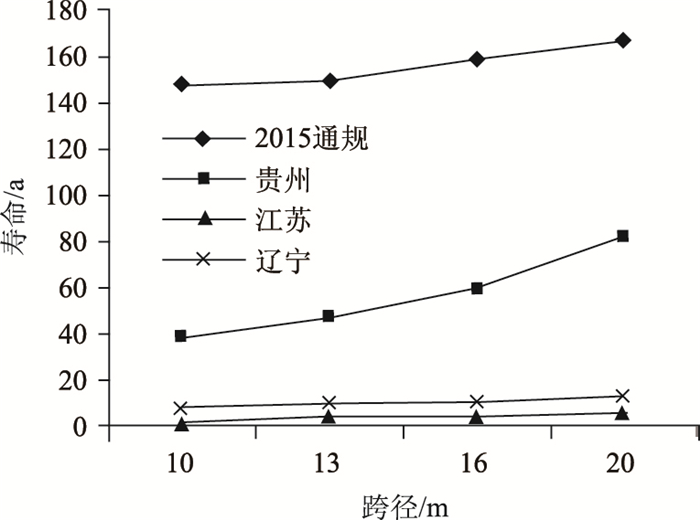
从表 12和图 6、9、10可看出,不同的S-N曲线对计算年限影响非常大。应用文献[7]中的构件S-N曲线和欧洲钢结构协会中的钢筋S-N曲线计算得到的年限相近,应用日本土木工程师学会和我国铁路规范中钢筋S-N曲线计算得到的年限相近,但年限偏大很多,不建议直接应用于钢筋混凝土构件中。在今后计算钢筋混凝土桥梁的工作年限时,推荐采用欧洲钢结构协会中的钢筋S-N曲线方程。
|
| 图 9 不同跨径不同荷载下的T梁计算年限(构件的S-N曲线) Fig. 9 Calculated lives of T-beams with different spans and loads (S-N curves of components) |
| |
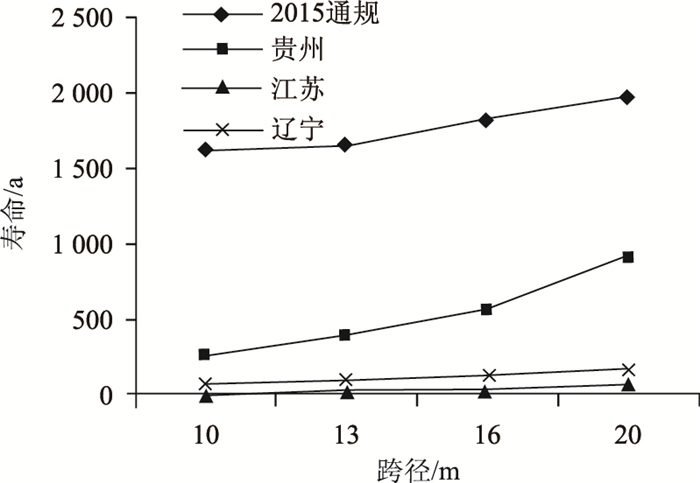
|
| 图 10 不同跨径不同荷载下的T梁计算年限(我国铁路规范中的S-N曲线) Fig. 10 Calculated lives of T-beams with different spans and loads (S-N curves in China railway specification) |
| |
6 结论
(1) 本研究提出了公路桥梁正常工作年限的概念,既包括规范上规定的静载工作年限,又包括车辆反复荷载下的正常工作年限,两者均需满足设计使用年限要求。
(2) 本研究提出了一种快速计算公路钢筋混凝土桥梁工作年限的计算方法,适用于各种形式的钢筋混凝土桥梁。
(3) 桥梁的工作年限与车辆荷载关系很大,在2015年规范疲劳车辆荷载下,T梁桥的工作年限远远满足设计使用年限要求。不同地区调查的车辆荷载差别较大,相比贵州地区,江苏和辽宁地区车辆荷载偏大,尤其是单车重35 t以上的车流量大,导致不满足设计使用年限要求。
(4) 随着跨径的增大,T梁桥工作年限相应增大,这与配筋率随着跨径增大而增大有一定关系。
(5) 横隔板的设置对T梁桥工作年限影响很大,不同跨径T梁桥不设横隔板比设置横隔板的工作年限降低了18%~63%,年限降低程度与荷载、跨径有关,跨径越大年限降低的程度越小。
(6) 钢筋配筋率对T梁工作年限影响较大,各种跨径T梁配筋率减少0.6%~0.7%左右,年限减少33%~57%,配筋率越低,年限减少速率越快。
(7) 车辆荷载和S-N曲线方程的选取对工作寿命计算准确性影响很大。今后在计算工作年限时,建议获取桥址位置附近的车辆荷载数据,并推荐选用欧洲钢结构协会中的变形钢筋的S-N曲线。
| [1] |
JTG D60-2015, 公路桥涵设计通用规范[S]. JTG D60-2015, General Specifications for Design of Highway Bridges and Culverts[S]. |
| [2] |
宋玉普. 混凝土结构的疲劳性能及设计原理[M]. 北京: 机械工业出版社, 2005. SONG Yu-pu. Fatigue Behavior and Design Principle of Concrete Structures[M]. Beijing: China Machine Press, 2005. |
| [3] |
张彦玲, 李运生, 王新敏. 提速后钢筋混凝土梁疲劳寿命估算方法研究[J]. 石家庄铁道学院学报, 2004, 17(2): 54-57. ZHANG Yan-ling, LI Yun-sheng, WANG Xin-min. A Study of the Evaluation Method of Fatigue Life of Reinforced Concrete Beams after Speed-lifting[J]. Journal of Shijiazhuang Tiedao University, 2004, 17(2): 54-57. |
| [4] |
朱红兵, 余志武, 蒋丽忠. 基于Corten-Dolan累积损伤准则的等效等幅疲劳应力幅值计算方法[J]. 公路交通科技, 2010, 27(1): 54-57. ZHU Hong-bing, YU Zhi-wu, JIANG Li-zhong. Calculation Method of Equivalent Constant Amplitude Fatigue Stress Amplitude Based on Corten-Dolan Cumulative Damage Criterion[J]. Highway Traffic Science and Technology, 2010, 27(1): 54-57. |
| [5] |
曾志斌, 李之榕. 普通混凝土梁用钢筋的疲劳S-N曲线研究[J]. 土木工程学报, 1999, 32(5): 10-14. ZENG Zhi-bin, LI Zhi-rong. Research on Fatigue S-N Curves of Reinforcing Bars in Common Reinforced Concrete Beams[J]. China Civil Engineering Journal, 1999, 32(5): 10-14. |
| [6] |
TB 10092-2017, 铁路桥涵混凝土结构设计规范[S]. TB 10092-2017, Code for Design of Concrete Structures of Railway Bridge and Culvert[S]. |
| [7] |
徐学东. 既有铁路混凝土桥梁疲劳寿命预测及可靠性分析[J]. 铁道标准设计, 1996, 14(3): 28-35. XU Xue-dong. Fatigue Life Prediction and Reliability Analysis of Existing Railway Concrete Bridges[J]. Railway Standard Design, 1996, 14(3): 28-35. |
| [8] |
周泳涛, 翟辉, 鲍卫刚. 公路桥梁标准疲劳车辆荷载研究[J]. 公路, 2009(12): 21-25. ZHOU Yong-tao, ZHAI Hui, BAO Wei-gang. Research on Standard Fatigue Vehicular Load for Highway Bridges[J]. Highway, 2009(12): 21-25. |
| [9] |
BS5400, Steel, Concrete and Composite Bridges, Part 10-Code of Practices for Fatigue[S].
|
| [10] |
AASHTO. AASHTO LRFD Bridge Design Specifications (SI Units 4th edition)[S]. Washington, D.C.: AASHTO, 2007.
|
| [11] |
BS EN 1991-2: 2003 Eurocode 1, Actions on Structures. Part 2: Traffic Loads on Bridges[S].
|
| [12] |
童乐为, 沈祖炎. 城市道路桥梁的疲劳荷载谱[J]. 土木工程学报, 1997, 30(5): 20-27. TONG Le-wei, SHEN Zu-yan. Fatigue Load Spectrum for Urban Road Bridges[J]. Journal of Civil Engineering, 1997, 30(5): 20-27. |
| [13] |
王荣辉, 池春. 广州市高架桥疲劳荷载车辆模型研究[J]. 东南理工大学学报:自然科学版, 2004, 32(12): 94-96. WANG Rong-hui, CHI Chun. Study on the Model of the Fatigue-loaded Vehicles in Guangzhou Trestle Bridges[J]. Journal of Southeast University of Science and Technology:Natural Science Edition, 2004, 32(12): 94-96. |
| [14] |
陈敏.公路桥梁疲劳车辆荷载模型研究[R].上海: 同济大学, 2009. CHEN Min. Research on Fatigue Vehicle Load Models of Highway and Bridge[R]. Shanghai: Tongji University, 2009. |
| [15] |
李少骏.中小跨径混凝土桥梁疲劳荷载模型和疲劳性能研究[R].杭州: 浙江大学, 2015. LI Shao-jun. Fatigue Load Model and Fatigue Performance of Medium and Small Span Concrete Bridges[R]. Hangzhou: Zhejiang University, 2015. |
| [16] |
JT-GQS 025-1984, 公路桥涵设计图装配式钢筋混凝土T型梁[S]. JT-GQS 025-1984, Road Bridge and Culvert Design Drawing-Prefabricated Reinforced Concrete T-beams[S]. |
| [17] |
朱宏兵.公路钢筋混凝土简支梁桥疲劳试验与剩余寿命预测方法研究[D].长沙: 中南大学, 2011. ZHU Hong-bing. Research on Fatigue Test and Residual Life Prediction Method of Highway Reinforced Concrete Beam Bridges[D]. Changsha: Central South University, 2011. http://cdmd.cnki.com.cn/article/cdmd-10533-1011177885.htm |
| [18] |
陶然.考虑长期性能退化的混凝土梁桥疲劳寿命研究[R].南京: 东南大学, 2016 TAO Ran. Research on Fatigue Life of Concrete Girder Bridges Considering Long-term Performance Degradation[R]. Nanjing: Southeast University, 2016. |
 2019, Vol. 36
2019, Vol. 36