扩展功能
文章信息
- 蔡俊华
- CAI Jun-hua
- 反复水位作用下的深厚滩涂路基沉降及预测研究
- Study on Settlement and Prediction of Subgrade in Deep Shoal under Repeated Water Level
- 公路交通科技, 2019, 36(8): 37-46
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(8): 37-46
- 10.3969/j.issn.1002-0268.2019.08.006
-
文章历史
- 收稿日期: 2018-06-07
2. 三明市交通建设集团有限公司, 福建 三明 365000
2. Sanming Transport Construction Group Co., Ltd., Sanming Fujian 365000, China
滩涂作为重要的土地后备资源,为沿海地区的发展提供了广阔的土地资源和空间。目前,随着“五纵七横”战略的提出,高速公路不断在我国滩涂地区兴建。由于滩涂地区具有潮涨淹没、潮落露出的特点,路基往往会受到反复涨落水位作用的影响。工程经验表明,在反复水位作用下,深厚滩涂路基将会产生较大的沉降,甚至会引发工程事故。因此研究反复水位作用下深厚滩涂路基的沉降规律及预测方法有着十分重要的意义。
针对反复水位作用下沉降规律的研究,国内外学者已经做了很多的研究。Dong等[1]针对高速铁路桥墩在雨季、旱季桥基的下沉问题,利用ABAQUS软件建立三维有限元模型,讨论了地下水位变化对地基沉降的影响规律,揭示了地应力场和变形场的特征。Roslan[2]等通过CBR试验研究了不同浸水情况下路面填土材料的承载力和沉降变化规律。张英平[3]采用模拟试验,研究了在水位循环升降作用下粉土孔隙水压力、土压力周期性的变化规律及由此产生的变形沉降特性。张文杰[4]利用土-水特征曲线和水渗透性函数对水位上升和下降情况下的非饱和岸坡进行了非稳态渗流分析,研究了负孔隙水压力对非饱和土抗剪强度及岸坡稳定性的贡献,分析了水位升降对非饱和土质岸坡稳定性的影响。何忠明[5]采用有限元软件定量分析了在水位下降过程中的渗流特性,并在此基础上分析了不同路堤填筑形式及不同水位下路堤稳定性系数的变化规律。
针对沉降预测方法的研究,Liu等[6]提出了一种改进的GA-BP神经网络软土地基沉降预测方法,并证明了GA-BP神经网络方法具有精度高、收敛速度快等优点。秦亚琼[7]依据现场实测沉降数据,利用灰色GM(1, 1)模型对荷载稳定时的路基沉降进行预测,取得了较为吻合的结果。张涛[8]根据软土路基沉降特点,采用Weibull模型预测路基沉降的新方法,并验证了该方法的可靠性。秦晓光[9]通过对路基观测数据进行等时距变换,采用灰色理论GM(1, 1)模型、双曲线法、三点法分别对工后沉降进行了预测,并通过对灰色理论预测模型进行精度检验,发现灰色理论预测结果更接近实测值。
虽然反复水位作用下路基沉降与预测方法的研究已经获得较多的成果,但仍存在很多的不确定性,很少有专家针对反复水位作用下的深厚滩涂路基开展数值模拟分析,探究滩涂路基的沉降固结演化规律,并且几乎没有专家学者针对潮涨潮落特殊工况研发沉降预测系统,指导工程实践。本研究结合福建霞浦某路基工程,基于现场工程地质状况,通过数值模拟软件Plaxis2D对反复水位作用下深厚滩涂路基的沉降及预测方法开展研究,并利用GM(1, 1)模型编制一个反复水位作用下深厚滩涂路基沉降预测程序,以实现堆载过程中和反复水位作用下滩涂路基的沉降和固结度的预测。
1 工程地质条件路基工程段位于福建省宁德市霞浦县内,地处福建省东北部,位居台湾海峡西北岸,是我国南北海岸线的中点,北连长江三角洲,南接珠江三角洲,东与台湾岛隔海相望,是连接沿海两大经济发达地区的必经之地。由于地质构造上的原因,流速巨大的河流挟带的大量泥沙在河口三角洲及平原沿海地带不断堆积淤涨,形成了沿海地区大面积的滩涂地段。根据水位监测资料分析,霞浦历年最高潮位5.25 m,最低潮位-4.34 m,多年平均高潮位3.08 m,多年平均低潮位-2.72 m,最大潮差8.38 m。
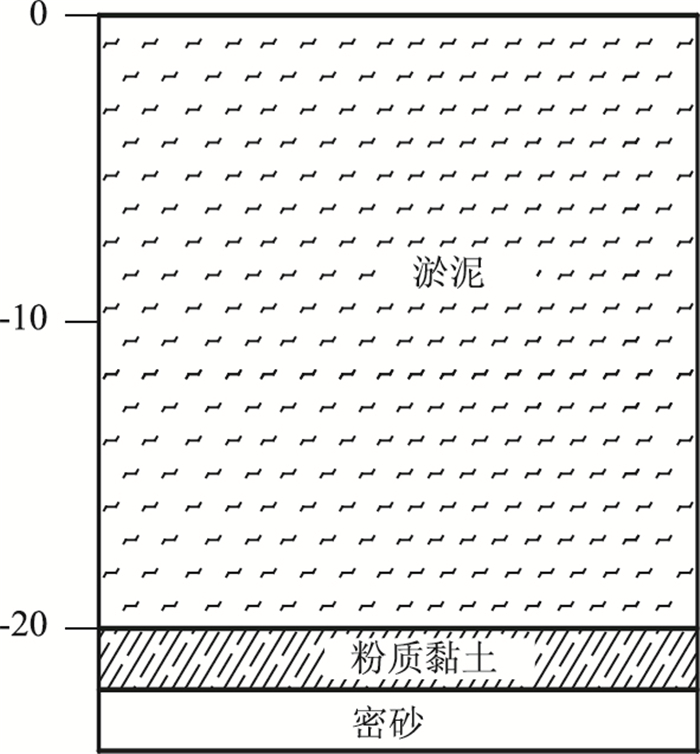
为了开展反复水位作用下深厚滩涂路基的沉降及预测研究,通过钻探取样,发现滩涂地区软基淤泥厚度可达20 m,典型工程地质剖面如图 1所示。针对深厚淤泥开展了一系列的室内试验,获取了相关的物理特性指标,如表 1所示。
|
| 图 1 地质剖面(单位:m) Fig. 1 Geological profile(unit:m) |
| |
| 物理指标 | 含水量/% | 天然密度/(g·cm-3) | 孔隙比 | 液限/% | 塑限/% | 塑性指数 | 液性指数 | 压缩系数/MPa-1 | 压缩模量/MPa | 固结系数/(10-3 cm2·s-1) | 渗透系数/(10-7 cm·s-1) | 无侧限强度/kPa |
| 范围 | 58.7~85.5 | 1.52~1.62 | 1.50~1.75 | 46.1~64.7 | 26.4~31.7 | 14.3~37.3 | 1.35~1.99 | 1.62~2.66 | 1.03~1.53 | 0.73~2.05 | 0.85~2.04 | 8.8~17.9 |
表 1中滩涂区淤泥的液性指数为1.35~1.99,呈流塑状态,土质较软;天然含水量高(58.7%~85.5%),天然孔隙比可达1.50~1.75,压缩系数为1.03~1.53 MPa-1,无侧限强度约为8.8~17.9 kPa,表明土的压缩性大,抗剪切强度低;固结系数为0.73×10-3~2.05×10-3 cm2/s,说明固结所需要时间较长;渗透系数属10-7数量级,渗透系数低,表明滩涂区淤泥固结沉降和强度增长所需时间长[10]。
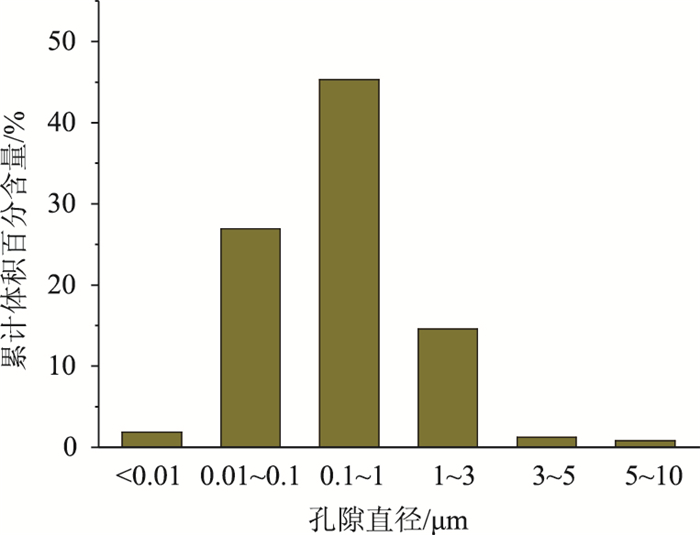
通过压汞试验,不难发现孔隙直径r主要分布在0.01~3 μm之间,孔隙直径在0.1~1 μm范围内分布最多,且孔隙直径在0.1~3 μm之间的孔隙含量占70%以上,如图 5所示。根据微观孔隙分类原则,当孔隙直径r>2 μm,为大孔隙土;当孔隙直径0.2 μm < r < 2 μm,为中等孔隙的土;当孔隙直径0.02 μm < r < 0.2 μm,为亚孔隙土;当孔隙直径r < 0.02 μm,为微孔隙土,显然滩涂淤泥为中等孔隙或者大孔隙土。
|
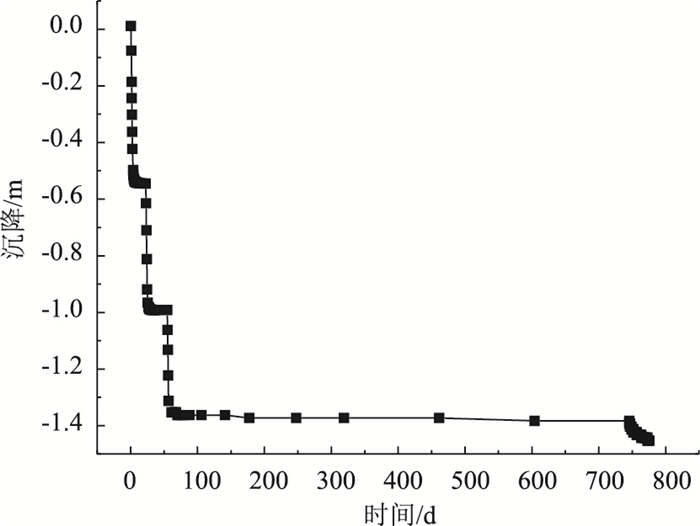
| 图 5 沉降-时间曲线 Fig. 5 Settlement-time curve |
| |
图 2为不同孔径下累计体积的百分含量。
|
| 图 2 不同孔径下累计体积百分含量 Fig. 2 Cumulative volume percentage at different pore sizes |
| |
2 数值模拟及结果分析 2.1 模型建立及模型参数
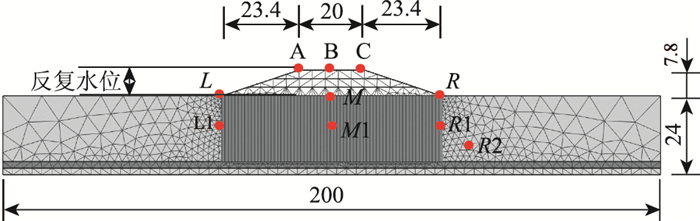
采用有限元数值软件Plaxis2D对本工程典型断面的沉降进行模拟分析[11]。路面宽度约为20 m,路基坡度为1:3。其中在深厚滩涂淤泥地段(淤泥厚度约为20 m),采用堆载预压的地基处理方法加固软土地基,排水板的间距为1 m,排水板插入深度20 m,路基填筑高度约7.8 m,分3次堆填,模型建立如图 3所示。
|
| 图 3 土体模型(单位:m) Fig. 3 Soil model(unit: m) |
| |
地基尺寸为200 m×24 m,选择平面应变模型,单元选取15个节点,网格划分的疏密程度设置为中等,共2 966单元,23 997个节点。针对淤泥、密砂和路堤填土均采用土体硬化模型,该模型可以模拟土体在主压缩条件下的不可逆压缩变形,可以考虑土体刚度的应力相关性,属于二阶双曲线弹塑性本构模型。针对粉质黏土采用软土模型,即剑桥模型(Cam-clay),可以模拟土体在主压缩条件下的不可逆压缩变形。
土体参数如表 2所示。结合室内三轴试验和现场勘查的试验结果,模型左右两侧及底部边界条件均设置为透水边界。计算时考虑土体的初始条件,设定初始应力系数k0=0.5,用来生成初始水平应力。采用的施工步为:(1)初始地应力平衡;(2)填筑第1层(2 d);(3)第1阶段固结(20 d);(4)填筑第2层(2 d);(5)第2阶段固结(30 d);(6)填筑第3层(2 d);(7)第3阶段固结(685 d);(8)反复水位作用(30 d)。
| 土层名称 | 天然重度/(kN·m-3) | 饱和重度/(kN·m-3) | 变形模量/kPa | 泊松比 | 黏聚力/kPa | 摩擦角/(°) | 渗透系数/(m·d-1) | |
| 水平 | 竖向 | |||||||
| 淤泥 | 17 | 19.1 | 5 | 0.35 | 26 | 15 | 6×10-4 | 5×10-4 |
| 粉质黏土 | 14 | 16 | 1.92 | 0.35 | 1 | 30 | 1×10-3 | 1×10-3 |
| 密砂 | 17 | 20 | 45 | 0.22 | 0 | 33 | 7.128 | 7.128 |
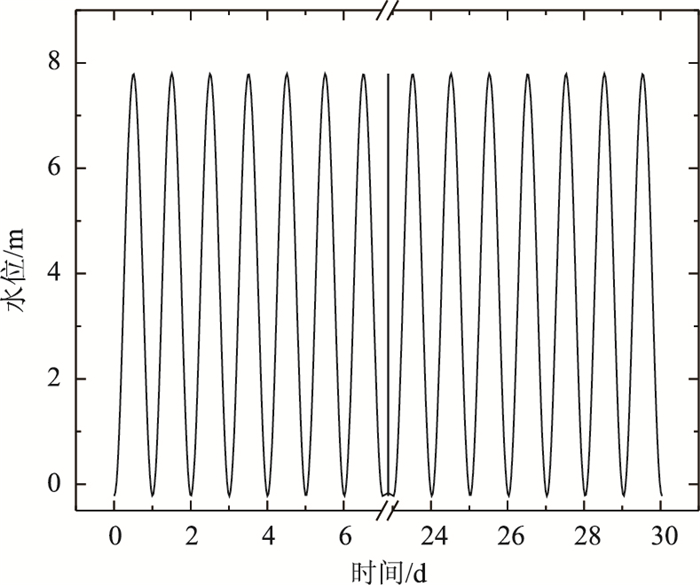
针对潮涨潮落对路基变形特性的影响,在第3层固结结束后, 于路基左侧添加反复水位变化施工步。初始水位为地下潜水位-0.2 m,水位随时间呈半正弦变化,周期为1 d,振幅为8 m,总时间为30 d,如图 4所示。
|
| 图 4 模拟方案 Fig. 4 Simulation scheme |
| |
2.2 模拟结果分析 2.2.1 沉降分析
为了研究软土路基沉降规律,首先选取路堤下方中心点处M点,发现M点的最大沉降量随着时间的增加而增加,沉降-时间曲线呈现出阶梯状发展趋势,如图 5所示。在第1层堆载阶段,沉降-时间曲线近似直线发展,沉降突增至0.56 m;在第1阶段固结的20 d内,沉降增加为0.58 m,沉降增量为0.02 m。在第2层堆载阶段,沉降突增为1.02 m; 在第2阶段固结的20 d内,沉降基本保持不变,沉降增量为0.01 m。同样,在第3层堆载阶段,沉降突增至1.38 m,第3阶段固结过程中,沉降增量为0.03 m。但在反复水位作用下滩涂路基的沉降可达1.459 m,沉降增量约为0.072 m,约占总沉降量的5%,显然,反复水位对路基的工后沉降影响较大。
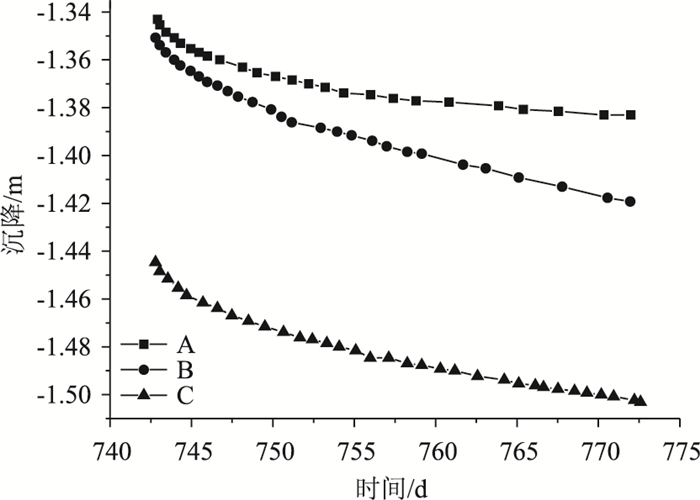
为了说明反复水位作用对差异沉降的影响,选取了路肩A点和C点,选取路中B点。图 6证明了在反复水位作用下,路堤顶部右侧C点的沉降量大于左侧A点的沉降量,两侧沉降差约为36 cm,但两侧的累计沉降量均小于路堤顶部中间的累计沉降量1.503 m。原因是滩涂路基模量太小,导致路堤下方土体向两侧挤出,中间的沉降量相对较大。同时,在反复水位作用下,B点沉降速率小于C点沉降速率且大于A点沉降速率,其中B点沉降速率为8.76×10-5 m/d,C点的沉降速率为9.43×10-5 m/d,A点的沉降速率为4.35×10-5 m/d。这表明反复水位作用会导致滩涂路基右侧出现较大沉降,引起路基不均匀沉降。
|
| 图 6 控制点A, B, C沉降曲线 Fig. 6 Settlement curves of control point A, control point B and control point C |
| |
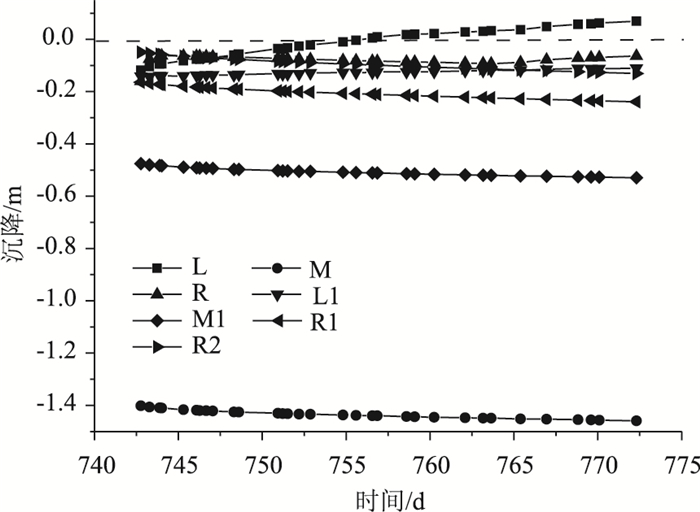
为了研究反复水位作用对路基的影响范围,选取控制点L,M,R,L1,M1,R1和R2。图 7表明路基左侧坡脚处L及深度范围内L1的沉降变小,坡脚处土体甚至有向上拱起趋势。而路基中心处及右侧土体沉降在反复水位作用下逐渐增大,中心点处M累计沉降量为1.459 m,路基右侧R1和R2两点在反复水位作用阶段的沉降均超过了0.1 m。
|
| 图 7 其他各控制点沉降曲线 Fig. 7 Settlement curves of other control points |
| |
2.2.2 固结度分析
在工程实践中,固结度是评价土体固结程度和是否满足工程验收的重要性指标,固结度可以根据孔压的比值计算,也可以采用沉降量的比值计算[12]。本研究选取M点作为固结度计算控制点,通过累计沉降量与计算最终沉降量的比值得到土体的固结度U, 公式为:
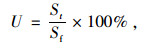
|
(1) |
式中,St为t时刻预压荷载下地基的沉降量; Sf为预压荷载下地基的最终沉降量,其计算公式为:
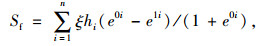
|
(2) |
式中,e0i为预压前淤泥的孔隙比; e1i为预压后淤泥的孔隙比; hi为土体分层厚度; ξ为经验系数,根据预压土的实际情况,取ξ=1.4。
根据场地勘察报告及室内试验资料,预压前淤泥的孔隙比e0i=1.53,预压后孔隙比e1i=1.3,利用式(1)计算得到滩涂路基的固结度,如表 3所示。
| 施工阶段 | 时间/d | 沉降量/m | 固结度/% |
| 阶段1:第1层填筑及固结 | 1 | -0.197 | 10.24 |
| 5 | -0.546 | 28.29 | |
| 10 | -0.552 | 28.64 | |
| 16 | -0.554 | 28.72 | |
| 22 | -0.555 | 28.75 | |
| 阶段2:第2层填筑及固结 | 23 | -0.719 | 37.28 |
| 25 | -0.974 | 50.48 | |
| 27 | -0.993 | 51.48 | |
| 30 | -0.999 | 51.81 | |
| 35 | -1.002 | 51.93 | |
| 41 | -1.003 | 52.00 | |
| 54 | -1.004 | 52.07 | |
| 阶段3:第3层填筑及固结 | 60 | -1.357 | 70.34 |
| 71 | -1.366 | 70.83 | |
| 78 | -1.368 | 70.91 | |
| 87 | -1.369 | 70.99 | |
| 105 | -1.372 | 71.11 | |
| 140 | -1.375 | 71.28 | |
| 176 | -1.377 | 71.40 | |
| 246 | -1.38 | 71.56 | |
| 317 | -1.382 | 71.67 | |
| 459 | -1.385 | 71.79 | |
| 601 | -1.386 | 71.85 | |
| 742 | -1.387 | 71.88 | |
| 阶段4:反复水位作用 | 745 | -1.417 | 73.46 |
| 750 | -1.43 | 74.13 | |
| 755 | -1.439 | 74.58 | |
| 760 | -1.444 | 74.87 | |
| 765 | -1.45 | 75.19 | |
| 770 | -1.456 | 75.50 | |
| 772 | -1.459 | 75.64 |
表 3表明,随着时间的增加,固结度呈增长趋势,当第3次固结完成时,固结度超过了70%,为71.88%。为了合理描述和预测滩涂淤泥的固结度,采用幂函数公式进行拟合,相关系数R2可达85%以上,如图 11(a)~(c)所示,幂函数表达式为:
|
| 图 11 灰色预测程序流程图 Fig. 11 Flowchart of gray prediction Program |
| |
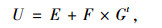
|
(3) |
式中,E,F,G均为试验参数; t为固结时间,具体拟合结果详见表 4。
| 参数 | E | F | G | 拟合公式 | R2 |
| 阶段1:第1层堆载和固结 | -0.562 | 0.604 | 0.535 | U=-0.562+0.604×0.535t | 0.983 |
| 阶段2:第2层堆载和固结 | -1.003 | 1.135 | 0.421 | U=-1.003 +1.135×0.421t | 0.988 |
| 阶段3:第3层堆载和固结 | -0.379 | 37.853 | 0.89 | U=-0.379+37.853×0.890t | 0.866 |
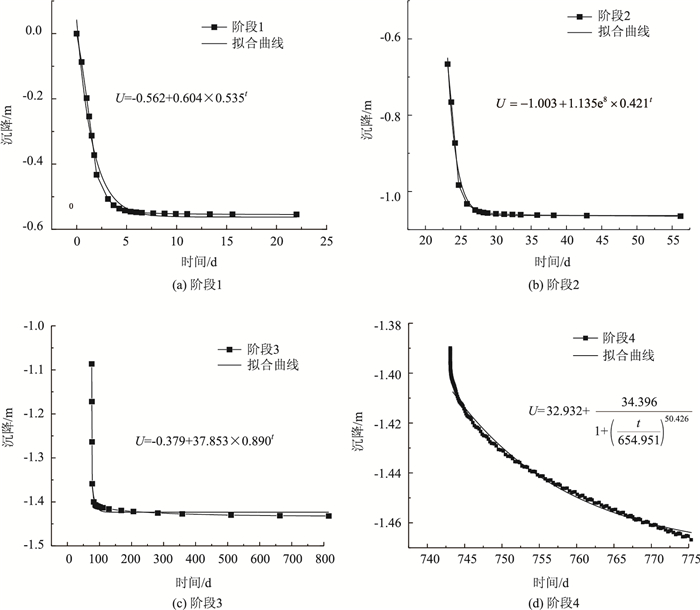
研究发现,滩涂路基在反复水位作用阶段,沉降量与时间关系并不满足幂函数拟合公式。本研究选择Logistic函数模型拟合,发现相关系数R2可达99.4%以上,如图 8(d)所示,Logistic函数的表达式为:

|
(4) |
|
| 图 8 各阶段沉降拟合曲线 Fig. 8 Fitting curves of settlement at each stage |
| |
式中,A1,A2,t0,p均为试验参数; t为固结时间,具体拟合结果详见表 5。
| 参数 | A1 | A2 | t0 | p | R2 |
| 数值 | 67.328 | 32.932 | 654.951 | 50.426 | 0.994 |
2.2.3 孔压分析
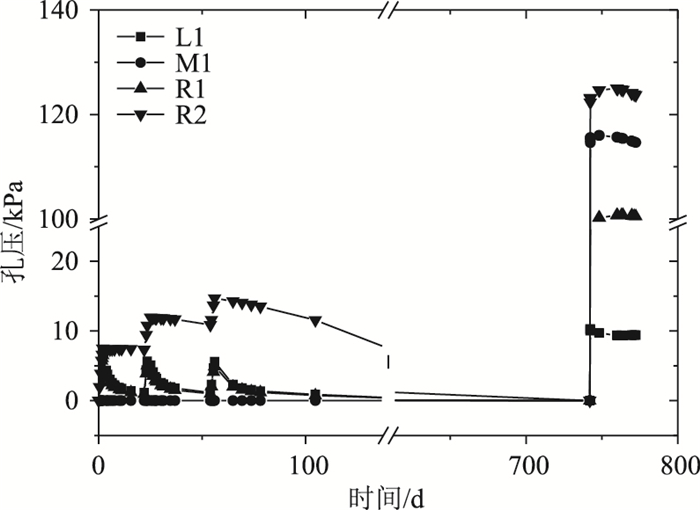
孔压是衡量土体固结沉降特性十分重要的指标,本研究选取了控制点L1,M1,R1,R2进行孔压分析,如图 9所示。显然在堆载和固结过程中,有排水板的地方,滩涂淤泥的孔隙水压力在堆载阶段呈现上升趋势,在固结阶段呈现出下降趋势,这主要是由于选择的控制点R1和L1一侧有排水板,一侧无排水板,孔隙水压力来不及消散,导致先升高后下降。其中M点处的孔压基本保持零不变,这主要是因为在整个过程中,土体处于排水状态。但在R2点处,孔压处于增长趋势,由于土体渗透系数较小,基本处于不排水状态。
|
| 图 9 孔压-时间曲线 Fig. 9 Curves of pore water pressure vs. time |
| |
当反复水位作用时,路基右侧R2处孔隙水压力忽然增高至120 kPa,随时间增加,孔隙水压力减小趋势不明显。路基中心处M1点的孔隙水压力增加到113 kPa。其次,路基右侧R1点处的孔隙水压力为101 kPa,路基左侧L1处的孔隙水压力为10 kPa,但仍比第1次堆载时产生的孔压高3 kPa。
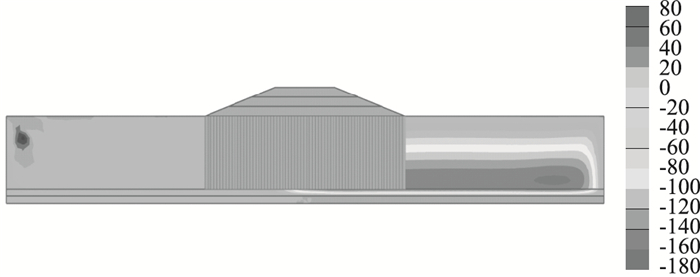
图 10为反复水位作用下孔压分布云图。可以看出,滩涂路基在沉降固结完成后,由于反复水位作用的影响,土体中各个测点处均会重新产生不同程度的孔隙水压力,尤其中间及右侧土体孔隙水压力明显大于左侧土体,根据有效应力原理,右侧土体有效应力将会减小,地基承载力降低,存在很大的安全隐患。
|
| 图 10 反复水位作用下孔压分布云图(单位:kN/m2) Fig. 10 Nephogram of pore water pressure distribution under repeated water level (unit: kN/m2) |
| |
3 预测方法
沉降量作为软基处理效果的主要判断依据,对软基处理工程具有重要意义。目前,适用于软土地基的常用沉降预测方法主要有双曲线法、指数曲线法、沉降速率法、三点法、灰色预测法等[13]。由于灰色预测具有原理简单、预测精度高、易于实现、便于编程等特点,本研究利用灰色预测方法进行软基处理的沉降量估算,并利用VB语言编制一个GM(1,1)小程序,输入部分沉降数据后即可自动计算沉降预测结果。
3.1 灰色预测的原理灰色预测方法GM(1,1)是我国邓聚龙教授基于不完全信息发明的一种预测方法。该方法能对短期的数据进行预测,灰色系统理论专门针对“贫信息”、“小样本”数据[14-15]进行分析,其特点是计算量小,对数据一般不需要假定服从什么分布,可直接从所面对的数据中提取信息。该理论主要包括以灰色朦胧集为基础的理论体系,以灰色关联空间为依托的分析体系,以灰色序列生成为基础的方法体系,以灰色模型GM(1,1)为核心的模型体系,以系统分析、评估、建模、预测、决策、控制和优化为主体的技术体系[16]。
但在求解参数u时,原始的求解方法是不合理的。为了进一步提高预测精度,根据杨华龙[17]提出的改进灰色GM(1,1)模型能很好地应用于工程中的短期预测,在确定参数u时,利用自动寻优定权的方法对参数进行迭代,直到参数取值满足预测值与实际值离差的平方和最小为止,并提出该方法尤其适用于深基坑开挖过程中周围管线沉降预测变化。具体原理步骤为:
(1) 由原始序列X(0)按下式计算累加生成序列:
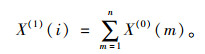
|
(5) |
(2) 根据式(5),采用最小二乘法和自动寻优定权的方法按式(6)确定模型的参数:
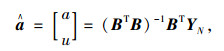
|
(6) |
要求u满足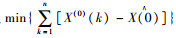
式(6)中
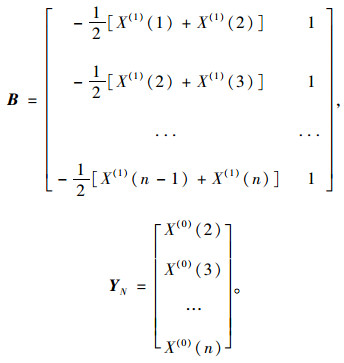
|
(7) |
(3) 建立预测模型,求出累加序列:
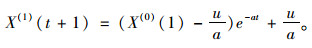
|
(8) |
(4) 采用残差分析法进行模型检验。
(5) 根据系统未来变化,确定预测值的上下界,来确定灰平面[18]。
(6) 用模型进行预测。利用上述模型预测是利用累加生成序列X(1)的预测,利用累减生成法将其还原,即可以得到原始X(0)的预测值。
3.2 反复水位作用下的深厚滩涂路基沉降预测系统为了实现反复水位作用下深厚滩涂路基沉降量的快速预测,基于GM(1, 1)基本原理,利用Visual Basic 6.0(VB 6.0)研发了该沉降预测系统。系统用户操作界面简单,选择3个Command Button,Caption属性分别为“GM(1, 1)”、“固结”、“退出”。在Command 1(GM(1, 1))事件下编写用于灰色预测的程序,用于在窗体中输出沉降;在Command 2(固结)事件下编写用于固结度预测的程序,并在文本框(text)中输出固结度;在Command 3(退出)事件下编写退出程序。在界面设计过程中,选取3个text,text1用于输入监测数据,text2用于输入固结时间,text3用于获取预测固结度的结果。
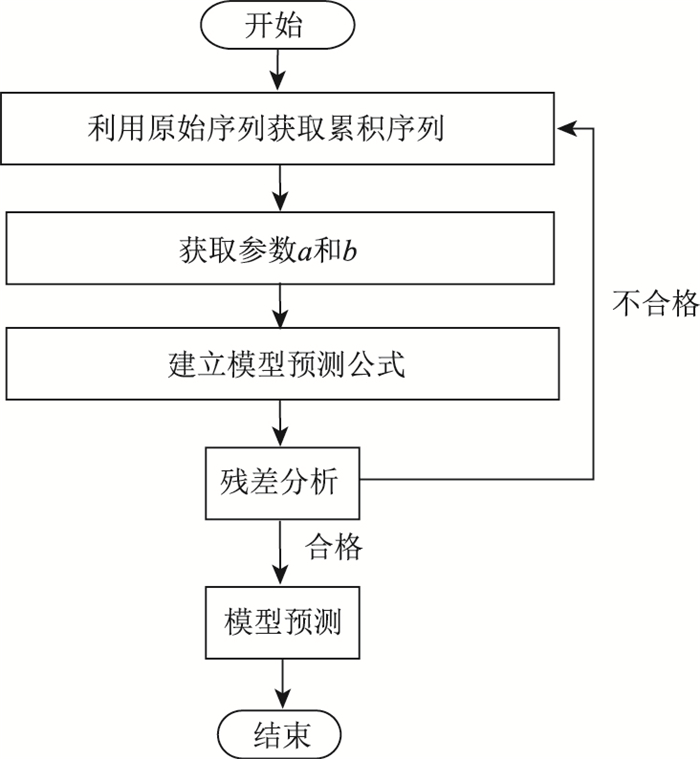
为了实现反复水位作用下深厚滩涂路基沉降预测系统的研发,根据以下顺序设计了内部程序[19]:首先,基于原始序列X(0)计算累积序列X(1);其次,根据方程(6)确定参数a和b;第三,建立预测模型获取增量序列;第四,利用残差分析检查模型;第五,利用模型进行模型,具体设计流程如图 11所示。此外,反复水位作用下深厚滩涂路基沉降预测系统可以利用经验公式(3)和(4)实现在反复水位作用下深厚滩涂路基固结度的预测。
为了验证程序的正确性,将4个施工阶段M点的沉降数据输入程序中,并获得如表 6所示的沉降预测结果。
| 施工阶段 | 时间/d | 沉降/m | 预测沉降/m | 误差值/% |
| 阶段1:第1层填筑及固结 | 1 | -0.197 | -0.191 | 3.05 |
| 5 | -0.546 | -0.532 | 2.56 | |
| 10 | -0.552 | -0.549 | 0.54 | |
| 16 | -0.554 | -0.553 | 0.18 | |
| 22 | -0.555 | -0.578 | 4.14 | |
| — | — | — | — | |
| — | — | — | — | |
| 阶段2:第2层填筑及固结 | 23 | -0.719 | -0.73 | 1.53 |
| 25 | -0.974 | -0.981 | 0.72 | |
| 27 | -0.993 | -1.031 | 3.83 | |
| 30 | -0.999 | -1.045 | 4.60 | |
| 35 | -1.002 | -1.048 | 4.59 | |
| 41 | -1.003 | -1.051 | 4.79 | |
| 54 | -1.004 | -1.053 | 4.88 | |
| 阶段3:第3层填筑及固结 | 60 | -1.357 | -1.299 | 4.27 |
| 71 | -1.366 | -1.299 | 4.90 | |
| 78 | -1.368 | -1.333 | 2.56 | |
| 87 | -1.369 | -1.356 | 0.95 | |
| 105 | -1.372 | -1.371 | 0.07 | |
| 140 | -1.375 | -1.376 | 0.07 | |
| 176 | -1.377 | -1.379 | 0.15 | |
| 246 | -1.38 | -1.384 | 0.29 | |
| 317 | -1.382 | -1.386 | 0.29 | |
| 459 | -1.385 | -1.389 | 0.29 | |
| 601 | -1.386 | -1.392 | 0.43 | |
| 742 | -1.387 | -1.398 | 0.79 | |
| 阶段4:反复水位作用 | 745 | -1.417 | -1.411 | 0.42 |
| 750 | -1.43 | -1.418 | 0.84 | |
| 755 | -1.439 | -1.429 | 0.69 | |
| 760 | -1.444 | -1.433 | 0.76 | |
| 765 | -1.45 | -1.454 | 0.28 | |
| 770 | -1.456 | -1.461 | 0.34 | |
| 772 | -1.459 | -1.471 | 0.82 |
表 6表明,大部分沉降误差可以控制在5%范围以内,可以利用本程序对工后沉降进行预测。
4 结论本研究结合福建霞浦某路基工程,基于现场的工程地质条件,通过数值模拟软件Plaxis2D对反复水位作用下的深厚滩涂路基沉降及预测系统开展了研究,并获得如下结论:
(1) 在反复水位作用下,路基会产生差异沉降,路堤的顶部右侧C点的沉降量大于左侧A点的沉降,两侧沉降差约为36 cm。并且B点的沉降速率小于C点的沉降速率且大于A点的沉降速率,B点沉降速率为8.76×10-5 m/d,C点的沉降速率为9.43×10-5 m/d,A点的沉降速率为4.35×10-5 m/d。
(2) 幂函数形式可以很好地描述滩涂淤泥在堆载和固结过程中固结度变化规律,但在反复水位作用阶段,滩涂淤泥的固结度建议采用Logistic函数表达式。
(3) 在反复水位作用下,路基右侧的孔隙水压力比路基左侧孔隙水压力要大,R2,M1,R1和L1处孔隙水压力分别为120,113,101,10 kPa。
(4) 基于灰色理论建立的反复水位作用下的深厚滩涂路基沉降预测系统,可以将沉降误差控制在5%范围之内,并应用于工程实践。
| [1] |
DONG L, NIU B, HU S, et al. Research on the Influence Law of Bridge Foundation Settlement with Seasonal Underground Water Level Change on High Speed Railway[J]. Japanese Geotechnical Society Special Publication, 2015, 2(39): 1407-1411. |
| [2] |
GHANI A N A, ROSLAN N I, HAMID A H A. Road Submergence during Flooding and Its Effect on Subgrade Strength[J]. International Journal of Geomate:Geotechnique, Construction, Materials & Environment, 2016, 10(21/22): 1848-1853. |
| [3] |
张英平, 唐益群, 徐杰, 等. 水位循环升降作用下粉土变形及沉降机理[J]. 同济大学学报:自然科学版, 2017, 45(12): 1773-1782. ZHANG Ying-ping, TANG Yi-qun, XU Jie, et al. Deformation Law and Settlement Mechanism of Silt Caused by Cyclic Rise-fall of Water Table[J]. Journal of Tongji University:Natural Science Edition, 2017, 45(12): 1773-1782. |
| [4] |
张文杰, 詹良通, 凌道盛, 等. 水位升降对库区非饱和土质岸坡稳定性的影响[J]. 浙江大学学报:工学版, 2006, 40(8): 1365-1370, 1428. ZHANG Wen-jie, ZHAN Liang-tong, LING Dao-sheng, et al. Influence of Reservoir Water Level Fluctuations on Stability of Unsaturated Soil Banks[J]. Journal of Zhejiang University:Engineering Science Edition, 2006, 40(8): 1365-1370, 1428. |
| [5] |
何忠明, 史振宁, 付宏渊, 等. 水位下降对沿湖路堤边坡渗流特征及稳定性的影响[J]. 中南大学学报:自然科学版, 2014, 45(9): 3227-3233. HE Zhong-ming, SHI Zhen-ning, FU Hong-yuan, et al. Influence of Water Decline on Seepage Characteristic and Slope Stability of Embankment along Lake[J]. Journal of Central South University:Science and Technology Edition, 2014, 45(9): 3227-3233. |
| [6] |
LIU J, GAN Y, TANG X, et al. Study on the Settlement Prediction Methods of Soft Ground[J]. Boletin Tecnico, 2017, 55(14): 562-571. |
| [7] |
秦亚琼.基于实测数据的路基沉降预测方法研究及工程应用[D].长沙: 中南大学, 2008. QIN Ya-qiong. Prediction Method and Engineering Application of Subgrade Settlement Based on Measured Data[D]. Changsha: Central South University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10533-2008165151.htm |
| [8] |
张涛, 蔡国军, 刘松玉. 基于Weibull模型的软土路基沉降预测方法[J]. 岩土工程学报, 2013, 35(增2): 212-216. ZHANG Tao, CAI Guo-jun, LIU Song-yu. Settlement Prediction of Soft Ground Based on Weibull Model[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 212-216. |
| [9] |
秦晓光, 杨龙才. 灰色预测在高铁路基沉降预测中的应用[J]. 华东交通大学学报, 2011, 28(5): 88-92. QIN Xiao-guang, YANG Long-cai. Application of Grey Prediction in Settlement Prediction of High-speed Railway[J]. Journal of East China Jiaotong University, 2011, 28(5): 88-92. |
| [10] |
刘红军, 成华雄, 单炜, 等. 不同深度沼泽湿地软粘土压缩固结特性[J]. 公路交通科技, 2011, 28(8): 41-45. LIU Hong-jun, CHENG Hua-xiong, SHAN Wei, et al. Compression and Consolidation Characteristics of Marsh Soft Clay in Different Depths[J]. Journal of Highway and Transportation Research and Development, 2011, 28(8): 41-45. |
| [11] |
刘志祥, 张海清. PLAXIS高级应用教程[M]. 北京: 机械工业出版社, 2015. LIU Zhi-xiang, ZHANG Hai-qing. PLAXIS Advanced Application Tutorial[M]. Beijing: China Machine Press, 2015. |
| [12] |
吴陆军, 汪小云, 林钟喜. 堆载预压法处理软土时计算固结度的几种方法[J]. 土工基础, 2009, 23(4): 66-68. WU Lu-jun, WANG Xiao-yun, LIN Zhong-xi. Several Calculation Methods of Consolidation Degree During Soft Soil Treatment by Preloading Method[J]. Soil Engineering and Foundation, 2009, 23(4): 66-68. |
| [13] |
赵明华, 刘建华, 刘煜, 等. 滨海公路软土路基变形机理及其沉降预测研究[J]. 公路交通科技, 2006, 23(1): 32-35. ZHAO Ming-hua, LIU Jian-hua, LIU Yu, et al. Deformation Mechanism and Settlement Forecast of Soft Clay Embankment in Coastal Region[J]. Journal of Highway and Transportation Research and Development, 2006, 23(1): 32-35. |
| [14] |
党耀国, 王正新. 灰色预测与决策模型研究[M]. 北京: 科学出版社, 2009: 1-15. DANG Yao-guo, WANG Zheng-xin. Research on Grey Prediction and Decision-making Model[M]. Beijing: Science Press, 2009: 1-15. |
| [15] |
杨和平, 湛文涛, 赵文建, 等. 基于GM(1, 1)模型的膨胀土填料CBR指标快速确定方法[J]. 公路交通科技, 2012, 29(9): 1-7. YANG He-ping, ZHAN Wen-tao, ZHAO Wen-jian, et al. Rapid Determination Method of CBR Indices for Expansive Soil Filler Based on GM(1, 1) Model[J]. Journal of Highway and Transportation Research and Development, 2012, 29(9): 1-7. |
| [16] |
李燕.灰色预测模型的研究及其应用[D].杭州: 浙江理工大学, 2012. LI Yan. Research and Application of Grey Forecast Model[D]. Hangzhou: Zhejiang Sci-Tech University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10338-1014229928.htm |
| [17] |
杨华龙, 刘金霞, 郑斌. 灰色预测GM(1, 1)模型的改进及应用[J]. 数学的实践与认识, 2011, 41(23): 39-46. YANG Hua-long, LIU Jin-Xia, ZHENG Bin. Improvement and Application of Grey Prediction GM(1, 1) Model[J]. Mathematics in Practice and Theory, 2011, 41(23): 39-46. |
| [18] |
张俊荣, 陈保国, 易贤龙, 等. 两侧水位变化时路堤渗流特征及稳定性分析[J]. 公路交通科技, 2017, 34(2): 35-41. ZHANG Jun-rong, CHEN Bao-guo, YI Xian-long, et al. Analysis on Seepage Characteristics and Stability of Embankment with Water Level Change on both Sides[J]. Journal of Highway and Transportation Research and Development, 2017, 34(2): 35-41. |
| [19] |
刘柞秋, 周翠英. 软粘土地基非线性一维大变形固结的有限差分法分析[J]. 中山大学学报:自然科学版, 2005, 44(3): 25-28. LIU Zuo-qiu, ZHOU Cui-ying. One-dimensional Non-linear Large Deformation Consolidation Analysis of Soft Clay Foundation by FDM[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2005, 44(3): 25-28. |
 2019, Vol. 36
2019, Vol. 36
