扩展功能
文章信息
- 程龙虎, 聂如松, 刘飞
- CHENG Long-hu, NIE Ru-song, LIU Fei
- 裂隙性黄土单轴抗压强度离散元分析
- Discrete Element Analysis on Uniaxial Compressive Strength of Fractured Loess
- 公路交通科技, 2019, 36(8): 29-36
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(8): 29-36
- 10.3969/j.issn.1002-0268.2019.08.005
-
文章历史
- 收稿日期: 2018-03-20
2. 西安科技大学 地质与环境学院, 陕西 西安 710054;
3. 高速铁路建造技术国家工程实验室, 湖南 长沙 410075
2. School of Geology and Environment Engineering, Xi'an University of Science and Technology, Xi'an Shaanxi 710054, China;
3. National Engineering Laboratory for High Speed Railway Construction, Changsha Hunan 410075, China
与岩体相同,土体内部也存在着许多裂隙、节理等不连续面,土体中存在的裂隙等不连续面会对土体的稳定性造成显著的影响[1]。孔德坊[2]、邓京萍[3]等通过对裂隙黏土的研究发现:黏性土中裂隙角度的不同对裂隙性黏土力学特性的影响显著。George[4]开展裂隙性黏土填方工程稳定性研究,发现土体中裂隙的存在对黏土的力学性质产生弱化现象。Vallejo[5]通过室内无侧限抗压强度试验,研究不同含水率和裂隙倾角下黏土变形破坏的机理。裂隙性黄土在西部黄土高原地区广泛存在,其抗压强度对工程的安全性和稳定性产生重要影响[6]。黄土体内部分布大量不同时期、产状、成因、尺度以及力学性质的裂隙[7-8],改变黄土体本身的结构构造,导致了黄土体的各向异性,使土体性质发生恶化,继而诱发黄土高原地区诸多工程地质问题[9]。关于裂隙性黄土的力学特性,卢全中[10]通过对裂隙性黄土试样进行三轴试验,对其本构模型进行了研究,并探索了裂隙性黄土的工程灾害效应;周彬[11]以裂隙性黄土为研究对象,通过平面应变压缩试验以及数值模拟手段研究了裂隙性黄土在平面应变条件下的压缩特性;孙萍[12-13]以单轴拉伸与三轴剪切试验为手段,分别研究裂隙的存在及其倾角的变化对裂隙性黄土试样的抗拉和剪切特性的影响规律;贾晖等[14]基于离散元法对节理黄土进行单轴压缩试验模拟,分析了不同节理角度对黄土力学行为的影响;程龙虎等[15]采用无侧限单轴抗压强度试验,研究了裂隙性黄土中裂隙的倾角变化对其抗压强度的影响规律,并对其破裂面进行分析,发现裂隙的存在及倾角的变化对其破裂面的形成具有重要的影响。虽然裂隙性黄土的力学性质研究已取得了一些成果,但是,由于裂隙性黄土试样制取的困难,尤其是不同裂隙倾角的原状裂隙性黄土试样制取的困难,目前针对裂隙性黄土开展大规模试验研究仍具有一定的困难性。近年来,随着岩土工程数值计算的不断发展,越来越多的数值计算方法被用于岩土工程问题的分析中。岩土工程数值分析方法作为理论分析和试验研究的辅助工具,通过对岩土体进行数值分析能直观地得到岩土体的行为特性[16-17]。因此,采用数值模拟方法能够克服不同裂隙倾角的黄土试样制取的困难性,同时可进行大量的重复性试验且试验数据获取更加高效、方便。
为此,在黄土常规物理力学试验以及裂隙性黄土室内试验结果的基础上,基于离散元软件3DEC建立不同裂隙倾角的裂隙性黄土数值模型,开展单轴压缩条件下不同裂隙倾角的裂隙性黄土试样的数值试验研究,分析裂隙倾角对裂隙性黄土抗压强度的影响,并对单轴压缩条件下裂隙性黄土试样的破坏模式进行探讨。
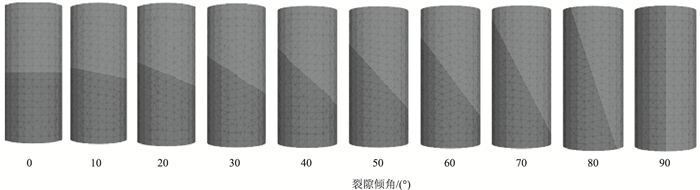
1 裂隙性黄土单轴抗压离散元模型的建立及验证 1.1 数值模型的建立首先利用离散元软件3DEC内嵌fish语言编写程序建立直径为39.1 mm,高度为80.0 mm的圆柱体模型,模型尺寸与室内试验所用试样的尺寸一致,然后以jset命令在圆柱体模型中生成1条贯通的裂隙面,且裂隙面通过圆柱体的中心点,最后采用GENERATE edge命令对圆柱体模型进行离散化。通过对模型试样裂隙倾角的改变,生成了具有不同角度的裂隙性黄土试样模型,10组不同裂隙倾角的裂隙性黄土试样模型如图 1所示。
|
| 图 1 离散后不同裂隙倾角的裂隙性黄土试样模型 Fig. 1 Discreted fracture loess specimen models with different fracture angles |
| |
1.2 室内试验
将制备的重塑黄土利用自行设计加工的具有不同倾角的PVC裂隙模具分别制成0°,10°,20°,30°,40°,45°,50°,60°,70°,90°等10组不同裂隙倾角的裂隙性黄土试样,其中试样直径为39.1 mm,高度为80.0 mm,分别对每组裂隙倾角的裂隙性黄土试样进行无侧限抗压强度试验。本次试验加载的应变速率为4×10-2 mm/s,以摄像机记录试验过程,当量力百分表开始出现“回转”时,表示试样已经破坏,终止试验。
1.3 模型参数的选取离散元软件3DEC中提供了5种内置块体本构模型和两种内置节理本构模型,根据其适用的研究对象和适用范围,并结合本研究的实际情况,本次数值试验所选取的本构模型为块体Mohr-Coulomb塑性模型,节理面接触库伦滑移模型。根据室内黄土试样的基本物理力学试验结果以及裂隙性黄土单轴抗压强度室内试验结果,经过对模型参数的多次标定,确定数值模型的参数,其中块体物理力学参数如表 1所示,裂隙面力学参数如表 2所示。
| 密度/(kg·m-3) | 弹性模量/MPa | 泊松比μ | 体积模量/MPa | 剪切模量/MPa | 黏聚力/kPa | 内摩擦角/(°) | 拉伸强度/kPa |
| 1 630 | 15 | 0.35 | 16.7 | 5.6 | 60 | 31.0 | 25.0 |
| 法向刚度/(MPa·m-1) | 剪切刚度/(MPa·m-1) | 黏聚力/kPa | 内摩擦角/(°) | 拉伸强度/kPa |
| 80 | 60 | 30 | 32 | 0.3 |
1.4 试验与数值结果对比分析
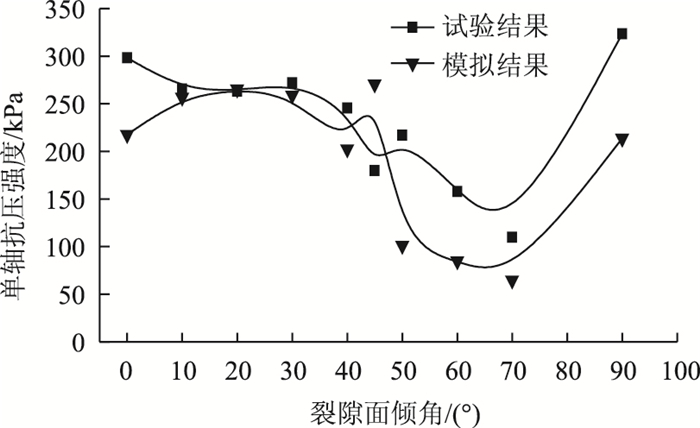
为了验证本次数值试验结果的可靠性,将本次数值试验结果与笔者先前裂隙性黄土室内试验结果[15]绘制于同一坐标轴下进行对比分析,如图 2所示。从图 2可以看出,数值试验结果与室内试验结果均表明随着试样中裂隙倾角的增大,裂隙性黄土试样的抗压强度呈现先减小后增大的变化规律,且均存在相同的最不利裂隙倾角区间。从整体趋势上看,室内试验结果与数值试验结果的单轴抗压强度随裂隙面倾角的变化规律相一致,不同之处是裂隙性黄土试样的裂隙倾角为45°时,单轴抗压强度的室内试验结果低而数值试验结果高。出现这种现象的可能原因有:(1)数值试验时裂隙参数认为是均一的,与实际裂隙性黄土试样可能有一定的差别;(2)室内试验所用的试验仪器对试样的两端会产生一定的摩擦作用,对试验结果有一定的影响;(3)数值试验所选用的本构模型为Mohr-Coulomb塑性模型,而摩尔-库伦准则对裂隙性黄土的适用性有待研究。卢全中[7]通过裂隙性黄土试样的三轴试验,认为大多数裂隙性黄土试样的破坏不符合Mohr-Coulomb准则。基于上述分析,虽然两者存在一定的差异,但是数值模拟结果从总体上能够反映裂隙倾角变化对裂隙性黄土试样单轴抗压强度的影响规律,因此认为采用离散元软件3DEC所建立的裂隙性黄土单轴抗压离散元模型对不同裂隙倾角的裂隙性黄土试样在单轴压缩条件下的强度及破坏特性进行分析具有一定的合理性。
|
| 图 2 室内试验与数值试验结果对比 Fig. 2 Comparison between laboratory test and numerical simulation results |
| |
2 裂隙性黄土单轴抗压特性数值分析 2.1 数值试验设计
为研究不同裂隙倾角对裂隙性黄土试样单轴抗压强度的影响,将裂隙倾角定义为裂隙面与试样轴向压应力作用面之间的夹角,数值试验中建立裂隙倾角分别0°,10°,20°,30°,40°,45°,50°,60°,70°,90°等10组不同圆柱体裂隙模型试样。试验时模型侧面为自由边界,通过对模型上、下表面以速度加载方式实现单轴压缩数值试验,加载速率为0.04 m/s,采用plot命令实时记录模型试件顶部应力及位移的关系曲线,当模型试件顶部应力达到峰值并开始下降时,根据应力及位移的关系曲线判断计算是否停止。试验结束后用hist命令将试验过程中记录的应力和位移导入到Excel文件中,然后通过origin软件进行数据处理,绘制各模型的应力与应变曲线。
2.2 裂隙性黄土试样的应力-应变曲线分析开展了不同裂隙倾角的裂隙性黄土试样单轴压缩数值试验,获得10组不同裂隙倾角的裂隙性黄土试样的应力-应变曲线,如图 3所示。
|
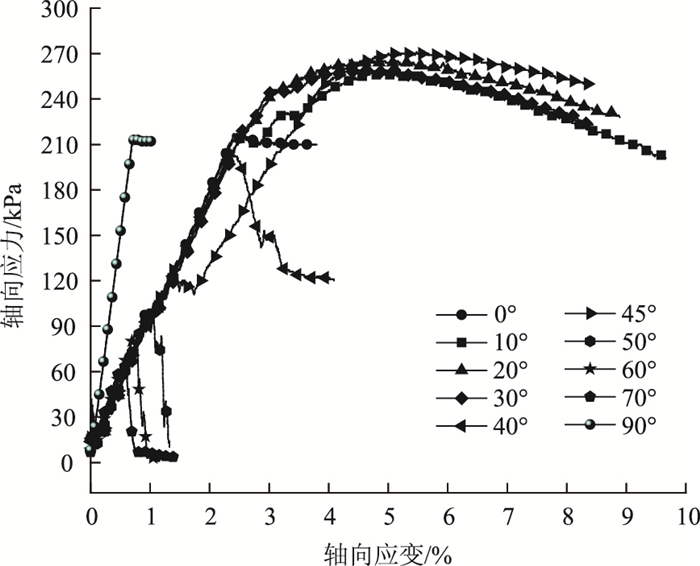
| 图 3 不同裂隙倾角的裂隙性黄土试样应力-应变曲线 Fig. 3 Stress-strain curves of fractured loess specimens with different fractured angles |
| |
由图 3可以看出裂隙性黄土试样在单轴压缩条件下的应力-应变关系曲线具有下列特点:
(1) 当裂隙性黄土试样的裂隙倾角为0°和90°时,其裂隙性黄土试样的应力-应变关系曲线没有明显的应力峰值点,即当裂隙性黄土试样发生很小变形时试样就发生压裂破坏,破坏时试样轴向应力发生较小的变化,从而没有明显的应力降。其他裂隙性黄土试样的应力-应变关系曲线具有相对明显的应力峰值点,且具有明显的应力降,试样表现为一定的脆性破坏;此外,其他不同裂隙倾角的裂隙性黄土的应力-应变关系曲线的形态也不尽相同,曲线的峰值强度及其应力降的程度也表现出相对明显的差异。
(2) 当裂隙性黄土试样的裂隙倾角为10°~30°时,其试样的应力-应变关系曲线表现出4个明显的阶段:第1阶段当试样的应变较小时,其应力-应变曲线的斜率不断波动但数值较小,为试样裂隙的压密阶段;第2阶段裂隙性黄土试样的应力-应变曲线近似直线,其直线斜率大于第一阶段曲线斜率,为裂隙试样的弹性变形阶段;第3阶段随着变形的增大其应力-应变曲线斜率逐渐减小直至轴向应力出现峰值,为裂隙试样的塑性屈服阶段;第4阶段相应地应力-应变曲线表现出明显的应力降,为试样破坏阶段。当裂隙性黄土试样的裂隙倾角为40°~70°时,试样的应力-应变关系曲线与裂隙倾角为10°~30°时不同,无4个明显的阶段,不仅应力-应变关系曲线的弹性变形阶段较长且基本上无塑性屈服阶段,而且裂隙试样的应变较小时,其应力-应变关系曲线就达到了应力峰值继而出现应力陡降,试样突然破坏;当裂隙性黄土试样的裂隙倾角为45°时,试样的应力-应变曲线呈现4个明显的阶段,且试样压缩过程中相应地应力-应变曲线出现较小的屈服台阶,即在试样的轴向应变还比较小时,试样的应力-应变曲线经历了应力屈服,继而随裂隙性黄土试样应变的增大而应力逐渐增大,对于裂隙倾角为45°时试样的应力-应变曲线出现的这种特殊情况,下文结合试样的单轴抗压强度以及破坏特性对其进行了讨论。
(3) 当裂隙性黄土试样的裂隙倾角为0°和90°时,裂隙性黄土试样应力-应变曲线的形状和峰值强度较为接近,均无明显的应力降,且均在较小应变时试样发生破坏,说明当试样的裂隙倾角与作用在试样上的轴向应力垂直或平行时,裂隙试样中裂隙的存在对其裂隙性黄土试样的强度影响较小。当裂隙性黄土试样的裂隙倾角为0°时,由于裂隙性黄土试样在轴向压力作用下需要经历裂隙压密阶段,与试样的裂隙倾角为90°时相比,裂隙倾角为0°时试样的应力-应变曲线的应变相对较大。
2.3 裂隙倾角对抗压强度的影响分析为了便于直观地分析不同裂隙倾角对试样单轴抗压强度的作用规律,将数值试验结果中裂隙试样单轴抗压强度随裂隙倾角的变化曲线绘制在下图中,见图 4。
|
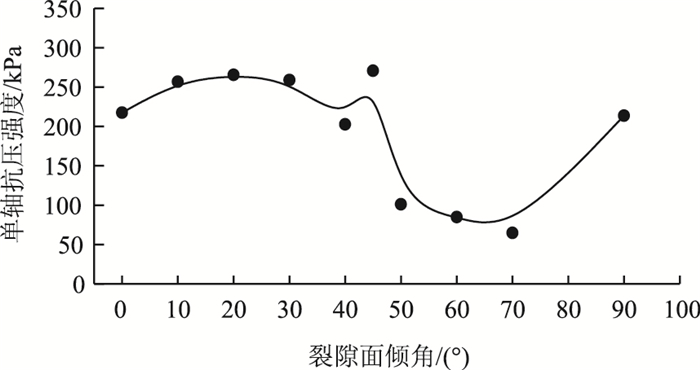
| 图 4 裂隙倾角与裂隙性黄土试样单轴抗压强度关系 Fig. 4 Relationship between fracture angle and uniaxial compressive strength of fractured loess specimens |
| |
由图 4可知裂隙性黄土试样中裂隙倾角的存在以及倾角的不同对其单轴抗压强度有着明显的影响,随裂隙性黄土试样中裂隙倾角的不断增大,裂隙性黄土的抗压强度表现出先减小后增大的变化规律。当裂隙性黄土试样的裂隙倾角为0°~30°时,裂隙性黄土试样的抗压强度比较接近,裂隙倾角在此范围内变化时,试样的抗压强度受裂隙倾角的影响较小。
当裂隙性黄土试样的裂隙倾角在40°~50°范围内变化时,试样的抗压强度表现出先增大后降低的变化规律,裂隙倾角为45°时抗压强度最大。当裂隙性黄土试样的裂隙倾角在60°~70°范围内,裂隙性黄土试样抗压强度出现最小值,说明当裂隙性黄土试样的裂隙倾角为60°~70°时为最不利裂隙倾角区间。对于裂隙性黄土试样的倾角为0°和90°的情况,裂隙性黄土试样抗压强度基本相同,且与裂隙倾角为0°~30°时所对应的单轴抗压强度近似,说明当裂隙试样的倾角很小或很大时,裂隙试样中倾角的变化对裂隙性黄土试样单轴抗压强度影响较小。
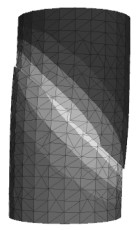
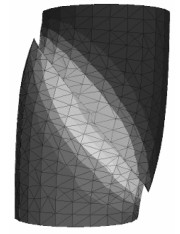
2.4 单轴压缩破坏特性分析为了便于对裂隙性黄土试样在单轴压缩条件下的破坏特性进行分析,将裂隙倾角为0°~90°的裂隙性黄土试样单轴压缩条件下破坏图汇总如表 3所示。
| 裂隙倾角/(°) | 试样破坏图 | 破坏类型 |
| 0 |  |
压裂破坏 |
| 20 |  |
滑移压剪复合破坏 |
| 40 |  |
滑移压剪复合破坏 |
| 50 |  |
滑移破坏 |
| 70 |  |
压裂滑移混合破坏 |
| 10 |  |
滑移压剪复合破坏 |
| 30 |  |
滑移压剪复合破坏 |
| 45 |  |
滑移压剪复合破坏 |
| 60 |  |
滑移破坏 |
| 90 |  |
压裂破坏 |
(1) 当裂隙性黄土试样中的裂隙倾角为0°和90°时,单轴压缩条件下裂隙性黄土试样的破坏形式均为压裂破坏,即在轴向压应力作用下试样内部处于受拉状态,试样破坏由裂隙中心开始破裂进而不断向外延伸扩展。裂隙性黄土试样的裂隙倾角不同,试样破裂时自裂隙中心的扩展方向不同,裂隙倾角为0°时,试样的破裂是自裂隙面上、下沿轴向逐渐扩展至试样顶、底端;裂隙倾角为90°时,试样的破裂由中心向两边不断扩展。尽管前述裂隙倾角不同,但裂隙性黄土试样破坏痕迹均不明显,其原因是试样发生较小变形所对应的轴向应力已达到最大且无明显的应力降,终止计算时试样的变形很小,故试样破坏时没有明显的破坏痕迹,这与本研究前期的室内试验结果[9]相符。
(2) 当试样中裂隙的倾角在10°~45°范围变化时,由于轴向压力与裂隙面存在一定角度且裂隙倾角相对较小,随轴向压力的增加,裂隙性黄土试样沿裂隙面的滑移破坏与试样整体的压剪破坏基本上同时发生,故试样破坏类型为滑移压剪复合破坏。试样破坏沿裂隙面方向和轴向方向均有较大变形,试样破坏痕迹较明显。
(3) 当裂隙性黄土试样的裂隙倾角为50°和60°时,裂隙性黄土试样破坏形式为滑移破坏。因裂隙倾角较大,随轴向压力的增大,试样主要发生沿裂隙的滑移变形直至试样的破坏,且破坏时峰值强度和应变相对较小。
(4) 裂隙倾角为70°时,陡倾的裂隙面受试样顶、底部的约束与支撑,轴向压力作用较小时,试样沿裂隙面滑移受到限制,随轴向压力增大,裂隙面尖端首先产生破裂,然后随轴向压应力的继续增大,试样逐渐沿裂隙产生一定的滑移破坏。该结果与罗世林等[18]进行的层状岩体单轴压缩破坏结果类型中的倾斜破坏比较类似,本研究根据试样在单轴压缩作用下破裂产生的顺序,将该类型破坏称为压裂滑移混合破坏。
3 讨论 3.1 裂隙倾角对试样抗压强度的理论分析本研究的试验结果和数值模拟结果都表明随着裂隙倾角的不断增大,裂隙性黄土试样的抗压强度整体上都呈现出先减小后增大的趋势,且都存在最不利裂隙倾角区间,但是数值模拟结果与试验结果还存在一定的差异。为了进一步验证数值模拟结果的合理性,下面从理论上对抗压强度随裂隙倾角的变化进行说明,并与数值模拟结果进行对比。
由Mohr-Coulomb准则,当试样沿裂隙面发生剪切破坏时,符合式(1):
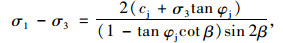
|
(1) |
式中,cj和φj分别为裂隙面的黏聚力和内摩擦角,根据表 2的数据可知:cj=30 kPa,φj=32°;β为裂隙面倾角;σ1为最大主应力;σ3为最小主应力。
当试样沿着土体本身发生破坏时,满足式(2):
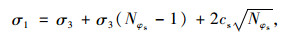
|
(2) |
式中,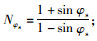
由式(1)和式(2)可知:当β≤φj=32°和β=90°时,试样的抗压强度由土体本身的强度控制;而当β≥φj=32°时试样的抗压强度由裂隙面强度控制,且当β=45°+φj/2=61°时裂隙试样的抗压强度取得最小值,这与试验结果和数值模拟结果一致。
将裂隙性黄土试样抗压强度的理论值与模拟值列于表 4,从表 4中可以看出,理论计算也表明随着裂隙倾角的增大,抗压强度也呈现出先减小后增大的趋势,不同的是当β≤φj=32°和β=90°时试样的抗压强度理论值相同,但是通过试验可以看出当β≤φj和β=90°抗压强度虽变化较小,但还有一定的变化,说明数值模拟结果比理论计算结果更加符合实际情况。除此之外值得注意的是,当裂隙倾角为40°~50°范围时,理论结果为40°时抗压强度达到最大,而数值模拟结果为45°时抗压强度达到最大。当裂隙倾角为0°和90°时抗压强度的数值结果和理论结果基本相同。
| 裂隙倾角/(°) | 抗压强度模拟值/kPa | 抗压强度理论值/kPa |
| 0 | 217.5 | 212.1 |
| 10 | 256.7 | 212.1 |
| 20 | 265.5 | 212.1 |
| 30 | 258.8 | 212.1 |
| 40 | 202.6 | 238.8 |
| 45 | 270.6 | 160.0 |
| 50 | 101.0 | 128.1 |
| 60 | 84.8 | 108.4 |
| 70 | 64.8 | 120.8 |
| 90 | 213.6 | 212.1 |
3.2 对倾角为45°时数值计算结果的讨论
针对裂隙倾角在40°~50°范围内变化时,裂隙倾角为45°时试样应力应变曲线以及抗压强度出现的特殊情况,下面结合裂隙倾角为40°,45°,50°试样的应力应变曲线和试样破坏图对其进行讨论。
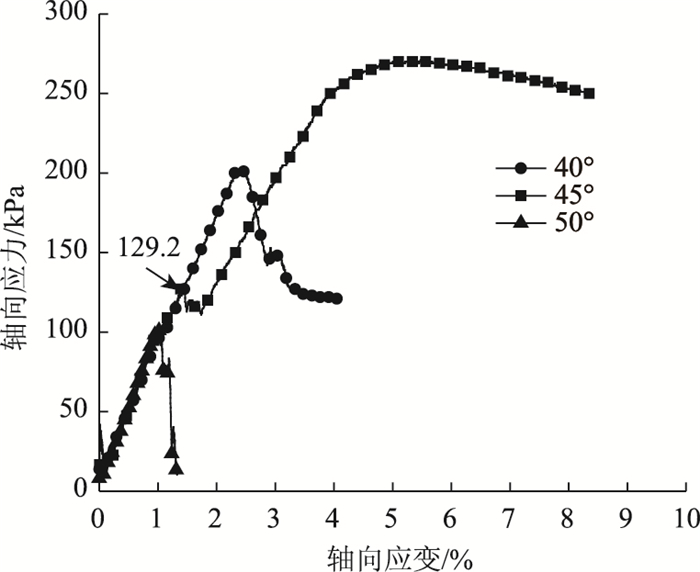
从3种不同倾角的试样破坏图(表 5)和裂隙试样的应力应变关系曲线(图 5)中可以看出,在轴向应力作用下,试样首先是沿着裂隙面发生微小变形,此时裂隙试样的强度受裂隙面控制,试样沿着裂隙面发生较小的滑移破坏,试样的应力-应变曲线出现峰值点,峰值点所相对应的峰值应力即受裂隙面控制时试样峰值强度。若以此峰值应力作为裂隙试样的抗压强度,如图 5中所示此时裂隙倾角为45°的试样对应的抗压强度为129.2 kPa,此时裂隙倾角为40°,45°,50°试样的抗压强度随倾角的变化规律就与理论计算结果一致。然而不同的是随着应变的增大,裂隙倾角为45°的试样不像裂隙倾角为40°和50°那样具有明显的应力降,而是发生较小的应力下降之后轴向应力随着应变的增大继续增大,因此倾角为45°的裂隙试样具有更高的抗压强度,即裂隙倾角为45°时试样的抗压强度除了受裂隙面的影响外还受土体本身强度的控制。此外,从试样破坏图中看出,裂隙倾角为45°的试样除了沿着裂隙面发生破坏外,试样在轴向方向上也发生了较大变形,具有明显的滑移和鼓胀现象,而裂隙倾角为40°和50°时试样的破坏主要沿着裂隙面发生滑移破坏。故裂隙倾角为40°和50°时试样的抗压强度受裂隙面强度的控制,而裂隙倾角为45°时试样的抗压强度除了受裂隙面强度的控制外还受土体本身强度的控制。因此裂隙倾角为45°时裂隙性黄土试样单轴抗压强度比其他裂隙倾角所对应的单轴抗压强度更大。
|
| 图 5 裂隙性黄土试样应力-应变曲线 Fig. 5 Stress-strain curves of fractured loess specimens |
| |
4 结论
本研究基于离散元法开展了不同裂隙倾角的裂隙性黄土在单轴压缩条件下试样的抗压强度和破坏特性的数值试验研究,得出如下结论:
(1) 裂隙性黄土试样中裂隙角度的不同,单轴压缩条件下试样的应力-应变关系曲线的形状和峰值应力具有较大的变化。裂隙性黄土试样中裂隙的角度为0°和90°时,试样的应力-应变关系曲线无明显应力降且应变较小。裂隙性黄土试样中裂隙的角度在10°~30°范围内变化时,试样的应力-应变关系曲线具有典型的裂隙压密、弹性变形、强度屈服以及峰后破坏等4个阶段。裂隙性黄土试样中裂隙的角度在40°~70°范围内变化时,试样的应力-应变关系曲线没有塑性屈服阶段,应变较小时,应力出现陡降;裂隙性黄土试样中裂隙的角度为45°时,试样的应力-应变曲线中间存在一段较小的屈服阶段。
(2) 裂隙试样中倾角的存在及其角度的变化对试样的单轴抗压强度的作用明显。随着裂隙试样中角度的不断增大,裂隙性黄土试样的抗压强度表现出先减小后增大的变化规律,且试样的单轴抗压强度存在最不利裂隙倾角区间(60°~70°),数值模拟与室内试验均有相同的结论。因此,在实际工程中应该对黄土中发育的裂隙、节理等不连续面的倾角予以充分重视。
(3) 裂隙性黄土中裂隙的存在及其角度的不同,试样在单轴压缩条件下的破坏模式不同,其破坏模式可以分为压裂、滑移、滑移压剪复合破坏以及压裂滑移混合破坏等4种破坏模式。
| [1] |
XU L, DAI F C, THAM L G, et al. Investigating Landslide-related Cracks along the Edge of Two Loess Platforms in Northwest China[J]. Earth Surface Processes & Landforms, 2012, 37(10): 1023-1033. |
| [2] |
孔德坊. 裂隙性黏土[M]. 北京: 地质出版社, 1994: 3-21. KONG De-fang. Fracture Clay[M]. Beijing: Geological Publishing House, 1994: 3-21. |
| [3] |
邓京萍, 张惠英. 成都黏土的裂隙性对力学性能的控制作用[J]. 水文地质工程地质, 1988, 15(2): 42-46. DENG Jing-ping, ZHANG Hui-ying. The Controlling of Fissure on the Mechanical Properties of Chengdu Clay[J]. Hydrogeology & Engineering Geology, 1988, 15(2): 42-46. |
| [4] |
OTOKO G R. Analysis of the Stability of Embankments on Clay Foundations[J]. International Journal of Engineering and Technology Research, 2014, 2(1): 1-11. |
| [5] |
VALLEJO L E. Compressive Strength of Unsaturated Fssured Clays[C]//Proceedings of 5th International Conference on Unsaturated Soils. Barcelona: CRC Press, 2010: 387-390.
|
| [6] |
高建伟, 余宏明, 李科. 黄土无侧限抗压强度的试验研究[J]. 安全与环境工程, 2014, 21(4): 132-137. GAO Jian-wei, YU Hong-ming, LI Ke. Experimental Research on Unconfined Compression Strength of Loess[J]. Safety and Environmental Engineering, 2014, 21(4): 132-137. |
| [7] |
王景明. 地裂缝及其灾害的理论与应用[M]. 西安: 陕西科学技术出版社, 2000. WANG Jing-ming. Theory of Ground Fissure and Its Disasters and Application[M]. Xi'an: Shannxi Science and Technology Press, 2000. |
| [8] |
李彦武. 黄土地区路基防护与支挡工程病害及防治措施[J]. 公路交通科技, 2009, 26(9): 53-58. LI Yan-wu. Diseases of Subgrade Protection and Retaining Engineering in Loess Area and Control Measures[J]. Journal of Highway and Transportation Research and Development, 2009, 26(9): 53-58. |
| [9] |
谢定义. 试论我国黄土力学研究中的若干新趋向[J]. 岩土工程学报, 2001, 23(1): 3-13. XIE Ding-yi. Exploration of Some New Tendencies in Research of Loess Soil Mechanics[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(1): 3-13. |
| [10] |
卢全中.裂隙性黄土的力学特性及其工程灾害效应研究[D].西安: 长安大学, 2007. LU Quan-zhong. Study on Mechanical Property of Fractured Loess and Engineering Hazard Effects[D].Xi'an: Chang'an University, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1529085 |
| [11] |
周彬.裂隙性黄土平面应变压缩试验研究[D].西安: 长安大学, 2013. ZHOU Bin. Fissured Loess Plane Strain Compression Test[D]. Xi'an: Chang'an University, 2013. |
| [12] |
SUN P, PENG J B, CHEN L W, et al. An Experimental Study of the Mechanical Characteristics of Fractured Loess in Western China[J]. Bulletin of Engineering Geology and the Environment, 2016, 75: 1639-1647. |
| [13] |
孙萍, 彭建兵, 吴树仁, 等. 裂隙性黄土力学特性试验研究[J]. 中南大学学报:自然科学版, 2015, 46(6): 2188-2195. SUN Ping, PENG Jian-bing, WU Shu-ren, et al. An Experimental Study on Mechanical Properties of Fractured Loess[J]. Journal of Central South University:Science and Technology Edition, 2015, 46(6): 2188-2195. |
| [14] |
贾晖, 和耀林, 杨世贤. 节理对黄土破坏形态和力学性质的影响研究[J]. 中国农村水利水电, 2011, 36(11): 77-81. JIA Hui, HE Yao-lin, YANG Shi-xian. Rupture and Mechanics Behavior of Loess Affected by Joints in it[J]. China Rural Water and Hydropower, 2011, 36(11): 77-81. |
| [15] |
程龙虎, 聂如松, 刘飞. 裂隙性黄土单轴抗压试验研究[J]. 水文地质工程地质, 2017, 44(5): 80-85, 91. CHENG Long-hu, NIE Ru-song, LIU Fei. An Experimental Study of the Uniaxial Compressive Strength of Fractured Loess[J]. Hydrogeology & Engineering Geology, 2017, 44(5): 80-85, 91. |
| [16] |
何忠明, 彭振斌, 曹平, 等. 层状岩体单轴压缩室内试验分析与数值模拟[J]. 中南大学学报:自然科学版, 2010, 41(5): 1906-1912. HE Zhong-ming, PENG Zhen-bin, CAO Ping, et al. Test and Numerical Simulation for Stratified Rock Mass under Uniaxial Compression[J]. Journal of Central South University:Science and Technology Edition, 2010, 41(5): 1906-1912. |
| [17] |
张华, 陆阳, 余建华. 连续-离散介质动力耦合模型在斜坡堆积体地震响应分析中的应用[J]. 公路交通科技, 2011, 28(5): 6-11, 27. ZHANG Hua, LU Yang, YU Jian-hua. Application of Continuum and Discrete Medium Dynamic Coupling Model in Seismic Response Analysis of a Deposit Covered Slope[J]. Journal of Highway and Transportation Research and Development, 2011, 28(5): 6-11, 27. |
| [18] |
罗世林, 万文, 赵延林, 等. 层状岩体单轴压缩破坏数值研究[J]. 矿业工程研究, 2016, 31(2): 50-56. LUO Shi-lin, WAN Wen, ZHAO Yan-lin, et al. Numerical study of Layered Rock Mass under Uniaxial Compression Failure[J]. Mineral Engineering Research, 2016, 31(2): 50-56. |
 2019, Vol. 36
2019, Vol. 36