扩展功能
文章信息
- 王浩, 陈冬
- WANG Hao, CHEN Dong
- 城市交叉口群的聚类分析分类算法
- Clustering Analysis and Classification Algorithm for Urban Intersections
- 公路交通科技, 2019, 36(7): 121-126, 142
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(7): 121-126, 142
- 10.3969/j.issn.1002-0268.2019.07.015
-
文章历史
- 收稿日期: 2018-04-10
为了提升道路网整体运行效益,协调控制(划分子区)逐渐成为解决运行效益的主流方法[1-2]。但协调各个交叉口,往往会忽视交叉口的差异性,无法为每一个交叉口配置个性化的配时方案[3-4]。基于交叉口流量数据的交叉口分类算法,较好地兼顾了协调控制和个性化配时方案两方面,同一类的交叉口配时方案相似,地理位置或距离相近(易于划分子区)。当前对于交叉口流量数据的分析主要分为两类,一种是基于支持向量机的研究,另外一种是建立在隐马尔可夫模型上的研究[5-6]。但是针对交通流量数据而言,并不是所有的参数都具有相同的重要性,无法排除弱势参数对最终结果的过度干扰[7-8]。
道路交叉口所具有的大数量的流量数据,比较适合运用聚类算法对数据进行分析。目前有两种基本类型的聚类算法:层次聚类和划分聚类[9]。划分聚类算法通常分为两步程序。首先确定划分聚类的集群个数k和用于度量的目标函数。其次,将每个对象分配给与其特征“最为接近”的集群[10]。Ng & Han讨论了在一个集群中数据库如何确定“自然”数k的方法。对于每个发现的聚类,计算轮廓系数,最后选择具有最大轮廓系数的聚类作为“自然”聚类。但是对于数据库的数据个数n而言,这种方法的运行时间是令人失望的缓慢,无法满足现实的快速需求[11]。同时,划分聚类分析还要求所划分的聚类个数一般是在2~15个之间。城市交叉口的交通参数维数众多,每天都可以产生大量的数据,交通流量具有临近性、周期性、趋势性,而且对于固定区域的交叉口分类个数一般是保持在10个以内的,部分城区更是可以将交叉口分类个数确定在5个以内。综上所述,划分聚类分析满足交叉口分类算法的需求[12]。
1 使用流量作为交叉口分类依据的可行性分析交叉口的交通流量是确定交叉口绿信比、相位相序和饱和度的基础参数,同时也是判定早晚高峰和优化信号的时段划分的基本依据。应用交通流量优化交叉口时段划分两种方式,其中一种是根据交叉口的总流量进行判断[13],较为优化的方法是应用各个支路的交通分流量为时段划分提供更加精确的数据基础[14]。基于RBF神经网络的交通流量预测算法为后续的智能交通控制与管理提供了基础数据[15-16],同时基于车型聚类的交通流参数检测算法也为交通流数据的获取提供了新的思路[17]。交通流量为交叉口的分类提供了基础的数据依据和较为可靠的分类标准。
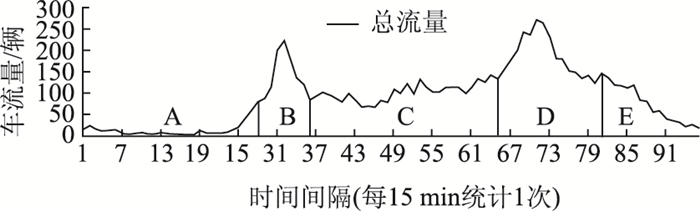
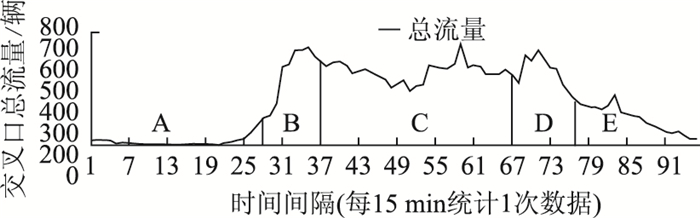
一般交叉口的总流量如图 1所示,通常可以将全天的时间划分为5个主要段落。
|
| 图 1 一般交叉口时间段划分示意图 Fig. 1 Schematic diagram of time division for general intersection |
| |
由于本研究着眼于苏州工业园区的路网和交叉口,并且在统计单位时间内的流量时,每15 min为一单位,全天一共96个单位,以后时间的变化就以单位时间的序号为准。根据苏州工业园区107个交叉口的统计数据,对早高峰和晚高峰的起止单位时间的序号求平均数,求得统一的起止单位时间序号,作为后续研究的根据。
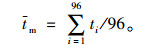
|
(1) |
确定该交叉口的各主要段落,本研究统一规定:
A.时段0~28为高峰前期;B.早高峰:时段29~37;C.时段38~67为平谷期; D.晚高峰:时段68~77;E.时段78~96为高峰后期。
2 分类基准参数模型的确立五数概括是数据处理中最为基础的数据特征,其中包括中位数(Q2)、四分位数Q1和Q3、最小和最大观测值,通常按照次序Minimum,Q1,Median,Q3,Maximum写出[9]。本研究建立了以下新型的“五数概括”,用以描述流量的特征,方便以后的聚类分析。
SC为C段的平均值;σC2为C段的平方差;σ2SC-max为C2段的最大值;Q1为第1个四分位数(即从大到小排第25位);Q3为第3个四分位数(即从大到小排第72位);
由此我们确立了可以与每一个交叉口一一对应的多维向量:
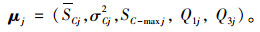
|
(2) |
在划分方法中,质点被分为若干组并根据给定的规则改组成最有粘性的族群。因为K均值聚类方法是基于均值的,所以它对异常值是敏感的。一个更稳健的方法是围绕中心点的划分(PAM)。与其用质心(变量均值向量)表示类,不如用一个最有代表性的观测值来表示(称为中心点)。K均值聚类一般使用欧几里得距离,而PAM可以使用任意的距离来计算。因此,PAM可以容纳混合数据类型,并且不仅限于连续变量[18-20]。
PAM算法如下:
(1) 随机选择K个观测值(每个都称为中心点):
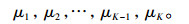
|
(3) |
(2) 计算观测值到各个中心的距离/相异性,取任意一个观测值,计算其与K个中心点μ1,μ2,…, μK-1, μK的距离:
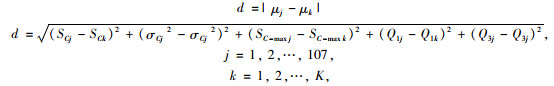
|
(4) |
(3) 把每个观测值分配到最近的中心点:
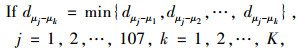
|
then μj∈Xμk,Xμk为以μk为中心点的集合。
(4) 计算每个中心点到每个观测值的距离总和(总成本)。
计算随机聚类的某一个组群的群内非中心点到中心点的欧氏距离之和:
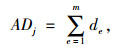
|
(5) |
式中, m为某一个组群内所有观测值的个数;e为某一个组群内所有观测值的编号;ADi为某一个组群内所有非中心点到中心点的欧氏距离之和,i为随机聚类组群的编号。
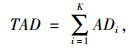
|
(6) |
式中TAD为该群观测值的所有随机聚类组群欧氏距离之和的总和。
(5) 选择一个该类中不是中心的点,并和中心点互换:
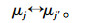
|
(7) |
(6) 重新把每个点分配到距它最近的中心点:
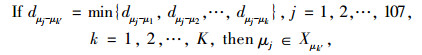
|
式中Xμk′为以μk′为中心点的集合。
(7) 再次计算总成本:
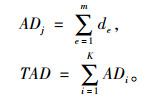
|
(8) |
(8) 如果总成本比步骤(4)计算的总成本少,把新的点作为中心点。
(9) 重复步骤(5)~(8)直到中心点不再改变。
最终得到每一类的最终中心点集合{*μ1,*μ2,…, *μK-1, *μK},这些中心点的参数SCj, σCj2, SC-maxj, Q1j, Q3j,能够代表本类的平均水平,是本类各项特征的综合体现。在同一类的观测值与彼此之间的距离或者说相似程度都要比类外各个观测值要近或者说相似程度高。
围绕中心点的划分(Partitioning Around Medoid)PAM算法,有时也称为k-中心点算法,是指用中心点来代表一个簇。PAM算法的目的是对n个数据对象给出k个划分。PAM算法的基本思想:PAM算法的目的是对成员集合D中的N个数据对象给出k个划分,形成k个簇,在每个簇中随机选取1个成员设置为中心点,然后在每一步中,对输入数据集中目前还不是中心点的成员根据其与中心点的相异度或者距离进行逐个比较,看是否可能成为中心点。用簇中的非中心点到簇的中心点的所有距离之和来度量聚类效果,其中成员总是被分配到离自身最近的簇中,以此来提高聚类的质量。
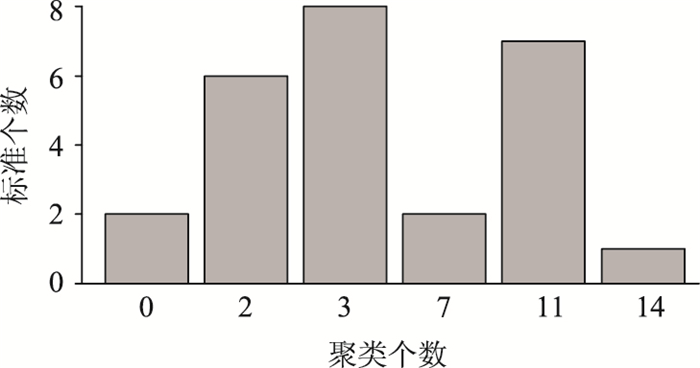
4 划分的分类个数(类的个数确定)本研究使用两种办法确定交叉口类的个数,一种是使用R语言中的Nbclust方法。首先计算机系统定义了几十个评估指标,接着聚类数目从2遍历到15(计算机系统自己设定),然后通过这些指标看分别在聚类数为多少时达到最优,最后选择指标支持数最多的聚类数目就是最佳聚类数目。如图 2所示,是在R语言环境下,调用Nbclust方法,对107个交叉口进行可能的分类个数的预测。由图 2可以看出,针对这107个交叉口,本研究在使用Nbclust方法后,“根据多数规则,最好的数目是3”。
|
| 图 2 Nbclust方法确定分类个数统计图 Fig. 2 Determining number of categories by Nbclust method |
| |
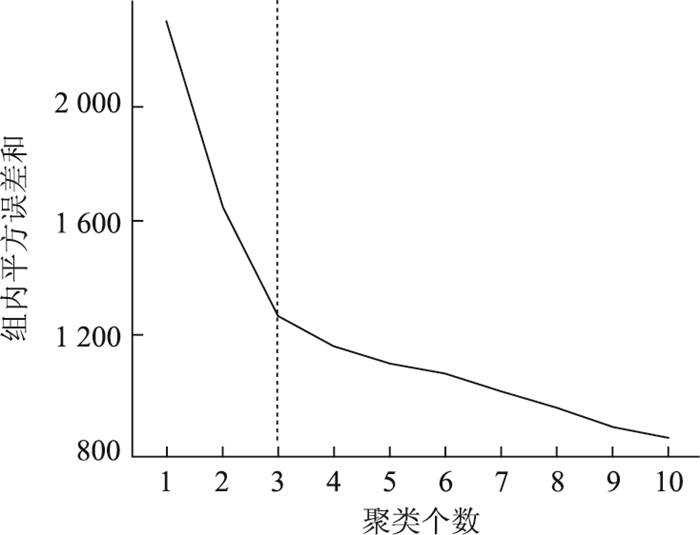
另外一种方法是使用组内平方误差和拐点图,在R语言中,本研究使用wssplot()函数来实现该功能,如图 3所示。想必之前动辄几十个指标,这里就用一个最简单的指标——sum of squared error (SSE)组内平方误差和来确定最佳聚类数目。这个方法是自定义的一个求组内误差平方和的函数。
|
| 图 3 wssplot()函数结果示意图 Fig. 3 Schematic diagram of result of wssplot () function |
| |
随着聚类数目增多,每一个类别中数量越来越少,距离越来越近,因此WSS值肯定是随着聚类数目增多而减少的,所以关注的是斜率的变化,但WWS减少得很缓慢时,就认为进一步增大聚类数效果也并不能增强,存在得这个“肘点”就是最佳聚类数目,从1类到3类下降得很快,之后下降得很慢,所以最佳聚类个数选为3。
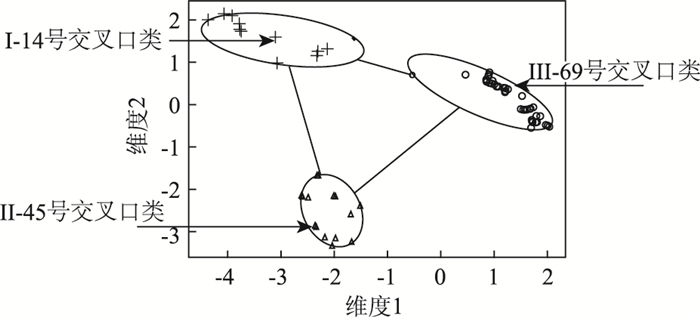
5 聚类分析交叉口划分的结果由上文所提及的交叉口的分类方法和类的个数确定。本研究使用R语言环境,对苏州工业园区107个交叉口进行聚类分析,得到的结果如图 4所示。“这两个参数解释了89.2%的点变化性”,PAM划分聚类算法认为向量μj=(SCj, σCj2, SC-maxj, Q1j, Q3j)中的两个维度为如下分类可能性提供了89.2%的支持。
|
| 图 4 分类结果示意图 Fig. 4 Schematic diagram of classification result |
| |
由图 4可以看出,应用聚类分析将107个交叉口分为3个大的族群,其中3大族群的中心点分别如图 5所示,可以看出第1类的中心点为代号是14的交叉口,第2类的中心点为代号是45的交叉口,第3类的中心点为代号是69的交叉口。

|
| 图 5 族群中心点输出 Fig. 5 Output of community centers |
| |
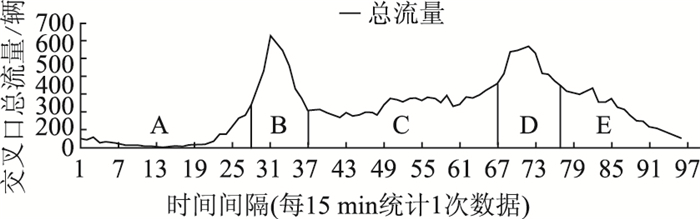
根据图 4提供的3个族群的中心点信息,本研究可以在苏州工业园区中找到对应的交叉口流量变化示意图。图 6~图 8由上到下分别为族群Ⅰ的中心点14号交叉口,族群Ⅱ的中心点45号交叉口,族群Ⅲ的中心点69号交叉口的流量变化示意图。
|
| 图 6 族群Ⅰ的中心点14号交叉口流量 Fig. 6 Traffic volume at Intersection 14 (center point of community Ⅰ) |
| |
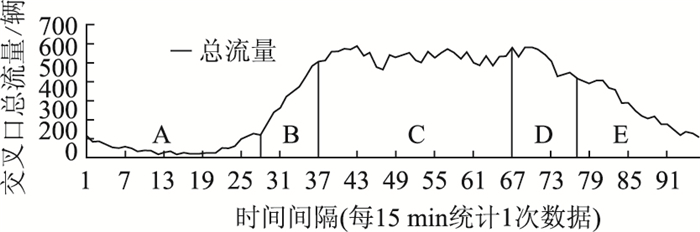
|
| 图 7 族群Ⅱ的中心点45号交叉口流量示意图 Fig. 7 Traffic volume at Intersection 45 (center point of community Ⅱ) |
| |
|
| 图 8 族群Ⅲ的中心点69号交叉口流量示意图 Fig. 8 Traffic volume at Intersection 69 (center point of community Ⅲ) |
| |
6 聚类结果的验证
根据上文,将苏州工业园区的107个交叉口分为3类,每一类的中心点能够体现本类中各点的集体特点,是本类各项特征的综合体现。接下来,本研究根据每一类中心点交叉口的数据,使用synchro7软件对该交叉口进行自动配时优化、周期优化和绿信比优化。最后,将中心点交叉口的管理方案应用到本类的其他交叉口。原本4号交叉口(钟南街-方洲路)45号交叉口(万盛路-旺墩街)和69号交叉口(星湖街-钟园路)的总停车时间为90.325,77.575,81.025 h。根据Wang Hao, ChenDong的研究[14],分别对14号交叉口(钟南街-方洲路)45号交叉口(万盛路-旺墩街)和69号交叉口(星湖街-钟园路)提出优化方案,并将方案应用到本类的其他交叉口。表 1~表 3为应用优化方案后3个交叉口的总停车时间。
| 时间段编号 | 起止时间 | 每小时停车时间/h | 时间段时长/h | 总停车时间/h |
| A | 6:45—9:15 | 7.25 | 2.50 | 18.125 |
| B | 9:15—13:15 | 2.90 | 4.00 | 11.600 |
| C | 13:15—15:45 | 4.00 | 2.50 | 10.00 |
| D | 15:45—20:00 | 5.80 | 4.25 | 24.650 |
| E | 20:00—22:15 | 4.00 | 2.25 | 9.000 |
| F | 22:15—6:45 | 1.40 | 8.50 | 11.900 |
| 合计 | — | — | 24 | 85.275 |
| 时间段编号 | 起止时间 | 每小时停车时间/h | 时间段时长/h | 总停车时间/h |
| A | 7:15—9:15 | 5.0 | 2.00 | 10.000 |
| B | 9:15—13:00 | 2.9 | 3.75 | 10.875 |
| C | 13:00—15:45 | 3.3 | 2.75 | 9.075 |
| D | 15:45—19:30 | 6.7 | 3.75 | 25.125 |
| E | 19:30—21:45 | 3.8 | 2.25 | 8.550 |
| F | 21:45—7:15 | 0.9 | 9.50 | 8.550 |
| 合计 | — | — | 24.00 | 72.175 |
| 时间段编号 | 起止时间 | 每小时停车时间/h | 时间段时长/h | 总停车时间/h |
| A | 7:15—9:15 | 5.0 | 2.00 | 10.000 |
| B | 9:15—13:00 | 2.9 | 3.75 | 10.875 |
| C | 13:00—15:45 | 3.3 | 2.75 | 9.075 |
| D | 15:45—19:30 | 5.80 | 3.75 | 21.750 |
| E | 19:30—21:45 | 4.00 | 2.25 | 9.000 |
| F | 21:45—7:15 | 1.40 | 9.50 | 13.300 |
| 合计 | — | — | 24.00 | 73.70 |
由表 4可以看出,在107个交叉口中有80个交叉口的总停车时间减少了,占到了所有交叉口的74.8%,所有交叉口一共减少了241.325 h的停车时间,平均每个交叉口减少2.26 h。但是各类的交叉口优化比例却不一致,Ⅰ-14号交叉口类只有15个交叉口停车时间得到了优化,所占比例仅是45.50%,类内交叉口总停车时间为31.25 h,平均下来一个交叉口仅仅优化了不到1 h。而Ⅱ-45号交叉口类和Ⅲ-69号交叉口类表现了较好的优化,两类交叉口一共减少了210.075 h,平均每个交叉口节省了近3 h。
| 大类 | 类内交叉口个数/个 | 类内交叉口总停车时间/h | 停车时间减少的交叉口个数/个 | 停车时间增加的交叉口个数/个 | 停车时间持平的交叉口个数/个 | 比例/% |
| Ⅰ-14号交叉口类 | 33 | 31.25 | 15 | 16 | 2 | 45.50 |
| Ⅱ-45号交叉口类 | 27 | 69.075 | 24 | 2 | 1 | 88.90 |
| Ⅲ-69号交叉口类 | 47 | 141.00 | 41 | 4 | 2 | 87.20 |
| 合计 | 107 | 241.325 | 80 | 22 | 5 | — |
7 结论
城市交叉口数目众多,可以通过合理化地分类算法,对交叉口进行分类,进而对每一类交叉口统一管理或者分配交通管理方案,提高交叉口通过效率。本研究通过使用划分聚类分析的算法,对苏州工业园区的107个交叉口进行分类,通过建立相异性函数,衡量聚类中交叉口的相似性。最终将苏州工业园区107个交叉口分为3类,每一类都对族群内各个交叉具有较高的相似性,对族群外的交叉口差别较大。每一族群的中心交叉口对本族群具有良好的代表性,集中体现了本族群交叉口的特征,为以后各类交叉口设计合理的交通管理方案,提供了良好的基础。在107个交叉口中有80个交叉口的总停车时间减少了,占到了所有交叉口的74.8%,所有交叉口一共减少了241.325 h的停车时间,平均每个交叉口减少2.26 h。
| [1] |
GHODS A H, FU L P, RAHIMI-KIAN A. An Efficient Optimization Approach to Real-time Coordinated and Integrated Freeway Traffic Control[J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(4): 873-884. |
| [2] |
徐洁琼, 姚佼, 倪枫. 城市干道的多时段协调控制优化[J]. 公路交通科技, 2017, 34(8): 114-122, 129. XU Jie-qiong, YAO Wei, NI Feng. Arterial Time-of-day Coordinated Control Optimization in Urban Area[J]. Journal of Highway and Transportation Research and Development, 2017, 34(8): 114-122, 129. |
| [3] |
赵靖, 马万经, 汪涛, 等. 基于宏观基本图的相邻子区协调控制方法[J]. 交通运输系统工程与信息, 2016, 16(1): 78-84. ZHAO Jing, MA Wan-jing, WANG Tao, et al. Coordinated Perimeter Flow Control for Two Subareas with Macroscopic Fundamental Diagrams[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(1): 78-84. |
| [4] |
张逊逊, 许宏科, 闫茂德. 基于MFD的城市区域路网多子区协调控制策略[J]. 交通运输系统工程与信息, 2017, 17(1): 98-105. ZHANG Xun-xun, XU Hong-ke, YAN Mao-de. Coordinated Control Strategy for Multi-subarea Based on MFD in Urban Zonal Road Networks[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(1): 98-105. |
| [5] |
AOUDE G S, DESARAJU V R, STEPHENS L H, et al. Driver Behavior Classification at Intersections and Validation on Large Naturalistic Data Set[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2): 724-736. |
| [6] |
BISHOP C M. Pattern Recognition and Machine Learning (Information Science and Statistics)[M]. New York: Springer-verlag, 2006.
|
| [7] |
MAJI S, BERG A C, MALIK J. Classification using Intersection Kernel Support Vector Machines is Efficient[C]//2008 IEEE Conference on Computer Vision and Pattern Recognition. Anchorage, USA: IEEE, 2008: 1-8. https://www.researchgate.net/publication/221363163_Classification_using_intersection_kernel_support_vector_machines_is_efficient
|
| [8] |
VELAN P, ČERMÁK M, ČELEDA P, et al. A Survey of Methods for Encrypted Traffic Classification and Analysis[J]. International Journal of Network Management, 2015, 25(5): 355-374. |
| [9] |
HAN J. Data Mining:Concepts and Techniques[M]. .
|
| [10] |
ESTER M, KRIEGEL H P, XU X. A Density-based Algorithm for Discovering Clusters a Density-based Algorithm for Discovering Clusters in Large Spatial Databases with Noise[C]//International Conference on Knowledge Discovery and Data Mining. Portland: AAAI Press, 1996: 226-231.
|
| [11] |
JAIN A K, DUBES R C. Algorithms for Clustering Data[J]. Technometrics, 1988, 32(2): 227-229. |
| [12] |
LOUHICHI S, GZARA M, ABDALLAH H B. A Density Based Algorithm for Discovering Clusters with Varied Density[C]//2014 World Congress on Computer Applications and Information Systems (WCCAIS). Hammamet, Tunisia: IEEE, 2014: 1-6.
|
| [13] |
李清泉, 曹晶, 乐阳, 等. 短时交通流量模式提取及时变特征分析[J]. 武汉大学学报:信息科学版, 2011, 36(12): 1392-1396. LI Qing-quan, CAO Jing, LE Yang, et al. Pattern Extraction and Temporal Evolution of Short-term Traffic Volume[J]. Journal of Wuhan University, 2011, 36(12): 1392-1396. |
| [14] |
WANG H, CHEN D. Traffic Signal Segmentation Algorithm Based on Two Dimensional Clustering of Traffic Volume and Vector Angles[C]// 2017 International Smart Cities Conference (ISC2). Wuxi: IEEE, 2017. https://ieeexplore.ieee.org/document/8090784
|
| [15] |
朱文兴, 龙艳萍, 贾磊. 基于RBF神经网络的交通流量预测算法[J]. 山东大学学报:工学版, 2007, 37(4): 23-27. ZHU Wen-xing, LONG Yan-ping, JIA Lei. Traffic Volume Forecasting Algorithm Based on RBF Neural Network[J]. Journal of Shandong University:Engineering Science Edition, 2007, 37(4): 23-27. |
| [16] |
管硕, 高军伟, 张彬, 等. 基于K-均值聚类算法RBF神经网络交通流预测[J]. 青岛大学学报:工程技术版, 2014, 29(2): 20-23. GUAN Shuo, GAO Jun-wei, ZHANG Bin, et al. Traffic Flow Prediction Based on K-means Clustering Algorithm and RBF Neural Network[J]. Journal of Qingdao University:Engineering & Technology Edition, 2014, 29(2): 20-23. |
| [17] |
吴聪, 李勃, 董蓉, 等. 基于车型聚类的交通流参数视频检测[J]. 自动化学报, 2011, 37(5): 569-576. WU Cong, LI Bo, DONG Rong, et al. Detecting Traffic Parameters Based on Vehicle Clustering from Video[J]. Acta Automatica Sinica, 2011, 37(5): 569-576. |
| [18] |
FEBBRARO A D, GIGLIO D, SACCO N. Urban Traffic Control Structure Based on Hybrid Petri Nets[J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(4): 224-237. |
| [19] |
KABACOFF R I. R in Action: Data Analysis and Graphics with R[M]. English ed. Beijing: Posts and Teleco Press, 2013.
|
| [20] |
王浩, 包林基, 云美萍. 交叉口直行待行区的车辆延迟启动策略分析[J]. 公路交通科技, 2016, 33(4): 108-112. WANG Hao, BAO Lin-ji, YUN Mei-ping. Analysis of Delayed Starting Strategy for Through Vehicles at Intersection Waiting-zone[J]. Journal of Highway and Transportation Research and Development, 2016, 33(4): 108-112. |
 2019, Vol. 36
2019, Vol. 36
