扩展功能
文章信息
- 张惠玲, 陈华伟, 敖谷昌
- ZHANG Hui-ling, CHEN Hua-wei, AO Gu-chang
- 基于级差效益的驾驶员个性化路径选择
- Driver's Personalized Route Choice Based on Differential Benefit
- 公路交通科技, 2019, 36(7): 114-120
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(7): 114-120
- 10.3969/j.issn.1002-0268.2019.07.014
-
文章历史
- 收稿日期: 2018-02-01
2. 重庆交通大学 交通运输学院, 重庆 400074
2. School of Traffic & Transportation, Chongqing Jiaotong University, Chongqing 400074, China
随着公路信息化与智能化水平的显著提升,路网信息的全方位、实时获取已成为可能,针对驾驶员的出行路径选择也成为了交通信息化领域的研究重点[1-2]。出行路径选择以ITS实时提供的路况信息和驾驶员的交通需求为输入,在一定的优化目标下,为驾驶员提供最合理的出行路径。由于驾驶员间出行需求的差异,对于最优路径的理解不尽相同。以往的路径选择研究侧重考虑出行时间最少或者距离最短,优化目标比较单一且忽略了驾驶员的个性化需求[3]。同时,由于优化目标相同,诱导系统向不同驾驶员提供了相同的最优路径,这将导致最优路径上的车辆过度聚集,造成路网中的交通流处于失衡状态[4]。因此,在公路成网和信息共享的前提下,研究多属性条件下的路径选择问题不仅很有必要,也成为了可能。
目前,国内外针对多属性路径选择问题进行了许多有益的尝试,包括龙琼等[5]提出的物理规划法,孙燕等[6]提出的灰色理论法,PANG G K H等[7]提出的模糊神经网络法以及龙雪琴等[8]提出的前景理论法。这些模型的公路属性的主观性较强。但在实际生活中,公路属性值是路网信息的反映,应该是客观的区间数,而不应该是驾驶员对客观公路状况的主观评价。因此,笔者首先利用公路评价指标的级差效益作为公路属性值,通过模糊分析法处理驾驶员的个性化需求,求得驾驶员个性化的属性权重,然后算出可行方案的综合级差效益,最后通过排序选择最优路径。这种模型既保留了目标属性的客观性,又能直观反映出驾驶员对出行路径选择的本质,即驾驶员追求自身利益的最大化。
1 不确定型多属性决策方法多属性决策是指为了实现一定目标,在考虑多个属性的情况下,选择最优备选方案或进行方案排序的过程[4]。对于多属性的路径选择而言,驾驶员往往以自身建立的路径评价指标体系为基础,对不同的路径进行综合比较,从而选出符合自身利益需要的出行路径。
公路网络是一个复杂的网络,路网信息具有很强的动态性和随机性[9],评价指标的指标值会随时间不断变化,所以路径评价具有不确定性[10]。对于动态出行路径选择的不确定型多属性决策问题,设可行方案集合为Y={yi|i=1, …, m}, m为可行路径方案数,决策属性集合为X={xj|j=1, …, n},属性的权重向量为W=(w1, …, wn)T,其中,wj=[wjL, wjU]为属性xj的权重区间,wjL和wjU分别为该权重区间的上下界; 属性权重应该满足∑wjL≤1和∑wjU≥1,且对于任意的wjL,wjU≥0。aij=[aijL, aijU]为可行方案yi关于属性xj的取值区间,aijL和aijU分别为该取值区间的上下界,则决策矩阵为:
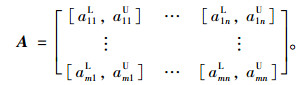
|
(1) |
考虑到属性类型之间存在的差异,为了消除不同属性之间物理量纲和数量级的差异对决策结果的影响,需要对决策矩阵进行规范化处理。
基于误差传递法[11],决策矩阵A=(aij)m×n可以写成误差分布形式,即A=[A-ΔA, A+ΔA],其中,A=(aij)m×n为中间值矩阵,ΔA=(Δaij)m×n为最大估计误差矩阵,对应的计算公式为:
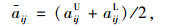
|
(2) |
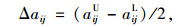
|
(3) |
式中, aij为中间值矩阵A的元素; Δaij为最大估计误差矩阵ΔA的元素。
当min(aijL) < 0时,为了保证决策矩阵的非负性,需对决策矩阵进行平移,平移后的决策矩阵为B=[B-ΔB, B+ΔB],其中,B=(bij)m×n为平移后的中间值矩阵,ΔB=(Δbij)m×n为平移后的最大估计误差矩阵,相关的计算公式为:
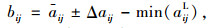
|
(4) |
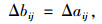
|
(5) |
式中,bij为平移后的决策矩阵B的元素;Δbij为平移后的最大估计误差矩阵ΔB的元素。
决策矩阵的规范化,首先对矩阵B=(bij)m×n进行规范化处理,得到规范化后的矩阵C=(cij)m×n。由于本研究的决策属性均为效益型,故采用的规范化公式如下:
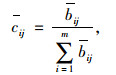
|
(6) |
式中, bij为平移后的中间值矩阵B的元素;cij为规范化后的研究中间值矩阵C的元素。
接着对矩阵ΔB=(Δbij)m×n进行规范化处理,得到规范化后的矩阵ΔC=(Δcij)m×n,公式为:
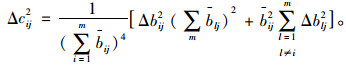
|
(7) |
最后得到规范化后的决策矩阵C=(cij)m×n,即C=[C-ΔC, C+ΔC]。
多属性决策的本质是各方案的综合属性值的比较。由方案yi的属性值ci=(ci1, …, cin)与属性权重向量W,即可算得方案yi的综合属性值zi:
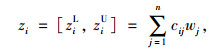
|
(8) |
式中,ziU和ziL分别为方案yi综合属性值区间的上下界。
由于zi=[ziL, ziU]仍是区间数,不能直接对方案进行排序,需定义区间数可能度的概念[4]。设zi=[ziL, ziU]和zj=[zjL, zjU](1≤i, j≤m),记zi区间的长度L(zi)=ziU-ziL,zj区间的长度L(zj)=zjU-zjL,则zi≥zj的可能度pij=P(zi≥zj)为[12]:
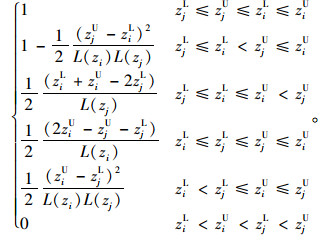
|
(9) |
根据方案属性值间的可能度pij,建立可能度互补矩阵P=(pij)m×m,采用行和归一化公式求得方案排序向量S=(s1, …, sm)T,其中元素si为[13]:
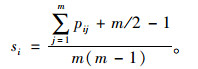
|
(10) |
按照方案排序向量S元素的大小对方案进行排序,即可得到最优方案。
2 公路单级差效益的定量化模型 2.1 相关概念参考相关[14],级差效益指相较于使用其他道路,出行者使用某条道路而获得的效益差。公路单级差效益是公路之间单一评价指标的级差效益,如成本级差效益、适应性级差效益。公路综合级差效益是指驾驶员行驶在不同公路上时,由于主观感受(如舒适性)和外界条件(如油耗成本)不同而产生的综合级差效益。公路的综合级差效益由单级差效益组成,为单级差效益的加权之和。
2.2 级差效益综合评价指标体系随着交通出行方式及出行路径的日趋多样化,驾驶员也越来越重视出行效益的高低。对于不同的驾驶员,出行效益的侧重也不同,例如有的驾驶员注重运输时间的节约,有的注重安全性的提高。为了更加系统地分析比较不同的出行路径,描述驾驶员的个性化需求,首先需要构建级差效益评价指标体系,确定驾驶员路径选择的评价内容。
级差效益评价指标体系与服务水平评价指标体系有关,服务水平评价指标体系主要考虑公路运输的高效性、便捷性、经济性、安全性、舒适性[15]。从驾驶员的角度考虑,理想最优路径的确定应综合考虑上述公路运输特性,并充分体现驾驶员的主观性[3]。笔者综合面向驾驶员的个性化需求,构建路径的评价指标集,即级差效益评价指标体系:
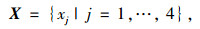
|
(11) |
式中,x1为运输时间;x2为运输成本;x3为交通安全;x4为舒适性。
基于选定的级差效益评价指标体系,建立单级差效益的定量化模型,包括时间效益模型、成本效益模型、安全效益模型、舒适性效益模型。
2.3 运输时间节约的效益运输时间节约的效益是指驾驶员在节约的行程时间中所创造的社会价值,与驾驶员的社会属性、路径里程和行程时间差值有关,定量化模型为:
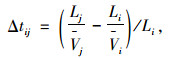
|
(12) |
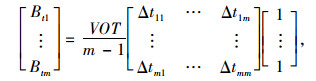
|
(13) |
式中,Bti为第i(1≤i≤m)条路径的运输时间节约的效益;VOT为驾驶员时间价值;m为可行路径数;Δtij为第j(1≤j≤m)条路径与第i条路径的相对时间差;Li和Lj分别为第i, j条路径的里程;Vi和Vj分别为第i, j条路径车辆的平均车速。
2.4 运输成本降低的效益运输成本降低的效益是指与其他路径相比,车辆在该路径上节约了运输成本而产生的潜在效益,与油耗、燃油价格和公路收费标准有关,其降低的效益模型为[16]:
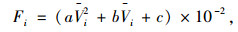
|
(14) |
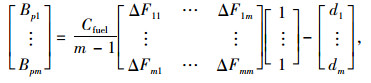
|
(15) |
式中,Bpi为第i条路径运输成本降低的效益;Cfuel为燃油价格;di为第i条路径的平均收费标准;Fi为第i条路径的油耗;ΔFij为第j条路径与第i条路径的油耗差(ΔFii=0);a, b, c为模型参数。
2.5 交通安全的效益交通安全的效益是指相对于其他路径,由于该路径事故经济损失风险低而在提高行驶安全性上产生的效益,与公路事故率和事故平均经济损失(包括直接经济损失和间接经济损失)有关。关于交通安全效益的定量化模型为:
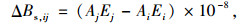
|
(16) |
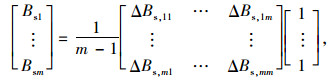
|
(17) |
式中,Bsi为第i条路径的交通安全效益;ΔBs, ij为第i条路径与第j条路径的安全效益差;Ai为第i条路径的交通事故率;Ei为第i条路径的交通事故平均经济损失。
2.6 舒适性的效益一般情况下,舒适性的效益是指驾驶员为获取较高的服务水平而乐于支付一定费用,当所选择路径的服务水平较高时,良好的驾驶体验所产生的潜在效益就是舒适性的效益。车辆行驶速度与行车舒适性密切相关,能最直观地体现行车舒适性[17],则舒适性的效益模型为:
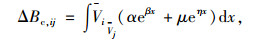
|
(18) |
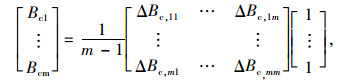
|
(19) |
式中,Bci为第i条路径的舒适性效益;α,β,μ,η为模型参数;ΔBc, ij为第i条路径与第j条路径的舒适性效益差。
3 基于级差效益的个性化路径选择 3.1 基本思路个性化路径选择的核心是个性化,个性化又通过指标权重反映。由于人的出行需求具有主观性和不确定性,所以需要通过对评价指标的相互比较,得到指标的判断矩阵,然后利用模糊分析方法,将驾驶员的主观判断转化成客观的指标权重向量。
基于级差效益的个性化路径选择,首先根据驾驶员对各指标的偏爱程度,对各指标进行赋权;然后根据之前计算的路径评价指标的级差效益值和指标权重,计算出该方案的综合级差效益值,并以此对方案进行排序。
3.2 个性化指标权重的确定一般情况下,驾驶员会根据个人需求选择路径,通过指标权重反映自身的个性化需求。模糊分析法的基本过程是以矩阵形式表达各级差效益评价指标对驾驶员的相对重要程度,从而建立相应的模糊判断矩阵:
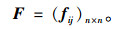
|
(20) |
由于驾驶员个性化需求具有模糊性和动态性,所以模糊判断矩阵的元素fij应该是一个标度区间,即fij=[fijL, fijU], 其中fijL和fijU分别为该区间的上下界。
采用0.1~0.9九标度建立模糊的判断矩阵,能较好地反映人们的实际估计[18],标度分布见表 1。
| 标度 | 定义 | 标度 | 定义 |
| 0.10 | n极度重要于m | 0.56 | m稍微重要于n |
| 0.14 | n强烈重要于m | 0.68 | m明显重要于n |
| 0.32 | n明显重要于m | 0.86 | m强烈重要于n |
| 0.44 | n稍微重要于m | 0.90 | m极度重要于n |
| 0.50 | m与同样重要n | — | — |
计算区间数互补判断矩阵F的行和并归一化,求出指标权重向量W的分量wi[19]:
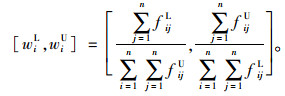
|
(21) |
从而得到级差效益综合评价指标体系的权重向量W=([w1L, w1U], …, [wnL, wnU])T。
通过引入指标权重,体现驾驶员对不同评价指标的偏爱程度,体现个性化路径选择问题的本质。
3.3 基于级差效益的个性化路径选择针对路网信息的不确定性,利用基于级差效益的个性化路径选择模型对所有可行路径进行综合排序,即得最优路径,主要步骤如下:
Step1:确定出行起讫点,并建立可行路径方案集合Y={yi|i=1, …, m}和级差效益评价指标集合X={xj|j=1, …, n}。
Step2:根据模型,建立关于级差效益的决策矩阵A=(Bt, Bp, Bs, Bc),各方案的单级差效益分别由式(10)~式(13)算得,并通过式(2)~式(5)对其进行平移、规范化处理。
Step3:通过式(14)~式(15),计算级差效益评价指标体系的权重向量W=(w1, …, wn)T。
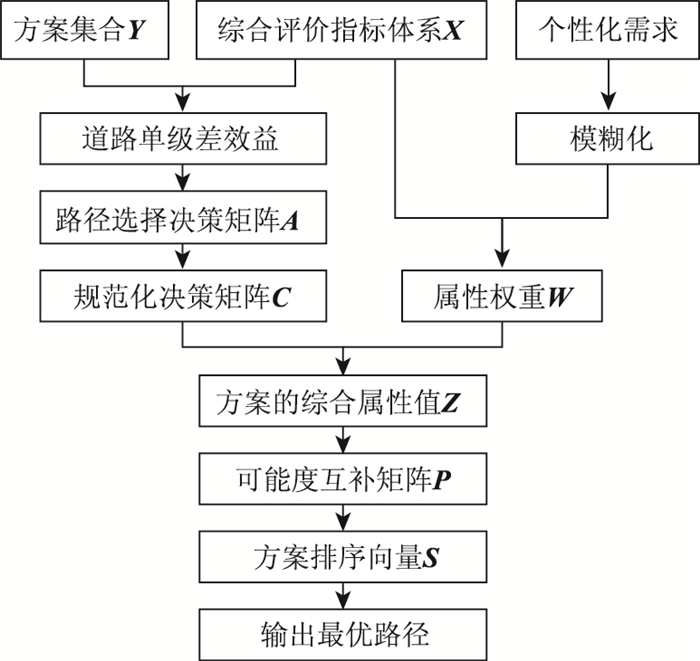
Step4:根据式(6),算得各可行路径的综合级差效益值,并通过式(7)~式(8)计算出可行路径方案的排序向量S=(s1, …, sm)T,以此对可行路径方案进行排序,选出最优路径。具体流程见图 1。
|
| 图 1 驾驶员个性化路径选择流程图 Fig. 1 Flowchart of driver's personalized route choice |
| |
4 案例分析
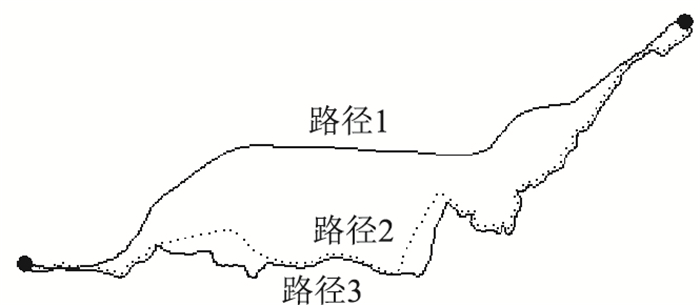
为了验证该个性化路径选择模型的可行性,笔者以重庆市黔江区公路网为背景,假设有两位具有不同指标偏好且偏好程度较高的驾驶员,分别对具有相同起终点的3条路径进行选择,路径分布及其说明分别见图 2和表 2。
|
| 图 2 可行路径分布 Fig. 2 Distribution of feasible routes |
| |
| 路径名称 | 里程/km | 公路等级 |
| 路径1 | 20.05 | 高速公路 |
| 路径2 | 26.00 | 二级公路 |
| 路径3 | 26.74 | 三级公路 |
通过调查,收集各单级差效益定量化模型所需的基础数据,计算出路径评价指标的级差效益,建立关于级差效益的决策矩阵,并对决策矩阵进行规范化处理,处理结果见表 3。
| 路径 | 时间 | 成本 | 安全性 | 舒适性 |
| 1 | [0.38 0.40] | [0.28 0.52] | 0.34 | [0.35 0.47] |
| 2 | [0.32 0.34] | [0.31 0.55] | 0.33 | [0.21 0.30] |
| 3 | [0.29 0.31] | [0.04 0.28] | 0.33 | [0.07 0.16] |
假设驾驶员1最关心成本,时间、安全性与舒适性次之,且3者相等,即x2>x1=x3=x4;假设驾驶员2最关心安全,时间、成本与舒适性次之,且3者相等,即x3>x1=x2=x4。根据驾驶员的偏好,建立相应的判断矩阵,由此得到两位驾驶员个性化的指标权重,结果见表 4。
| 驾驶员 | 时间 | 成本 | 安全 | 舒适 |
| 1 | [0.05 0.10] | [0.75 0.80] | [0.05 0.10] | [0.05 0.10] |
| 2 | [0.05 0.10] | [0.05 0.10] | [0.75 0.80] | [0.05 0.10] |
由此计算路径的综合级差效益值,并根据可行路径的综合级差效益值,建立可能度互补矩阵,从而得到可行路径方案的排序向量,排序结果见表 5。
根据驾驶员1的需求,该模型提供的路径排序为y2>y1>y3,最优路径方案是y2;根据驾驶员2的需求,该模型提供的路径排序为y1>y2>y3,最优路径方案是y1。从排序结果上看,该模型为不同需求的驾驶员提供了不同的公路,既保证了驾驶员的个性化需求,同时避免了部分公路上的车辆过度聚集,使路网中的交通流达到动态平衡。
5 结论利用路网信息建立基于公路级差效益的决策矩阵,既保留了目标因素的客观属性,又能直观地反映出驾驶员对出行路径选择的本质。同时引入指标权重,模糊了驾驶员的个性化出行需求,能更好地反映驾驶员对各指标的偏爱程度,将个性化路径选择问题转化成路径综合评价问题。
将本研究所讨论的模型汇编成计算机语言,并加载到车辆定位系统中。驾驶员通过车载计算机,输入路径导航的起终点,并标定对各属性的偏爱程度。车载计算机通过计算,寻找出最优路径,并通过地图显示和语音提示引导用户驾驶。随着交通信息共享平台和综合交通信息服务的推广应用,基于级差效益的驾驶员个性化路径选择模型具有较好的应用前景。
| [1] |
交通运输部.交通运输科技"十三五"发展规划[EB/OL]. (2016-05-27)[2016-07-25]. http://www.gov.cn. Ministry of Transport. Transportation Science and Technology Development Plan in 13th Five-year[EB/OL].(2016-05-27)[2016-07-25].http://www.gov.cn. |
| [2] |
李春燕, 陈峻, 孙正安, 等. ATIS条件下驾驶员出行途中路径选择行为研究[J]. 深圳大学学报:理工版, 2016, 33(2): 164-172. LI Chun-yan, CHEN Jun, SUN Zheng-an, et al. Drivers' Route Choice Behavior Analysis under ATIS[J]. Journal of Shenzhen University:Science and Engineering Edition, 2016, 33(2): 164-172. |
| [3] |
陈海鹏, 刘陪, 申铉京, 等. 实时环境下多目标的路径选择模型[J]. 哈尔滨工程大学学报, 2017, 38(8): 1285-1292. CHEN Hai-peng, LIU Pei, SHEN Xuan-jing, et al. Route Choice Model Based on Multi-objective in a Real-time Environment[J]. Journal of Harbin Engineering University, 2017, 38(8): 1285-1292. |
| [4] |
龙琼, 胡列格, 张谨帆, 等. 不确定性环境下个性化路径选择的多属性决策方法[J]. 中国公路学报, 2014, 27(9): 105-110. LONG Qiong, HU Lie-ge, ZHANG Jin-fan, et al. Multi-attribute Decision-making for Personalized Route Selection Under Uncertain Condition[J]. China Journal of Highway and Transport, 2014, 27(9): 105-110. |
| [5] |
龙琼, 胡列格, 张蕾, 等. 基于物理规划的路径诱导方法[J]. 中南大学学报:自然科学版, 2012, 43(8): 3287-3293. LONG Qiong, HU Lie-ge, ZHANG Lei, et al. Route Guidance Method Based on Physical Programming[J]. Journal of Central South University:Science and Technology Edition, 2012, 43(8): 3287-3293. |
| [6] |
孙燕, 陈森发, 亓霞, 等. 基于灰色系统理论的最优路径选择方法[J]. 土木工程学报, 2003, 36(1): 94-98. SUN Yan, CHEN Sen-fa, QI Xia, et al. Optical Route Selection Method Based on Gray System Theory[J]. China Civil Engineering Journal, 2003, 36(1): 94-98. |
| [7] |
PANG G K H, TAKABASHI K, YOKOTA T, et al. Adaptive Route Selection for Dynamic Route Guidance System Based on Fuzzy-neural Approaches[J]. IEEE Transactions on Vehicular Technology, 1999, 48(6): 2028-2041. |
| [8] |
龙雪琴, 宋嘉骐, 王建军, 等. 面向有限理性决策的出行者行为研究[J]. 公路交通科技, 2016, 33(5): 105-110. LONG Xue-qin, SONG Jia-qi, WANG Jian-jun, et al. Study on Traveler's Behavior for Bounded-rational Decision-making[J]. Journal of Highway and Transportation Research and Development, 2016, 33(5): 105-110. |
| [9] |
郑建湖, 伍雄斌, 黄明芳, 等. 有偏好的多属性灰色关联路径选择模型[J]. 交通运输系统工程与信息, 2014, 14(4): 168-172. ZHENG Jian-hu, WU Xiong-bin, HUANG Ming-fang, et al. Grey Relational Analysis for Multi-attributes Decision Making of Route Choice with Subjective Preference[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(4): 168-172. |
| [10] |
戢晓峰, 张玲, 冯川. 多源出行信息影响下的路径选择行为仿真研究[J]. 公路交通科技, 2016, 33(8): 127-132. JI Xiao-feng, ZHANG Ling, FENG Chuan. Simulation of Route Choice Behavior under Influence of Multi-source Travel Information[J]. Journal of Highway and Transportation Research and Development, 2016, 33(8): 127-132. |
| [11] |
胡明礼, 范成贤, 史开泉. 区间数决策矩阵规范化方法的性质分析[J]. 计算机科学, 2013, 40(10): 203-207. HU Ming-li, FAN Cheng-xian, SHI Kai-quan. Character Analysis of Standardization Methods of Decision Matrix with Intervals[J]. Computer Science, 2013, 40(10): 203-207. |
| [12] |
肖峻, 张跃, 付川. 基于可能度的区间数排序方法比较[J]. 天津大学学报, 2011, 44(8): 705-711. XIAO Jun, ZHANG Yue, FU Chuan. Comparison Between Methods of Interval Number Ranking Based on Possibility[J]. Journal of Tianjin University, 2011, 44(8): 705-711. |
| [13] |
徐泽水. 模糊互补判断矩阵排序的一种算法[J]. 系统工程学报, 2001, 16(4): 311-314. XU Ze-shui. Algorithm for Priority of Fuzzy Complementary Judgement Matrix[J]. Journal of Systems Engineering, 2001, 16(4): 311-314. |
| [14] |
王飞雄.基于级差效益的高速公路合理收费标准研究[D].广州: 华南理工大学, 2011. WANG Fei-xiong. Research on Toll Standard of Expressway Based on Differential Benefit[D]. Guangzhou: South China University of Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10561-1011189063.htm |
| [15] |
徐吉谦, 陈学武. 交通工程总论[M]. 北京: 人民交通出版社, 2008. XU Ji-qian, CHEN Xue-wu. Fundamentals of Traffic Engineering[M]. Beijing: China Communications Press, 2008. |
| [16] |
彭勃.高速公路汽车油耗模型研究[D].哈尔滨: 哈尔滨工业大学, 2014: 27-29. PENG Bo. Research about Model of Vehicle's Fuel Consumption in Expressway[D]. Harbin: Harbin Institute of Technology, 2014: 27-29. http://cdmd.cnki.com.cn/Article/CDMD-10213-1014083534.htm |
| [17] |
王海涛, 黄鑫, 陈火根. 公路行车广义舒适度评价指标体系研究[J]. 交通与运输, 2015(增1): 193-196. WANG Hai-tao, HUANG Xin, CHEN Huo-gen. Research on Evaluation Indexes of Generalized Comfort of Highway Driving[J]. Traffic & Transportation, 2015(S1): 193-196. |
| [18] |
林钧昌, 徐泽水. 模糊AHP中一种新的标度法[J]. 运筹与管理, 1998, 7(2): 37-40. LIN Jun-chang, XU Ze-shui. A New Scale in Fuzzy AHP[J]. Operations Research and Management Science, 1998, 7(2): 37-40. |
| [19] |
谢凤平, 曾雪兰, 段云艳. 基于区间粗糙数互补判断矩阵的一种排序方法[J]. 琼州学院学报, 2015, 22(5): 22-26. XIE Feng-ping, ZENG Xue-lan, DUAN Yun-yan. Priority Method for Complementary Judgement Matrix Based on Interval Rough Number[J]. Journal of Qiongzhou University, 2015, 22(5): 22-26. |
 2019, Vol. 36
2019, Vol. 36
