扩展功能
文章信息
- 周和祥, 马建林, 李军堂, 张凯, 杨柏
- ZHOU He-xiang, MA Jian-lin, LI Jun-tang, ZHANG Kai, YANG Bai
- 深大沉井下沉阻力的现场监测
- Field Monitoring of Sinking Resistance of Large and Deep Caisson
- 公路交通科技, 2019, 36(7): 81-89
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(7): 81-89
- 10.3969/j.issn.1002-0268.2019.07.010
-
文章历史
- 收稿日期: 2018-02-06
2. 中铁大桥局集团有限公司, 湖北 武汉 430050
2. China Railway Major Bridge Engineering Group Co., Ltd., Wuhan Hubei 430050, China
如何确保沉井安全平稳下沉是沉井基础的关键问题[1-4],下沉系数与稳定系数是沉井下沉的重要参数,两项参数均与沉井刃脚土阻力和侧壁摩阻力直接相关,分析刃脚土阻力与侧壁摩阻力的大小和变化规律是沉井设计计算的重要内容,对于刃脚土阻力的计算,目前通用的主要有以下3种方法:根据规范提供的地基土极限承载力表格确定[5]、按照规范中所给的经验公式进行计算[6-8]、利用极限承载力理论公式计算[9]。对于侧壁摩阻力的计算,目前主要采用规范中所给的分布图形[5],该分布规律是通过对大直径桩和小型沉井下沉机理分析得出的[10]。上述的计算方法是否适用于大型沉井基础的设计计算,还需进一步验证。因此,在大型沉井下沉施工过程中有必要进行现场监测,并分析沉井下沉机理与下沉阻力分布特征,为设计计算方法的优化提供参考。
1 现场监测 1.1 工程概况沪通长江大桥是沪通铁路的控制性工程[11],桥位距上游江阴长江公路大桥45 km,距下游苏通长江公路大桥40 km。为减小工程建设成本, 充分利用宝贵的桥位资源,大桥采用沪通铁路通苏嘉城际铁路、锡通高速公路共通道建设,为四线铁路六车道公路合建桥梁。其中沪通铁路为两线Ⅰ级干线,设计速度为200 km/h。通苏嘉城际铁路为两线客运专线,设计速度为250 km/h,公路为双向六车道高速公路[12]。
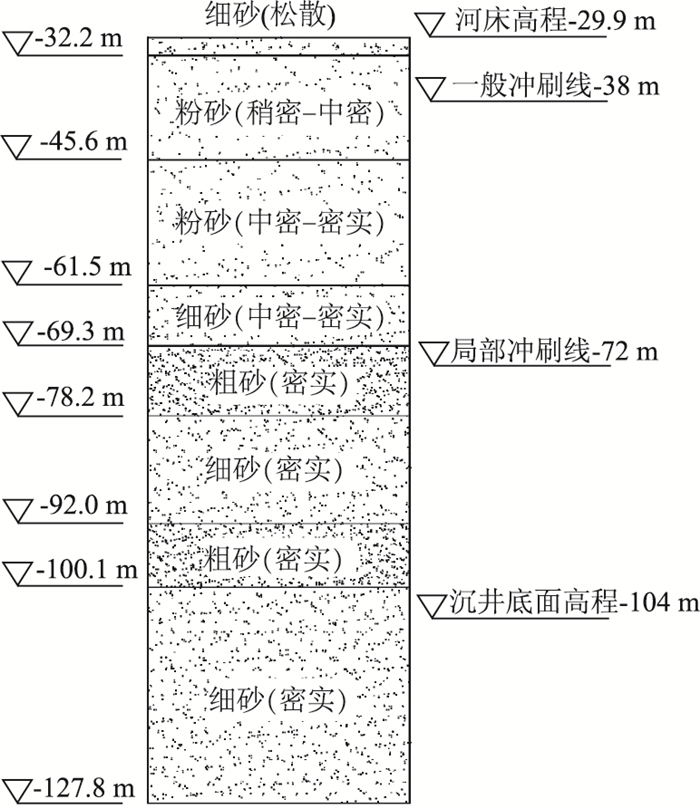
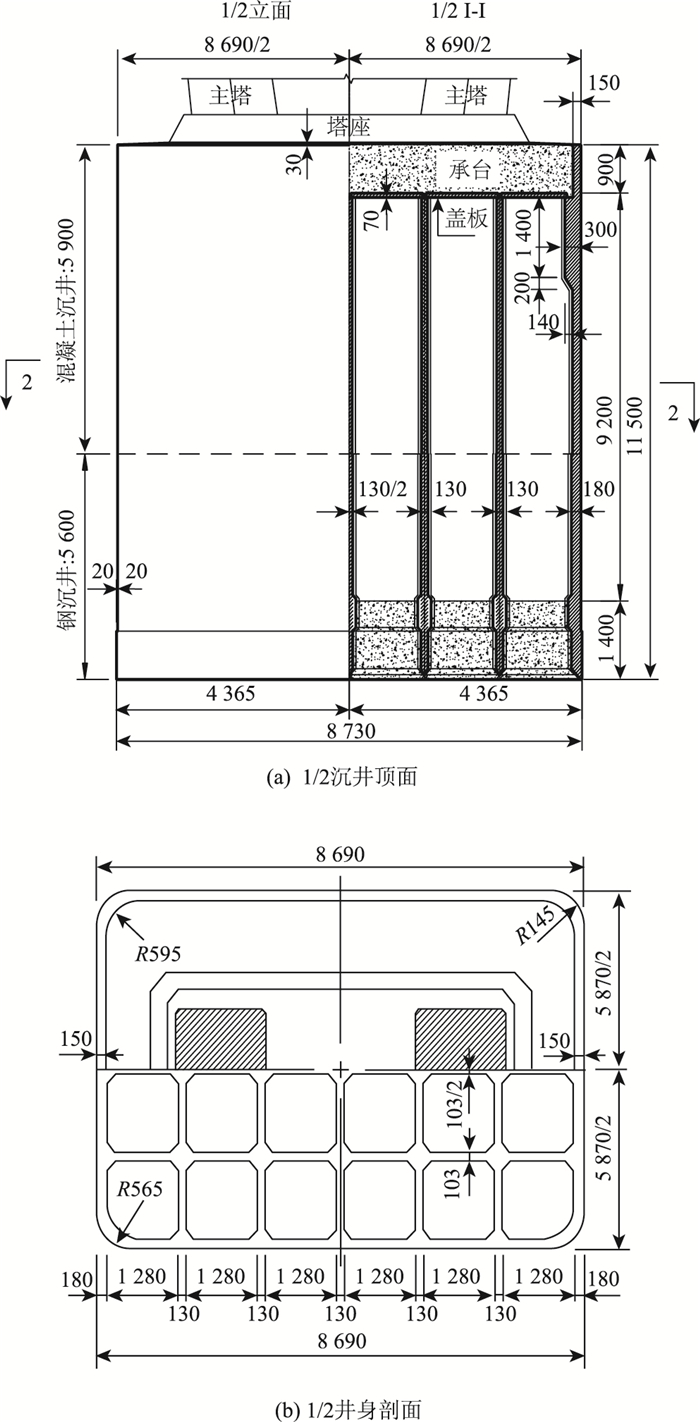
主航道桥采用双塔斜拉桥,全长2 296(140+462+1 092+462+140)m,其中29#主墩基础位于240 m厚的典型的深厚沉积土层,沉井地基土层分布见图 1,各层地基土层主要物理力学参数见表 1。经多方案比选,采用倒圆角的矩形沉井基础方案。矩形沉井平面尺寸为86.9 m×58.7 m,倒圆半径为7.45 m,沉井总高115 m,如图 2所示。其中下部56 m采用钢沉井,上部59 m采用混凝土沉井,考虑主墩基础建成以后对冲刷以及河床变迁的影响,持力层选用密实细砂层。为避免船舶撞击,设计沉井顶面标高+8.0 m,高于最高通航水位以上3 m。
|
| 图 1 沉井地基土层分布 Fig. 1 Soil layer distribution of caisson foundation |
| |
| 地层代号 | 土层类别 | 层厚/m | 天然密度ρ/(g·cm-3) | 内摩擦角φc/(°) | 黏聚力Cc/kPa | 泊松比ν | 基本承载力σ0/kPa |
| ①4 | 细砂(松散) | 2.34 | 2.01 | 42.1 | 6.8 | 0.25 | 100 |
| ②3 | 粉砂(稍密-中密) | 13.36 | 1.91 | 36.4 | 14.1 | 0.25 | 100 |
| ③3 | 粉砂(中密-密实) | 15.94 | 1.93 | 36.4 | 11.1 | 0.25 | 120 |
| ③4 | 细砂(中密-密实) | 7.76 | 1.95 | 37.1 | 10.8 | 0.25 | 210 |
| ③6 | 粗砂(密实) | 8.94 | 1.98 | 40.8 | 7.5 | 0.25 | 550 |
| ④2 | 细砂(密实) | 13.78 | 1.99 | 38.3 | 8.9 | 0.25 | 300 |
| ④4 | 粗砂(密实) | 8.08 | 1.93 | 39.3 | 10.0 | 0.25 | 550 |
| ⑤3 | 细砂(密实) | 27.74 | 1.98 | 36.6 | 12.0 | 0.25 | 300 |
|
| 图 2 29#墩沉井基础结构(单位:cm) Fig. 2 Structure of caisson foundation of pier No.29(unit:cm) |
| |
钢沉井在干船坞内整体制造、拼装并浮运至墩位处,采用大直径钢管桩锚碇系统及液压千斤顶多向快速定位技术,精确调节着床位置,分段接高混凝土井壁并分次下沉,直至设计高程[13]。
1.2 现场监测内容及测点布置(1) 刃脚踏面土压力监测
在沉井下沉过程中,刃脚直接挤压沉井下部土体,刃脚土压力能够直观反映在下沉过程中遇到的地层阻力,是沉井下沉过程中的重要监控指标。
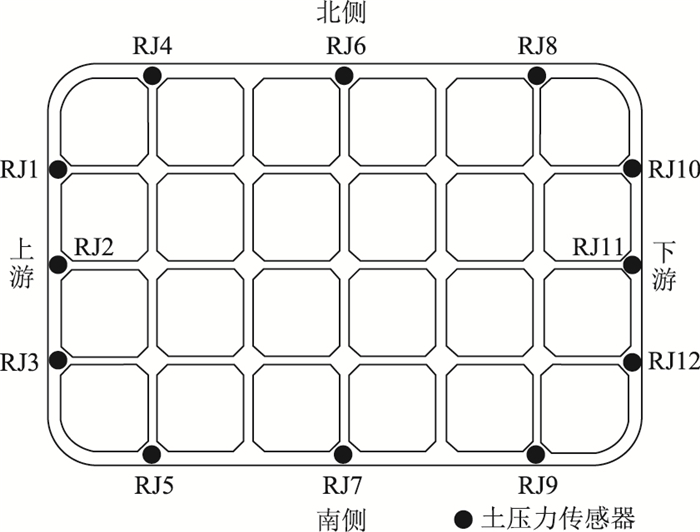
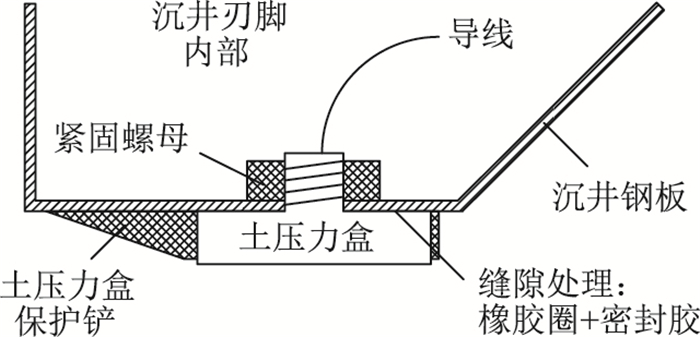
通过在沉井不同位置处的刃脚踏面布置土压力传感器,实时监测沉井下沉过程中刃脚土压力变化情况。传感器安装位置如图 3所示。在沉井着床与下沉过程中,刃脚位置要承受巨大的土压力,为避免土压力传感器遭到破坏,专门设计了一种土压力传感器保护方案[14],如图 4所示。首先,在沉井刃脚踏面相应位置开孔,通过满焊将土压力传感器保护铲固定在踏面上,然后利用密封胶和密封圈将土压力传感器安装至保护铲内,最后从沉井内部将螺母旋紧。经现场水压试验测试,该方案在2 MPa水压环境中无渗水现象,证明了方案的可靠性。安装完成后的土压力传感器如图 5所示。
|
| 图 3 刃脚土压力传感器安装位置 Fig. 3 Location of earth pressure sensors at blade foot |
| |
|
| 图 4 刃脚土压力传感器防水措施 Fig. 4 Waterproofing measures for earth pressure sensors at blade foot |
| |

|
| 图 5 刃脚土压力传感器安装 Fig. 5 Installation of earth pressure sensor at blade foot |
| |
传感器导线通过在沉井侧壁相应位置满焊角钢进行保护。
(2) 侧壁土压力监测
沉井侧壁土压力反映了沉井下沉时不同深度土层对沉井侧壁的正压力,是影响沉井设计与施工的重要指标。通过测量沉井下沉过程中的侧壁土压力,可计算得到侧壁摩阻力。
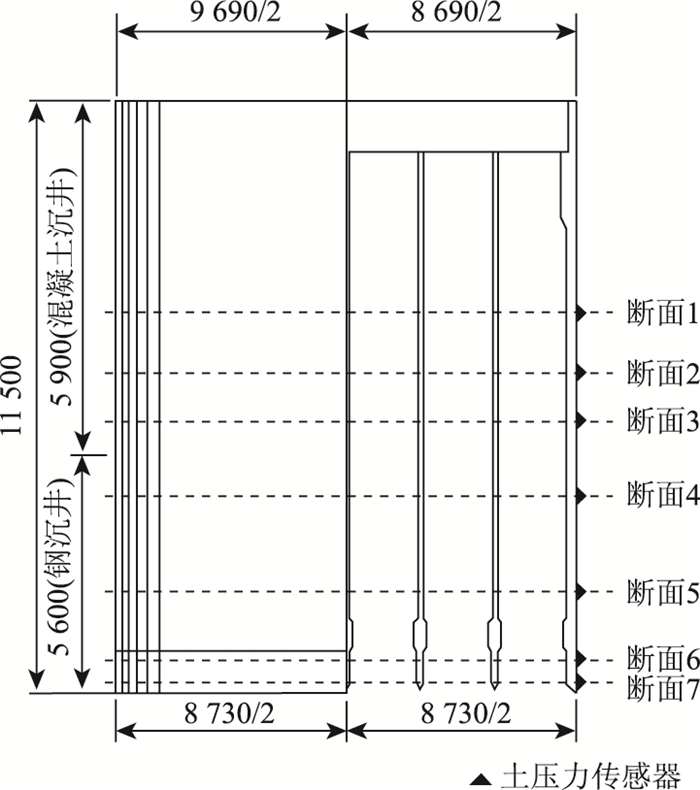
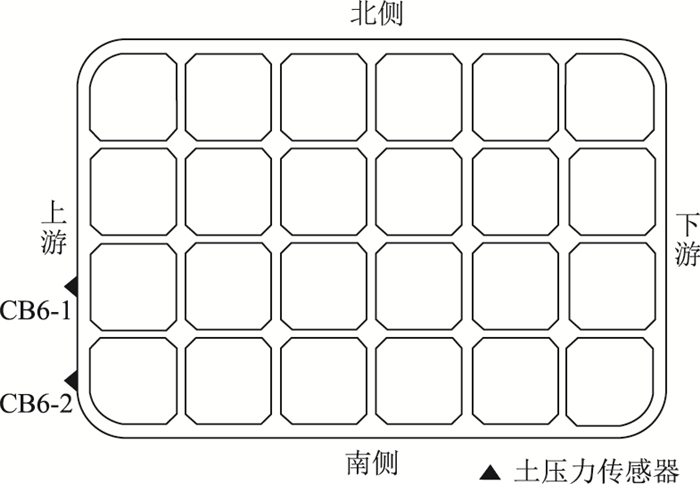
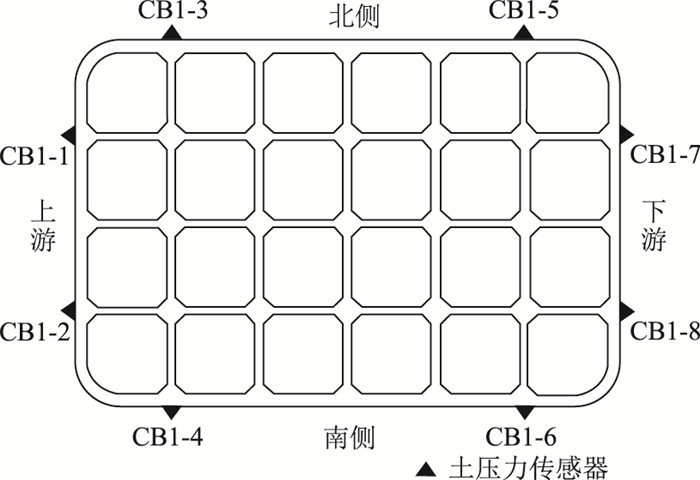
沿沉井外壁四周不同高度设置7个监测断面,断面高度分别为刃脚以上2, 5, 19, 37, 51, 60, 72 m,并依据断面标高从高到低的顺序依次编号为断面1~断面7,侧壁土压力传感器监测断面布置如图 6所示。其中,除刃脚以上5 m高度的断面布置两个土压力盒外,其余6个断面均布置8个土压力盒,且布置形式相同,侧壁土压力传感的器编号形式为CBx-y,其中x代表断面号,y代表土压力传感器在每个断面的位置,如图 7、图 8所示。
|
| 图 6 侧壁土压力传感器监测断面布置(单位:mm) Fig. 6 Layout of monitoring sections of earth pressure sensors on side wall(unit:mm) |
| |
|
| 图 7 侧壁土压力传感器(断面6)安装位置 Fig. 7 Location of earth pressure sensors on side wall (Section 6) |
| |
|
| 图 8 侧壁土压力传感器(除断面6外其余断面)安装位置 Fig. 8 Location of earth pressure sensors on side wall (the sections except section 6) |
| |
(3) GPS沉井姿态监测
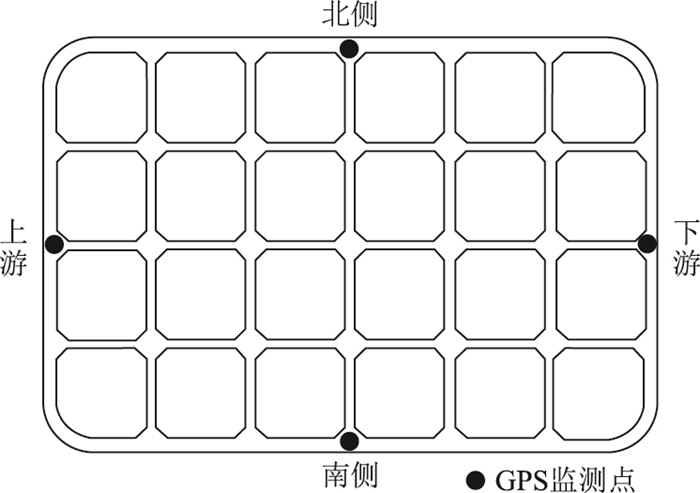
选取沉井的4条边的中心位置布设4个GPS数据接收器,并在南岸设置GPS基准站,二者共同构成了沉井GPS姿态监测系统,如图 9所示。该系统可通过无线组网的方式,将4个监测点的GPS定位数据实时传输到监控中心。通过对4个监测点的平面坐标和高程进行分析,可以实时得到沉井顶面中心位置、顶面标高、平面扭角、倾斜度等姿态数据。另外,利用GPS载波相位差分技术,平面定位精度可达±1.5 cm,高程定位精度可达±2.5 cm。
|
| 图 9 GPS监测系统布置 Fig. 9 Layout of GPS measurement systems |
| |
2 试验结果及分析 2.1 下沉曲线
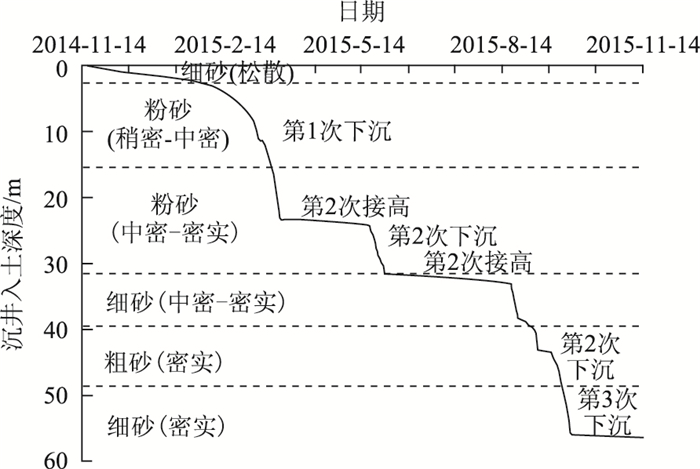
根据施工方案,沉井基础采用不排水吸泥下沉,分4次下沉3次接高,其中前3次下沉和接高的沉降曲线见图 10。
|
| 图 10 沉井下沉曲线 Fig. 10 Sinking curve of caisson |
| |
第1次下沉量为23.43 m,历时75 d,平均下沉速率为0.26 m/d。前期由于沉井要穿过河床表面2 m厚的防冲刷拋填碎石区,故下沉曲线斜率较小,后期沉井进入细砂层和稍密-中密粉砂层后,由于土质松软,且下沉通道已经形成,故下沉曲线斜率较大。
第2次下沉量为6.24 m,历时19 d,平均下沉速率为0.33 m/d,穿越中密-密实粉砂层。
第3次下沉量为23.35 m,历时44 d,平均下沉速率为0.52 m/d,先后穿越中密-密实细砂层、密实粗砂层、密实细砂层。下沉速率与前两次下沉相比较快,这是由于第3次下沉时间历时较长,后期下沉通道形成后,下沉速率保持在较快水平。
2.2 下沉阻力分析(1) 刃脚土阻力
目前的刃脚土阻力计算可借鉴以下方法:
(a) 根据《给排水工程钢筋混凝土沉井结构设计规程》[5]提供的地基土极限承载力表格确定。该规范规定,当下沉系数较大,或在下沉过程中遇有软弱土层时,应根据实际情况进行沉井的下沉稳定验算。其中沉井刃脚、隔墙和底梁下地基土的极限承载力可按表 2选用。
| 土的种类 | 极限承载力 |
| 泥炭 | 60~70 |
| 淤泥 | 80~100 |
| 淤泥质黏土 | 10~120 |
(b) 按照《铁路桥涵地基和基础设计规范》、《公路桥涵地基与基础设计规范》、《建筑地基基础设计规范》[3-5]中所给的经验公式进行计算,以《铁路桥涵地基和基础设计规范》为例,刃脚土阻力为:
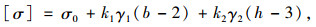
|
(1) |
式中,[σ]为地基的容许承载力;σ0为地基的基本承载力;b为基础的短边宽度,大于10 m时按10 m计算;h为基础底面的埋置深度;γ1为基底以下持力层土的天然容重;γ2为基底以上土的天然容重的平均值;k1,k2为宽度、深度修正系数,按持力层土确定。
上述经验公式计算得到的地基容许承载力安全系数一般为2~3,在本研究计算中将地基极限承载力与容许承载力的比值取为3,通过地基容许承载力计算地基极限承载力。
(c) 利用Prandtl-Vesic,Terzaghi,Meyerhof,Hansen等[6]极限承载力理论公式计算:
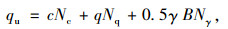
|
(2) |
式中,qu为地基极限承载力;c为地基土的内聚力;q为地基土顶面过载;γ为地基土的容重;B为基础的宽度;Nc,Nq,Nγ为无量纲承载力系数。
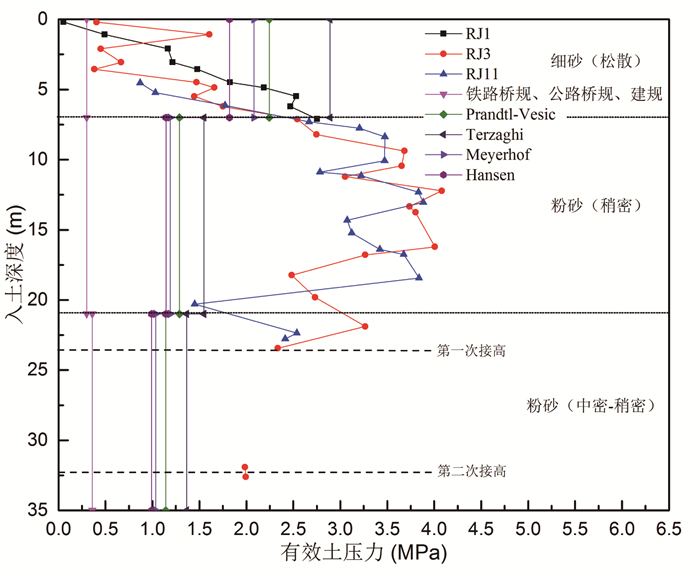
通过现场监测得到刃脚土压力随入土深度之间的关系曲线,并与现有的《铁路桥涵地基和基础设计规范》、《公路桥涵地基与基础设计规范》、《建筑地基基础设计规范》等设计规范和Prandtl-Vesic,Terzaghi,Meyerhof,Hansen计算理论进行对比,如图 11所示。
|
| 图 11 刃脚土压力-入土深度关系曲线 Fig. 11 Curve of earth pressure vs. depth at blade foot |
| |
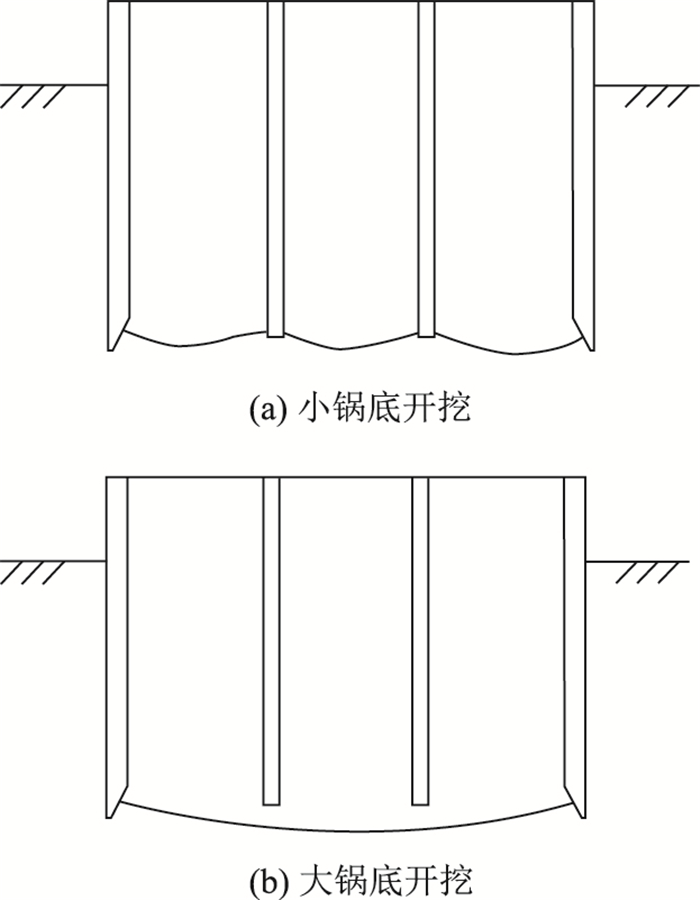
由图可见,在沉井第1次吸泥下沉初期,沉井入土深度为0~12 m时,刃脚土压力随着沉井基础入土深度的增大近似呈线性增大,分析对应深度土层性质发现,上层细砂的内摩擦角大于下层粉砂的内摩擦角,显然上层土的物理力学性质要好于下层土,说明土层性质并不是导致此处刃脚土压力增大的主要因素。经分析,刃脚所在土层的前期固结压力与土层深度线性相关,根据相关文献研究结论[15],前期固结压力对砂性土峰值强度影响显著,峰值强度随着超固结比呈现线性增加,因此,随着沉井下沉深度的增加,土体极限承载力也显著提高,且二者近似呈线性关系。在沉井第1次吸泥下沉中后期,沉井入土深度为12~23 m时,随着入土深度的进一步增大,侧壁摩阻力增加,且开挖方式逐渐由“小锅底”开挖转为“大锅底”开挖,如图 12所示,刃脚插入泥面深度降低,部分刃脚位置甚至出现脱空,导致刃脚土压力降低。
|
| 图 12 沉井不同开挖方式 Fig. 12 Different excavation methods of caisson |
| |
无论沉井下沉深度如何,铁路桥规、公路桥规、建规计算值均明显小于实测值。当沉井下沉深度较小时(不大于7 m),Prandtl-Vesic,Meyerhof,Hansen理论计算值与实测值较为接近,Meyerhof理论计算值偏大;当沉井下沉深度较大时,Prandtl-Vesic,Terzaghi,Meyerhof,Hansen理论计算值均明显偏小。综上可知,以上刃脚土阻力计算方法仅Prandtl-Vesic,Meyerhof,Hansen理论适用于沉井下沉深度较小的工况,而当沉井下沉深度较大时,以上刃脚土阻力计算方法均不适用。分析原因为:目前刃脚土阻力设计计算方法均未考虑刃脚所在土层前期固结压力的影响,而将刃脚处土体破坏模式视作简单的浅基础破坏,采用此类计算方法,在沉井入土深度较小、刃脚所在土层前期固结压力较小的情况下可以适用,但当沉井入土深度较大、刃脚所在土层前期固结压力较大时,计算值明显小于实测值。
(2) 侧壁摩阻力
侧壁摩阻力计算一般采用规范法,参见《给排水工程钢筋混凝土沉井结构设计规程》(CECS 137—2015)[5]规定如下:
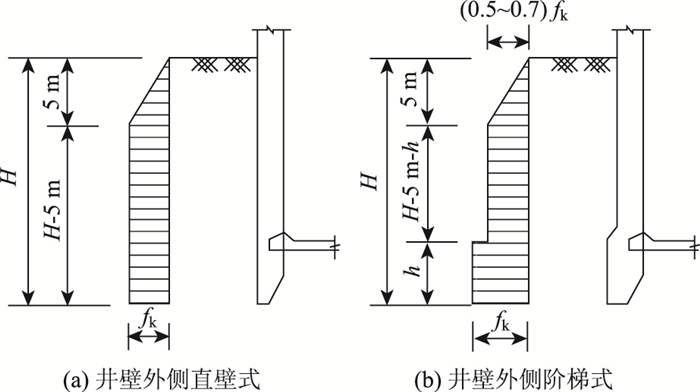
(a) 当沉井井壁外侧为直壁时,入土深度0~5 m范围内时,侧壁摩阻力呈三角形分布,在5 m深处达到fk,入土深度大于5 m时,侧壁摩阻力呈矩形分布,并保持fk不变,如图 13(a)所示;
|
| 图 13 摩阻力沿井壁外侧的分布(CECS 137—2015) Fig. 13 Distributions of frictional resistance along outside of side wall(CECS 137—2015) |
| |
(b) 当沉井井壁外侧为阶梯形时,入土深度0~5 m范围内时,侧壁摩阻力呈三角形分布,在5 m深处达到(0.5~0.7)fk,入土深度大于5 m时,侧壁摩阻力呈矩形分布,并保持(0.5~0.7)fk不变,在台阶处增大到fk,如图 13(b)所示。
其中fk为单位摩阻力标准值,可根据土层类别按照表 3规定选用。
| 土层类别 | fk/kPa |
| 流塑状态黏性土 | 10~15 |
| 可塑、软塑状态黏性土 | 12~25 |
| 硬塑状态黏性土 | 25~50 |
| 泥浆套 | 3~5 |
| 砂性土 | 12~25 |
| 砂砾土 | 15~20 |
| 卵石 | 18~30 |
| — | — |
通过现场实时监测得到沉井下沉期间的侧壁土压力,然后通过下式计算可得侧壁摩阻力:
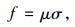
|
(3) |
式中,f为侧壁摩阻力;σ为侧壁土压力;μ为土体与井壁的摩擦系数。根据相关文献[16-17]查证,可知砂性土与混凝土井壁摩擦系数基本集中在0.4~0.5之间,砂性土与钢井壁摩擦系数略小,仍处在此范围内,考虑到本试验的近似性,并结合现场土层的物理力学特性指标,将μ取值为0.45。
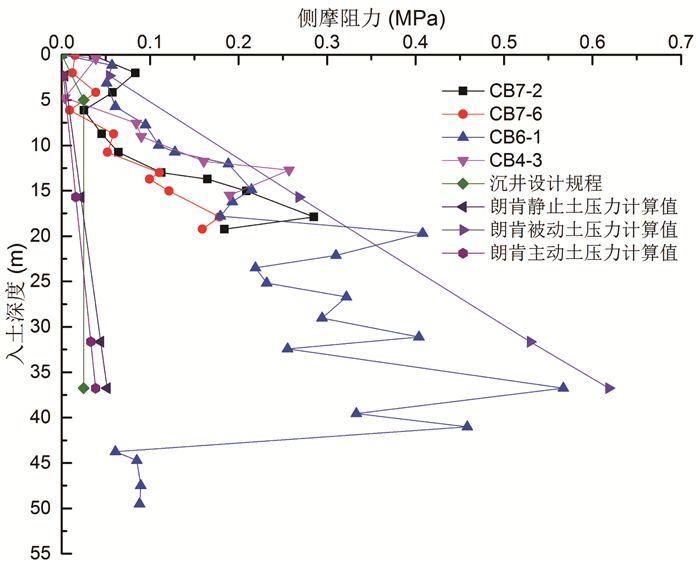
分析现场数据可得侧壁摩阻力随土压力盒入土深度之间关系曲线,并与规范结果对比,如图 14所示。
|
| 图 14 侧壁摩阻力-对应土压力盒入土深度关系曲线 Fig. 14 Curves of frictional resistance of side wall vs. depth of earth pressure cell |
| |
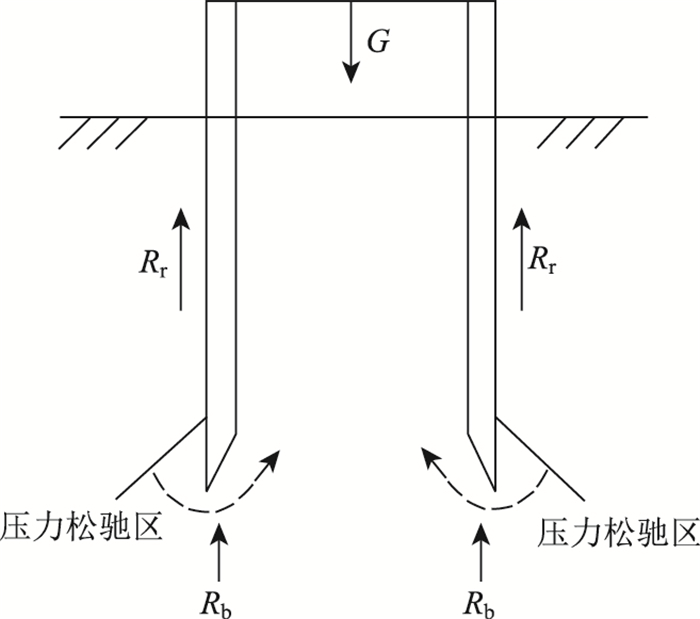
由图可见,当入土深度在0~37 m时,随着入土深度的增加,沉井侧壁受到的土压力增大,侧壁摩阻力也相应增大,入土深度与侧壁摩阻力近似呈线性关系,从数值上来看,侧壁摩阻力实测值介于朗肯理论静止土压力计算值与被动土压力计算值之间,远大于《给排水工程钢筋混凝土沉井结构设计规程》取值,初步分析可能与沉井下沉时的姿态有关。当入土深度大于37 m时,CB6-1侧摩阻力值随入土深度的增加迅速降低,这是由于随着沉井下沉深度不断增加,沉井侧壁受到的摩阻力也越来越大,此时沉井若要顺利下沉,须在刃脚以下掏挖更深,使得沉井刃脚附近压力松弛效应[18]显著增强,成为影响刃脚附近侧壁土压力重要因素,在压力松弛区内,由于沉井内侧不断开挖,土体具有由外向内流动的趋势,使得刃脚附近处侧壁土压力相对较小。CB6-1在刃脚以上5 m位置,当入土深度达到37 m以上时,其侧壁摩阻力降低至侧壁摩阻力最大值的1/5左右,说明该测点受到了压力松弛区的影响,压力松弛区在刃脚以上的影响高度≥5 m。
将实测值与《给排水工程钢筋混凝土沉井结构设计规程》取值比较可知,当入土深度不大于5 m时,实测值与规范取值较为接近,当下沉深度大于5 m时,实测值远大于规范取值。另外,实测值与规范取值分布形式也有很大区别,规范规定侧壁摩阻力三角形分布区域为入土深度0~5 m范围,而实测三角形分布区域为入土深度0~37 m范围。另外,由于目前学术界对于压力松弛问题还没有定论,规范中也没有考虑压力松弛区对沉井刃脚附近侧壁摩阻力的影响。
|
| 图 15 沉井压力松弛区 Fig. 15 Relaxation zone of caisson pressure |
| |
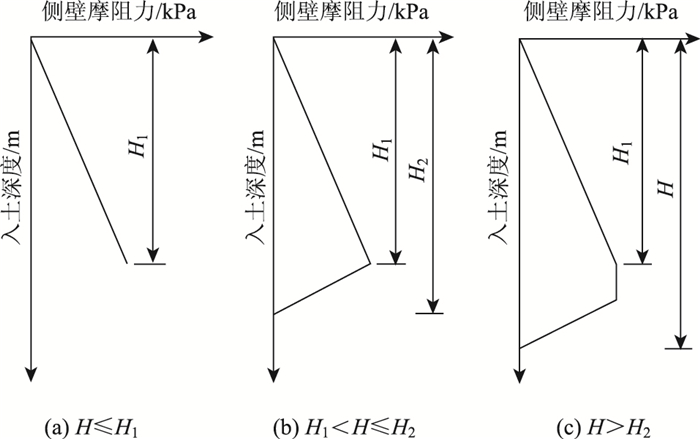
分析现场实测数据,建立侧壁摩阻力分布模式图,如图 16所示,其数学计算模型为:
|
| 图 16 侧壁摩阻力计算模式图 Fig. 16 Calculation mode of frictional resistance on side wall |
| |
当H≤H1时:
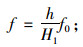
|
(4) |
当H1 < H≤H2时:
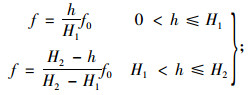
|
(5) |
当H≥H2时:
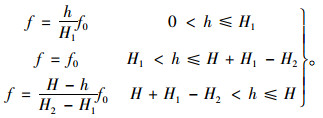
|
(6) |
上述式中,f为侧壁摩阻力;h为入土深度;H1为侧壁摩阻力达到最大值时的入土深度,H1建议取值为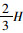
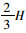
上述数学模型可做如下表达:
当H≤H1时,压力松弛效应较弱,此时朗肯土压力理论适用,侧壁摩阻力随沉井入土深度的增加呈三角形分布;当H1≤H≤H2时,压力松弛效应显著增强,侧壁摩阻力在0~H1深度范围内呈三角形分布,在H1~H2深度范围呈倒三角形分布;当H>H2时,压力松弛区随沉井入土深度的增加而向下移动,中间段侧壁摩阻力则保持f0不变。
本次监测结果表明:H1=37 m,压力松弛区H2-H1≥5 m。
侧壁摩阻力最大值f0可采用朗肯土压力理论进行计算:
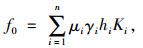
|
(5) |
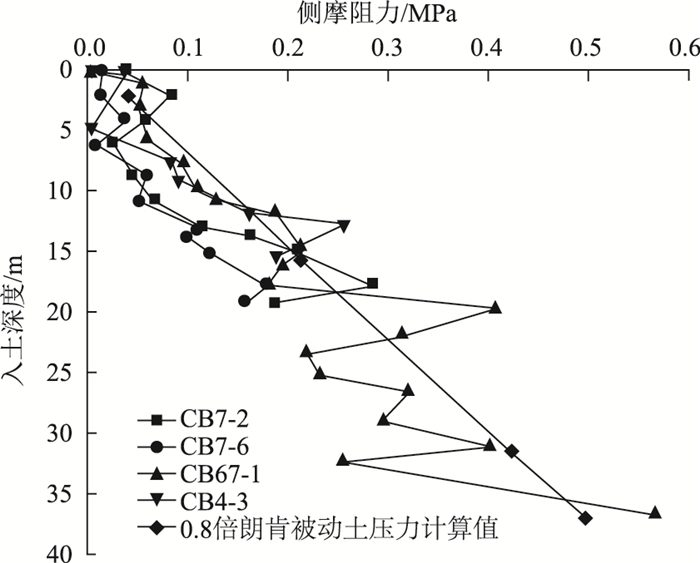
式中,μ为第i层土体与井壁的摩擦系数;γi为第i层土的浮重度; hi为第i层土的厚度;Ki为第i层土的朗肯土压力系数。本次监测结果表明,Ki取值介于静止土压力系数K0与被动土压力系数Kp之间,约为0.8Kp,如图 17所示。
|
| 图 17 侧壁摩阻力对比 Fig. 17 Comparison of different frictional resistances on side wall |
| |
上述数学计算模型可于砂性土中大型沉井的下沉计算。如图 17所示,在侧壁摩阻力增加段,计算模型与现场实测结果吻合较好。由于现场施工条件限制,无法在刃脚位置处埋设侧壁土压力传感器,因此无法得到刃脚位置处的侧壁摩阻力,这里假设刃脚位置处的侧壁摩阻力为0,这样会导致该模型在计算压力松弛区范围内侧壁摩阻力时会有一定误差。
3 结论经上述讨论分析,可得出以下结论:
(1) 刃脚土阻力与土层性质、下沉深度、开挖方式等因素有关。目前的设计计算方法均未考虑刃脚所在土层前期固结压力的影响,此类计算方法适用于沉井入土深度较小、刃脚所在土层前期固结压力不大的情况。当沉井入土深度较大时,计算值与实际值相比明显偏小。
(2) 本次监测结果表明:沉井侧壁摩阻力随入土深度的增大呈先增大后减小的变化规律,最大值出现在入土深度等于37 m位置处,当入土深度小于37 m时,侧壁摩阻力随入土深度的增大而增大,二者近似呈线性关系,侧壁摩阻力介于朗肯理论静止土压力计算值与被动土压力计算值之间,远大于规范取值。当入土深度超过37 m时,沉井刃脚附近压力松弛效应显著增强,导致刃脚附近侧壁摩阻力较小,侧壁摩阻力降低至侧壁摩阻力最大值的1/5左右,压力松弛区影响高度≥5 m。
(3) 根据本次试验结果提出了侧壁摩阻力分布简化模型,分为以下3个阶段:第1阶段为线性增加阶段,侧壁摩阻力分布模式为三角形分布;第2阶段为压力松弛影响阶段,侧壁摩阻力分布模式为三角形分布+倒三角形分布;第3阶段为压力松弛下移阶段,摩阻力分布模式为梯形分布。
(4) 简化模型中,侧壁摩阻力最大值f0可采用朗肯土压力理论进行计算,即式(1)。其中Ki的取值与沉井下沉时的姿态有关,在本次监测中,Ki取值介于静止土压力系数K0与被动土压力系数Kp之间,约为0.8Kp。
| [1] |
穆保岗, 王岩, 朱建民, 等. 大型沉井实测下沉阻力分析[J]. 土木建筑与环境工程, 2012, 34(增1): 107-115. MU Bao-gang, WANG Yan, ZHU Jian-min, et al. Analysis of Large Caisson Sinking Measured Resistance[J]. Journal of Civil, Architectural & Environmental Engineering, 2012, 34(S1): 107-115. |
| [2] |
吉林, 阮静, 王陶. 泰州大桥三塔两跨悬索桥关键技术[J]. 公路交通科技, 2015, 32(2): 94-99. JI Lin, RUAN Jing, WANG Tao. Key Technology of 3-pylon 2-span Suspension Bridge of Taizhou Bridge[J]. Journal of Highway and Transportation Research and Development, 2015, 32(2): 94-99. |
| [3] |
穆保岗, 朱建民, 龚维明, 等. 悬索桥大型沉井排水下沉控制的关键问题分析[J]. 中国公路学报, 2013, 26(6): 118-127. MU Bao-gang, ZHU Jian-min, GONG Wei-ming, et al. Key Issues about Drainage Sinking Control of Large Caissons in Suspension Bridge[J]. China Journal of Highway and Transport, 2013, 26(6): 118-127. |
| [4] |
郑大超, 朱斌. 武汉杨泗港长江大桥2号墩钢沉井施工关键技术[J]. 桥梁建设, 2017, 47(6): 106-110. ZHENG Da-chao, ZHU Bin. Key Techniques for Construction of Steel Open Caisson of Pier No.2 of Yangsigang Changjiang River Bridge in Wuhan[J]. Bridge Construction, 2017, 47(6): 106-110. |
| [5] |
CECS 137-2015, 给水排水工程钢筋混凝土沉井结构设计规程[S]. CECS 137-2015, Specification for Structural Design of Reinforced Concrete Sinking Well of Water Supply and Sewerage Engineering[S]. |
| [6] |
TB 10002.5-2005, 铁路桥涵地基和基础设计规范[S]. TB 10002.5-2005, Code for Design on Subsoil and Foundation of Railway Bridge and Culvert[S]. |
| [7] |
JTG D63-2007, 公路桥涵地基与基础设计规范[S]. JTG D63-2007, Code for Design of Ground Base and Foundation of Highway Bridges and Culverts[S]. |
| [8] |
GB 50007-2011, 建筑地基基础设计规范[S]. GB 50007-2011, Code for Design of Building Foundation[S]. |
| [9] |
郑大同. 地基极限承载力的计算[M]. 北京: 中国建筑工业出版社, 1979. ZHENG Da-tong. Calculation of Ultimate Bearing Capacity of Foundation[M]. Beijing: China Architecture & Building Press, 1979. |
| [10] |
穆保岗, 朱建民, 龚维明. 大型沉井设计、施工及监测[M]. 北京: 中国建筑工业出版社, 2015. MU Bao-gang, ZHU Jian-min, GONG Wei-ming. Design, Construction and Monitoring of Large Caisson[M]. Beijing: China Architecture & Building Press, 2015. |
| [11] |
徐力, 高宗余, 梅新咏. 沪通长江大桥公铁合建斜拉桥桥塔基础设计[J]. 桥梁建设, 2015, 45(3): 7-12. XU Li, GAO Zong-yu, MEI Xin-yong. Design of Pylon Foundations for Rail-cum-road Cable-stayed Bridge of Hutong Changjiang River Bridge[J]. Bridge Construction, 2015, 45(3): 7-12. |
| [12] |
高宗余, 梅新咏, 徐伟, 等. 沪通长江大桥总体设计[J]. 桥梁建设, 2015, 45(6): 1-6. GAO Zong-yu, MEI Xin-yong, XU Wei, et al. Overall Design of Hutong Changjiang River Bridge[J]. Bridge Construction, 2015, 45(6): 1-6. |
| [13] |
李军堂. 沪通长江大桥主航道桥沉井施工关键技术[J]. 桥梁建设, 2015, 45(6): 12-17. LI Jun-tang. Key Techniques for Construction of Open Caissons of Main Ship Channel Bridge of Hutong Changjiang River Bridge[J]. Bridge Construction, 2015, 45(6): 12-17. |
| [14] |
胡伟明, 马建林, 李军堂, 等. 超大截面沉井着床行为判别分析[J]. 桥梁建设, 2016, 46(2): 115-120. HU Wei-ming, MA Jian-lin, LI Jun-tang, et al. Judgment Analysis of Behavior of Landing Super Large Section Caisson onto Riverbed[J]. Bridge Construction, 2016, 46(2): 115-120. |
| [15] |
孟颂颂.不同前期固结压力下粉砂类滑带土抗剪强度环剪试验研究[C]//2016年全国工程地质学术年会论文集.北京: 中国地质学会工程地质专业委员会, 2016: 1355-1361. MENG Song-song. Shear Strength Behavior of Silty Sand Type Landslide Soil under Different pre-consolidation Pressures in Ring Shear Tests[C]//Proceedings of the National Engineering Geology Conference. Beijing: Engineering Geology Professional Committee of China Geological Society, 2016: 1355-1361. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-GCDZ201610001200.htm |
| [16] |
大桥局桥梁研究所. 沉井下沉时土阻力的测量[J]. 桥梁建设, 1974(3): 33-43. Bridge Research Institute of Bridge Bureau. Measurement of Soil Resistance in Settlement of Sinking Wells[J]. Bridge Construction, 1974(3): 33-43. |
| [17] |
李宗哲, 朱婧, 居炎飞, 等. 大型沉井群的沉井下沉阻力监测技术[J]. 华中科技大学学报:城市科学版, 2009, 26(2): 43-46, 51. LI Zong-zhe, ZHU Jing, JU Yan-fei, et al. Monitoring Technique for Sinking Resistance of Large Caisson Group[J]. Journal of Huazhong University of Science and Technology:Urban Science Edition, 2009, 26(2): 43-46, 51. |
| [18] |
陈晓平, 茜平一, 张志勇. 沉井基础下沉阻力分布特征研究[J]. 岩土工程学报, 2005, 27(2): 148-152. CHEN Xiao-ping, QIAN Ping-yi, ZHANG Zhi-yong. Study on Penetration Resistance Distribution Characteristic of Sunk Shaft Foundation[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(2): 148-152. |
 2019, Vol. 36
2019, Vol. 36
