扩展功能
文章信息
- 袁卓亚, 王旭, 朱伟庆, 胡强
- YUAN Zhuo-ya, WANG Xu, ZHU Wei-qing, HU Qiang
- 陕西地区桥梁结构温度作用特点
- Characteristics of Thermal Action on Bridge Structures in Shaanxi Province
- 公路交通科技, 2019, 36(7): 73-80
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(7): 73-80
- 10.3969/j.issn.1002-0268.2019.07.009
-
文章历史
- 收稿日期: 2017-06-12
2. 西安公路研究院, 陕西 西安 710065;
3. 长安大学 公路学院, 陕西 西安 710064
2. Xi'an Highway Research Institute, Xi'an Shaanxi 710065, China;
3. School of Highway, Chang'an University, Xi'an Shaanxi 710064, China
近年来,我国西北地区交通建设的脚步不断加快,不同等级的公路桥梁在西北地区不断兴建。由于西北地区独特的气候特征,在桥梁设计计算时要着重关注桥梁的温度效应。陕西省地处我国内陆,地域呈现南北狭长、东西较窄的特点,陕西气温的分布基本上是由南向北逐渐降低,我国《公路桥涵设计通用规范》(JTG D60—2015)[1]将全国各地域气温划分为严寒地区、寒冷地区以及温热地区3类。陕西地区由南向北依次处于温热地区、寒冷地区和严寒地区,气候特征较为复杂。同时,不同的温度作用模式下的桥梁结构温度效应也不一样[2-5],因此,研究陕西地区桥梁结构的温度作用特点十分必要。
袁磊等[6]根据珠三角地区某高速公路预应力混凝土连续箱梁桥桥面铺装前后箱梁温度场的实测数据,分析了混凝土桥面铺装对箱梁温度场的影响规律,提出了基于《公路桥涵设计通用规范》的混凝土铺装箱梁桥温度梯度修正模型。刘文丽等[7]通过模型梁测试研究了不同厚度和不同类型铺装层对T形梁温度梯度的影响。高大峰等[8]基于传热学经典理论,建立数值模型研究了陕北榆林地区混凝土箱梁温度梯度,并通过与实测温度梯度值的分析比较,采用回归分析方法,推导出适用于陕北地区冬季混凝土箱梁温度梯度的计算模式。李长凤等[9]结合某实际箱梁桥,考虑寒流作用、日气温变化和桥面铺装,采用有限元分析了寒冷地区混凝土箱梁温度作用。以上研究表明,温度作用具有明显的地域特征,温度作用的选取如果不考虑当地的实际情况,而完全按照《公路桥涵设计通用规范》中在缺乏实际调查资料时的推荐值选取,可能导致桥梁设计偏于不安全。同时,已有研究大多针对温度梯度模式,目前还未见对结构有效温度标准值的取值和陕西地区桥梁结构温度作用特点的相关系统研究。因此,本研究采用数学统计和有限元数值模拟相结合的方法,探讨陕西地区桥梁结构温度作用特点,包括结构有效温度标准值和竖向温度梯度分布,以期为陕西地区桥梁结构的设计提供参考。
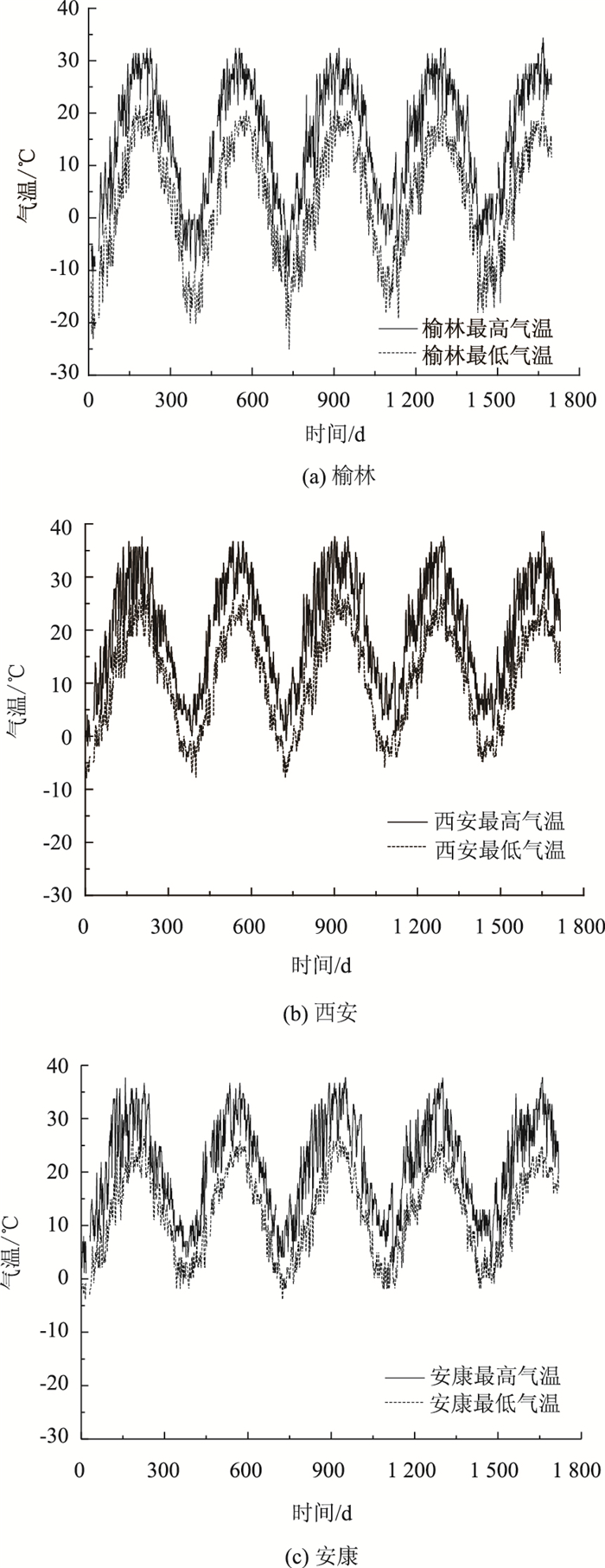
1 陕西地区桥梁结构有效温度标准值 1.1 最高日平均气温和最低日平均气温统计根据陕西地区的气候特点,选取榆林、西安、安康3个城市分别代表陕北严寒地区、关中寒冷地区以及陕南的温热地区。通过统计这3个城市近5 a中的日最高、最低气温(图 1),分别统计分析得到这3个城市近5 a最高日平均气温及最低日平均气温(表 1)。由图 1和表 1可知,陕西3个地区夏季最高日平均气温与历年最高温度均较高,且各地区差别不大;而3个地区的冬季历年最低日平均气温与历年最低温度差别非常大。
|
| 图 1 三个典型城市的日最高气温、最低气温统计 Fig. 1 Statistics of maximum and minimum daily air temperatures in 3 typical cities |
| |
| 气温 | 榆林 | 西安 | 安康 |
| 历年最高日平均气温 | 30 | 32 | 33 |
| 历年最低日平均气温 | -16 | -4 | -0.5 |
| 历年最高气温 | 35 | 39 | 38 |
| 历年最低气温 | -25 | -8 | -4 |
1.2 结构有效温度标准值
在统计历年最高、最低日平均气温和历年最高、最低气温数据的基础上,根据我国《公路桥涵设计通用规范》中的计算方法,得到不同气温区域的结构有效温度标准值。当气温在20~45 ℃之间时,对于钢桥面板钢桥:
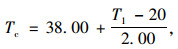
|
(1) |
对于混凝土桥面板钢桥:
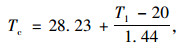
|
(2) |
对于混凝土桥、石桥:
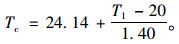
|
(3) |
当气温在-2~-50 ℃之间时,对于钢桥面板钢桥:
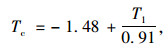
|
(4) |
对于混凝土桥面板钢桥:

|
(5) |
对于混凝土桥、石桥:
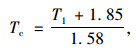
|
(6) |
式中,Tc为结构有效温度标准值;T1为气温,对混凝土结构可取当地历年最高日平均气温或最低日平均气温,对钢结构可取当地历年最高气温或最低气温。当为0 ℃以下时取负值。
计算得到的陕西不同气温区域的结构有效温度标准值如表 2所示,表 2中同时列出了《公路桥涵设计通用规范》在缺乏实际调查资料时对于不同气温区域结构有效温度标准值的取值。对比计算值与规范取值可知:(1)对于混凝土结构的最高有效温度标准值,陕西3个气温区域的规范取值与计算值吻合较好,且略偏于保守;(2)对于钢结构桥梁(钢桥面钢桥、混凝土桥面钢桥)的最高有效温度标准值,规范取值与计算值较为接近,但是在寒冷地区和温热地区,规范取值略偏于不安全;(3)对于结构最低有效温度标准值,规范取值均低于计算值,且根据近5 a的统计数据,规范取值过于保守(有可能是由于统计数据有限导致)。因此,根据以上结果,由于陕西地区气温特点,应尽可能在当地统计气温资料的基础上进行陕西地区桥梁的设计和建造,同时也可在《公路桥涵设计通用规范》的基础上,细化陕西3个气温区域结构有效温度标准值的取值,使得设计的桥梁更加安全和经济。
| 气温区域 | 钢桥面板钢桥 | 混凝土桥面板钢桥 | 混凝土、石桥 | ||||||||||||||
| 计算值 | 规范取值 | 计算值 | 规范取值 | 计算值 | 规范取值 | ||||||||||||
| 最高 | 最低 | 最高 | 最低 | 最高 | 最低 | 最高 | 最低 | 最高 | 最低 | 最高 | 最低 | ||||||
| 严寒地区(榆林) | 45.5 | -29.0 | 46 | -43 | 38.6 | -20.8 | 39 | -32 | 31.3 | -9.0 | 34 | -23 | |||||
| 寒冷地区(西安) | 47.5 | -10.3 | 46 | -21 | 41.4 | -6.7 | 39 | -15 | 32.7 | -1.4 | 34 | -10 | |||||
| 温热地区(安康) | 47.0 | -5.9 | 46 | -9 | 40.7 | -3.4 | 39 | -6 | 33.4 | 0 | 34 | -3 | |||||
2 陕西地区桥梁结构竖向温度梯度分布 2.1 梁体竖向温度场二维分析方法 2.1.1 分析基本假定
桥梁结构的温度场分析以Fourier热传导微分方程为理论基础[10]。在进行桥梁等一维构件(长度方向较截面方向尺寸大得多、且截面形式和尺寸沿梁体纵向变化不剧烈)的温度场分析时,可做如下两个假定:
(1) 沿梁体纵向的热传导可忽略,即可简化为平面热传导问题进行分析。
(2) 截面中不同材料部件之间的界面(如钢-混组合梁中的钢混界面)满足温度与热流密度连续的条件,即第4类边界条件[11]。
2.1.2 太阳辐射作用下竖向温度梯度分析边界条件陕西3个地区的太阳辐射强度可按照各自的维度、海拔以及从元旦算起的日序数等较为合理地确定[12-15]。在太阳辐射作用下,桥梁结构表面法向热传导微分方程可表示为:
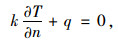
|
(7) |
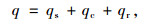
|
(8) |
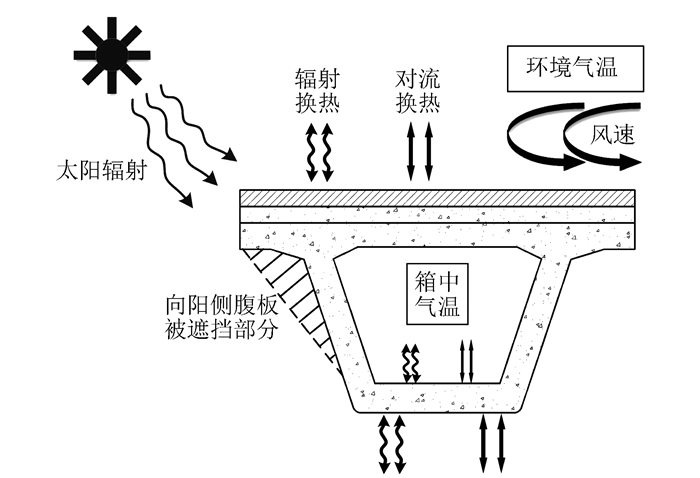
式中,T为桥梁结构温度;k为材料的导热率,n为法向方向;q为热流荷载;qc为结构表面与环境之间的对流换热,qr为结构表面与周围环境的辐射换热(梁体与环境热交换如图 2所示)。qs为结构表面吸收的太阳辐射,可按下式计算:
|
| 图 2 梁体与环境热交换 Fig. 2 Heat exchange between girder and surroundings |
| |
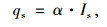
|
(9) |
式中,α为结构表面材料对太阳辐射强度的短波吸收率,主要与表面颜色和光洁度有关,若无试验测定的准确值,可参考文献[13, 16]进行取值;Is为结构表面的太阳辐射强度,可按下式计算:
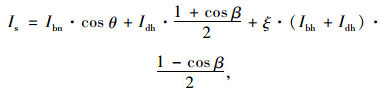
|
(10) |
式中,θ为太阳入射角;β为结构表面的倾角;ξ为地面对太阳辐射的反射率,一般取0.2[17];Ibn,Ibh,Idh分别为法向和水平面的太阳直接辐射强度以及水平面上的散射辐射强度。等号右边3项分别为太阳直接辐射强度、大气对太阳辐射的散射辐射强度、地面对太阳直接辐射和大气散射的反射辐射强度。同时,对于直接辐射还应考虑翼缘板对腹板的遮挡作用[18]。
结构表面与周围环境的对流换热热流密度qc由牛顿冷却公式[19]计算:
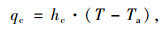
|
(11) |
式中,T和Ta分别为结构表面温度和气温;hc为对流换热系数,与环境风速v有关,对于箱梁可根据凯尔别克的测试分析得到:
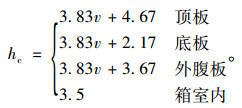
|
(12) |
结构表面的辐射换热热流密度qr可按下式计算:
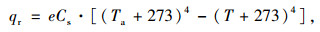
|
(13) |
式中,e为结构表面辐射率;Cs为Stefan-Boltzmann常数,可取5.67×10-8 W/m2。
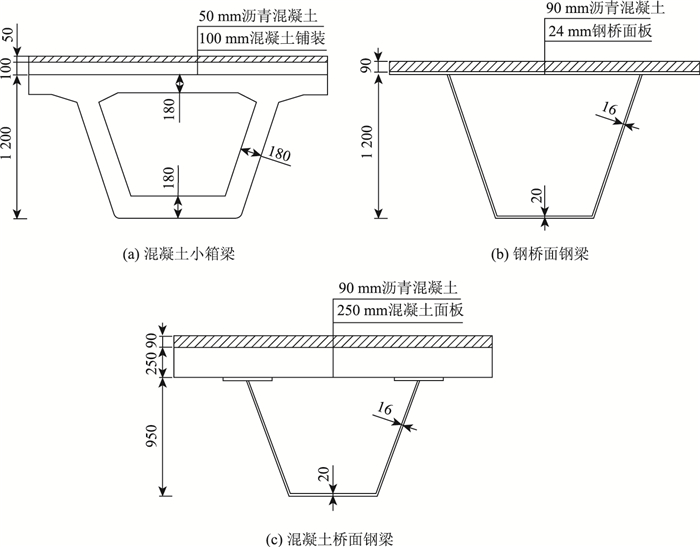
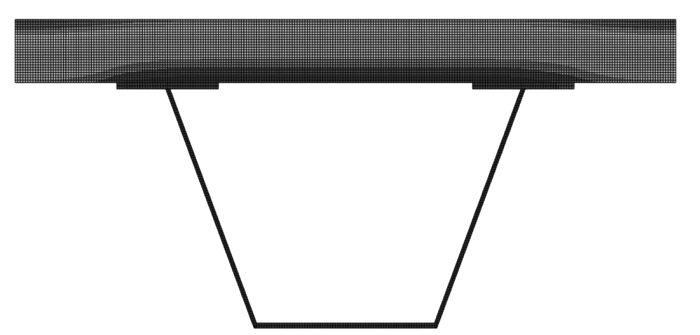
2.1.3 有限元模型的建立选取某实际工程中混凝土小箱梁,以及钢桥面钢梁和混凝土桥面钢梁3种截面形式进行梁体竖向温度梯度模式分析(如图 3所示)。采用ABAQUS有限元软件进行温度场数值仿真分析。有限元建模时选用四节点线性传热四边形单元(DC2D4),按照2.1.2节选取边界条件,各边界的对流换热系数hc可根据式(13)计算得到,各材料热工参数可按表 3选取。太阳辐射强度按照3个城市各自的维度、海拔以及从元旦算起的日序数等较为合理地确定[12-15],风速选取较为不利的较低风速1.0 m/s。选取本研究统计的气温数据中气温最高日的气温数据进行计算,其中,榆林(严寒地区)选取2015年7月30日,最低温度22 ℃,最高温度35 ℃;西安(寒冷地区)选取2016年7月20日,最低温度28 ℃,最高温度39 ℃;安康(温热地区)选取2015年8月3日,最低温度23 ℃,最高温度38 ℃。由此建立二维温度场有限元模型(如图 4所示)。
|
| 图 3 箱梁截面形式(单位:mm) Fig. 3 Cross-section types of box girders (unit: mm) |
| |
| 热工参数 | C50混凝土 | 钢 | 沥青混凝土 |
| 密度/(kg·m-3) | 2 500 | 7 850 | 2 100 |
| 比热容/[J·(kg·℃)-1] | 880 | 475 | 1 680 |
| 传导率/[W·(m·℃)-1] | 2.50 | 55 | 1.05 |
| 吸收率 | 0.65 | 0.3 | 0.90 |
| 辐射率 | 0.88 | 0.8 | 0.90 |
|
| 图 4 温度场计算有限元模型 Fig. 4 FE model for calculating temperature field |
| |
2.2 计算结果与分析
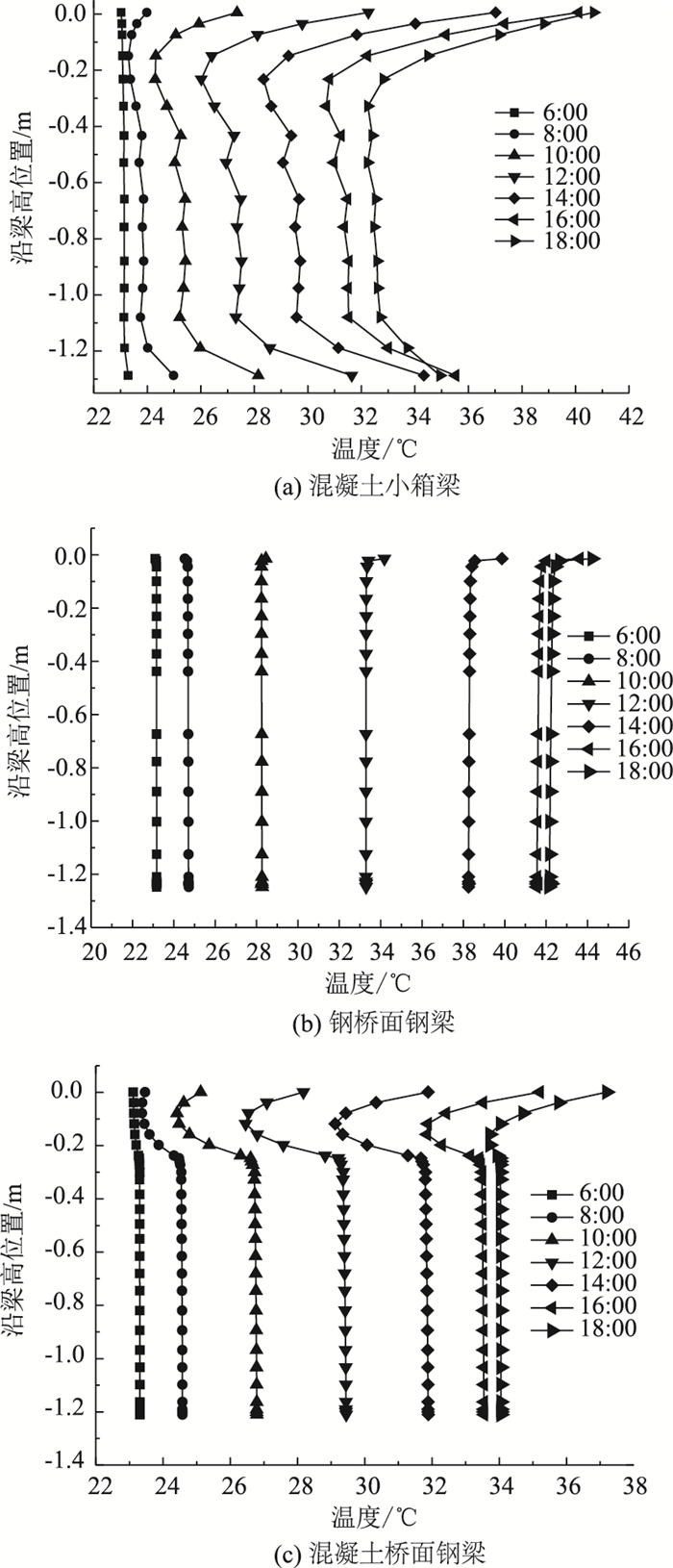
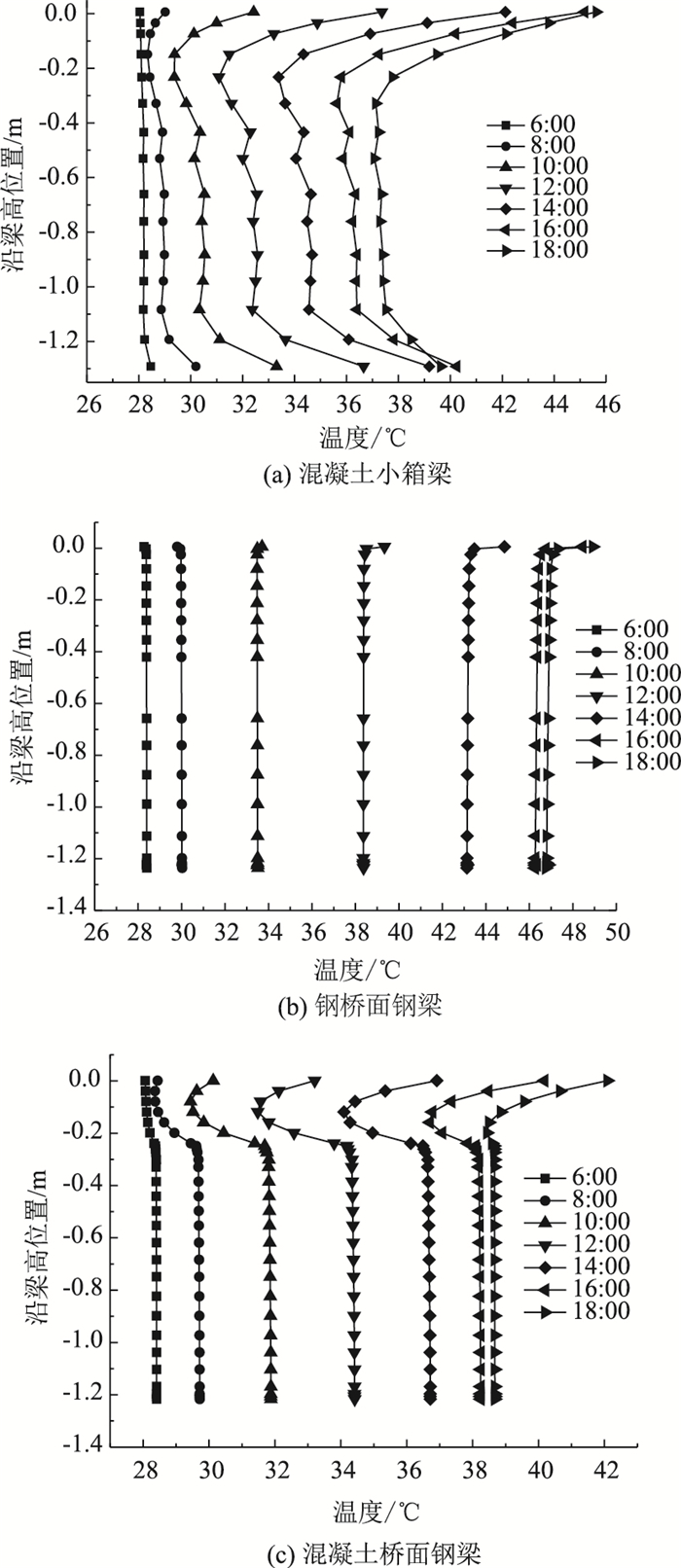
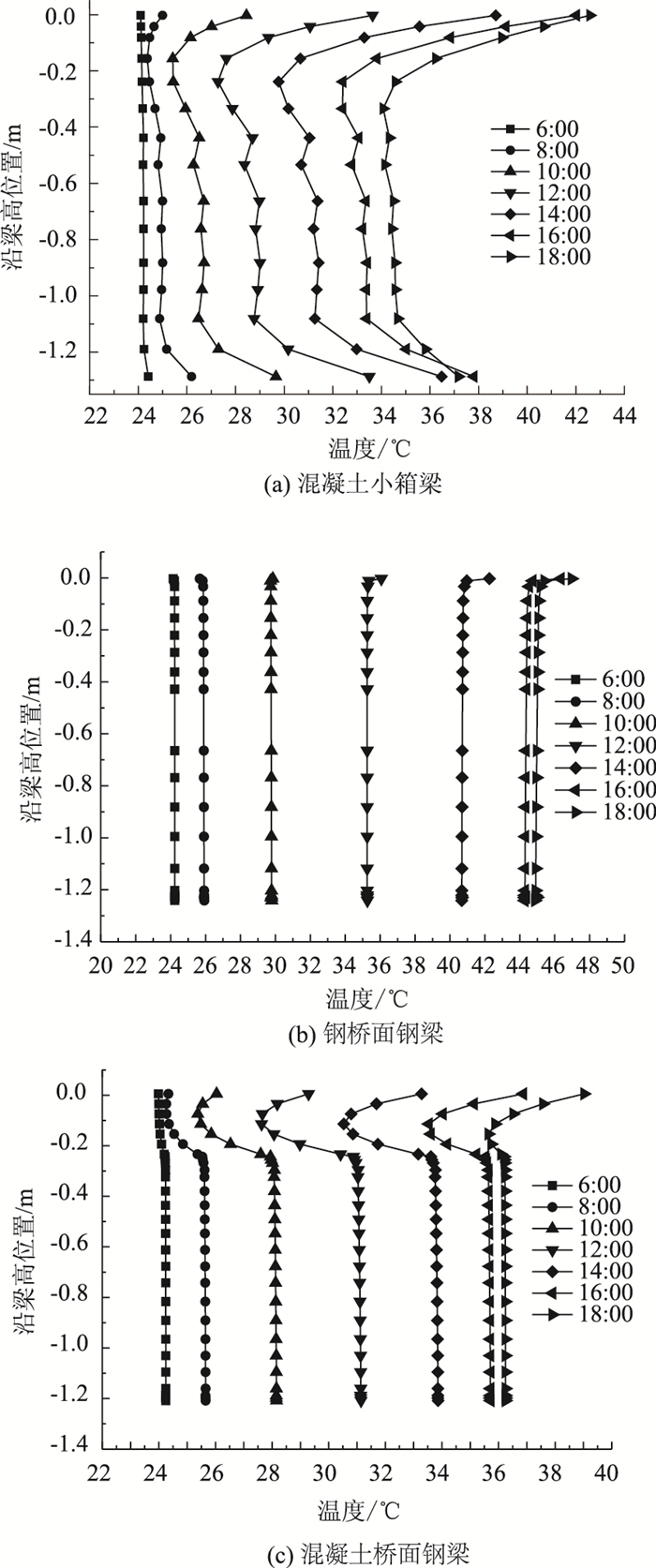
图 5~图 7分别给出了按照榆林、西安、安康气候资料计算得到的不同时刻的混凝土小箱梁、钢桥面钢梁、混凝土桥面钢梁温度沿梁高的分布。可以看出:(1)受太阳辐射的影响,3种不同截面形式的梁在沿梁高方向存在明显的非线性温度梯度。(2)3种不同截面形式的梁中,混凝土小箱梁截面平均温度最小、但沿梁高方向竖向温差最大,而钢桥面钢梁截面平均温度最大、但在沿梁高方向竖向温差最小。主要原因是混凝土导热系数小,热量传递速度慢,导致温差较大,而钢的导热系数很大,热量传递速度快,故温差较小。(3) 3种不同截面形式的梁中,混凝土小箱梁底板厚度方向存在明显的负温差,钢桥面钢梁和混凝土桥面钢梁底板厚度方向无明显的温差。主要原因是混凝土小箱梁底板厚度较厚,且混凝土导热系数较小、热量传递速度慢,导致底板内外侧存在明显的温差。(4)对比3个地区温度分布曲线可以看出,同一种梁在3个地区最不利时刻的截面温度分布模式基本一致,地区差异较小。同时,通过对比图 5~图 7与《公路桥涵设计通用规范》给出的温度梯度模式,可以看出陕西3个不同气温区域桥梁结构竖向温度梯度分布与规范中的温度梯度模式也存在一定的差异:3种不同截面形式的梁的顶板位置温度梯度均比规范值偏小,主要原因是沥青铺装起到一定的隔热作用;混凝土小箱梁底板位置最大负温差达5.3 ℃。
|
| 图 5 榆林地区不同截面形式主梁沿梁高度的温度分布 Fig. 5 Vertical temperature gradient distribution of girders with different sections along depth in Yulin |
| |
|
| 图 6 西安地区不同截面形式主梁沿梁高度的温度分布 Fig. 6 Vertical temperature gradient distribution of girders with different sections along depth in Xi'an |
| |
|
| 图 7 安康地区不同截面形式主梁沿梁高度的温度分布 Fig. 7 Vertical temperature gradient distribution of girders with different sections along depth in Ankang |
| |
3 结论
为得到陕西地区温度作用的特点,本研究根据陕西地区的气候特点,选取典型城市分别代表陕北严寒地区、关中寒冷地区及陕南温热地区。在统计得到的历年最高和最低日平均气温,以及历年最高和最低气温数据的基础上,根据《公路桥涵设计通用规范》的计算方法得到了陕西不同气温区域的结构有效温度标准值。其次,选取某实际工程中混凝土小箱梁以及钢桥面钢梁和混凝土桥面钢梁,分别建立了有限元模型,计算分析了其在不同气温区域时的竖向温度梯度分布。对比计算结果与规范得出以下结论:
(1) 对于混凝土结构的最高有效温度标准值,陕西3个不同气温区域的规范取值与计算值吻合较好,且略偏于保守;对于钢桥面钢桥、混凝土桥面钢桥的最高有效温度标准值,规范取值与计算值较为接近,但是在寒冷地区和温热地区时,规范取值略偏于不安全;对于结构最低有效温度标准值,规范取值均低于计算值,且根据近5 a的统计数据,规范取值过于保守。
(2) 受太阳辐射的影响,不同截面形式的梁在沿梁高方向存在明显的非线性温度梯度;同一种梁在3个地区最不利时刻的截面温度分布模式基本一致,地区差异较小。不同截面形式的梁中,混凝土小箱梁截面平均温度最小,但沿梁高方向竖向温差最大;而钢桥面钢梁截面平均温度最大,但在沿梁高方向竖向温差最小。规范中竖向温度梯度分布模式较计算结果偏于安全,但是规范没有考虑混凝土小箱梁底板位置明显的负温度梯度的情况。
| [1] |
JTG D64-2015, 公路钢结构桥梁设计规范[S]. JTG D64-2015, Specifications for Design of Highway Steel Bridge[S]. |
| [2] |
何翔, 方诗圣, 方飞, 等. 不同梯度温度作用下曲线桥梁的温度效应分析[J]. 合肥工业大学学报:自然科学版, 2012, 35(8): 1087-1092. HE Xiang, FANG Shi-sheng, FANG Fei, et al. Analysis of Temperature Effects of Curved Bridge under Different Gradient Temperature Load[J]. Journal of Hefei University of Technology:Natural Science Editin, 2012, 35(8): 1087-1092. |
| [3] |
季德钧, 刘江, 张瑑芳, 等. 高原高寒地区钢-混凝土组合梁斜拉桥温度效应分析[J]. 建筑科学与工程学报, 2016, 33(1): 113-119. JI De-jun, LIU Jiang, ZHANG Zhuan-fang, et al. Temperature Effect Analysis of Steel-concrete Composite Girder Cable-stayed Bridge in Arctic-alpine Region[J]. Journal of Architecture and Civil Engineering, 2016, 33(1): 113-119. |
| [4] |
杨佐, 赵勇, 苏小卒. 国内外规范的混凝土桥梁截面竖向温度梯度模式比较[J]. 结构工程师, 2010, 26(1): 37-43. YANG Zuo, ZHAO Yong, SU Xiao-zu. Comparison of Vertical Temperature Gradients at Cross Sections of Concrete Bridges in Bridge Design Codes of Different Countries[J]. Structural Engineers, 2010, 26(1): 37-43. |
| [5] |
马毓泉, 汪屏, 冯云成. 中、英、美规范温度梯度效应的分析比较[J]. 交通科技, 2008(5): 67-70. MA Yu-quan, WANG Ping, FENG Yun-cheng. Comparison of Effect of Temperature Difference among Specifications of China, America and British[J]. Transportation Science and Technology, 2008(5): 67-70. |
| [6] |
袁磊, 王石磊, 张勇. 混凝土铺装箱梁桥的合理温度梯度[J]. 铁道建筑, 2015(4): 1-5. YUAN Lei, WANG Shi-lei, ZHANG Yong. Rational Temperature Gradient of Box Girder Bridges with Concrete Pavement[J]. Railway Engineering, 2015(4): 1-5. |
| [7] |
刘文丽, 贡金鑫, 张秀芳. 铺装层对T形梁桥梁竖向温度梯度的影响[J]. 公路交通科技, 2014, 31(10): 45-50. LIU Wen-li, GONG Jin-xin, ZHANG Xiu-fang. Impact of Pavement Layer on Vertical Temperature Gradient of T-girder Bridge[J]. Journal of Taiyuan University of Technology, 2014, 31(10): 45-50. |
| [8] |
高大峰, 何新成, 任禹州. 陕北榆林地区混凝土箱梁温度梯度分析[J]. 太原理工大学学报, 2012, 43(2): 212-215. GAO Da-feng, HE Xin-cheng, REN Yu-zhou. Concrete Box Girder Temperature Gradient Analysis of Yulin District[J]. Journal of Taiyuan University of Technology, 2012, 43(2): 212-215. |
| [9] |
李长凤, 王岚, 赵延林, 等. 寒冷地区混凝土箱梁温度作用影响[J]. 黑龙江科技学院学报, 2013, 23(2): 169-172. LI Chang-feng, WANG Lan, ZHAO Yan-lin, et al. Research on Temperature Effect on Reinforced Box Girder in Cold Region[J]. Journal of Heilongjiang Institute of Science and Technology, 2013, 23(2): 169-172. |
| [10] |
梅飞鸣, 章熙, 任泽霈. 传热学[M]. 5版. 北京: 中国建筑工业出版社, 2007. MEI Fei-ming, ZHANG Xi, REN Ze-pei. Heat Transfer Theory[M]. 5th ed. Beijing: China Architecture & Building Press, 2007. |
| [11] |
朱伯芳. 大体积混凝土的温度应力与温度控制[M]. 2版. 北京: 中国电力出版社, 2012. ZHU Bo-fang. Temperature Stress and Temperature Control of Mass Concrete[M]. 2nd ed. Beijing: China Electric Power Press, 2012. |
| [12] |
李申生. 太阳能物理学[M]. 北京: 首都师范大学出版社, 1996. LI Shen-sheng. Solar Energy Physics[M]. Beijing: Capital Normal University Press, 1996. |
| [13] |
凯尔别克F.太阳辐射对桥梁结构的影响[M].刘兴法, 等译.北京: 中国铁道出版社, 1981. KEHLBECK F. Influence of Solar Radiation on Bridge Structure[M]. LIU Xing-fa, et al translated. Beijing: China Railway Publishing House, 1981. |
| [14] |
刘广龙, 刘江, 刘永健, 等. 西北极寒地区混凝土箱梁温度场实测与仿真分析[J]. 公路交通科技, 2018, 35(3): 64-71. LIU Guang-long, LIU Jiang, LIU Yong-jian, et al. Measurement and Simulation of Temperature Field of Concrete Box Girder in Northwest Severe Cold Area[J]. Journal of Highway and Transportation Research and Development, 2018, 35(3): 64-71. |
| [15] |
FU H C, NG S F, CHEUNG M S. Thermal Behavior of Composite Bridges[J]. Journal of Structural Engineering, 1990, 116(12): 3302-3323. |
| [16] |
ELBADRY M M, GHALI A. Temperature Variations in Concrete Bridges[J]. Journal of the Structural Engineering, 1983, 109(10): 2355-2374. |
| [17] |
向学建, 董军, 刘昊苏, 等. 高原冬季环境下桥梁温度场各参数的确定[J]. 公路交通科技, 2012, 29(3): 58-63. XIANG Xue-jian, DONG Jun, LIU Hao-su, et al. Determination of Parameters of Temperature Field of Box-girder Bridge in Winter Weather of Plateau[J]. Journal of Highway and Transportation Research and Development, 2012, 29(3): 58-63. |
| [18] |
彭友松.混凝土桥梁结构日照温度效应理论及应用研究[D].成都: 西南交通大学, 2007. PENG You-song. Studies on Theory and Application of Solar Radiation Thermal Effects on Concrete Bridges[D]. Chengdu: Southwest Jiaotong University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10613-2008178072.htm |
| [19] |
杨世铭. 传热学[M]. 北京: 高等教育出版社, 1998. YANG Shi-ming. Heat Transfer Theory[M]. Beijing: Higher Education Press, 1998. |
 2019, Vol. 36
2019, Vol. 36
