扩展功能
文章信息
- 黄海林, 刘光伟, 朱慧, 黄曙, 曾垂军
- HUANG Hai-lin, LIU Guang-wei, ZHU Hui, HUANG Shu, ZENG Chui-jun
- 带剪力键的GFRP-混凝土空心箱型组合板受力性能试验研究
- Experimental Study on Mechanical Behavior of GFRP-concrete Hollow Box-type Composite Slabs with Shear Connectors
- 公路交通科技, 2019, 36(7): 63-72
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(7): 63-72
- 10.3969/j.issn.1002-0268.2019.07.008
-
文章历史
- 收稿日期: 2018-02-01
2. 中建五局广西公司, 广西 南宁 530022;
3. 长沙市人防工程质量监督定额管理站, 湖南 长沙 410013
2. Guangxi Construction Co., Ltd., of China Construction Fifth Engineering Bureau, Nanning Guangxi 530022, China;
3. Civil Air Defense Engineering Quality Supervision Station of Chansha, Changsha Hunan 410043, China
玻璃纤维增强塑料(Glass Fiber Reinforced Polymer,GFRP)是由合成树脂和玻璃纤维经复合工艺制作而成的一种新型功能型材料。GFRP具有强度高、轻质、耐腐蚀性好、可设计性强等优点,已被各国应用于全GFRP结构或GFRP-混凝土组合结构中[1-4]。目前,GFRP材料的利用已逐渐成为组合结构及新材料应用研究的重要方向[5-7]。GFRP箱梁、GFRP工字梁、GFRP组合板等试验研究表明, 全GFRP构件的刚度偏低,受压区GFRP容易压屈,使得GFRP的强度得不到充分发挥[8-9]。为此,可将GFRP置于受拉区、混凝土置于受压区形成GFRP-混凝土组合结构。国内外学者对GFRP-混凝土组合板展开了大量理论与试验研究[10-15],结果表明,GFRP-混凝土组合板能充分利用材料的特性,在减轻自重的情况下,能显著改善结构的受力性能。
GFRP-混凝土组合结构中的剪力键是保证底部GFRP构件与上部混凝土面层连接成整体而协同工作的关键,其连接程度决定了GFRP-混凝土组合结构的整体工作性能。剪力键具有承载力高、延性好、抗疲劳等优点,在钢-混凝土组合结构中已得到了广泛的研究与应用。如:栓钉剪力键[16]、开孔板剪力键[17]、T形开孔肋剪力键[18]、Y形剪力键[19]等。目前国内外学者主要通过推出试验对剪力键的破坏机理、极限承载力、荷载-滑移关系等进行研究,基于试验结果,提出了诸多模型用于预测其抗剪承载力公式。但对带剪力键的GFRP-混凝土空心箱型组合板在静力荷载作用下的研究较为少见。Kong等[20]进行了一种带圆形空心截面剪力键的GFRP-混凝土组合板试验研究,发现组合截面实现了部分复合作用,连接件的力学性能可影响组合结构的承载能力和刚度。卓一泽等[21]进行了6个带T形穿孔肋剪力键的GFRP-混凝土组合桥面板的试验研究,考虑了开孔间距、有无弯曲钢筋、GFRP复合材料表面处理质量、桥面板深度、钢筋类型5个试验参数,发现配置弯曲钢筋、对GFRP表面喷砂处理、增加甲板厚度可以提高桥面板的极限强度,而开孔间距和钢筋类型对桥面板板极限承载力的影响可以忽略不计。
尽管剪力键在钢-混凝土组合结构中的研究已经比较成熟,对开展GFRP-混凝土组合结构中剪力键的研究提供了参考,但GFRP与钢两种材料的力学性能完全不同,导致GFRP-混凝土组合结构与钢-混凝土组合结构中剪力键的受力性能与破坏形态存在差异,有必要开展GFRP-混凝土组合结构中对剪力键受力性能的研究。为此,本研究提出一种带剪力键的GFRP-混凝土空心箱型组合板,组合板底部由GFRP空心箱型构件组成,在构件上部增设T形或矩形肋剪力键。为保证剪力键与GFRP空心箱型构件共同受力,整个GFRP空心箱型构件采用拉挤工艺一次成型。本研究进行在不同因素下4个GFRP-混凝土空心箱型组合板受弯性能试验,重点研究剪力键的截面形式、贯穿钢筋、开孔间距3个因素对GFRP-混凝土空心箱型组合板受力性能的影响。基于试验结果得到试件的破坏机制,提出并建立带剪力键的GFRP-混凝土空心箱型组合板的抗弯承载力计算方法。
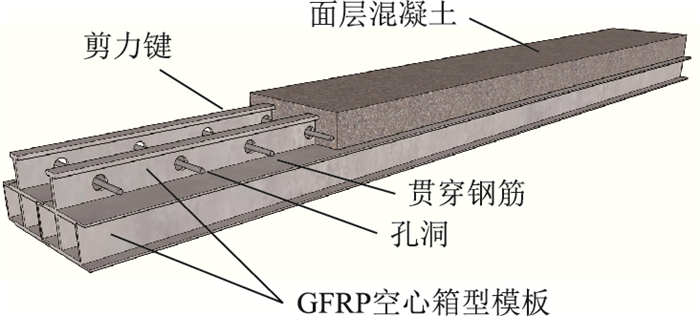
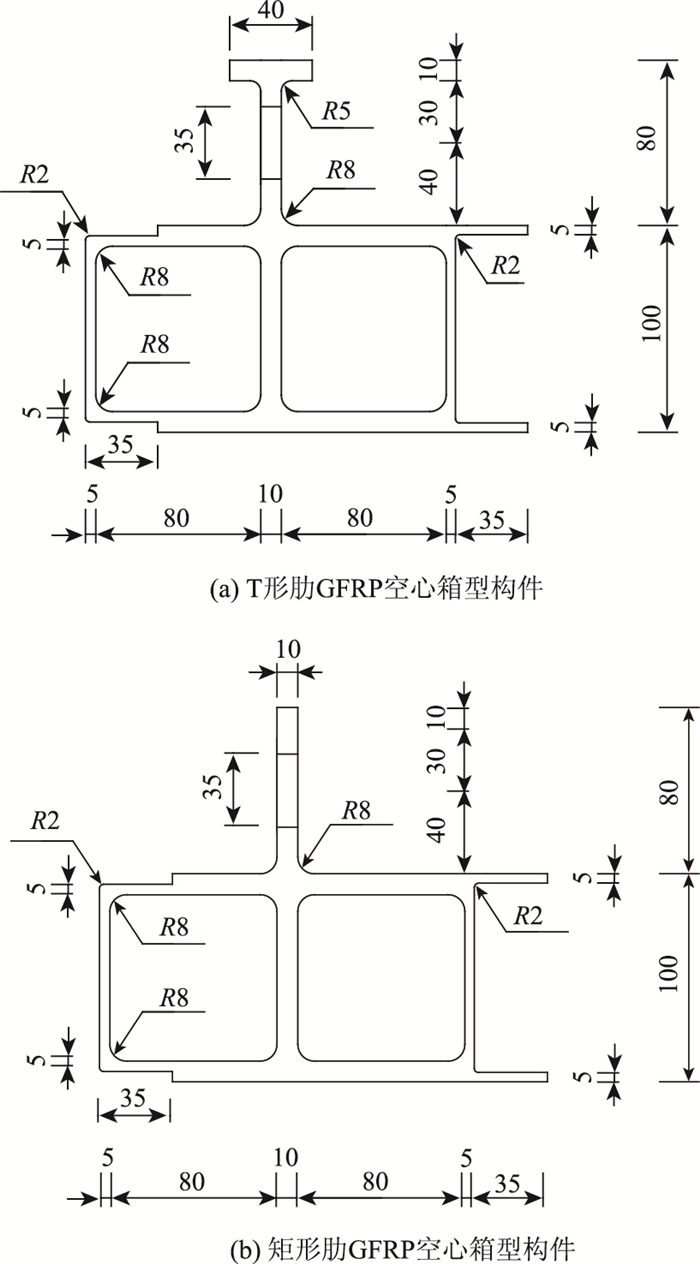
1 试验概况 1.1 试件设计参考现行规范,设计了4根带剪力键的GFRP-混凝土空心箱型组合板试件,编号从试件1~试件4,重点研究剪力键的截面形式、贯穿钢筋、开孔间距3个因素对组合板受力性能的影响。组合板三维模型见图 1,试件净跨为2 880 mm,总长为3 100 mm,板宽为394 mm,板高为200 mm。面层混凝土厚度为100 mm。GFRP空心箱型构件由上部剪力键与下部空心箱型底板采用拉挤工艺一次成型。GFRP空心箱型构件截面设计见图 2,变化参数包括剪力键的截面形式、贯穿钢筋、开孔间距。各组合板试件所采用的GFRP空心箱型构件主要参数见表 1。
|
| 图 1 GFRP-混凝土空心箱型组合板三维模型 Fig. 1 3D model of GFRP-concrete hollow box-type Composite slab |
| |
|
| 图 2 GFRP空心箱型构件截面设计(单位:mm) Fig. 2 Section design of GFRP hollow box-type members (unit:mm) |
| |
| 试件编号 | 净跨/ mm | 剪力键截面形式 | 贯穿钢筋直径/mm | 开孔间距/ mm | 是否开孔 |
| 1 | 2 880 | T形 | 12 | 200 | 是 |
| 2 | 2 880 | T形 | 12 | 100 | 是 |
| 3 | 2 880 | T形 | — | — | 否 |
| 4 | 2 880 | 矩形 | 12 | 100 | 是 |
1.2 材料性能
GFRP空心箱型构件为某公司生产的拉挤型材,基体采用间苯型不饱和聚酯树脂,纤维采用4800TEX无碱玻璃纤维。GFRP材料性能参数见表 2。混凝土立方体抗压实测强度平均值为38.1 MPa。孔内贯穿钢筋选用ϕ12,实测平均屈服强度、极限强度分别为551,689 MPa。
| 拉伸强度/MPa | 压缩强度/MPa | 拉伸弹模/GPa | 压缩弹模/GPa |
| 473 | 265 | 13.8 | 9.8 |
1.3 试件制作
本研究制作的GFRP空心箱型构件由上、下两部分组成。下部为单箱室GFRP型材粘结拼装而成;上部经切割、开孔、粘接等工艺,形成带有不同肋截面形式与开孔间距的GFRP空心箱型构件。在对GFRP型材构件进行拼装时,采用80目粗砂纸进行人工打磨,然后用ESTA-TJ碳纤维粘贴胶涂刷GFRP空心构件拼装面,最后对齐拼装,形成空心箱型构件。为保证单箱室GFRP型材连接紧密,拼装完成后在GFRP构件侧壁用橡胶锤敲打并在室温下养护数日。为避免加载过程中支座端部在局部压力作用下出现应力集中而导致局压破坏的情况,在GFRP空心箱端部空腔内灌注长度为150 mm的混凝土块。
1.4 试验装置、加载方案及测点布置试验采用跨中两点对称静力加载,试验装置为DH3816静态应变测试系统、JMZX实心荷载传感器、读数仪、100 t千斤顶、50 mm广陆防震机械百分表等。试验装置如图 3所示。

|
| 图 3 试验装置 Fig. 3 Test equipment |
| |
试验加载分为预加载和正式加载两个阶段。预加载阶段:在正式加载之前取每级4 kN荷载加载至0.1倍计算承载力荷载,之后分级卸载。正式加载阶段:力控制加载阶段按每级4 kN加载,直至跨中挠度达到1 mm,每级加载完成持荷5 min后读数。位移控制加载阶段按每级1 mm加载,每级加载完成后,若5 min内滑移量增量小于0.05 mm则持荷完毕,进行读数。试件最终破坏标志:板顶跨中混凝土完全压溃且板顶主裂缝贯通整个截面,试件不能继续承受荷载。
测试内容主要包括跨中实际挠度、GFRP与混凝土界面相对滑移、GFRP、混凝土和贯穿钢筋处应变等。
2 试验结果及现象分析试件主要试验结果见表 3。其中,Pu为试件加载过程中的峰值荷载,Pcr为试件出现第1条裂缝时的荷载,Pc为跨中板顶混凝土达到极限压应变时的极限荷载,Po为挠跨比达到1/50时的荷载,Sc为Pc荷载作用时的端部界面滑移量。
| 试件编号 | Pu/kN | Pcr/kN | Pc/kN | Po/kN | Sc/mm | 破坏形式 |
| 1 | 184 | 106 | 175 | 146 | 2.4 | 跨中板顶混凝土被压碎 |
| 2 | 256.2 | 181 | 256 | 195 | 1.0 | |
| 3 | 249.2 | 136 | 160 | 149 | 14.9 | |
| 4 | 302.3 | 148 | 212 | 232 | 1.3 |
2.1 受力全过程及破坏机理
试件1:加载106 kN时,混凝土侧壁出现第1条从交界面斜向上延伸的剪切裂缝。184 kN时,试件发生一声巨响,右端部箱型腹板侧壁与顶板在剪应力集中处出现纤维撕裂现象,跨中侧壁与上板顶出现鼓曲现象,此时挠度急剧增加。随后跨中上部混凝土侧壁出现第1条横向裂缝。随着裂缝进一步增大,上部混凝土裂缝在纯弯段由中心向四周迅速发散,呈放射状。最终剪力键翼缘被压断,顶部混凝土压碎。
试件2:加载180.9 kN时,弯剪段靠近加载点处沿垂直方向出现沿45°方向细小斜裂缝。挠度增加至33.4 mm时,剪力键部位出现脆性响声。交界面上部同时出现多条垂直裂缝,并迅速向上延伸。加载256.2 kN时,由于端部剪应力过大,箱型腹板与顶板被剪断。混凝土纵、横两个方向上出现多条裂缝,挠度进一步增大。继续加载,裂缝贯穿整个截面,板顶混凝土出现压溃现象,试件达到破坏。该试件侧壁并未出现鼓曲剥离现象,T形剪力键根部被剪断,但翼缘未被压断。卸载后,由于GFRP材料弹性恢复性能比混凝土强,导致试件右部混凝土板出现翘曲现象。
试件3:加载136 kN时,支座端部沿T形剪力键截面位置产生竖向裂缝。同时,加载点侧壁处出现短而密的竖向剪切裂缝。当加载至249.2 kN,挠度达到42.3 mm时,右端部箱型腹板、侧壁与底板在剪应力集中处出现撕裂现象。GFRP侧壁与上下腹板发生剥离,试件出现局部破坏,此后采用位移控制加载。继续加载,交界面位置处的裂缝不再向上发展,混凝土侧壁中部位置横向裂缝扩展增宽,呈现明显一字形分布。此时板顶裂缝向整个截面延伸,板顶混凝土出现掀起现象。最终T形剪力键翼缘被压断,混凝土压碎区贯穿整个截面,试件破坏。
试件4:加载148.4 kN时,听到细微响声,左加载点下端混凝土表面出现树状形裂缝,宽度未超过0.02 mm,长度约为16 mm,该裂缝沿垂直面呈45°向上发展,此后新的剪切裂缝未在侧壁出现。直至加载302.3 kN,侧壁靠近中点附近出现横向裂缝,GFRP-混凝土界面滑移程度增大,发出轻脆的劈裂声,支座处出现明显的错位现象。左加载点附近箱型腹板局部被撕裂,侧壁剪切裂缝急剧增加,交界面突然出现众多斜向裂缝。继续加载,端部剪力键腹板与箱型顶板被完全剪断。左加载点处板顶混凝土突然出现集中破坏,右加载点处板顶混凝土基本完整。可见,该试件左右加载点附近混凝土受力不均匀,这取决于加载时集中荷载的对中程度。卸载后,混凝土板翘曲,矩形剪力键根部直接被剪断。
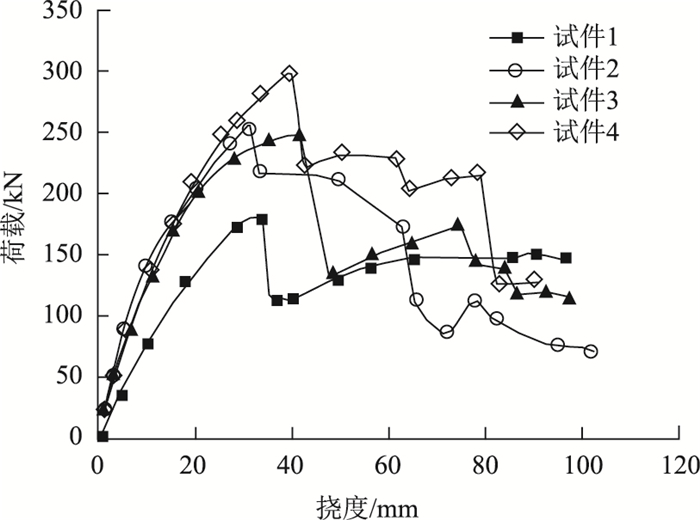
2.2 荷载-挠度曲线试件的跨中板底荷载-挠度曲线如图 4所示。试件的荷载-挠度曲线可分为线性阶段、非线性阶段、下降阶段3个阶段。
|
| 图 4 跨中板底荷载-挠度曲线 Fig. 4 Load-deflection curves in bottom of slab at midspan |
| |
线性阶段:在试验初期,试件处于线性阶段,刚度较大,加载点侧壁处出现少量剪切裂缝。GFRP和混凝土之间没有明显的滑移,共同受力,协同变形,基本呈现相同变化规律,跨中荷载-挠度曲线呈线性关系,斜率反映了试件的初始刚度。
非线性阶段:随着荷载的持续增长,试件跨中挠度增长速率明显快于初期。端部交界面开始出现明显滑移,纯弯段出现多条裂缝且向上发展,刚度有所下降。当达到最大承载力时,GFRP-混凝土界面滑移程度增大,支座处出现明显的错位现象,试件刚度进一步下降。由于GFRP型材没有明显的屈服平台,且弹性模量较低,所以组合板在达到最大荷载时突然破坏,挠度突然增大。试件的承载力迅速下降但并未完全丧失,有一个下降台阶,在下降到某稳定值后又缓慢增长。此时两种材料界面发生相互错动,由于剪力键的存在,在一定程度上降低了滑移的速率。
下降阶段:跨中受压区混凝土局部压溃并有部分脱落,组合作用逐步消失,试件刚度明显减小。当滑移很大时,两种材料已不再作为一个整体共同工作,跨中混凝土被压溃,试件完全破坏。此时试件荷载-挠度曲线存在一定的离散性,在某范围内波动。
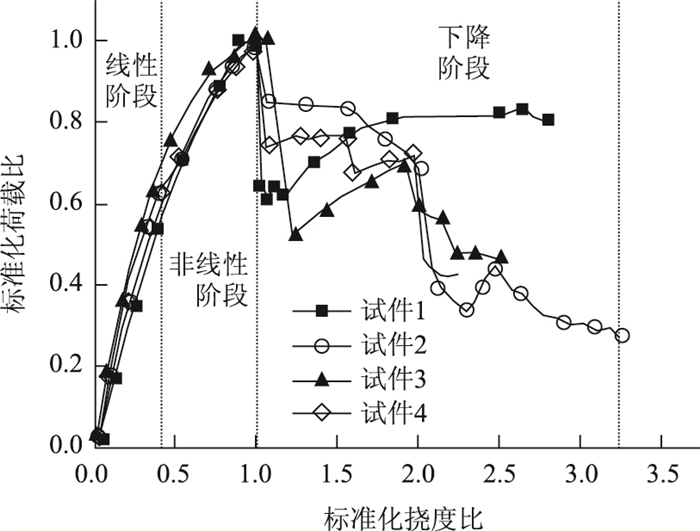
为了便于区分各试件的受力阶段并比较其弹性阶段的抗弯刚度,对各试件的荷载-挠度曲线进行归一化处理后进行分析,如图 5所示。从图 5可以看出,开孔间距对试件的抗弯刚度有一定的影响,而截面形式对抗弯刚度无影响。在线性阶段,开孔间距越大的试件抗弯刚度越低,主要原因是剪力键腹板开孔削弱了截面的刚度,但开孔后形成的混凝土榫的面积越大,对试件整体刚度下降的弥补作用越强。
|
| 图 5 标准化的跨中板底荷载-挠度曲线 Fig. 5 Standardized load-deflection curves in bottom of at midspan |
| |
2.3 荷载-应变曲线 2.3.1 板顶荷载-应变曲线
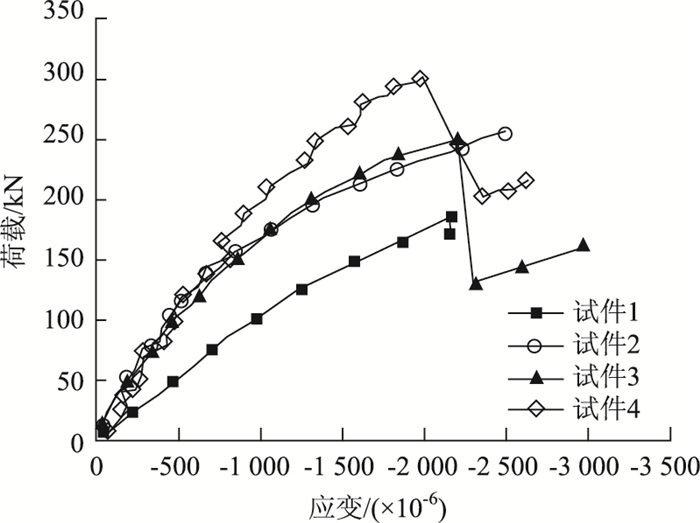
试件跨中混凝土板顶荷载-应变曲线如图 6所示。试验初期,板顶的荷载-应变曲线大致呈线性发展。在同级荷载作用下,试件1板顶的压应变明显大于其余试件。混凝土开裂后,GFRP与混凝土之间开始出现滑移,其界面应力开始重新分布。试件最终破坏时,混凝土顶面压应变迅速增加,此时试件的混凝土压应变存在一个下降段,说明表面的混凝土不是瞬间压溃,而是经历了一个过程。
|
| 图 6 跨中板顶荷载-应变曲线 Fig. 6 Load-strain curves in top of slab at midspan |
| |
2.3.2 板底荷载-应变曲线
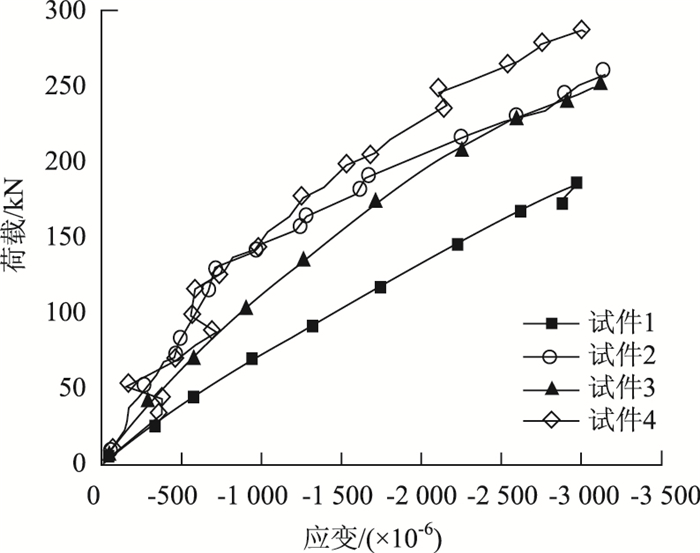
试件跨中GFRP板底荷载-应变曲线如图 7所示。达到最大荷载之前,GFRP箱型组合板板底跨中应变值增长较缓慢。达到最大荷载之后,GFRP箱型组合板板底的应变值较初期应变增长速率有所增加,各试件板底应变在最大荷载时拉应力相近。试件最终破坏时,试件GFRP空心箱型板底的最大拉应变为3 147×10-6,板底的GFRP纵向纤维均未被拉断,试件底部基本完整,远未达到GFRP材料自身的极限拉应变,试件具有较大的安全储备。
|
| 图 7 跨中板底荷载-应变曲线 Fig. 7 Load-strain curves in bottom of slab at midspan |
| |
2.3.3 剪力键翼缘荷载-应变曲线
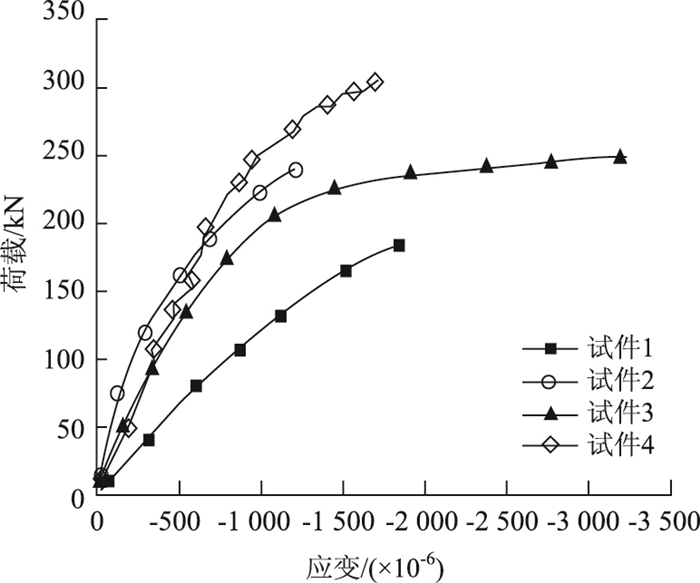
剪力键翼缘荷载-应变曲线如图 8所示。剪力键翼缘在整个加载过程中处于受压状态。试件加载至最大荷载时,GFRP剪力键翼缘处最大压应变为3 245×10-6。最大压应力约为31.7 MPa,为GFRP型材纵向抗压强度的14%。由于剪力键翼缘压应力大于混凝土的极限压应力,剪力键有效起到连接GFRP与混凝土作用。直至试件最终破坏时,试件1、试件3剪力键翼缘被压断,试件2、试件4剪力键根部被剪断。
|
| 图 8 剪力键翼缘荷载-应变曲线 Fig. 8 Load-strain curves of shear connector flange |
| |
试件3由于未开孔,其界面滑移量明显高于其他3个试件,滑移量增大使组合作用变弱,达到最大荷载时剪力键翼缘应变达到最大值。应变测试结果与GFRP剪力键翼缘断裂现象相吻合。
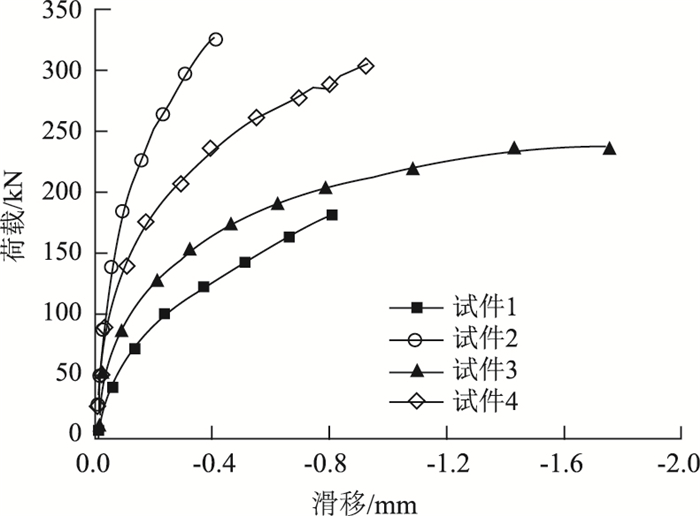
2.4 荷载-滑移曲线试件端部荷载-滑移曲线如图 9所示。剪力键连接程度较高的试件其滑移量均较小,达到最大荷载时,除试件3外,其余试件最大滑移量未超过1 mm。说明试件开孔间距及贯穿钢筋数量对滑移量影响较大。其荷载-滑移曲线可分为线性阶段和非线性阶段两个阶段。
|
| 图 9 端部荷载-滑移曲线 Fig. 9 Load-slip curves at end |
| |
线性阶段:试验初期荷载-滑移曲线呈线性关系。GFRP和混凝土交界面没有明显滑移现象,剪力键的增设有效抑制了受压区混凝土开裂与GFRP之间的滑移,使GFRP和混凝土协同受力,从而增强了组合板整体刚度。
非线性阶段:随着荷载增大,滑移发展加快,当荷载接近最大承载力时,试件交界面出现明显的滑移。荷载-滑移曲线出现明显转折,曲线斜率降低,近似呈水平直线。混凝土板顶出现贯通裂缝,导致整体刚度降低,滑移量进一步增大。各试件GFRP-混凝土组合板板顶混凝土一旦被压溃,两种材料不再作为一个整体进行工作,试件无法继续承力,达到破坏。
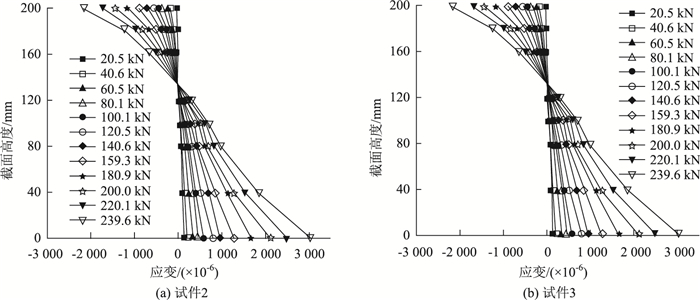
2.5 跨中沿截面高度应变分布典型试件的跨中沿截面高度应变分布如图 10所示。各个试件跨中截面处应变沿梁高近似符合平截面假定,由于试件3未开孔,因此在交界面处滑移应变值较大,各试件中和轴在各受力阶段位置基本保持不变,距离GFRP板底约140 mm。
|
| 图 10 跨中沿截面高度应变分布 Fig. 10 Strain distributions at midspan along section height |
| |
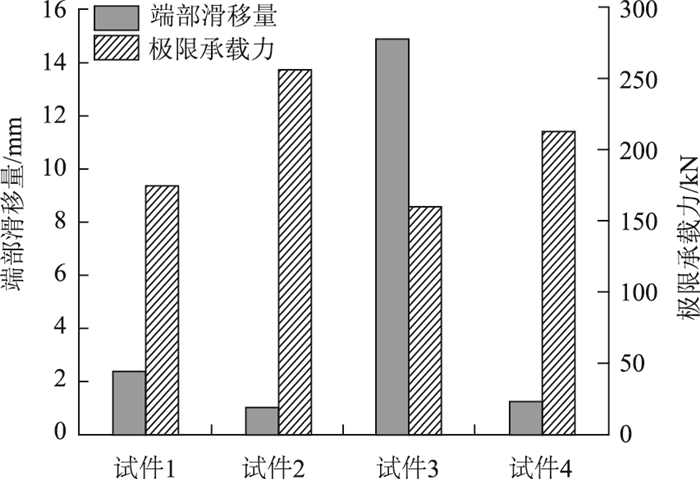
2.6 参数对比分析 2.6.1 开孔间距对比
图 11为各试件的端部滑移量与极限承载力对比柱状图。由图 11可知,试件2比试件1极限承载力提高了39.2%,相对滑移量减小了58.3%。对比分析试件1与试件2、试件3,通过观察荷载-挠度曲线、荷载-滑移曲线可知,试件1的刚度、极限承载力明显低于其他试件。在少量开孔的情况下,开孔孔径对剪力键腹板本身具有一定破坏作用,使得组合结构整体性能有所削弱,试件极限承载力有一定程度的降低。而试件3的相对滑移明显高于其他试件,可见剪力键内形成的混凝土榫能在一定程度上限制GFRP与混凝土之间的滑移,提高试件整体受力性能。
|
| 图 11 滑移量与极限承载力对比柱状图 Fig. 11 Comparative histogram of slippage and ultimate bearing capacity |
| |
2.6.2 截面形式对比
T形肋截面增加了GFRP中剪力键翼缘受压区的接触面积。试件2出现第1条裂缝的时间远远迟于试件4的时间。且试件2剪力键翼缘并未被压断,侧壁未出现鼓曲剥离现象。由图 11可知,试件4的极限承载力比试件2的极限承载力略提高17.9%,但其相对滑移量却增大了30%。
3 抗弯承载力计算试验结果表明,试件最终的破坏形态为跨中板顶混凝土受压破坏。因此,定义GFRP-混凝土空心箱型组合板跨中顶部混凝土达到极限压应变,且GFRP板底尚未拉断时的跨中截面弯矩为控制截面所能承担的最大弯矩。为简化计算,引入正截面抗弯承载力计算假定:
(1) 达到承载力极限状态时,GFRP空心箱型构件和混凝土之间没有明显滑移,剪力能有效传递。
(2) GFRP-混凝土组合板截面应变保持平截面。
(3) 不计GFRP-混凝土组合板受拉区混凝土、受压区纵向钢筋以及剪力键腹板对试件抗弯承载力的作用。
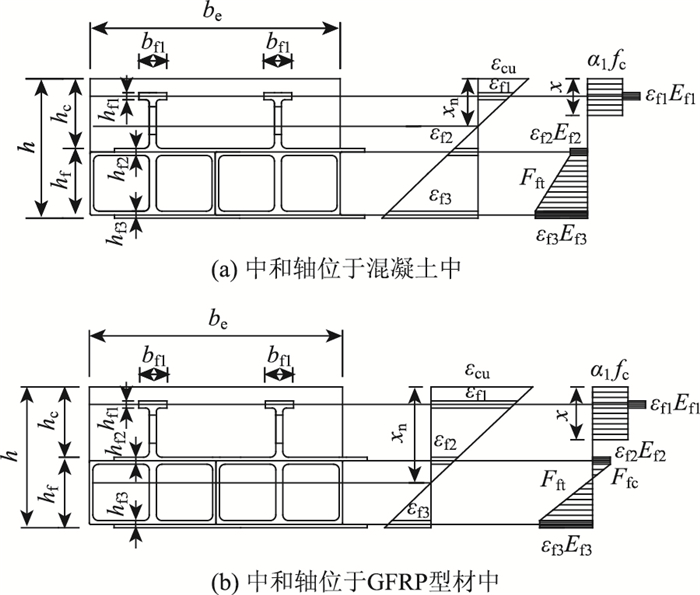
根据以上假定,GFRP-混凝土空心箱型组合板抗弯承载力极限状态有两种情况,即组合截面中和轴位于混凝土中和GFRP空心箱型构件中。其计算简图如图 12所示。
|
| 图 12 带剪力键的GFRP-混凝土组合板计算简图 Fig. 12 Calculation diagram of GFRP-concrete composite slabs with shear connectors |
| |
试件抗弯承载力Mu计算公式如下:
(1) 第1类情况。当中和轴位于混凝土中,即x≤hc时,组合板截面的塑性中和轴位于混凝土翼板内,根据内力平衡方程,此时应满足条件:
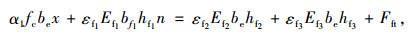
|
(1) |
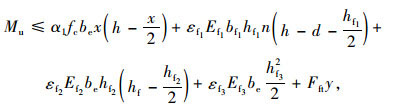
|
(2) |
式中,α1为混凝土受压区翼板的等效矩形应力系数;fc为混凝土轴心的抗压强度设计值;be为混凝土翼板的宽度;x为GFRP-混凝土组合板有效受压区的高度;n为截面剪力键的排数;εf1,εf2,εf3分别为剪力键、GFRP构件顶板和底板高度处截面的等效应变;Ef1,Ef2,Ef3分别为剪力键翼缘、GFRP构件顶板和底板沿板纵向的等效弹性模量;bf1为剪力键翼缘宽度;hf1,hf2,hf3分别为剪力键翼缘、GFRP箱型上翼缘、下翼缘高度;Mu为不考虑滑移效应的GFRP-混凝土组合板的弯矩设计值;h为组合板的总高;d为剪力键翼缘到混凝土板顶的距离;hf为GFRP空心箱型构件的高度;Fft为GFRP空心箱型构件腹板的等效拉应力;y为GFRP空心箱型构件腹板等效应变形心至板底的距离。
由于混凝土强度等级不超过C50,β取为0.8。
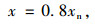
|
(3) |
式中xn为GFRP-混凝土组合板截面中性轴距梁顶面的高度。
根据平截面假定,各处应变符合下列几何方程关系:
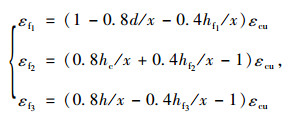
|
(4) |
式中,hc为混凝土翼板的厚度;εcu为混凝土顶面的极限压应变。
空心箱型腹板截面应变保持平截面假定,求出等效应力Fft和形心距板底距离y:
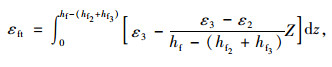
|
(5) |
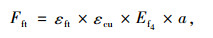
|
(6) |
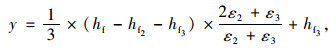
|
(7) |
式中,εft为GFRP空心箱型构件腹板处的等效截面应变;εcu为混凝土顶面的极限压应变;Ef4为GFRP腹板沿板纵向的等效弹性模量;a为GFRP空心箱型构件腹板总宽度。
(2) 第2类情况。当中和轴位于GFRP中时,即x>hc时,组合板截面的塑性中和轴位于GFRP内,根据内力平衡条件,此时应满足条件:
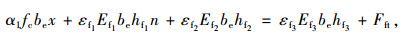
|
(8) |
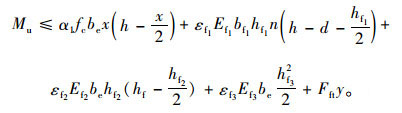
|
(9) |
空心箱型腹板截面应变保持平截面假定,求出等效拉力Fft和形心距板底距离y:
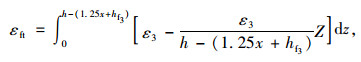
|
(10) |
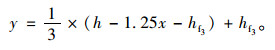
|
(11) |
上述公式虽然计算相对简单,物理概念明确,但未考虑GFRP与混凝土界面的相对滑移,导致计算值偏于不安全。在试验过程中,滑移效应是不可避免的,由于界面滑移会使组合结构抗弯承载力降低,而单纯理论计算滑移效应对极限承载力的影响过于复杂,考虑实际需要,引入抗弯承载力折减系数φ来考虑交界面滑移效应的影响。
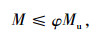
|
(12) |
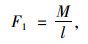
|
(13) |
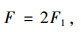
|
(14) |
式中,M为考虑滑移效应的GFRP-混凝土组合板弯矩设计值;φ为与剪力键数量相关的抗弯承载力折减系数,主要反映了剪力键对组合结构整体连接性能的影响;F1为考虑滑移效应的GFRP-混凝土组合板支座反力;l为加载点至支座端部中心点的距离;F为考虑滑移效应的GFRP-混凝土组合板跨中反力。本研究参考文献[22]并根据试验结果,对开孔间距100 mm、开孔间距200 mm、无开孔试件的抗弯承载力折减系数φ1,φ2,φ3分别取为1.0,0.9,0.8。
根据式(1)~(12),组合板抗弯承载力试验值与计算值对比如表 4所示。由于公式忽略了剪力键腹板对试件抗弯承载力的影响,简化了计算结果,使结果偏于安全,因此试件抗弯承载力计算值均小于试验实测值。研究表明,组合板的交界面滑移随着抗剪连接程度的降低而增大。在完全抗剪连接中,剪力键数量相对较多,整体刚度较大,相对滑移较小,试验值在组合效应作用下有明显提高,因此试件2与试件4的计算值与试验值相差较大。在部分抗剪连接或无抗剪连接中,剪力键数量相对较少,相对滑移较大,使组合板抗弯强度降低明显,组合结构的性能得不到充分发挥。在简化计算过程中,引入抗弯承载力折减系数φ来考虑交界面滑移效应的影响,使得计算值偏于安全,因此试件1与试件3的计算值较接近试验值。本研究所提出的抗弯极限承载力方法具备一定的安全富余程度,可供工程设计参考。
| 试件编号 | 计算值M/ (kN·m) | 计算值F/ kN | 试验值F/ kN | 计算值/试验值 |
| 1 | 75.83 | 157.98 | 175 | 0.90 |
| 2 | 84.25 | 175.52 | 256 | 0.70 |
| 3 | 67.4 | 140.42 | 160 | 0.88 |
| 4 | 81.45 | 169.69 | 212 | 0.80 |
4 结论
(1) 带剪力键的GFRP-混凝土组合板的最终破坏形态为跨中截面受压区混凝土压碎,GFRP型材底部基本完整。由于界面出现滑移导致剪力键破坏,但其整体工作性能良好,表明此新型组合结构具有良好的受力性能及协同变形能力。
(2) 开孔间距的变化对试件承载力提高明显。在少量开孔的情况下,开孔孔径对剪力键腹板本身具有一定破坏作用,使得组合结构整体性能有所削弱,试件极限承载力有一定程度的降低。随着开孔间距减小,孔内贯穿钢筋数量增多,试件的承载力明显提高,整体受力性能变好。
(3) 剪力键的截面形式对试件的承载力影响不明显。在相同条件下,矩形肋截面试件比T形肋截面试件的抗弯承载力性能稍有提高,但T形肋截面试件的滑移量却远小于矩形肋截面试件。
(4) 基于试验结果并考虑剪力键对界面滑移的影响,引入抗弯承载力折减系数φ来考虑交界滑移效应的影响。提出了一种带剪力键的GFRP-混凝土空心箱型组合板抗弯承载力简化计算方法。所得抗弯承载力计算值均小于试验实测值,有一定的安全储备,可供工程设计参考。
| [1] |
NELSON M S, FAM A Z, BUSEL J P, et al. Fiber-reinforced Polymer Stay-in-place Structural Forms for Concrete Bridge Decks:State-of-the-art Review[J]. ACI Structural Journal, 2014, 111(5): 1069-1079. |
| [2] |
LI G, LI N, KANG J. Development of FRP-concrete Composite Bridge Deck in Korea:A State-of-the-art Review[J]. Cold Regions Science and Technology, 2006, 45(3): 193-201. |
| [3] |
CHENG L, KARBHARI V M. New Bridge Systems Using FRP Composites and Concrete:A State-of-the-art Review[J]. Progress in Structural Engineering & Materials, 2010, 8(4): 143-154. |
| [4] |
冯鹏. 复合材料在土木工程中的发展与应用[J]. 玻璃钢/复合材料, 2014(9): 99-104. FENG Peng. Development and Application of Composite in Civil Engineering[J]. Fiber Reinforced Plastics/Composites, 2014(9): 99-104. |
| [5] |
CORREIA J R, BAI Y, KELLER T. A Review of the Fire Behaviour of Pultruded GFRP Structural Profiles for Civil Engineering Applications[J]. Composite Structures, 2015, 127: 267-287. |
| [6] |
BANK L C. Progressive Failure and Ductility of FRP Composites for Construction:Review[J]. Journal of Composites for Construction, 2013, 17(3): 406-419. |
| [7] |
HOLLAWAY L C. A Review of the Present and Future Utilisation of FRP Composites in the Civil Infrastructure with Reference to Their Important In-service Properties[J]. Construction and Building Materials, 2010, 24(12): 2419-2445. |
| [8] |
冯鹏, 叶列平. 外部纤维缠绕增强FRP桥面板受力性能试验研究[J]. 土木工程学报, 2009, 42(9): 61-67. FENG Peng, YE Lie-ping. Experimental Study on Exterior Filament-wound Strengthening Fiber-reinforced Polymer Bridge Decks[J]. China Civil Engineering Journal, 2009, 42(9): 61-67. |
| [9] |
王言磊, 欧进萍. FRP-混凝土组合梁/板研究与应用进展[J]. 公路交通科技, 2007, 24(4): 99-104. WANG Yan-lei, OU Jin-ping. Hybrid FRP-concrete Beam/Deck Systems-state-of-the-art Review[J]. Journal of Highway and Transportation Research and Development, 2007, 24(4): 99-104. |
| [10] |
范海丰, 刘玉擎, 代亮. GFRP-混凝土组合桥面板设计及试验研究[J]. 防灾减灾工程学报, 2010, 30(增1): 356-360. FAN Hai-feng, LIU Yu-qing, DAI Liang. Design and Experimental Study of GFRP-concrete Composite Bridge Deck[J]. Journal of Disaster Prevention and Mitigation Engineering, 2010, 30(S1): 356-360. |
| [11] |
黄辉, 王文炜, 戴建国. 两跨连续GFRP-混凝土空心组合板受力性能试验研究[J]. 建筑结构学报, 2015, 36(10): 59-65. HUANG Hui, WANG Wen-wei, DAI Jian-guo. Experimental Study on Structural Performance of Two-span Continuous GFRP-concrete Composite Hollow Slabs[J]. Journal of Building Structures, 2015, 36(10): 59-65. |
| [12] |
NOЁL M, FAM A. Design Equations for Concrete Bridge Decks with FRP Stay-in-place Structural Forms[J]. Journal of Composites for Construction, 2016, 20(5): 4016024. |
| [13] |
HASSELHOFF J, CHENG L, WAIMER F, et al. Design, Manufacturing and Testing of Shear-cone Connectors Between CFRP Stay-in-place Formwork and Concrete[J]. Composite Structures, 2015, 129: 47-54. |
| [14] |
杨勇, 刘玉擎, 范海丰. FRP-混凝土组合桥面板疲劳性能试验研究[J]. 工程力学, 2011, 28(6): 66-73. YANG Yong, LIU Yu-qing, FAN Hai-feng. Experimental Study on the Fatigue Behavior of FRP-concrete Composite Decks[J]. Engineering Mechanics, 2011, 28(6): 66-73. |
| [15] |
朱慧.带剪力键的GFRP-混凝土组合板受弯性能试验及设计方法[D].湘潭: 湖南科技大学, 2016. ZHU Hui. Flexural Behavior and Design Method of GFRP-concrete Composite Deck with Shear Connector[D].Xiangtan: Hunan University of Science and Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10534-1016792581.htm |
| [16] |
HANSWILLE G, PORSCH M, USTUNDAG C. Resistance of Headed Studs Subjected to Fatigue Loading:Part Ⅰ:Experimental Study[J]. Journal of Constructional Steel Research, 2007, 63(4): 475-484. |
| [17] |
ZHENG S, LIU Y, YODA T, et al. Parametric Study on Shear Capacity of Circular-hole and Long-hole Perfobond Shear Connector[J]. Journal of Constructional Steel Research, 2016, 117: 64-80. |
| [18] |
RODRIGUES J P C, LAÍM L. Experimental Investigation on the Structural Response of T, T-block and T-perfobond Shear Connectors at Elevated Temperatures[J]. Engineering Structures, 2014, 75: 299-314. |
| [19] |
KIM S, CHOI K, PARK S, et al. Experimental Shear Resistance Evaluation of Y-type Perfobond Rib Shear Connector[J]. Journal of Constructional Steel Research, 2013, 82: 1-18. |
| [20] |
KONG S Y, YANG X, LEE Z Y. Mechanical Performance and Numerical Simulation of GFRP-concrete Composite Panel with Circular Hollow Connectors and Epoxy Adhesion[J]. Construction and Building Materials, 2018, 184: 643-654. |
| [21] |
ZUO Y, MOSALLAM A, XIN H, et al. Flexural Performance of a Hybrid GFRP-concrete Bridge Deck with Composite T-shaped Perforated Rib Connectors[J]. Composite Structures, 2018, 194: 263-278. |
| [22] |
付果, 姚大海, 张磊. 部分抗剪连接钢-混凝土组合梁抗弯极限承载力的实用计算方法[J]. 交通科学与工程, 2010, 26(3): 31-35. FU Guo, YAO Da-hai, ZHANG Lei. Applied Method on Ultimate Flexural Capacity of Steel-concrete Composite Beams with Partial Shear Connection[J]. Journal of Transport Science and Engineering, 2010, 26(3): 31-35. |
 2019, Vol. 36
2019, Vol. 36
