扩展功能
文章信息
- 周芬, 丘友威, 杜运兴, 聂逸悠, 袁兰
- ZHOU Fen, QIU You-wei, DU Yun-xing, NIE Yi-you, YUAN Lan
- 填料应力控制的预应力筋预拉力的合理取值
- Reasonable Value of Prestress of Prestressed Reinforcement Controlled by Filler Stress
- 公路交通科技, 2019, 36(7): 38-46
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(7): 38-46
- 10.3969/j.issn.1002-0268.2019.07.005
-
文章历史
- 收稿日期: 2018-04-02
2. 中国电建地产集团有限公司, 北京 102300
2. POWERCHINA Real Estate Group Co., Ltd., Beijing 102300, China
无黏结预应力加筋土挡墙是一种新型加筋土挡墙,该类挡墙结构由墙面板、侧压板、预应力筋及填料组成。其中预应力筋两端连接了侧压板与墙面板,在挡墙填筑完毕后,对预应力筋施加预拉力,使侧压板与墙面板间的填料受到挤压,产生水平方向的约束,以提高挡墙强度与稳定性。基于上述原理,挡墙内部的水平应力分布是影响其力学性能的重要因素,而填料的水平应力与预应力筋的预拉力密切相关。因此,该类挡墙设计关键在于如何确定预应力筋的预拉力值。
填料应力的状态既可采用试验方法测量也可以采用数值仿真方法获得。试验方法是获得加筋土挡墙破坏形态与填料应力变化最直接有效的方法。杜运兴等[1]通过试验研究预应力加筋土路堤的静力性能,研究表明筋带对填料有着可靠的约束能力。Yang等[2]通过室内试验分析了挡墙主动土压力系数,结果显示在不同模式下的库仑主动土压力系数都要大于主动土压力系数的实测值。黄向京等[3]对某高速公路一新型组合格宾挡墙进行了现场监测,结果表明垂直土压力实测值基本小于理论值。试验可以观测到挡墙在荷载作用下的真实反应,但试验方法不仅有着可重复性差、耗资大的缺点,还由于测点数量有限而难以全面反映挡墙的变形特征与受力状态。在1967年,Clough等[4]首次将有限元方法应用于岩土领域,此后许多学者开始采用数值模拟方法对加筋土结构进行研究。Liu等[5]采用有限单元法计算挡墙加筋区后填料侧向土压力,利用其分布规律给出了在长期荷载作用下挡墙主要在顶部发生蠕变的解释。Chen等[6]采用有限差分法分析研究了挡墙的破坏模式、控制因素以及挡墙在附加荷载作用下塑性区的发展。Yu等[7]对比了挡墙数值分析结果与工程实测,文献认为数值模拟可以对材料属性、几何布局类似的结构等进行参数分析,为挡墙设计提供相应依据。
采用数值模拟研究加筋土挡墙内填料的应力状态时,合理选择填料的本构关系对正确分析填料内部应力有着重要影响。应用较为广泛的填料本构模型有邓肯张模型[8-9]、摩尔库仑模型[10-11]。Huang等[12]采用这两种本构关系进行了模拟研究,其计算结果与实测值吻合良好。材料之间的界面关系是建立数值模型同样需要注意的关键点,Gu等[13]在模拟挡土墙材料间的接触关系时,引入了考虑抗剪强度折减的界面单元,界面参数由经验公式确定,计算表明,格栅拉力、墙面板位移等方面的模拟值和实测值吻合良好。
对于预应力加筋土挡墙的的仿真分析还需要考虑预应力筋预拉力的仿真方法。常用的预应力模拟方法有等效荷载法、初始应变法以及降温法[14-16],3种方法各具优缺点,但都难以全面满足本研究分析的需求。郁大照等[17]对螺栓固件的疲劳裂缝进行模拟研究时采用了伺服连接法,即在螺栓上建立了多点约束来实现施加预紧力,该方法具有操作简单、概念明确以及精度高的优点。
本研究采用有限元方法对单层预应力筋加筋土挡墙内的应力分布、塑性区大小及筋带预拉力合理取值进行研究。在此基础上选取填料的内摩擦角、黏聚力,预应力筋长度与挡墙高度比等进行参数分析,以研究各参数对预拉力合理取值的影响。
1 数值方法验证 1.1 建模方法在有限元模型中采用四节点四边形平面应变单元来模拟填料、侧压板、墙面板以及地基,采用梁单元模拟预应力筋,采用两节点平面应变单元模拟玻纤格栅。使用摩尔库伦模型作为填料的本构模型,其余材料均设置为线弹性模型。模型的边界条件:非加筋区填料未被支挡的一侧和地基两侧设置水平向位移约束,对地基底部同时设置水平向和竖向的位移约束。
采用伺服连接法模拟预拉力。首先分割某一预应力筋单元,其界面将生成重复节点,如图 1所示。之后建立一个外部控制节点,该点仅在沿预拉力方向上不受约束。在界面重复节点与外部控制点间建立伺服连接,使得:
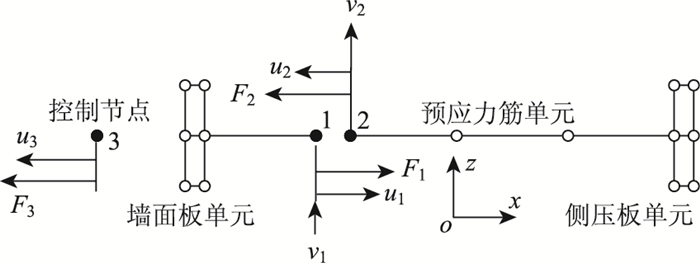
|
| 图 1 预拉力施加图 Fig. 1 Application of pretension |
| |
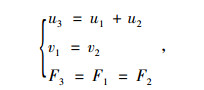
|
(1) |
式中,u1, u2为被分割位置相邻预应力筋单元节点对应的水平位移;v1, v2为竖向位移;u3为控制节点的水平位移;F1, F2为被分割位置相邻预应力筋单元节点对应的水平拉力;F3为施加于外部控制节点的水平集中力。
最后,对外部控制点施加集中力即可实现预拉力的模拟。预拉力的大小可以用预拉力系数(Npi)表示,该系数为无量纲系,定义如下:
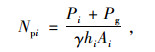
|
(2) |
式中,Pi,Pg分别为挡墙第i层预应力筋施加的预拉力值和由重力荷载引起的拉力值,二者之和在试验中可通过力传感器测量获取;γ为填料的重度;hi为第i层预应力筋距挡墙顶部的距离;Ai为第i层墙面板的面积。Npi大小等于第i层墙面板处受到的拉力值与该位置对应的土静压力合力的比值。
试验中保证预应力钢绞线表面润滑并置于PVC管中,使其在管中可以自由滑动,还不与填料发生接触,本研究根据节点自由度之间的相互关系模拟预应力筋与填料之间的相互约束关系,在图 2(a)中,1~4,9~12号节点属于平面应变单元,而5~8号节点属于平面梁单元,前者具有2个自由度,后者则有3个自由度,模型所建立的连接应使1~4,9~12号的各个节点与对应位置的5~8号节点水平位移相互独立却又拥有相同的竖向位移,可通过在模型中建立一个只约束z向位移自由度的节点连接来加以实现。
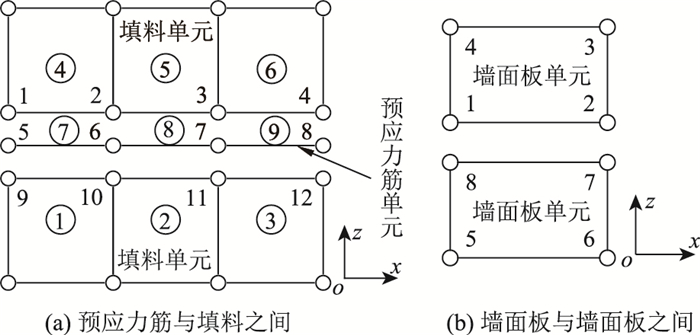
|
| 图 2 界面节点连接 Fig. 2 Connection of interface nodes |
| |
墙面板与墙面板之间的界面关系如图 2(b)所示。因为模块式墙面板具有较小的水平向相对位移,而具有基本一致的竖向位移。在计算模型中,x向使用弹簧节点连接,弹簧刚度越大即表示墙面板间越难产生相对位移;z向则设置节点连接使界面节点拥有相同的竖向位移。
填料与地基、墙面板、侧压板间的界面抗剪强度由摩尔库仑失效准则来定义。法向刚度kn、切向刚度ks以及界面的摩擦角δ由下列公式[13]确定:
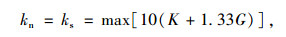
|
(3) |
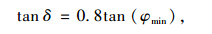
|
(4) |
式中,K是体积模量;G是剪切模量;φmin则为内摩擦角的最小值。
正常使用情况下,挡墙中的玻纤格栅与填料的滑移量非常小,可以忽略不计,在模拟中可假设二者变形协调,计算模型中的约束格栅单元节点与其周围填料单元节点水平向、竖向位移一致。
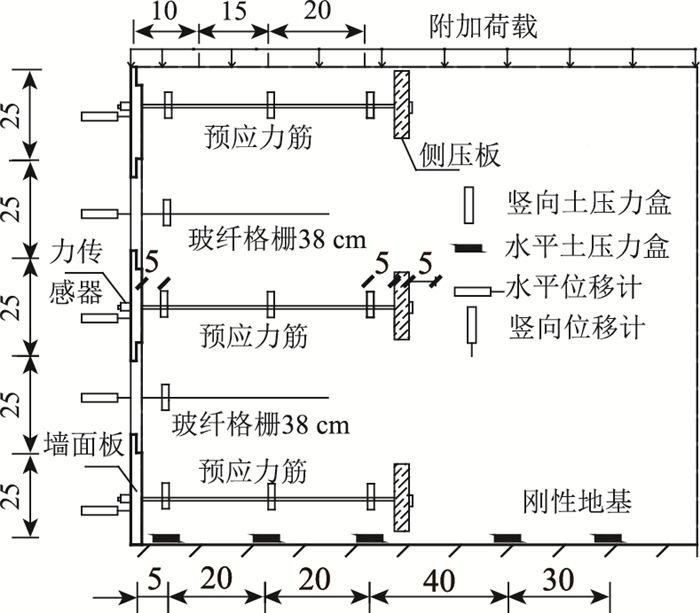
1.2 模型验证计算模型采用无黏结预应力筋/普通格栅混合加筋土挡墙的缩尺模型试验进行验证,模型试验所用玻纤格栅的弹性模量为72 GPa,泊松比为0.3。挡墙截面与测量元件布置情况见图 3。该挡墙放置在刚性地基上,从下往上第1,3,5层铺设预应力加筋,预应力筋长度(L)为墙高(H)的0.5倍,第2,4层铺设玻纤格栅,玻纤格栅长度(L)为墙高(H)的0.3倍。该试验采用增大填料密度法[18]解决模型相似比问题,用钢砂代替砂土作为无黏性填料,相似常数n=3。挡墙填筑完成后,对第1, 3, 5层预应力筋依次施加8,4,1 kN的预拉力。墙顶附加荷载为13.32 kPa。
|
| 图 3 数值模拟原型(单位:cm) Fig. 3 Prototype of numerical simulation(unit:cm) |
| |
模型试验与计算模型中填料的内摩擦角均为35°,黏聚力均为0 kPa;预应力筋的抗拉强度均为1 860 MPa,最大伸长率均为3.5%,其余材料参数见表 1。根据式(3), 式(4),填料与侧压板、墙面板的界面刚度均为3.33×105 MPa,与地基间则为807 MPa;侧压板、墙面板、地基与填料间的界面摩擦角均为29°。通过墙面板位移的实测值与模拟结果可推测得到相邻墙面板间的弹簧刚度K的大小为1×108 N/m。
| 参数 | 材料 | 数值 | |
| 模型试验 | 计算模型 | ||
| 弹性模量/MPa | 填料 | 60 | 60 |
| 地基、侧压板、墙面板 | 3.0×104 | 3.0×104 | |
| 预应力筋 | 2.0×105 | 2.0×105 | |
| 泊松比 | 地基、填料 | 0.3 | 0.3 |
| 重度/(kN·m-3) | 侧压板、墙面板 | 0.2 | 0.2 |
| 侧压板、墙面板 | 25 | 25 | |
| 填料 | 52 | 18 | |
| 公称直径/mm | 预应力筋 | 5.8 | 15.7 |
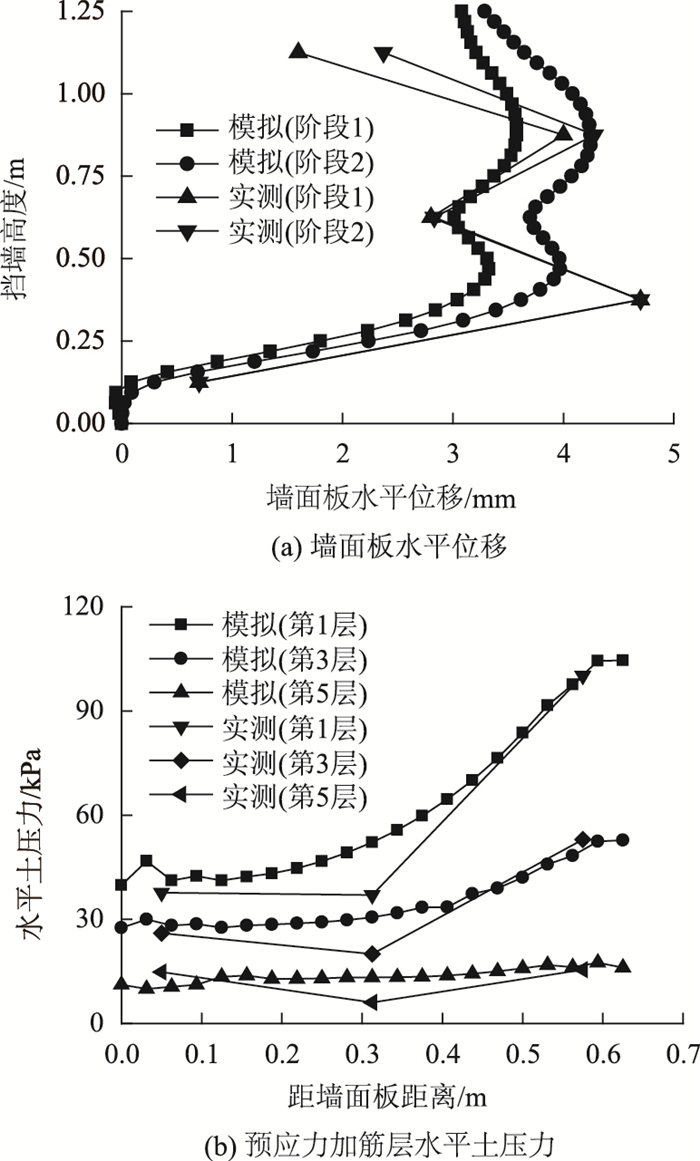
图 4(a)是预拉力施加完成后(阶段1)、堆载完成后(阶段2)挡墙墙面板水平位移的模拟结果与试验实测结果的对比,模拟值与实测值在各层墙面板位移的变化趋势上基本一致,在第1,3,5层水平位移较小,而在第2,4层出现较大的水平位移。2,5层的模拟值与试验值误差略大,但考虑到试验中各种不确定因素的影响,试验实测值会存在一定的随机性,因此本研究认为墙面板水平位移的模拟结果与实测值吻合良好。预拉力施加完成后,第1,3,5层填料水平土压力对比情况如图 4(b)所示。从图中可以看出,虽然在挡墙中部区域模拟值略大于实测值,但在整体趋势上模拟与实测结果都具有较好的一致性,在侧压板前、墙面板后的结果也基本吻合,从而验证了采用数值模拟方法分析该类挡墙是合理的。
|
| 图 4 结果对比 Fig. 4 Comparison of results |
| |
2 预应力筋预拉力的合理取值 2.1 基本工况
基本工况为10层全预应力加筋土挡墙,几何尺寸如图 5所示。挡墙中预应力筋间距沿墙高间隔0.8 m布置,侧压板与墙面板的厚度均为0.12 m,侧压板边长为墙面板边长的0.6倍。界面参数和材料参数与本研究模型验证部分的设置一致。
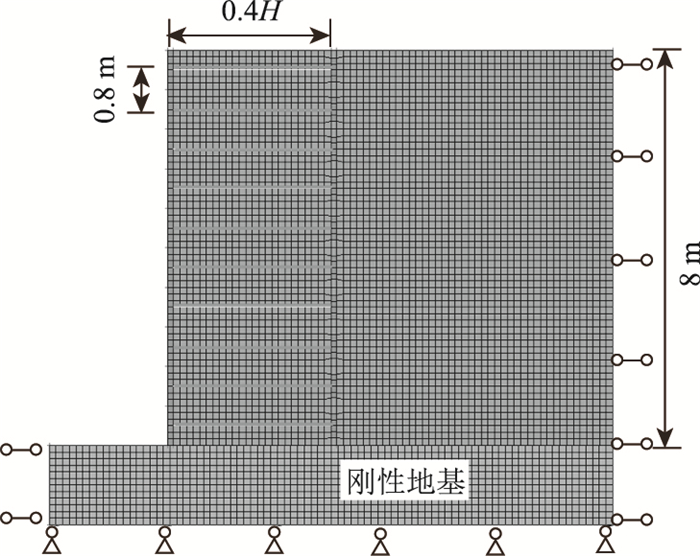
|
| 图 5 基本工况模型 Fig. 5 Model of basic case |
| |
2.2 塑性区分布
依次对模型1~10层的预应力筋施加预拉力,研究表明,挡墙塑性区的发展规律具有一致性。以在第5层施加预应力为例,在重力荷载作用下,挡墙的等效塑性应变云图如图 6(a)所示,可以观察到填料的塑性区主要集中墙面板后方的墙址处以及侧压板后方非加筋区域的中上部,这是由于填料在重力荷载的作用下挡墙有着绕墙趾外倾的趋势。逐级施加预拉力,每级增量为5.6 kN,随着预拉力增长,在侧压板上下端开始形成塑性区并向着墙面板一侧扩展,由于侧压板有着向墙面板一侧移动的趋势进一步扩大了侧压板后方填料的塑性区范围。如图 6(c)所示,当第5层预应力筋的预拉力值P5达到268.8 kN时,侧压板附近的填料中出现贯通的塑性区并迅速向墙面板发展,贯通点距侧压板的距离约等于侧压板的边长。如图 6(d)所示,当P5达到560 kN时,塑性区已经延伸到墙面板附近。挡墙变形方面,侧压板与墙面板出现了显著的水平位移,并且第5层之上的挡墙出现了向外倾倒的趋势。规范[19]中墙面板最大位移与墙高比值的限值为0.5%,而此时该挡墙的这一比值已经达到了0.47%。因此为保证该类挡墙的正常使用状态,预拉力的增加应避免侧压板附近填料出现贯通的塑性区。

|
| 图 6 挡墙整体等效塑性应变云图 Fig. 6 Nephogram of equivalent plastic strain of retaining wall |
| |
图 7是距第5层侧压板一倍边长(0.48 m)处填料的等效塑性应变曲线,该位置作为填料的特征点。当P5达到156.8 kN前该位置基本不出现塑性应变;当P5超过156.8 kN后,随着预拉力的增长,该位置塑性应变也随之增大。由于预拉力-塑性应变曲线不存在显著的标志点,所以取该曲线起点与终点的切线,将二者交点的位置作为标志点,此时对应的预拉力值为300 kN,接近于图 6(c)中的268.8 kN。由于通过观察等效塑性应变云图来判断塑性区贯通存在着较大的主观性,本研究取标志点对应的预拉力作为侧压板附近填料出现贯通塑性区的标志。
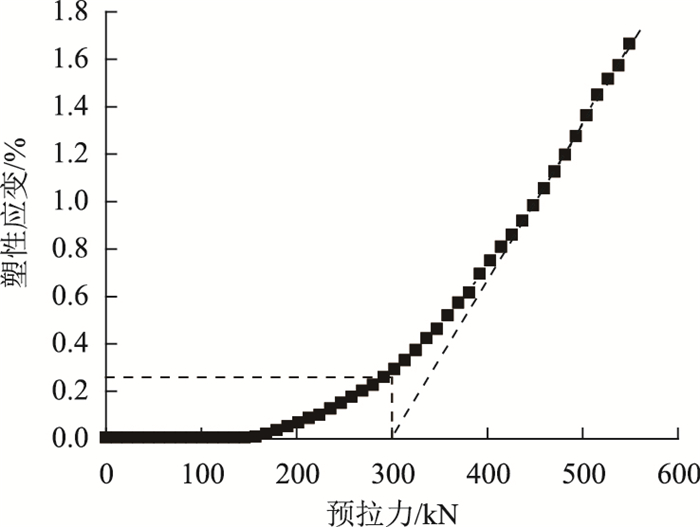
|
| 图 7 填料特征点等效塑性应变 Fig. 7 Equivalent plastic strain of filler feature point |
| |
2.3 填料应力分布
图 8是在不同预拉力作用下第5层预应力筋附近填料的土压力变化曲线。σx,σy为水平应力; σx方向沿预应力筋纵向; σy方向与预应力筋垂直; σz为竖向应力。如图 8所示,随着预拉力增长,3个应力中σx的增长率最大,σy次之,σz最小。靠近侧压板与墙面板的填料其σx增长最快,使得σx沿预应力筋呈现出中间小两端大的分布形态。在预拉力作用下,填料的应力状态变化分为两个阶段进行:第1阶段,如图 8(a)~(c)所示,当P5=0 kN时,挡墙在重力荷载作用下,σz,σx分别接近于大主应力σ1和小主应力σ3,σy则和中主应力σ2完全相同;施加预拉力使P5增大到95.2 kN的过程中,σx逐渐增大并超过σz成为3个应力中的最大值,此时,σx,σz分别接近于σ1和σ2,σy则与σ3完全相同。第二阶段,如图 8(c)~(e)所示,继续施加预应力使P5达到162.4 kN的过程中,σy也将超过σz,σz成为3个应力中的最小值,此时σx,σy,σz分别与σ1,σ2,σ3完全重合。增大P5到268.8 kN时,如图 8(f)所示,σx,σy,σz始终与σ1,σ2,σ3重合,σ1,σ2明显出现增大,σ3则基本保持不变。
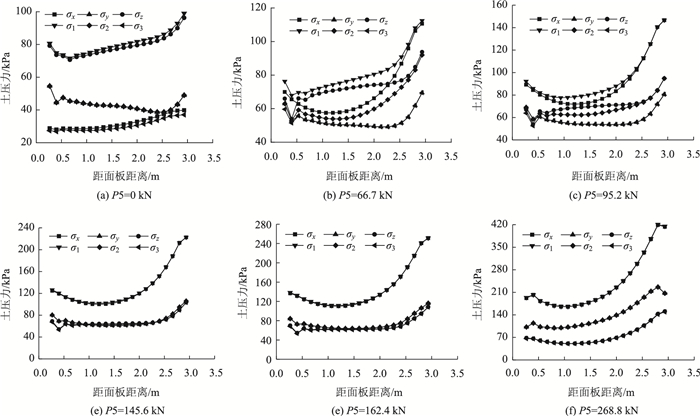
|
| 图 8 第5层预应力筋附近填料土压力 Fig. 8 Soil pressure around 5th-layer prestressed reinforcement |
| |
通过填料中某点的主应力值σ1和σ3可以确定一个摩尔圆,本研究以选取的第5层填料的特征点为例。其应力状态在预拉力作用下的改变情况如图 9所示。
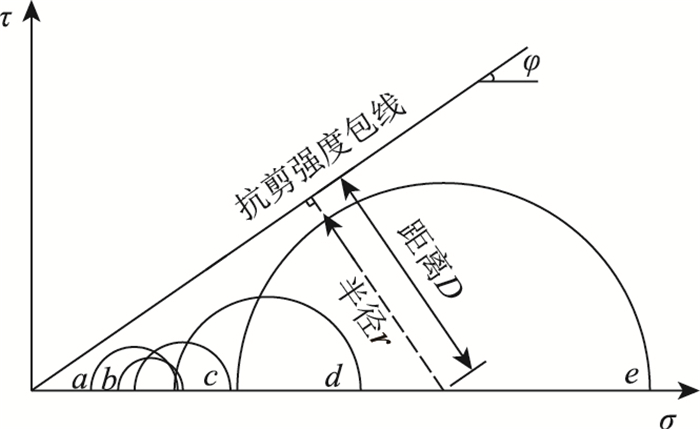
|
| 图 9 摩尔圆与抗剪强度包线关系 Fig. 9 Relationship between Mole circle and shear strength envelope |
| |
图 9中(a)~(e)分别是P5等于0,66.7,95.2,162.4,268.8 kN时的摩尔圆。如图 9所示,摩尔圆的圆心随着预拉力增大向右偏移,但其半径r先减小后增大,说明在预拉力增大的过程中填料存在一个最优的安全状态。为表示填料的应力达到抗剪强度的比例,本研究定义破坏比系数f为:
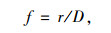
|
(5) |
式中,D为摩尔圆圆心到抗剪强度包线的距离;r为摩尔圆半径。当f<1时,填料处于安全状态;当f=1时,填料处于极限平衡状态;当f>1时,填料已经剪切破坏。
图 10反映了第5层填料特征点的破坏比系数与预拉力系数的关系,可以看出,破坏比系数随着预拉力系数增大呈现出先减小后增大的趋势。曲线存在一个极小值点,即Np5=1.43,f=0.47。当预拉力系数小于极小值点时,曲线斜率较大,填料很快达到极小值对应的最优安全状态;当预拉力系数大于极小值点时,随着预拉力的增大,曲线的斜率逐渐减小为0,使得f逐渐增大最后趋于1.0,曲线出现屈服平台。
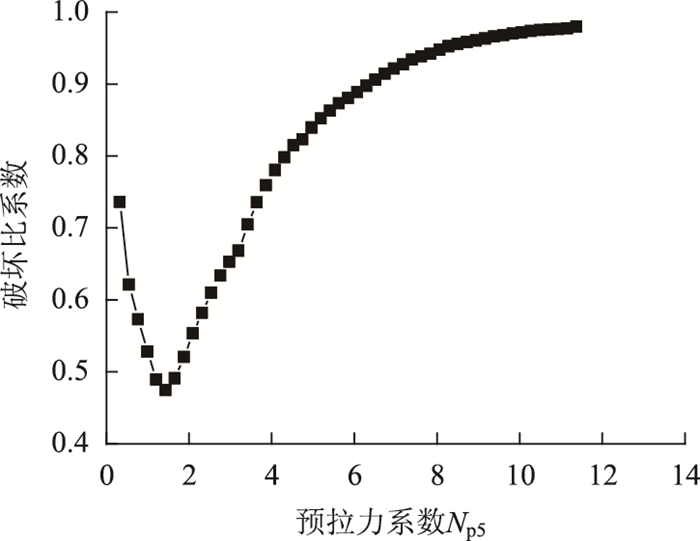
|
| 图 10 填料特征点的破坏比系数 Fig. 10 Failure ratio coefficient of filler feature point |
| |
2.4 预拉力的合理取值
为了研究各层填料破坏比系数与各层预拉力系数的关系,在各层沿预应力筋长度方向等间距取预应力筋附近填料的10个位置,分别求得各层这些填料位置的破坏比系数平均值,将其定义为平均破坏比系数。图 11是各层平均破坏比系数与预拉力系数的关系曲线。将图 11(a)中第5层曲线与图 10对比,表明第5层填料特征点的破坏比系数曲线和第5层填料的平均破坏比系数曲线的变化规律是一致的。
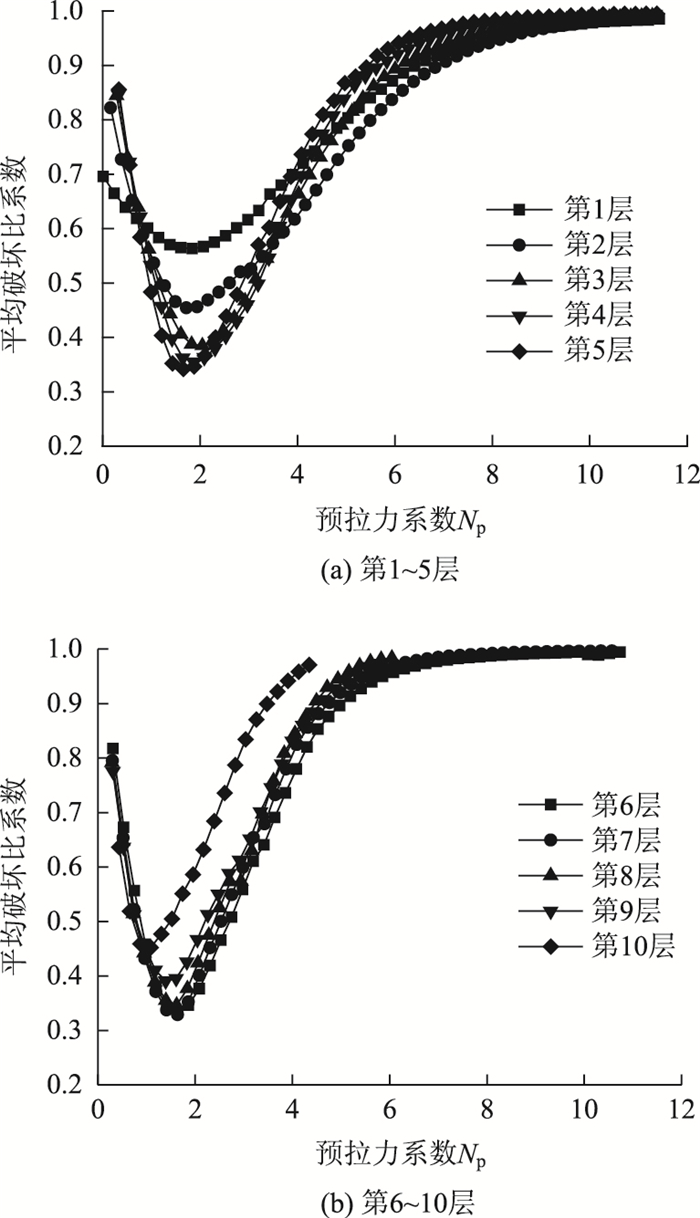
|
| 图 11 挡墙各层预应力筋附近填料的平均破坏比系数 Fig. 11 Average failure ratio coefficient of filler around prestressed reinforcements in each layer |
| |
由图 11可见,顶层的填料平均破坏比系数的极小值fmin对应的预拉力系数Nmin约为1.1,而其余各层的Nmin都约为2.0,其原因在于顶层的筋带埋深较浅,在预拉力作用下该层填料相比于其他层更容易发生局部破坏。
取各层填料特征点在预拉力作用下塑性应变出现突变时的预拉力值,由式(2)求出对应的预拉力系数,进一步由图 11确定对应的平均破坏比系数,得填料各层的平均破坏比系数在0.84~0.98之间。从设计角度考虑,取挡墙各层填料的平均破坏比系数为0.80,记为f0.8,意味着其达到0.80时,表明侧压板附近填料即将出现贯通的塑性区,相应的预拉力系数记作N0.8。
综上,由填料的最优安全状态和侧压板附近是否出现贯通的塑性区可确定预应力筋预拉力的合理取值。图 12反映了第1~10层填料的平均破坏比系数达到fmin与f0.8时对应的预拉力系数Nmin与N0.8。该图表明,除顶层之外,各层预应力筋的埋深对Nmin影响不大,顶层预应力筋的Nmin约为0.3Kp,其余的Nmin接近于0.48 Kp,Kp为被动土压力系数。每层预应力筋的N0.8随墙高的增加逐渐减小并趋于Kp,第2层预应力筋有着最大的N0.8,达到了1.56 Kp,而顶层预应力筋的N0.8最小,仅为0.83 Kp,N0.8沿墙高的分布形态近似为三角形。
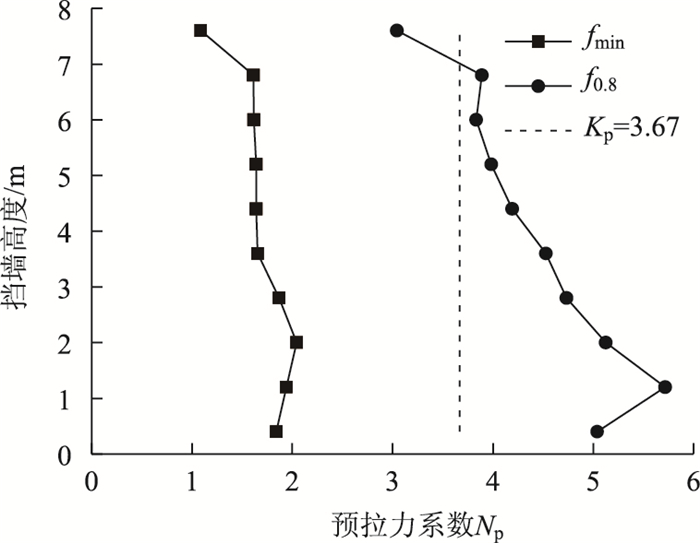
|
| 图 12 预拉力合理取值范围 Fig. 12 Reasonable value range of pretension |
| |
3 参数分析
为使研究成果更具普遍性,本研究分析了如表 2所列参数的影响。每次计算只变动表 2中的一个计算参数,其他参数与表中的基本工况相同。
| 参数 | 内摩擦角φ/(°) | 黏聚力c/kPa | 筋长/墙高L/H |
| 减小参数 | 25 | — | 0.3 |
| 基本工况 | 35 | 0 | 0.4 |
| 增大参数 | 45 | 10, 20, 30 | 0.5 |
由图 13(a)可见,各层预应力筋的Nmin, N0.8受内摩擦角的影响较大,内摩擦角每增大10°,Nmin平均增幅为21.5%,N0.8则为44.6%。这是因为填料的抗剪强度会随着内摩擦角的增大而提高,需要更大的预拉力才能使填料平均破坏比系数达到fmin和f0.8。

|
| 图 13 不同参数对预拉力系数的影响 Fig. 13 Influence of parameters on pretension coefficient |
| |
由图 13(b)可见,黏聚力对Nmin影响较小,但对N0.8影响较大。黏聚力每增大10 kPa,Nmin平均增幅为2.9%,N0.8平均增幅为15.2%。同时,N0.8受黏聚力的影响程度与筋带埋深具有相关性,黏聚力的影响随着筋带埋深的增加而减小。这表明黏性填料能提高挡墙顶部填料的抗剪强度,有效避免顶部填料因预拉力作用产生局部破坏的问题。
由图 13(c)可见,当挡墙高度固定时,预应力筋长度对预拉力系数Nmin,N0.8都有较大影响。预应力筋长度每增加0.1 H,Nmin平均增幅为22%,N0.8平均增幅为16.1%。填料抗剪强度会随着该层预应力筋长度的增长而提高,在其他因素不变的情况下,就需要更大的预拉力使填料平均破坏比系数达到某一值。
4 结论文章研究了无黏结预应力加筋土挡墙中预应力筋预拉力的合理取值,通过有限元分析得到了该挡墙在单层预应力筋施加预拉力情况下的填料应力分布及塑性区分布情况,在此基础上进行了参数分析,获得了如下研究成果。
(1) 对预应力筋施加过大的预拉力将导致侧压板附近的填料出现贯通的塑性区,随着预拉力的增加塑性区向墙面板发展,并使墙面板的位移增加。
(2) 填料的水平应力受预拉力的影响较大并且沿预应力筋纵向呈现出中间小两端大的分布形态,竖向应力受到的影响比较小。随着预拉力逐渐增大,主应力大小方向不断变化,在达到某一值后,x,y,z向的应力大小分别等于大、中、小主应力。
(3) 本研究采用一个破坏比系数f来表示填料的应力达到抗剪强度的比例,随预拉力系数增大,发现破坏比系数先减小后增加,表明填料存在最优的安全状态。
(4) 该类挡墙预拉力的合理取值由填料的最优安全状态和侧压板附近是否出现贯通的塑性区来控制。
(5) 预应力筋长度与挡墙高度比的增加可以提高填料的抗剪强度,预拉力合理取值的上限和下限相应增加。
| [1] |
杜运兴, 龙述尧, 尚守平. 预应力加筋中砂路堤模型静力试验研究[J]. 湖南大学学报:自科版, 2008, 35(2): 27-30. DU Yun-xing, LONG Shu-yao, SHANG Shou-ping. Static Model-test Study on Reinforced Medium-sandy Embankment with Prestress[J]. Journal of Hunan University:Natural Science Edition, 2008, 35(2): 27-30. |
| [2] |
YANG M, TANG X. Rigid Retaining Walls with Narrow Cohesionless Backfills under Various Wall Movement Modes[J]. International Journal of Geomechanics, 2017, 17(11): 04017098. |
| [3] |
黄向京, 许桂林, 杨果林, 等. 加筋格宾新型组合支挡结构试验研究[J]. 公路交通科技, 2011, 28(2): 7-13. HUANG Xiang-jing, XU Gui-lin, YANG Guo-lin, et al. Experimental Research on a New Kind of Compound Supporting and Retaining Structure with Reinforced Gabion Retaining Wall[J]. Journal of Highway and Transportation Research and Development, 2011, 28(2): 7-13. |
| [4] |
CLOUGH R W, WOODWARD R J. Analysis of Embankment Stresses and Deformations[J]. Journal of Soil Mechanics and Foundations Division, 1967, 93(4): 529-549. |
| [5] |
LIU H B. Long-term Lateral Displacement of Geosynthetic-reinforced Soil Segmental Retaining Walls[J]. Geotextiles and Geomembranes, 2012, 32(2): 18-27. |
| [6] |
CHEN R H, WU C P, HUANG F C, et al. Numerical Analysis of Geocell-reinforced Retaining Structures[J]. Geotextiles and Geomembranes, 2013, 39(8): 51-62. |
| [7] |
YU Y, BATHURST R J, MIYATA Y. Numerical Analysis of a Mechanically Stabilized Earth Wall Reinforced with Steel Strips[J]. Soils and Foundations, 2015, 55(3): 536-547. |
| [8] |
曹喜仁, 赵振勇, 赵明华. 高填石路堤地基沉降计算方法研究[J]. 公路交通科技, 2005, 22(6): 38-41. CAO Xi-ren, ZHAO Zhen-yong, ZHAO Ming-hua. Study on Settlement Calculation Method for Subgrade of High Rockfill Embankment[J]. Journal of Highway and Transportation Research and Development, 2005, 22(6): 38-41. |
| [9] |
CHEN X B, ZHANG J S, LI Z Y. Shear Behaviour of a Geogrid-reinforced Coarse-grained Soil Based on Large-scale Triaxial Tests[J]. Geotextiles and Geomembranes, 2014, 42(4): 312-328. |
| [10] |
周世良, 汪承志, 何光春, 等. 台阶式格栅加筋挡墙潜在破裂面计算模式研究[J]. 公路交通科技, 2007, 24(11): 15-20. ZHOU Shi-liang, WANG Cheng-zhi, HE Guang-chun, et al. Study on Rational Model of Potential Fractured Surface for Stepped Geogrid Reinforced Soil Retaining Wall[J]. Journal of Highway and Transportation Research and Development, 2007, 24(11): 15-20. |
| [11] |
YU Y, BATHURST R J, ALLEN T M, et al. Physical and Numerical Modelling of a Geogrid-reinforced Incremental Concrete Panel Retaining Wall[J]. Canadian Geotechnical Journal, 2016, 53(12): 1883-1901. |
| [12] |
HUANG B Q, BATHURST R J, HATAMI K. Numerical Study of Reinforced Soil Segmental Walls Using Three Different Constitutive Soil Models[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(10): 1486-1498. |
| [13] |
GU M X, COLLIN J G, HAN J, et al. Numerical Analysis of Instrumented Mechanically Stabilized Gabion Walls with Large Vertical Reinforcement Spacing[J]. Geotextiles and Geomembranes, 2017, 45(4): 294-306. |
| [14] |
张社荣, 祝青, 李升. 大型渡槽数值分析中预应力的模拟方法[J]. 水力发电学报, 2009, 28(3): 97-100, 90. ZHANG She-rong, ZHU Qing, LI Sheng. Simulation Methods of Prestress in Numerical Analysis of Large Aqueduct[J]. Journal of Hydroelectric Engineering, 2009, 28(3): 97-100, 90. |
| [15] |
何琳, 王家林. 模拟有效预应力的等效荷载-实体力筋降温法[J]. 公路交通科技, 2015, 32(11): 75-80. HE Lin, WANG Jia-lin. Method of Equivalent Load and Temperature Reduction on Prestressing Tendon for Effective Prestress Simulation[J]. Journal of Highway and Transportation Research and Development, 2015, 32(11): 75-80. |
| [16] |
熊欢, 李鹏辉, 李庆斌, 等. PCCP受载响应分析中三种预应力施加方法的比较研究[J]. 水力发电学报, 2010, 29(6): 178-186. XIONG Huan, LI Peng-hui, LI Qing-bin, et al. Comparative Study of Three Methods for the Prestressing Simulation in the Analysis of Load-bearing Response of a PCCP[J]. Journal of Hydroelectric Engineering, 2010, 29(6): 178-186. |
| [17] |
郁大照, 陈跃良. 含裂纹螺接件应力强度因子三维有限元分析[J]. 机械工程学报, 2011, 47(20): 121-126. YU Da-zhao, CHEN Yue-liang. Stress Intensity Factor of Cracks in Bolted Joints Based on Three-dimensional Finite Element Analysis[J]. Journal of Mechanical Engineering, 2011, 47(20): 121-126. |
| [18] |
杜运兴, 周芬, 梁强. 双根无黏结预应力筋加筋体力学性能研究[J]. 长江科学院院报, 2017, 34(2): 45-51. DU Yun-xing, ZHOU Fen, LIANG Qiang. Mechanical Properties of Reinforced Body with Double Unbonded Prestressed Reinforcements[J]. Journal of Yangtze River Scientific Research Institute, 2017, 34(2): 45-51. |
| [19] |
BS 8006-1: 2010, Code of Practice for Strengthened/Reinforced Soils and Other Fills[S].
|
 2019, Vol. 36
2019, Vol. 36
