扩展功能
文章信息
- 刘川昆, 陈铭颢, 王芷芸, 鹿腾, 孙畅
- LIU Chuan-kun, CHEN Ming-hao, WANG Zhi-yun, LU Teng, SUN Chang
- 基于模拟退火的地下物流通道网络设计
- Network Design of Underground Logistics Channel Based on Simulated Annealing
- 公路交通科技, 2019, 36(6): 151-158
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(6): 151-158
- 10.3969/j.issn.1002-0268.2019.06.019
-
文章历史
- 收稿日期: 2018-03-15
2. 西南交通大学 信息科学与技术学院, 四川 成都 610031
2. School of Information Science and Technology, Southwest Jiaotong University, Chengdu, Sichuan 610031, China
近年来,随着城市化进程的不断加快,大量人口向城市集中,城市规模的不断扩大,将不同程度的导致城市交通拥堵、环境污染等问题,严重制约了现代城市的可持续发展[1]。Heney Liu[2]等针对纽约市地下物流技术与经济进行了可行性研究并以此引发对世界其他城市地下物流建设的启示。大量实践证明,通过扩张传统路网容量来解决城市交通拥堵问题,难以满足日益增长的交通发展需求[3-5]。
导致城市交通拥堵的主要原因是交通需求激增所带来的地面道路上车辆、车次数量巨增,而其中相当一部分是由于货物物流的需求增长所致。为解决物流运输所带来的交通拥堵问题,未来物流系统将逐步转向地下,目前,荷兰、美国等国家针对地下物流网络规划展开了大量的研究和实践工作[6]。
国内学者针对地下物流网络的构建进行了一定的探索。马祖军[7]分析了城市地下物流系统的研究与发展现状,提出了城市地下物流系统设计的主要步骤;闫文涛等[8]提出了地下物流节点选址双层规划模型及研究算法;易美等[9]通过建立数学模型研究分析了城市地下物流的网络规划;曾令慧等[10]基于遗传算法对城市地下物流网络进行了路径优化;贺政纲等[11]结合遗传算法和禁忌搜索算法对报废汽车回收物流网络进行建模及分析;戢晓峰等[12]构建了交通管制时限条件下的城市物流配送优化双层规划模型,并对比分析了交通管制时限期与整个配送期的配送时间及成本;王来军等[13]基于MapGIS对城市配送网络的优化问题进行分析研究。
上述研究成果针对城市物流网络节点选址、路径优化进行了初步研究,但是鲜少考虑区域交通拥堵系数对地下物流通道网络的规划进行研究,本文建立以总成本最小为优化目标,以通道容量限制及交通拥堵系数限制为约束条件的线性规划模型,并通过模拟退火算法进行优化求解,设计地下物流网络通道,改善交通拥堵状况。
1 问题背景 1.1 地下物流网络(1) 网络节点
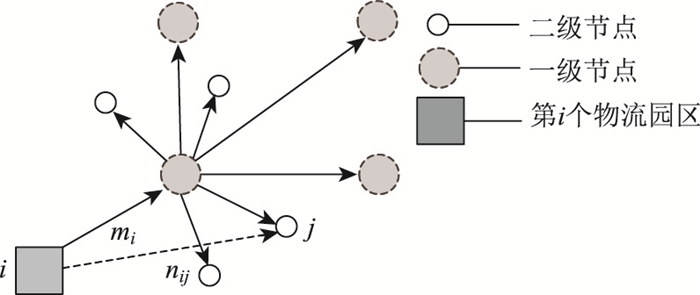
第i个物流园区与其隶属节点关系连接如图 1所示。对于第i个物流园区,对应一个一级节点与其直接相连,一系列二级节点通过此一级节点与其间接相连,如图 1所示。mi为第i个物流园区的总出货量;nij为第i个物流园区通过对应一级节点发往二级节点j的货运量。
|
| 图 1 物流园区与节点连接 Fig. 1 Connection of logistics park and nodes |
| |
(2) 网络结构
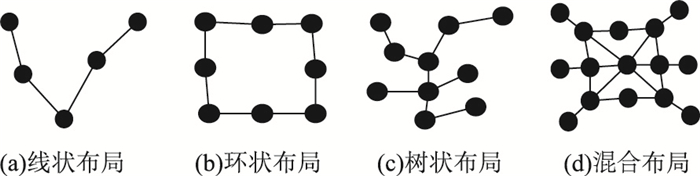
网络通道与各网络节点互相连接称为地下物流网络的结构形态。如图 2所示,按其连接方式的不同分为线状布局、环状布局、树状布局及混合布局等类型[14-15]。城市地下物流网络结构要充分结合城市的交通、地形、环境等具体情况,因地制宜。
|
| 图 2 地下物流网络布局类型 Fig. 2 Layouts of underground logistics network |
| |
1.2 概况及基本假设
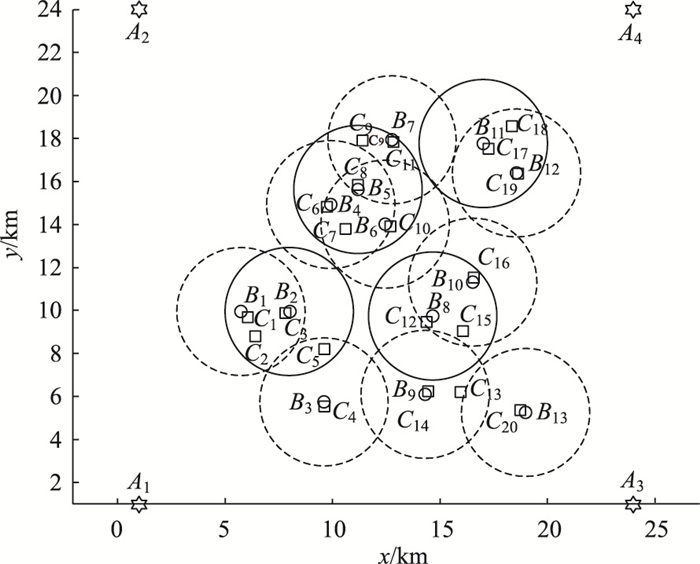
现有某地区交通货运区域划分图(图 3)及相应的货运流量矩阵(表 1)、各区域中心点及区域面积、各区域交通拥堵系数(表 1),为缓解某地区交通拥堵现状、降低物流运输成本,需设计节点间的地下通道网络,确定通道的位置以及类型,从而建立城市地下物流系统,实现该地区物流运输的多式联运。
|
| 图 3 物流节点示意图 Fig. 3 Schematic diagram of logistics nodes |
| |
| 区域编号 | C1 | C2 | C3 | C4 | C5 |
| 总货运量/t | 1 477.4 | 1 346.1 | 1 497.5 | 1 302.0 | 1 444.5 |
| 拥堵系数 | 4.48 | 6.57 | 6.79 | 6.53 | 5.33 |
| 区域编号 | C6 | C7 | C8 | C9 | C10 |
| 总货运量/t | 1 245.4 | 1 336.0 | 1 243.3 | 1 457.7 | 1 274.2 |
| 拥堵系数 | 6.35 | 6.64 | 6.78 | 6.41 | 6.79 |
| 区域编号 | C11 | C12 | C13 | C14 | C15 |
| 总货运量/t | 1 503.1 | 1 267.6 | 1 270.8 | 1 404.8 | 1 388.4 |
| 拥堵系数 | 7.03 | 6.96 | 6.53 | 6.08 | 6.42 |
| 区域编号 | C16 | C17 | C18 | C19 | C20 |
| 总货运量/t | 1 253.4 | 1 501.7 | 1 436.2 | 1 503.9 | 1 486.6 |
| 拥堵系数 | 6.64 | 7.22 | 6.49 | 6.50 | 5.40 |
针对该问题,作出以下假设:
(1) 所有节点的服务半径在3 km范围内自由选择,节点间距离不受限制;
(2) 地下节点及通道内的货物每天要清仓;
(3) 每两个相邻节点间地下物流通道双向尺寸一致,以单向流量最大的为设计原则;
(4) 每天的总成本由货物的运输成本和地下物流通道与节点的折旧构成;
(5) 假设每吨货每公里的平均运输成本始终相等,约为1元/t·km,与所经过的通道尺寸无关。
地下物流通道与节点的建设成本如表 2所示,设计年限100 a,年综合折旧率均为1%。
| 序号 | 通道与节点类型 | 建设成本 |
| 1 | 双向四轨(10 t) | 5亿元/km |
| 2 | 双向双轨(10 t) | 4亿元/km |
| 3 | 双向四轨(5 t) | 3.5亿元/km |
| 4 | 双向双轨(5 t) | 3亿元/km |
| 5 | 一级节点 | 1.5亿元/个 |
| 6 | 二级节点 | 1亿元/个 |
该地区地下物流网络节点群固定不变,物流园区及物流节点概况如表 3所示,物流网络节点示意如图 3所示。其中,C1~C20代表各货运区域中心点。
| 物流园区 | 对应一级节点 | 下属二级节点 |
| A1 | B2 | B1,B3 |
| A2 | B5 | B4,B6,B7 |
| A3 | B8 | B9,B10,B13 |
| A4 | B11 | B12 |
2 地下物流通道网络设计
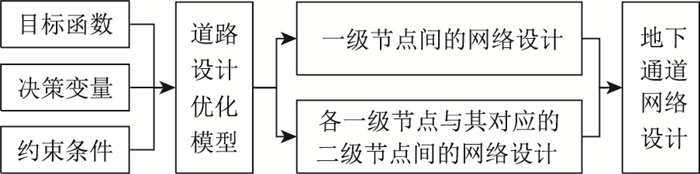
根据物流节点的位置、服务范围以服务节点与物流园区间的对应关系。为使各区域间能够相互连通,还需在各物流节点之间建立通道从而建立地下通道网络。结合网络可行流的思想,建立以总成本最小为目标的优化模型,如图 4所示。
|
| 图 4 地下通道网络设计模型的建立流程图 Fig. 4 Flowchart of establishing design model of underground channel network |
| |
2.1 决策变量的确定
为得到地下通道网络,即需最终确定通道的位置、类型与实际流量。首先引入0-1变量rijm:
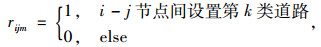
|
(1) |
式中m的取值情况如表 4所示。
| m值 | 道路类型 | cm |
| 1 | 不设置道路 | 0 |
| 2 | 双向四轨(10 t) | 18×5×8×10×2 |
| 3 | 双向双轨(10 t) | 18×5×8×10 |
| 4 | 双向四轨(5 t) | 18×5×8×5×2 |
| 5 | 双向双轨(5 t) | 18×5×8×5 |
某条通道的实际流量实际为经过此条通道运输的所有货运量之和,引入决策变量fijkl,其表示第k个节点发往第l个节点的流在i-j通道上的流量,则i-j通道的实际流量为:
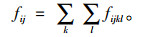
|
(2) |
以地下物流系统网络的总成本最小为目标函数,考虑货物的运输成本与地下物流通道与节点的折旧构成,即:
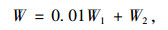
|
(3) |
式中,W1为地下物流通道和节点的修建成本; W2为货物的运输成本。
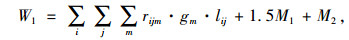
|
(4) |
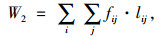
|
(5) |
式中,gm为第m类道路的造价; lij为i-j通道的长度(i, j节点间的距离); M1,M2分别为建设的一级节点与二级节点个数。
2.3 约束条件的确定(1) 可行流的平衡条件
现有第k个节点要将货物发往第l个节点,选择的节点与通道可以看做为一个可行流,对于这条可行流上的每一个节点,都需要满足收发平衡条件。
对于中间节点vi(i≠k, l),其流出量等于流入量,即:
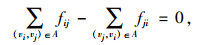
|
(6) |
式中,(vi, vj)表示vi点到vj点的弧,而A表示所有弧的集合;fij, fji为i-j通道的实际流量。
对于发点vk,有:
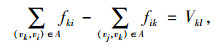
|
(7) |
式中,fki, fik为k-i通道的实际流量。
对于收点vl,有:
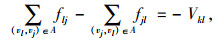
|
(8) |
式中,flj, fjl为j-l通道的实际流量; Vkl看作第k个节点通过地下物流网络发往第l个节点的净输出量,Vkl具有如下关系:
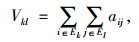
|
(9) |
式中,aij表示第i个区域通过地下物流网络发往第j个区域的净输出量;Ek表示第k个节点所分担的区域集; El为第l个节点所分担的区域集。
(2) 通道容量限制条件
首先,第k个节点发往第l个节点的流在i-j通道上的流量总是大于等于0,即:
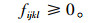
|
(10) |
其次,对于i-j通道来讲,在此条道路上的实际流量应小于该条道路的道路运送能力,即:
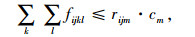
|
(11) |
式中,cm为第m类道路的运送能力。根据题意,每个节点每天最多运营18 h,每小时最多发车5班,每班车最多8节车辆,而车辆的类型由道路类型决定,cm的取值如表 4所示。
(3) 交通拥堵系数限制
根据交通拥堵系数的取值范围,为缓解交通拥堵直至交通畅通,至少基本畅通,地面交通的拥堵系数应低于4。近似地认为区域交通拥堵系数与区域总货运量成正比,根据每个区域交通拥堵系数与总货运量的比值ki,计算出满足道路基本畅通时的路面货运量Qi。
为考虑节点间在地下通道上的流量需求,将重新求解各区域间在地下物流系统里的货运OD流量矩阵。该地下物流系统的OD流量矩阵需满足以下两方面的关系:
一方面,地面交通拥堵系数与货运量成正比,即地下物流系统承担的货运量越多,地面交通情况越好,既对于每一个区域,有:
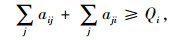
|
(12) |
另一方面,地下物流OD矩阵中的货运量一定不能高于初始OD矩阵的货运量,即:
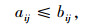
|
(13) |
式中,bij表示第i个区域通过地面与地下发往第j个区域的货运总量。
考虑到地下物流成本远远高于地面物流成本,投入地下物流网络的货运量在缓解地面交通的情况下应该尽可能的小,即:
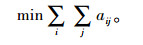
|
(14) |
综上所述,可得到道路设计优化的最终模型为:
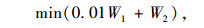
|
(15) |
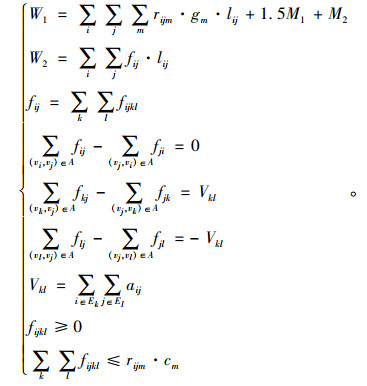
|
(16) |
为实现对模型结果的全局搜索,采用模拟退火算法[16-18]求解规划模型,通过如下基本步骤,最终得到通道网络设计最优解。
Step1:选取一个起始点z,并设定起始温度T,令迭代次数k等于1;
Step2:求目标函数(能量函数)E=f(x1x2…xi…xj…xn)=0.01W1+W2的函数值;
Step3:采用两点变异法,任选序号i和j,随机改变xi,xj的取值,得到新解x1x2…xi′…x′j…xn;
Step4:由上计算费用差有Δf = f(x1x2…xi…xj…xn)-f(x1x2…x′i…x′j…xn);
Step5:若Δf < 0,则接受新方案,否则以概率e-Δf/T接受新的方案;
Step6:选定α=0.9的降温系数进行降温,则新的温度为αT;
Step7:若T < e(e为终止温度),则输出结果,否则返回Step3。
4 求解分析通过MATLAB编程求解,地下物流通道及节点的建设成本W1=466.16亿元,货物运输成本W2=3.91亿元/年,按照年综合折旧率1%进行计算,得到地下物流网络总成本W=0.01W1+W2=8.57亿元/年。
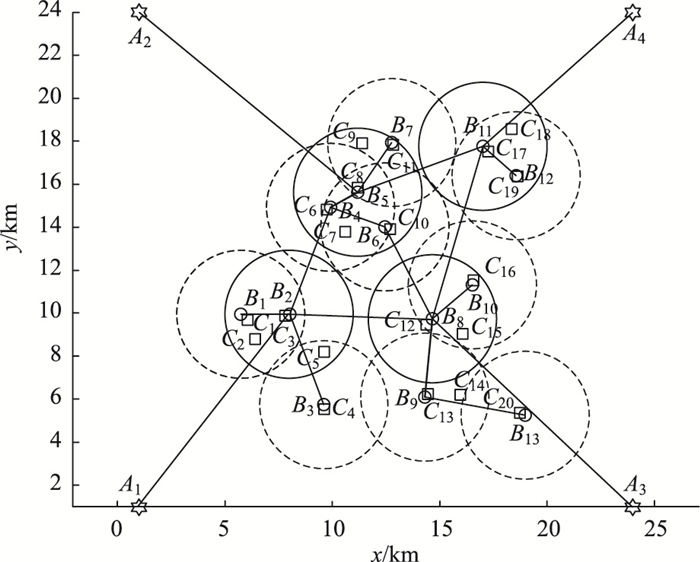
该地区地下物流系统所有通道示意如图 5所示,其中,A1—B2,A2—B5,A3—B8,A4—B11表示一级节点与物流园区通道, 其余线条表示一级节点之间或一级节点与同区域二级节点之间的通道设计。
|
| 图 5 地下物流系统所有通道设计示意图 Fig. 5 Schematic diagram of design of all channels of underground logistics system |
| |
4.1 一级节点与物流园区之间的通道设计结果
表 5为一级节点与物流园区之间的通道设计结果,除A4物流园区与B11一级节点采用双向双轨(10 t)之外,其余物流园区与对应一级节点均采用双向四轨(10 t),主要是由于为满足货物的需求,从物流园区运出的货物数量较大,因此对道路的要求更高。
| 序号 | 连接通道 | 道路类型 |
| 1 | A1—B2 | 双向四轨(10 t) |
| 2 | A2—B5 | 双向四轨(10 t) |
| 3 | A3—B8 | 双向四轨(10 t) |
| 4 | A4—B11 | 双向双轨(10 t) |
4.2 一级节点与一级节点之间的通道设计结果
表 6为一级节点之间的通道设计结果,各一级节点之间均采用双向双轨(5 t),其轨道数量和货运量上限均为一级节点与物流园区之间通道的一半,主要是由于从某一物流园区运送到对应一级节点的货物,部分已经由该区域二级节点运送到货物需求点。
| 序号 | 连接通道 | 道路类型 |
| 1 | B2—B5 | 双向双轨(5 t) |
| 2 | B2—B8 | 双向双轨(5 t) |
| 3 | B5—B11 | 双向双轨(5 t) |
| 4 | B8—B11 | 双向双轨(5 t) |
4.3 一级节点与同区域二级节点间的通道设计结果
表 7为一级节点与同区域二级节点之间的通道设计结果,除B5一级节点与B4二级节点、B8一级节点与B9二级节点之间采用双向四轨(5 t)之外,其余一级节点与同区域二级节点之间的通道均采用双向双轨(5 t)。
| 序号 | 连接通道 | 道路类型 |
| 1 | B1—B2 | 双向双轨(5 t) |
| 2 | B2—B3 | 双向双轨(5 t) |
| 3 | B4—B5 | 双向四轨(5 t) |
| 4 | B5—B7 | 双向双轨(5 t) |
| 5 | B6—B8 | 双向双轨(5 t) |
| 6 | B8—B9 | 双向四轨(5 t) |
| 7 | B8—B10 | 双向双轨(5 t) |
| 8 | B11—B12 | 双向双轨(5 t) |
4.4 同区域二级节点之间的通道设计结果
表 8为同区域二级节点之间的通道设计结果,由表可知,B4二级节点与B6二级节点之间、B9二级节点与B13二级节点之间均采用双向双轨(5 t),对于B9二级节点的设置,主要是为了满足C13,C14两个需求点的货运量。
| 序号 | 连接通道 | 道路类型 |
| 1 | B4—B6 | 双向双轨(5 t) |
| 2 | B9—B13 | 双向双轨(5 t) |
4.5 货运量求解结果
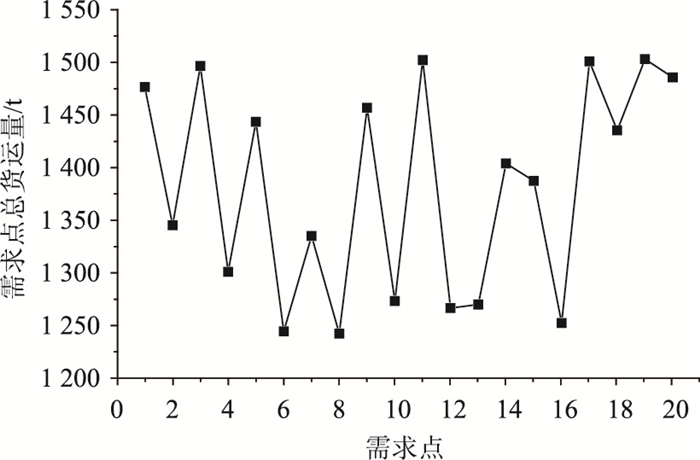
通过计算得到该地区每个物流需求点Ci的总货运量及各个物流园区Ai分别对该物流需求点的货运量。图 6为所有物流园区对各需求点的总货运量,由图 6可知,需求点C1,C3,C5,C9,C11,C17,C18,C19,C20的货物需求量较大,均在1 450以上,而其他需求点货物需求量相对较小。
|
| 图 6 所有物流园区对各需求点的总货运量 Fig. 6 Total freight volume of all logistics parks for demand points |
| |
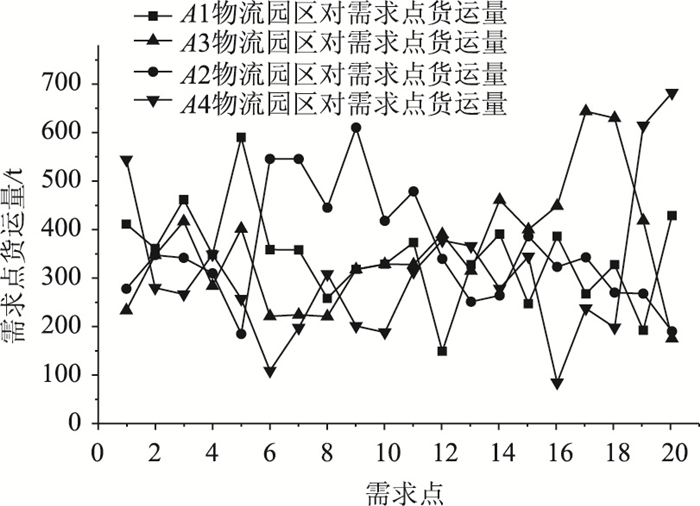
图 7为各个物流园区对需求点的货运量,由图 7可知,4个物流园区对所有需求点的总货运量偏差不大,对各个需求点的货运量均在400左右波动,其中A2—C6,C7,C9的货运量较其他需求点明显增大,主要是由于这3个需求点的位置与A2物流园区的距离较近所致。
|
| 图 7 各物流园区对需求点的货运量 Fig. 7 Freight volume of each logistics park for demand points |
| |
通过MATLAB编程求解,得到满足优化目标的13个服务节点与其对应服务需求点的货运量如表 9所示。由表可知,B1~B13各个服务节点对C1~C20各个需求点的货运量各不相同,除C3,C8,C10,C19外,其余需求点货物运输均来自于单一服务节点。结合图 5的地下物流系统所有通道设计结果,以B1服务节点为例,B1总是对局部相邻的C1,C2,C3需求点进行货物运输,因此考虑路径优化及运输成本,服务节点及物流需求点均遵循就近原则,即每个物流需求点会尽可能从最近的服务节点获取物流。
| 服务节点 | 对应需求点及货运量/t | ||
| B1 | C1 | C2 | C3 |
| 1 477.41 | 1 346.13 | 176.46 | |
| B2 | C3 | C5 | — |
| 1 321.01 | 1 444.45 | — | |
| B3 | C4 | — | — |
| 1 301.98 | — | — | |
| B4 | C6 | C7 | C8 |
| 1 245.41 | 1 335.95 | 418.64 | |
| B5 | C8 | C9 | C10 |
| 824.61 | 1 457.74 | 717.65 | |
| B6 | C10 | — | — |
| 556.56 | — | — | |
| B7 | C11 | — | — |
| 1 503.06 | — | — | |
| B8 | C12 | C15 | — |
| 1 267.6 | 1 388.36 | — | |
| B9 | C13 | C14 | — |
| 1 270.82 | 1 404.82 | — | |
| B10 | C16 | — | — |
| 1 253.44 | — | — | |
| B11 | C17 | C18 | C19 |
| 1 501.65 | 1 436.24 | 62.11 | |
| B12 | C19 | — | — |
| 1 441.83 | — | — | |
| B13 | C20 | — | — |
| 1 486.61 | — | — | |
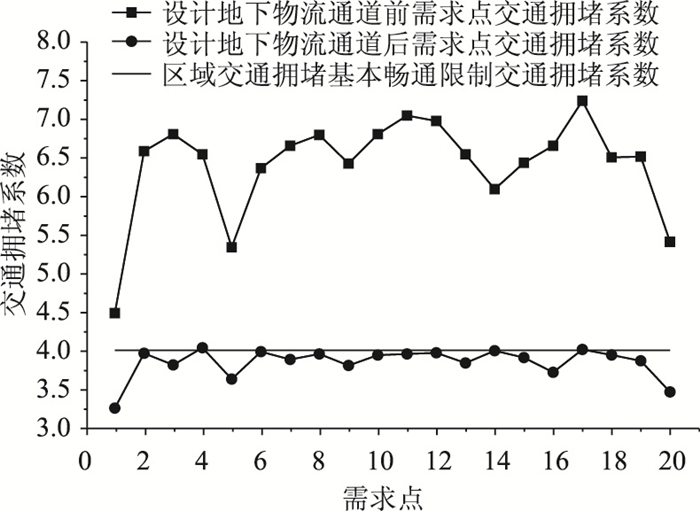
图 8为设计地下物流通道前后需求点的交通拥堵系数对比情况,由图 8可知,各需求点在设计地下物流通道前交通拥堵系数在4.5~7.5之间,均为轻度拥堵或中度拥堵,通过将部分货运量转至地下物流通道,交通拥堵系数降到4.0及以下,各区域需求点交通状况均达到基本畅通的要求。
|
| 图 8 设计地下物流通道前后需求点交通拥堵系数对比 Fig. 8 Comparison of traffic congestion factors of demand points before and after designing underground logistics channel |
| |
5 结论
以国内某地区物流概况为研究背景,结合国内外地下物流系统研究成果,考虑路径优化与运输成本,建立以总成本最小为优化目标的线性规划模型,并通过模拟退火算法进行优化求解,得到以下结论:
(1) 基于模拟退火算法得到该地区地下物流网络通道设计全局最优解,地下物流通道及节点的建设成本为466.16亿元,货物运输成本为3.91亿元/a,按照年综合折旧率1%进行计算,地下物流网络总成本为8.57亿元/a。
(2) 从物流园区运送出的货物通过地下物流通道运输的量较大,物流园区与一级节点之间的通道均为双向四轨(10 t)或双向双轨(10 t),表明其通道设计要求更高。
(3) 所有物流园区对各需求点的总货运量表现出明显的波动性,而各物流园区对所有需求点的总货运量偏差不大,对各个需求点的货运量均在400 t左右波动。
(4) 各个服务节点对各个需求点的货运量各不相同,但大部分需求点的货物运输均来自于单一服务节点,且每个物流需求点会尽可能从最近的服务节点获取物流。
(5) 各需求点在设计地下物流通道前交通拥堵系数在4.5~7.5之间,均为轻度拥堵或中度拥堵,通过将部分货运量转至地下物流通道,交通拥堵系数降到4.0及以下,各区域需求点交通状况均达到基本畅通的要求。
| [1] |
李鹏, 朱合华, 王璇, 等. 地下物流系统对城市可持续发展的作用探讨[J]. 地下空间与工程学报, 2007, 3(1): 1-4. LI Peng, ZHU He-hua, WANG Xuan, et al. Underground Logistics System: Towards the Sustainable Development of the City[J]. Journal of Underground Space and Engineering, 2007, 3(1): 1-4. |
| [2] |
LIUH, 崔建强, 林冬, 等. 纽约市地下物流可行性研究及对世界其他主要城市的启示[J]. 现代交通技术, 2008, 5(4): 86-92. LIU H, CUI Jian-qiang, LIN Dong, et al. Feasibility of Underground Freight Transport in New York City and Lessons Learned and Implications to Other Major Cities in the World[J]. Modern Transportation Technology, 2008, 5(4): 86-92. |
| [3] |
CHEN Z L, DONG J M, REN R. Urban Underground Logistics System in China: Opportunities or Challenges[J]. Underground Space, 2017, 2(3): 195-208. |
| [4] |
ZEVGOLIS I E, MAVRIKOS A A, KALIAMPAKOS D C. Construction, Storage Capacity and Economics of an Underground Warehousing: Logistics Center in Athens, Greece[J]. Tunnelling and Underground Space Technology, 2004, 19(2): 165-173. |
| [5] |
莫海熙, 郜振华, 陈森发. 基于AHP和目标规划的物流配送中心选址模型[J]. 公路交通科技, 2007, 24(5): 150-153. MO Hai-xi, GAO Zhen-hua, CHEN Sen-fa. Location Model of Distribution Center Besed on Analytic Hierarchy Process and Goal Programming[J]. Journal of Highway and Transportation Research and Development, 2007, 24(5): 150-153. |
| [6] |
钱七虎, 郭东军. 城市地下物流系统导论[M]. 北京: 人民交通出版社, 2007. QIAN Qi-hu, GUO Dong-jun. Introduction to Urban Underground Logistics System[M]. Beijing: China Communications Press, 2007. |
| [7] |
马祖军. 城市地下物流系统及其设计[J]. 物流技术, 2004(10): 12-15. MA Zu-jun. Urban Underground Logistics System and Its Design[J]. Logistics Technology, 2004(10): 12-15. |
| [8] |
闫文涛, 覃燕红. 地下物流节点选址的双层规划模型及算法研究[J]. 地下空间与工程学报, 2016, 12(4): 870-874. YAN Wen-tao, QIN Yan-hong. Research on Bi-level Programming Model and Algorithm of Underground Logistics Node Location[J]. Journal of Underground Space and Engineering, 2016, 12(4): 870-874. |
| [9] |
易美, 周爱莲. 一类城市地下物流网络规划模型研究[J]. 交通科学与工程, 2016, 32(3): 93-98. YI Mei, ZHOU Ai-lian. Research on a Logistics Network Planning Model of the Urban Underground[J]. Journal of Transport Science and Engineering, 2016, 32(3): 93-98. |
| [10] |
曾令慧, 周爱莲. 基于遗传算法的城市地下物流网络优化模型[J]. 交通科学与工程, 2016, 32(2): 89-93. ZENG Ling-hui, ZHOU Ai-lian. Optimizing Path of Urban Underground Logistics Network Based on Genetic Algorithm[J]. Journal of Transport Science and Engineering, 2016, 32(2): 89-93. |
| [11] |
贺政纲, 邹晔, 杨晓. 报废汽车物流网络选址-路径问题建模与求解算法研究[J]. 公路交通科技, 2016, 33(3): 138-145. HE Zheng-gang, ZOU Ye, YANG Xiao. Research of Modeling and Algorithm for ELV Logistics Network Location-routing Problem[J]. Journal of Highway and Transportation Research and Development, 2016, 33(3): 138-145. |
| [12] |
戢晓峰, 普永明, 梁斐雯, 等. 交通管制时限条件下城市物流配送优化双层规划模型[J]. 公路交通科技, 2014, 31(12): 145-152. JI Xiao-feng, PU Yong-ming, LIANG Fei-wen, et al. Bi-level Programming Model for City Logistics Distribution Optimization under Time Restrict Condition Caused by Traffic Control[J]. Journal of Highway and Transportation Research and Development, 2014, 31(12): 145-152. |
| [13] |
王来军, 郭捷, 宣登殿, 等. 基于MapGIS的城市配送网络优化设计[J]. 公路交通科技, 2015, 32(8): 143-149. WANG Lai-jun, GUO Jie, XUAN Deng-dian, et al. Optimization Design of City Distribution Network Based on MapGIS[J]. Journal of Highway and Transportation Research and Development, 2015, 32(8): 143-149. |
| [14] |
徐国峰.城市地下物流系统构架研究[D].武汉: 华中科技大学, 2012. XU Guo-feng. Research on Urban Underground Logistics System Framework[D]. Wuhan: Huazhong University of Science and Technology, 2012. http://d.wanfangdata.com.cn/Thesis/D228277 |
| [15] |
穆树录.城市地下物流系统线路规划研究[D].石家庄: 石家庄铁道大学, 2015. MU Shu-lu. The Research of Route Planning of Urban Underground Logistics System[D]. Shijiazhuang: Shijiazhuang Tiedao University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10107-1015424626.htm |
| [16] |
赵振亚, 贺国先. 基于模拟退火算法的应急物流仓库选址优化[J]. 大连交通大学学报, 2010, 31(3): 102-106. ZHAO Zhen-ya, HE Guo-xian. Optimization of Emergency Logistic Warehouse Location Based on Simulation Annealing Algorithm[J]. Journal of Dalian Jiaotong University, 2010, 31(3): 102-106. |
| [17] |
郎茂祥. 装卸混合车辆路径问题的模拟退火算法研究[J]. 系统工程学报, 2005, 20(5): 41-47. LANG Mao-xiang. Study on Simulated Annealing Algorithm for Vehicle Routing Problem with Backhauls[J]. Journal of Systems Engineering, 2005, 20(5): 41-47. |
| [18] |
查伟雄, 孙敬. 基于模拟退火算法的危险货物道路运输路径优化双层规划模型[J]. 公路交通科技, 2012, 29(4): 101-106. ZHA Wei-xiong, SUN Jing. Bi-level Programming Model for Road Transport Route Optimization of Dangerous Goods Based on Simulated Annealing Algorithm[J]. Journal of Highway and Transportation Research and Development, 2012, 29(4): 101-106. |
 2019, Vol. 36
2019, Vol. 36
