扩展功能
文章信息
- 吴芳芸, 朱小林
- WU Fang-yun, ZHU Xiao-lin
- 基于轴辐式理论的冷链物流网络优化模型
- Cold Chain Logistics Network Optimization Model Based on Hub-and-Spoke Theory
- 公路交通科技, 2019, 36(6): 144-150
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(6): 144-150
- 10.3969/j.issn.1002-0268.2019.06.018
-
文章历史
- 收稿日期: 2017-06-30
现阶段,由于中国生鲜电商市场的快速发展和人们对生鲜类、奶制品类等各类易腐品消费的快速增长,冷链运输需求旺盛,其作为物流行业中进入壁垒较高,市场空间巨大的一个领域,前景广阔,成为电商和物流企业抢占的高地。且2017文件《关于深入推进农业供给侧结构性改革加快培育农业农村发展新动能的若干意见》中的第14条明确指出,要加强冷链物流基础设施网络建设。因此冷链物流网络节点的设计是否科学,冷链物流网络的布局是否合理,更是至关重要。
由于冷链物流起步较晚,目前国内外学者对冷链物流网络设计取得较少的成果:袁群、左奕等人[1]建立了以总成本最低为目标函数,同时考虑时间窗、货物品质及客户服务水平,利用贪婪算法改进交叉算子的混合遗传算法对模型求解,进行冷链物流网络设计; 杨晓芳等人[2]结合冷链运输对时间的敏感性特点,建立了客户满意度最大化和物流成本最小化的双目标优化模型进行网络设计; 杨华龙等人[3]为优化冷链物流网络布局, 建立非线性规划模型, 设计遗传算法;BD Song等人[4]研究了冷藏, 一般类型的多种易腐食品的冷链物流网络设计; R Haijema[5]提出了一种新的MILP模型和一种混合优化“仿真”(HOS)方法,以在产品质量要求下识别成本最优的冷链物流网络设计。JC Kuo[6]提出了在设计冷链物流网络时采用一种基于多温度联合分配系统的发展物流服务模型,即MTJD,运用于食品冷链。M Lütjen[7]等人在冷链物流网络中提出能够自主决定其运输货物状况的新型运输系统“智能集装箱”。Hasani A等人[8]研究如何在冷链品运输中通过缩短生产和交付之间的时间间隔来提高这些食品的质量。尚成国等人[9]考虑了在电子商务的背景下,生鲜农产品物流网络设计与鲁棒性有关,构建成本最小化目标函数。梁海红[10]结合生鲜农产品易损耗特点, 基于线性规划构建“互联网+”时代农产品物流配送中心选址模型。
综观上述研究现状,学者们多数只对于冷链传统直通式物流网络的结构模式进行研究,而据中物联冷链委统计,现冷链市场需求和资源碎片化趋势严重且冷链运输多为小批量多批次。因此直通式网络会导致冷链物流企业承担大量小规模的运输,增加物流总成本,且运输次数的频繁导致道路网络的拥挤,增加社会总成本。
因此,本研究构建基于轴辐式理论的冷链物流网络优化模型。轴辐式物流网络(Hub-and-Spoke network)是由枢纽点(Hub)与非枢纽点(Spoke)通过干线和支线连接而成的运输网络,在航空、通讯、物流等行业[11-14]中运用广泛。在轴辐式物流网络中,OD流先汇聚到枢纽点,由枢纽点转运至指定的辐节点,这一方式比直通式物流网络使用了更少的连线连接多对OD流,并且依靠枢纽点的集散货功能,增大了运输网络中干线的货物流量,从而利用干线运输的规模经济效应降低了物流总运输成本[15-16]。一定程度上改善了直通式网络成本高和效率低的情况,促进冷链需求和资源集中化,提高冷链物流网络的效率,降低冷链物流网络总成本,达到运输经济效益最大化。
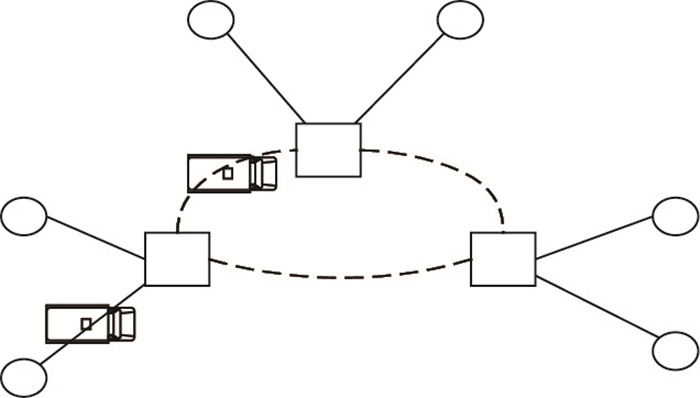
1 基于轴辐式理论的冷链物流网络优化模型 1.1 问题描述与假设全国各地冷链物流运输公司由于中小客户较多,易腐品等需求量较小且批次多,经常会出现冷藏车非满载运输的情况,一方面增加了公司的车辆成本和人工成本,另一方面导致区域范围内道路拥挤,降低了运输效率和服务质量,增加了物流总成本。在上述情况下,冷链物流运输公司在一定的时间范围内(保持新鲜度)先把大量来自不同出发地的易腐品聚集到合适的冷链配送中心,再按目的地不同重组后各自发往目的地,利用冷链配送中心的干线大规模运输降低总的物流总成本,缓解交通拥挤。本研究要解决的问题就是在最小化冷链物流运输公司总物流成本(运输成本,制冷成本以及新鲜度造成的货损成本)和最小运输时间的双重约束下确定冷链配送中心的个数和其具体位置,以及其和需求节点之间的分配关系(如图 1所示)。
|
| 图 1 冷链物流网络 Fig. 1 Cold chain logistics network |
| |
假设如下:
(1) 冷链配送中心之间的运输为干线运输,需求点与冷链配送中心之间的运输为支线运输,干线上冷藏车的满载率等因素形成规模效应;
(2) 为了降低模型难度,每个需求节点只能与一个冷链配送中心相连;
(3) 冷链配送中心彼此相连,由于需求点冷链品小批量多批次,必须至少经过一个或两个冷链配送中心进行干线运输达到降低成本;
(4) 冷链配送中心之间的干线单位运输成本有一个规模效应经济系数λ,其中0<λ<1;
(5) 冷链配送中心的容量不受限制,且各节点间的时间、运量、距离和费率已知;
(6) 冷链的新鲜度随时间指数下降,该网络中的货损成本只与新鲜度损失率相关,不考虑其他人为因素。
1.2 建立基于轴辐式理论的冷链物流网络模型(1) 集合
i, j, k, l∈N, 网络中节点个数为N个,i, j为需求节点,k和l为枢纽节点。
(2) 参数
为冷链配送中心(枢纽点)的建设成本;tij为需求点i, j之间运输时间;Tij为需求点i, j之间运输时间限制;dik为需求点i到冷链配送中心k的距离;wij为需求点i和j之间的流量;δ, λ, ε分别为需求点到冷链配送中心,冷链配送中心转运以及到达需求点的单位运输成本;κ为单位制冷成本;θ为新鲜度单位损失率;ρ为冷链单位损失成本;p为冷链配送中心个数。
(3) 决策变量
xik为1表示需求点i被分配到冷链配送中心k,否则为0;xkk为1表示k为冷链配送中心;xijkl为1表示需求点i和j之间的流量经过冷链配送中心k,l否则为0;ykli为易腐品从需求点i经过冷链配送中心k,l的干线运输的流量。
(4) 基于新鲜度的货损成本的表示
冷链的新鲜度在整个冷链轴辐式网络运输途中会随着时间的增加而减少,从变质率角度产生一定的货损成本,整个冷链轴辐式网络运输分为3段,需求节点到冷链配送中心的时间,冷链配送中心之间转运的时间以及冷链配送中心运往需求节点之间的时间,根据Osvald等人[17]和张建等人[18]的文献,新鲜度函数φ(t)=(1-θ)t,其中θ>0,易腐品从需求节点i运输到节点j的新鲜度为:φij=(1-θ)∑k∑l(tik+tkl+tlj)xijkl,所以货损成本表示为:

|
(5) 模型建立
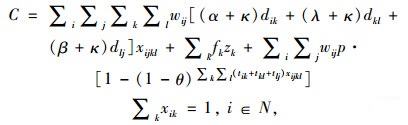
|
(1) |
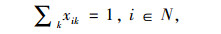
|
(2) |
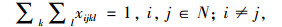
|
(3) |
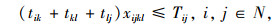
|
(4) |
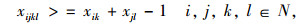
|
(5) |
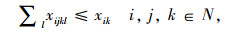
|
(6) |
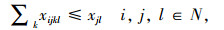
|
(7) |
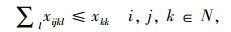
|
(8) |
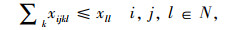
|
(9) |
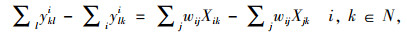
|
(10) |
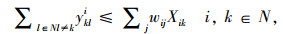
|
(11) |
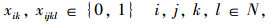
|
(12) |
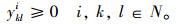
|
(13) |
目标函数求整个冷链物流网络的总运输成本,制冷成本和货损成本最小。各约束代表的含义描述如下:式(1)为冷链品需求节点只能被分配到一个冷链配送中心;式(2)确保必须建立总共p个冷链配送中心;式(3)为每个O-D对(i,j)和选择一个冷链配送中心对(k,l);式(4)为需求节点间时间约束,以保证冷链品的新鲜度;式(5)~式(7)为通过冷链品需求节点i→k和l→j之间的线路的存在来确保路径i-j-k-l存在;式(8)和式(9)要求如果需求节点i,j,k和l之间存在路径,则冷链配送中心选址为k和l;式(10)为流量平衡;式(11)为从需求节点i点发送到冷链配送中心的流量小于从需求节点发出的总量; 式(12)为0-1变量;式(13)为非负变量。
2 算例 2.1 算例描述本研究考虑20个需求节点(N=20)的冷链物流轴辐式网络,数据由某冷链运输公司提供,γ=σ=1元,α=0.65。单位新鲜度损失率为0.005,单位损失成本为150,制冷成本为1.5,需求节点部分相关数据见表 1和表 2。使用CPLEX12.5求解。为验证CPLEX商业求解器的求解规模,将设计的基于改进权重的粒子群算法(由于篇幅限制此处不做详述)和CPLEX在不同规模下进行对比,如表 3所示。当问题规模较小时,CPLEX和算法最优解接近,计算时间更快; 当N=30和40时,CPLEX已经无法计算结果。因此本研究N=20下的基于新鲜度的冷链物流网络模型适合CPLEX求解。
| 需求点 编号 | 横坐 标/km | 纵坐 标/km | 建设成本/ (×106元) |
| 点01 | 100.09 | 23.88 | 204 |
| 点02 | 100.25 | 23.48 | 345 |
| 点03 | 98.59 | 24.44 | 146 |
| 点04 | 104.24 | 23.37 | 267 |
| 点05 | 102.71 | 25.05 | 232 |
| 点06 | 99.71 | 27.83 | 125 |
| 点07 | 105.33 | 27.41 | 156 |
| 点08 | 109.17 | 27.67 | 189 |
| 点09 | 116.28 | 39.54 | 204 |
| 点10 | 117.11 | 39.01 | 345 |
| 点11 | 117.35 | 32.93 | 189 |
| 点12 | 115.82 | 32.90 | 325 |
| 点13 | 118.29 | 29.71 | 235 |
| 点14 | 118.46 | 32.03 | 221 |
| 点15 | 116.32 | 37.46 | 246 |
| 点16 | 119.45 | 32.20 | 217 |
| 点17 | 120.15 | 33.37 | 197 |
| 点18 | 118.87 | 28.96 | 186 |
| 点19 | 121.48 | 31.25 | 247 |
| 点20 | 119.51 | 35.42 | 278 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 1 | 0 | 0.19 | 0.4 | 0.3 | 0.2 | 0.36 | 0.26 | 0.16 | 0.82 | 0.61 | 0.42 | 0.32 | 0.96 | 0.45 | 0.65 | 0.79 | 0.35 | 0.46 | 0.78 | 0.39 |
| 2 | 0.3 | 0 | 0.2 | 0.38 | 0.36 | 0.34 | 0.32 | 0.14 | 0.36 | 0.57 | 0.32 | 0.36 | 0.79 | 0.95 | 0.4 | 0.46 | 0.78 | 0.23 | 0.56 | 0.75 |
| 3 | 0.2 | 0.27 | 0 | 0.85 | 0.42 | 0.82 | 0.61 | 0.46 | 0.56 | 0.78 | 0.23 | 0.56 | 0.95 | 0.41 | 0.46 | 0.35 | 0.25 | 0.46 | 0.45 | 0.26 |
| 4 | 0.38 | 0.26 | 0.38 | 0 | 0.66 | 0.12 | 0.56 | 0.79 | 0.46 | 0.95 | 0.41 | 0.46 | 0.35 | 0.25 | 0.56 | 0.45 | 0.26 | 0.66 | 0.75 | 0.66 |
| 5 | 0.36 | 0.78 | 0.23 | 0.56 | 0 | 0.62 | 0.82 | 0.46 | 0.85 | 0.42 | 0.82 | 0.62 | 0.46 | 0.56 | 0.78 | 0.23 | 0.56 | 0.54 | 0.43 | 0.64 |
| 6 | 0.34 | 0.29 | 0.46 | 0.5 | 0.43 | 0 | 0.75 | 0.32 | 0.34 | 0.58 | 0.26 | 0.89 | 0.55 | 0.71 | 0.76 | 0.65 | 0.55 | 0.66 | 0.75 | 0.36 |
| 7 | 0.32 | 0.36 | 0.79 | 0.95 | 0.4 | 0.46 | 0 | 0.15 | 0.64 | 0.49 | 0.24 | 0.64 | 0.53 | 0.52 | 0.64 | 0.57 | 0.64 | 0.86 | 0.57 | 0.36 |
| 8 | 0.14 | 0.28 | 0.46 | 0.76 | 0.8 | 0.52 | 0.8 | 0 | 0.56 | 0.78 | 0.23 | 0.56 | 0.95 | 0.41 | 0.46 | 0.35 | 0.25 | 0.46 | 0.45 | 0.26 |
| 9 | 0.66 | 0.68 | 0.53 | 0.46 | 0.35 | 0.61 | 0.56 | 0.83 | 0 | 0.46 | 0.45 | 0.56 | 0.75 | 0.35 | 0.66 | 0.85 | 0.66 | 0.36 | 0.55 | 0.86 |
| 10 | 0.56 | 0.78 | 0.33 | 0.66 | 0.45 | 0.51 | 0.67 | 0.38 | 0.39 | 0 | 0.65 | 0.66 | 0.57 | 0.67 | 0.89 | 0.58 | 0.38 | 0.63 | 0.68 | 0.98 |
| 11 | 0.35 | 0.68 | 0.53 | 0.67 | 0.49 | 0.46 | 0.59 | 0.69 | 0.38 | 0.58 | 0 | 0.26 | 0.35 | 0.41 | 0.46 | 0.67 | 0.78 | 0.69 | 0.67 | 0.46 |
| 12 | 0.82 | 0.56 | 0.55 | 0.72 | 0.83 | 0.64 | 0.45 | 0.56 | 0.78 | 0.23 | 0.56 | 0 | 0.43 | 0.22 | 0.74 | 0.68 | 0.57 | 0.78 | 0.79 | 0.46 |
| 13 | 0.32 | 0.36 | 0.59 | 0.76 | 0.85 | 0.57 | 0.68 | 0.65 | 0.35 | 0.47 | 0.58 | 0.39 | 0 | 0.42 | 0.84 | 0.68 | 0.89 | 0.36 | 0.57 | 0.37 |
| 14 | 0.35 | 0.46 | 0.78 | 0.95 | 0.76 | 0.84 | 0.66 | 0.48 | 0.59 | 0.75 | 0.33 | 0.66 | 0.87 | 0 | 0.14 | 0.38 | 0.69 | 0.96 | 0.67 | 0.57 |
| 15 | 0.65 | 0.36 | 0.58 | 0.57 | 0.68 | 0.79 | 0.78 | 0.36 | 0.55 | 0.47 | 0.58 | 0.59 | 0.48 | 0.57 | 0 | 0.48 | 0.59 | 0.76 | 0.87 | 0.53 |
| 16 | 0.85 | 0.78 | 0.89 | 0.67 | 0.87 | 0.97 | 0.87 | 0.66 | 0.57 | 0.48 | 0.69 | 0.36 | 0.49 | 0.55 | 0.41 | 0 | 0.51 | 0.72 | 0.33 | 0.27 |
| 17 | 0.46 | 0.45 | 0.29 | 0.36 | 0.78 | 0.38 | 0.98 | 0.48 | 0.38 | 0.59 | 0.67 | 0.38 | 0.39 | 0.46 | 0.56 | 0.72 | 0 | 0.42 | 0.63 | 0.47 |
| 18 | 0.75 | 0.26 | 0.39 | 0.54 | 0.98 | 0.54 | 0.76 | 0.65 | 0.45 | 0.36 | 0.56 | 0.53 | 0.65 | 0.87 | 0.47 | 0.75 | 0.55 | 0 | 0.23 | 0.49 |
| 19 | 0.39 | 0.67 | 0.58 | 0.67 | 0.98 | 0.48 | 0.57 | 0.65 | 0.34 | 0.51 | 0.57 | 0.48 | 0.93 | 0.76 | 0.57 | 0.46 | 0.78 | 0.76 | 0 | 0.53 |
| 20 | 0.65 | 0.57 | 0.51 | 0.63 | 0.48 | 0.39 | 0.56 | 0.76 | 0.63 | 0.79 | 0.83 | 0.39 | 0.69 | 0.66 | 0.78 | 0.73 | 0.77 | 0.41 | 0.72 | 0 |
| 规模大小 | 项目 | 基于改进的粒子群算法 | CPLEX12.5 |
| N=10 | 成本最低值/百万元 计算时间/s | 4.521 17.2 | 4.523 17 |
| N=20 | 成本最低值/百万元 计算时间/s | 9.632 36.1 | 9.622 34.4 |
| N=30 | 成本最低值/百万元 计算时间/s | 14.820 37.339 | 15.120 63.339 |
| N=40 | 成本最低值/百万元 计算时间/s | 28.945 67.197 0 | — |
| 注:—表示CPLEX无法求出结果。 | |||
2.2 试验设置
为了证明冷链物流轴辐式网络具有优越性, 设置了表 4中3个试验。
| 试验 序号 | 试验目的 | 模型调整及分析过程 |
| 1 | 分析新鲜度按时间分段对结果的影响(目标函数中冷链的货损成本是一个非线性函数,利用分段技术求解) | (1)保持运输成本、时间等参数不变。 (2)按时间段划分新鲜度 (3)试验结果见图 2~图 4及表 5 (4)分析试验结果 |
| 2 | 观测冷链物流轴辐式网络具有经济效应,对比传统冷链物流网络, 为冷链物流网络设计者提供参考依据 | (1)保持运输成本、时间等参数不变。 (2)调节λ的大小 (3)试验结果见表 6 (4)分析试验结果 |
| 3 | 验证冷链配送中心个数的选择影响整个冷链物流网络的结构和总成本,证明轴辐式网络对于冷链需求和资源碎片化现象具有改善作用,在冷链运输多为小批量多批次的情况下集中需求共同配送,减少冷链物流网络总成本,利于规模小的冷链物流企业合作。 | (1)保持运输成本、时间等参数不变。 (2)调整冷链配送中心个数 (3)试验结果见表 7; (4)分析试验结果 |
2.3 试验分析
(1) 新鲜度分段函数分析
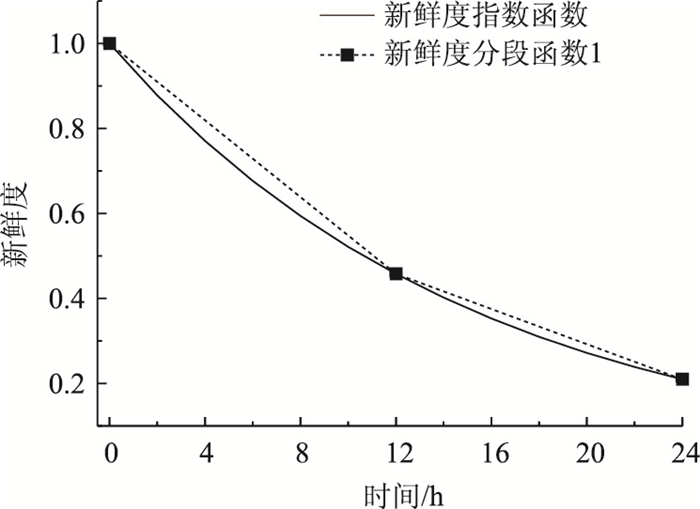
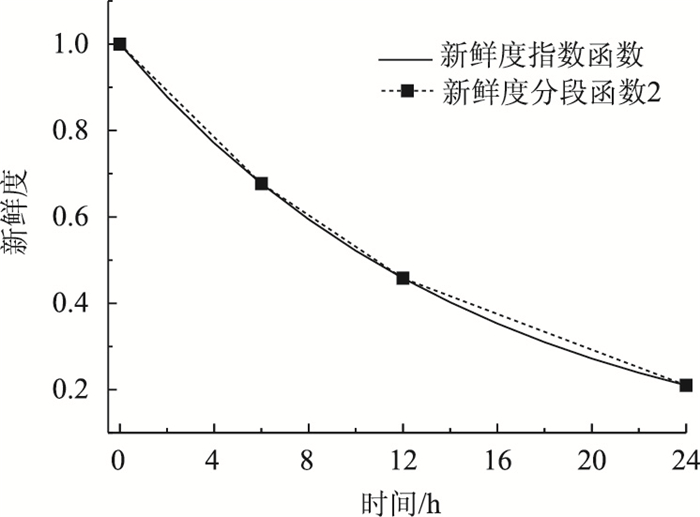
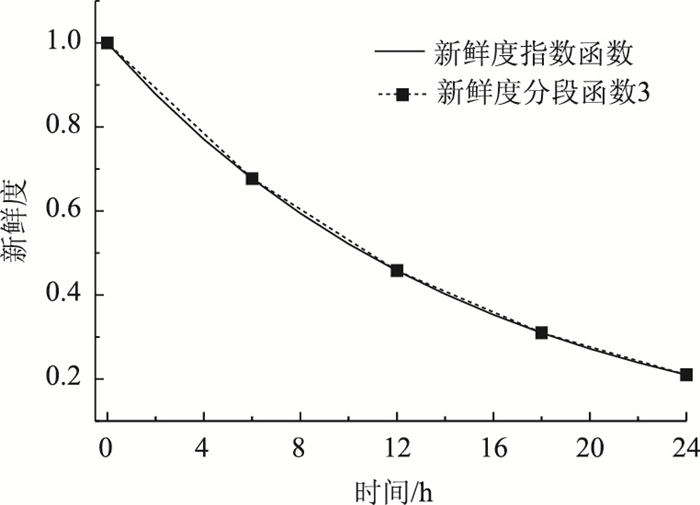
试验1结果中如图 2~图 4所示,将新鲜度按冷链生命周期分别划分为2, 3, 4段,新鲜度分段函数在3种情形下的新鲜度表示都接近于新鲜度指数表达,且新鲜度的精确度与分段的数目呈正比关系,如图 4的新鲜度分段函数3将新鲜度按4个时间段划分,其走向和新鲜度指数几乎重合,验证了采用该技术符合冷链新鲜度按时间指数下降的实际情况。且如表 5所示,通过模型求解,新鲜度分段函数表达形式下的冷链物流网络总成本接近新鲜度指数函数表达形式下的总成本,误差分别为1.6%,0.5%,0.3%。且分段函数3情况下(0.3%的误差)更接近新鲜度指数函数的总成本。以上验证了新鲜度函数分段表达的可行性。
|
| 图 2 新鲜度指数函数与分段函数1对比 Fig. 2 Contrast of freshness index function and piecewise function 1 |
| |
|
| 图 3 新鲜度指数函数与分段函数2对比 Fig. 3 Contrast of freshness index function and piecewise function 2 |
| |
|
| 图 4 新鲜度指数函数与分段函数3对比图 Fig. 4 Contrast of freshness index function and piecewise function 3 |
| |
| 新鲜度表示 | 总成本/百万元 | 新鲜度表示 | 总成本/百万元 | 新鲜度表示 | 总成本/百万元 |
| 新鲜度分段函数1 | 9.816 | 新鲜度分段函数2 | 9.711 | 新鲜度分段函数3 | 9.690 |
| 新鲜度指数函数 | 9.662 | 新鲜度指数函数 | 9.662 | 新鲜度指数函数 | 9.662 |
| 误差 | 1.6% | 误差 | 0.5% | 误差 | 0.3% |
(2) 对规模经济系数λ敏感分析
试验2结果中表 6为了直观地观测冷链物流轴辐式网络具有经济效应,对λ进行固定处理,通过保持其他参数不变的情况下改变规模经济系数λ,当规模经济系数λ为0.5时,总成本为9.662,是传统冷链物流网络总成本的40. 5%,而规模经济系数从0.5增加到0.85时,总成本分别为9.163×106,9.329×106,9.502×106,9.622×106都低于传统直通式冷链物流网络的总成本,成本节约率分别为40.5%,39.7%,38.6%,37.8%。相对于传统冷链物流网络总成本,轴辐网络总成本约占37%~40%。而规模经济系数的大小和运输的流量密切相关。因此相关人员可根据冷链物流中小企业的货运量进行整个物流网络的优化,通过该网络,企业可采用共同配送的方式减少冷藏车辆总量、提高冷藏车辆的装载率、消除封闭性的冷链物流网络、扩大物流冷链市场范围,利于营造冷链物流企业共建共享的环境。
| λ | 目标值/百万元 |
| 0.5 | 9.163 |
| 0.65 | 9.329 |
| 0.75 | 9.502 |
| 0.85 | 9.622 |
| 直通式物流网络 | 15.474 |
(3) 对冷链配送中心个数p(枢纽点)的分析
试验结果3中表 7表示限制冷链配送中心个数p(即冷链运输转运的次数)对结果的影响,在保持运输成本、制冷成本等参数不变的前提下,当枢纽中心个数为1-4时,基于新鲜度的冷链物流轴辐式网络总成本随着枢纽个数的增加而不断降低。一方面表明冷链物流运输网络通过配送中心转运,产生规模经济效应从而降低冷链物流网络的总成本。另一方面配送中心个数增加可优化生鲜品配送路线,低成本的同时减少道路拥挤,减少生鲜品运输的货损成本;而当枢纽中心个数大于4时,则与前相反。这表明考虑到整个冷链物流的服务范围,冷链配送中心个数不能无限制建设,否则将造成额外的建设成本,绕道成本和货损成本。由于目前冷链市场中相关企业规模小集中度差、冷链需求和资源碎片化现象严重,冷链运输多为小批量多批次。所以相关人员规划冷链物流网络时可根据网络覆盖范围以及冷链中小企业的需求特点等进行整个网络的优化。
| δ | λ | β | 枢纽点数目 | 枢纽点 | 目标值/百万元 |
| 1 | 0.85 | 1 | 1 | 2 | 15.33 |
| 1 | 0.85 | 1 | 2 | 2, 4 | 10.92 |
| 1 | 0.85 | 1 | 3 | 2, 3, 4 | 10.69 |
| 1 | 0.85 | 1 | 4 | 2, 3, 4, 8 | 9.662 |
| 1 | 0.85 | 1 | 5 | 2, 3, 4, 5, 8 | 16.96 |
试验结果3中表 7得不论冷链配送中心个数如何变化,一些节点总是被选择成为冷链配送中心,例如节点4。可能原因是节点的地理位置处于整个冷链物流轴辐式网络的中间地带,以便服务更多的需求点,配送时可以减少运输距离,生鲜品新鲜度损失率降低,且经济规模效应更为明显,因此降低总成本;该试验结果可启示冷链物流网络设计者在固有的冷链物流网络基础上优化冷链配送中心位置及需求点的分配关系,可减少价格昂贵的冷链配送中心的重复建设,对于整个冷链物流网络总成本降低具有重要意义。
3 结论针对冷链物流网络优化问题,构建了以时效最优,成本最低的基于轴辐式理论的冷链物流网络模型。
(1) 由于冷链物流企业规模小和集中度差、冷链需求和资源碎片化现象严重和冷链运输多为小批量多批次,导致整个冷链物流市场运营成本高。而本研究提出的基于新鲜度的冷链物流轴辐式网络在保持易腐品新鲜度最大情况下利于冷链需求和资源集中化,运输网络高效化和低成本化。结果表明冷链物流轴辐式网络相对冷链物流传统直通式网络更有优势。
(2) 相对于冷链物流传统网络,冷链物流轴辐式网络中枢纽点的转运会导致生鲜品货损成本增加。而文中通过枢纽点个数的优化,证明干线运输的规模效应下总体的运输经济效益仍为最大化,为冷链物流运输决策者网络设计提供一定的参考,且该网络利于冷链物流中小企业合作,共同配送达到利益最大化。
(3) 针对冷链物流网络规模小的模型采用CPLEX商业软件,大规模采用基于优先权重的粒子群算法,为冷链物流网络设计者提供技术支持。
(4) 未来研究方向:①有关冷链新鲜度函数的参数的设定有待商榷,对于货损成本函数的研究未来仍将继续深入;②针对生鲜品具有高损耗的特点,未来将继续研究冷链混合轴辐式网络结构,允许生鲜品需求量较大的起始节点采用直达运输,减少行驶距离和装卸费用;③对于大规模的求解算法进一步地深入研究。
| [1] |
袁群, 左奕. 基于改进混合遗传算法的冷链物流配送中心选址优化[J]. 上海交通大学学报, 2016, 50(11): 1795-1800. YUAN Qun, ZUO Yi. Selection of Cold Chain Logistics Distribution Center Location Based on Improved Hybrid Genetic Algorithm[J]. Journal of Shanghai Jiaotong University, 2016, 50(11): 1795-1800. |
| [2] |
杨晓芳, 姚宇, 付强. 基于新鲜度的冷链物流配送多目标优化模型[J]. 计算机应用研究, 2016, 33(4): 1050-1053, 1074. YANG Xiao-fang, YAO Yu, FU Qiang. Multi-objective Optimization Model of Cold Chain Logistics Distribution Based on Freshness[J]. Application Research of Computers, 2016, 33(4): 1050-1053, 1074. |
| [3] |
杨华龙, 计莹峰, 刘斐斐. 生鲜农产品物流网络节点布局优化[J]. 大连海事大学学报, 2010, 36(3): 47-49. YANG Hua-long, JI Ying-feng, LIU Fei-fei. Layout Optimization of Logistics Network Nodes for Fresh Agricultural Products[J]. Journal of Dalian Maritime University, 2010, 36(3): 47-49. |
| [4] |
SONG B D, KO Y D. A Vehicle Routing Problem of Both Refrigerated-and General-type Vehicles for Perishable Food Products Delivery[J]. Journal of Food Engineering, 2016, 169: 61-71. |
| [5] |
HAIJEMA R. A New Class of Stock-level Dependent Ordering Policies for Perishables with a Short Maximum Shelf Life[J]. International Journal of Production Economics, 2013, 143(2): 434-439. |
| [6] |
KUO J C, CHEN M C. Developing an Advanced Multi-temperature Joint Distribution System for the Food Cold Chain[J]. Food Control, 2010, 21(4): 559-566. |
| [7] |
LVTJEN M, DITTMER P, VEIGT M. Quality Driven Distribution of Intelligent Containers in Cold Chain Logistics Networks[J]. Production Engineering, 2013, 7(2/3): 291-297. |
| [8] |
HASANI A, ZEGORDI S H, NIKBAKHSH E. Robust Closed-loop Supply Chainnetwork Design for Perishable Goods in Agile Manufacturing under Uncertainty[J]. International Journal of Production Research, 2012, 50(16): 4649-4669. |
| [9] |
尚成国, 来瑶媛. 电子商务下生鲜农产品物流鲁棒性的网络设计[J]. 经济问题, 2015(12): 99-102. SHANG Cheng-guo, LAI Yao-yuan. The Network Design of Fresh Agricultural Products Logistics Robustness under Electronic Commerce[J]. On Economic Problems, 2015(12): 99-102. |
| [10] |
梁海红. "互联网+"时代物流配送中心选址优化模型构建[J]. 统计与决策, 2016(22): 51-53. LIANG Hai-hong. Optimization Modeling for"Internet+"Era Logistics Distribution Center Location[J]. Statistics and Decision, 2016(22): 51-53. |
| [11] |
ALUMUR S A, NICKEL S, SALDANHA-DA-GAMA F. Hub Location under Uncertainty[J]. Transportation Research Part B:Methodological, 2012, 46(4): 529-543. |
| [12] |
傅少川, 胡梦飞, 唐方成. 禁忌搜索算法在单分配多枢纽轴辐式物流网络中的应用[J]. 中国管理科学, 2012, 20(3): 145-151. FU Shao-chuan, HU Meng-fei, TANG Fang-cheng. The Optimization of Hub and Spoke Logistics Network Design Based on Tabu Search Algorithm[J]. Chinese Journal of Management Science, 2012, 20(3): 145-151. |
| [13] |
杨斌, 邓志慧, 胡志华. 考虑Hub网络拥堵的轴辐式网络优化[J]. 重庆交通大学学报:自然科学版, 2016, 35(1): 138-144. YANG Bin, DENG Zhi-hui, HU Zhi-hua. Hub and Spoke Network Optimization Based on Hub Network Congestion[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2016, 35(1): 138-144. |
| [14] |
李莉, 丁以中. 轴辐式快递网络的枢纽选址和分配优化[J]. 上海海事大学学报, 2012, 33(2): 33-39, 75. LI Li, DING Yi-zhong. Optimization of Hub Location and Allocation for Hub-spoke Express Delivery Network[J]. Journal of Shanghai Maritime University, 2012, 33(2): 33-39, 75. |
| [15] |
王雁凤, 黄有方. 大规模零担物流轴辐式网络决策优化[J]. 华中师范大学学报:自然科学版, 2016, 50(4): 530-535. WANG Yan-feng, HUANG You-fang. Optimization for Large-scale LTL Logistics Hub-and-spoke Network[J]. Journal of Central China Normal University:Natural Science Edition, 2016, 50(4): 530-535. |
| [16] |
SAHUGUET N, WALCKIERS A. A Theory of Hub-and-spoke Collusion[J]. International Journal of Industrial Organization, 2017, 53: 353-370. |
| [17] |
OSVALD A, STIRN L Z. A Vehicle Routing Algorithm for the Distribution of Fresh Vegetables and Similar Perishable Food[J]. Journal of Food Engineering, 2008, 85(2): 285-295. |
| [18] |
张建, 傅少川.新鲜度影响需求的生鲜食品配送中心选址研究[C]//中国优选法统筹法与经济数学研究会会议论文集.北京: 《中国管理科学》编辑部, 2011: 473-476. ZHANG Jian, FU Shao-chuan. Study on Location of Fresh Food Distribution Center with Demand Influenced by Freshness[C]//Conference of Chinese Society of Optimization, Overall Planning and Economic Mathematics. Beijing: Editorial Department of Chinese Journal of Management Science, 2011: 473-476. |
 2019, Vol. 36
2019, Vol. 36
