扩展功能
文章信息
- 王淑云, 马文秀
- WANG Shu-yun, MA Wen-xiu
- 基于保鲜努力的生鲜农产品库存和协调优化
- Fresh Agricultural Products Inventory and Coordinative Optimization Based on Fresh Keeping Effort
- 公路交通科技, 2019, 36(6): 125-134
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(6): 125-134
- 10.3969/j.issn.1002-0268.2019.06.016
-
文章历史
- 收稿日期: 2018-11-02
近年来,生鲜农产品在居民生活中的比重不断攀升,与此同时,社会公众的消费安全意识也趋于增强,对我国生鲜农产品的冷链物流运作提出了更高挑战。生鲜农产品作为一类特殊的变质产品,在采摘后仍具有持续的易腐易损性[1]。这种特性不仅体现在流通过程中因装卸操作不规范,湿度、温度控制不合理等造成的数量损耗,也体现在质量上的损耗,如:果蔬打蔫、脱水等,会同时带来数量损耗及质量下降,进而影响销售量及销售收益。因此,在平衡物流成本的情况下,供应链成员投入适当的保鲜成本以控制数量、质量的双重损耗,对生鲜农产品供应链的有效管理具有重要意义。
国内外关于生鲜农产品的研究主要集中在库存与定价管理、供应链协调两方面,但对腐损控制的考虑通常只涉及数量或质量损耗的某一方面。Hsu等[2]首先研究了保鲜投入对降低产品腐败率的易腐产品库存模型,文中假设保鲜投入所减缓的腐败率服从负指数分布,在固定需求环境下讨论了单级易腐品最优补货周期、补货量及保鲜投入的最优决策问题。Dye和Hsieh[3]对易腐品腐败率的假设与Hsu等[2]基本一致,只是假设基础变质率为线性时变函数,研究了允许部分短缺情形下的库存模型。Mishra[4]在两参数Weibull函数的基础上引入保鲜投入刻画变质率函数,在允许库存短缺的条件下以总成本最小化寻求最佳库存策略。Dye和Yang[5]研究的则是非即可变质情形,将市场需求视为售价、消费者参考价格和时间的函数,以利润最大化为目标寻求最优定价、保鲜投入及补货策略。杨磊等[6]侧重于比较分析集中决策与独立决策两种模式下的定价策略与系统利润,其中,变质率为保鲜努力的减函数,数据分析表明,保鲜努力的付出对于供应链利润的提高有着至关重要的作用。在质量控制方面,Rong等[7]重点考虑了质量控制对易腐品生产与配送决策的影响,研究表明质量控制对短生命周期的产品运营具有很强的借鉴意义。王磊和但斌[8-9]基于消费者效应的视角,构建了受保鲜努力影响的线性新鲜度函数,并分别考虑了供应商、零售商保鲜投资时的库存策略。Chen等[10]则构建了保鲜投入呈负指数分布的质量损耗函数,对供应链系统的动态定价和库存决策问题进行了联合求解。陈奕娟等[11]研究了需求受新鲜度影响的生鲜食品动态定价模型,并证明了动态定价时的利润优于单一定价。
事实上,在生鲜农产品的流通过程中,数量损耗与质量损耗是共存的,其均会对系统决策产生不同程度的影响。现有研究中,少数文献同时考虑了保鲜投入对数量损耗与质量损耗的影响。如Qin等[12]、Cai和Chen等[13]在此基础上分别研究了单级、两级供应链系统下保鲜和库存策略的联合决策问题,其中,Qin等[12]在生鲜品的单周期库存系统中引入两参数Weibull函数用以表示其数量与品质变化,Cai和Chen等[13]则分别构建了易腐品新鲜度与生存函数。马雪丽、王淑云等[14]对三级冷链模式下的库存策略进行了研究,考虑了包含第三方物流提供商的三级供应链系统的协调优化,设计了“成本共担+收益共享”协调机制,其中,变质率与新鲜度函数分别设为数量弹性、质量弹性的函数。
对于生鲜农产品供应链的协调问题,现有文献已做了大量研究,所采用的契约机制主要有收益共享[15-17]、回购契约[18]、数量折扣[19]、收益共享与成本共担的组合契约[20]等。其中,林略、杨书萍等[15]引入库存因子对鲜活农产品三级供应链进行了收益再分配,结果表明收益共享契约参数在一定范围内可有效实现三方共赢。Xiao等[16]研究了产品质量、服务质量、售价共同影响市场需求时的供应链最优服务和价格联合决策模型,并设计了收益共享契约以实现系统最优。Zhang等[20]在考虑供应双方均进行保鲜成本分担的情形中,针对零售商利润受损问题,进一步结合收益共享契约对分散型供应链进行了优化协调。
上述文献为生鲜农产品库存、定价决策及供应链的协调优化研究提供了很好的借鉴与参考,但对数量或质量腐损控制多进行的是单独研究,且忽略了时间因素。本研究与以往研究的区别在于,一是,考虑了生鲜农产品的“双重损耗”并突出质量下降与数量变化之间的内在联系,且同时引入保鲜努力与时间因素对数量损耗进行刻画;二是,综合考虑了价格与质量水平对市场需求的影响。鉴于此,本研究从腐损保鲜的视角出发,构建供应双方均实施保鲜投资情形下的二级冷链库存模型,以利润最大化为决策依据研究集中决策与分散决策两种模式下的库存与定价联合决策,并基于系统利润最优建立有效协调分散型供应链的收益共享契约模型,以期为冷链的协同与优化研究提供理论和方法支持。
1 问题描述 1.1 研究问题本文研究有限期内,一个生产商与一个零售商组成的两级供应链系统销售单品种生鲜农产品的情形。对于生鲜农产品而言,在仓储及销售过程中存在着质量和数量的“双重损耗”,为减缓产品新鲜度的下降速率、降低数量损耗,供应链各节点企业有必要投入适量的保鲜成本。因此,为了刻画保鲜努力对生鲜农产品质变损耗的影响,借鉴Hsu[2]等对保鲜投入下产品数量损耗的研究,用函数θ(u)=θ0·e-ηu表示质量损耗率。其中,θ0为无冷链投资时商品品质下降的速率,0 < θ0 < 1;u为保鲜努力,0 < u < 1,随保鲜努力的增加商品品质下降速率得以减缓,即满足θ(u)′ < 0, 且θ(u)″>0,是一个减速递减过程,符合投资的边际递减规律,契合生鲜农产品的保鲜和变质特性;η>0为保鲜努力对质量损耗率的敏感因子;由数量损耗的函数可知,0 < θ < θ0,当θ≈0时,商品品质几乎不发生下降,θ≈1时,商品整体品质100%发生腐坏。
事实上,生鲜农产品的数量损耗速率会随质量损耗速率的增加而增加,即二者存在同向变化关系,此外,即便投资水平一定,商品的数量损耗依然会随着仓储时间的延长而逐渐递增。因此,充分考虑商品数量损耗与质量损耗的内在关系,并将时间因素纳入数量损耗的函数之中,将其设定为:λ(θ, t)=ln[θ(u)+1](α+βt),且满足0 < ln[θ(u)+1] < 1,其中α>0,β < 1为数量损耗的时间敏感因子。因数量损耗率是质量损耗率的增函数(保鲜努力u的减函数),同时又是时间的增函数,故函数假设与实际情况相符。保鲜需要一定的冷链投资成本,投资成本函数为:C(u)=1/2ρ·u2,其中ρ>0表示保鲜努力对冷链投资成本的敏感系数,ρ越大意味着相同保鲜努力需要的成本越高,并且C(u)满足C′(u)>0,C″(u)>0,即边际成本也呈增加的趋势。
生鲜农产品是生活必需品,在不发生突变事件的情况下,需求比较稳定,主要受新鲜度和价格的影响。参考文献[6], 以乘积形式的需求函数刻画这种市场特征,即:d(p, θ)=-ln[θ(u)](a-bp),其中p为单位商品售价,a>0表示商品在不受质量损耗率和价格影响下的最大需求率,b>1为需求价格弹性。由需求率函数可知,市场需求与价格、质量损耗率成反比,且当质量损耗率θ(u)趋于1时,无论价格如何调整,市场需求均为0,这些均与实际情况一致。
1.2 模型假设(1) 在一个供应商与一个零售商组成的两级冷链系统中,供应商只通过零售商向最终消费者销售生鲜农产品。
(2) 供应商处于市场主导地位,且为了产品保鲜,供应双方各自进行保鲜投资。
(3) 不考虑零售商缺货情形,系统瞬时补货,不考虑提前期,同时由于生鲜农产品具有时鲜性与易变质性,不允许退货。
(4) 假设供应链成员之间不存在信息不对称的情形,并且参与者都是风险中性的,决策双方绝对理性。
(5) 系统中不考虑打折销售的情况。
1.3 符号说明模型中的其他符号及定义见表 1。
| w | 供应商对零售商的单位产品批发价格 |
| q | 供应商的生产速率 |
| cp | 供应商的单位产品生产成本 |
| Km | 供应商的单次批量生产准备成本 |
| Kr | 零售商的单次批量订购成本 |
| hr,hm | 零售商、供应商的单位产品库存保管成本 |
| cdr,cdm | 零售商、供应商的单位产品量变损耗处理成本 |
| θ0r,θ0m | 零售商、供应商未采取保鲜投入时的产品质变损耗率 |
| ur,um | 零售商、供应商的保鲜努力水平 |
| ηr,ηm | 零售商、供应商的保鲜投资敏感系数 |
| βr,βm | 零售商、供应商处量变损耗率的时间敏感系数 |
| αr, αm | 零售商、供应商处产品的初始变质率 |
| λr(θr, t), λm(θm, t) | 零售商、供应商的产品量变损耗率 |
| θr(ur), θm(um) | 零售商、供应商的产品质变损耗率 |
| Ir(t),Im(t) | 零售商、供应商t时刻的库存水平 |
| ϕ | 零售商处的销售收入分享给供应商的比例,且满足0 < ϕ < 1 |
| Qrk | 零售商在模式k(I, D, C)下的单个周期订购量,I, D, C分别表示一体化决策、分散决策、基于收益共享的供应链协调优化决策 |
| Πik | 供应链成员i(sc, m, r)在模式k(I, D, C)下的周期总利润,sc, m, r分别表示供应链整体、供应商、零售商 |
2 模型构建 2.1 零售商库存模型
零售商的补货周期为T,在t=0的时刻,库存水平为初始订购量Q,以一个周期[0, T]内的库存变化为例,对其进行成本收益分析。生鲜农产品到达零售商处开始销售,其库存水平同时受到消费者需求与商品变质的影响,该过程可用微分方程表示:
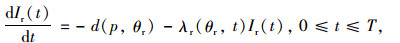
|
(1) |
其中,λr(θr, t)=ln[θ0r·e-ηrur+1](αr+βrt)。
方程满足临界条件Ir(T)=0,通过求解微分方程,可得到: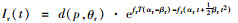
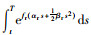
据此可得出零售商的期初库存量,即单次补货量:
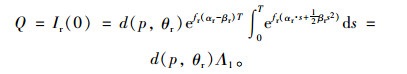
|
(2) |
零售商在一个补货间隔期内的总成本包括订货处理成本、采购成本、库存持有成本、量变损耗处理成本、保鲜投入成本,其具体核算如下:
量变损耗处理成本为:Cdr=cdr(Q-D),D=d(p, θr)T为周期内的市场总需求量;
库存持有成本为:Hr=hr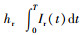
其中,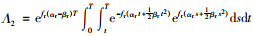
故零售商在某一个周期内的利润函数为:
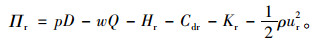
|
(3) |
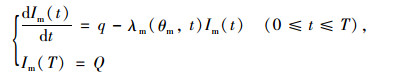
|
(4) |
式中,λm(θm, t)=ln[θ0m·e-ηmum+1](αm+βmt)。
求解微分方程,可得供应商t时刻的库存水平:
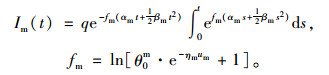
|
最优生产速率:
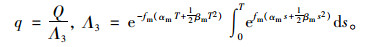
|
供应商单个生产周期T内的库存总量为:Gm=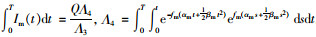
供应商在单个周期内的总成本包括生产准备成本、生产成本、库存持有成本、量变损耗处理成本与保鲜投入成本,其具体核算如下:
量变损耗处理成本为:Cdm=cdm(qT-Q);
库存持有成本为: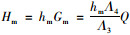
故供应商在某一周期内的利润函数为:
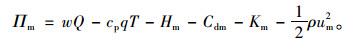
|
(5) |
因此,单位周期内供应链总利润函数为:
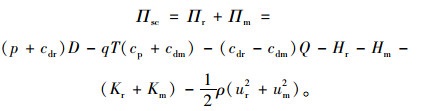
|
(6) |
分散决策下,供应商与零售商之间的交易为动态博弈过程,二者同样作为理性决策者追求各自利润最大化。运用逆序求解法,首先对零售商单个订货周期内的利润函数式(3)求解关于p的一阶导数并令其等于零,整理可得:
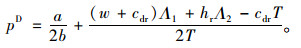
|
(7) |
将式(7)代入供应商的利润函数式(5)中,分别求解关于批发价格w的一阶与二阶导数:
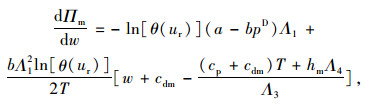
|
(8) |
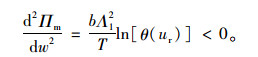
|
(9) |
由式(9)可知,供应商的利润函数是批发价格的上凸函数。根据其一阶导数等于0,即可得最优批发价格wD*为:
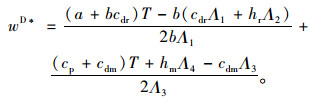
|
(10) |
将wD*代入式(7)可得分散决策下零售商的最优销售价格为:
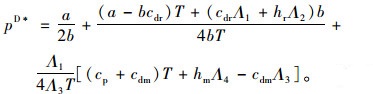
|
(11) |
定理1:当零售商的定价是其利润最大化时的最优定价,其订货量是经济订货批量。
证明:在利润最大化原则下,零售商的经济订货批量Q*为利润函数关于Q的一阶导数为零时的取值。由式(2)可知,Q是p的函数,在推导最优价格时可进行如下变换:
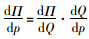
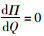
因此,依据定理1,将pD*代入式(2)中可得零售商在一个订货周期内的经济批量QD*。同理,将wD*, pD*分别代入式(3)与式(5)中,即为分散决策下零售商与供应商在单位周期内的最优利润值ΠrD*与ΠmD*。
3.2 集中决策模式分析在集中决策下,供应商与零售商作为利益共同体统一进行决策,不考虑供应链成员间的转移支付,以系统整体利润最大化寻求最优的售价、订货量。因此,对供应链总利润函数式(6)求解关于销售价格p的一阶和二阶导数:
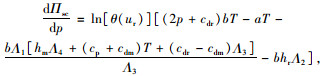
|
(12) |
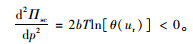
|
(13) |
由式(13)可知,供应链总利润是销售价格的上凸函数。根据其一阶导数等于0,即可得集中决策下零售商的最优销售价格为:
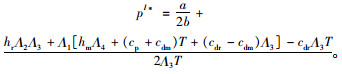
|
(14) |
将其分别代入式(2)、式(6)中,即可得一体化决策下的最优订货量QI*及系统最优利润ΠscI*。
命题1:生鲜农产品的集中决策售价低于分散决策下的售价,集中决策订货量高于分散决策下的订货量,且供应链的集中决策系统总利润高于分散决策下的系统总利润,即pI* < pD*, QI*>QD*, Πsc(pI*)>Πsc(pD*)。
证明:Δp=pD*-pI*=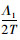
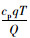
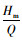
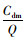
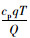
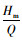
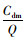
另,Q=d(p, θr)Λ1=-ln[θ(ur)](a-bp)Λ1,已知pI* < pD*,故QI*>QD*。此外,系统利润函数Πsc=Πr(p)+Πm(p),pI*为一元上凸函数Πsc的最优解,pD*为一元上凸函数Πsc的可行解,且存在pI* < pD*,所以必然有Πsc(pI*)>Πsc(pD*)。故,命题1得证。
命题1表明,集中决策与分散决策相比,零售商趋于降低销售价格,提升单次补货量/降低订货频率,并使得系统利润最优。因此,欲使分散状态下的系统决策及利润达到集中决策时的水平,供应商需适当降低批发价格,但若无契约激励机制,供应商不会单方面将批发价格降至一体化最优时的水平。因此,供应链系统需要设计有效的契约激励机制,对分散决策下各自的收益进行有效协调。
3.3 收益共享协调契约为了使分散型供应链达到有效协调,系统引入收益共享契约。该契约通过设定供应商的批发价格w、收入分享比例ϕ,对双方利润进行再分配,其实质是通过供应商降低批发价格的行为刺激零售商订购有利于供应链总收益的补货量,同时要求以一定比例分享零售商的销售收入,从而在保证双方利润的同时也达到系统最优。
命题2:当供应商给零售商的批发价格wc(wc* < wD*)满足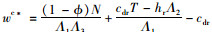
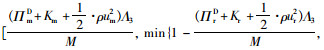
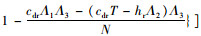
证明:(1)根据收益共享契约,供应商与零售商协调后的利润函数如下:
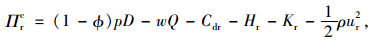
|
(15) |
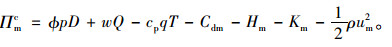
|
(16) |
由于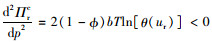
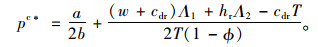
|
(17) |
① 渠道协调条件
根据收益共享契约的协调要求可知,供应链各节点成员必须采取与一体化最优决策相一致的策略,即满足渠道协调条件pc*=pI*。因此,可得到:
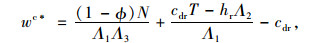
|
(18) |
式中,N=hrΛ2Λ3+Λ1[hmΛ4+(cp+cdm)T+(cdr-cdm)Λ3]-cdrΛ3T,由式(18)可以看出,零售商分配给供应商的收入比例系数ϕ越高,则供应商给予的批发价折扣越大,w越低。
因供应商处的批发价格必须满足wc*≥0,可得:
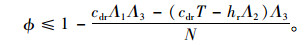
|
(19) |
② 利润分配条件
为了使系统各成员发达到一体化决策时的纳什均衡状态,协调后的各成员利润除了满足上述参与约束原则外,必须同时满足激励相容原则,即协调后的各方利润应不小于其独立决策时的利润。因此,须满足Πrc*≥ΠrD*, Πmc*≥ΠmD*,将pc*,wc*,ΠscI*分别代入式(15)与式(16)中,可得协调后的零售商与供应商利润函数为:
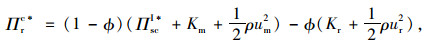
|
(20) |
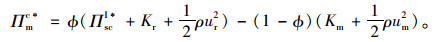
|
(21) |
由上式可知,契约协调后的供应链各方利润函数为系统最优利润的仿射函数,且Πrc*+Πmc*=ΠscI*,即协调后的各方利润不会造成系统最优利润的减少。
将其与独立决策时的利润函数相比可以得到:
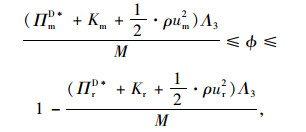
|
式中,M=-ln[θ(ur)](a-bpI*)(Λ3pI*T-N)。结合式(19)即可得ϕ的取值范围。
(2) 另外,要证wc* < wD*,只需证ϕ>1-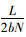
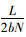
综上,命题2得证。其表明,收益共享参数在一定范围内取值时,能够实现分散型供应链的协调与优化,但具体取值范围则取决于双方的领导地位、讨价还价能力及其他影响因素。在后续灵敏度分析部分,将具体探讨相关系统参数变动对协调方案的影响。
4 算例及灵敏度分析 4.1 算例数据及结果分析为验证模型的合理性及协调契约的有效性,利用MATLAB工具进行数值仿真计算,并进一步探讨相关参数变化对系统利润、最优决策及收益共享参数的影响。参考Dye等[5]、Zhang等[20],部分参数取值为:T=2, ρ=1 600,其他相关参数赋值详见表 2、表 3。
| θ0m | ηm | αm | βm | cp | Km | um | hm | cdm |
| 0.2 | 3.5 | 0.2 | 0.1 | $10 | $80 | 0.35 | $3 | $1 |
| θ0r | ηr | αr | βr | a | b | Kr | ur | hr | cdr |
| 0.4 | 3 | 0.25 | 0.15 | 450 | 5 | $50 | 0.7 | $5 | $1.5 |
将上述参数代入模型中,通过计算,可分别得到集中决策与分散决策两种模式下的供应链最优决策与利润, 见表 4。
| p* | w* | Q* | Πr* | Πm* | Πsc* | |
| 集中决策 | 54.370 | — | 1 103 | — | — | 37 671 |
| 分散决策 | 72.185 | 47.937 | 551.705 | 9 131 | 18 968 | 28 099 |
通过对比两种决策模式下的最优策略与利润发现,集中决策下产品销售价格为$54.370,较分散决策低了25%,同时,订购量提高了近一倍,供应链总利润也提升了34%,再一次验证了命题1的结论。这是因为,一体化决策环境下,价格的降低会刺激更多的消费者参与购买,而市场需求的大幅激增也会促使零售商提高订购量,从而使得系统获得更多的收益。与此同时,消费者也能从降价中获得更多的消费者剩余。这也表明,一体化决策不仅有利于增加生鲜农产品的订单量/加快流通速率、提升系统总利润,也有利于实现更多的消费者福利,提升顾客满意度。
4.2 系统参数灵敏度分析由于生鲜农产品的特殊性,新鲜度是影响市场需求的重要因素之一,保鲜努力水平的增加,一方面减少了产品流通过程中的数量损耗,降低了成本,另一方面也会因为新鲜度的保证而增加市场需求,此外,价格弹性因子也会对系统决策及利润产生不同程度的影响。这两个参数对系统决策及利润影响的灵敏度分析如表 5所示。
| 参数变量 | pI* | pD* | wD* | QD* | QI* | ΠmD* | ΠrD* | ΠscD* | ΠscI* | |
| ur | -30% | 54.589 | 72.294 | 46.965 | 443.547 | 887.1 | 14 783 | 7 239 | 22 022 | 29 503 |
| -20% | 54.501 | 72.250 | 47.352 | 479.490 | 959.0 | 16 181 | 7 879 | 24 060 | 32 240 | |
| -10% | 54.429 | 72.214 | 47.672 | 515.534 | 1 031.1 | 17 576 | 8 510 | 26 086 | 34 963 | |
| +10% | 54.323 | 72.161 | 48.154 | 588.012 | 1 176.0 | 20 355 | 9 743 | 30 098 | 40 365 | |
| +20% | 54.284 | 72.142 | 48.332 | 624.458 | 1 248.9 | 21 739 | 10 345 | 32 084 | 43 043 | |
| +30% | 54.252 | 72.126 | 48.478 | 661.041 | 1 322.1 | 23 120 | 10 936 | 34 056 | 45 705 | |
| b | -30% | 73.656 | 101.114 | 66.720 | 595.232 | 1 190.5 | 31 659 | 15 477 | 47 136 | 63 054 |
| -20% | 65.620 | 89.060 | 58.894 | 580.723 | 1 161.4 | 26 338 | 12 816 | 39 154 | 52 412 | |
| -10% | 59.370 | 79.685 | 52.806 | 566.214 | 1 132.4 | 22 229 | 10 761 | 32 990 | 44 193 | |
| +10% | 50.279 | 66.049 | 43.952 | 537.195 | 1 074.4 | 16 324 | 7 809 | 24 133 | 32 384 | |
| +20% | 46.870 | 60.935 | 40.632 | 522.686 | 1 045.4 | 14 143 | 6 718 | 20 861 | 28 021 | |
| +30% | 43.986 | 56.608 | 37.822 | 508.177 | 1 016.4 | 12 317 | 5 806 | 18 123 | 24 371 | |
(1) 保鲜投入水平ur的灵敏度分析
大型、规范化的供应商一般都设有冷库、冷藏车等保鲜设施,以满足生产和销售需要。为此,这里仅对零售商处的保鲜投入进行灵敏度分析。分析发现,无论是分散决策还是一体化决策模式,零售商保鲜投入水平的变化均会引发订货量和各方利润较大幅度的同向变化,如ur增幅30%时,订货量和各方利润提升了20%左右。同时还可发现,价格是随之小幅反向波动的。事实上,保鲜投入的增加,价格略有下降,主要是由于保鲜努力的投入使得产品品质有了保证,可以吸引更多的顾客消费量。即在产品新鲜度得到保障的前提下,价格的略微降低会较大幅度地引发市场需求的增加,零售商采取走量的形式更能使得供应链双方及系统获得更多利润。
由此可见,作为销售终端,零售商在保鲜投入上扮演着非常重要的角色。因此,欲使供应链整体绩效达到最优,关键在于提高零售商处的保鲜努力水平,增强其保鲜动力,比如,可以通过供应商的回购策略、保鲜成本分担等方式提高零售商的保鲜意愿。
(2) 价格弹性因子b的灵敏度分析
表 5中的数据展示了价格弹性因子b的变动对系统决策及利润的影响。对比分析发现,市场需求对价格越敏感,供应商与零售商的售价、补货量以及利润越低,其中,订货量Q随价格弹性因子的增大呈小幅下降趋势,价格和利润则发生更大程度的反向波动。如b上浮20%时,补货量的下降比率为5%左右,价格和利润的下降比率则分别达到了15%与25%左右。其主要原因在于:价格弹性的增强会直接引发需求对新鲜度依赖程度的减弱,为避免需求的快速下降,此时零售商会被迫通过调低售价的方式以减少利润损失。即消费者对价格较敏感时,进行适当的降价促销活动反而会获得更多利润,因此,对于生鲜农产品市场的零售商而言,必须充分了解消费者的消费偏好,根据不同情形制定不同的定价策略。此时,还可发现,随价格弹性b的增加,分散决策的效率(ΠscD*/ΠscI*)有所降低。
4.3 协调契约的灵敏度分析(1) 协调因子ϕ的变动对供应双方各自利润的影响
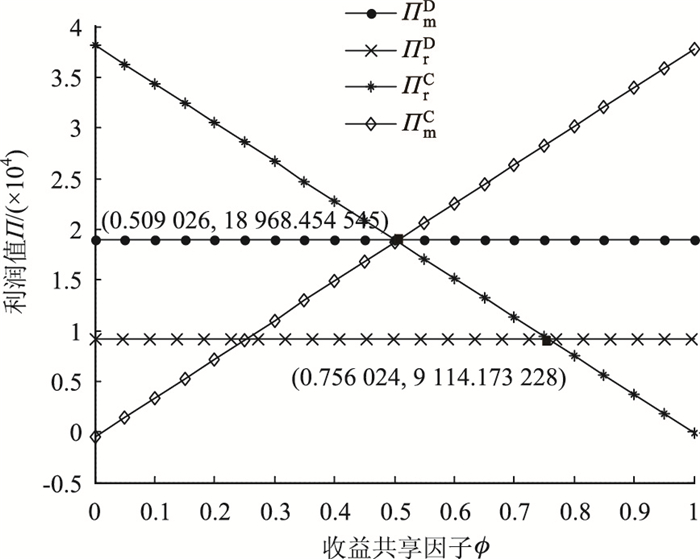
本文构建的收益共享契约以一体化利润为标杆,对分散型供应链进行了优化协调,旨在既实现系统利润的最大化,又确保各自利润不低于独立决策情形。在不同的协调因子ϕ下,其利润协调结果是不同的,各自获得利润的具体情况如图 1所示。
|
| 图 1 协调因子ϕ的取值范围 Fig. 1 Range of coordination factor ϕ |
| |
由命题2的讨论可知,批发价格与供应商分享所得的销售收入比例之间是线性负相关的。这表明,为采取更有利于一体化的定价、订购策略,供应商可以通过控制批发价格的大小调整契约协调因子,反之,零售商也可以通过设定契约参数的取值调节供应商的批发价格。但为使供应双方自觉参与契约协调,此时各自利润都要不低于其独立决策时的取值,即满足v∈[0.509 0, 0.756 0]。
对于生鲜农产品而言,新鲜度是其区别于一般产品的显著特征,不同的腐损特征与保鲜效果均会引起市场需求与价格的波动,进而影响系统收益,并对供应链协调方案产生不同程度的影响。因此,针对零售商的质变损耗率、保鲜投入敏感因子作简要的灵敏度分析。
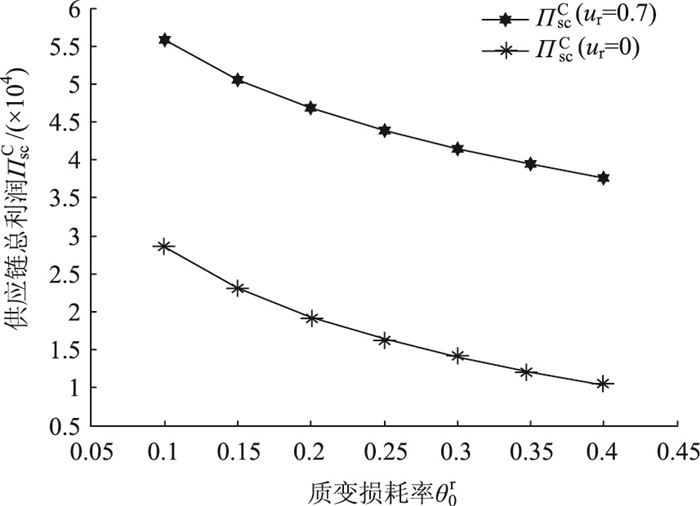
(2) 质变损耗率θ0r的变动对协调方案及系统利润的影响
已知θ0r为零售商未保鲜情形下的质量腐损率,如果该值较大,显然不利于销售。因此,本文仅对低于基础θ0r值做灵敏度分析。分析发现,契约协调因子ϕmin, ϕmax随质变损耗率的下降未发生明显变化,其值大约稳定在[0.50, 0.75]左右。但观察图 2可知,质变损耗率θ0r的降低却会引起系统总利润的大幅提升,如θ0r降低至原来的50%时,系统利润提升约24%;同时,对比零售商进行保鲜投入与未进行保鲜投入两种情形下的系统总利润发现,零售终端的保鲜投入显然能够较大程度地增加系统总利润。这说明,在本文假设条件下,生鲜农产品的易腐属性虽不会对协调方案产生较大影响,但其易腐性越强,一体化总利润越低。此外,除特殊情形,对于一般的生鲜农产品,不论其易腐属性如何,零售商都有必要进行适度的保鲜努力投入。
|
| 图 2 θ0r对协调契约下系统总利润的影响 Fig. 2 Effect of θ0r on total profit of system under coordination contract |
| |
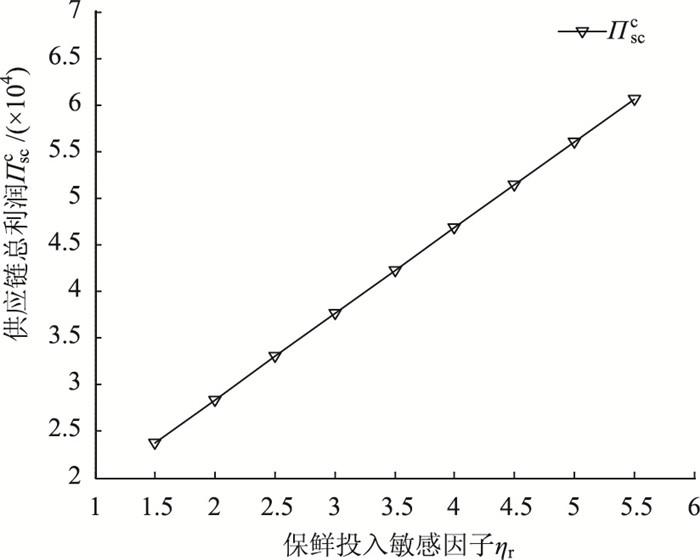
(3) 零售商保鲜投入敏感因子ηr的变动对协调方案及系统利润的影响
通过对ηr的灵敏度分析发现,契约协调因子ϕ的空间大小不会发生明显波动,其取值范围为[0.499 0, 0.751 3]。另外,观察图 3可知,提高保鲜技术的保鲜敏感度显然能明显改善供应链的整体绩效水平,如ηr增加一倍时,整体绩效提升率为56%左右。其表明,ηr的变动虽不会对契约协调方案产生太大影响,但若保鲜投入敏感因子越大即保鲜技术对生鲜农产品的保质保鲜水平越高,系统总利润则越大。因此,生鲜农产品供应链应加大对保鲜技术的研发力度,不断提高技术的成熟度/有效性,如:加强冰温、气调保鲜、超高压保鲜、生物保鲜剂、低剂量辐射保鲜等各种保鲜技术与新型包装的复合研究与应用。
|
| 图 3 ηr对协调契约下系统总利润的影响 Fig. 3 Effect of ηr on total profit of system under coordination contract |
| |
综上,无论系统参数(θ0r, ηr)如何变动,收益共享契约协调因子都大致稳定在[0.50, 0.75]范围内。同时,质变损耗率θ0r的降低与保鲜投入敏感因子ηr的提高均有益于系统总利润的提升,且受ηr变动的影响更大。
5 结论本文基于生鲜农产品数量腐损严重以及质量安全问题趋于增强的现实,考虑供应双方均进行保鲜投资以减缓数量与质量“双重折损”的情形,针对集中与分散两种决策模式分别寻求其最优库存与价格联合决策。研究中,充分考虑了时间与质变损耗对量变损耗的综合影响,除价格影响因素外,在需求函数构建中同时引入质变损耗,使得模型更符合实际。研究结论如下:(1)集中决策环境下较分散决策,产品售价更低、订货量更高,同时系统总利润也更优。这表明生鲜农产品供应链一体化运作不仅有利于加快产品流通速率,增强冷链系统的获利能力,还有助于实现更多消费者福利。(2)以一体化利润为标杆,收益共享契约既可以实现系统利润的最大化,又可以实现合作双赢。同时,通过契约协调因子的灵敏度分析发现,ϕ∈[0.509 0, 0.758 0]时,即可达到有效协调分散型供应链的目的。(3)灵敏度分析还发现,提高零售商处的保鲜努力对提升供应链双方及系统利润的提升均有显著成效。因此,对于生鲜农产品供应链而言,增强系统效益的关键在于增强零售商的保鲜动力。(4)对生鲜农产品市场的零售商而言,必须充分了解消费者的消费偏好,根据不同情形制定不同的定价策略。当消费者对价格较敏感时,进行适当的降价促销活动反而会获得更多利润。(5)在本文假设情形下,质变损耗率及保鲜努力敏感因子的变动均不会对协调结果产生较大影响,ϕ值基本稳定在[0.50, 0.75]范围内,但降低质变损耗率及提高保鲜努力敏感因子则会增加供应链系统的总利润。
本研究主要考虑了单一协调契约下的供应链协调,今后可进一步将其扩展为与成本共担、数量折扣、回购协议等契约相结合的组合契约协调情形。此外,还可依据DC物流配送、增值服务功能日趋增强的实际,构建以DC为中枢的更复杂情况下的多级供应链库存与定价决策模型。
| [1] |
李琳, 范体军. 零售商主导下生鲜农产品供应链的定价策略对比研究[J]. 中国管理科学, 2015, 23(12): 113-123. LI Lin, FAN Ti-jun. Comparison and Analysis on Pricing Policies for Fresh Agricultural Produce Supply Chain with Dominant Retailer[J]. Chinese Journal of Management Science, 2015, 23(12): 113-123. |
| [2] |
HSU P H, WEE H M, TENG H M. Preservation Technology Investment for Deteriorating Inventory[J]. International Journal of Production Economics, 2010, 124(2): 388-394. |
| [3] |
HSIEH T P, DYE C Y. A Production-inventory Model Incorporating the Effect of Preservation Technology Investment When Demand is Fluctuating with Time[J]. Journal of Computational and Applied Mathematics, 2013, 239(1): 25-36. |
| [4] |
MISHRA V K. Deteriorating Inventory Model Using Preservation Technology with Salvage Value and Shortages[J]. Advances in Production Engineering & Management, 2013, 8(3): 185-192. |
| [5] |
DYE C Y, YANG C T, LEV B. Optimal Dynamic Pricing and Preservation Technology Investment for Deteriorating Products with Reference Price Effects[J]. Omega, 2016, 62: 52-67. |
| [6] |
杨磊, 肖小翠, 张智勇. 需求依赖努力水平的生鲜农产品供应链最优定价策略[J]. 系统管理学报, 2017, 26(1): 142-153. YANG Lei, XIAO Xiao-cui, ZHANG Zhi-yong. Optimal Pricing Policies of Fresh Agricultural Product Supply Chain with Effort Level Dependent Demand[J]. Journal of Systems and Management, 2017, 26(1): 142-153. |
| [7] |
RONG A, AKKERMAN R, GRUNOW M. An Optimization Approach for Managing Fresh Food Quality throughout the Supply Chain[J]. International Journal of Production Economics, 2011, 131(1): 421-429. |
| [8] |
王磊, 但斌. 考虑零售商保鲜和消费者效用的生鲜农产品供应链协调[J]. 运筹与管理, 2015, 24(5): 44-51. WANG Lei, DAN Bin. Coordination of Fresh Agricultural Supply Chain Considering Retailer's Freshness-keeping and Consumer Utility[J]. Operations Research and Management Science, 2015, 24(5): 44-51. |
| [9] |
王磊, 但斌. 考虑消费者效用的生鲜农产品供应链保鲜激励机制研究[J]. 管理工程学报, 2015, 29(1): 200-206. WANG Lei, DAN Bin. The Incentive Mechanism for Preservation in Fresh Agricultural Supply Chain Considering Consumer Utility[J]. Journal of Industrial Engineering and Engineering Management, 2015, 29(1): 200-206. |
| [10] |
CHEN J, DONG M, CHEN F F. Joint Decisions of Shipment Consolidation and Dynamic Pricing of Food Supply Chains[J]. Robotics and Computer-Integrated Manufacturing, 2017, 43(2): 135-147. |
| [11] |
陈奕娟, 何利芳, 张诚一. 考虑新鲜度的生鲜食品动态定价模型[J]. 统计与决策, 2016(8): 47-50. CHEN Yi-juan, HE Li-fang, ZHANG Cheng-yi. Dynamic Pricing Model of Fresh Food Considering Freshness[J]. Statistics and Decision, 2016(8): 47-50. |
| [12] |
QIN Y Y, WANG J J, WEI C M. Joint Pricing and Inventory Control for Fresh Produce and Foods with Quality and Physical Quantity Deteriorating Simultaneously[J]. International Journal of Production Economics, 2014, 152(2): 42-48. |
| [13] |
CAI X Q, CHEN J, XIAO Y B, et al. Optimization and Coordination of Fresh Product Supply Chains with Freshness-keeping Effort[J]. Production and Operations Management, 2010, 19(3): 261-278. |
| [14] |
马雪丽, 王淑云, 金辉, 等. 考虑保鲜努力与数量/质量弹性的农产品三级供应链协调优化[J]. 中国管理科学, 2018, 26(2): 175-185. MA Xue-li, WANG Shu-yun, JIN Hui, et al. Coordination and Optimization of Three-echelon Agricultural Product Supply Chain Considering Freshness-keeping Effort and Quantity/Quality Elasticity[J]. Chinese Journal of Management Science, 2018, 26(2): 175-185. |
| [15] |
林略, 杨书萍, 但斌. 收益共享契约下鲜活农产品三级供应链协调[J]. 系统工程学报, 2010, 25(4): 484-491. LIN Lue, YANG Shu-ping, DAN Bin. Three-level Supply Chain Coordination of Fresh and Live Agricultural Products by Revenue-sharing Contracts[J]. Journal of Systems Engineering, 2010, 25(4): 484-491. |
| [16] |
XIAO T J, YANG D Q, SHEN H C. Coordinating a Supply Chain with a Quality Assurance Policy via a Revenue-sharing Contract[J]. International Journal of Production Research, 2011, 49(1): 99-120. |
| [17] |
代建生, 孟卫东. 风险规避下具有促销效应的收益共享契约[J]. 管理科学学报, 2014, 17(5): 25-34. DAI Jian-sheng, MENG Wei-dong. Revenue Sharing Contract for a Risk-averse Supply Chain with Promotional Effect[J]. Journal of Management Science in China, 2014, 17(5): 25-34. |
| [18] |
杨亚, 范体军, 张磊. 新鲜度信息不对称下生鲜农产品供应链协调[J]. 中国管理科学, 2016, 24(9): 147-155. YANG Ya, FAN Ti-jun, ZHANG Lei. Coordination of Fresh Agricultural Supply Chain with Asymmetric Freshness Information[J]. Chinese Journal of Management Science, 2016, 24(9): 147-155. |
| [19] |
吴忠和, 陈宏, 赵千. 时间约束下鲜活农产品供应链应急协调数量折扣契约研究[J]. 运筹与管理, 2014, 23(3): 146-156. WU Zhong-he, CHEN Hong, ZHAO Qian. Supply Chain Disruptions Coordination of Fresh Agricultural Products under Time Constraints with Quantity Discount Contracts[J]. Operations Research and Management Science, 2014, 23(3): 146-156. |
| [20] |
ZHANG J X, LIU G W, ZHANG Q, et al. Coordinating a Supply Chain for Deteriorating Items with a Revenue Sharing and Cooperative Investment Contract[J]. Omega, 2015, 56(3): 37-49. |
 2019, Vol. 36
2019, Vol. 36
