扩展功能
文章信息
- 赵建峰, 袁细国, 梁伯栋, 陈球霞
- ZHAO Jian-feng, YUAN Xi-guo, LIANG Bo-dong, CHEN Qiu-xia
- 基于车联网及云计算的电动物流车智能调度算法
- An Electric Logistics Vehicle Intelligent Scheduling Algorithm Based on Internet of Vehicles and Cloud Computing
- 公路交通科技, 2019, 36(6): 112-124
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(6): 112-124
- 10.3969/j.issn.1002-0268.2019.06.015
-
文章历史
- 收稿日期: 2018-09-21
2. 西安电子科技大学 计算机学院, 陕西 西安 710071
2. School of Computer, Xidian University, Xi'an Shaanxi 710071, China
电动汽车取代传统燃油汽车对于缓解城市空气污染具有重要意义,然而,当前相比传统燃油车,电动汽车价格昂贵、充电时间长、续航里程短,特别是充电桩不足,极大地影响了电动车的推广。尽管国家一再出台鼓励新能源汽车(含电车)发展的措施,电车在城市的普及率并不高。相比将电动车推广到家用市场的种种困难,将其推广到物流领域却有自身的优势:(1)物流企业通常可以提供固定的充电位;(2)电动货车对比燃油汽车其单位运行成本具有较大的优势[1],物流企业较高的年均使用里程使其具有经济优势。因而,各个城市在继公交电动化后,开始大力推动物流企业市内运输的电动化,目前,深圳市已经开始制定相关的鼓励政策。可以预见,电动车在市内物流替代燃油车是发展趋势。
物流车辆调度问题最早由Dantzig和Ramser[2]中提出,其目标是在一定的约束条件下,如:车辆载重、货物体积等的限制下,寻求最佳的货物车辆装配,亦称车辆排程问题(Vehicle Scheduling Problem),或者寻求车辆最佳的行驶路径,亦称车辆路径问题(Vehicle Routing Problem),进而使得总的配送成本最低。因此,物流车辆的调度问题是典型的NP问题,当采用电动车进行运输后,受充电、续航的影响,其求解难度更加复杂。近年来,以新能源汽车为载体的物流调度问题统称为Green Vehicle Routing Problem (GVRP)。
GVRP问题的研究最早可以追溯到欧盟发起的电动车物流测试项目,从1998年到2002年,欧盟将电动车应用于物流领域(Electric Vehicle City Distribution,ECLIDIS)进行测试,项目非常成功,然而当时的电动车的价格及其电池的寿命限制其推广[3]。2010年,Conrad和Figliozzi在传统的车辆路由问题Vehicle Routing Problem (VRP)的基础上,考虑到电动车充电特性及充电速度的影响,提出了Electric Vehicle Routing Problem (EVRP)[4]。
随后,SevgiĚrdogan, Elise Miller-Hooks考虑了新能源车的物流调度问题,正式提出了GVRP[5],即:给定一个由客户节点、能源补充点、仓储节点等组成的完备图,GVRP在限定的时间内寻找一个最短的调度路径经过所有的客户节点并且满足新能源车辆的能源约束。由此,GVRP正式成为研究者关注的一个典型NP问题。
1 国内外研究现状 1.1 国内外研究成果国外的研究较早,然而由于GVRP问题也比较新,经典研究文献并不多。文献[6]对2014年以前的EVRP研究现状进行了综述,文章从电动车技术背景,包含车辆类型和电池,与传统燃油车费用对比,包含车辆编组,路径选择和最佳路径等几个方面进行了综述,同时,给出了可能的研究方向。
近两年来,比较有代表性的研究成果有:Michael Schneider研究团队对时间和充电站约束下的车辆调度问题进行了研究[7-9]。文献[7]采用了一种新的混合启发式算法对此进行求解,新算法结合了可变的领域搜索和禁忌搜索算法,在标准集上进行测试,取得了较好的效果。文献[8-9]对不同类型电动车的混合编队问题进行了研究,模型中,以运输时间、运输费用、车辆负载等为约束,采用基于自适应大规模的领域搜索算法(Adaptive Large Neighborhood Search)改进的分支定价算法(branch-and-price)进行求解,试验表明,该算法有效。除了Schneider团队外,文献[10]对时间约束下的不同调度路径下的不同的电车充电情况进行了研究,通过对每条调度路径上是否具有多个充电站和每次充电是否必须充满得到4种组合,采用分支定价及修剪算法(branch-price-and-cut algorithms)进行求解。研究表明,在达到100个客户,21个充电站的情况下,4种组合都有解,对比4种路径规划,多充电桩在不是必须满充的情况下相比其他3种情况更有优势。文献[11]则提出了一种通用的EVRP模型,模型中以最小运输时间、最小能量消耗和最少运输车辆为约束,经过每个客户且只经过每个客户一次。不同于以往的模型,该建模中考虑的车辆不同负载下的电力消耗问题。在该模型下,由于其可行解空间不大,因此,采用计算机对其进行精确求解。
国内,目前也有少量的学者开始EVRP的研究,其中华中科技大学研究团队的研究最有代表性。如:学者杨珺[12]等将换电站的选址和物流运输路径规划一起研究,建立了整数规划模型,并设计了禁忌搜索-改进Clarke-Wright节省的两阶段启发式算法来对模型进行求解。文献[13-14]以不同类型的电动车混合运输的基础上,建立了一个含时间窗的多车型电动汽车车辆路径问题的混合整数规划模型,模型采用分支定价算法进行求解,并在求解过程中采用下界-上界的方法减少求解空间的规模以达到快速求解的目标,算法的有效性也得以验证。
除此之外,文献[15-16]用数据挖掘的方法对北京市政府支持下的70辆北汽新能源纯电封闭式货车的充电行为进行了分析,发现了用户的充电规律。文献[17]从低碳排放的角度出发,建立了一个以能耗和碳排放为最小目标,并考虑租车费用的求解模型,并采用禁忌搜算法进行求解。李英等[18]则从文献分析的角度以Web of Science数据库中的GVRP问题的相关文献进行了统计,从宏观的文献年载量、来源期刊、核心作者、学术机构和国家(地区)分布和微观的高频关键词和共被引文献两个方面进行了分析。文章认为,GVRP正处于快速发展阶段。
另外,国内也有部分学者开始在对基于云计算、车联网或电动物流车辆的智能调度问题进行研究。基于云计算的如:宋钰[19]等提出了一种新的有关云计算和神经网络相结合的物流作业调度算法。试验结果表明,改进算法不仅能满足用户的多种需求,提高了用户的满意度,同时也提高了资源调度率和系统资源的利用率。基于智能算法的如:叶勇等[20]根据物流车辆调度的具体特征设计了一种新的二维编码方法,并采用了增强的狼群觅食算法进行问题的求解,并与禁忌搜索算法、遗传算法、改进蚁群算法和混合粒子群算法等常见智能优化算法进行了对比,试验结果表明,狼群算法不仅具有收敛速度快和搜索质量高等优点,而且拥有良好的稳定性和求解效果。邵丽丽[21]则采用蚁群优化自适应遗传算法对物流车辆的调度问题进行求解,其基本思路是,首先采用自适应遗传算法对物流车辆的调度问题进行求解,然后使用遗传算法的求解结果,初始化蚁群算法的信息素,并采用蚁群算法再次进行求解,其求解结果相比标准遗传算法、自适应遗传算法和蚁群算法具有优势。其中,文章所采用的计算模型为一个配送中心、多个客户的模型。李秀娟等[22]则提出了一种改进的蚁群优化算法并将其应用在物流车辆调度中,对比固定车辆调度算法具有明显优势。针对蚁群算法存在局部收敛及收敛速度不够快的2个问题,引入了扰动因子和最优路径策略来改善其求解结果,在标准的TSP问题测试集测试表明,改进后的蚁群算法效果较好。最后,将改进的蚁群算法应用于物流车辆的调度问题进行了仿真。金涛[23]提出了一种基于改进差分进化算法的多配送中心物流车辆调度模型,首先对车辆的调度进行了模拟,然后采用了差分算法变异过程中动态自适应地调整缩放因子,在交叉过程中通过高斯扰动增加种群的多样性,在变异操作之后加入新的选择机制等措施对差分算法进行改进,最后以3个配送中心为例,对算法进行了测试,取得了较好效果。李明燏等[24]在提出了带有时间窗和异构车队的车辆路径问题的基础上,建立了带有时间窗和异构车队的车辆路径问题的模型,并提出一种改进的禁忌搜索算法来对模型进行求解,演算结果证明了这种创新算法在解决带有时间窗和异构车队的车辆路径问题上是有效的。
1.2 研究存在的问题尽管现在的研究成果很多,然而EVRP作为一个新问题,还有许多亟待解决的问题,如:(1)研究规模偏小,这是由NP问题的特性所决定;(2)研究范围局限于一个或几个物流分发中心,限于物流中心到客户的终端物流研究,缺少对城市间物流中心的调度配送的研究;(3)未能充分考虑实际的应用情况,如:假设到顾客的道路运输时间是固定的,顾客的服务时间也是随时可以得到等,这与实际路况及货物派送的实际情况相背离;(4)未能充分考虑大规模电动车应用于物流企业时,新技术特别是车联网和云计算平台对物流企业技术变革的影响;(5)车辆装配和车辆路径寻找分开研究,未能一体规划。
针对上述问题,本文提出了一种基于车联网及云计算平台的电动车物流的多目标优化智能调度算法(下称“智能调度算法”)。其核心是:假定车联网及云计算平台已经应用于物流企业,在车辆及货物信息能充分获得的基础上,对城市间物流中心间的电动车货运装配及路径规划进行了一体建模,确定了调度算法的评价目标。为提高求解效率,采用多目标优化算法进行求解。该算法基于企业调研,具有较强的实际应用价值,同时,通过仿真试验表明,该算法能正确安排车辆调度及其运行路径,通过大规模数据测试,对比当前物流企业所使用的人工调度算法具有非常明显的经济效益。
2 电动车物流智能调度模型 2.1 智能调度模型的建模 2.1.1 模型假设条件随着车联网的发展及各大物流开始对物流云计算平台的建设,未来的物流业一定能够做到以下技术要求:
(1) 车联网技术能够实时收集电动轻型货车的位置、剩余载重、剩余体积、剩余续航里程等信息;
(2) 基于云计算平台的物流平台能够记录每个货物的ID、质量、体积、时限、位置等信息;
(3) 所有的物流仓库都设有充电桩,可以满足车辆随时进行充电的需要。
限于篇幅,本文不对车联网技术及云计算平台的具体实现进行描述。参考相关研究,如文献[25]所研究的托盘技术可以用于云计算平台的物流数据的采集,而文献[26-27]则对车联网环境下的车辆定位进行了研究。从多个文献的研究成果及最新的技术进展出发,可以判定本文的假设是合理的。
本文假定随着未来车联网技术及云计算平台的建成,本调度模型所需的计算参数能依赖于车联网及云平台实时获取(条件1, 2),同时条件3保证在任何一个物流仓,车辆空闲时均可以进行充电,此条件为车辆状态转换成立的必要条件。实践中,当车辆的剩余形式里程大于规划路径时,即可将车辆投入运营中。如存在一个物流仓储不能满足车辆随时进行充电的需求,则车辆无法直接从卸货状态转换为充电状态,而是需要将车辆先调度到可以充电的仓库才可以进行转换,而此时如果该车辆电量不足,则无法被调度,出现车辆状态转换矛盾,调度模型不成立。
基于以上技术条件展开本研究。
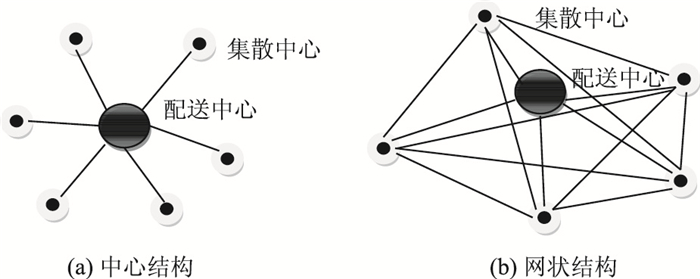
2.1.2 模型的抽象及符号集目前,所有的城市物流配送(分拣)中心站点都是把地理位置作为主要选址因素进行建设,然后,以该站点为圆心,辐射其周边区域,并建立相应的集散站点。因此,在研究中许多学者将其抽象为一个中心点,多个辐射点的模型,以中心点代表配送中心,客户为辐射点,如图 1(a)所示。
|
| 图 1 抽象物流节点 Fig. 1 Abstract logistics nodes |
| |
本研究认为,辐射模型配送效率低下,未来随着物流云计算中心的建设,配送中心派出车辆不仅仅是给一个集散中心运输货物,也可以同时给几个集散中心运输货物;同时,物流车辆在非满载的情况下,可以到下一个集散中心装载货物后,再到达配送中心,因此本文提出将一个城市物流调度节点图抽象网状结构,如图 1(b)所示。图中,各个集散中心的节点线路也是连通的,运输车辆可以一次给多个集散中心运输货物,也可以经过多个集散中心收集货物后到达配送中心。
为便于读者阅读,先简略给出本文主要的数学符号:G为运输的物流货物的集合;W为配送中心及集散点的集合;V为物流电动车的集合;L为路网集合;S为调度方案集合,即每个车辆的货物装载信息及其运输路径。
下面对各个符号进行详细介绍。
设G(ID, Wei, Des, Time)表示货物,其中,ID表示货物的ID,用ij表示,i表示货物仓储的ID,j表示货物发往目的地仓储ID,Wei表示货物的质量,Des表示货物的目的地,Time表示货物剩余的到达时间。
设在图中有一个配送中心W(ID, Cap, G, CL),其中,ID表示配送中心的ID,用自然数1表示,Cap表示仓库的容积,单位t;CL表示充电桩个数;设有n-1个集散中心W2, W3, …Wn,Wi具有属性Wi(ID, Cap, G, CP),其中,ID用自然数2,3,…,n表示。由于W与Wi的属性一致,为表达方便,后期也用W1表示W,同时,在不严格区分是配送中心还是集散中心时,统称仓储中心。配送中心的货物的目的地可以是Wi中的任意一个,而集散中心的货物的目的地只能是配送中心W1,当货物从配送中心到达集散中心时,将被集散中心派送到最终的客户手中,同时集散中心从客户中收取相应的物流快件。当货物从集散中心到达配送中心时,经过分拣,本地货物将被发送到其他集散中心,外地货物将通过城际连接线发送到下一个配送中心。
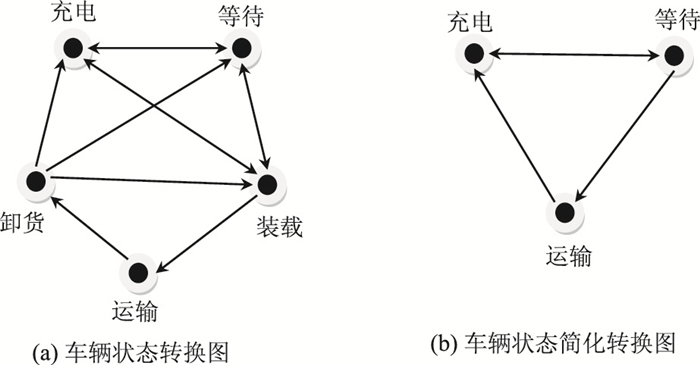
设m辆电动物流车辆Vi(ID, TL, RL, ML, Sta, Loc, Path),其中,i=1, 2, …, m,表示车辆的数量,ID表示车辆的ID,用自然数1, 2, …, c表示,TL为总载重,RL为剩余载重,ML为车辆的续航里程,Sta为车辆状态,Loc为车辆当前位置,Path为车辆的调度形式路径。根据物流企业的实际情况,车辆的状态及相关状态转换图可以通过图 2(a)表示,其中,箭头表示该状态可以由其尾部所连接的状态转换得到。考虑到车辆装卸时间要远远小于车辆运输的时间,同时,装载、运输、卸货有极强的顺序性和相关性,因此,车辆状态转换图可以简化为图 2(b)的状态,即将装载、卸货、运输3个点抽象为一个连接点。不同于其他研究文献先通过确定车辆的配送路径来决定车辆装载的货物,本文是将车辆的装载和车辆的运输路径作为一个整体来进行求解,因此,本文将建立的模型是包含货物装配及车辆路径规划一体的调度模型。
|
| 图 2 车辆状态转换 Fig. 2 Vehicle state transition |
| |
设lij表示从仓储i到达仓储j的路网代价,实践中,每个企业对路网代价的定义不同,如:可以表示经过此路的运输时间、路桥费、运输距离等,也可以是混合代价,本研究中选取运输时间作为道路运输代价。应用推广中,根据企业要求进行设置,因此,L={lij|i, j∈W(ID)}为路网集。
2.2 智能调度模型优化目标在给定本模型符号集的基础上,依据EVRP问题的需求,确定本模型的求解目标及约束条件。
算法目标,给定一个车辆装配及车辆行驶路径,使得整个物流具有最小的物流成本、最快的物流运输速度,同时保证货物在限定时间内到达目的地。从成本方面分析,物流企业的在运输中的成本主要包含3个方面,即:道路成本、仓储成本及装卸成本。因此,用形式化的语言可以描述为:
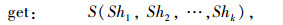
|
(1) |
其中,k≤m, Shi为车辆的调度状态
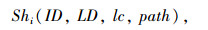
|
(2) |
式中,ID为车辆的ID; LD为车辆货物装配的负载(ld1, ld2, …, ldn); ldi为车辆将装配目的地为Ji的负载; lc为车辆当前的位置; path为车辆的运行路径(pt1, pt2, …, ptn); pti为路径节点。
s.t在调度S下有
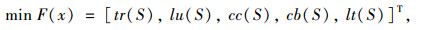
|
(3) |
式中,tr(S)为平均道路运输成本,研究中,成本为道路运输时间,应用推广中,可以根据企业的需求进行设定,如:道路运输时间、道路运输距离、过路费或者加权后的混合代价。
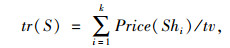
|
(4) |
式中,Price(Shi)为在给定车辆Shi和Lc的情况下,用最短路径法求得的车辆将所有货物运输到目的地后的代价;tv为在调度Shi下车辆的总运量;lu(S)为平均车辆的装卸成本。物流企业实际运输中,装配一个车辆,其满载或者只装卸一部分货物,对装卸一辆车的成本影响可以忽略不计,为简化模型的计算,研究中,根据调度S所包含的装卸次数进行计算,这也符合企业的实际情况。
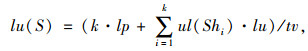
|
(5) |
式中,k为装配的次数;lp为车辆装配一次的成本;ul(Shi)为在调度Shi下的卸载次数;lu为车辆卸载一次的成本。
cc(S),表示仓库的仓储成本:
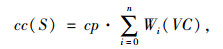
|
(6) |
式中,cp为每吨货物的仓储成本;VC为Wi在调度S下剩余的仓储量,因此有:
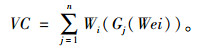
|
(7) |
cc(S)的约束是为了在一次调度中使得车辆尽量多装载货物,以降低仓库的库存,减少物流企业的成本;cb(S)为仓库的仓储均衡度,
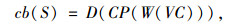
|
(8) |
式中,VC为在调度S下仓储Wi剩余的仓储量;CP()为仓储率,即Wi当前所存储的货物与其总容量的比值;D()为各个仓库Wi的均方差。
cb(S)约束是为了保证各个仓库仓储率相对一致,如果取消此约束,算法为了追求更低的运输成本,可能会出现一些仓库仓储率过高,进而影响后续货物的到达或者会出现某仓库的货物运输时间较长的问题。
lt(S)为装载货物的剩余物流时间:
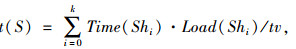
|
(9) |
式中,Time(Shi)为在车辆的调度状态Shi下车上所载货物剩余的到达时间;Load (Shi)为在车辆的调度状态Shi下,车上所载货物的总量。
lt(S)是为了保证货物的运输时间,即在云计算平台下,物流企业可以记录货物的预期到达时间,当货物已经临近预期时间时,则表明该货物具有较高的运输优先级,该约束保证同等经济条件下总是最紧急的货物将被最快运往目的地。
调度目标,tr(S),lu(S),cc(S)的最优,可以达到物流企业追求的物流成本最低和物流速度最快,而目标lt(S)则保证了最紧急的货物将被最先运输。cb(S)则保证各个仓库的库存较为均衡,以保证后面货物顺利到达以及各个仓库货物能较为均衡地到达客户手中。
从建立的模型目标中可以看到,本模型的求解目标包含5个求解目标,tr(S),lu(S),cc(S),lt(S),cb(S),此目标的建立,为采用多目标优化算法求解创造了条件。
同时,调度必须满足约束
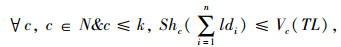
|
(10) |
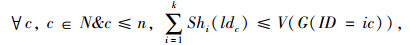
|
(11) |
式中,约束(10)表示在车辆的调度状态Shi下,车载货物的总质量,不能超过车辆的额定载重。约束(11)表示在调度状态Shi下,车辆所装载的仓配中心i到达目为c的货物,不能超出仓储中心i所有的到达目的为c的货物总量。
2.3 智能调度模型与其他模型的区别从以上对模型的描述中可以看出,不同于以往的学者通过先确定车辆的行驶路径,再确定车辆的装载货物建立的模型,本文提出的模型有以下几个不同:
(1) 车辆的装载过程与车辆的行驶路径一起确定,只要给出一个调度方案S,便确定了车辆的装载及运输路径。
(2) 基于物流企业的云计算平台精确获取了当前仓储的物流状态,通过车联网精确获取了当前车辆的状态,通过实时路况,能实时查询当前的路线信息,因此,调度能够进行车辆与货物的精确匹配,大大提升了调度效率和降低了物流企业的成本。
(3) 模型的约束中,只考虑了两个约束,即不能超载和车辆所装载的货物不能超过仓储中心目前的配送货物,没有建立其他任何约束,诸如一个配货点只能经过一次的约束、车辆必须满载的约束等,大大提升了模型的实用性。
(4) 考虑了时间约束,未来的物流业的竞争将更加激烈,“限时达”将是一种普遍存在的现象,本模型可以很完美地达到将剩余到达时间最短的货物优先送达。
(5) 模型计算目标没有包含微分积分的复杂运算,大多数运算为加法,及少量的乘法和除法,因而求解过程很快,单次求解规模可以达到很大数值。仿真试验中,车辆的运输规模最大可以达到25辆,仓储中心的数量最大可以达到50个,其单次求解过程不超过5 min,这完全在调度平台的可接受范围内。
3 求解算法 3.1 智能调度算法总体框架在建模的基础上,提出本文对模型进行求解的算法,即:基于车联网及云计算平台的电动车物流的多目标优化智能调度算法,如图 3所示。

|
| 图 3 基于车联网及云计算平台的物流车辆调度总算法 Fig. 3 Logistics vehicle scheduling algorithm based on internet of vehicle and cloud computing platform |
| |
智能调度算法的核心思想是:依据云计算平台获得的货物信息,如载重、体积、剩余运输时间等,依据车联网平台获取的车辆信息,如:载重、位置等,以及当前的路况等状态,采用多目标优化算法,依据本文的建模及提出的优化目标进行求解,进而给出每个车辆的最佳装载及行驶路线。
算法中G1的目的地是各个集散点Wi,由于集散点不具有分拣功能,因此,Wi的货物Gi的目的地为分拣中心W1。算法的5~8步保证即将到达限定运输时间的货物优先装车,保证“限时达”的货物能按时到达。步骤9则对不紧急的货物,按照最优的经济原则进行调度。步骤9的核心是依据仓储状态、车辆状态、路况等综合因素,以本文所建立的优化目标为求解目标,采用多目标优化算法进行求解。具体的求解步骤,详见2.2及2.3节叙述。
车辆状态,依据建模中的车辆状态转换图进行转换,具体算法中,车辆状态Vi(sta)依赖下列规则进行转换:
规则1:如果车辆当前状态为充电状态且车辆当前续航里程已经超过经过所有节点Wi的最长路径的续航,则车辆进入等待状态。
规则2:如果车辆在等待状态且车辆当前续航里程已经超过经过所有节点Wi的最长路径的续航,且当前有货物需要运输,则进入运输状态;如果需要补充电量,则进入充电状态。否则保持当前状态。
规则3:如果车辆在运输状态,如果车辆GPS定位显示其已经到达运输路线的终点,且当前有充电空余位置,则进入充电状态。否则进入等待状态。
3.2 智能调度算法编码算法采用二进制编码,对于任意一个解,∀pi,其长度为k·n,其中,k为等待调度车辆的数量,n为仓库的数量,因此:
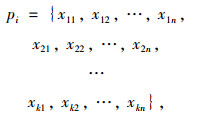
|
当j < n,xij=1时表示向车辆i装载到达集散点j的货物;当xij=0时,则不装。考虑实际情况中,存在空车调度的情况,xin表示是否将空车发往仓储量最大的仓库。因此,问题的解空间为:
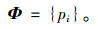
|
(12) |
算法的种群空间为:
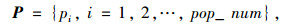
|
(13) |
式中pop_num表示种群的数量。
∀pi,若xij= 0,j≤n-1, 且xin= 1,则
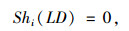
|
(14) |
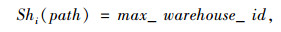
|
(15) |
其中,max_warehouse_id表示剩余仓储量最大的仓库。
否则,设
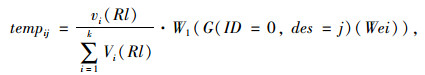
|
(16) |
则:
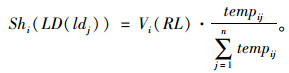
|
(17) |
Shi(path)则为在给定的货物分配下,经过将货物运输到目的地的所有节点时,在给定的L下,经过最短路径算法求解的最小运输代价的运输路径。本研究采用最短路径遍历的算法,如图 4所示,求解问题的近似解,在本文的研究范围内,通常也是问题的最优解。

|
| 图 4 基于最短路径的遍历算法 Fig. 4 Traversal algorithm based on shortes path |
| |
3.3 智能调度算法的步骤
算法的主要步骤采集经典的NSGAII算法[28],如图 5所示。算法中,种群的编码采用本文提出的编码方式,其优化目标为本模型所建立的tr(S),lu(S),cc(S),lt(S),cb(S),算法的迭代则采用经典的交叉,变异,Pareto最优选择步骤进行。

|
| 图 5 基于车联网及云计算平台的智能调度算法 Fig. 5 Intelligent scheduling algorithm based on internet of vehicle and cloud computing platform |
| |
4 试验及结果对比分析
依据实际调研结果,本文做如下数据假设:
(1) 电动货运车辆的载重为0.5~2.5 t之间;
(2) 电动车平均续航里程为200 km,在快速充电下,2 h可以充满80%,4 h可以完全充满;
(3) 电动车运输一次的平均距离为30 km,运输时间加装载卸货时间为2 h,完成一次周期调度的时间为4 h;
(4) 市内调度路价以运输时间为单位进行衡量,根据实际情况,本文考虑市内交通运输时间在0.5~2 h之间;
(5) 根据车辆的运量,以4 h为单位,考察最小不少于4 h的车辆运量,最大总仓储容量仓储不超过8 h的车辆运量。
本文将在上述数据范围内,随机生成相关数据,展开相应的仿真研究。
智能调度算法关键参数根据经验设置如下:
| 参数 | 值 |
| 种群个体数量p_num | 20 |
| 基因长度gene_num | n·m |
| 进化迭代次数ite_num | 200 |
| 交叉率p_cross | 0.9 |
| 变异率p_mute | 1/gene_num |
试验中选用目前物流中心使用人工调度的方法(下称,人工调度算法)为对比算法,其调度方式为:将最大载重的车辆装载仓库中库存最大的货物发往对应的集散点,然后再从集散点载物返回。
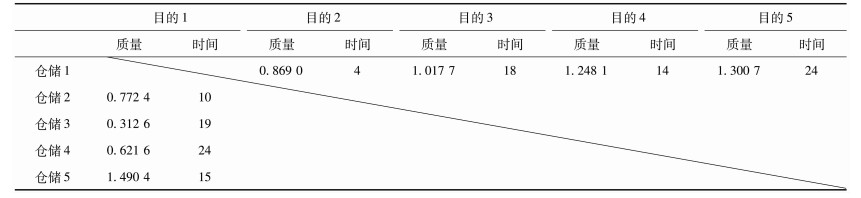
4.1 算法正确性的验证为便于观察调度结果,本文假定仓储节点个数n=5,车辆个数m=4,具体数据如表 2所示。
车辆载重分别为:0.5,1.5,1,2.5路价如图 6所示。计算结果如表 3所示。
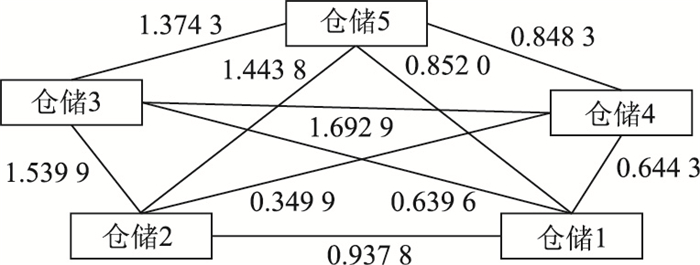
|
| 图 6 仓储节点路径代价示意图 Fig. 6 Schematic diagram of warehouse node path cost |
| |
| 基因 | 装载 | 路径 | 仓储结果 | 结果 | |||||||
| W1 | others | tr | lu | cc | cb | lt | |||||
| 00000 | V1 | 0 0 0 0 0.312 6 | 3 | 0 | 0 | ||||||
| 00011 | V2 | 0 0 0 1.300 7 1.490 4 | 5 | 0 | 0 | ||||||
| 10001 | V3 | 0.869 0 0 0 0 0.772 4 | 2 | 0 | 0 | 1.026 7 | 1.965 3 | 0 | 0 | 5.756 3 | |
| 01100 | V4 | 0 1.011 7 1.24 8 | 3 | 0 | 0 | ||||||
| 0 0.639 6 1.692 9 | 4 | ||||||||||
| 00001 | V1 | 0 | 0 | 0.869 0 | 0.772 4 | 0.543 7 | 2.325 6 | 7.632 5 | 0.032 4 | 2.084 3 | |
| 00001 | V2 | 0 | 0 | 1.017 7 | 0.919 0 | ||||||
| 00001 | V3 | 0 | 0 | 1.248 1 | 0.621 6 | ||||||
| 00001 | V4 | 0 | 0 | 1.300 7 | 1.490 4 | ||||||
| 01001 | V1 | 0 0.500 0 0 0 0.312 6 | 3 | 0 | 0 | 0.864 1 | 2.488 9 | 0.517 7 | 0.001 8 | 4.233 6 | |
| 00011 | V2 | 0 0 0 1.300 7 1.490 4 | 5 | 0.517 7 | 0 | ||||||
| 10001 | V3 | 0.869 0 0 0 0 0.772 4 | 2 | 0 | 0 | ||||||
| 00101 | V4 | 0 0 1.248 1 0 0.621 6 | 4 | 0 | 0 | ||||||
| 人工 | V1 | 0.500 0 0 0 0 0.500 0 | 2 | 0.369 0 | 0.272 4 | 0.881 6 | 2.294 5 | 0.659 2 | 0.012 4 | 3.945 5 | |
| V2 | 0 0 1.248 1 0 0.621 6 | 4 | 0.017 7 | 0 | |||||||
| V3 | 0 1.000 0 0 0 0.312 6 | 3 | 0 | 0 | |||||||
| V4 | 0 0 0 1.300 7 1.490 4 | 5 | 0 | 0 | |||||||
表 3的第1列,基因的1, 2, 3行是从多目标优化算法中找出的具有代表性的解结果,“人工”表示人工调度的结果。装载列给出了各个车辆需要装载的货物质量,路径表示车辆需要行驶经过的节点并回到出发点。仓储结果表示在该调度算法下,经过调度后车辆的仓储的库存容量。结果表示各个调度结果评价指标。
从表 3结果中可以看出:智能算法对应于不同的求解目标,可以找个各个进化目标的近似最优解,进而满足仓储管理的不同需要。如:有的企业如果仓库容量较小,且仓储价格特别贵,则可以选用基因1的调度结果,这样可以做到企业运行成本最小。反之,如果车辆运输的道路成本最高,则该企业可以选用基因3的调度结果。需要特别说明的是,基因2的调度结果,表示本次调度所有车辆原地待命,不参加运输。这是考虑到可以等待一段时间,在后期货物增加,且车辆增加的情况再进行调度,从而获取更加高效的企业效率和调度成本。
从表 3一次的调度结果可知,智能调度算法能获取不同类型的解,企业可以根据实际情况选择所需要的解。算法的结果也验证了算法的可行性和正确性,通过一次调度对比人工调度算法也具有一定的优势。
4.2 不同情况下算法对比结果单次调度结果并不能代表智能调度算法的优势,本文从不同负载,不同车辆数量,不同仓库数量情况下,求解其100次随机生成的调度结果,并与人工调度结果进行对比。
4.2.1 不同alpha系数下调度结果比较在大规模调度下,仓库的仓储能力与车辆的运输能力的比值是影响调度的一个重要指标,本文简称alpha系数,即:
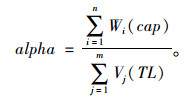
|
(18) |
图 7给出了各个调度指标随着alpha系数的变化,其中n=20,m=20。同时,本文选择一个所有指标和最小的解(min)作为企业可能的选择之一与人工调度进行对比。事实上,各个指标简单的相加只是简单地反映了智能调度算法的优势,并不能完全反映智能调度算法的优势,各个企业可以根据自己的实际情况,在对各个指标加权后相加,进而得到最适合企业实际情况的解。
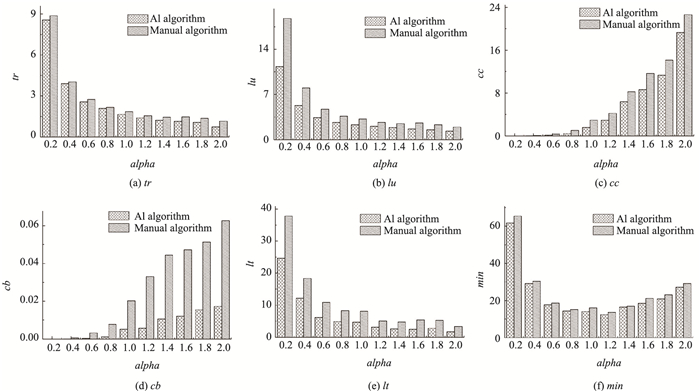
|
| 图 7 调度评价指标随着alpha系数变化 Fig. 7 Scheduling evaluation index varying with alpha coefficient |
| |
从图中可以看出,随着alpha系数的增加,tr,lu,lt3个指标逐渐下降,因为,随着alpha系数的增加,每车能够装载的货物会增加,直至满载,因此,单位货物的平均指标就会下降。另外,随着alpha系数的增加,cc和cb也逐步增加,这是由于alpha系数的增加,导致剩余的仓储货物增加,进而导致cc和cb的增加。min指标则随着alpha系数的增加,先减少,在alpha指数为1~1.2时,达到最小值,可见当运载车辆的总载重与货物运输需求的总载重接近时,调度总体成本最小。
4.2.2 不同车辆数量下调度算法的效果比较不同的物流公司,物流调度集散点的数量差异较大,本文以一个典型的节点数量20为例进行研究。下面给出在货物集散点数量一定的情况下,不同调度车辆情况下,对比智能调度算法100次调度后,人工调度算法的平均调度结果,其中,在不同的车辆数量下,货物仓储数量随着车辆数量随机变化,平均alpha系数约为100%。
图 8表明,随着调度车辆的增加,cc,cb呈下降趋势,因为,车辆数量的增加导致有更多的车辆可以进行安排,使得车辆的载重更加接近需要装载的货物,从而使得调度的效率更高。而tr,lu,lt,min随着车辆数量的增加,无明显的变化,这是因为,随着车辆数量的增加,alpha系数稳定的情况下,货物的数量也在增加,因此,几个指标变化不明显。
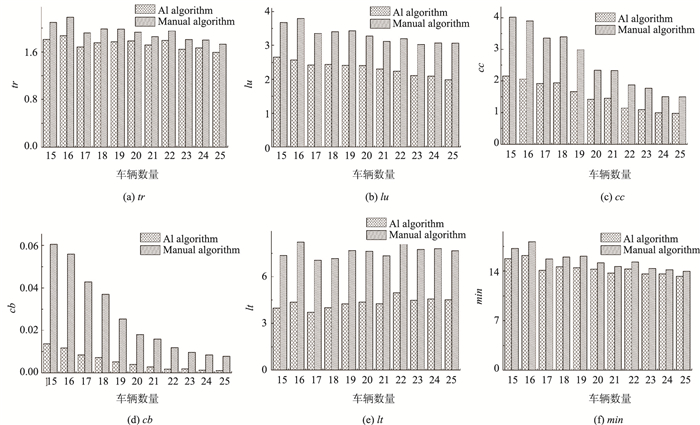
|
| 图 8 调度评价指标随着车辆数量的变化 Fig. 8 Scheduling evaluation index varying with vehicles number |
| |
4.2.3 不同仓储节点数量下调度算法调度效果比较
仓储节点数量的不同,对算法调度的影响效果也不同,下面给出,仓储节点从5~50个节点,每隔5个节点的调度结果,其中,根据节点数量不同,车辆选取与仓储节点等同数量的节点,平均alpha系数约为100%。
m=20,alpha=1,从图 9可以看出,与车辆对调度的影响相反,随着调度仓储节点的增加,cc,cb呈增加趋势,这是因为,随着仓储节点的增加,调度的难度增加,总剩余的货物也开始增加。而tr,lu,lt,min随着仓储节点数量的增加,变化不明显,原因同车辆变化的影响,这几个指标只与alpha系数有强相关。

|
| 图 9 调度评价指标随着仓储节点的变化 Fig. 9 Scheduling evaluation index varying with warehouse nodes |
| |
5 结论
针对目前物流车辆的调度都是人工调度,其效率低下的问题,着眼于未来云计算平台和车联网技术发展,本文提出了一种新的物流调度模型,并创立了一种多目标优化的智能物流车辆调度算法。首先使用一个实际案例验证了算法的可行性、正确性;然后,通过大规模的仿真数据测试,对比人工调度算法,在不同的仓储货物载重比, 不同的载重车辆个数, 不同的仓储节点个数下,智能物流车辆调度算法在平均道路运输成本、平均装卸成本、平均仓储成本、平均仓储均衡度、平均货物的物流时间等方面均有较好的结果。
仿真结果表明,本文的算法具有可行性、正确性。大规模的仿真数据测试表明,对比人工调度算法,在不同的仓储货物载重比,不同的载重车辆个数,不同的仓储节点个数下,智能调度算法在平均道路运输成本、平均装卸成本、平均仓储成本、平均仓储均衡度、平均货物的物流时间等方面均有较好的结果。
相比其他研究者提出的算法,本文的算法是装载、路径规划一体求解的算法,同时可以实时获取仓储货物,车辆及道路的实际情况,是实时调度,弥补了当前研究主要通过参数假设的情况来实现调度。此外,智能调度算法的仿真充分考虑了物流企业的现实情况,其平台数据的设计,如路网的代价、仓储的数量,可以调度的车辆、alpha系数等都是在对深圳几家主要物流公司调研的基础上拟定的,具有非常重要的现实应用意义。
| [1] |
DAVIS B A, FIGLIOZZI M A. A Methodology to Evaluate the Competitiveness of Electric Delivery Trucks[J]. Transportation Research Part E:Logistics and Transportation Review, 2013, 49(1): 8-23. |
| [2] |
DANTZIG G B, RAMSER J H. The Truck Dispatching Problem[J]. Management Science, 1959, 6(1): 80-91. |
| [3] |
VERMIE T. Electric Vehicle City Distribution: Final Report[R].[S.l.]: European Commission, 2002.
|
| [4] |
CONRAD G R, FIGLIOZZI M A. The Recharging Vehicle Routing Problem[C]//Proceedings of the 2011 Industrial Engineering Research Conference.Reno, USA: Curran Associates.Inc., 2011: 2785-2792.
|
| [5] |
ERĎOGAN S, MILLER-HOOKS E. A Green Vehicle Routing Problem[J]. Transportation Research Part E:Logistics and Transportation Review, 2012, 48(1): 100-114. |
| [6] |
PELLETIER S, JABALI O, LAPORTE G. 50th Anniversary Invited Article-Goods Distribution with Electric Vehicles:Review and Research Perspectives[J]. Transportation Science, 2016, 50(1): 3-22. |
| [7] |
SCHNEIDER M, STENGER A, GOEKE D. The Electric Vehicle Routing Problem with Time Windows and Recharging Stations[J]. Transportation Science, 2014, 48(4): 500-520. |
| [8] |
BRUGLIERI M, PEZZELLA F, PISACANE O, et al. A Variable Neighborhood Search Branching for the Electric Vehicle Routing Problem with Time Windows[J]. Electronic Notes in Discrete Mathematics, 2015, 47: 221-228. |
| [9] |
HIERMANN G, PUCHINGER J, ROPKE S, et al. The Electric Fleet Size and Mix Vehicle Routing Problem with Time Windows and Recharging Stations[J]. European Journal of Operational Research, 2016, 252(3): 995-1018. |
| [10] |
DESAULNIERS G, ERRICO F, IRNICH S, et al. Exact Algorithms for Electric Vehicle-routing Problems with Time Windows[J]. Operations Research, 2016, 64(6): 1388-1405. |
| [11] |
LIN J, ZHOU W, WOLFSON O. Electric Vehicle Routing Problem[J]. Transportation Research Procedia, 2016, 12: 508-521. |
| [12] |
杨珺, 冯鹏祥, 孙昊, 等. 电动汽车物流配送系统的换电站选址与路径优化问题研究[J]. 中国管理科学, 2015(9): 87-96. YANG Jun, FENG Peng-xiang, SUN Hao, et al. Battery Exchange Station Location and Vehicle Routing Problem in Electric Vehicles Distribution System[J]. Chinese Journal of Management Science, 2015(9): 87-96. |
| [13] |
揭婉晨, 杨珺, 杨超. 多车型电动汽车车辆路径问题的分支定价算法研究[J]. 系统工程理论与实践, 2016, 36(7): 1795-1805. JIE Wan-chen, YANG Jun, YANG Chao. Branch-and-price Algorithm for Heterogeneous Electric Vehicle Routing Problem[J]. Systems Engineering-Theory & Practice, 2016, 36(7): 1795-1805. |
| [14] |
揭婉晨, 杨珺, 陆坚毅. 基于分支定价算法的电动汽车车辆路径问题[J]. 运筹与管理, 2016, 25(4): 93-100. JIE Wan-chen, YANG Jun, LU Jian-yi. Electric Vehicle Routing Problem Based on A Branch-and-price Algorithm[J]. Operations Research and Management Science, 2016, 25(4): 93-100. |
| [15] |
毕军, 张文艳, 赵小梅, 等. 基于数据驱动的物流电动汽车充电行为分析[J]. 交通运输系统工程与信息, 2017, 17(1): 106-111. BI Jun, ZHANG Wen-yan, ZHAO Xiao-mei, et al. Charging Behavior Analysis of Electric Logistic Vehicle Based on Data Driven[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(1): 106-111. |
| [16] |
张文艳.基于数据驱动的城市配送电动汽车充电行为分析及模型建立[D].北京: 北京交通大学, 2017. ZHANG Wen-yan. Modeling and Analyzing of Charging Behavior of Electric Vehicle Usage for City Distirbution Based on Data Driven[D]. Beijing: Beijing Jiaotong University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10004-1017051134.htm |
| [17] |
李进, 傅培华, 李修琳, 等. 低碳环境下的车辆路径问题及禁忌搜索算法研究[J]. 中国管理科学, 2015(10): 98-106. LI Jin, FU Pei-hua, LI Xiu-lin, et al. Study on Vehicle Routing Problem and Tabu Search Algorithm under Low-carbon Envionment[J]. Chinese Journal of Management Science, 2015(10): 98-106. |
| [18] |
李英, 李惠, 成琪. 基于文献计量和知识图谱的国际绿色车辆路径问题研究发展分析[J]. 中国管理科学, 2016(增1): 206-216. LI Ying, LI Hui, CHENG Qi. The Development Analysis of International Green Vehicle Routing Problem Based on Bibliometric and Knowledge Mapping[J]. Chinese Journal of Management Science, 2016(S1): 206-216. |
| [19] |
宋钰, 何小利, 何先波, 等. 基于云计算神经网络物流车辆调度算法研究[J]. 计算机仿真, 2012(4): 367-370. SONG Yu, HE Xiao-li, HE Xian-bo, et al. Study on the Logistics Vehicle Scheduling Based on Cloud Computing and Neural Network[J]. Computer Simulation, 2012(4): 367-370. |
| [20] |
叶勇, 张惠珍. 求解带时间窗车辆路径问题的狼群算法[J]. 公路交通科技, 2017, 34(10): 100-107. YE Yong, ZHANG Hui-zhen. Wolf Pack Algorithm for Solving Vehicle Routing Problem with Time Windows[J]. Journal of Highway and Transportation Research and Development, 2017, 34(10): 100-107. |
| [21] |
邵丽丽. 蚁群优化自适应遗传算法物流车辆调度实现[J]. 计算机测量与控制, 2012, 20(5): 1423-1425, 1441. SHAO Li-li. Ant Colony Optimizing Adaptive Gene Algorism Resolving Logistics Vehicle Schedule[J]. Computer Measurement & Control, 2012, 20(5): 1423-1425, 1441. |
| [22] |
李秀娟, 杨玥, 蒋金叶, 等. 蚁群优化算法在物流车辆调度系统中的应用[J]. 计算机应用, 2013, 33(10): 2822-2826. LI Xiu-juan, YANG Yue, JIANG Jin-ye, et al. Application of Ant Colony Optimization to Logistics Vehicle Dispatching System[J]. Journal of Computer Applications, 2013, 33(10): 2822-2826. |
| [23] |
金涛. 多配送中心物流车辆调度的改进差分进化算法[J]. 计算机工程与应用, 2014(3): 232-235. JIN Tao. Multi Distribution Center Logistics Vehicle Scheduling Problem Based on Improved Differential Evolution[J]. Computer Engineering and Applications, 2014(3): 232-235. |
| [24] |
李明燏, 梁丽萍, 鲁燕霞, 等. 基于改进禁忌搜索算法的车辆路径问题模型[J]. 公路交通科技, 2017, 23(10): 108-114. LI Ming-yu, LIANG Li-ping, LU Yan-xia, et al. A Model of Vehicle Routing Problem Based on Improved Tabu Search Algorithm[J]. Journal of Highway and Transportation Research and Development, 2017, 23(10): 108-114. |
| [25] |
王征宇, 任建伟, 马钰淇, 等. 基于城市共同配送系统的托盘共用调度随机规划模型[J]. 公路交通科技, 2018, 35(4): 146-152. WANG Zheng-yu, REN Jian-wei, MA Yu-qi, et al. A Stochastic Programming Model for Pallet Pooling Based on Urban Collaborative Distribution System[J]. Journal of Highway and Transportation Research and Development, 2018, 35(4): 146-152. |
| [26] |
郑坤.基于RFID的车辆定位系统设计及定位方法研究[D].长春: 吉林大学, 2016. ZHENG Kun. Research on Vehicle Positioning System Design and Positioning Method Based on RFID[D]. Changchun: Jilin Unversity, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10183-1016079129.htm |
| [27] |
郭彬, 赵燕. 车联网环境中基于RFID的车辆定位方法[J]. 公路交通科技, 2016, 33(12): 140-144, 158. GUO Bin, ZHAO Yan. A Vehicle Positioning Method Based on RFID in Internet of Vehicles[J]. Journal of Highway and Transportation Research and Development, 2016, 33(12): 140-144, 158. |
| [28] |
DEB K, PRATAP A, AGARWAL S, et al. A Fast and Elitist Multiobjective Genetic Algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. |
 2019, Vol. 36
2019, Vol. 36