扩展功能
文章信息
- 柳祖鹏, 李克平, 何雅琴, 许彩霞
- LIU Zu-peng, LI Ke-ping, HE Ya-qin, XU Cai-xia
- 基于时间距离轨迹的公交站点布设优化
- Optimization of Bus Stop Layout Based on Time Distance Trajectory
- 公路交通科技, 2019, 36(6): 103-111
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(6): 103-111
- 10.3969/j.issn.1002-0268.2019.06.014
-
文章历史
- 收稿日期: 2017-12-22
2. 同济大学 道路与交通工程教育部重点实验室, 上海 201804;
3. 湖北省邮电学校, 湖北 武汉 430079
2. Key Laboratory of Road and Traffic Engineering of Ministry of Education, Tongji University, Shanghai 201804, China;
3. Hubei Posts and Telecommunications School, Wuhan Hubei 430079, China
干线协调控制是城市道路交通常用的信号控制方式,设计良好的协调控制方案可以使机动车连续通过多个交叉口。公交优先是通过设置公交专用道、公交优先信号等,给予公交车辆更高的优先通行权,可以提高公共交通的运行效率。在干线协调控制背景下,社会车辆以合适的速度行驶,从而可以获得较好的绿波控制效果。但是公交车辆受到交叉口信号控制和公交进站停靠的双重约束,很难实现不停车连续通过多个交叉口,公交运行与绿波控制之间存在不协调。
公交站点布设方案与绿波控制之间存在着相互影响和制约关系,国内外学者对公交站点的最佳布设方案进行了很多研究。其中,公交站位置布设在交叉口上游或下游时,对信号控制的影响各不相同。
公交站布设在交叉口上游:Lee等基于公交出行时间预测模型,结合交叉口上游的公交站,提出一种公交优先信号控制方法[1]。Kim基于车辆到达时间预测模型和公交停靠时间模型,建立一种适用于交叉口上游公交站的公交信号优先控制系统[2]。Zheng等建立公交延误理论模型,探索交叉口上游公交站对公交延误的影响,并提出了最优的公交优先控制策略[3]。Dion等以交叉口上游公交站为研究对象,通过VISSIM仿真研究了公交停靠时间对公交信号优先的影响[4]。赵胜建立了公交站点元胞自动机模型,分析公交站位置对下游交叉口进口道通行能力的影响,给出了在不同的信号控制方案下的最佳公交站点位置,使其对进口道通行能力影响最小[5]。
公交站布设在交叉口下游:Ludwick等指出将停靠站布设在交叉口下游更有利于发挥公交优先效益;公交站布设在交叉口上游时,公交停靠时间的不确定性影响车辆到达交叉口的时刻,导致公交优先控制不容易实现[6]。Byrne等对交叉口上游和下游的公交站进行仿真测试和分析,结果表明公交站布设在交叉口下游时公交优先效果比较好[7]。Wang等提出公交优先控制策略下公交站点位置的优化建议:在道路条件允许的情况下,选择在交叉口下游设置港湾式公交站,公交优先控制效果更好[8-9]。吕林在中观、微观层面对公交站点优化进行研究,从公交自身停靠延误、对交叉口影响及交通安全方面考虑,得出交叉口停靠站优于在路段停靠站,交叉口出口道站点优于进口道站点[10]。葛宏伟对交叉口上游和下游公交进行了详细的对比,表明下游公交站点均优于上游公交站点[11]。
以交通干线为研究背景,考虑公交站在干线上的布设及优化研究:FITZPATRICK等通过仿真对郊区主干道上不同的公交站设计进行分析和评价,研究结果可以为公交站位置和形式选择提供参考[12]。SATIENNAM等以两车道主干路为研究对象,提出一种针对交叉口上游公交站的公交优先控制策略[13]。吴志周等通过模型计算和仿真分析,比较了协调干线上相邻公交站不同设置方式的优劣,结果表明两个公交站分别布设在上游交叉口的进口道和下游交叉口的出口道时,公交车辆延误最小[14]。Liu等基于大量的微观仿真试验,提出了一种干线协调背景下的公交站点布设的理想模型[15]。赵尘、DEWI等利用GIS的空间分析功能对公交线上的站点位置进行优化,以提高公共交通系统的吸引力[16-17]。
已有相关研究中,单点交叉口上下游的公交站位置优化有一定的局限性,无法应用于干线协调背景下的布设优化。考虑多个公交站的相关研究中,通过模型或仿真得出了最优的布设方案,但是缺少更深入的原因分析。本文以干线协调控制为背景,以公交专用道上公交车辆的时间距离轨迹为基础,深入分析交叉口信号控制和公交站布设之间的关系,提出一种基于公交车辆行驶轨迹的公交站点布设优化方法。
1 时间距离轨迹时间距离图是以时间为纵坐标、距离为横坐标的二维平面图,用于绘制车辆的行驶轨迹。在干线协调控制的图解法中,纵坐标表示信号控制的红绿灯时间,横坐标表示沿线多个交叉口及其间距,在时间距离图的第一象限中选择合理的绿波带速度进行协调控制方案设计。
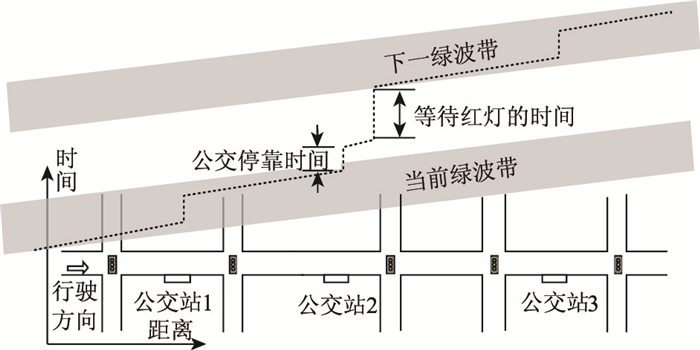
1.1 公交车辆的行驶轨迹线融合干线协调的绿波带和车辆的行驶轨迹,有助于分析公交车流在干线上的运行情况。在公交专用道条件下,采集公交车辆在干线上行驶时的时间和距离数据,在时间距离图上将(x=距离,y=时间)数据点连接成线得到该车的行驶轨迹线,如图 1所示。
|
| 图 1 时间距离图上公交车辆的行驶轨迹线 Fig. 1 Travel trajectory of transit vehicle on time distance chart |
| |
由图 1可见,当公交车辆进入公交站2进行停靠时,行驶轨迹表现为一段垂直向上的线段,其长度表示公交进站的停靠时间。当公交车离开公交站2后遇到下游交叉口的红灯信号,等待红灯之后再进入下一个绿波带。从该轨迹线可见,公交车经公交站1和公交站2进站停靠后,无法继续保留在当前绿波带,只能延后至下一个绿波带。
1.2 公交车流在路段上的行驶轨迹分布在时间距离轨迹图中,单辆公交车的行驶轨迹不具有代表性,因此需要从宏观上分析公交车流整体的行驶轨迹分布情况。绘制公交车流行驶轨迹需要调查的数据有干线的道路条件、信号控制方案、公交车流的速度分布、公交进站停靠时间分布等。
上下游交叉口之间的路段上可能布设的公交站数量有0个、1个和2个共3种情况,因此公交行驶轨迹变化情况各不相同。
(1) 路段上无公交站
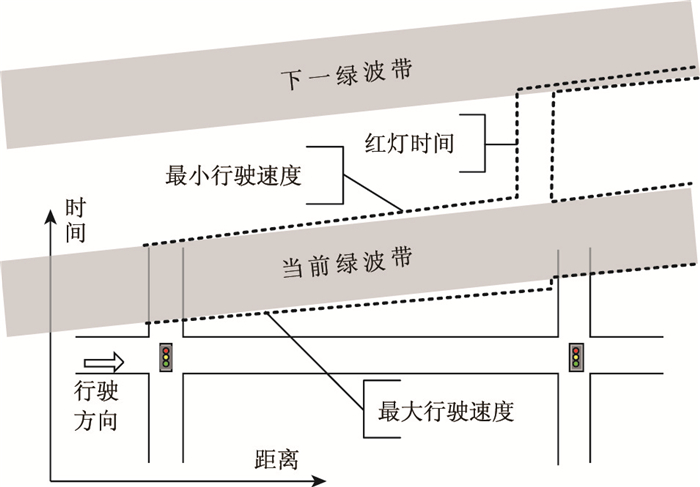
以上游交叉口停车线上的绿波带为起点,公交车流轨迹沿着行驶方向有较小幅度的扩散,在下游交叉口受信号控制影响被分为两个部分,轨迹分布如图 2所示。
|
| 图 2 路段上无公交站的行驶轨迹分布 Fig. 2 Travel trajectory distribution of road section without bus stop |
| |
图 2中的虚线表示公交车流行驶轨迹分布的范围,其上、下界限分别是公交车速分布中的最小行驶速度和最大行驶速度。当最小行驶速度低于绿波带速时,速度较慢的公交车将往上延后至绿波带外面,在下游交叉口遇到红灯,然后在下一绿波带的初期继续行驶,即这部分公交车将被延后至下一绿波带。当最大行驶速度高于绿波带速时,速度较快的公交车将往下超前于当前绿波带,并在下游交叉口等待较短的红灯后重新进入当前绿波带。
由图 2可以看出,受到公交车辆在路段行驶速度差异和下游交叉口信号控制的影响,公交行驶轨迹分布在下游交叉口停车线上可以分解为两个部分:大部分保持在当前绿波带,少量延后至下一绿波带,其中延后的比例与绿波带速和公交车速分布有关系[18]。
根据路段上交叉口间的距离和公交车速分布,可以构建路段离散的转移矩阵TD, i,根据信号控制参数和绿灯启亮后车队离散的车头时距分布,可以构建信号控制的转移矩阵TC, i[18]。在上游交叉口的公交车辆到达分布Ai已知的前提下,通过矩阵乘法运算得到下游交叉口的公交车辆到达分布Ai+1[18]。
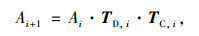
|
(1) |
式中,Ai+1为路段下游交叉口的公交到达分布;Ai为路段上游交叉口的公交到达分布;TD, i为路段离散的转移矩阵;TC, i为下游交叉口的信号控制转移矩阵。
(2) 路段上有一个公交站
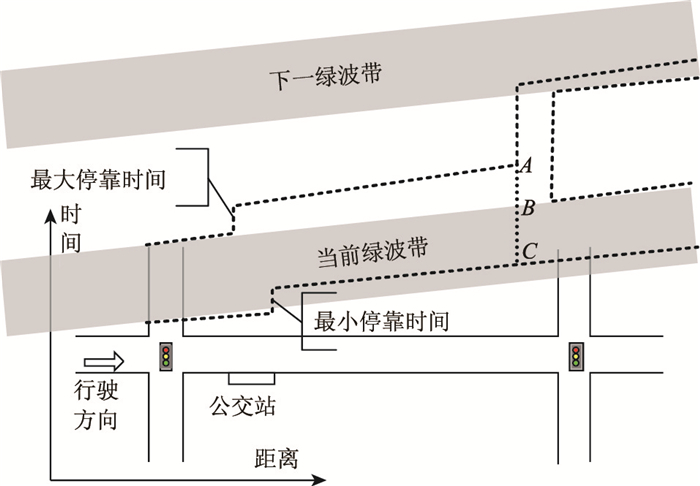
当路段上有一个公交站时,公交车辆必须进站停靠,公交车流的行驶轨迹分布范围沿纵向时间轴向上移动,在下游交叉口受信号控制影响被分为两个部分,轨迹分布如图 3所示。
|
| 图 3 路段上有一个公交站的行驶轨迹分布 Fig. 3 Travel trajectory distribution of road section with one bus stop |
| |
在图 3中,公交行驶轨迹分布在公交站处有一个台阶式的上移:下边界在公交站上移的时间长度为公交停靠时间分布中的最小停靠时间,上边界在公交站上移的时间长度为最大停靠时间。
在整个路段中,由于公交车流存在速度差异,行驶轨迹分布仍然有较小幅度的扩散。由于公交车流在下游交叉口受到信号控制的影响,其行驶轨迹分布被分解为两个部分,如图中的点线ABC所示,其中AB表示公交车是在红灯时间内到达交叉口,需要等待红灯并在绿灯初期进入下一绿波带,即“延后”部分;BC表示公交车仍然保留在当前绿波带内,即“保留”部分。
由图 3可以看出,受到公交车流在路段行驶速度差异、公交进站停靠和下游交叉口信号控制的共同影响,公交行驶轨迹在公交站上移一个台阶,在下游交叉口被分解为“延后”和“保留”两个部分[19]。与路段上无公交站的情况相比,此处“延后”的比例有所增加。
根据公交车辆的车头时距分布、公交车辆进站和出站时间分布、停靠时间分布等,计算得到公交车辆的延后时间分布,再扩展到延后的转移矩阵TS, j,结合路段离散转移矩阵TD, i和信号控制转移矩阵TC, i[19]。在上游交叉口的公交车辆到达分布Ai已知的前提下,通过矩阵乘法运算得到下游交叉口的公交车辆到达分布Ai+1[19]。
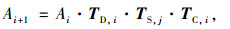
|
(2) |
式中,Ai+1为路段下游交叉口的公交到达分布;Ai为路段上游交叉口的公交到达分布;TS, j为路段上进入公交站j停靠后的转移矩阵。
(3) 路段上成对布设公交站
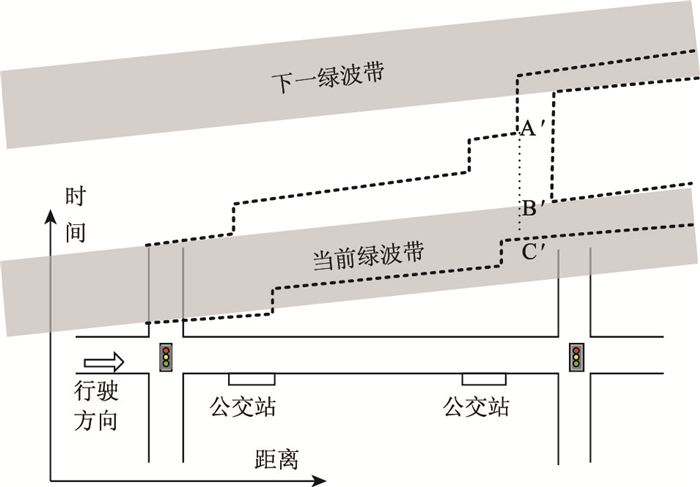
当路段上有2个公交站时,通常将公交站布设在路段两端,即公交站在路段上成对布设。公交车流的行驶轨迹分布沿纵向时间轴向上移动两次,在下游交叉口受信号控制影响被分为2个部分,轨迹分布如图 4所示。
|
| 图 4 路段上有两个公交站的行驶轨迹分布 Fig. 4 Travel trajectory distribution of road section with two bus stops |
| |
在图 4中,公交行驶轨迹分布依次在2个公交站各上移一个台阶,同时受到公交车行驶速度差异和下游交叉口信号控制的影响,公交车流行驶轨迹分布在下游交叉口也被分解为“延后”和“保留”两个部分,如图中的A′B′和B′C′段所示。与路段上只有一个公交站的情况相比,此处“延后”的比例相对较大。
同理,根据转移矩阵乘法运算规则,可以计算得到受两个公交站(j和j+1)影响的下游交叉口公交车辆到达分布Ai+1。

|
(3) |
式中,Ai+1为路段下游交叉口的公交到达分布;Ai为路段上游交叉口的公交到达分布;TS, j+1为路段上进入公交站j+1停靠后的转移矩阵。
1.3 公交车流在干线上的行驶轨迹分布以整条干线为研究对象时,先根据道路条件绘制时间距离图,再根据协调控制方案在图上绘制绿波带。以干线上第1个交叉口停车线上的绿波带为起点,沿公交行驶方向依次绘制下游各路段的行驶轨迹分布,最终可以得到公交车流在整条干线上的行驶轨迹分布情况。
假设该干线由n个交叉口和m个公交站组成,则在干线末端交叉口的下游,公交车辆的到达分布可以由上游各路段、交叉口、公交站的转移矩阵计算得到。计算方法是以每个交叉口的停车线为关键断面,沿着公交车辆行驶方向,依次计算每个关键断面的公交车辆到达分布,直到干线末端交叉口下游的关键断面An。
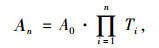
|
(4) |
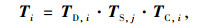
|
(5) |
式中,An为干线末端交叉口下游的公交到达分布;A0为干线上游起始断面的公交到达分布;Ti为交叉口i上游路段的总转移矩阵。
在干线的公交行驶轨迹分布图上,可以深入分析每个交叉口上行驶轨迹与绿波带之间的关系,有利于针对性地选择合适的公交优先信号控制策略。
在公交行驶轨迹分布的末端,根据行驶轨迹的分布情况,选择公交车流的行驶时间或延误时间较小者作为最优的协调控制方案。
2 公交站与交叉口的典型组合在干线协调背景下考虑多个公交站和交叉口时,不同的组合方案导致不同的公交行驶轨迹分布,具有代表性的组合有以下几种。
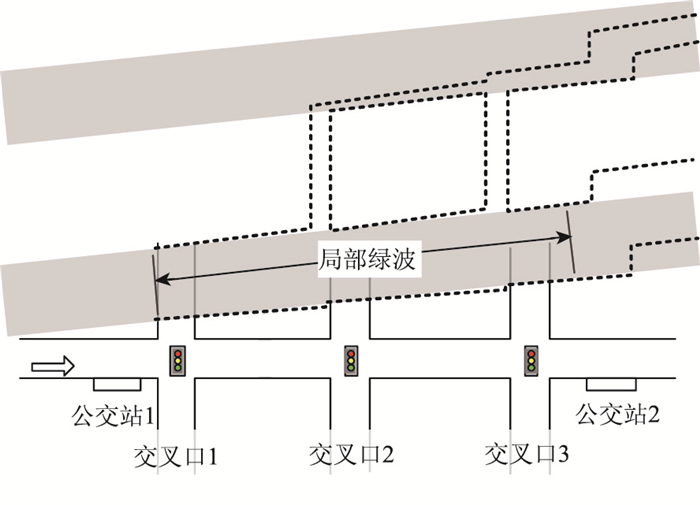
2.1 公交站间的交叉口群当2个公交站之间存在2个或多个交叉口(或信控的人行横道)时,上下游公交站及站间交叉口群形成一种典型组合,公交行驶轨迹分布如图 5所示。
|
| 图 5 公交站间交叉口群的行驶轨迹分布 Fig. 5 Travel trajectory distribution of intersections group between bus stops |
| |
在图 5的例子中,公交站1和公交站2之间有3个信号控制交叉口,公交车流离开公交站1进入绿波带,大部分公交车可以连续通过3个交叉口,少量速度较慢的公交车在交叉口2和交叉口3延后到下一绿波带。对公交车流而言,这种典型组合在两个公交站之间形成了一段有效的局部绿波。
2.2 成对布设与交叉口群的组合当考虑干线上更多的交叉口和公交站时,公交站在路段上成对布设与公交站间交叉口群的衔接可以形成另一种典型组合,公交行驶轨迹分布如图 6所示。

|
| 图 6 成对布设与交叉口群组合的行驶轨迹分布 Fig. 6 Travel trajectory distribution of combination of paired layout and intersections group |
| |
在图 6的例子中,公交站1和公交站2在路段上成对布设,在公交站2和公交站3之间有3个连续的交叉口。当公交车在公交站1和公交站2的停靠时间之和大于绿波带的绿灯时间时,公交行驶轨迹在交叉口2全部延后至下一绿波带,且集中于信号控制的绿灯初期。绿灯启亮后,公交车流进入一段由3个交叉口组成的局部绿波,连续通过交叉口2,3和4之后在公交站3进站停靠,出站后仍有大部分公交车保留在该绿波带中。
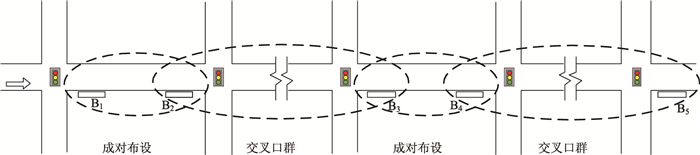
2.3 成对布设与交叉口群的交错衔接在干线上以公交站为衔接点,路段上成对布设与站间交叉口群交错衔接,可以形成非常理想的公交站点布设方案,如图 7所示。
|
| 图 7 成对布设与交叉口群的交错衔接 Fig. 7 Staggered connection of paired layout and intersections group |
| |
在图 7的理想布设方案中,公交车辆可以在成对布设的路段充分利用绿波带以外的红灯时间进站停靠,然后在下游交叉口过渡到下一绿波带。公交车流的延误主要集中在站间交叉口群中的首个交叉口,如图中的公交站B2下游的首个交叉口,而在局部绿波中其他交叉口对公交车流的影响非常小;公交车流再经下一成对布设的公交站进入下一个局部绿波。
3 站点布设优化在不改变干线协调控制方案的前提下,不同的公交站点布设方案将导致不同的公交车辆行驶轨迹,据此可以分析公交车流的运行效益,确定最优的站点布设方案。新建道路和改建道路在工程上有不同的特点,公交站点布设优化在新建和改建场景中有不同的操作流程。
3.1 新建道路的站点布设优化新建道路通常先规划再建设,规划中的公交站具有更多的位置调整空间。操作流程如下:
(1) 制订公交站点布设方案
将规划设计的公交站点布设情况定义为规划方案;在规划方案的基础上,根据道路条件参考“成对布设”与交叉口群“交错布设”方案,可以得到“理想方案”。
(2)绘制时间距离轨迹图
根据道路条件绘制时间距离图,按照协调控制参数绘制绿波带,先将规划方案、理想方案中的公交站位置标注在距离轴上,再按照前述方法分别绘制两种方案下的行驶轨迹分布情况,计算公交车流的到达分布,在干线末端得到最终的公交行驶轨迹分布。
(3)对比公交行驶轨迹分布
分析规划方案和理想方案的行驶轨迹分布情况,对比公交站移动前后的车辆到达分布变化情况。干线末端的行驶轨迹分布范围更靠下对应公交车流延误更少,即为最优的公交站点布设方案。
3.2 改建道路的站点布设优化对于已经建成的道路网络,由于受到公交规划、市政工程等各种条件的限制,公交站点位置只能进行局部微调。公交站位置在交叉口间的同一路段上移动时,对公交运行轨迹分布和到达分布的影响很小;但是公交站从一个路段移动到另一个路段上(跨越了一个交叉口)时,公交车流的轨迹分布有很大的变化。因此建议以“成对布设”为参考,或者重点考虑直行相位绿灯时间较短的关键交叉口,将公交站的位置在交叉口上游和下游进行微调。
将现有公交站点布设情况定义为现状方案。在现状方案基础上对公交站位置进行调整,即选择有条件移动位置的公交站,将其从交叉口上游移动至交叉口下游,或者反之。改变位置后的方案定义为优化方案。
按照同样的操作流程依次绘制现状方案和优化方案的时间距离轨迹图,计算关键断面的车辆到达分布,对比干线末端的公交行驶轨迹分布和到达分布,选择公交车流延误较小的方案作为最优的站点布设方案。
4 仿真试验与结果分析为了验证上述公交站点布设优化方法,在VISSIM仿真软件中构建干线仿真模型,分别设置现状方案、优化方案和理想方案,运行仿真试验,统计公交车流的延误,记录车辆位置和时间数据用于绘制轨迹线。
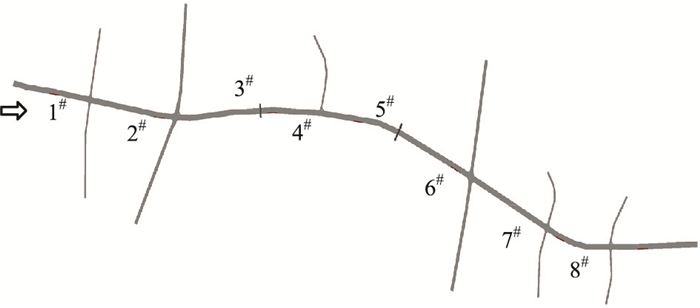
4.1 构建干线仿真模型以武汉市雄楚大道为背景构建仿真模型,如图 8所示。干线上共设有6个信控交叉口和2个信控人行横道(3#和5#)。根据道路条件和交通条件设置由西向东的单向绿波。信号控制方案的公共周期为90 s,其中2个关键交叉口(2#和6#)的直行绿灯时间为35 s,其余信号控制方案中的直行绿灯时间为50 s。干线上设有公交专用道,沿线共设有7个直线式公交站。
|
| 图 8 仿真软件VISSIM中的主干道模型 Fig. 8 Arterial road model in simulation software VISSIM |
| |
4.2 公交站点布设方案
3种公交站点布设方案如图 9所示。现状方案就是现有道路条件下的公交站点位置。在现状方案基础上,将交叉口6#上游的公交站进行微调,即由交叉口6#上游移动到下游,如图 9中的箭头所示,得到站点布设的优化方案。

|
| 图 9 3种公交站点布设方案示意图 Fig. 9 Schematic diagram of 3 layout schemes of bus stops |
| |
为了验证理想布设方案的优化效果,根据道路条件和公交站位置及约束关系,制订了成对布设与交叉口群交错衔接的理想方案,如图 9中最下一行所示。
在图 9的理想方案中,公交站在交叉口1#和2#、4#和5#及6#和7#之间成对布设,在交叉口2#~4#、5#~ 6#及7#~8#之间形成3个交叉口群。由图 9可见,调整后的公交站间距离有较大的变动,交叉口群两端的公交站间距离较大,成对布设的公交站间距离较小。
4.3 运行微观仿真试验在VISSIM仿真软件中,设置相同的流量、路径及公交发车班次等,采用相同的绿波协调控制方案,根据3种公交站点布设方案设置公交站点位置,作为3种仿真试验场景。
运行多个随机种子的仿真试验,统计公交车流在干线上的延误时间。仿真运行时,记录公交专用道上每辆公交车的路段坐标、仿真时间、车辆编号信息为(x, y, z),用于绘制公交行驶轨迹。
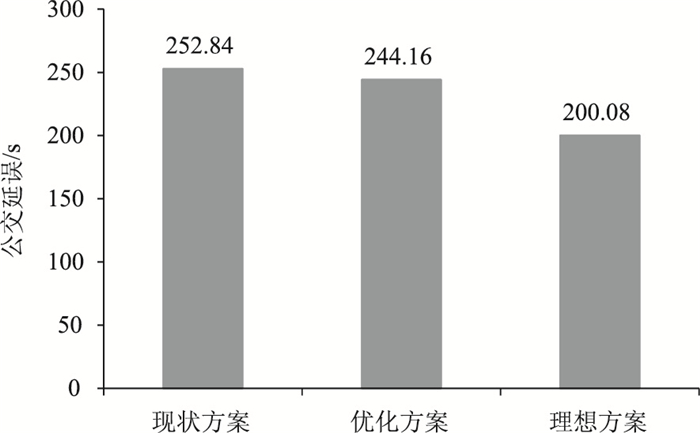
4.4 公交延误对比分析统计多次仿真试验的延误评价结果,3种公交站点布设方案的公交延误如图 10所示。
|
| 图 10 3种公交站点布设方案的公交延误对比 Fig. 10 Comparison of transit delays of 3 layout schemes of bus stops |
| |
由图 10可见,优化方案的公交延误比现状方案降低了3.8%,优化效果不明显。理想方案的公交延误比现状方案降低了22%,优化效果非常明显。此外,3种公交站点布设方案中,社会车辆的直行车流延误未见显著差异。
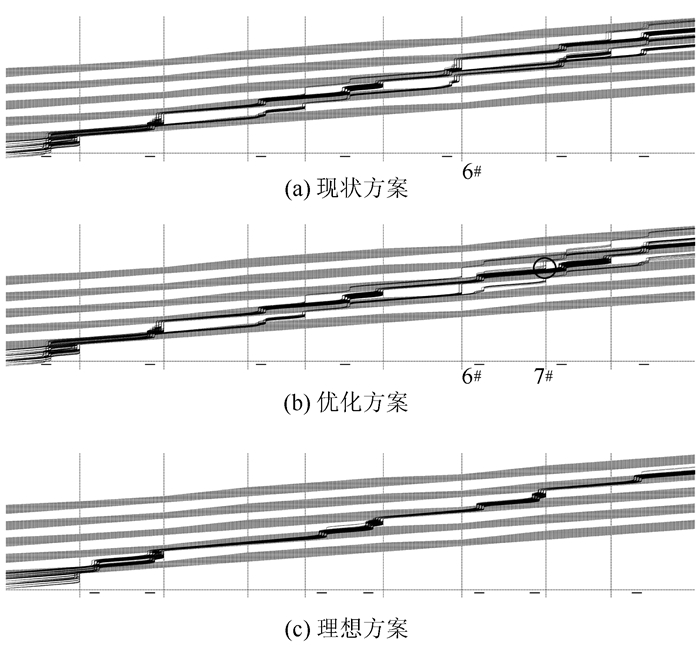
4.5 公交行驶轨迹分析根据仿真统计的车辆行驶距离和时间信息,在AutoCAD软件中绘制公交行驶轨迹线。为了便于对比分析,将所有公交车的轨迹线以周期为单位下移到第1个周期中,分别得到3种站点布设方案的公交行驶轨迹分布情况,如图 11所示。
|
| 图 11 3种公交站点布设方案的行驶轨迹分布 Fig. 11 Travel trajectory distribution of 3 layout schemes of bus stops |
| |
由图 11可见,在现状方案与优化方案中,移动前后的公交站分别位于交叉口6#的上游和下游,对公交行驶轨迹的影响也不一样。由于交叉口6#是直行绿灯时间相对较短的关键交叉口,公交站设在下游使更多的公交车先通过该交叉口再进入公交站,出站后仍保留在该绿波带中,并且大部分公交车在绿灯时间内通过了下游的交叉口7#,见图(b)中圆圈标示。
理想方案行驶轨迹分布的最大特点是车辆行驶轨迹非常集中,并且可以在公交站成对布设的路段过渡到下一个绿波带,在站间交叉口群内形成稳定的局部绿波带。在干线的末端,行驶轨迹绝大部分集中在第4个绿波带,因此该方案下的公交延误相对其他方案要小一些。
5 结论在干线协调控制背景下,利用时间距离图上的绿波带和公交行驶轨迹,可以深入分析公交站点不同位置对公交运行的影响。通过分析干线上交叉口和公交站位置的不同组合,提出公交站成对布设与站间交叉口群交错衔接的理想布设方案。改建场景中的公交站点位置受到公交规划和市政工程等方面的限制,只能在交叉口上下游进行微调;已规划未建设的公交站点布设可以参考理想布设方案进行整体优化。本研究是基于已设置公交专用道的假设,其研究成果也适用于BRT、有轨电车等公共交通系统的站点布设优化。由于仅考虑了公交专用道条件,公交车流与社会车流混行条件下的行驶轨迹将更加复杂和多变,其站点布设优化还有待进一步深入研究。
| [1] |
LEE J, SHALABY A, GREENOUGH J, et al. Advanced Transit Signal Priority Control with Online Microsimulation-based Transit Prediction Model[J]. Transportation Research Record, 2005, 1925: 185-194. |
| [2] |
KIM W, RILETT L. Improved Transit Signal Priority System for Networks with Nearside Bus Stops[J]. Transportation Research Record, 2005, 1925: 205-214. |
| [3] |
ZHENG J, WANG Y, LIU H, et al. Modeling Impact of Near-side Bus Stop on Transit Delays at Transit Signal Priority Enabled Intersections[C]//Proceedings of Transportation Research Board 86th Annual Meeting. Washington, D.C.: Transportation Research Board, 2007.
|
| [4] |
DION F, GHANIM M. Impact of Dwell Time Variability on Transit Signal Priority Performance at Intersections with Nearside Bus Stop[C]//Proceedings of Transportation Research Board 86th Annual Meeting. Washington, D.C.: Transportation Research Board, 2007.
|
| [5] |
赵胜. 港湾式公交站位置对交叉口通行能力影响模拟分析[J]. 公路与汽运, 2017(5): 17-19. ZHAO Sheng. Simulation Analysis of Influence of Harbour Bus Station on Intersection Capacity[J]. Highways & Automotive Applications, 2017(5): 17-19. |
| [6] |
LUDWICK Jr, JOHN S. Bus Priority System: Simulation and Analysis[R]. Washington, D.C.: U.S. Department of Transportation, 1976.
|
| [7] |
BYRNE N, KOONCE P, BERTINI R L, et al. Using Hardware-in-the-loop Simulation to Evaluate Signal Control Strategies for Transit Signal Priority[J]. Transportation Research Record, 2005, 1925: 227-234. |
| [8] |
WANG D, YE Z. Effects of Bus Stop Location on the Efficiency of Bus Priority for Arterials with Segmented Signal Progression Control[C]//Proceedings of 15th COTA International Conference of Transportation Professional. Reston: American Society of Civil Engineers, 2015.
|
| [9] |
王达琳.公交优先信号协调控制下的站点位置优化研究[D].南京: 东南大学, 2016. WANG Da-lin. Optimization of Bus Stop Location under Bus Priority Signal Coordination Control[D]. Nanjing: Southeast University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10286-1016326948.htm |
| [10] |
吕林.城市公交站点优化设计方法研究[D].南京: 东南大学, 2006. LÜ Lin. Research on Optimization Design Method of Urban Bus Station[D]. Nanjing: Southeast University, 2006. http://cdmd.cnki.com.cn/article/cdmd-10286-2007031734.htm |
| [11] |
葛宏伟.城市公交停靠站点交通影响分析及优化技术研究[D].南京: 东南大学, 2006. GE Hong-wei. Traffic Impact Analysis and Optimization Technology of Urban Bus Stops[D]. Nanjing: Southeast University, 2006. http://d.wanfangdata.com.cn/Thesis/Y1040713 |
| [12] |
FITZPATRICK K, NOWLIN R L. Effects of Bus Stop Design on Suburban Arterial Operations[J]. Transportation Research Record, 1997, 1571: 31-41. |
| [13] |
SATIENNAM T, FUKUDA A, MUROI T, et al. An Enhanced Public Transportation Priority System for Two-lane Arterials with Nearside Bus Stops[C]//Proceedings of the Eastern Asia Society for Transportation Studies. Kawana, Japan: EASTS, 2005: 1309-1321.
|
| [14] |
吴志周, 马万经, 杨晓光. 考虑信号优先的相邻公交停靠站最佳布置方法[J]. 公路交通科技, 2008, 25(1): 146-150. WU Zhi-zhou, MA Wan-jing, YANG Xiao-guang. Optimal Location of Adjacent Bus Stops on Condition of Bus Signal Priority[J]. Journal of Highway and Transportation Research and Development, 2008, 25(1): 146-150. |
| [15] |
LIU Z, LI K, NI Y. Optimization of Bus Stops Layout Under the Conditions of Coordinated Control[J]. Transport Research Procedia, 2017, 25: 1585-1596. |
| [16] |
赵尘. 基于GIS的站点选址优化:以龙岩市新罗区2路公交车为例[J]. 信息与电脑, 2018(6): 3-5. ZHAO Chen. Bus Stops Site Selection Optimization Based on GIS:Taking the No.2 Bus in Xinluo District of Longyan City as an Example[J]. China Computer & Communication, 2018(6): 3-5. |
| [17] |
DEWI D, RAKHMATULLOH A, ANGGRAINI P. Mapping Between Bus Rapid Transit Shelter and High School Location in Semarang[C]//2nd Geoplanning-International Conference on Geomatics and Planning.Surakarta, Indonesia: [s.l.] 2018.
|
| [18] |
柳祖鹏, 倪颖, 李克平. 干线关键断面的到车率分布预测[J]. 同济大学学报:自然科学版, 2014, 42(5): 714-720. LIU Zu-peng, NI Ying, LI Ke-ping. Prediction of Arrival Flow Profile on Critical Section of Arterial[J]. Journal of Tongji University:Natural Science Edition, 2014, 42(5): 714-720. |
| [19] |
柳祖鹏, 李克平, 倪颖. 考虑停靠服务的公交到车率分布预测[J]. 中国公路学报, 2015, 28(1): 87-94. LIU Zu-peng, LI Ke-ping, NI Ying. Prediction of Distribution of Arrival Flow Rates of Public Traffic with Bus Stopping Service Considered[J]. China Journal of Highway and Transport, 2015, 28(1): 87-94. |
 2019, Vol. 36
2019, Vol. 36
