扩展功能
文章信息
- 杜明洋, 程琳, 李雪峰
- DU Ming-yang, CHENG Lin, LI Xue-feng
- 基于自适应粒子群小波网络的公共自行车出行需求预测
- Prediction of Public Bike Trip Demand Based on APSO-WNN
- 公路交通科技, 2019, 36(6): 94-102
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(6): 94-102
- 10.3969/j.issn.1002-0268.2019.06.013
-
文章历史
- 收稿日期: 2018-03-09
公共自行车作为解决城市“最后一公里”的有效出行工具,具有低碳排放、绿色出行的优良特性[1-2]。然而,由于交通潮汐性现象,早晚高峰时段常出现双向流量严重不平衡,部分租赁点单一方向借车需求大,而另一方向还车需求大,系统中不同租赁点的需求差异明显[3]。尤其在高峰时段,部分租赁点无车可借而部分站点停车位满载,这都直接影响运营者的效益、自行车的周转率以及用户的满意度[4]。然而,对各租赁点不同时段需求进行合理的预测是实现城市公共自行车运营供需平衡的关键,同时这也是解决“租/还车难”问题的有效途径。
目前,学者们主要聚焦于构建数学模型对公共自行车出行需求进行预测。REGUE[5]以站点历史出行数据、天气、日期、时间为基础,建立了一种基于梯度提升机方法的需求预测模型,结合调度需求和调度车辆路径模型使系统性能提升7%,降低了不满意用户数量;Kaltenbrunner[6]从时间上分析了里昂、巴塞罗那公共自行车的动态特征并基于此构建了自行车动态预测模型;何流[7]在研究需求等待、转移和消退变化规律的基础上,基于历史借还信息建立了短期多时段的需求预测模型,并将其与调度计划模型结合实现动态需求预测;温惠英[8]考虑不同时段的租借人次、周转率、用地类型、居住人口和建筑面积等因素,构建了自行车需求预测的迭代回归模型,该模型能充分利用短期调查数据,更准确地确定新租赁点投放自行车的数量;吴瑶[9]以未来年居民出行OD为基础,考虑公共自行车分担率、停车桩周转率等因素,对城市公共自行车需求及停车桩规模进行预测;解小平[10]利用连续30 d工作日公共自行车需求量,基于改进的Elman神经网络建立了单点需求预测模型,该模型能较好地对租赁点某时段的需求量进行预测,降低调度的盲目性,改善供需不平衡的状态。以上研究本质上是考虑公共自行车租赁点自身特征以及外部环境因素进行需求预测,并未考虑到租赁点之间需求的相互影响,而相邻租赁点的借还需求具有相似性,并且在一定程度上能够缓解用户的借还车需求,是自行车出行需求预测不可忽视的重要因素。此外,学者把借还车需求用同一个模型来度量,忽略了借车和还车的需求差异性,由此来预测对模型的准确性具有一定的影响。
基于此,本文尝试使用关联租赁点出行信息,结合租赁点的周转特性,以及本租赁点历史出行信息作为影响因子分别进行自行车借、还需求预测。考虑到小波神经网络是小波分析和神经网络的直接融合,自适应粒子群算法具有快速的全局搜索能力。本文构建了自适应粒子群小波神经网络的自行车出行需求预测模型,通过动态变化惯性权重并基于群体适应度变化率自适应地进行变异操作来优化小波神经网络的初始参数,最后用美国纽约市公共自行车系统的出行数据进行实例分析验证模型的有效性。
1 公共自行车系统借还影响因素分析公共自行车系统借还需求受许多因素的影响,选取合理的影响因素是进行准确预测的基础。国内外研究主要考虑系统历史借还数据、天气、时间、日期以及外部环境等作为影响因素[11]。本文尝试基于系统的借还特性以及相邻租赁点的相似、互补特性来合理选取出行需求的影响因素,为预测模型的建立做好铺垫。
1.1 公共自行车系统借还特性分析(1) 周转特性
公共自行车借还周转率分为自行车周转率和停车桩周转率,其中,前者是指单位时间内每辆自行车平均被借出的次数,反映了自行车的使用效率;后者是指单位时间内每个停车桩停放归还自行车的次数, 反映了停车桩的使用效率,是租赁点还车特性的重要体现[12]。二者的计算如下:
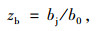
|
(1) |
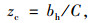
|
(2) |
式中, zb和zc分别为自行车周转率和停车桩周转率;bj和bh分别为单位时间内自行车借出和归还次数;b0为初始时刻自行车辆数;C为停车桩数量。
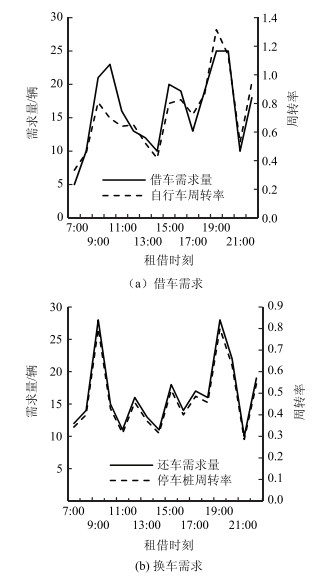
以纽约市公共自行车系统Broadway & E 14 S租赁点2017年6月23日的出行数据以1 h为间隔统计其借还需求,结合租赁点的停车桩数量和估算的初始时刻自行车数量,绘制借还需求和周转率的关系如图 1所示。由于此租赁点附近有两处地铁换乘站并靠近Union square park,故系统的借还需求存在明显的高峰特性。从图中可知早高峰借车需求和周转率在8:00—10:00最大,平均为22辆/h和0.76,还车需求和停车桩周转率在8:00—9:00最大,平均为28辆和0.8;晚高峰在18:00—20:00也存在相似的现象。这可能是因为早晚高峰期间居民在此进行地铁换乘。在非高峰时段,由于周边用地性质的影响,借还需求量并非很低,平均维持在15辆/h。
|
| 图 1 自行车借、还车需求和周转率关系图 Fig. 1 Relationship between bike borrowing/returning demand and turnover rate |
| |
由上述分析可知,公共自行车系统的借还需求变化趋势和周转率变化趋势较为相似。因此,在借还需求预测时可考虑周转率因素对需求的影响,另外,由于借还周转率的指标不同,故应将借还需求分别预测。
(2) 相似和互补性
在单个租赁点的周边范围内,相邻租赁点用地性质类似,此特性定义为相邻租赁点借还需求的功能相似性。互补性是指公共自行车系统中相邻租赁点具有一定的替代作用,当出行者到达租赁点无车可借时可去相邻租赁点借车,当车位满载时只能选择去相邻租赁点还车。
实际情况中,距离越远,出行者去相邻租赁点借车概率越小,放弃自行车而选择其他出行方式的概率越大,故距离对借车相邻租赁点的选取起关键作用;然而,当出行者发现无位可还时,只能选择去相邻租赁点还车,但不同的是还车点未必是最近的租赁点。如图 2所示,A点周边有两个相邻租赁点B和C,用户的目的地D距离C点80 m,当租赁点A车位满载时,用户应当选择租赁点C而非B还车,因为B离用户的目的地越来越远,此时C点称为A的关联租赁点。因此,在选择还车关联租赁点时,不能仅依据距离,还应结合借还需求的相关系数进行综合考虑。

|
| 图 2 关联租赁点示意图 Fig. 2 Schematic diagram of associated rental stations |
| |
为了对借、还关联租赁点进行合理的选取,本研究参考El-Geneidy等研究的居民可接受的最大步行距离[13-14],选取租赁点周边600 m服务半径进行相邻租赁点的功能相似和互补性分析,并定义如下指标:
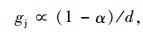
|
(3) |
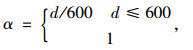
|
(4) |
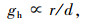
|
(5) |
式中,gj,gh分别为相邻借、还车租赁点出行需求关联度;d为待选取的相邻租赁点与预测的目标租赁点之间的步行距离;α为放弃系数,即放弃选择自行车而选择其他替代方式出行的比例;r为待选取的相邻还车租赁点与预测的目标还车租赁点间的相关系数。
以纽约市公共自行车系统2017年6月的出行数据为例,选取Cooper Square & E 7 St租赁点及周边600 m服务半径内的7个租赁点(分别距离253,260,307,405,529,566,585 m),以1 h为间隔统计其工作日和周末的借、还需求进行相关系数的计算,然后结合7个租赁点距离的分布进行需求关联度的计算,最后绘制相邻租赁点关联度变化图如图 3所示。

|
| 图 3 相邻租赁点关联度变化图 Fig. 3 Correlation degree change curves of neighboring rental stations |
| |
从图中可以看出,租车关联度变化曲线在工作日和周末重合,且随着距离的增大由2.3迅速下降到接近于0,主要因为在借车关联租赁点的选取上,距离起到关键性作用。相对而言,还车关联度变化曲线在工作日和周末呈现出类似的变化趋势,主要因为在还车关联租赁点的选取上,距离和借还需求相关系数同时发挥作用;在距离260, 307, 566, 585 m共4个相邻租赁点处出现回升现象,即还车用户在租赁点车位满载时选择的相邻租赁点并非为距离最近的租赁点,还车租赁点还和用户的目的地位置有关。因此,本例中借、还车关联租赁点应分别选取260,307 m处的租赁点。
由上述分析可知,关联租赁点与预测租赁点借还需求在相近时刻具有功能相似性和互补性,比如:A在早高峰8:00的出行需求会受到关联租赁点C在8:00附近出行需求(简称关联租赁点的即时出行需求)的影响。由于关联租赁点的即时出行需求在预测前同样不能及时获取,因此,本文对关联租赁点的即时出行需求预测仅从关联租赁点的历史出行信息中进行预测得到。
(3) 周期稳定特性
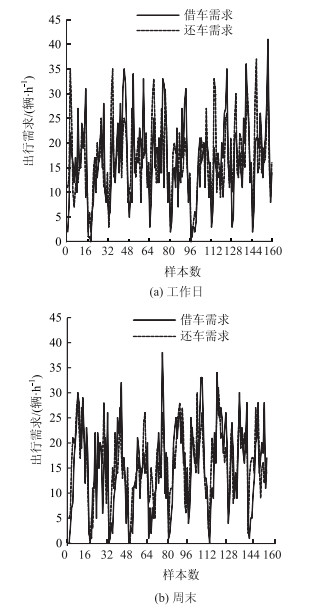
对纽约市公共自行车系统Broadway & E 14 S租赁点2017年5—6月份每日6:00—22:00的出行数据,以1 h为间隔统计其工作日和周末的借还需求,如图 4所示。图中横轴一个间隔(16 h)代表一天的数据,由图中趋势可以看出,公共自行车系统的借还需求具有周期性变化的特征。另外,工作日的出行具有早晚两个高峰,周末只有一个午后高峰,这可能与工作日通勤交通较大,周末午后居民购物娱乐出行增加有关,因此工作日和周末的出行需求应分别预测。
|
| 图 4 公共自行车工作日(左)、周末(右)借还需求变化 Fig. 4 Borrowing/returning demand changes of public bikes in weekdays and weekend |
| |
为进一步说明本租赁点历史出行信息对出行需求预测的影响,本文利用上述数据分别构造出公共自行车某日某时段的借还需求与相邻天、上周同天及相邻天对应时段借还需求的样本并进行相关性分析,相关性采用斯皮尔曼等级相关系数(Spearman)[15]表示,计算公式如下所示:
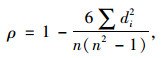
|
(6) |

|
(7) |
式中,ρ为相关性系数:n为样本总数量;di为秩次之差;x′i,y′i分别为第i个自变量和对应的因变量在从大到小排列后数据所在的位置,i=1, 2, …, n,自变量为预测日相邻天、上周同天及相邻天对应时段的借还需求,因变量为预测日某时段的借还需求。
相关系数的计算结果如表 1、表 2所示,从表中可以看出,本租赁点工作日的出行需求与前一天和上周同天的相关系数较大;周末的出行需求与上周同天的相关系数较大。
| 本租赁点 | 上周前天 | 上周同天 | 上周后天 | 前3天 | 前2天 | 前1天 |
| 租车 | 0.51 | 0.70 | 0.52 | 0.46 | 0.48 | 0.55 |
| 还车 | 0.46 | 0.66 | 0.42 | 0.40 | 0.46 | 0.46 |
| 本租赁点 | 上周同天 | 前1天 |
| 租车 | 0.68 | 0.46 |
| 还车 | 0.52 | 0.47 |
1.2 公共自行车系统借还影响因素选取
通过上一小节的分析表明,相邻租赁点间的需求相似、互补性以及借还周转特性是出行需求预测不可忽视的重要因素,基于此,本文选取本租赁点相同时段历史不同天的出行需求和周转率、关联租赁点相同时段历史不同天的出行需求和周转率以及时间作为本文预测的主要影响因素。
(1) 相同时段历史出行需求(时间特性)
对于历史出行日期的选取,在工作日,本文选取前1天及上周同天的出行需求作为主要影响因素;周末则选取上周同天的出行需求作为主要因素。
(2) 相同时段历史周转特性
由于周转率和借还需求之间有较强的相关关系,本文在对工作日和周末的借还需求预测时,借车以时间特性中所选取日期的自行车周转率作为影响因素,还车以时间特性中选取日期的停车桩周转率作为预测影响因素构建模型。
(3) 相同时段即时空间关联特性
由于关联租赁点的即时出行需求对本租赁点的借还需求具有空间上的相似性和互补性,故将关联租赁点的即时借还需求作为预测影响因素代入模型。具体而言,关联租赁点的即时借还需求预测可由关联租赁点的历史时间特性数据和周转特性数据作为影响因素进行预测。
2 求解算法小波神经网络(简称“小波网络”)通过平移和伸缩对信号进行多尺度分析,是一类通用函数逼近器[16],本文中的小波神经网络采用融合型小波网络。
粒子群算法(PSO)是一种基于群体协作的人工智能优化技术[17]。其中惯性权值ω对算法的收敛性能具有一定的影响,粒子的全局搜索能力随着其值的变大而增强,局部搜索能力则相反。为了兼顾两者,本文采用非线性函数下降策略动态变化惯性权重来控制算法进程:
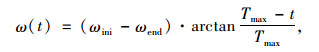
|
(8) |
式中,ωini为初始惯性权重;ωend为进化至最大代数时的惯性权重;Tmax为最大迭代次数;t为当前迭代次数,本文ωini,ωend分别取0.8,1.2。
粒子群优化算法结构简单,求解速度快,但该算法容易陷入局部最优,出现“早熟”现象。针对上述不足,本文通过对gbest自适应变异操作可提高种群多样性以实现算法改进[18-19]。
在迭代次数达到阈值,适应度变化率满足条件时进行自适应变异操作,适应度变化率k:
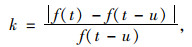
|
(9) |
式中,f(t)为第t代的适应度;f(t-u)为第(t-u)代的适应度;u为适应度连续不变代数的阈值,本文取5;k为种群在u代数内适应度的变化率,k的临界取值为5%;文中迭代次数设定的阈值为300代。
对于gbest的自适应变异操作,本文采取增加随机扰动的方式,变异概率取0.08,gBestk表示全局极值gBest的第k维变量,η是服从Gauss(0, 1)分布的随机变量,则:
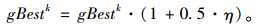
|
(10) |
本文算法的适应度函数选用神经网络训练误差的均方误差(Mean Squared Error):
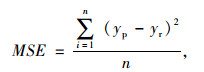
|
(11) |
式中,yp为借、还车需求预测值;yr为借、还车需求真实值;n为训练样本数。
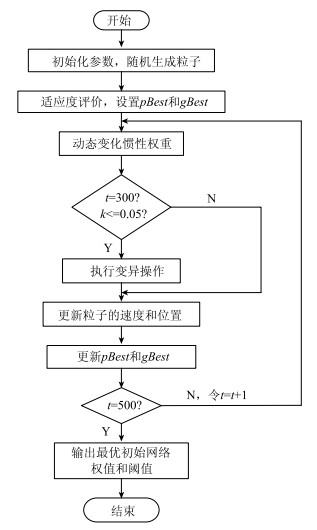
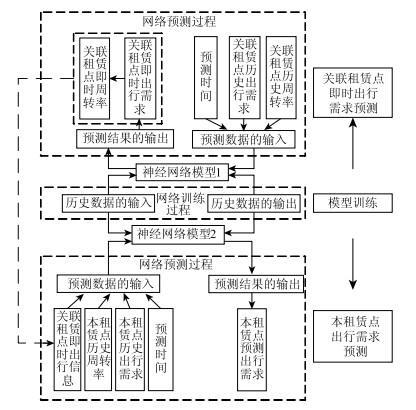
自适应粒子群小波神经网络训练流程如图 5所示,公共自行车系统借还需求预测整体流程如图 6所示。具体的预测流程如下:
|
| 图 5 自适应粒子群小波网络训练流程图 Fig. 5 Flowchart of APSO-WNN training |
| |
|
| 图 6 公共自行车系统借还需求预测流程图 Fig. 6 Flowchart of borrowing/returning demand prediction for public bike system |
| |
(1) 根据1.1小节的方法选取待预测目标租赁点的借、还车关联租赁点,并将工作日和周末各个时段的借、还出行需求分别进行预测。
(2) 构造关联租赁点相同时段历史出行需求、周转特性、时间数据作为输入,各时段即时借还需求作为输出的样本,进行训练得到神经网络模型1;构造本租赁点相同时段历史出行需求、周转特性、时间数据、关联租赁点的即时借还信息作为输入,本租赁点各时段借还需求作为输出的样本,进行训练得到神经网络模型2。
(3) 将待预测目标租赁点的关联租赁点相同时段历史出行需求、周转率以及时间作为输入代入神经网络模型1,得到关联租赁点各时段的即时出行信息(即时出行需求和即时周转率)。
(4) 将关联租赁点的即时出行信息、待预测目标租赁点相同时段的历史出行需求、周转率以及时间作为输入代入神经网络模型2,最终得到待预测目标租赁点各时段的借还需求。
3 实例分析 3.1 模型对比分析本文以美国纽约市公共自行车系统Broadway & E 14 S租赁点2017年5月和6月每日6:00—22:00的出行数据进行统计分析。其中工作日选取6月1日至28日的数据进行训练,用6月29日的数据进行测试;周末数据中6月17日、18日由于天气原因出行量极少将其从样本中排除,最终选取5月6日至6月10日的周末数据进行训练,用6月11日的数据进行测试。
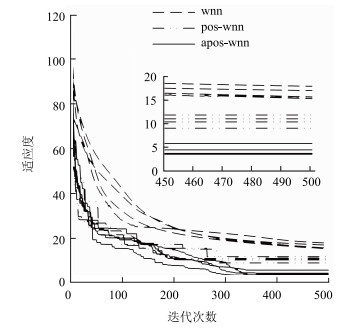
为检验模型的优化效果,本文分别采用小波网络(wnn)、粒子群优化的小波网络(pso-wnn)、自适应粒子群优化的小波网络(apso-wnn)进行预测来比较三者的适应度。为消除参数随机初始化造成的影响,本文分别选取4组预测结果进行适应度对比,结果如图 7所示。由图中可以看出,pso-wnn和apso-wnn的适应度明显低于wnn,且当迭代次数大于450次时,适应度值基本不再变化,说明粒子群算法以及自适应操作可以使模型跳出局部最优,有效降低小波网络的训练误差。
|
| 图 7 适应度曲线对比图 Fig. 7 Comparison of fitness curves |
| |
3.2 预测结果对比分析
文中采用平均相对误差(Mean Relative Error)和均方误差来说明模型预测的准确性,平均相对误差的计算公式见式(12):
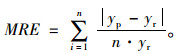
|
(12) |
租赁点工作日和周末借还需求预测结果如表 3和表 4所示,其中层结构表示输入层、隐含层、输出层最终选择的最优节点数目。由数据分析可得出:apso-wnn在工作日和周末借还需求预测的平均相对误差分别为11.05%和12.27 %,相比于wnn来说平均相对误差下降26.45%,均方误差减少36.31%;相比于pso-wnn来说平均相对误差下降15.81%,均方误差减少25.01%。可以看出,apso-wnn相比之下预测精度更高,稳定性更好,具有较强的可靠性。
| 预测模型 | wnn | pso-wnn | apso-wnn | |
| 租车 | 层结构 | 25-10-1 | 25-10-1 | 25-10-1 |
| MRE/% | 19.02 | 14.75 | 10.78 | |
| MSE | 24.88 | 21.56 | 15.25 | |
| 还车 | 层结构 | 25-11-1 | 25-11-1 | 25-12-1 |
| MRE/% | 16.23 | 13.85 | 11.33 | |
| MSE | 12.50 | 9.31 | 8.69 | |
| 预测模型 | wnn | pso-wnn | apso-wnn | |
| 租车 | 层结构 | 9-9-1 | 9-9-1 | 9-9-1 |
| MRE/% | 14.65 | 13.19 | 11.39 | |
| MSE | 23.25 | 21.88 | 9.94 | |
| 还车 | 层结构 | 9-6-1 | 9-6-1 | 9-6-1 |
| MRE/% | 20.67 | 16.48 | 13.15 | |
| MSE | 29.38 | 20.13 | 13.19 | |
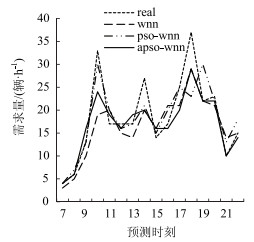
3种神经网络模型在工作日和周末借还车需求预测结果与真实值的对比如图 8~图 11所示。由结果可以看出,大部分时段中apso-wnn预测都较为精准,与实际需求更为接近,反映了apso-wnn相比于其他两种模型的优越性。仅有部分高峰时刻的预测需求比真实需求偏低,可能与高峰时刻存在的不可控因素(如交通拥堵所导致的短途出行对公共自行车利用率增加)有关。
|
| 图 8 租赁点工作日租车需求预测结果 Fig. 8 Prediction result of rental demand of rental station in weekdays |
| |
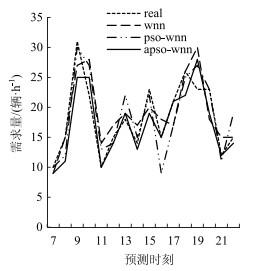
|
| 图 9 租赁点工作日还车需求预测结果 Fig. 9 Prediction result of returning demand of rental station in weekdays |
| |
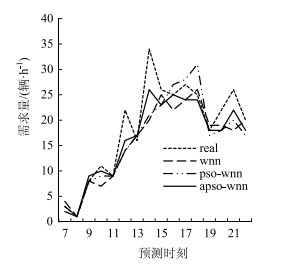
|
| 图 10 租赁点周末租车需求预测结果 Fig. 10 Prediction result of rental demand of rental station in weekend |
| |
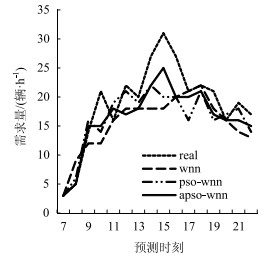
|
| 图 11 租赁点周末还车需求预测结果图 Fig. 11 Prediction result of returning demand of rental station in weekend |
| |
为进一步说明选取影响因素的有效性,本文在只考虑本租赁点历史出行信息和时间因素的条件下再次利用wnn,pso-wnn,apso-wnn这3个模型进行需求预测,得到的结果与综合考虑关联租赁点出行信息、租赁点周转特性以及本租赁点历史出行信息和时间因素所得的结果进行比较,得到图 12的结果。从图中可以看出,与只考虑本租赁点历史出行信息的模型相比较,综合考虑关联租赁点、周转率和本租赁点历史出行信息的模型,其预测精度在3个模型中均有不同程度的提高,并且apso-wnn预测精度的提高率最高,达到4%左右。

|
| 图 12 考虑关联租赁点、周转特性模型精度提高率 Fig. 12 Model prediction accuracy enhancement considering associated rental station and turnover characteristics |
| |
4 结论
本文在对公共自行车系统出行特性分析的基础上,综合关联租赁点的相似、互补特性、租赁点周转特性以及本租赁点历史出行信息和时间因素,并考虑工作日与周末的出行差异,提出利用自适应粒子群优化的小波神经网络分别进行公共自行车借、还需求预测。以美国纽约市的公共自行车系统出行数据为例对模型进行验证。通过wnn,pso-wnn,apso-wnn这3个模型的对比分析,结果表明:带自适应操作的粒子群优化算法能有效降低网络的训练误差;考虑关联租赁点相似、互补以及周转特性时能有效提高模型预测的准确度,工作日和周末的出行需求预测的平均相对误差分别为11.05%和12.27%。目前,在互联网和移动支付的背景下,无桩式的共享单车已成为城市居民短距离出行的重要交通工具,其与公共自行车在功能上存在一定的竞争和替代关系,如何将共享单车的出行影响考虑到公共自行车的出行需求预测中将是进一步研究的重点。
| [1] |
陈飞, 诸大建. 城市低碳竞争力理论与发展模式研究[J]. 城市规划学刊, 2011(4): 15-22. CHEN Fei, ZHU Da-jian. Research on the Theory and Development Model of Urban Low Carbon Competitiveness[J]. Urban Planning Forum, 2011(4): 15-22. |
| [2] |
RAVIV T, KOLKA O. Optimal Inventory Management of a Bike-sharing Station[J]. ⅡE Transactions, 2013, 45(10): 1077-1093. |
| [3] |
林燕平, 窦万峰. 基于ARIMA模型的城市公共自行车需求量短期预测方法研究[J]. 南京师范大学学报:工程技术版, 2016, 16(3): 36-40. LIN Yan-ping, DOU Wan-feng. Research on Short-Term Prediction Method of Demand Number in Urban Public Bicycle Based on the ARIMA Model[J]. Journal of Nanjing Normal University:Engineering and Technology Edition, 2016, 16(3): 36-40. |
| [4] |
ALVAREZ-VALDES R, BELENGUER J M, BENAVENT E, et al. Optimizing the Level of Service Quality of a Bike-Sharing System[J]. Omega, 2016, 62: 163-175. |
| [5] |
REGUE R, RECKER W. Proactive Vehicle Routing with Inferred Demand to Solve the Bikesharing Rebalancing Problem[J]. Transportation Research Part E:Logistics and Transportation Review, 2014, 72: 192-209. |
| [6] |
KALTENBRUNNER A, MEZA R, GRIVOLLA J, et al. Urban Cycles and Mobility Patterns:Exploring and Predicting Trends in a Bicycle-based Public Transport System[J]. Pervasive & Mobile Computing, 2010, 6(4): 455-466. |
| [7] |
何流, 李旭宏, 陈大伟, 等. 公共自行车动态调度系统需求预测模型研究[J]. 武汉理工大学学报:交通科学与工程版, 2013, 37(2): 278-282. HE Liu, LI Xu-hong, CHEN Da-wei, et al. Research on the Demand Forecast Model of Public Bike Dynamic Scheduling System[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2013, 37(2): 278-282. |
| [8] |
温惠英, 杨曌照. 基于迭代回归法的公共自行车投放量预测研究[J]. 武汉理工大学学报:交通科学与工程版, 2014, 38(2): 245-248. WEN Hui-ying, YANG Zhao-zhao. Iterative Regression-based Research on Demand Forecasting of Public Bicycle[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2014, 38(2): 245-248. |
| [9] |
吴瑶, 陈红, 鲍娜, 等. 基于多项logit模型的城市公共自行车租借需求预测模型[J]. 大连交通大学学报, 2013, 34(1): 19-24. WU Yao, CHEN Hong, BAO Na, et al. A Model Development of Public Bicycle Rental Demand Based on Multinomial Logit[J]. Journal of Dalian Jiaotong University, 2013, 34(1): 19-24. |
| [10] |
解小平, 邱建东, 汤旻安. 基于Elman神经网络的公共自行车单站点需求预测[J]. 计算机工程与应用, 2017, 53(16): 221-224. XIE Xiao-ping, QIU Jian-dong, TANG Min-an. Demand Prediction of Public Bicycle Rental Station Based on Elman Neural Network[J]. Computer Engineering and Applications, 2017, 53(16): 221-224. |
| [11] |
陆凯韬, 董红召, 陈宁. 基于LSTM的公共自行车服务点租还需求量预测[J]. 计算机测量与控制, 2017, 25(9): 178-181. LU Kai-tao, DONG Hong-zhao, CHEN Ning. Demand Prediction for Service Point of Public Bicycle System Based on LSTM[J]. Computer Measurement & Control, 2017, 25(9): 178-181. |
| [12] |
刘冰, 曹娟娟, 周于杰, 等. 城市公共自行车使用活动的时空间特征研究:以杭州为例[J]. 城市规划学刊, 2016(3): 77-84. LIU Bing, CAO Juan-juan, ZHOU Yu-jie, et al. A Study on the Temporal-spatial Features of Bicycle-sharing Activities:A Case of Hangzhou[J]. Urban Planning Forum, 2016(3): 77-84. |
| [13] |
李敏迪. 车辆供给和距离效应对公共自行车借车行为影响[J]. 公路交通科技, 2017, 34(2): 121-128. LI Min-di. Effect of Bike Supply and Distance Effect on Behavior of Borrowing Public Bikes[J]. Journal of Highway and Transportation Research and Development, 2017, 34(2): 121-128. |
| [14] |
EL-GENEIDY A, GRIMSRUD M, WASFI R, et al. New Evidence on Walking Distances to Transit Stops:Identifying Redundancies and Gaps Using Variable Service Areas[J]. Transportation, 2014, 41(1): 193-210. |
| [15] |
严利鑫, 吴超仲, 高嵩, 等. 驾驶人个体因素对驾驶愤怒情绪影响关系研究[J]. 交通信息与安全, 2013, 31(6): 119-124. YAN Li-xin, WU Chao-zhong, GAO Song, et al. Relationship between Driver's Temperament and Driving Anger[J]. Journal of Transport Information and Safety, 2013, 31(6): 119-124. |
| [16] |
季彦婕, 陆佳炜, 陈晓实, 等. 基于粒子群小波神经网络的公交到站时间预测[J]. 交通运输系统工程与信息, 2016, 16(3): 60-66. JI Yan-jie, LU Jia-wei, CHEN Xiao-shi, et al. Prediction Model of Bus Arrival Time Based on Particle Swarm Optimization and Wavelet Neural Network[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(3): 60-66. |
| [17] |
齐琳, 姚俭, 王心月. 基于改进粒子群算法的电动汽车充电站布局优化[J]. 公路交通科技, 2017, 34(6): 136-143. QI Lin, YAO Jian, WANG Xin-yue. Optimizing Layout of Electric Vehicle Charging Station Based on Improved Particle Swarm Optimization Algorithm[J]. Journal of Highway and Transportation Research and Development, 2017, 34(6): 136-143. |
| [18] |
吕振肃, 侯志荣. 自适应变异的粒子群优化算法[J]. 电子学报, 2004, 32(3): 416-420. LÜ Zhen-su, HOU Zhi-rong. Particle Swarm Optimization with Adaptive Mutation[J]. Acta Elfctronica Sinica, 2004, 32(3): 416-420. |
| [19] |
阳春华, 谷丽姗, 桂卫华. 自适应变异的粒子群优化算法[J]. 计算机工程, 2008, 34(16): 188-190. YANG Chun-hua, GU Li-shan, GUI Wei-hua. Particle Swarm Optimization Algorithm with Adaptive Mutation[J]. Computer Engineering, 2008, 34(16): 188-190. |
 2019, Vol. 36
2019, Vol. 36
