扩展功能
文章信息
- 王景春, 林佳秀, 靳俊中
- WANG Jing-chun, LIN Jia-xiu, JIN Jun-zhong
- 基于改进K-Means聚类模型的公路隧道施工风险分析及其应用
- Analysis on Highway Tunnel Construction Risk Based on Improved K-Means Clustering Model and Application
- 公路交通科技, 2019, 36(6): 58-64
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(6): 58-64
- 10.3969/j.issn.1002-0268.2019.06.008
-
文章历史
- 收稿日期: 2018-04-26
2. 河南省第二公路工程有限公司, 河南 郑州 450052
2. Henan Provincial Second Highway Engineering Co., Ltd., Zhengzhou Henan 450052, China
随着我国交通需求量的不断增加和山区公路建设的快速发展,公路隧道以其独特优势在山区公路建设中持续高速发展[1]。公路隧道工程由于受到施工环境恶劣、作业空间狭小等固有条件的限制,普遍存在作业风险高、安全生产事故频发等问题[2-3]。2012年11月19日,厦成高速公路雷公山隧道在进行初期支护钢拱架安装作业时出现拱顶塌方,引发4死2伤的较大安全生产事故;2013年11月29日,夏蓉高速公路徐家寨隧道因冒顶事故致使4人死亡。进行公路隧道施工风险分析,预先识别潜在危险源,采取措施规避风险,提高施工安全生产水平是保障公路隧道建设又快又好发展的现实需求。
目前我国公路隧道施工风险研究常用到层次分析法、模糊分析法等。程远等[4]通过层次分析法识别公路隧道施工各环节中的风险因素,将综合权重作为隧道施工风险等级的考量依据;李孜军等[5]提出一种组合式的隧道施工风险评估模型,利用模糊综合评价法得到隧道施工风险值,通过粗糙集约简学习样本,应用神经网络训练学习样本得出隧道施工安全水平;温世儒等[6]在传统模糊综合评价模型的基础上加入地质雷达预报,通过确定风险事件权重矩阵对隧道进行对比性风险评估。
上述方法从多个角度进行了隧道风险评判,仍存在以下几点不足。从研究对象来讲,上述文献主要研究隧道施工的综合风险等级,对于隧道施工工序具体细节的风险描述有所欠缺,不利于各施工环节的风险预判与风险规避。从研究方法来讲,层次分析法和模糊综合评价法的计算模型多依赖于基础运算,对数据的挖掘深度不够,具有较强的主观性与随意性。
本研究提出一种改进的K-Means聚类模型,对公路隧道施工组织各环节进行全周期风险测评。采用WBS-RBS分析法对隧道施工作业开展风险识别,通过耦合作业分解树与风险分解树梳理复杂的施工风险系统,为动态评估创造条件。针对公路隧道评价指标复杂多变的特点,提出将事故发生的可能性L、人员暴露于危险环境中的频繁程度E和发生事故或危险事件可能产生的后果C这3个因素,作为K-Means中的样本指标,并指定5组样本作为初始聚类中心。该模型通过计算机的大量运算进行数据挖掘,降低了评估过程的主观性与随意性,提高了准确性和可靠性,具有一定的理论依据和应用价值。
1 K-Means聚类基本原理K-Means聚类算法是1967年由J. B. Macqueen提出的,按照相似度将样本集分成多个类簇[7]。该算法简单高效,具有良好的局部搜索能力,是一种典型的基于质心距离的无监督或半监督迭代聚类方法,运用数据分类算法将数据样本划分为不同类别,每个数据样本属于唯一确定的类[8-11]。采用对象间的距离作为相似度指标,对象间距离越近,相似度越高,反之相似度越低。距离的定义方法有很多,应用最广泛的为欧氏距离[12-14],计算如下:
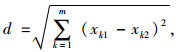
|
(1) |
式中,d为两个样本点间的欧氏距离;xk1为第1个样本点的第k维坐标;xk2为第2个样本点的第k维坐标。
将n个对象在欧式空间中建立样本点,按照某种标准从n个样本中选取k个点作为初始聚类中心,计算剩余n-k个样本点到初始中心点的距离。根据所求距离大小把每个样本数据划分到最近中心点所在的簇,对新簇进行均值运算得到下一环节的聚类中心[15-16]。不断重复此运算,当结果能够满足以下两个终止条件中的任何一个,K-Means运算结束。聚类终止条件为:
(1) 达到最大迭代次数;
(2) 目标函数达到最优,即对于不同的距离度量,目标函数往往不同。欧氏距离对应的目标函数如下:

|
(2) |
式中,E为误差函数值;k为聚类簇数;xj为第i个簇中的样本;ti为第i个簇中的样本数;ωi为第i个簇的聚类中心。
2 WBS-RBS隧道施工作业风险识别公路隧道具有施工工期长、工序复杂、风险易变等特点,随着施工进程、作业位置和周边环境的不同,施工风险类型也在不断变化。WBS-RBS是一种不仅可以把握工程风险全局,还可以兼顾工程风险细节的分析模型,采用WBS-RBS可以更加准确、全面地辨识隧道施工组织的潜在风险单元,具体步骤如下[17]:
(1) 构建WBS作业分解树:将工程项目自上而下逐层划分,构建便于风险研判的作业单元体系(Work Breakdown Structure, WBS),组成WBS体系最末端的工作单元称为作业包(Work Package)。
(2) 构建RBS风险分解树:将整个工程可能存在的风险因素逐层分解,明确风险所属的领域及产生的原因,所形成的风险判别体系称为RBS (Risk Breakdown Structure)。
(3) 构建WBS-RBS耦合矩阵:以WBS项目作业包为列向量,以RBS基本风险指标为行向量,建立WBS-RBS耦合矩阵,实现作业活动与风险之间的动态映射。判断该风险源在特定的项目作业包中是否存在,存在则为1,不存在或者发生可能性极小且后果很轻微则为0,进而判断项目所需关注的潜在风险事件及所处位置。
3 改进的K-Means聚类风险评估模型风险评估是对风险识别的深入应用与量化研究,通过数学运算对各风险事件发生的可能性及其带来损失的大小进行量化,进而转化为定性化等级描述。本研究提出对K-Means聚类算法进行改进并应用于公路隧道施工风险评估,具体步骤如下:
(1) 建立风险事件样本集U={u1, u2, …, un}:通过WBS-RBS耦合矩阵识别出项目中的n个风险事件,构成K-Means样本集U={u1, u2, …, un},对n个风险事件做进一步风险评估。
(2) 建立风险评估指标集V={L, E, C}:对n个风险事件进一步评估,提出将事故发生的可能性L,人员暴露于危险环境中的频繁程度E和发生事故或危险事件可能产生的后果C作为风险评估指标,具体如表 1所示。以传统LEC法的设计思想和取值标准为依据[18],以K-Means聚类风险评估模型的设计需求为目标,进行如下改进与创新。针对传统LEC法存在的数量级不统一、分级过于精细和分级档次差异等问题,进行针对性的修正改善,便于后续进行K-Means聚类运算。首先将L,E,C这3个指标的取值区间统一到[0, 10],然后对一些过于精细的分级进行重新整合,最终将L,E,C的定性描述与定量表达划分为5个等级,其具体划分细节不能与传统LEC法完全脱节,需在借鉴传统划分方法的基础上进行适当权衡。
| 参数 | 取值依据 | 取值范围 |
| 事故发生的可能性L | 非常可能 | [7, 10] |
| 可能,但不经常 | [4, 7) | |
| 可能性小 | [2, 4) | |
| 很不可能,可以设想 | [1, 2) | |
| 不可能 | [0, 1) | |
| 人员暴露于危险环境的频繁程度E | 连续暴露 | [7, 10] |
| 每天工作时间内暴露 | [4, 7) | |
| 每周1次或偶然暴露 | [2, 4) | |
| 每月1次暴露 | [1, 2) | |
| 几乎不暴露 | [0, 1) | |
| 发生事故可能产生的后果C | 10人以上死亡或直接经济损失100万以上 | [8, 10] |
| 3~9人死亡或直接经济损失30~100万 | [6, 8) | |
| 1~2人死亡或直接经济损失10~30万 | [4, 6) | |
| 严重伤残或经济损失1~10万 | [2, 4) | |
| 损失1~105工作日的失能伤害 | [0, 2) |
(3) 建立样本数据矩阵B:邀请5位相关领域工作人员根据施工现场实际情况对样本进行量化取值,为降低专家打分的主观性和随意性,对5位专家打分分值进行均值处理,得到样本数据矩阵:
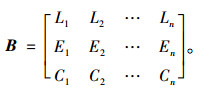
|
(4) 设置初始值k和μ:查阅相关资料,根据改进后L,E,C的取值标准和传统LEC法的取值标准,将风险等级D划分为Ⅰ到Ⅴ级。k为聚类结果的簇数(分组数),参照风险等级D划分为5个等级确定k=5;μ为最大迭代次数。值得注意的是,μ取值过小会导致局部最优,这里取μ=100。
(5) 设置初始聚类中心:确定初始聚类中心最常见的方法是从样本点中随机选取k个对象。该方法的缺陷是随着每次运行过程中初始聚类中心不同,每次运行的效果也不同。为了克服上述问题,本研究指定5组样本A={A1, A2, A3, A4, A5}作为初始聚类中心,保证运行结果输出的一致性。分别对应5个风险等级选取5组特殊样本作为初始聚类中心,具体取值及风险等级如表 2所示。其中Ai(i=1, 2, 3, 4, 5)的3个样本指标(L,E,C)取值按式(3)计算:
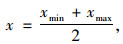
|
(3) |
| 标号 | 风险等级 | 风险描述 | L值 | E值 | C值 |
| A1 | Ⅰ | 微小风险 | 0.5 | 0.5 | 1 |
| A2 | Ⅱ | 较小风险 | 1.5 | 1.5 | 3 |
| A3 | Ⅲ | 一般风险 | 3 | 3 | 5 |
| A4 | Ⅳ | 较大风险 | 5.5 | 5.5 | 7 |
| A5 | Ⅴ | 重大风险 | 8.5 | 8.5 | 9 |
式中,x为样本指标L,E,C的取值;xmin为取值区间的最小值;xmax为取值区间的最大值。
(6) 模型实现与结果分析:应用SPSS软件实现K-Means聚类计算,得到n个风险事件的风险等级,根据风险等级结果制定行之有效的防范措施。
4 实例分析 4.1 工程背景某高速公路隧道全长1 971 m,路段内有两大背斜和3条断裂带,常伴有崩塌、碎落和泥石流等病害。区内年平均降雨量725.3 mm,7—9月份降雨集中,段内地下水较丰富,以松散岩石的孔隙水、基岩裂隙水和裂隙岩溶水形式赋存。隧道采用复合式衬砌设计,喷锚构筑法施工,具有工作面小、施工难度大、质量要求高和施工环境差等特点。
4.2 构造WBS作业分解树根据逐级逐层分解的原则对该公路隧道工程进行WBS分解,得到预加固支护、隧道开挖、初期支护、防水工程、二次衬砌和其他等6个主要阶段,在此基础上向下进一步分解,得到如图 1所示19个项目作业包。
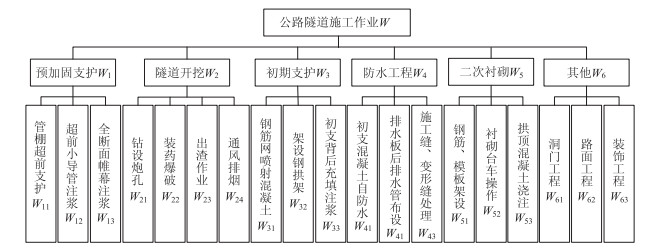
|
| 图 1 公路隧道施工作业分解树 Fig. 1 Work breakdown structure of highway tunnel construction |
| |
4.3 构造RBS风险分解树
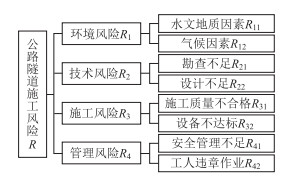
按照风险来源将该项目初步划分为环境风险、技术风险、施工风险和管理风险4部分,根据风险产生的具体原因进行下一步分解,得到风险分解树如图 2所示。
|
| 图 2 公路隧道施工风险分解树 Fig. 2 Risk breakdown structure of highway tunnel construction |
| |
4.4 构造WBS-RBS耦合矩阵
将RBS的末端风险因素与WBS的末端项目单元进行两两耦合,得到如表 3所示的风险耦合矩阵。由于篇幅有限,本研究仅选取预支护加固作业W1和隧道开挖作业W2两道工序进行风险分析,得到W11R22管棚超前支护设计不足,W11R31管棚超前支护施工质量不合格等20项可能风险事件。其他工序风险分析类似,本研究不予赘述。
| 风险因素 | W1 | W2 | … | ||||||||
| W11 | W12 | W13 | W21 | W22 | W23 | W24 | … | ||||
| R1 | R11 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | … | ||
| R12 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | … | |||
| R2 | R21 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | … | ||
| R22 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | … | |||
| R3 | R31 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | … | ||
| R32 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | … | |||
| R4 | R41 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | … | ||
| R42 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | … | |||
4.5 独立性检验
公路隧道施工系统的内部是复杂交错的,经过WBS-RBS风险梳理,构造出如表 3所示的风险耦合矩阵。然而所得风险耦合矩阵并不能保证各项风险指标之间的独立性,需进一步考察各指标之间的相互影响程度以及携带信息熵的重叠程度,提高风险评价体系的可靠性。由于Spearman秩相关系数可适用于等级数据的自由分布,对于定性数据或含有异常值的情况尤其适用,因此可选取Spearman法对WBS-RBS耦合矩阵进行独立性检验[19]。得到风险指标Rij与Rmn之间的Spearman秩相关系数rij-mn如表 4所示。从相关程度检验和可接受程度检验两个角度对rij-mn进行判别,检验各风险指标间的独立性:
| 风险指标 | R11 | R12 | R21 | R22 | R31 | R32 | R41 | R42 |
| R11 | 1 | 0.300 | 0.645 | -0.091 | -0.091 | 0.300 | 0.300 | 0.091 |
| R12 | — | 1 | 0.645 | -0.730 | -0.091 | 0.300 | 0.300 | -0.548 |
| R21 | — | — | 1 | -0.471 | 0.354 | 0.645 | -0.258 | -0.354 |
| R22 | — | — | — | 1 | 0.417 | -0.730 | -0.091 | 0.167 |
| R31 | — | — | — | — | 1 | -0.091 | -0.730 | -0.417 |
| R32 | — | — | — | — | — | 1 | -0.400 | 0.091 |
| R41 | — | — | — | — | — | - | 1 | 0.846 |
| R42 | — | — | — | — | — | — | — | 1 |
标准1:相关程度检验。
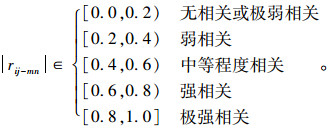
Spearman秩相关系数的大小可以直接反映两个元素之间的关联程度,如下所示。
|
(4) |
rij-mn < 0为负相关,rij-mn>0为正相关;|rij-mn|与1越靠近,说明两个指标之间关联程度越大。
观察表 4发现,R42与R41极强相关,R21与R11、R12强相关,R22与R12强相关,R32与R21、R22强相关,R41与R31强相关。在进行后续风险评估与规避操作时,需重视以上风险指标之间的强相关性,例如W21R42(钻设炮孔作业工人违章作业)的风险等级为一般,在制定风险规避措施时除了加强工人钻设炮孔作业的规范管理,还要扩展到提高钻设炮孔作业的整体安全管理水平。
标准2:接受度检验。
通过查询《Spearman秩相关系数检验临界值表》可得,当样本容量n=7,显著水平α=0.01的情况下,临界值rsα=0.893。根据表 4可得,max|rij-mn|=r42-41=0.846 < 0.893,故表 3所示耦合矩阵符合独立性检验要求。
4.6 K-Means聚类风险评估将前文所述得到的20项可能风险事件作为K-Means聚类的样本对象,应用专家打分法对20个样本的L,E,C这3个指标进行打分,得到如表 5所示的样本数据。按照前述改进的K-Means聚类风险评估方法,借助SPSS软件进行计算,得出20组样本的风险等级结果,如表 6所示。
| 事件 | L | E | C |
| W11 R22 | 1.4 | 2.0 | 1.8 |
| W11 R31 | 2.1 | 2.0 | 3.0 |
| W11 R42 | 3.3 | 2.1 | 2.2 |
| W12 R22 | 1.2 | 1.8 | 1.3 |
| W12 R31 | 2.7 | 1.8 | 4.0 |
| W13 R22 | 1.5 | 2.4 | 2.5 |
| W13 R31 | 4.0 | 2.4 | 5.8 |
| W21 R32 | 2.0 | 4.0 | 2.2 |
| W21 R42 | 4.1 | 4.0 | 2.3 |
| W22 R11 | 4.8 | 4.7 | 5.0 |
| W22 R22 | 2.0 | 4.7 | 3.5 |
| W22 R41 | 1.1 | 4.7 | 2.3 |
| W22 R42 | 4.9 | 4.7 | 4.0 |
| W23 R12 | 1.0 | 2.1 | 1.1 |
| W23 R41 | 4.0 | 2.1 | 1.5 |
| W24 R11 | 3.0 | 4.5 | 4.0 |
| W24 R12 | 3.0 | 4.7 | 3.6 |
| W24 R21 | 2.1 | 4.5 | 2.1 |
| W24 R31 | 1.3 | 4.5 | 3.3 |
| W24 R32 | 2.0 | 4.5 | 4.1 |
| 风险等级 | 风险描述 | 风险事件 |
| Ⅰ | 微小风险 | W11 R22、W12 R22、W23 R12 |
| Ⅱ | 较小风险 | W11 R31、W11 R42、W12 R31、W13 R22、W21 R32、W23 R41 |
| Ⅲ | 一般风险 | W13 R31、W21 R42、W22 R22、W22 R41、W22 R42、W24 R11、W24 R12、W24 R21、W24 R31、W24 R32 |
| Ⅳ | 较大风险 | W22 R11 |
| Ⅴ | 重大风险 | 无 |
4.7 分析结果
对20项基本风险事件的风险评估结果进行汇总,管棚超前支护设计不足、超前小导管注浆设计不足等3项风险等级为Ⅰ级(微小风险);管棚超前支护施工质量不合格、全断面帷幕注浆设计不足等6项风险等级为Ⅱ级(较小风险);钻射炮孔工人违章作业、通风排烟设备不达标等10项风险等级为Ⅲ级(一般风险);装药爆破的水文地质条件风险等级为Ⅳ级(较大风险)。钻爆是隧道围岩开挖能否得到控制的关键因素,该公路隧道围岩质量差,地下水丰富,钻爆过程中很容易引起超欠挖,进而引起岩爆、坍塌、突水突泥等安全事故,与本研究风险评估结果相吻合。
5 结论(1) 应用WBS-RBS开展项目风险识别,通过耦合矩阵确定项目中潜在的基本风险事件,准确、全面地反映了隧道施工风险系统的结构;提出了应用改进的K-Means聚类模型对各基本风险事件进行风险评估,将耦合矩阵确定的风险事件作为K-Means样本对象。
(2) 提出了以事故发生的可能性L,人员暴露于危险环境中的频繁程度E和发生事故或危险事件可能产生的后果C作为K-Means聚类的样本指标,L,E,C对所有风险事件具有普适性,是K-Means模型能够进行全周期动态风险评估的理论基础;对应Ⅰ到Ⅴ级风险指定5组样本数据作为初始聚类中心,确保了多次运算结果的一致性。
(3) 应用改进的K-Means聚类算法对某公路隧道进行风险评估,选取预支护加固W1和隧道开挖W2两道作业工序进行风险分析,结果显示装药爆破的水文地质条件风险等级为Ⅳ级,为较大风险,评估结果与工程实际基本相符,证明了应用该模型进行公路隧道施工风险评判的有效性。
| [1] |
孙闯, 贾宝新, 张涛. 大跨径公路交叉隧道施工安全性研究[J]. 中国安全科学学报, 2015, 25(12): 111-115. SUN Chuang, JIA Bao-xin, ZHANG Tao. Research on Surrounding Rock Stability of Large Span and Small Space Highway Crossing Tunnel[J]. China Safety Science Journal, 2015, 25(12): 111-115. |
| [2] |
杨玉宝, 高国红, 王晓安, 等. 公路隧道施工新型应急救援通道设计[J]. 科学技术与工程, 2013, 13(1): 248-252. YANG Yu-bao, GAO Guo-hong, WANG Xiao-an, et al. Design of the New Emergency Rescue Passage in Highway Tunnel Construction[J]. Science Technology and Engineering, 2013, 13(1): 248-252. |
| [3] |
谢洪涛. 一种改进模糊期望值决策法在隧道施工安全评价中的应用[J]. 安全与环境学报, 2013, 13(3): 248-251. XIE Hong-tao. Application of the Improved Fuzzy Expectancy Value Decision-making Method to the Risk Assessment on Tunnel Excavation[J]. Journal of Safety and Environment, 2013, 13(3): 248-251. |
| [4] |
程远, 刘志彬, 刘松玉, 等. 基于层次分析法的大跨浅埋公路隧道施工风险识别[J]. 岩土工程学报, 2011, 33(增1): 198-202. CHENG Yuan, LIU Zhi-bin, LIU Song-yu, et al. Risk Recognition of Construction of Large-span and Shallow Buried-highway Tunnels Based on Analytic Hierarchy Process[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(S1): 198-202. |
| [5] |
李孜军, 石东平. 基于粗糙集-模糊评判-神经网络的隧道施工安全状态评估[J]. 安全与环境学报, 2011, 11(6): 231-235. LI Zi-jun, SHI Dong-ping. Renovated Security Status Evaluation System for Tunnel Construction Based on the Rough Sets-fuzzy Evaluation-neural Network[J]. Journal of Safety and Environment, 2011, 11(6): 231-235. |
| [6] |
温世儒, 吴霞, 杨晓华, 等. 基于地质雷达预报的隧道施工风险评估[J]. 西南大学学报:自然科学版, 2014, 36(8): 201-205. WEN Shi-ru, WU Xia, YANG Xiao-hua, et al. Risk Evaluation for Tunnel Construction Based on GPR Geological Forecast[J]. Journal of Southwest University:Natural Science Edition, 2014, 36(8): 201-205. |
| [7] |
曹永春, 蔡正琦, 邵亚斌. 基于K-means的改进人工蜂群聚类算法[J]. 计算机应用, 2014, 34(1): 204-207, 217. CAO Yong-chun, CAI Zheng-qi, SHAO Ya-bin. Improved Artificial Bee Colony Clustering Algorithm Based on K-means[J]. Journal of Computer Applications, 2014, 34(1): 204-207, 217. |
| [8] |
杨博, 刘钰洋, 潘懋. 基于Minkowski泛函和K-means聚类算法的岩石类型划分[J]. 科学技术与工程, 2017, 17(22): 63-67. YANG Bo, LIU Yu-yang, PAN Mao. Rock-type Classification Based on Minkowski Functionals and K-means Cluster Analysis[J]. Science Technology and Engineering, 2017, 17(22): 63-67. |
| [9] |
胡志刚, 徐维祥. 聚类分析在隧道开挖变形速率中的应用[J]. 公路交通科技, 2011, 28(2): 97-102. HU Zhi-gang, XU Wei-xiang. Application of Cluster Analysis in Deformation Rate of Tunnel Excavation[J]. Journal of Highway and Transportation Research and Development, 2011, 28(2): 97-102. |
| [10] |
侯寒冰.地铁建设项目施工风险评价方法与准则研究[D].大连: 大连理工大学, 2011. HOU Han-bing. Research on Risk Assessment and Risk Acceptance Criteria of Subway Construction Risk[D]. Dalian: Dalian University of Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10141-1012276001.htm |
| [11] |
谢雪莲, 李兰友. 基于云计算的并行K-means聚类算法研究[J]. 计算机测量与控制, 2014, 22(5): 1510-1512. XIE Xue-lian, LI Lan-you. Research on Parallel K-means Algorithm Based on Cloud Computing Platform[J]. Computer Measurement & Control, 2014, 22(5): 1510-1512. |
| [12] |
游峰, 张荣辉, 李福樑, 等. 基于K-means算法的行人检测方法研究[J]. 公路交通科技, 2014, 31(7): 143-147. YOU Feng, ZHANG Rong-hui, LI Fu-liang, et al. Research on Pedestrian Detection Method Based on K-means Algorithm[J]. Journal of Highway and Transportation Research and Development, 2014, 31(7): 143-147. |
| [13] |
杜巍, 赵春荣, 黄伟健. 改进的K-means聚类算法在客户细分中的应用研究[J]. 河北经贸大学学报, 2014, 35(1): 118-121. DU Wei, ZHAO Chun-rong, HUANG Wei-jian. Application Research on Improved K-means Cluster Algorithm in Customer Segmentation[J]. Journal of Hebei University of Economics and Business, 2014, 35(1): 118-121. |
| [14] |
李浩然, 吴超仲, 褚端峰, 等. 基于K均值聚类的高速公路汽车碰撞事故分析[J]. 中国安全科学学报, 2013, 23(11): 91-96. LI Hao-ran, WU Chao-zhong, CHU Duan-feng, et al. Statistical Analysis of Car Crash on Freeways Based on K-means Clustering[J]. China Safety Science Journal, 2013, 23(11): 91-96. |
| [15] |
赵莉, 候兴哲, 胡君, 等. 基于改进K-means算法的海量智能用电数据分析[J]. 电网技术, 2014, 38(10): 2715-2720. ZHAO Li, HOU Xing-zhe, HU Jun, et al. Improved K-Means Algorithm Based Analysis on Massive Data of Intelligent Power Utilization[J]. Power System Technology, 2014, 38(10): 2715-2720. |
| [16] |
钱蕾, 韩印, 姚佼. 基于改进K-Means算法的交叉口影响路段行程速度估计[J]. 公路交通科技, 2017, 34(12): 115-122. QIAN Lei, HAN Yin, YAO Jiao. Estimation of Travel Speed on Intersection Influenced Link Based on Improved K-Means Algorithm[J]. Journal of Highway and Transportation Research and Development, 2017, 34(12): 115-122. |
| [17] |
陈国华, 吴武生, 徐三元, 等. 基于WBS-RBS与AHP的跨海桥梁工程施工HSE风险评价[J]. 中国安全科学学报, 2013, 23(9): 51-57. CHEN Guo-hua, WU Wu-sheng, XU San-yuan, et al. Assessment HSE Risk of during Sea-crossing Bridges Project Construction Based on WBS-RBS and AHP[J]. China Safety Science Journal, 2013, 23(9): 51-57. |
| [18] |
周靖轩, 刘培, 宋文华, 等. 基于模糊层次-LEC法的罐区多米诺事故预防研究[J]. 南开大学学报:自然科学版, 2016, 49(4): 97-103. ZHOU Jing-xuan, LIU Pei, SONG Wen-hua, et al. Study on the Domino Accident Prevention of Storage Tank Area by Fuzzy Hierarchy-LEC Method[J]. Acta Scientiarum Naturalium Universitatis Nankaiensis:Natural Science Edition, 2016, 49(4): 97-103. |
| [19] |
李木楠, 李志娟, 李素清, 等. 山西阳泉矿区煤矸石山自然定居植物群落优势种种间关系[J]. 应用与环境生物学报, 2015, 21(6): 1143-1149. LI Mu-nan, LI Zhi-juan, LI Su-qing, et al. Interspecific Association of Dominant Species in Naturally Colonized Plant Communities on Coal Gob Piles of the Yangquan Mining Area in Shanxi, China[J]. Chinese Journal of Applied and Environment Biology, 2015, 21(6): 1143-1149. |
 2019, Vol. 36
2019, Vol. 36
