扩展功能
文章信息
- 姜腾蛟, 楚玺, 唐见, 唐亮, 周志祥
- JIANG Teng-jiao, CHU Xi, TANG Jian, TANG Liang, ZHOU Zhi-xiang
- 基于变形轮廓线跟踪的结构整体变形监测方法
- An Overall Deformation Monitoring Method of Structure Based on Tracking Deformation Contour
- 公路交通科技, 2019, 36(6): 48-57
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(6): 48-57
- 10.3969/j.issn.1002-0268.2019.06.007
-
文章历史
- 收稿日期: 2017-08-17
2. 自贡市交通运输局, 四川 自贡 643000
2. Zigong Traffic and Transportation Bureau, Zigong Sichuan 643000, China
结构在服役过程中,由于外界荷载、环境侵蚀、材料疲劳效应等多因素耦合作用,结构往往受到不同程度的损伤并逐渐积累,其最重要的外在表现形式是关键部位的变形不断加剧。结构变形监测是结构健康监测的重要组成部分,是安全性评价的一项重要指标[1-2]。传统的结构变形监测方法有水准仪人工测量或点式位移计直接测量,后来出现大地测量、GPS测量,这些测量方法的不足之处在于只局限于有限关键点的测量,不能实现结构整体监测,特别对于大型结构物,测量点众多,难以获得能够表征结构整体及局部安全状况的变形信息。
近些年来,国内外研究学者致力于研究通过数字图像处理技术获取结构变形的方法。Ghorbani等[3]通过三维数字图像相关技术对在水平循环荷载作用下的砌体墙的位移场进行了测量,通过该技术测得钢筋混凝土构造柱与砌体之间的偏移、角度变化和界面滑移,并与PWS测量方法进行了比较。王国辉[4]等人通过手持普通相机借助近景摄影测量技术对隧道洞室位移进行了监测。潘兵等[5]对基于数字图像中亚像素的相关位移测量方法进行了研究,对多种算法精度和效率进行比较,结果表明基于空域相关函数迭代的牛顿-拉普森方法计算结果最为精确、稳定。张国建等[6]通过近景摄影测量技术对动态桥梁进行瞬间实时变形监测,观测范围广,精度较高,但试验前需要布置人工标记点,且只局限于有限的点观测。胡朝辉等[7]利用数字图像处理技术获取简支梁受载状况下位移场,并通过小波技术对位移场进行噪声滤除,精度和去噪结果较为理想,但试验中始终保持垂直简支梁立面获取数字图像,未考虑现实中任意角度倾斜拍摄更具有实用价值。
本研究综合考虑桥梁等大型结构物周边地形地貌较为复杂,往往难以获取结构物立面正轴投影的数字图像,以及结构物轮廓线局部缺陷等问题,基于透视变换和边缘检测数字图像处理技术,提出一种用于结构整体变形监测的方法。并在钢桁-混凝土组合架加载试验中对该技术进行了系统的应用研究,以期能够准确、方便、经济地获取结构整体变形监测数据。
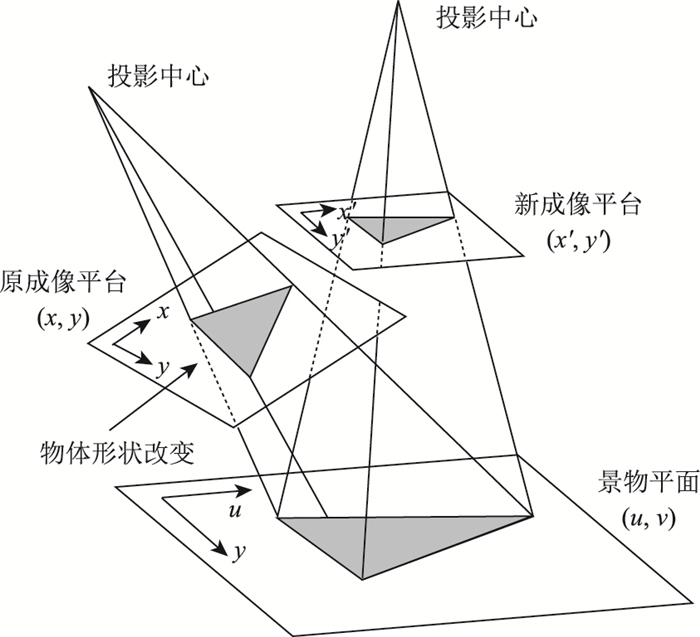
1 数字图像处理技术 1.1 图像透视变换图像几何变换是指在不改变原始图像内容的基础上对图像像素点位置进行几何变换,主要包括平移、旋转、缩放、反射和错切等。透视变换等复合变换都是由基本变换组合而来,相机倾斜拍摄目标结构物在原成像平面上所形成的图像会发生变形。若将该图像映射到目标结构物所在平面,即相当于相机垂直目标结构物所在平面拍摄,则可获取目标结构物的真实形状,这样将相机进行正投影属于透视变换,透视变换模型见图 1。
|
| 图 1 透视变换 Fig. 1 Perspective transformation |
| |
其中,以相机投影中心作为原点建立三维直角坐标系,设其成像平面为xy平面,焦点在[0, 0, f]T处(f>0)。在景物所在平面建立一个二维直角坐标系,此坐标系原点在相机坐标系中为[x0, y0, z0]T。x轴方向单位向量为[u1, u2, u3]T,y轴方向单位向量为[v1, v2, v3]T,可知:
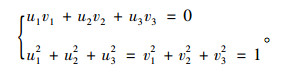
|
(1) |
则景物平面中坐标为[u, v]T的点,在相机坐标系中可表示成:
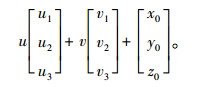
|
(2) |
假设该点在成像平面中的成像点坐标为[x, y, 0]T,则必∃k∈R满足
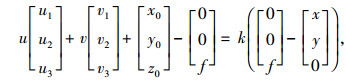
|
(3) |
可得
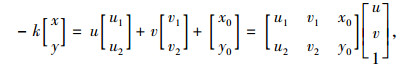
|
(4) |
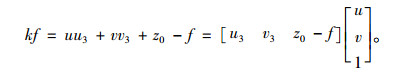
|
(5) |
由式(5)得
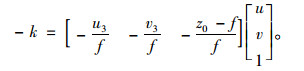
|
(6) |
结合式(4)得
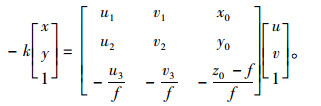
|
(7) |
引入参数矩阵M,记M为:
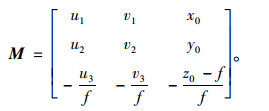
|
(8) |
若景物平面不通过焦点[0, 0, f]T,则矩阵M必为可逆矩阵。而正常工作状态下,焦点都不会位于景物平面上,因此矩阵M恒为可逆矩阵。当相机转换到新位置对目标结构物进行拍摄时,此时相机的空间位置和焦距发生改变,即相机和目标结构物的相对空间位置改变。该变化可等价于假设相机成像平面不动,而焦距和目标结构物的实际空间位置相应发生改变。令相机焦点的坐标变为[0, 0, f′]T,景物平面的原点变为[x0′, y0′, z0′]T。在景物平面的x,y轴的单位向量分别变成为[u1′, u2′, u3′]T、[v1′, v2′, v3′]T。同样∃k′∈R使得景物平面上坐标点[u, v]T与该点对应的成像点[x′, y′, 0]T满足:
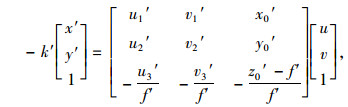
|
(9) |
记参数矩阵M ′为:
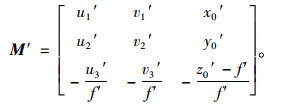
|
(10) |
结合式(7)、式(9)可得:
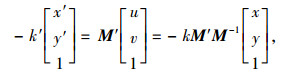
|
(11) |
设
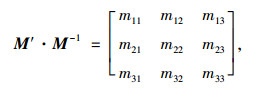
|
(12) |
则可得到:
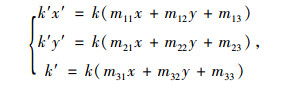
|
(13) |
于是有:
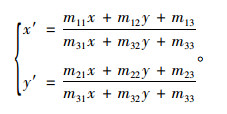
|
(14) |
(x, y)为原始图像成像点,经透视变换后转变成新成像点(x′, y′)。将原先倾斜拍摄的结构物影像通过基本变换组合转换成正射投影影像[8-9]。
1.2 边缘检测边缘检测是图像分析的主要特征提取手段。边缘检测的实质是通过算法识别出图像中景物与背景灰度值变化剧烈的连续点,从而获取景物与背景的交界线[10-11]。利用灰度的导数可更直观量化边缘点的变化程度。
在一维状况下,阶跃边缘与图像的一阶导数局部峰值有着相应联系,而函数的变化程度可用梯度来表示。图像函数f (x, y)在点(x, y)的梯度G (x, y)(即一阶微分)是一个具有方向和大小的矢量:
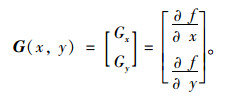
|
(15) |
可得向量G (x, y)的方向就是函数f (x, y)增大时的最大变化率方向。
梯度的幅值:
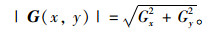
|
(16) |
在实际应用中,常用绝对值来近似梯度幅值:
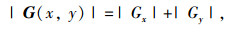
|
(17) |
或
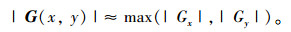
|
(18) |
由向量分析可知,梯度的方向定义为:
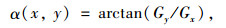
|
(19) |
式中α角是相对x轴的角度。
从而图像灰度的变化程度可用梯度的离散逼近函数来检测,增强图像中所需检测的区域,对梯度进行阈值运算,若梯度值大于所设限定值,则存在边缘[12]。
2 钢桁-混凝土组合梁受载性能试验 2.1 百分表测量试验受载性能试验加载对象为钢桁混凝土组合梁,其中桥道板采用C50预制混凝土桥道板,纵向共7个节段拼装而成,共有两种长度规格,其中两端节段为长度1 080 mm的桥道板,中间5个节段为长度1 000 mm的桥道板。
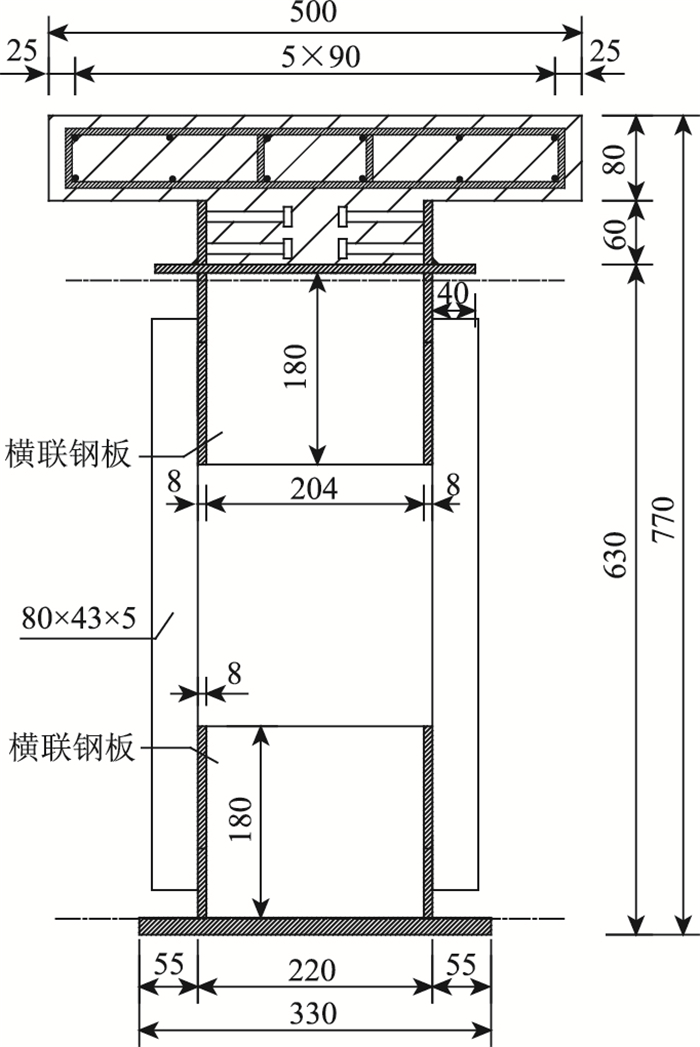
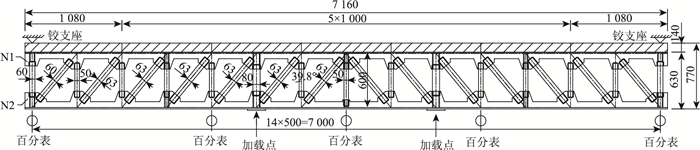
加载点分别距离试验梁两端2 580 mm,采用千斤顶竖直向上对试验梁进行负弯矩加载试验。该加载用于模拟连续刚构桥的墩顶区段受负弯矩作用。铰支座安装在两端桥道板与反力架之间,提供向下的支承反力。对具有代表性的L/4,L/2,3L/4这3个断面布置百分表获取位移量,同时在两端铰支座处分别布置百分表进行支座刚体位移测量。每个断面横向对称安装2个,共计10个百分表。钢桁混凝土组合梁具体构造及加载示意见图 2、图 3。
|
| 图 2 钢桁混凝土组合梁横截面尺寸(单位:mm) Fig. 2 Cross-sectional dimensions of steel truss-concrete composite beam (unit:mm) |
| |
|
| 图 3 钢桁混凝土组合梁构造及加载图(单位:mm) Fig. 3 Structure and loading diagram of steel truss-concrete composite beam (unit:mm) |
| |
将试验梁以20 kN为增量从0~100 kN反复进行3次的弹性预加载,检查百分表工作情况是否正常和数据合理。正式加载以50 kN为增量从0~600 kN缓慢分级加载,每个工况加载完毕后维持荷载2 min再进行试验梁影像采集和百分表数据获取。
2.2 摄影测量试验在整个试验加载过程中,采集每个工况试验梁的数字图像,保持相机所处空间位置和自身方位角度不发生任何改变。为了防止相机受扰动,采用电脑控制相机进行拍摄。同时,由于试验持续时间较长,从早到晚实验室内光照条件不断在改变,可通过电脑实时观看图像质量及时调节相机ISO等参数,确保每个工况试验梁形态轮廓对比度较高。
现实中,实桥周边的地形地貌往往使得获取桥梁立面正轴投影图像较为困难,一般只能在桥梁两岸倾斜立面正轴拍摄。
结合实际应用需求,在实验室内模拟该实际情况,将相机任意选定一个倾斜角度对试验梁进行拍摄。如图 4所示,相机离地垂直高度约3.5 m,水平离试验梁约3 m,与试验梁立面正轴在水平方向有水平夹角,在竖直方向有俯仰角。

|
| 图 4 相机安放位置 Fig. 4 Camera placement position |
| |
试验采用非量测普通单镜头反光式取景照相机,Nikon-D810单机和Nikon AF-S 50 mm f/1.8 G定焦镜头。待每个工况加载到位持荷2 min后获取试验梁影像形态。图 5为其中一个工况的试验梁形态数据采集结果,试验梁的右侧铰支座附近接近800 mm梁长图像信息被反力架遮挡。

|
| 图 5 试验梁形态数据采集 Fig. 5 Collecting shape data of experimental beam |
| |
3 影像数据处理及结果分析 3.1 试验梁影像透视变换
利用透视变换原理,在MATLAB中编写算法,首先对尺寸为450 mm×450 mm标准的正方形棋盘进行验证试验。任意选定一个倾斜角度对正方形棋盘进行拍摄,获取的图像中棋盘形状呈现为不规则四边形。通过MATLAB对图像进行透视变换,将实际棋盘表面作为正投影面,棋盘经透视变换已变成矩形,但还未完全变换成正方形,长宽比约为1.266,因此在透视变换后需要进行进一步标定。
同样,通过该透视变换算法对试验梁每一工况的数字图像进行处理,将试验梁的正立面作为正投影面,其中一个工况透视变换如图 6所示。经过透视变换,试验梁从倾斜投影(x, y)变成了正视投影(x′, y′),变换后的图像完整地保留了试验梁的全部细节。由于最终需要获取的是试验主梁的轮廓线形等数据,因此其余环境部分的图像出现畸变失真等情况并不影响后期结构形态数据获取。经过透视变换的数字图像过滤了原图像中的RGB信息,将图像转变成灰度图,方便后期边缘检测以及轮廓线形数据提取。

|
| 图 6 受载试验梁透视变换 Fig. 6 Perspective transformation of experimental beam under loading |
| |
3.2 试验梁边缘轮廓线获取
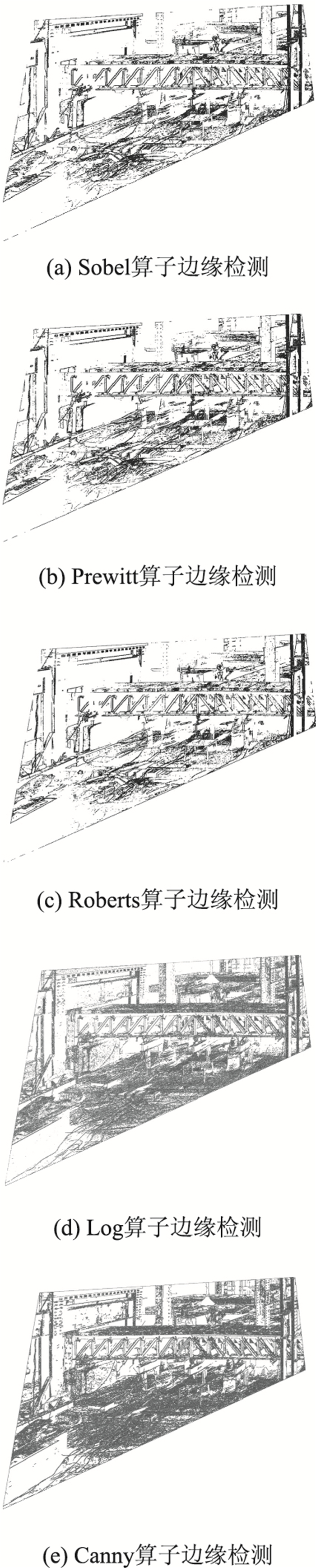
图像边缘检测算子按计算导数近似值的方式不同可分为Sobel算子[13]、Prewitt算子[14]、Roberts算子[15]、Log算子[16]、Canny算子[17]。在MATLAB中,分别采用这5种算子,对经透视变换后的试验梁正视投影图进行边缘检测,如图 7所示。除Log算子外,其他4种算子边缘检测结果不太理想,主要表现为边缘双线性或边缘信息缺失较多[18],对后期检测精度影响较大。而Log算子边缘检测结果较为理想,更适合应用于结构的边缘检测中。
|
| 图 7 5种边缘检测算子对比 Fig. 7 Comparison of 5 kinds of edge detection operators |
| |
Log算子原理在于先对原始图像f (i, j)用高斯空间滤波器做最佳平滑,然后用拉普拉斯算子对滤波后的图像提取零交叉点,以克服噪声对边缘检测的影响[19]。拉普拉斯算子是一种二阶边缘检测算子,它的表达式为:
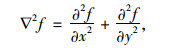
|
(20) |
式中,
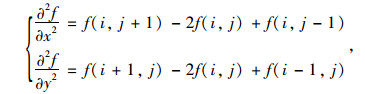
|
(21) |
式中i, j为图像坐标。
图像经过二阶微分之后,在边缘处产生一个陡峭的零交叉,根据这个零交叉就可判断出边缘点。
由于试验过程中试验梁受到阳光直射,全梁光强分布不一致。受到阳光直射的试验梁边缘位置灰度变化不强烈,导致边缘检测算子不能成功识别部分边缘。在边缘检测图像中,出现了局部区域的边缘不连续现象。因此边缘检测结果的完整性和准确性有待后期进一步通过算法提升来处理完善。
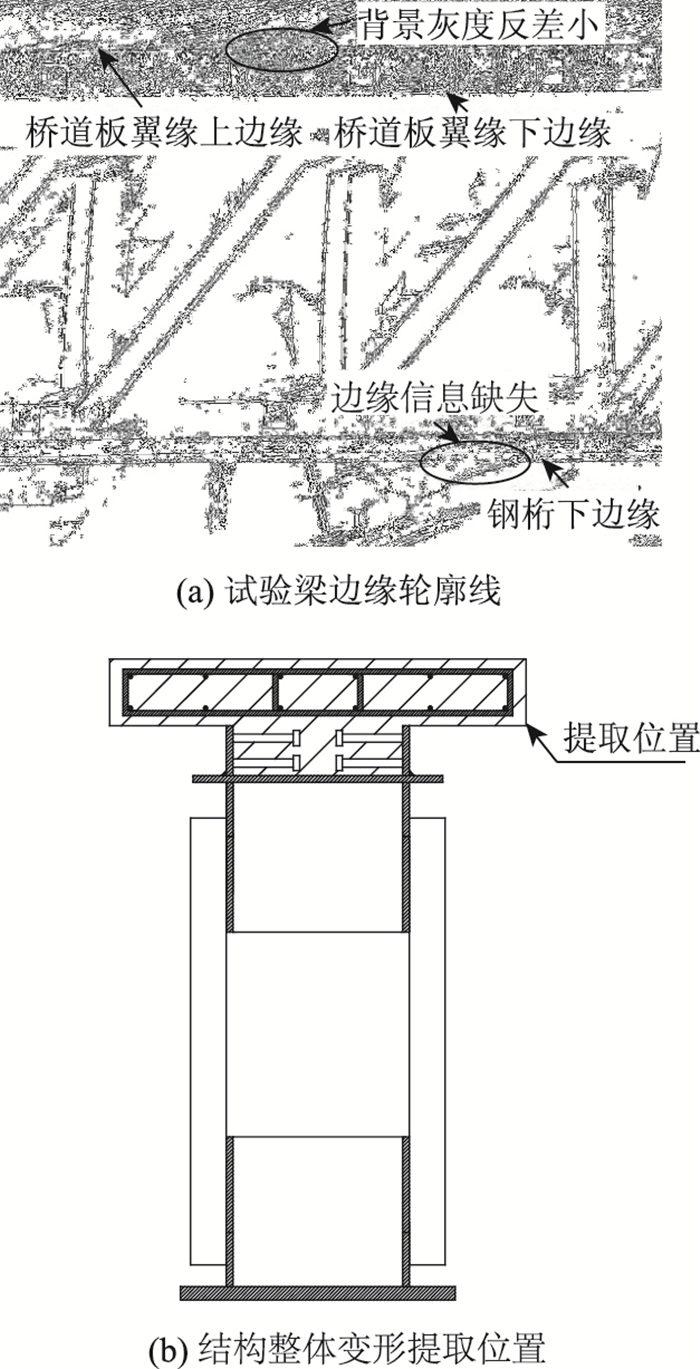
所采用的钢桁-混凝土组合梁为等截面直线梁,因此桥道板翼缘上下边缘或钢桁下边缘均能作为该试验梁的特征轮廓线来表征结构的整体变形。图 8(a)所示,受阳光照射、背景杂物灰度相近等外在条件影响,桥道板翼缘上边缘和钢桁下边缘检测结果受到影响较大。而桥道板翼缘下边缘较为连续,背景灰度反差较大易于提取,优于其他两条轮廓线检测结果。因此将桥道板翼缘下边缘作为该试验梁的特征轮廓线来提取结构整体变形。可通过图像二值化减少部分环境噪音点,将图像二值化阈值区间设置为[250, 255]来获取真实边缘信息。
|
| 图 8 特征轮廓线提取 Fig. 8 Feature contour extraction |
| |
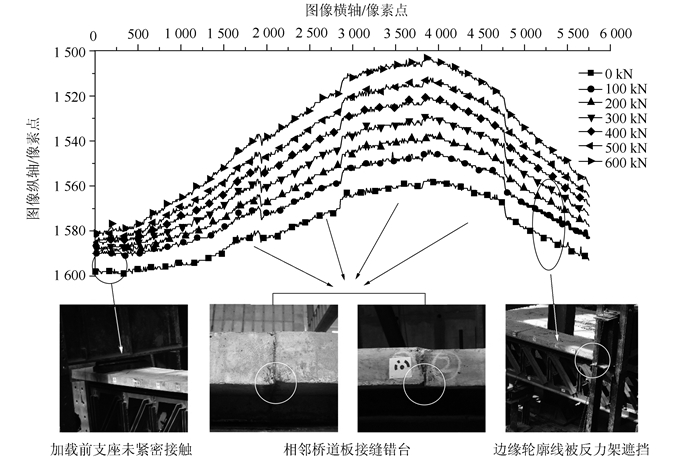
由于采集数字图像时,相机的空间位置相对于试验梁自始至终从未改变。同时,每个工况透视变换采用相同处理方法,变换后正射投影图保持一致,因此每个工况无需寻找不动点即可对边缘轮廓线提取并直接对比。以每个工况试验梁正视投影图左上角使得边缘线最左侧X轴坐标归零处为坐标原点,以像素为单位提取翼缘下边缘的像素点坐标,得到0~600 kN每个工况结构的原始边缘轮廓线,如图 9所示。
|
| 图 9 桥道板翼缘原始边缘轮廓线形 Fig. 9 Original edge contour of flange of bridge plate |
| |
图 9结果表明在负弯矩作用下,0~600 kN各工况的试验梁呈现中间位移大两端位移小,不断拱起的趋势,完整地反映了试验梁全梁的受载变形全过程。右侧支座位置处的边缘轮廓线受到反力架遮挡,线形信息缺失。左侧支座位置处的边缘轮廓线信息较为完整,从轮廓线各级变化信息表明在每个荷载工况下,试验梁均发生了刚体位移。从未加载的0 kN到初加载的50 kN,刚体位移幅度最大。而从50~600 kN的各级工况,刚体位移大小较为接近,每级的刚体位移均远小于0~50 kN工况下的刚体位移。主要原因在于加载前,支座未与反力架紧密接触。而50 kN之后支座与反力架接触紧密,因此刚体位移大幅减小,但由于反力架在荷载作用下仍会产生变形,因此每个工况仍会存在刚体位移。
图 9从单个工况线形来看,呈现分段式连续,横坐标大致每隔1 000个像素点即出现跳跃现象。主要原因在于装配式钢桁-混凝土组合梁在装配过程中,通过环氧树脂将相邻桥道板相连,接缝位置会存在错台现象,而图中轮廓线跳跃位置即为接缝错台位置。
3.3 轮廓线叠差获取变形曲线各预制桥道板实际长度已知,两端预制桥道板的实际长度为1 080 mm,中间5块预制桥道板的实际长度为1 000 mm。基于此,对以像素点为单位的结构边缘轮廓线进行尺寸标定,可将其转化为拥有实际结构尺寸的轮廓线形。
图 9中所获取的线形直接反映全梁桥道板在各级荷载工况下的原始轮廓线形(包含错台等信息)。而相对于位移的量级,错台变形相对甚小,且钢桁-混凝土组合梁刚度较大,因此错台微小变形可忽略不计。因此在加载过程中,可认为错台只产生了刚体位移。基于此,本研究提出基于影像轮廓线“叠差”(Post-Stack Difference,PSD)算法[20]消除边界局部缺陷影响的处理方法,即根据桥道板原始轮廓线平整度特征信息,搜寻各级荷载工况之间的匹配点对,通过计算两个工况全梁匹配点对之间的欧式距离(变形值),来消除错台位置的线形突变对变形数据计算的影响,得到连续的荷载位移曲线。
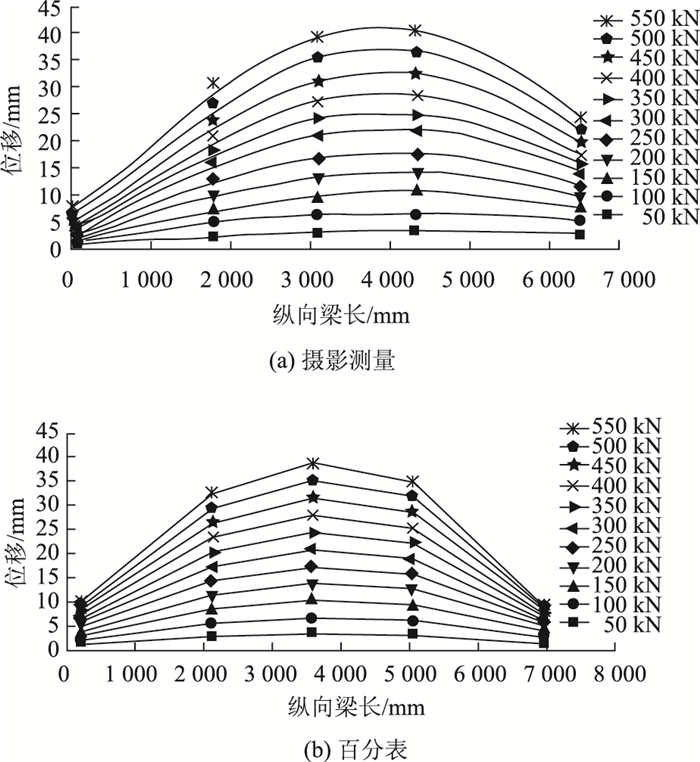
由于0~50 kN支座接触不紧密刚体位移较大,而50 kN之后支座与反力架紧密接触,因此将50 kN作为初始工况。在MATLAB中,将100~600 kN各工况边缘轮廓线与50 kN轮廓线进行叠差,并进行尺寸标定,得到50~550 kN荷载位移曲线,如图 10 (a)所示。
|
| 图 10 荷载位移曲线 Fig. 10 Load-displacement curves |
| |
从图 10(a)可知,每个工况的荷载位移曲线均较为平滑,相邻工况间的位移值随荷载等级的增加,基本呈线性增加的模式,与百分表数据相对比,其位移趋势基本相同。同时可以得出,在600 kN荷载作用下,钢桁-混凝土组合梁仍处于弹性阶段。
3.4 摄影测量误差对比分析由于试验梁影像获取时,右侧支座受到反力架遮挡导致右侧支座的刚体位移不能在影像中获得,同时传统点测量(百分表)获取的原始数据同样包含刚体位移,因此两者数据可以直接对比,不需要减去支座处的刚体位移。同样以50 kN荷载工况作为起始工况,将百分表原始数据进行处理得到荷载位移曲线,如图 10(b)所示。
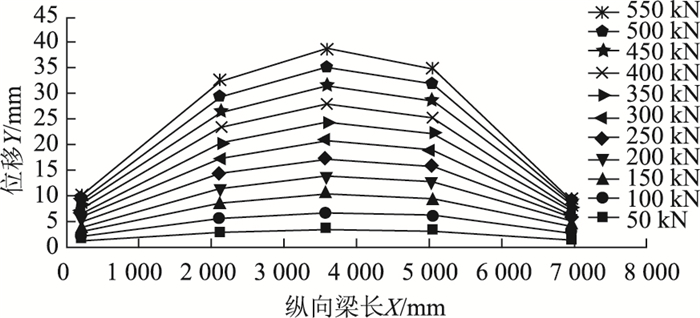
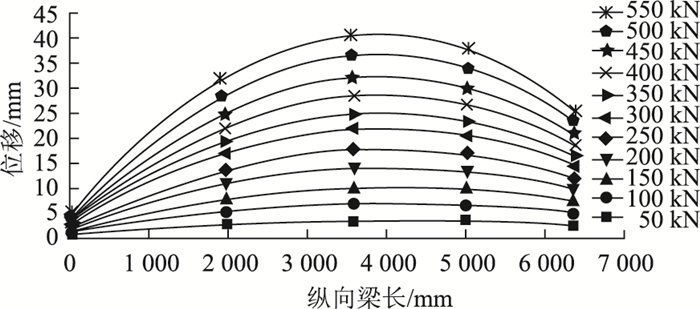
受环境噪声的影响,荷载位移曲线在局部出现锯齿状,为了去除噪音同时准确提取试验梁各个位置的位移值,在MATLAB中对各个工况的荷载位移曲线进行非线性拟合,如图 11所示。根据百分表实际位置坐标,在各工况的拟合曲线方程中进行近似插值计算得到各测点位移值,将其与百分表位移值进行对比,部分对比结果如表 1所示。并对L/2、3L/4百分表测点处的位移值分别进行对比,如图 12所示。数据对比结果可知:100 kN荷载工况下,在L/2位置处摄影测量差值为0.58 mm,此时误差最大为8.68%,除此之外其他工况误差均小于5%。且从图 12可知,摄影测量测得的数据与百分表较为吻合,表明摄影测量精度满足试验表相观测和变形精度的要求。且相对于传统的点测量(百分表),采用摄影测量方法观测范围更广,可以获取钢桁-混凝土组合梁任意截面的位移值,更能全方位体现结构的整体位移和变形状况。
|
| 图 11 拟合后的荷载位移曲线(摄影测量) Fig. 11 Fitted load-displacement curves of photogrammetry |
| |
| 加载 工况/ kN |
百分表 位置 |
百分表 实测值 R1/mm |
摄影测量钢桁 提取挠度值 R2/mm |
|R2-R1|= S/mm |
误差 S/R1/% |
| 50 | L/2 | 3.36 | 3.50 | 0.14 | 4.17 |
| 3L/4 | 3.18 | 3.19 | 0.01 | 0.31 | |
| 100 | L/2 | 6.68 | 7.26 | 0.58 | 8.68 |
| 3L/4 | 6.21 | 6.32 | 0.11 | 1.77 | |
| 200 | L/2 | 13.91 | 14.22 | 0.31 | 2.23 |
| 3L/4 | 12.76 | 12.57 | 0.19 | 1.49 | |
| 300 | L/2 | 20.87 | 21.52 | 0.65 | 3.11 |
| 3L/4 | 18.97 | 18.71 | 0.26 | 1.37 | |
| 400 | L/2 | 28.03 | 28.32 | 0.29 | 1.03 |
| 3L/4 | 25.42 | 24.54 | 0.88 | 3.46 | |
| 500 | L/2 | 35.35 | 36.17 | 0.82 | 2.32 |
| 3L/4 | 31.97 | 31.23 | 0.74 | 2.31 | |
| 550 | L/2 | 38.87 | 40.21 | 1.34 | 3.45 |
| 3L/4 | 35.08 | 34.63 | 0.45 | 1.28 |
|
| 图 12 测点处位移对比 Fig. 12 Comparison of displacements at measuring points |
| |
4 结论
本研究基于透视变换和边缘检测数字图像处理技术,提出一种用于结构整体变形监测的方法,并应用到钢桁-混凝土组合架加载试验中,与百分表测量数据进行了对比分析。得到主要结论如下:
(1) 综合考虑桥梁等大型结构物周边地形地貌较为复杂往往难以获取结构物立面正轴投影的数字图像问题,提出通过图像透视变换来获取结构物正视投影,精度对比结果表明,该方法较为可靠,获取的正视投影图像质量较高,能较好反映实际结构物立面轮廓线形,具有较好的实用价值。
(2) 分别采用5种常见的边缘检测算子对试验梁正视投影图进行处理,对比后得出,基于图像二阶微分的Log算子边缘检测结果较为理想,不会出现边缘双线性或边缘信息缺失较多等现象,更好地适用于该整体变形监测方法。
(3) 综合考虑结构物轮廓线可能存在局部缺陷的问题,提出基于影像轮廓线叠差算法消除边界局部缺陷影响的处理方法,使之较好地获取结构物整体连续变形,结果表明局部缺陷影响大致得到消除,结构物变形数据切合实际。
(4) 试验梁整体变形形态能在拟合后的荷载位移曲线图中得以直观体现,不只局限于有限关键点的测量,对试验梁任意位置均可进行变形监测,测量对比结果表明该摄影测量方法能满足试验表相观测和变形精度的要求。
(5) 另外关于横向不同轴线的一致性问题和通视问题,需要后期进一步开展试验研究,寻找相关处理方法,从而进一步提高该结构整体变形监测方法的精度、适用性和鲁棒性,从而更好地推广应用到实际工程结构变形监测。
| [1] |
刘智, 张宿峰, 蔡曙日, 等. 大坡度高落差桥梁挠度监测方案试验研究[J]. 公路交通科技, 2015, 32(11): 88-93. LIU Zhi, ZHANG Su-feng, CAI Shu-ri, et al. Experimental Study on Deflection Monitoring Scheme of Steep Gradient and High Drop Bridge[J]. Journal of Highway and Transportation Research and Development, 2015, 32(11): 88-93. |
| [2] |
段元锋, 姜平安, 叶贵如, 等. 应用数字散斑相关法测量结构振动位移和频率[J]. 公路交通科技, 2011, 28(6): 75-82. DUAN Yuan-feng, JIANG Ping-an, YE Gui-ru, et al. Measurement of Structural Vibration Displacement and Frequency by Using Digital Speckle Correlation Method[J]. Journal of Highway and Transportation Research and Development, 2011, 28(6): 75-82. |
| [3] |
GHORBANI R, MATTA F, SUTTON M A. Full-field Deformation Measurement and Crack Mapping on Confined Masonry Walls Using Digital Image Correlation[J]. Experimental Mechanics, 2015, 55(1): 227-243. |
| [4] |
王国辉, 马莉, 杨腾峰, 等. 手持普通相机监测隧道洞室位移的研究与应用[J]. 岩石力学与工程学报, 2005, 24(增2): 5885-5889. WANG Guo-hui, MA Li, YANG Teng-feng, et al. Study and Application of Deformation Monitoring to Tunnel with Amateur Camera[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(S2): 5885-5889. |
| [5] |
潘兵, 谢惠民, 戴福隆. 数字图像相关中亚像素位移测量算法的研究[J]. 力学学报, 2007, 39(2): 245-252. PAN Bing, XIE Hui-min, DAI Fu-long. An Investigation of Sub-pixel Displacements Registration Algorithms in Digital Image Correlation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(2): 245-252. |
| [6] |
张国建, 于承新. 数字近景摄影测量在桥梁变形观测中的应用[J]. 全球定位系统, 2016, 41(1): 91-95. ZHANG Guo-jian, YU Cheng-xin. The Application of Digital Close-range Photogrammetry in the Deformation Observation of Bridge[J]. GNSS World of China, 2016, 41(1): 91-95. |
| [7] |
胡朝辉, 袁向荣, 刘敏. 简支梁位移场小波去噪的试验研究[J]. 广州大学学报:自然科学版, 2010, 9(6): 50-53. HU Zhao-hui, YUAN Xiang-rong, LIU Min. Study on Wavelet Transform in Displacement Field De-noising of Simply Supported Beams[J]. Journal of Guangzhou University:Natural Science Edition, 2010, 9(6): 50-53. |
| [8] |
牛彦. 关于透视变换的研究[J]. 计算机辅助设计与图形学学报, 2001, 13(6): 549-551. NIU Yan. Discussion about Perspective Transform[J]. Journal of Computer-Aided Design & Computer Graphics, 2001, 13(6): 549-551. |
| [9] |
刘勇, 施万昌, 徐玉兰. 图像差异的分析与识别[J]. 复旦学报:自然科学版, 2000, 39(5): 472-476. LIU Yong, SHI Wan-chang, XU Yu-lan. Analysis of Difference and Recognition of Images[J]. Journal of Fudan University:Natural Science Edition, 2000, 39(5): 472-476. |
| [10] |
段瑞玲, 李庆祥, 李玉和. 图像边缘检测方法研究综述[J]. 光学技术, 2005, 31(3): 415-419. DUAN Rui-ling, LI Qing-xiang, LI Yu-he. Summary of Image Edge Detection[J]. Optical Technique, 2005, 31(3): 415-419. |
| [11] |
姜腾蛟, 唐亮, 周志祥, 等. 近景摄影三维重建在结构试验中的应用[J]. 实验室研究与探索, 2016, 35(11): 26-29, 46. JIANG Teng-jiao, TANG Liang, ZHOU Zhi-xiang, et al. Study on Application of Close-range Photogrammetric 3D Reconstruction in Structural Tests[J]. Research and Exploration in Laboratory, 2016, 35(11): 26-29, 46. |
| [12] |
甘金来.图像边缘检测算法的比较研究[D].成都: 电子科技大学, 2005. GAN Jin-lai. A Comparative Study of Image Edge Detection Algorithms[D]. Chengdu: University of Electronic Science and Technology of China, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10614-2005094954.htm |
| [13] |
ABBASI T A, ABBASI M U. A Novel FPGA-based Architecture for Sobel Edge Detection Operator[J]. International Journal of Electronics, 2007, 94(9): 889-896. |
| [14] |
PREWITT J. Object Enhancement and Extraction in Picture Process and Psychopictorics[M]. New York: Academic Press, 1970.
|
| [15] |
ROBERTS L. Machine Perception of Three-dimensional Solids[D]. Cambridge: Massachusetts Institute of Technology, 1963.
|
| [16] |
WANG X. Laplacian Operator-based Edge Detectors[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2007, 29(5): 886. |
| [17] |
DING L, GOSHTASBY A. On the Canny Edge Detector[J]. Pattern Recognition, 2001, 34(3): 721-725. |
| [18] |
唐见.基于定点摄影的钢桁-混凝土组合梁受力形态变化试验研究[D].重庆: 重庆交通大学, 2017. TANG Jian. Experimental Study on Morphological Changes of Steel Truss-concrete Composite Beam Based on Fixed-point Photography[D]. Chongqing: Chongqing Jiaotong University, 2017. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y3225184 |
| [19] |
王咏胜, 付永庆. 噪声目标的边缘检测算法研究[J]. 弹箭与制导学报, 2008, 28(6): 235-237. WANG Yong-sheng, FU Yong-qing. Study on Edge Detection Algorithm for Noise Objects[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(6): 235-237. |
| [20] |
姜腾蛟.基于桥面形态的钢-混凝土组合梁损伤状态试验研究[D].重庆: 重庆交通大学, 2018. JIANG Teng-jiao. Experimental Study on Damage Conditions of Steel-concrete Composite Beam Based on Bridge Surface[D]. Chongqing: Chongqing Jiaotong University, 2018. |
 2019, Vol. 36
2019, Vol. 36
