扩展功能
文章信息
- 楚玺, 向小菊, 周志祥, 侯旭, 何松霖
- CHU Xi, XIANG Xiao-ju, ZHOU Zhi-xiang, HOU Xu, HE Song-lin
- 欧拉运动放大算法在桥梁振动分析中的试验研究
- Experimental Study on Euler Motion Amplification Algorithm in Bridge Vibration Analysis
- 公路交通科技, 2019, 36(6): 41-47, 57
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(6): 41-47, 57
- 10.3969/j.issn.1002-0268.2019.06.006
-
文章历史
- 收稿日期: 2018-09-03
桥梁的振动状态是反映桥梁健康状况的重要参数,桥梁的振动监测是桥梁健康监测的一项重要内容,其中动态挠度是评价桥梁整体结构性能的控制指标。对桥梁结构的动态挠度进行科学可靠的测试至关重要。目前,测定桥梁振动特性的常用仪器为加速度计,但加速度计存在位移精度不高、连续实时监测困难、测点单一等缺点,难以满足现代桥梁实时动态位移监测的要求。其他的常规测量方法如水准仪、百分表和全站仪等难以进行动态测量,GPS虽能实现动态测量,但调试安装非常繁琐,复杂的桥梁地域工作环境和卫星、天气等因素都能影响到测量的精度和测量的时间。因此,结合现有的非接触式测量手段,发展新的桥梁动态位移识别和分析方法是值得研究和探索的问题。
微小运动放大技术是一种用于改变连续运动图像序列中感兴趣信号变化幅度的技术,这类技术可以将原本人眼无法感知的微弱变化放大到可以观察的幅度,达到视觉增强的效果,从而挖掘出有价值的信息[1]。对于常规的微小运动放大,一般的解决方法是拉格朗日法[2-5],这类方法的根本依据是广义流体力学理论,跟踪粒子随时间变化的路径,从而达到放大微小运动的目的。该方法的缺点是需要依赖相对精确的微小运动估计,需要在计算前提出显微运动的参数,否则放大计算难以准确反映微小运动的变化轨迹,因此基于拉格朗日的运动放大算法并不适用于具有复杂场景的图像序列,也不具备工程振动监测领域的应用前景。近年来,WU H Y等[6-9]提出了一种欧拉影像放大技术的方法,其基本思想是放大像素亮度的变化值,采用空间多尺度分析,不需要进行光流运动估计,只需要通过设置合适的滤波器放大确定位置的像素颜色变化值,可以获得较好的运动放大效果。但是,欧拉运动放大算法在滤波和视频重建过程中不可避免地会造成噪声溢出,导致连续图像序列瑕疵,造成放大后的图像模糊不清。Wadhwa[10-11]等对这项技术进行了改进,提出了基于相位的图像序列运动处理技术,基于相位的运动放大技术在放大微小运动的同时不会放大噪声,只是将已经存在的噪声进行平移,因而可以达到比较好的运动放大效果。然而,在提高放大效果的同时,其空域相位分解算法更为复杂,严重制约了放大计算效率。为此,Taj-Eddin[12-14]等对相位放大再一次进行了改进,提出了基于金字塔的快速相位运动放大算法,利用变换对正余弦信号进行近似处理,可以达到同相位运动放大相近的放大效果,同时提高了算法速率。
运动放大处理技术目前在影像处理、动画制作、医学研究等领域有所涉及,但受运动放大算法中伴随噪声的影响,该技术在以桥梁为代表的大型结构振动监测中的应用一直存在技术瓶颈,以致于目前尚无人开展相关研究。伴随着数学图像学和数字图像处理技术的快速发展,目前已临近运动放大处理技术在桥梁全息动态位移测量应用的突破口。本研究利用欧拉运动放大算法,结合数字图像处理技术,提出了一种新的桥梁非接触式的动态位移分析方法。
1 欧拉运动放大算法欧拉运动放大算法的根本是对连续图像序列中的微小运动信号进行捕获并放大,进而得到可量化和处理的物体运动信息。欧拉运动放大算法对连续图像序列处理过程如图 1所示[15]。

|
| 图 1 欧拉运动放大算法框架 Fig. 1 Framework of Euler motion amplification algorithm |
| |
欧拉运动放大算法首先要对输入的图像序列进行空间域分解,得到不同的空间频率分布[16]。对得到的不同空间频率分布使用包含对微弱运动敏感频段的时域带通滤波器进行滤波,得到连续图像序列中的微小运动,进而提取出需要放大的部分,再对其进行线性放大。
假设需要放大部分是一维运动信号I (x, t),δ (t)为位移函数即变化信号,在t=0时刻,I (x, 0)= f (x);在任意时刻t,I (x, t)=f [x+δ (t)]。最终希望得到放大α倍的信号为[17]:
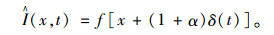
|
(1) |
将I (x, t)用一阶泰勒级数展开
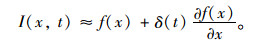
|
(2) |
由式(2)看出,此一维信号中变化部分为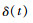
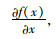
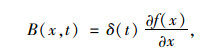
|
(3) |
式中,B (x, t)为需要放大部分的信号,将变化信号放大α并加到原始信号I (x, t),得到放大后信号为:
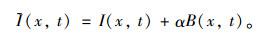
|
(4) |
比较上述公式可得:
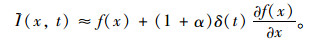
|
(5) |
因试验对象为微弱运动,因此假定此一维信号按泰勒级数展开包含放大后的信号(1+α)δ(t),对比式(5)与式(2)可知放大α倍的一维信号为:
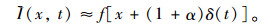
|
(6) |
式(6)表示原图像f(x)在t时刻将存在的变化信号δ(t)放大α倍得到信号。
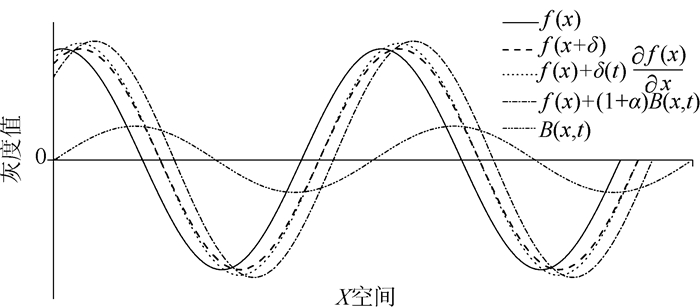
将提取变化部分经上述线性放大,再与原图像序列进行重建,得到微弱运动被放大的图像序列。图 2演示了使用欧拉运动放大算法处理一个余弦波的过程和结果。余弦信号在时刻t的灰度值为I(x, t)=f(x),在时刻t+1的灰度值为I(x, t+1)=f(x+δ),可以看出I(x, t+1)关于x的一阶泰勒级数有一个很好的近似效果,通过对其进行带通滤波处理并加到原信号中,得到了明显的放大效果。
|
| 图 2 一维余弦信号的泰勒级数逼近和放大过程 Fig. 2 Taylor series approximation and amplification process of 1D cosine signals |
| |
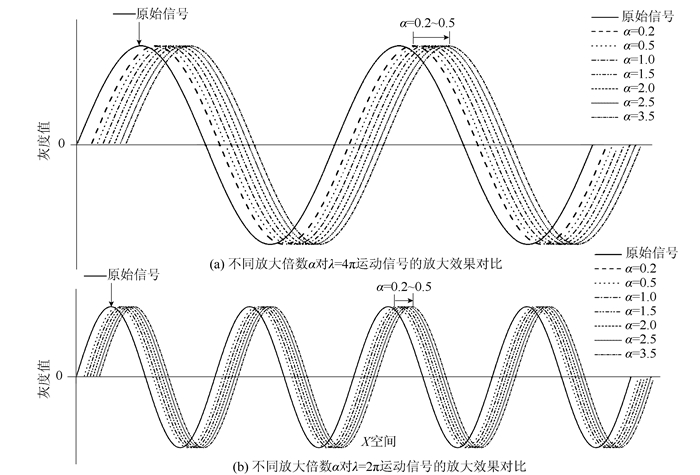
图 3展示了一维运动信号在不同空间波长λ和不同放大倍数α下的对比效果。上图信号的波长为λ=4π,t=1时刻的运动量为δ (1)=π/8;下图信号的波长为λ=2π,t=1时刻的运动量为δ (1)= π/8。黑色连续线为没有被放大的原始信号。其他间断线表示不同放大倍数下得到的波形图。从图 3可知,运动放大算法只是放大了目标图像的位移量,并没有放大图像的强度。
|
| 图 3 不同空间频率和放大系数处理的结果对比 Fig. 3 Comparison of processing results of different spatial frequencies and magnification coefficients |
| |
综上所述,可以利用欧拉运动放大算法对位移信号敏感且具备显微运动的这一特性,来研究桥梁结构图像序列的振动位移信息。
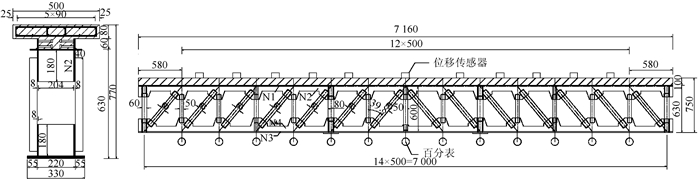
2 室内钢桁混凝土组合梁桥非接触式动态位移测量试验 2.1 试验概况为探索基于欧拉运动放大算法的显微振动放大处理技术在桥梁结构全息动态位移测量中应用的可行性,专门制作了一个钢桁混凝土组合梁试件来进行试验,该试件主体为钢桁架结构,桥道板为预制预应力混凝土桥道板,试件的具体尺寸见图 4。
|
| 图 4 钢桁混凝土组合梁试件构造图(单位:mm) Fig. 4 Structural drawing of steel truss concrete composite beam(unit:mm) |
| |
试验结果是通过布置在试件上的位移传感器和百分表来进行对比分析的,位移传感器和百分表布置如图 4所示。试件的激励方法采用人工势能激励,激励位置位于试件的跨中,开始测试时,试验人员从试件的跨中原地起跳,起跳前1 s开启传感器和千分表通道采样,起跳后4 s通道全部关闭,数据采集结束。整个试验过程中,通过普通民用相机对试件的激励过程和自由振动过程进行拍摄,相机投影方向为试件的正轴投影,位置距试件5 m处,拍摄采样频率为24帧/s。考虑到刚度对钢桁结构的振动响应影响非常明显,本次试验以刚度作为控制条件,对试件进行了不同程度的人工损伤来设置不同的工况,试验工况设置见表 1。
| 工况 | 损伤位置 | 损伤特征 |
| 1 |  |
完整工况 |
| 2 |  |
2根斜杆对称损伤 |
| 3 |  |
4根斜杆对称损伤 |
| 4 |  |
6根斜杆对称损伤 |
2.2 试验数据分析
试件激振过程和自由振动过程的非接触采样是通过普通民用相机拍摄完成的,本次试验所采用的相机为Canon5DSR,每个工况拍摄时间为5 s,即每个工况的初始数据源为一段5 s的视频。将每个工况下的初始数据源用图像序列运动放大相关算法进行处理,对微小的试件振动进行放大分析。
为了将试件的振动分析进行量化,试验开始前,在试件上画上人工标记点以便于识别试件上的特征点在时间域内的位移变化。试件上人工标记点位于每一根斜杆和竖杆的端部,为十字形,其特征明显,便于绘制,在图像序列中便于跟踪和分析。
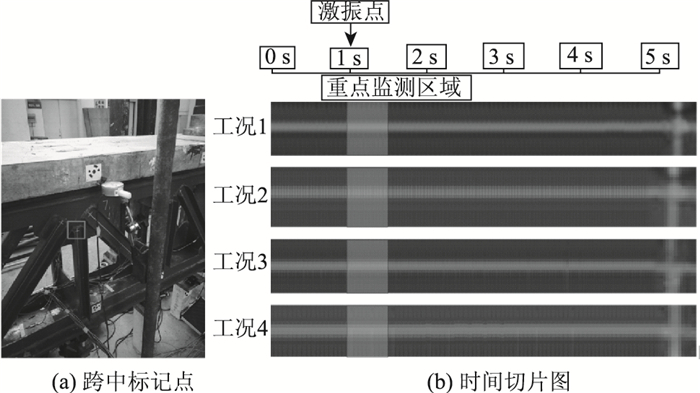
由钢桁结构的组成可知,其结构刚度大,振幅小,振动频率高,振动衰减速度快。因此重点分析激振开始后1 s范围内的图像序列运动放大数据。在进行运动放大算法处理前后,分别对单个标记点的位置进行时间切片,时间切片反映了标记点在整个时间域上的位移变化,是对运动放大效果最直观的反映,也是后期量化分析单个标记点在时间域上位移变化的基础。各工况下的跨中标记点未进行运动放大算法处理前的时间切片如图 5所示。
|
| 图 5 各工况跨中标记点运动放大算法处理前的时间切片图 Fig. 5 Time slicing diagram of marking points on mid-span under different working conditions before processed by motion amplification algorithm |
| |
由图 5可知,未进行运动放大处理的跨中人工标记点在时间域上基本无法观测到结构的任何振动特征,标记点的轨迹平滑,发展过程稳定,运动趋势在激振点前后无明显变化,无法针对该时间切片进行科学量化的分析。
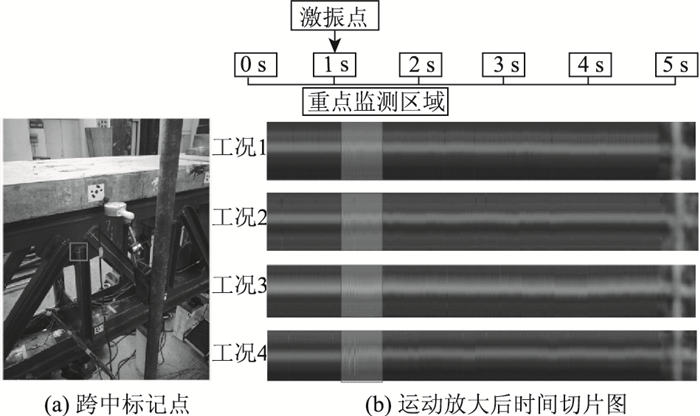
对每一个工况下初始数据源运用欧拉运动放大算法进行处理,本次算法参数取值如下:运动区域入口阈值ϑ为0.9;运动细节增强系数ξ为5;平滑参数σs为16;σr为0.2,放大倍数α为30倍。各工况跨中标记点运动放大后的时间切片如图 6所示。
|
| 图 6 各工况跨中标记点运动放大30倍后的时间切片图 Fig. 6 Time slicing diagram of marking points on mid-span under different working conditions after magnifying 30 times by motion amplification algorithm |
| |
图 6可知,试件在人工势能激励下产生的细微振动被空间分解后,较好地被滤波器识别出来,并通过运动细节增强过程得到了振动信号的放大与合成。放大后的图像序列时间切片图反映出了跨中人工标记点在时间域上的振动特征,特别是在激振开始后,时间切片图上相应区域的扰动十分明显,基本反映出了标记点在激振后的动态位移变化。但是时间切片图只能够直观地进行观察,初步判断结构振动的一些表面信息,比如起振点、起振方向、振动时长等,而要量化结构的振动特性,则需要对时间切片图所含信息进行更深层次的研究。时间切片图其实质是由一系列经放大算法处理后的图像序列所组成的,在时间域内具备可分解的特性,将激振前后需要重点分析的连续图像序列进行分解,就可以通过分解后的单张图像,来找寻动态位移的细节,达到量化振动特点的目的。
由相机拍摄的连续图像序列参数可知,在1 s内人工标记点的连续图像序列可以被分解成24幅图像,对这24幅图像进行分析,即可获得其中所包含的位移信息。要对位移进行量化,首先需要明确标记点的确切边界,因为在放大算法执行过程时,空间分解,滤波降噪和重新放大合成的过程都会增加图像的噪声,使得图像的像素质量降低,图像模糊不清,由图 6可知标记点在放大算法处理后已经出现边界模糊的情况,其准确边界已经无法通过常规手段识别,因此需要利用数学图像学和图像处理相关技术对模糊的标记点图像进行特征识别,以便于准确定位标记点边缘,进行位移分析。
图像的边缘检测是计算机视觉和图像处理中重要的内容,准确可靠的边缘检测方法对研究起到至关重要的作用。研究采用的人工标记点放大后分解图像,具有高噪声的细节特征,而分析过程又要求边缘定位准确,综合对比各种边缘检测算法发现Canny算子具备很好的信噪比和检测精度,且对单一边缘仅有唯一响应[18],适合针对本次试验的标记点进行边缘定位分析。将标记点边缘在时间域上重新排列,就可以得到起跳前后1 s内标记点各工况跨中标记点边缘位移。
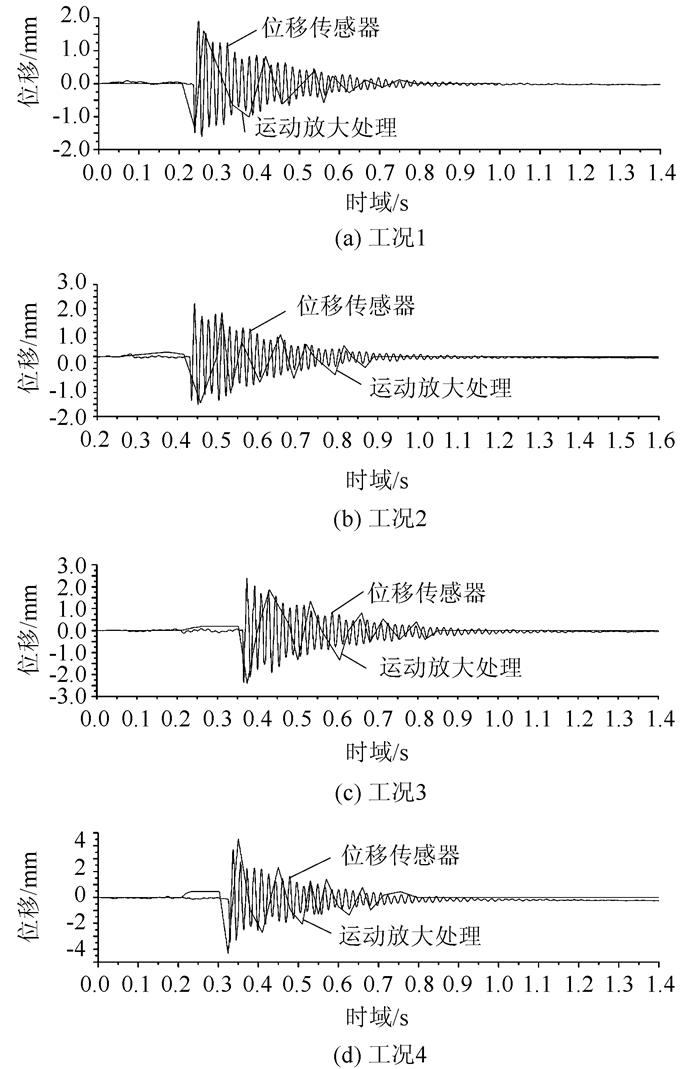
将相机进行标定,可以得到本次试验所得图像的物面分辨率为0.754 mm,再对像素点进行坐标解算,将整像素点的位移值乘以相机的物面分辨率,可以到各工况下人工标记点的位移曲线,将运动放大算法处理的跨中标记点位移曲线和跨中布置的位移传感器获得的位移曲线对比如图 7所示。
|
| 图 7 各工况跨中位移对比 Fig. 7 Contrast of mid-span displacements under different working conditions |
| |
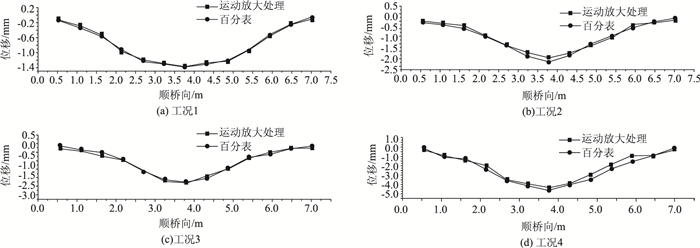
由图 7可知,运动放大算法处理后提取出的单个标记点的位移采样频率偏低,其原因在于本次试验采用的普通民用相机的采样频率仅为24帧/s,而且运动放大算法处理后不可避免地增加了图像的噪声,导致图 7中部分采样点出现了丢失和采样位置偏移、采样间距失真等问题。但是,本次试验过程中采用的运动放大算法基本正确反映出了桥梁的振动幅值、振动衰减特性、起振点、起振方向等动态振动信息。对单个标记点的分析验证了运动放大技术在桥梁振动分析中应用的可行性,继续探索桥梁全息动态位移,需要将试件的全部标记点进行如上运动放大处理,得到各工况下桥梁试件的全息最大振动位移与百分表对比如图 8所示。
|
| 图 8 各工况全部标记点与百分表的最大振动位移对比 Fig. 8 Contrast of maximum vibration displacements obtained by all marking points motion amplification and dial indicator under different working conditions |
| |
将标记点的最大振动位移与百分表的实测位移进行对比,得到经运动放大算法处理的各工况下标记点位移误差如表 2所示。
| 工况1 | |||||||||||||
| 百分表 | -0.15 | -0.34 | -0.56 | -0.93 | -1.24 | -1.29 | -1.38 | -1.31 | -1.21 | -0.92 | -0.51 | -0.26 | -0.06 |
| 标记点 | -0.13 | -0.29 | -0.52 | -0.97 | -1.2 | -1.21 | -1.34 | -1.28 | -1.23 | -0.93 | -0.55 | -0.25 | -0.11 |
| 误差/% | 13.3 | 14.7 | 7.1 | 4.3 | 3.2 | 6.2 | 2.8 | 2.2 | 1.6 | 10.8 | 7.8 | 3.8 | — |
| 工况2 | |||||||||||||
| 百分表 | -0.25 | -0.37 | -0.56 | -0.93 | -1.34 | -1.87 | -2.15 | -1.81 | -1.31 | -0.92 | -0.51 | -0.26 | -0.09 |
| 标记点 | -0.21 | -0.32 | -0.42 | -0.91 | -1.37 | -1.71 | -1.94 | -1.74 | -1.35 | -0.96 | -0.4 | -0.28 | -0.17 |
| 误差/% | 16.0 | 13.5 | 25 | 2.1 | 2.2 | 8.6 | 9.8 | 3.9 | 3.1 | 4.3 | 21.6 | 7.7 | — |
| 工况3 | |||||||||||||
| 百分表 | -0.15 | -0.38 | -0.53 | -0.96 | -1.61 | -2.13 | -2.28 | -2.04 | -1.46 | -0.81 | -0.61 | -0.31 | -0.18 |
| 标记点 | -0.31 | -0.42 | -0.71 | -0.98 | -1.57 | -2.21 | -2.31 | -1.91 | -1.49 | -0.86 | -0.53 | -0.31 | -0.27 |
| 误差/% | — | 10.5 | 34.0 | 2.1 | 2.5 | 3.8 | 1.4 | 6.4 | 2.1 | 6.2 | 13.1 | 9.7 | — |
| 工况4 | |||||||||||||
| 百分表 | -0.15 | -0.98 | -1.23 | -2.36 | -3.61 | -4.13 | -4.63 | -4.04 | -3.46 | -2.31 | -1.51 | -0.91 | -0.18 |
| 标记点 | -0.31 | -0.92 | -1.41 | -1.98 | -3.45 | -3.91 | -4.33 | -3.91 | -2.99 | -1.86 | -0.93 | -0.91 | -0.27 |
| 误差/% | — | -6.1 | 14.6 | 16.1 | 4.4 | 5.3 | 6.4 | 3.2 | 13.6 | 19.5 | 38.4 | 7.7 | 27.8 |
由表 2可知,各标记点经过运动放大处理后得到的试件动态最大位移与百分表所得到的动态最大位移吻合较好,最大误差发生在工况4的支座附近,为38.4%,导致误差偏大的原因是运动放大算法处理过程会不可避免地增强图像序列的噪声,导致标记点的边缘定位丢失、边缘偏移,进而影响了最终的分析结果。除了部分点的误差明显偏高外,其余标记点的位移误差能够控制在15%以内,所采用的运动放大算法和动态位移分析方法得到的试件动态位移基本正确反映出了试件的动态位移特性,基本能够满足桥梁动态位移测量的应用需求,也能够针对桥梁的某些振动特性,如振型、频率、振幅等开展初步的定量分析。
3 结论本研究提出并成功实践了利用欧拉运动放大算法和数字图像处理技术来进行桥梁振动分析的方法,得到如下结论:
(1) 针对桥梁振动的连续性和高频特性,提出采用基于欧拉运动放大算法的桥梁振动细节增强方法,在实验室内获取了桥梁试件的振动放大合成影像。试验结果表明,采用的欧拉运动放大算法能够准确地表征桥梁振动的细节。
(2) 提出对结构连续图像序列中的人工标记点或自然标记点进行边缘检测,用以进行桥梁结构动态位移的测量和分析。试验结果表明,本研究提出采用具备较好信噪比和检测精度的Canny算子进行图像序列中标记点的边缘定位,其边缘定位结果基本能够正确反映标记点在时间历程上的位移变化,为单个标记点的动态位移分析和整个桥梁全息动态位移测量提供了量化基础。
(3) 本研究所采用的桥梁振动分析方法能够基本准确地反映桥梁单点的振动幅值、振动衰减特性、起振点、起振方向等动态振动信息,验证了运动放大方法和数字图像处理技术在桥梁振动分析中应用的可行性。经过运动放大处理后试件动态最大位移与百分表所得到的动态最大位移吻合较好,最大误差为38.4%,一般误差能够控制在15%以内。所采用的动态位移分析方法得到的试件全息动态位移基本正确反映出了试件的动态位移特性,基本能够满足桥梁动态位移测量的应用需求,也能够针对桥梁的某些振动特性,如振型、频率、振幅等开展初步的定量分析。
(4) 在与位移传感器的对比发现,本研究提出的普通民用相机非接触式振动分析方法存在以下问题:①视频采样率低导致图像序列不足,体现在位移时程曲线上则是曲线信息不完整。因此,本研究所采用的方法尚无法开展深入的结构振动特性分析、振动参数分析、结构损伤识别等研究工作。但随着高速、高清摄影器材的不断发展,采样频率低的问题会得到有效的缓解和解决。②本研究所采用的图像序列运动放大算法在一定程度上有效抑制了图像分解过程中的不可避免的噪声,但是在后期标记点边缘定位的过程中,Canny边缘检测算子仍然受到了噪声的影响,位于支座附近的标记点边缘定位明显失真,导致分析结果误差偏大。综合上述两点问题,并结合误差分析结果可知,本研究所采用的桥梁振动分析方法精度还有较大的提升空间。
| [1] |
POH M Z, MCDUFF D J, PICARD R W. Non-contact, Automated Cardiac Pulse Measurements Using Video Imaging and Blind Source Separation[J]. Optics Express, 2010, 18(10): 10762-10774. |
| [2] |
LIU C, TORRALBA A, FREEMAN W T, et al. Motion Magnification[J]. ACM Transactions on Graphics, 2005, 24(3): 519-526. |
| [3] |
SAND P, TELLER S. Particle Video:Long-range Motion Estimation Using Point Trajectories[J]. International Journal of Computer Vision, 2008, 80(1): 72. |
| [4] |
TORRALBA A, MURPHY K P, FREEMAN W T. Shared Features for Multiclass Object Detection[J]. Toward Category-Level Object Recognition, 2006, 4170: 345-361. |
| [5] |
FREEMAN W T, WILLSKY A S, SUDDERTH E B. Graphical Models for Visual Object Recognition and Tracking[J]. Thesis Massachusetts Institute of Technology, 2006, 15(3): 66-76. |
| [6] |
WU H Y, RUBINSTEIN M, SHIH E, et al. Eulerian Video Magnification for Revealing Subtle Changes in the World[J]. ACM Transactions on Graphics, 2012, 31(4): 65. |
| [7] |
RUBINSTEIN M, SHAMIR A, AVIDAN S. Improved Seam Carving for Video Retargeting[J]. ACM Trans Graphics, 2008, 27(3): 1-9. |
| [8] |
BENNETT S L, GOUBRAN R, KNOEFEL F. The Detection of Breathing Behavior Using Eulerian-enhanced Thermal Video[C]//2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). Milan: IEEE, 2015.
|
| [9] |
HOLDSWORTH S J, RAHIMI M S, NI W W, et al. Amplified Magnetic Resonance Imaging (aMRI)[J]. Magnetic Resonance in Medicine, 2016, 75(6): 2245-2254. |
| [10] |
WADHWA N, RUBINSTEIN M, DURAND F, et al. Complex-valued Phase-based Eulerian Motion Modulation: US, 20140072229 A1[P]. 2014-07-22.
|
| [11] |
WADHWA N, RUBINSTEIN M, DURAND F. Phase-based Video Motion Processing[J]. ACM Transactions on Graphics, 2013, 32(4): 1-10. |
| [12] |
TAJ-EDDIN I A T F, AFIFI M, KORASHY M, et al. Can We See Photosynthesis? Magnifying the Tiny Color Changes of Plant Green Leaves Using Eulerian Video Magnification[J]. Journal of Electronic Imaging, 2017, 26(6): 1-4. |
| [13] |
CHENG M M, ZHANG G X, MITRA N J, et al. Global Contrast Based Salient Region Detection[C]// 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Colorado Springs: IEEE, 2011.
|
| [14] |
LIU Y F, VUONG C, WALKER P C, et al. Noninvasive Free Flap Monitoring Using Eulerian Video Magnification[J]. Case Reports in Otolaryngology, 2016, 16(4): 1-4. |
| [15] |
PARK S, KIM D. Subtle Facial Expression Recognition Using Motion Magnification[J]. Pattern Recognition Letters, 2009, 30(7): 708-716. |
| [16] |
CHEN J G, WADHWA N, CHA Y J, et al. Modal Identification of Simple Structures with High-speed Video using Motion Magnification[J]. Journal of Sound & Vibration, 2015, 345: 58-71. |
| [17] |
DAVIS A, BOUMAN K L, CHEN J G, et al. Visual Vibrometry: Estimating Material Properties from Small Motions in Video[C]// 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 5335-5343.
|
| [18] |
高尚兵, 颉正, 潘志庚, 等. 一种新的路面裂缝自动检测算法[J]. 系统仿真学报, 2017, 29(9): 2009-2015. GAO Shang-bing, XIE Zheng, PAN Zhi-geng. Novel Automatic Pavement Crack Detection Algorithm[J]. Journal of System Simulation, 2017, 29(9): 2009-2015. |
 2019, Vol. 36
2019, Vol. 36
