扩展功能
文章信息
- 孙婧, 张志强, 李地元, 林杭, 朱泉企
- SUN Jing, ZHANG Zhi-qiang, LI Di-yuan, LIN Hang, ZHU Quan-qi
- 软层对土质边坡破坏模式及稳定性影响的数值分析
- Numerical Analysis on Influence of Soft Layer on Failure Mode and Stability of Soil Slope
- 公路交通科技, 2019, 36(6): 17-24
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(6): 17-24
- 10.3969/j.issn.1002-0268.2019.06.003
-
文章历史
- 收稿日期: 2018-02-02
2. 西安理工大学 岩土工程研究所, 陕西 西安 710048
2. Institute of Geotechnical Engineering, Xi'an University of Technology, Xi'an Shaanxi 710048, China
力学性能较差的软层在实际路基边坡工程中较为常见,也是路基边坡的控制性弱面,软层的存在使得边坡稳定性分析更为复杂。边坡稳定性计算常用极限平衡法,如W. Fellenius[1]提出的瑞典圆弧法、Janbu法[2]及Sarma法[3]。1975年Zienkiewicz等[4]提出了通过折减岩土材料强度的方法来求解岩土工程的安全系数,即强度折减法。文献[5]比较了极限平衡法和强度折减法取得的边坡安全系数和临界滑动面,发现极限平衡法计算的安全系数略低于强度折减法。文献[6]提出了一种广义二分搜索算法用于强度折减有限元法,以减少从统计角度出现计算不收敛的可能性。文献[7]提出了考虑软弱夹层的岩质边坡稳定性分析方法。文献[8]基于Sarma极限平衡法和有限元强度折减法分别探讨了层状岩质边坡在不同岩层倾角、边坡坡角、结构面间隔距离条件下的安全系数与滑动面的变化规律。文献[9]采用离心模型和数值分析研究了含软弱夹层路基边坡的稳定性及破坏模式。文献[10]开展大型地质力学模型试验,揭示了降雨入渗对含软弱夹层顺层边坡性状的影响,表明降雨导致的层间错动受岩层倾角影响较大。文献[11]考虑土体参数空间变异性,分析了某含水平软弱夹层边坡,表明软弱夹层显著影响边坡稳定性、失效路径及可靠度。文献[12]利用有限元软件研究了加抗滑桩的含软弱夹层边坡,表明当桩距较小时,滑动面从坡脚向坡顶发展。文献[13]改进了已有平动-转动组合破坏机构,提出了一种便于工程应用的直线滑动破坏机构。文献[14]应用GEO-SLOPE、ANSYS及FLAC3D软件对开挖70°的含多层软弱夹层边坡进行了稳定性研究,得到边坡的稳定系数及其潜在滑动面。文献[15]建立了某含软弱夹层花岗岩残积土边坡模型,表明软弱夹层的存在不仅造成了边坡总体变形的增大,还决定了边坡滑动面的位置。文献[16]分析了不同坡高及不同坡度下黏聚力c、内摩擦角φ值对边坡安全系数的影响, 结果表明黄土c值控制低边坡稳定性,而黄土φ值控制高边坡稳定性,中间存在一段过渡坡高段,c和φ值对边坡稳定性都有较大影响。文献[17]运用RFPA对多级边坡在开挖卸荷条件下的变形失稳过程进行了数值模拟,表明边坡的软弱夹层附近更易产生局部应力集中并且最早出现初始裂纹。
以上的软层对边坡破坏模式及稳定性影响的多个实例中,研究对象多集中在岩质边坡,对工程实际中常见的土质边坡涉及较少,且只分析某特定含软层边坡的破坏模式,对于不同软层性质边坡的破坏模式较少涉及。本研究基于某土质边坡,运用有限差分分析软件建立多分层(坡体分4层,坡基分2层)层状土质边坡。结合强度折减法,将软层分为由内摩擦角φ控制的软层(φ 较小的软层)及由黏聚力c控制的软层(c较小的软层),分析软层对土质边坡的破坏模式及稳定性的影响。
1 数值方法 1.1 数值模型采用平面应变法建立计算模型,模型边界采用张鲁渝等[18]的建议:坡顶至右边界的距离为2.5H(H为边坡的坡高),左边界至坡脚的距离取1.5H,坡顶部到底部边界的距离为2H。位移边界条件为上部自由、下部固定、左右两侧水平约束,初始应力为自重地应力。为简化研究,不考虑沉积面和软层厚度对土质边坡稳定性的影响,建立水平层状边坡模型,坡脚为45°,层间为均质,其坡体均分为4层,坡基均分为两层,模型几何尺寸、边界条件及分层情况如图 1所示。
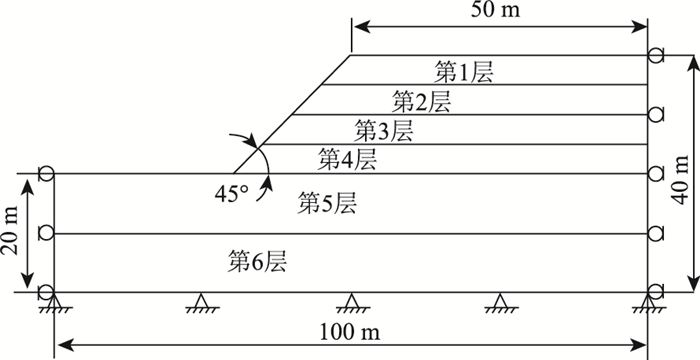
|
| 图 1 计算模型 Fig. 1 Calculation model |
| |
运用FLAC3D建立数值模型,模型包含2 300个单元,3 678个节点,数值模型如图 2所示,采用计算不收敛判据作为边坡失稳判据。
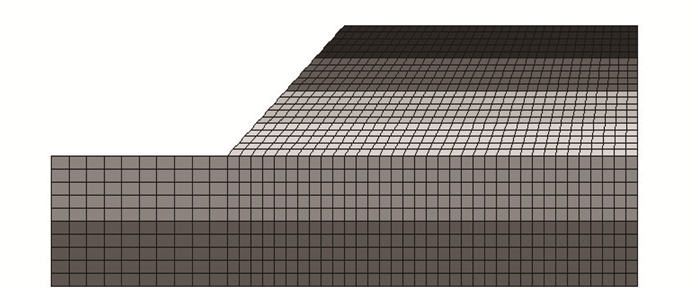
|
| 图 2 数值模型 Fig. 2 Numerical model |
| |
1.2 屈服准则
采取Mohr-Coulomb屈服准则,该准则能同时考虑关联流动拉伸屈服及非关联流动剪切屈服[19]。采用非关联流动法则,不考虑剪胀角Ψ的影响,即剪胀角Ψ值取0。
(1) 剪切屈服准则
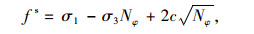
|
(1) |
式中,fs为岩土体的抗剪强度;c和φ分别为岩土体的黏聚力及内摩擦角;σ1和σ3分别为第1和第3主应力。
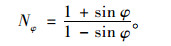
|
(2) |
(2) 拉伸屈服准则
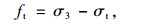
|
(3) |
式中,ft为岩土体的抗拉强度;σt为抗拉强度。
2 软层位置的影响 2.1 边坡参数取值(1) 参数取值
该非均质边坡按连续介质处理,只是材料参数不同。其中软层为粉质黏土层,其内摩擦角或黏聚力低于周围土层。仅考虑内摩擦或黏聚力及其相邻层间差异性的影响。本研究参数按文献[20]选取,内摩擦角相邻层间差异值f_ 2°,f_ 3°,f_ 5°分别为2°,3°,5°,内摩擦角按不同参数组取值,如表 1所示。与内摩擦角类似,coh_ 4kPa,coh_ 8kPa,coh_ 12kPa分别表示黏聚力相邻层间差异值为4,8,12 kPa,黏聚力的取值如表 2所示。
| 参数组 | 编号 | |||||
| 1(软层) | 2 | 3 | 4 | 5 | 6 | |
| f_2°/(°) | 20 | 22 | 24 | 26 | 28 | 30 |
| f_3°/(°) | 18 | 21 | 24 | 27 | 30 | 33 |
| f_5°/(°) | 14 | 19 | 24 | 29 | 34 | 39 |
| 参数组 | 编号 | |||||
| 1(软层) | 2 | 3 | 4 | 5 | 6 | |
| coh_4kPa/kPa | 36 | 40 | 44 | 48 | 52 | 56 |
| coh_8kPa/kPa | 28 | 36 | 44 | 52 | 60 | 68 |
| coh_12kPa/kPa | 20 | 32 | 44 | 56 | 68 | 80 |
(2) 参数分布
考虑工程实际,选取如下4种常见的软层分布方式:①软层分布在边坡顶部,即参数编号由1到6;②软层分布在边坡底部,即参数编号由6到1;③软层分布在边坡顶部和底部,即参数编号由1到3,再由3到1;④软层分布在边坡中部,即参数编号由3到1,再由1到3。考虑单一因素的影响,主要考虑内摩擦角及黏聚力如上4种分布以及不同分布情况下层间参数差异性对边坡稳定性的影响。
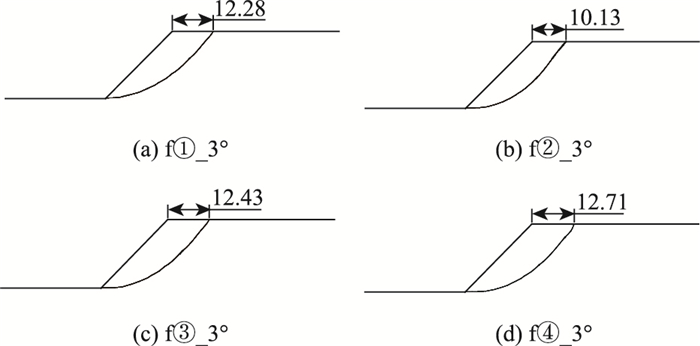
2.2 软层位置对滑动面的影响以参数组f_ 3°为例,计算边坡主要受土体自重力影响而产生的滑移力。为更好地反映边坡滑动面的位置,选取位移值为0.5 m的等值线作为边坡的滑动面[20],将该位移等值线与边坡上轮廓线取出,如图 3所示。分布①、③及④呈现为圆弧型破坏特征,分布②滑动面上边缘距坡顶距离明显低于分布①、③及④,表现为圆弧+直线型破坏,表明由内摩擦角控制的软层分布于边坡底部,使得边坡表现为圆弧+直线型破坏。
|
| 图 3 f_ 3°不同软层分布情况下边坡滑动面(单位: m) Fig. 3 Slip surface of slope with different distributions of soft layer in group of f_ 3°(unit: m) |
| |
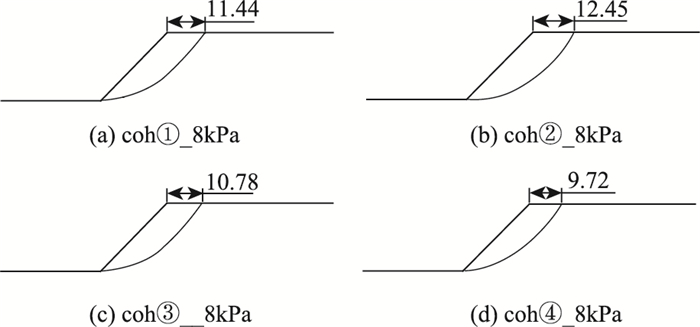
在不同分布情况下,由黏聚力控制的软层与由内摩擦角控制的软层对边坡破坏机制的影响具有显著差异。如图 4所示(以coh_ 8kPa参数组为例),表现为分布②呈明显的圆弧型破坏,且分布②具有最大的整体位移,即由黏聚力控制的软层分布于边坡底部,使得边坡表现为圆弧型破坏;分布④滑动面上边缘距坡顶距离最小,表现为明显的圆弧+直线型破坏;其余分布也表现为一定程度的圆弧+直线型破坏。
|
| 图 4 coh_ 8kPa不同软层分布情况下边坡滑动面(单位:m) Fig. 4 Slip surface of slope with different distributions of soft layer in group of coh_ 8kPa(unit: m) |
| |
2.3 软层位置对安全系数的影响
采用强度折减计算不收敛准则,计算f_ 3°和coh_ 8kPa共4种分布的安全系数,分别如表 3及表 4所示。内摩擦角安全系数的变化百分比为18.75%,黏聚力安全系数的变化百分比为27.08%。
| 软层 | |||
| ① | ② | ③ | ④ |
| 1.352 | 1.361 | 1.300 | 1.146 |
| 软层 | |||
| ① | ② | ③ | ④ |
| 1.333 | 1.406 | 1.279 | 1.106 |
可以看出,由黏聚力或内摩擦角控制的软层位置对边坡安全系数的影响效果一致,由式(4)[21]可知,黏聚力和内摩擦角联合反映土体抗剪强度τf,而抗剪强度的取值直接影响边坡稳定性:
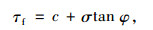
|
(4) |
式中c和φ分别为黏聚力和内摩擦角; σ为正应力。
由黏聚力或内摩擦角控制的软层位置中,分布②具有最高的安全系数,反映出软层位于边坡底部,坡体具有较大的整体稳定性,表明软层位于边坡底部对于工程安全影响较弱;分布④具有最低的安全系数,即软层位于边坡中部,显著降低坡体的整体稳定性,对边坡工程有显著不利影响,这也与工程实际、试验研究及理论分析[15-17]具有一致性。在实际施工过程中必须充分考虑对其进行加固。
2.4 软层位置不同分布情况下层间参数差异值的影响分别从滑动面上边缘距坡顶距离及边坡安全系数两方面评价软层不同分布情况下层间参数差异性的影响,主要考虑内摩擦角及黏聚力不同时的层间差异影响。如图 5所示,随层间参数差的提高,对内摩擦角控制的软层,在分布①时,边坡表现为滑动面上边缘距坡顶距离有微弱的增大,而由黏聚力控制的软层则稍有降低;在分布②时,内摩擦角控制的软层边坡滑动面上边缘距坡顶距离急剧减小,与之相反,黏聚力表现为使滑动面上边缘距坡顶距离有较为显著的增大;在分布③时,黏聚力层间差增大导致滑动面上边缘距稍有减小,内摩擦角层间差在增加较小时,滑动面上边缘距剧烈增加,但当其值持续增加时,其影响效果明显减弱;在分布④时,黏聚力层间差增大引起上边缘距剧烈减小,而内摩擦角层间差增大引起上边缘距稍有增大。
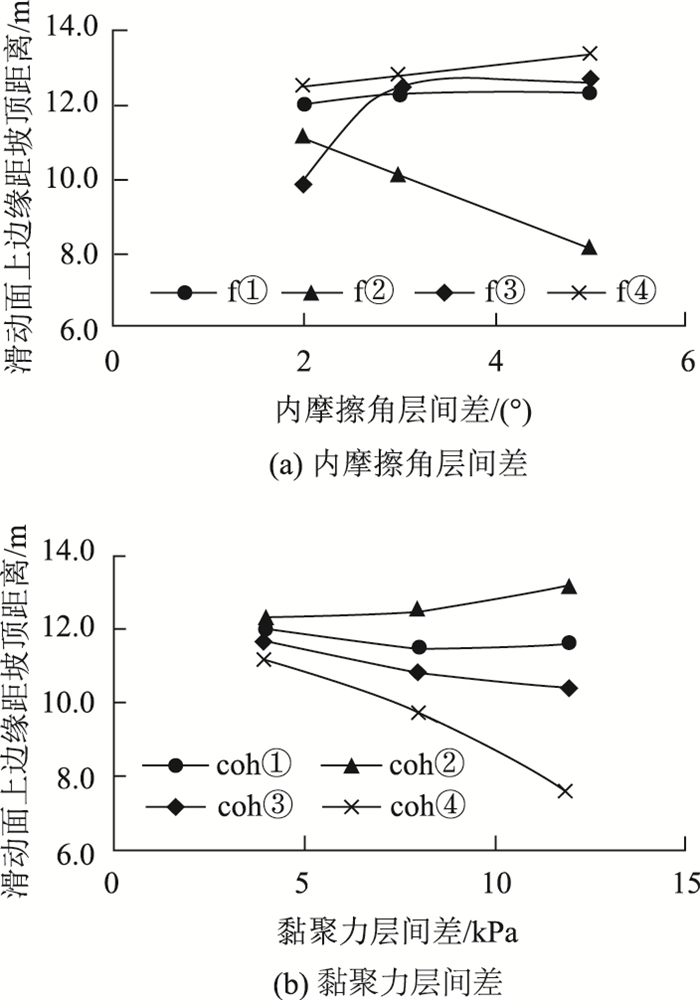
|
| 图 5 不同软层分布情况下层间差对应的滑动面上边缘距坡顶距离 Fig. 5 Distance from slip surface upper edge to slope top varying with interlayer difference in different soft layer distributions |
| |
因此,滑动面上边缘距不仅取决于边坡上层(第1层~第3层)土体的影响,而且受下层(第4层~第6层)土体的影响。对比f①与f③可知,在层间差较小时,因内摩擦角控制的软层分布于下层显著降低了滑动面上边缘距,随层间差的增加,下层较低的内摩擦角软层使滑动面上边缘距稍有增大;对比coh①与coh③,因黏聚力控制的软层分布于边坡底部使滑动面上边缘距有一定的降低,且该效果随层间差的增大而稍有增大。
如图 6所示,在安全系数方面,在分布①和②时,软层的内摩擦角及黏聚力随层间差的增大,安全系数都有所增大,且分布②的安全系数都较分布①大;分布③层间差影响不显著;在分布④时,内摩擦角及黏聚力随层间差增大,安全系数显著降低,主要由于层间差增大时,中间土层(第3和4层)取得的内摩擦角或黏聚力会明显减小,导致中间土层的抗剪强度显著降低, 表明位于边坡中部软层的抗剪强度会显著降低,其稳定性显著减低。
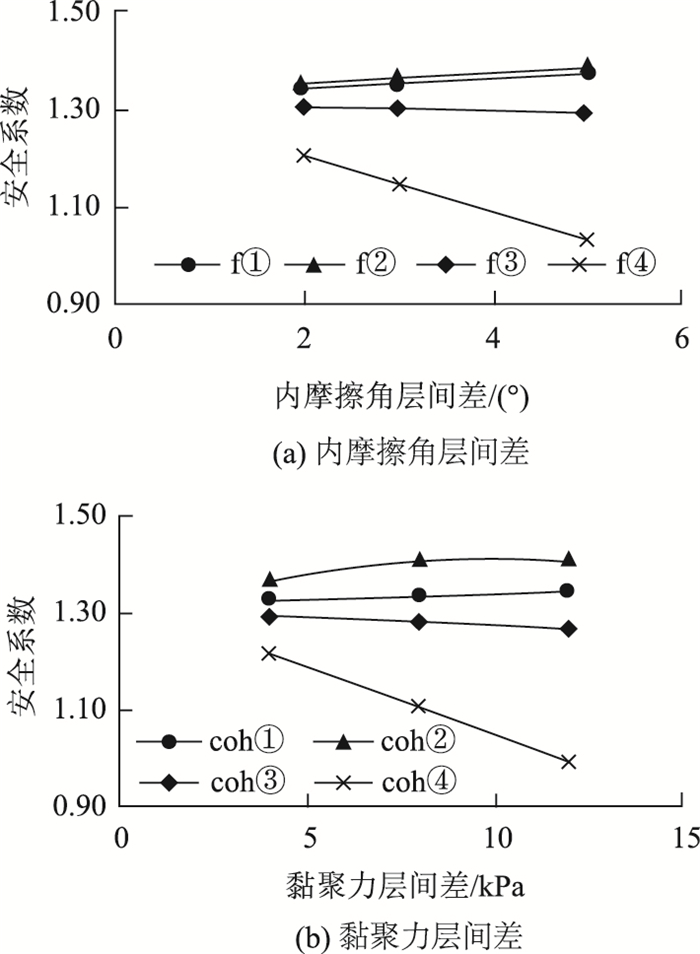
|
| 图 6 不同软层分布情况下层间差对应的边坡安全系数 Fig. 6 Safety factors of slope varying with interlayer difference in different soft layer distributions |
| |
综上所述得出如下结论:(1)软层内摩擦角和黏聚力的影响作用效果一致,因为内摩擦角和黏聚力联合决定了软层的抗剪强度,而软层的抗剪强度决定了边坡的稳定性;(2)边坡中间土层的内摩擦角和黏聚力的取值对边坡稳定性有显著的影响,当边坡中间土层的抗剪强度不发生改变时,上下土层的参数变化对其稳定性影响微弱(f③和coh③)。对比f④和coh④,当位于中间土层的软层抗剪强度降低时,会显著降低边坡的整体稳定性。土质边坡的剪切破坏始于坡脚,进而向坡体上边缘延伸,直至形成贯通的滑动面导致边坡失稳,故位于坡脚的低抗剪强度的软层使坡体易于发生剪切破坏,进而引起坡体失稳。
3 软层与周围土层相互作用的影响如上分析,位于坡体中部的软层对边坡的稳定性有显著影响。为探讨关键层是软层还是周围土层,有必要研究软层位于边坡中部时,软层与周围土层的相互作用机制对边坡稳定性的影响。
3.1 边坡参数取值内摩擦角的不同参数组取值如表 5所示,参数组F2至F6分别表示软层内摩擦角与其周围土层差异值为2°至6°,即研究在周围土层性质不变的情况下,软层内摩擦角减小对边坡稳定性的影响;参数组Fw_ 2至Fw_ 6分别表示在软层内摩擦角取值不变的情况下,周围土层差异值为2°至6°,即研究在软层性质不变的情况下,周围土层内摩擦角变化对边坡稳定性的影响。与内摩擦角类似,黏聚力的不同参数组取值如表 6所示。
| 内摩擦角/ (°) | 参数组编号 | 备注 | ||||
| F2 | F3 | F4 | F5 | F6 | φ2=22° | |
| φ1(软层) | 20 | 19 | 18 | 17 | 16 | φ3=24° |
| 内摩擦角/ (°) | 参数组编号 | 备注 | ||||
| Fw_2 | Fw_3 | Fw_4 | Fw_5 | Fw_6 | φ1=20° (软层) | |
| φ2 | 22 | 23 | 24 | 25 | 26 | |
| φ3 | 24 | 26 | 28 | 30 | 32 | |
| 黏聚力 | 参数组编号 | 备注 | ||||
| C4 | C8 | C12 | C16 | C20 | c2=40 kPa | |
| c1(软层) | 36 | 32 | 28 | 24 | 20 | c3=44 kPa |
| 黏聚力 | 参数组编号 | 备注 | ||||
| Cw_4 | Cw_8 | Cw_12 | Cw_16 | Cw_20 | c1=36 kPa (软层) | |
| c2 | 40 | 28 | 32 | 36 | 40 | |
| c3 | 44 | 36 | 44 | 52 | 60 | |
3.2 软层对边坡稳定性的影响
当边坡中存在软层时,随着软层内摩擦角的减小,边坡滑动面上边缘距坡顶距离不断增大(如图 7 (a)至 (d)所示),但当软层的内摩擦角减小到一定程度,边坡滑动面上边缘距坡顶距离反而降低,如图 7 (e)所示,其滑动面上边缘距坡顶距离有所降低,且随软层的内摩擦角的减小,边坡破坏模式趋向圆弧破坏。而边坡滑动面上边缘距坡顶距离随其软层黏聚力的降低而不断减小(如图 8所示),其破坏模式趋向圆弧+直线混合破坏。
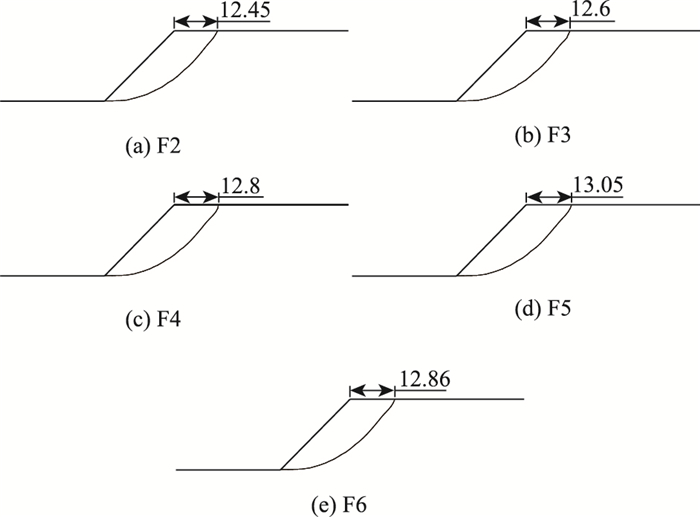
|
| 图 7 不同软层内摩擦角的边坡滑动面(单位:m) Fig. 7 Slip surfaces of slope with different internal friction angles of soft layer(unit: m) |
| |

|
| 图 8 不同软层黏聚力的边坡滑动面(单位:m) Fig. 8 Slip surfaces of slope with different cohesions of soft layer(unit: m) |
| |
随着边坡软层的内摩擦角和黏聚力的减小,其安全系数都逐渐递减(表 7、表 8)。内摩擦角安全系数的变化百分比为9.86 %,黏聚力安全系数的变化百分比为19.76 %。由此可知,边坡软层的抗剪强度对边坡的稳定性至关重要,在相关工程中必须对其进行加固处理。
| 软层 | F2 | F3 | F4 | F5 | F6 |
| 系数 | 1.203 | 1.177 | 1.150 | 1.122 | 1.095 |
| 软层 | C4 | C8 | C12 | C16 | C20 |
| 系数 | 1.217 | 1.164 | 1.117 | 1.069 | 1.016 |
3.3 软层周围地层对边坡稳定性的影响
当边坡中软层的抗剪强度确定时,软层周围土体内摩擦角的增大对其破坏形态无明显影响(如图 9所示)。而随软层周围土体黏聚力的提高,边坡破坏形态为圆弧破坏(图 10 (a)、图 10 (c)、图 10 (e))和圆弧+直线破坏(图 10 (b)、图 10 (d))交替出现。
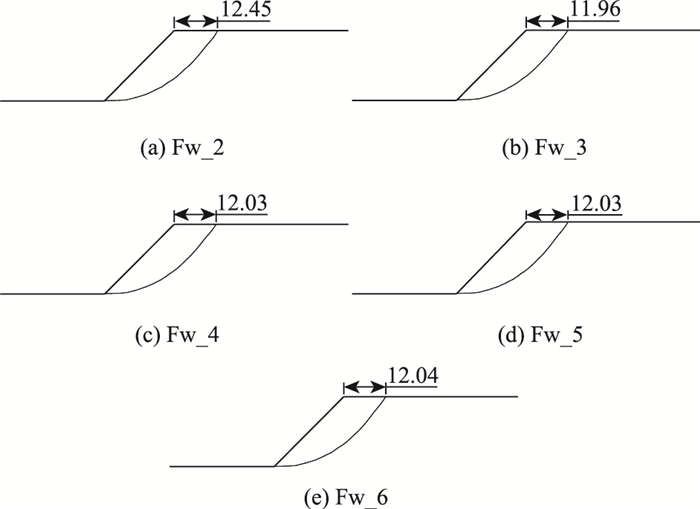
|
| 图 9 软层周围土层不同内摩擦角的边坡滑动面(单位: m) Fig. 9 Slip surfaces of slope with different internal friction angles of soil around soft layer (unit: m) |
| |

|
| 图 10 软层周围土层不同黏聚力的边坡滑动面(单位:m) Fig. 10 Slip surfaces of slope with different cohesions of soil around soft layer (unit: m) |
| |
随着边坡软层周围土层的内摩擦角和黏聚力的增大,安全系数有微弱的提升(表 9、表 10)。内摩擦角安全系数的变化率为1.26%,黏聚力安全系数的变化率为5.02%。软层周围土体的加强对边坡稳定性影响非常微弱,在施工过程中应重点加固软层,并适当对其周围土层进行补强。
| 软层 | ||||
| Fw_2 | Fw_3 | Fw_4 | Fw_5 | Fw_6 |
| 1.203 | 1.206 | 1.211 | 1.214 | 1.218 |
| 软层 | ||||
| Cw_4 | Cw_8 | Cw_12 | Cw_16 | Cw_20 |
| 1.217 | 1.228 | 1.252 | 1.267 | 1.278 |
4 结论
(1) 运用FLAC3D建立了能够反映复杂工况的多分层水平层状边坡,将软层分为由内摩擦角φ控制的软层(φ较小的软层)以及由黏聚力c控制的软层(c较小的软层),分析了由φ控制的软层和由c控制的软层位置及参数层间差值对土质边坡破坏模式及稳定性的影响。
(2) 由φ控制的软层分布于边坡顶部时,边坡表现为圆弧+直线型破坏,其他分布为圆弧破坏;由c控制的软层分布于边坡顶部时,边坡呈明显的圆弧型破坏,其余分布表现为一定程度的圆弧+直线型破坏。
(3) 由φ或c控制的软层位置对土质边坡安全系数影响效果一致,都表现为软层位于边坡底部对整体稳定性影响较小,软层位于边坡中部会显著降低其稳定性,在实际工程中应充分考虑该不利影响。滑动面上边缘距不仅取决于边坡上层土体,而且受下层土体的影响。不同软层分布工况下,φ或c对安全系数的影响效果一致。
(4) 对软层位于边坡中部情况的分析表明,软层自身的性质比其周围硬层性质对边坡破坏机制及稳定性的影响显著,施工中对软层进行加固能明显改善其不利影响,但对其周围硬层进行加固时,边坡的整体稳定性改善效果不明显。在相关施工中,应重点加固软层,并适当对其周围土层进行补强,可实现经济合理的支护方案。
| [1] |
FELLENIUS W. Earth Stability Calculations Assuming Friction and Cohesion on Circular Slip Surfaces[M]. Berlin: W. Ernst, 1927.
|
| [2] |
JANBU N. Slope Stability Computations Embankment Dam Engineering[M]. New York: John Wiley and Sons, Inc., 1973.
|
| [3] |
SARMA S K. Stability Analysis of Embankments and Slopes[J]. Geotechnique, 1973, 23(3): 423-433. |
| [4] |
ZIENKIEWICZ O C, HUMPHESON C, LEWIS R W. Associated and Non-associated Visco-plasticity and Plasticity in Soil Mechanics[J]. Geotechnique, 1975, 25(4): 671-689. |
| [5] |
LIU S Y, SHAO L T, LI H J. Slope Stability Analysis Using the Limit Equilibrium Method and Two Finite Element Methods[J]. Computers and Geotechnics, 2015, 63: 291-298. |
| [6] |
CHEN X, WU Y, YU Y, et al. A Two-grid Search Scheme for Large-scale 3-D Finite Element Analyses of Slope Stability[J]. Computers and Geotechnics, 2014, 62: 203-215. |
| [7] |
CHEN Z Y, MORGENSTERN N R. Extensions to the Generalised Method of Slices for Stability Analysis[J]. Canadian Geotechnical Journal, 1983, 20(1): 104-119. |
| [8] |
张社荣, 谭尧升, 王超, 等. 多层软弱夹层边坡岩体破坏机制与稳定性研究[J]. 岩土力学, 2014, 35(6): 1695-1702. ZHANG She-rong, TAN Yao-sheng, WANG Chao, et al. Research on Deformation Failure Mechanism and Stability of Slope Rock Mass Containing Multi-weak Interlayers[J]. Rock and Soil Mechanics, 2014, 35(6): 1695-1702. |
| [9] |
刘怡林, 黄茂松, 袁伟, 等. 斜坡含软夹层地基路堤离心模型试验与数值模拟[J]. 岩土力学, 2013(增2): 22-34. LIU Yi-lin, HUANG Mao-song, YUAN Wei, et al. Centrifugal Model Test and Numerical Simulation of Embankments on Sloping Ground with Weak Interlayer[J]. Rock and Soil Mechanics, 2013(S2): 22-34. |
| [10] |
李龙起, 罗书学, 魏文凯, 等. 降雨入渗对含软弱夹层顺层岩质边坡性状影响的模型试验研究[J]. 岩石力学与工程学报, 2013, 32(9): 1772-1778. LI Long-qi, LUO Shu-xue, WEI Wen-kai, et al. Model Tests of Rainfall Infiltration Effect on Bedding Rock Slope with Weak Interlayer[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(9): 1772-1778. |
| [11] |
蒋水华, 姚池, 杨建华, 等. 考虑参数空间变异性的非均质边坡可靠度分析[J]. 防灾减灾工程学报, 2016, 36(4): 572-579. JIANG Shui-hua, YAO Chi, YANG Jian-hua, et al. Reliability Analysis of Heterogeneous Slopes Considering Spatially Variable Soil Properties[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(4): 572-579. |
| [12] |
刘怡林, 宁兆轲, 姜瑞清, 等. 抗滑桩加固含软弱夹层边坡三维弹塑性数值分析[J]. 岩土工程学报, 2013, 35(增1): 216-221. LIU Yi-lin, NING Zhao-ke, JIANG Rui-qing, et al. 3D Elastoplastic Stability Analysis of Slopes with Weak Interlayers Reinforced by Piles Based on FEM[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S1): 216-221. |
| [13] |
汤祖平, 李亮, 赵炼恒, 等. 含软弱夹层边坡稳定性的极限分析上限解析[J]. 铁道科学与工程学报, 2014, 11(2): 60-64. TANG Zu-ping, LI Liang, ZHAO Lian-heng, et al. Stability Analysis of Slopes with Weak Interlayer Based on Upper Bound Limit Analysis[J]. Journal of Railway Science and Engineering, 2014, 11(2): 60-64. |
| [14] |
宋子岭, 杨添, 赵立春. 含多层软弱夹层的顺向岩质边坡稳定性评价方法对比分析[J]. 中国地质灾害与防治学报, 2016, 27(2): 20-25. SONG Zi-ling, YANG Tian, ZHAO Li-chun. Application of Combination Algorithm in Stability Analysis of Rock Slope with Contains Multilayer Weak Bedrock Layers[J]. The Chinese Journal of Geological Hazard and Control, 2016, 27(2): 20-25. |
| [15] |
陈玮, 简文彬, 董岩松, 等. 某含软弱夹层花岗岩残积土边坡稳定性研究[J]. 水利与建筑工程学报, 2014, 12(6): 107-112. CHEN Wei, JIAN Wen-bin, DONG Yan-song, et al. Stability Study of a Granite Residual Soil Slope with Weak Interlayers[J]. Journal of Water Resources and Architectural Engineering, 2014, 12(6): 107-112. |
| [16] |
张常亮, 李萍, 陶福平, 等. 黄土强度指标对边坡稳定性的影响研究[J]. 公路交通科技, 2011, 28(3): 20-25. ZHANG Chang-liang, LI Ping, TAO Fu-ping, et al. Research of Effect of Strength Index on Loess Slope Stability[J]. Journal of Highway and Transportation Research and Development, 2011, 28(3): 20-25. |
| [17] |
柴佳乐, 张拥军, 李博, 等. 开挖条件下软弱夹层对岩质边坡稳定性的影响[J]. 工程建设, 2017, 49(2): 1-6. CHAN Jia-le, ZHANG Yong-jun, LI Bo, et al. The Influences of Weak Interlayer on Rocky Slope Stability under the Condition of Excavation[J]. Engineering Construction, 2017, 49(2): 1-6. |
| [18] |
张鲁渝, 郑颖人, 赵尚毅, 等. 有限元强度折减系数法计算土坡稳定安全系数的精度研究[J]. 水利学报, 2003, 34(1): 21-27. ZHANG Lu-yu, ZHENG Yin-ren, ZHAO Shang-yi, et al. The Feasibility Study of Strength-reduction Method with FEM for Calculating Safety Factors of Soil Slope Stability[J]. Journal of Hydraulic Engineering, 2003, 34(1): 21-27. |
| [19] |
Itasca Consulting Group, Inc. Flac 3D User Manuals[M].Minneapolis: Itasca Consulting Group Inc., 2005.
|
| [20] |
孙书伟, 林杭, 任连伟. FLAC3D在岩土工程中的应用[M]. 北京: 中国水利水电出版社, 2011. SUN Shu-wei, LIN Hang, REN Lian-wei. Application of FLAC3D in Geotechnical Engineering[M]. Beijing: China Water and Power Press, 2011. |
| [21] |
陈祖煜, 汪小刚, 杨健, 等. 土质边坡稳定分析:原理·方法·程序[M]. 北京: 中国水利水电出版社, 2003. CHEN Zu-yu, WANG Xiao-gang, YANG Jian, et al. Soil Slope Stability Analysis:Theory, Methods and Procedures[M]. Beijing: China Water and Power Press, 2003. |
 2019, Vol. 36
2019, Vol. 36
