扩展功能
文章信息
- 徐冬青, 张东, 庄心怡, 边疆
- XU Dong-qing, ZHANG Dong, ZHUANG Xin-yi, BIAN Jiang
- 图像处理方法在粗集料形态评价中的应用研究进展
- Study Progress of Application of Image Analysis Methods in Evaluation of Coarse Aggregate Morphology
- 公路交通科技, 2019, 36(6): 1-9, 78
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(6): 1-9, 78
- 10.3969/j.issn.1002-0268.2019.06.001
-
文章历史
- 收稿日期: 2018-08-08
2. 南京工业大学 道路工程研究所, 江苏 南京 210009
2. Institute of Road Engineering, Nanjing Tech University, Nanjing Jiangsu 210009, China
粗集料是沥青混合料的主要成分之一,占总质量的50%~80%左右。沥青混合料是我国常用的路面铺筑材料。据我国交通运输部的统计数据,2010年至2016年间我国公路总里程每年约增加10万km。粗略计算,我国每年公路建设需要消耗20亿t左右的粗集料。国内外在粗集料对沥青混合料性能的影响方面已经有大量研究,并且得到了一些基本共识。在形状方面,针片状集料含量增加,会导致沥青混合料最佳油石比和空隙率增大,降低沥青混合料的高温稳定性、水稳定性和抗疲劳性能。在棱角方面,粗集料棱角性和沥青混合料高温稳定性之间的关系已经非常明确,提高粗集料的棱角性可以增强沥青混合料的永久变形性能。在纹理方面,粗集料纹理和沥青混合料性能之间关系密切,提高粗集料的纹理指标可以改善沥青混合料的高温稳定性、水稳定性和低温抗裂性。因此,准确评价粗集料的形态特征对于粗集料的质量控制和沥青混合料设计具有重要意义。
评价粗集料形态的方法主要有两类,即间接法和基于图像处理技术的方法。图像处理方法又分为基于二维图像的方法和基于三维图像的方法。近20 a以来,随着图像采集手段的进步和图像处理技术的发展,集料形态的评价方法和评价指标研究层出不穷。现有的研究综述主要分散在具体的研究论文中,并且是基于二维图像处理技术的部分成果。本研究通过大量文献调研,系统总结粗集料形态评价方面具有代表性的研究成果,并进行评述和展望。
1 间接方法ASTM D4791[1]使用规准仪手工测定粗集料中针片状集料的含量。ASTM D4791采用长细比(Flat and Elongated Ratio, FER)指标识别针片状颗粒。长细比FER是集料长轴长度Dl和短轴长度Ds的比值,如式(1)所示:
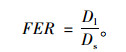
|
(1) |
通常将长细比超过5: 1或3: 1的粗集料定义为针片状集料。我国《公路工程集料试验工程》(JTG E42—2005)[2]也使用类似的方法测得针片状集料的含量。Prowell等[3]研究了ASTM D4791的测试精度,发现单人操作的变异系数可达26.1%,实验室之间的变异系数可达35.3%。ASTM D5821[4]通过人工计数断裂面的方法评价粗集料的棱角性。我国也采用了类似的方法[2]。ASTM D5821将断裂面定义为“集料颗粒的有棱角的、粗糙的面或者由外力造成的破坏面”。断裂面通过肉眼进行识别。
AASHTO TP56[5]通过粗集料的松装空隙率试验评价形状、棱角和纹理的复合效果。ASTM D3398[6]使用颗粒指数表征粗集料形状、棱角和纹理的复合效果。在试验中,每种粒径的粗集料被置于直径为6英寸、高为7英寸的圆柱形试模中,分别使用两种压实功(10次和50次)分层捣实。颗粒指数Ia的计算公式为:
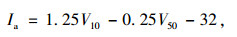
|
(2) |
式中,V10为分层捣实10次时粗集料中的空隙;V50为分层捣实50次时粗集料中的空隙。
间接方法费时、费力,测试精度取决于操作人员的熟练程度和经验。此外,AASHTO TP56和ASTM D3398无法将集料的形状、棱角和纹理特征分开研究。
间接方法主要基于手工测量、肉眼识别和简单试验,在控制集料质量方面具有一定作用,但只能做定性评价。采用现代化测试手段,快速、定量、精确评价粗集料的形状、棱角和纹理特征是该领域的研究课题之一,其中基于图像处理技术的方法是过去20 a的研究重点。
2 二维图像方法基于二维图像的方法,通过采集集料的二维图像,利用图像处理技术评价集料的形态特征。目前,已经研制了多种图像采集和分析系统。主要有Video Grader VDG 40系统[7]、WipShape系统[8]、集料图像系统AIMS[9]和AIMS2[10](第2代AIMS)以及伊利诺伊大学集料图像分析仪UIAIA[11]和E-UIAIA[12-13](第2代UIAIA)。基于二维图像,研究人员已经提出了多种指标评价集料的形态特征,以下进行综述。
2.1 基于图像尺寸和半径的方法岩石学家在20世纪30年代就对集料的形状进行了定量描述[14]。研究方法主要是基于集料的三维尺寸(长轴长度Dl、中轴长度Dm和短轴长度Ds)。通过这3个尺寸,可以得到一系列描述集料形状的指标,包括扁平比、细长比和形状因子。Wadell[15]使用球度来描述集料的三维形状特征,定义为具有与集料颗粒相同体积的球体的表面积与集料表面积的比值。Krumbein[16]根据球度的定义,提出了计算球度Ψ的简化公式:
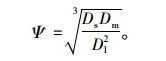
|
(3) |
使用形状因子、扁平比、细长比和球度可以将集料分为盘状、立方状、片状和棒状。Kuo等[17-18]基于粗集料的三维尺寸,提出形状因子(Shape Factor)表征粗集料的形状特征,如式(4)所示:
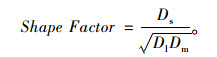
|
(4) |
基于粗集料几何尺寸提出的粗集料形状分类方法对后续研究具有启发意义,这种分类方法直到目前为止还被研究人员使用。
Wadell[15]基于集料二维图像,提出使用圆度(Roundness)评价集料的棱角性。圆度使用集料轮廓线上各拐角处的半径与最大内接圆半径的比值定义,计算公式为:

|
(5) |
式中,ri为拐角处半径;R为最大内接圆半径;N为拐角数目。
此外,还有一种使用图像轮廓线的周长和面积定义圆度的方法,如式(6)所示[19]:
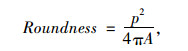
|
(6) |
式中,p为轮廓线的周长,A为图像的面积。
Lees[20]认为棱角不仅与拐角处内接圆的半径有关,而且与拐角顶点到内接圆的距离有关。由此提出了一个表征拐角尖锐程度的公式:
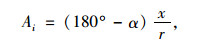
|
(7) |
式中,Ai是棱角度;α为拐角处顶角;x为拐角顶点到内接圆的的距离;r为拐角处内接圆的半径。
由于早期计算机图像处理技术尚未成熟,Wadell[15]和Lees[20]提出的公式在几何上是合理的,但是用图像处理方法难以实现。
Masad等[21]基于图像轮廓线半径的变化提出了形状指数(Form Index)和半径棱角指数(Radius Angularity Index)分别表征集料的形状和棱角,如式(8)和式(9)所示:
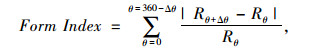
|
(8) |
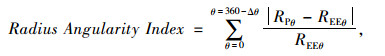
|
(9) |
式中,θ为方向角;Δθ为角度增量;R为轮廓线上点到图像形心的距离;RPθ为轮廓线上点到图像形心的距离; REEθ为图像等效椭圆上点到图像形心的距离。
Masad等 [21]基于现代图像处理技术提出的计算公式在粗集料二维形态评价方面具有一定的先进性,但式(8)和式(9)本质上都是评价棱角的指标,在形状指标上没有明确的物理意义。
2.2 腐蚀-膨胀法、分形维数法、梯度法和多边形拟合法腐蚀-膨胀法是一种常用的图像处理技术。腐蚀是指将图像中的像素移除,膨胀则是腐蚀的相反操作,是指增加图像的像素。腐蚀操作使图像失去棱角,图像轮廓线变得平滑,随后的膨胀操作将不能完全恢复失去的棱角。因此,图像的棱角性或纹理可以通过腐蚀-膨胀前后图像面积的变化描述,如式(10)所示:

|
(10) |
式中,Angularity为棱角指标;Texture为纹理指标;A1为腐蚀前图像的面积;A2为膨胀后图像的面积。
Masad等[22]使用这个方法分析低分辨率集料图像的棱角性和高分辨率集料图像的纹理。腐蚀-膨胀法是一种快速、简单的图像处理方法,在评价粗集料二维棱角方面是有效的,但是受到尺度的限制,并不具备评价纹理的意义。
分形方法也可以用于评价集料的棱角性[23]。二维集料图像在标准格栅上由像素点组成。每个像素点的灰度值在0~255之间,0表示黑色,255表示白色。分形维数分析通过图像的灰度变化算法实现。计算图像分形维数的主要步骤如下。首先,通过像素点的灰度变化识别集料图像的轮廓线。在某尺寸的格栅图上,包含集料图像轮廓线的网格数目可通过计算得到。然后,增加网格尺寸,得到不同尺寸格栅图上包含轮廓线的网格数目。最后,以网格尺寸为横坐标,以包含轮廓线的网格数目为纵坐标,绘制双对数曲线。曲线的坡度就是分形维数。对于完全光滑的边界(圆),分形维数等于1。对于极度不规则的边界,分形维数增加到最大值2。
Chandan等[24]提出了一种基于图像轮廓线梯度的方法评价集料的棱角性。这种方法的主要思想是,在图像轮廓线凸起处,相邻点梯度向量的方向变化很大。基于相邻点梯度向量方向角的差值,提出了梯度指数GI (Gradient Index)评价集料的棱角性:
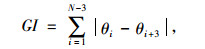
|
(11) |
式中,θi为方向角;i为点序号;N为轮廓线上点的数目。
基于梯度的方法在概念上是可行的,但是梯度指数值在一定程度上取决于图像轮廓线上点的数目,图像尺寸和像素会影响计算精度。
Rao等[23]使用等边多边形拟合集料图像的轮廓线,通过跟踪轮廓线坡度的变化表征图像的棱角性。首先,提取集料图像轮廓线上点的坐标,使用n边多边形拟合图像轮廓线。然后,计算相邻顶点顶角的差值,并绘制顶角差值的频率分布图(角度区间为10°),使用式(12)计算集料图像的棱角A:
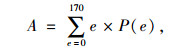
|
(12) |
式中,e为顶角,按每隔10°取值;P (e)为顶角差值在区间(e,e+10)内的概率。
最后,集料的棱角指数AI (Angularity Index)通过集料顶面、正面和侧面图像的棱角按面积加权平均计算:
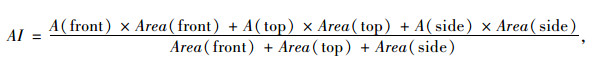
|
(13) |
式中,A (front)为正面图像棱角;Area (front)为正面图像面积;A (top)为顶面图像棱角;Area (top)为顶面图像面积;A (side)为侧面图像棱角;Area (side)为侧面图像面积。
Rao等[23]通过跟踪轮廓线坡度的变化表征图像棱角性的方法是准确的。并且他们使用粗集料顶面、正面和侧面图像按照面积加权平均的方法计算粗集料的棱角指标,这在一定程度上弥补了二维图像方法的缺陷。
2.3 霍夫变换法霍夫变换是图像处理中用于形状识别和形状检测的一种方法。在集料形态的研究中,霍夫变换主要用于检测图像轮廓线上的直线段。在早期,Wilson等[25]使用这种方法研究集料形态,提出了圆度指标和棱角指标分别评价集料的形状和棱角。Descantes等[26]使用霍夫变换检测集料图像轮廓线上的直线段,提出了评价集料棱角和纹理的指标ANG和RUG,计算公式分别为:
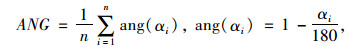
|
(14) |
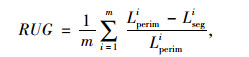
|
(15) |
式中,αi为两条相邻直线段之间的夹角;n为夹角的数目;m为直线段的数目;Lsegi为第i条直线段的长度;Lperimi为第i条直线段对应的轮廓线的长度。
基于霍夫变换法提出的棱角指标是可行的,但是使用这种方法得到的纹理指标(式(15))实际上是棱角和纹理的复合指标。
2.4 傅里叶变换法Wang等[27]使用傅里叶级数拟合集料图像的轮廓线,并基于此提出了评价粗集料形状、棱角和纹理的指标。设图像轮廓线上点到图像形心的距离为R (θ)(θ为轮廓线上点到形心之间直线与X轴的夹角),R (θ)可以用傅里叶级数表示成式(16)的形式:
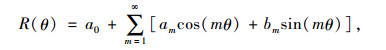
|
(16) |
式中,a0为轮廓线的平均半径;am和bm为幅度;m为频率;项amcos (mθ)+bmsin (mθ)反映了轮廓线的特征。
在频域,低频段部分代表形状,中频段部分代表棱角,高频段部分代表纹理。基于这个原理,构建了形状、棱角和纹理指标αs,αr和αt,计算公式分别为:
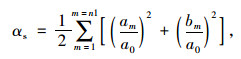
|
(17) |
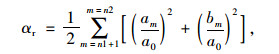
|
(18) |
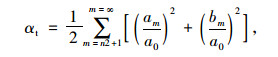
|
(19) |
式中,划分形状、棱角和纹理指标的临界频率n1和n2由图像的轮廓线特性决定。
类似地,Bangaru等[28]通过对集料二维图像的傅里叶变换,在频率域提出了评价集料形状、棱角和纹理的指标,在此不再细述。该方法的缺点是区分形状、棱角和纹理的临界频率具有不确定性,缺乏明确的依据。
2.5 小波变换法Chandan等[24]和Fletcher等[29]基于集料灰度图,提出了使用小波变换方法评价集料表面的纹理。在集料灰度图上,集料的表面纹理可由像素灰度值的局部变化来表征。小波变换的基本思想是在不同的分辨率水平下将图像分解成一个低分辨率的图像和一系列具体的图像。下面借助图 1说明小波变换的基本原理。原图像通过反复模糊,被分解成一个低分辨率的图像,如图 1(a)所示。图 1中的其余图像则包含了图 1(a)中丢失的细微强度变化信息(高频部分),图 1(b)中包含了y轴方向丢失的信息,图 1(c)中包含了x轴方向丢失的信息,图 1(d)中包含了x轴和y轴方向丢失的信息。图 1(a)可以进一步分解为更低分辨率的图像,用多尺度纹理分析。图 1(b)~图 1(d)中的高频部分表示集料表面的纹理,可以用细节系数(Detail Coefficient)定量描述。

|
| 图 1 小波分解图 Fig. 1 Images of wavelet decomposition |
| |
基于此,定义能量特征值(Energy Signature)指标表征纹理,如式(20)所示:
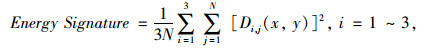
|
(20) |
式中,N为分解水平;Di, j (x, y)为细节系数;j为像素点序号。
在小波变换方法中,由于纹理由图像灰度值的局部变化来表征,因此,集料表面的灰尘和集料表面自身的颜色变化可能被当做纹理处理,这增加了这种方法的使用难度。此外,分解水平的确定也是个问题。
3 三维图像方法目前在三维空间形态方面的研究处于起步阶段。以下简述此方面的研究进展。
3.1 球谐变换法Garboczi[30]基于集料颗粒X射线CT扫描图像,给出了使用球谐分析(Spherical Harmonic Analysis)重构集料颗粒三维形态的方法。Zhou等[31]基于砂颗粒的X射线CT扫描数据,给出了使用球谐分析重构和表征砂颗粒三维形态的方法。使用球谐分析重构颗粒三维形态的原理简述如下。在球坐标下,颗粒表面的每一点可以用该点到颗粒形心的距离r (θ, ϕ)表示(θ和ϕ分别为颗粒表面点到形心之间直线和z轴、x轴的夹角)。同时,颗粒表面的任一点可以用球谐级数的展开式表示,如式(21)所示。Ynm (θ, ϕ)是球谐函数,如式(22)所示:
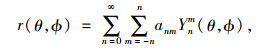
|
(21) |
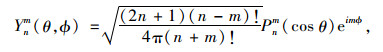
|
(22) |
式中,anm为球谐系数,需要根据计算确定;Pnm (x)为伴随勒让德函数;n和m分别为函数Pnm (x)的次和阶,根据拟合精度的不同,n的取值可以从0到∞,n的数值越大,拟合精度越高。
由式(21)可知,需要计算确定的球谐系数anm的总个数为(n+1)2。因此,在颗粒表面至少取(n+1)2个点,代入式(21),才可以确定所有球谐系数。求得球谐系数anm后,就可以根据式(21)重构颗粒的三维图像。在球谐分析重构的基础上,可以进一步使用球谐级数计算颗粒的体积和表面积等参数。
由式(21)可知,颗粒三维形态的球谐重构是随着球谐次n的增加而累进的过程。因此,可以将累加和分解为一系列具有独立频率的组分,如式(23)所示:
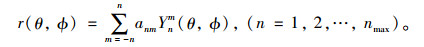
|
(23) |
随着频次n的增加,球谐系数的数值快速减小。当n超过10时,其值已经非常小。球谐系数对颗粒三维形态的影响表现在如下3个方面:第一,颗粒的总体形状由低频次的组分表达;第二,颗粒表面的棱角由中间频次的组分表达;第三,颗粒表面的细观纹理由高频次的组分表达。基于这个原理,Kutay等[32]提出使用球谐系数评价集料颗粒的三维形状指标FI3D、棱角指标AI3D和纹理指标MT3D,评价指标分别如式(24)~式(26)所示:
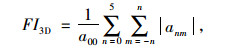
|
(24) |
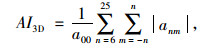
|
(25) |
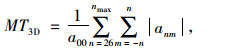
|
(26) |
式中,anm为球谐系数;a00为n为0时的球谐系数;n为次数,m为阶数。使用a00进行正规化,是为了消除评价指标的尺寸依赖性。这种方法的主要问题是划分形状、棱角和纹理指标的临界频次的确定具有主观性,很难确定一个客观的标准。
Joseph等[33]使用三维激光扫描仪获取集料的三维图像。首先将单个集料颗粒放置在设备中,然后用激光装置对颗粒的6个面进行扫描,最后在软件中生成集料颗粒的三维图像。利用该图像可以计算颗粒的表面积和体积。该设备的最高分辨率是0.1 mm。单个颗粒的扫描时间取决于颗粒大小和分辨率,平均扫描时间大约在25 min。Komba等[34]使用该仪器扫描集料颗粒,将集料三维数据导入到软件Matlab中,使用球谐变换方法重构了集料颗粒的三维形态,并利用球谐系数研究了集料的形状特性。
3.2 傅里叶变换法Wang等[35-36]研发了高分辨率傅里叶变换干涉(FTI)系统用于集料三维形态评价。FTI系统由摄像头、干涉光源和MATLAB程序组成。使用时,将集料颗粒摆放在斜镜下方的托盘上,摄像头从斜镜中采集颗粒的图像。用于后续分析的集料图像有3幅,分别是1幅可见光图像及两幅波长为675 nm和805 nm的激光图像。这3幅图像随后在MATLAB中使用傅里叶变换方法生成颗粒表面的三维坐标矩阵。最后,使用傅里叶变换方法进一步分析三维坐标矩阵,评价集料的棱角和纹理。棱角指标AF和纹理指标TF的计算公式分别如式(27)和式(28)所示:
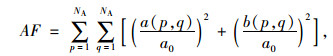
|
(27) |
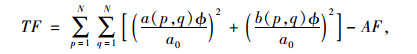
|
(28) |
式中,a0为颗粒表面三维坐标z (x, y)的平均值; a (p, q)ϕ和b (p, q)ϕ分别为傅里叶变换系数矩阵中p行、q列值的实部和虚部; N为三维坐标矩阵的大小; NA为计算棱角和纹理指标的临界值。这两个指标的物理意义和基于二维图像的傅里叶形态指标类似。与二维傅里叶变换法类似,该方法存在棱角和纹理指标临界值确定的问题。
3.3 小波变换法Kim等[37]研制了集料激光扫描系统LASS,用于获取集料的三维形态数据。对使用该设备获得的集料三维数据,Kim等[38]通过小波变换方法提出了评价集料形状、棱角和纹理的三维指标。在该方法中,首先将集料三维形态数据分解成6个层次,然后计算各个分解层次的能量指标E,最后使用不同层次的能量指标表征集料的形状指标Shape Index、棱角指标Angularity Index和纹理指标Texture Index,分别如式(29)~式(31)所示:
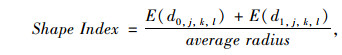
|
(29) |
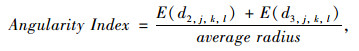
|
(30) |
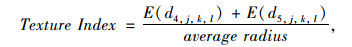
|
(31) |
式中,di, j, k, l为分解水平为i时的小波系数;j,k,l分别为像素点的三维坐标,average radius为平均半径; E (di, j, k, l)为分解水平为i时的能量指标。
小波变换方法的核心思想是,高分解水平(小尺度)对应的小波系数代表颗粒表面纹理,中等分解水平(中间尺度)对应的小波系数代表颗粒的棱角,低分解水平(大尺度)对应的小波系数代表颗粒的形状。该方法的优点是保持了3个指标在形式上的一致性。但是,表征形状、棱角和纹理的临界分解水平的确定具有主观性,缺乏明确的依据。对于不同形态的集料,临界分解水平可能不同。
3.4 腐蚀-膨胀法Lee等[39]研制了激光三角测量系统,用于获取集料颗粒上半部分的三维图像。通过对三维图像执行腐蚀-膨胀操作,提出使用图像的体积损失表征集料的棱角。在腐蚀操作中使用一个结构体(球或椭球)经过图像上的每个点进行腐蚀运算,然后对图像执行膨胀运算。最后,计算腐蚀-膨胀前后图像的体积损失,用于表征集料颗粒的棱角。
3.5 激光三维扫描技术 3.5.1 技术介绍随着三维扫描和曲面重建技术的发展,获取物体的三维图像已经不是难事。目前,市场上已经有多种激光三维扫描设备,扫描点间距可以达到0.05 mm,足以用于表征粗集料的形状、棱角和纹理。粗集料三维图像采集步骤如下:
(1) 在桌面上粘贴标志点。
(2) 将橡皮泥置于标志点中间,并将粗集料颗粒面积最小的面粘在橡皮泥上。
(3) 使用手持式激光扫描仪沿360°扫描粗集料颗粒,直至获得完整的粗集料三维图像。
(4) 重复步骤(2)~ (3),直至扫描完所有颗粒。
(5) 对扫描获得的三维图像进行处理,分离得到粗集料颗粒三维点云数据,并将其保存为stl格式。
在计算机中,粗集料三维图像通常采用相互连接的三角面片表征,三角面片由粗集料表面的点云相互连接而成。图 2显示了扫描得到的粗集料三角面片图像,图 3显示了粗集料三维点云图像。

|
| 图 2 粗集料三角面片图像 Fig. 2 Triangle mesh image of coarse aggregates |
| |

|
| 图 3 粗集料三维点云图像 Fig. 3 Point cloud image of coarse aggregates |
| |
使用激光三维扫描技术可以获取高精度粗集料三维图像,利用粗集料表面的点云坐标可以构建评价粗集料三维形状、棱角和纹理的指标,这将是今后的研究重点。
3.5.2 研究思路探讨研究思路是利用粗集料表面的点云坐标构建粗集料三维形状、棱角和纹理指标。限于篇幅,仅作简要探讨。
(1) 三维形状。形状反映了集料颗粒尺寸的比例关系,所以利用粗集料三维点云数据计算粗集料三维尺寸是首要问题。对于三维尺寸,可以编制算法用椭球拟合粗集料三维点云,然后分别计算椭球长轴、中轴、短轴与粗集料表面交点之间的长度,即是粗集料的三维尺寸。粗集料三维形状指标可以用三维尺寸计算获得,可以参考Chen等[40]的研究。
(2) 三维棱角。棱角反映了集料颗粒拐角的变化。对于棱角评价,可以编制算法删除粗集料表面凸起的点,然后采用处理前后粗集料的体积变化率表征三维棱角特性。图 4显示了这种算法的处理效果。

|
| 图 4 处理前后粗集料三维图像 Fig. 4 Coarse aggregate 3D images before and after processing |
| |
(3) 三维纹理。纹理反映了集料颗粒表面的粗糙程度。在三维图像处理中,可以采用平滑算法将粗集料表面纹理去除,然后采用处理前后粗集料表面积的变化表征粗集料的三维纹理。图 5显示了粗集料平滑前后的图像。

|
| 图 5 平滑前后粗集料三维图像 Fig. 5 Coarse aggregate 3D images before and after smoothing |
| |
4 结论
早在1980年,Barrett[41]就对集料形状、棱角和纹理作了明确定义。Barrett认为,集料形状、棱角和纹理是3个相互独立的特性。形状是第1特征,反映了集料颗粒尺寸的比例关系。棱角是第2特征,反映了集料颗粒拐角的变化。纹理是第3特征,是集料颗粒的表面形貌特性。近20 a来,二维图像被广泛用于评价粗集料的形态特征,提出了一系列评价指标。然而,粗集料在本质上是一种空间三维形体,其三维形态特征比二维图像更加复杂,尤其是棱角和纹理特征。二维集料图像仅反映了集料某个截面上轮廓的变化。基于二维图像的方法,即使其特征被准确表征,也只能给出真实三维形态的不完整描述。因此,研究基于三维图像的方法势在必行。在使用三维图像评价粗集料形态指标时,现有研究的局限性和需要进一步解决的问题如下:
(1) 现有基于球谐变换法、傅里叶变换法和小波变换法提出的粗集料形状、棱角和纹理指标具有类似的表达式,但是对这3个指标临界值的确定具有主观性,很难确定一个客观标准。而且,使用这3种方法提出的形态指标没有明确的物理意义。
(2) 随着激光三维扫描和曲面重建技术的发展,获取粗集料三维图像已经不是难事。基于粗集料三维点云数据,运用三维图像处理方法构建粗集料形状、棱角和纹理指标是今后的研究重点。
| [1] |
ASTM D4791, Standard Test Method for Flat Particles, Elongated Particles, or Flat and Elongated Particles in Coarse Aggregate[S].
|
| [2] |
JTG E42-2005, 公路工程集料试验规程[S]. JTG E42-2005, Test Methods of Aggregate for Highway Engineering.
|
| [3] |
PROWELL B D, WEINGART R. Precisions of Flat and Elongated Particle Tests ASTM D4791 and VDG-40 Video-grader[J]. Transportation Research Record, 1999, 1673: 73-80. |
| [4] |
ASTM D5821, Standard Test Method for Determining the Percentage of Fractured Particles in Coarse Aggregate[S].
|
| [5] |
ASTM C1252-03, Standard Test Methods for Uncompacted Void Content of Fine Aggregate (as Influenced by Particle Shape, Surface Texture, and Grading)[S].
|
| [6] |
ASTM D3398, Standard Test Method for Index of Aggregate Particle Shape and Texture[S].
|
| [7] |
Central Laboratory of Road and Bridge. Measurement of Particle Size Distribution of Granular Mixtures, P18-556[R]. Paris: Central Laboratory of Road and Bridge, 1994.
|
| [8] |
MAERZ N H. Technical and Computational Aspects of the Measurement of Aggregate Shape by Digital Image Analysis[J]. Journal of Computing in Civil Engineering, 2004, 18(1): 10-18. |
| [9] |
MASAD E. The Development of a Computer Controlled Image Analysis System for Measuring Aggregate Shape Properties[R]. Washington, D. C.: National Research Council, 2003.
|
| [10] |
GATES L, MASAD E, PYLE R, et al. Aggregate Imaging Measurement System 2(AIMS2): Final Report[R]. Washington, D. C.: FHWA, 2011.
|
| [11] |
RAO C, TUTUMLUER E, STEFANSKI J A. Coarse Aggregate Shape and Size Properties Using a New Image Analyzer[J]. Journal of Testing and Evaluation, 2001, 29(5): 461-471. |
| [12] |
MOAVENI M, WANG S, HART J M, et al. Evaluation of Aggregate Size and Shape by Means of Segmentation Techniques and Aggregate Image Processing Algorithms[J]. Transportation Research Record, 2013, 2335: 50-59. |
| [13] |
MOAVENI M, MAHMOUD E, ORTIZ E M, et al. Use of Advanced Aggregate Imaging Systems to Evaluate Aggregate Resistance to Breakage, Abrasion, and Polishing[J]. Transportation Research Record, 2014, 2401: 1-10. |
| [14] |
JANOO V C. Quantification of Shape, Angularity, and Surface Texture of Base Course Materials[R]. Hanover: Cold Regions Research & Engineering Laboratory, 1998.
|
| [15] |
WADELL H. Volume, Shape and Roundness of Rock Particles[J]. Journal of Geology, 1932, 40: 443-451. |
| [16] |
KRUMBEIN W C. Measurement and Geological Significance of Shape and Roundness of Sedimentary Particles[J]. Journal of Sedimentary Petrology, 1941, 11(2): 64-72. |
| [17] |
KUO C Y, FREEMAN R. Image Analysis Evaluation of Aggregates for Asphalt Concrete Mixtures[J]. Transportation Research Record, 1988, 1615: 65-71. |
| [18] |
KUO C Y, ROLLINGS R S, LYNCH L N. Morphological Study of Coarse Aggregates Using Image Analysis[J]. Journal of Materials in Civil Engineering, 1998, 10(3): 135-142. |
| [19] |
AL-ROUSAN T, MASAD E, TUTUMLUER E, et al. Evaluation of Image Analysis Techniques for Quantifying Aggregate Shape Characteristics[J]. Construction and Building Materials, 2007, 21(5): 978-990. |
| [20] |
LEES G. The Measurement of Particle Shape and Its Influence in Engineering Materials[J]. Journal of the British Granite and Whinestone Federation, 1964, 11(2): 1-22. |
| [21] |
MASAD E, OLCOTT D, WHITE T, et al. Correlation of Fine Aggregate Imaging Shape Indices with Asphalt Mixture Performance[J]. Transportation Research Record, 2001, 1757: 148-156. |
| [22] |
MASAD E, BUTTON J. Unifed Imaging Approach for Measuring Aggregate Angularity and Texture[J]. Computer-Aided Civil and Infrastructure Engineering, 2000, 15(4): 273-280. |
| [23] |
RAO C B. Development of 3-D Image Analysis Techniques to Determine Shape and Size Properties of Coarse Aggregate[D]. Urbana: University of Illinois at Urbana-Champaign, 2001.
|
| [24] |
CHANDAN C, SIVAKUMAR K, MASAD E, et al. Application of Imaging Techniques to Geometry Analysis of Aggregate Particles[J]. Journal of Computing in Civil Engineering, 2004, 18(1): 75-82. |
| [25] |
WILSON J D, KLOTZ L D, NAGARAJ C. Automated Measurement of Aggregate Indices of Shape[J]. Particulate Science and Technology, 1997, 15(1): 13-35. |
| [26] |
DESCANTES Y, FOSSSE Y, MILCENT F. Automated Measurement of Railway Ballast Angularity[J]. Journal of Materials in Civil Engineering, 2006, 18(4): 612-618. |
| [27] |
WANG L, WANG X, MOHAMMAD L, et al. Unifed Method to Quantify Aggregate Shape Angularity and Texture Using Fourier Analysis[J]. Journal of Materials in Civil Engineering, 2005, 17(5): 498-504. |
| [28] |
BANGARU R S, DAS A. Aggregate Shape Characterization in Frequency Domain[J]. Construction and Building Materials, 2012, 34: 554-560. |
| [29] |
FLETCHER T, CHANDAN C, MASAD E, et al. Measurement of Aggregate Texture and Its Influence on HMA Permanent Deformation[J]. Journal of Testing and Evaluation, 2002, 30(6): 524-531. |
| [30] |
GARBOCZI E J. Three-dimensional Mathematical Analysis of Particle Shape Using X-ray Tomography and Spherical Harmonics: Application to Aggregates Used in Concrete[J]. Cement and Concrete Research, 2002, 32: 1621-1638. |
| [31] |
ZHOU B, WANG J, ZHAO B. Micromorphology Characterization and Reconstruction of Sand Particles Using Micro X-ray Tomography and Spherical Harmonics[J]. Engineering Geology, 2015, 184: 126-137. |
| [32] |
KUTAY M E, OZTURK H I, ABBAS A R, et al. Comparison of 2D and 3D Image-based Aggregate Morphological Indices[J]. International Journal of Pavement Engineering, 2011, 12(4): 421-431. |
| [33] |
ANOCHIE-BOATENG J K, KOMBA J J, MVELASE G M. Three-dimensional Laser Scanning Technique to Quantify Aggregate and Ballast Shape Properties[J]. Construction and Building Materials, 2013, 43: 389-398. |
| [34] |
KOMBA J J, ANOCHIE-BOATENG J K, VAN DER MERWE STEYN W. Analytical and Laser Scanning Techniques to Determine Shape Properties of Aggregates[J]. Transportation Research Record, 2013, 2335: 60-71. |
| [35] |
WANG L, SUN W, LALLY E M, et al. Application of LADAR in the Analysis of Aggregate Characteristics[R]. Washington, D.C.: Transportation Research Board, 2012.
|
| [36] |
SUN W, WANG L, TUTUMLUER E. Image Analysis Technique for Aggregate Morphology Analysis with Two-dimensional Fourier Transform Method[J]. Transportation Research Record, 2012, 2267: 3-13. |
| [37] |
KIM H, HAAS C T, RAUCH A F, et al. A Prototype Laser Scanner for Characterizing Size and Shape Parameters in Aggregates[C]//Proceedings of the 9th Annual Symposium: Aggregates-concrete, Bases and Fines. Austin: International Center for Aggregates Research, 2001.
|
| [38] |
KIM H, HASS C T, RAUCH A F, et al. Wavelet-Based Three-dimensional Descriptors of Aggregate Particles[J]. Transportation Research Record, 2002, 1787: 109-116. |
| [39] |
LEE J R J, SMITH M L, SMITH L N. A New Approach to the Three-dimensional Quantification of Angularity Using Image Analysis of the Size and Form of Coarse Aggregates[J]. Engineering Geology, 2007, 91(2/3/4): 254-264. |
| [40] |
CHEN J S, SHIAH M S, CHEN H J. Quantification of Coarse Aggregate Shape and Its Effect on Engineering Properties of Hot-mix Asphalt Mixtures[J]. Journal of Testing and Evaluation, 2001, 29(6): 513-519. |
| [41] |
BARRETT P J. The Shape of Rock Particles, a Critical Review[J]. Sedimentology, 1980, 27(3): 291-303. |
 2019, Vol. 36
2019, Vol. 36
