扩展功能
文章信息
- 何民, 李沐轩, 税文兵, 钱慧敏
- HE Min, LI Mu-xuan, SHUI Wen-bing, QIAN Hui-min
- 可靠性和舒适性对响应式定制公交线路设计的影响
- Influence of Reliability and Comfort on Responsive Custom Bus Route Design
- 公路交通科技, 2019, 36(5): 145-151
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(5): 145-151
- 10.3969/j.issn.1002-0268.2019.05.020
-
文章历史
- 收稿日期: 2018-02-06
目前,随着信息技术的进步和支付能力的提高,城市居民出行行为发生了很大的改变,出行者希望服务供应商能够提供舒适、可靠及个性化的公共交通服务[1]。在国内外的很多城市中,出现了称为“响应式定制公交”的公共交通服务。因不同的出行者对公交的要求不同,所以根据部分出行者的特定需求,为乘客量身打造全新的公交运营模式,满足客户对时间、地点的特定要求。不同出行者可以通过响应式定制公交得到更加先进的服务,能够提高公共交通服务的灵活性和个性化,因为响应式定制公交具有“不定时、不定点、不定车、不定人、不定价”的特征,在国外已经拥有了比较成熟的运营经验,为我国提供了诸多可借鉴的因素。与传统的公共交通相比,在运营过程中,响应式定制公交系统的灵活性更强(如时间、路径等具有更多的选择),可以通过个性化设计来满足市场特征,最大限度地降低系统成本,吸引更多的出行者接受响应式定制公交服务[2]。如美国的印第安纳州的华沙由固定线路的常规公交转为需求响应公交后,公交载客量每日都可以提升41%,减少了24%的公交运行里程;明尼苏达州的沙科皮采用响应式定制公交后,每日载客量增加了将近3~5倍[3]。
可靠性和舒适性是影响响应式定制公交吸引乘客的关键因素。可靠性严格来说是一个概率数值,指公交系统在正常运营状态下,向客户收取合理费用,按照乘客的要求将乘客送达目的地,并保证提供安全、舒适的服务[4]。较高的可靠性可以通过灵活选择线路的响应式定制公交来实现。舒适性是指公交为出行者提供的乘车环境给出行者带来的感官认知[5]。舒适性越高,对出行者就有越强的吸引力,因此,将可靠性和舒适性因素作为响应式定制公交线路生成的首要条件才能够让响应式定制公交的吸引力得到提升,同时也能够增强其在同行业当中的竞争力。
然而,案例分析是现阶段研究响应式公交相关内容的主要方式,如Mcknight等[6]研究了芝加哥地区定制公交服务如何满足乘客的出行需求;Brake等[7]通过对意大利不同地区的情况进行分析,了解到响应型公交同时在佛罗伦萨、米兰等地区被提出。虽然对响应式定制公交来说,可靠性和舒适性的重要性已经得到了充分的认识,但是却缺少更加深入的研究,没有能够通过线路设计来研究如何提高可靠性和舒适性。如刘毅[8]建立了城市定制公交站点、路线规划模型及城市定制公交发展评价模型;李艳梅[9]研究了定制公交线网构建的优化模型,并设计了求解该模型的一种启发式算法;Ceder等[10]描述了公交网络设计问题,提出了比较完整的公共交通规划过程;Gao等[11]把公交线路网络设计问题分为上下两层。
对于公交可靠性的研究,目前主要集中在如何描述和计算公交的可靠性,很少将公交的可靠性与线路设计问题进行关联。如陈茜等[12]针对站点、线路、路网不同层面的公交可靠性,提出了一种改进的计算方法;Yin等[13]从公交系统运行时间、站点时刻表等角度评估了行程时间可靠性;Tumquist将[14]公交可靠性定义为公交运营车辆可以按照计划行车时间运行的能力,将公交车到站准点率作为公交可靠性的评价指标。对于公交舒适性的研究,目前主要是在公共交通服务质量评价的背景下进行的,很少从公交线路设计的角度研究提高舒适性。如Botzow[15]从乘客角度建立了基于公共交通的特征的综合评价模型,评价指标包括舒适性、安全性和便利性,余芯璇[16]建立了从乘客感知角度出发的快速公交系统(BRT)服务水平评估方法。
本研究结合已有的响应式定制公交的特点,研究如何从可靠性和舒适性两方面来满足乘客的出行需求,为乘客提供更好的出行体验,同时还将运营成本降到最小化,并按照这一标准进行响应式定制公交线路模型的设计。在所建立的模型中,成本最小化、出行者出行可靠性和舒适性要求的研究有所体现,并通过设计小规模仿真算例来验证,其求解过程通过LINGO软件完成。由于所建立的模型比较复杂,用精确算法难以在较短时间获得实际规模问题的解,因此设计基于遗传算法的模型求解方法,同时用一个较大规模算例验证该设计算法的有效性。
1 模型建立 1.1 问题的描述乘客通过网络或手机APP提前告知响应式公交运营企业上下车地点、上下车时间、人数、车型选择等信息。运营企业根据这些信息在最短时间内设计出不同车型车辆的线路,同时满足经济性、可靠性和舒适性的要求。影响经济性的因素包括运营商成本、不同车型车辆固定使用成本、可变成本等。
1.2 模型假设及参数设置模型通过如下假设来进行构建:(1)网络中可供不同车型车辆停放的停车场有多个;(2)停车场同时包含起始站和终点站;(3)几种不同的车型均可以经过每个需求节点,并且不同车型的载客能力有所限制;(4)根据不同车型进行个性化线路设计,并且不同车型能服务多个需求点;(5)所有车辆不限制行驶距离;(6)固定安排上下车时间,保持每个需求节点的运作规律;(7)路径选择可以依据车型和不同路段的行驶时间可靠性来选择。
首先,将一个完备图定义为G= (V, A),车场点集合定义为D,设计V= (1, 2, …, n)为节点集,需求点集用节点集V′表示,在需求点i同时经过不同车型的集合定义为C(不同车型可以到同一节点服务,C∈V′);另外,弧集或边集表示为A= { (i, j)|i, j∈V, i≠j}。
模型相关参数:(i, j) (i≠j),cijk为车型k的车辆从节点i行驶到节点j的可变成本,车型不会对这个数值造成影响,只能是零或正值;车辆类型的集合表示为K={1, 2, …, k};n为节点数量;pik为在节点i处车型k的上车需求,可记为pi;Qk为车型k在Q1 < Q2 < … < Qk条件下的最大载客能力;Fk为车型k在F1 < F2 < … < Fk条件下的固定成本;qik为节点i处车型k的下车需求,可记为qi;βk为不同车型线路可靠性要求;U1k为离开节点1(起点)时车型k的车辆上的乘客数量;T为任意车辆的实际行驶时间,t为给定的行驶时间;σij为经过路段i-j时车辆行驶时间的标准差;μij为车辆平均行驶时间;P为车辆行驶可靠度; Φ为正态分布概率。
对每条弧(i, j),决策变量定义为:

|
依据上述假设和参数设置,需求响应式定制公交线路生成模型如下:
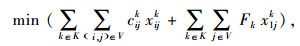
|
(1) |
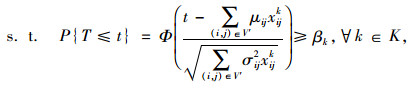
|
(2) |
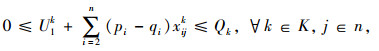
|
(3) |
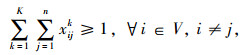
|
(4) |
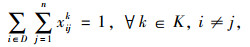
|
(5) |
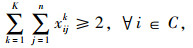
|
(6) |
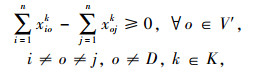
|
(7) |
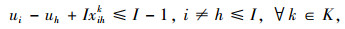
|
(8) |
式(1)是目标函数,车辆可变成本是第1部分,包括车辆维修、燃油、过路过桥、保险等成本;车辆固定成本是第2部分,主要为驾驶员及相关工作者的工资、车辆购买或租赁成本等;约束(2)用来计算车辆行驶可靠性,约束(3)表示不同出行者的出行需求由某车型来完成,乘客在每个需求节点完成上、下车之后,该车辆载客数要不小于该车辆车内乘客数;约束(4)表示要服务所有节点1次;约束(5)表示所有车辆要从初始站出发,在完成运输任务后必须回到附近的停车场;约束(6)表示至少两种以上的不同车型要确保经过部分需求节点;约束(7)表示车辆经过某个节点o完成服务后,该车辆必须从该节点o离开,以保持守恒的流量;消去回路的约束用约束(8)表示,式中ui,uh为回路顺序, I为节点数n。
2 算法设计上述建立的数学模型属于混合整数非线性规划模型中较复杂的类型,是一个典型的NP-困难问题,因此在有限时间内很难通过传统的精确求解方法来求解实际规模问题。本研究利用遗传算法的优点,设计遗传算法来求解构建的模型,以下是算法设计步骤。
2.1 编码的设计解决问题时,利用遗传算法的定义染色体编码方式,如二进制编码,十进制编码,自然数编码等[17]。本研究采用十进制编码,按需求点进行编码,如[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13],[2, 3, 4, 4, 5, 5, 6, 7, 8, 9, 10, 11, 12],遗传算法编码是第1行,实际对应的需求点是第2行。由于每辆车的起点都是从第1个点出发,因此,后面那行数据从第2个点开始。4,5经过两次并且不能是同一辆车。
2.2 初始种群的产生本研究运用随机方法产生k(k=1, 2, …, n)数目(k为种群中染色体的个数)的染色体inn作为种群,产生的每组染色体存在差异。
2.3 适应度函数的计算用约束条件判定种群的每个染色体,并求出可行解,再对可行解根据式(1)进行计算,并得出一个值fmax。由于适应度函数一般是最大化问题,但最小的出行总成本是本研究的目标函数,因此,适应度函数取为f=1/fmax,变为最小化问题。若染色体性能表现会随着适应度值f在式中的增加而增强,其对应的解就越接近最优解。
2.4 遗传操作(1) 选择
对有用的遗传信息进行保存,防止其丢失,是遗传算法中选择操作的目的,只有这样才能够使全局的收敛性和计算效率得到提高。轮盘赌选择是本研究采用的选择操作,其方法是回放式随机采样方法[17]。
(2) 交叉
交叉原则是对两个互相配对的染色体和部分基因以某种方式进行互换,以此产生新个体。所求问题的编码方式一般和交叉有关,均匀两点交叉的方法是本研究染色体交叉操作采用的方法[18]。
(3) 变异
遗传算法中的变异操作是对染色体上某些基因位的基因值做改动,其作用是维护种群多样性,它在维持种群多样性中只起辅助作用,以很小的概率进行变异,本研究采取对个体基因的某一值随机变异[18]。
(4) 终止条件
设置固定迭代次数,算法收敛,得到最优解,停止计算;否则继续优化,直到得到最优解。
3 算例分析 3.1 小规模算例为了检验所构建数学模型的正确性,设计能够用精确算法求解的小规模算例,同时使用遗传算法求解并对比两种算法的差异。假设网络中有13个需求点, 3种车型,其中1为出发车场,两种以上的不同车型能经过4,5这两个节点,10,11,12,13为终点车场,其余节点为中间需求点。表 1为各需求点之间车辆可变成本,表 2、表 3为模型中使用的相关参数。
| 可变成本 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 0 | 101 | 51 | 84 | 105 | 91 | 79 | 68 | 32 | 72 | 107 | 109 | 94 |
| 2 | 68 | 0 | 61 | 64 | 110 | 75 | 65 | 99 | 54 | 85 | 79 | 82 | 118 |
| 3 | 119 | 118 | 0 | 104 | 43 | 74 | 85 | 99 | 75 | 54 | 87 | 87 | 99 |
| 4 | 55 | 75 | 75 | 0 | 119 | 106 | 102 | 91 | 104 | 43 | 112 | 106 | 108 |
| 5 | 113 | 74 | 111 | 80 | 0 | 48 | 84 | 95 | 111 | 107 | 118 | 113 | 65 |
| 6 | 112 | 77 | 78 | 50 | 75 | 0 | 118 | 119 | 95 | 87 | 106 | 33 | 72 |
| 7 | 88 | 97 | 88 | 51 | 112 | 53 | 0 | 72 | 63 | 106 | 115 | 44 | 96 |
| 8 | 85 | 120 | 75 | 111 | 31 | 59 | 106 | 0 | 68 | 100 | 66 | 64 | 55 |
| 9 | 119 | 67 | 72 | 69 | 118 | 67 | 44 | 93 | 0 | 96 | 79 | 64 | 116 |
| 上下车需求点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 上车乘客数 | 3 | 2 | 2 | 1 | 1 | 4 | 3 | 3 | 2 |
| 下车乘客数 | 0 | 2 | 3 | 4 | 2 | 4 | 3 | 2 | 1 |
| 车型 | K1 | K2 | K3 |
| 固定成本/元 | 400 | 500 | 600 |
| 时间/min | 12 | 12 | 12 |
| 车辆载客能力/人 | 8 | 6 | 4 |
| 概率 | 0.91 | 0.935 | 0.955 |
运用遗传算法求解上述算例的参数设置如下:初始化种群数量为200,交叉概率为0.9,变异概率为0.000 1,最大迭代次数为50次。算法求解过程如图 1所示。为了对算法性能做比较,使用lingo11.0求解该算例,求解结果如表 4、表 5所示。
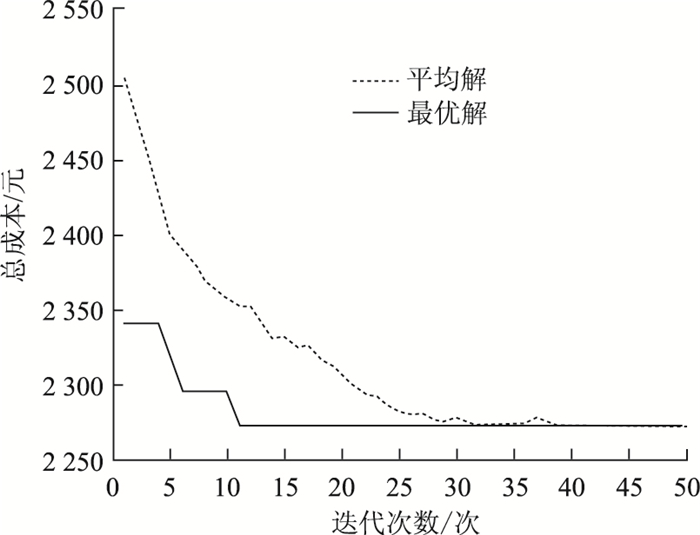
|
| 图 1 遗传算法迭代收敛曲线 Fig. 1 Genetic algorithm iterative convergence curve |
| |
| 路线 | 线路走向 | 可靠度 |
| 路线1 | 1-9-8-5-4-10 | 0.92 |
| 路线2 | 1-2-7-6-12 | 0.94 |
| 路线3 | 1-3-5-4-10 | 0.96 |
| 总成本/元 | 2 248 | |
| 路线 | 线路走向 | 可靠度 |
| 路线1 | 1-9-2-4-10 | 0.946 |
| 路线2 | 1-8-5-6-11 | 0.962 |
| 路线3 | 1-7-4-3-5-13 | 0.981 |
| 总成本/元 | 2 272 | |
从表 4可以看出,本研究构建的数学模型可以正常求解,求出的结果可以构成完整的线路,表明本研究构建模型的正确性。从图 1可以看出,遗传算法得出目标函数的最优解为2 272,即系统总成本为2 272元,lingo得出的系统总成本为2 248元,两者相差不大,说明了遗传算法的准确性。使用lingo软件运算所花费的时间是3 h 20 min 50 s,而在同样规模算例下使用遗传算法花费602.56 s的时间就能完成运算。所以,在运算效率上采用遗传算法优势更加明显。与线路1相比,路线3在时间相同的情况下需要更高的固定成本,且线路1的车型座位数更多。从可靠性来看,路线3的车型具有更高的可靠性,同时还具有更高的舒适性。反之,如果有较多的座位数,投入较低成本的车型,也必然会导致该车型不能拥有较高的可靠性和舒适性。在进行总成本计算时,遗传算法求出的总成本略高于精确算法的求解结果,并且求解结果中所有车型行驶线路的可靠性也都高于精确算法求解出的可靠性。
3.2 较大规模算例为了证明使用遗传算法在求解较大规模问题时能快速找到近似最优解的能力,设计一个接近实际问题的较大规模算例。假设网络中有50个需求点、6种车型,其中1为出发车场,两种以上的不同车型能经过4,5,6,7,8这5个节点,47,48,49,50为终点车场,其余为中间需求点。在excel表中在0~120之间随机生成一个46×50矩阵,得到各需求点之间车辆可变成本的相应数据,表 6、表 7为模型中使用的相关参数。
| 上下车需求点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 上车乘客数 | 18 | 1 | 2 | 2 | 3 | 5 | 1 | 3 | 1 | 2 | 3 | 5 | 6 | 2 | 2 | |
| 下车乘客数 | 0 | 2 | 2 | 3 | 2 | 3 | 2 | 3 | 2 | 3 | 1 | 4 | 5 | 4 | 3 | |
| 上下车需求点 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| 上车乘客数 | 3 | 2 | 1 | 4 | 5 | 2 | 2 | 1 | 3 | 2 | 2 | 1 | 5 | 4 | 3 | |
| 下车乘客数 | 2 | 4 | 3 | 2 | 4 | 5 | 2 | 2 | 3 | 2 | 3 | 3 | 5 | 3 | 3 | |
| 上下车需求点 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 |
| 上车乘客数 | 5 | 2 | 3 | 2 | 3 | 3 | 3 | 2 | 4 | 2 | 4 | 3 | 5 | 4 | 3 | 2 |
| 下车乘客数 | 3 | 3 | 6 | 2 | 3 | 6 | 5 | 3 | 6 | 4 | 2 | 5 | 5 | 2 | 5 | 3 |
| 车型 | 1 | 2 | 3 | 4 | 5 | 6 |
| 固定成本/元 | 345 | 400 | 500 | 555 | 600 | 650 |
| 时间/min | 21 | 21 | 21 | 21 | 21 | 21 |
| 车辆载客能力 | 15 | 12 | 10 | 8 | 6 | 4 |
| 概率 | 0.89 | 0.9 | 0.91 | 0.92 | 0.93 | 0.95 |
本研究运用遗传算法求解较大规模算例的参数设置如下:初始化种群数量设为100,交叉概率为0.9,变异概率为0.000 1,最大迭代次数为50次。取10次求解结果中最好的解作为该算例的最优解。遗传算法最后得出目标函数的最优解为8 762,即系统总成本为8 762元,程序运行时间为11 724.227 s。本研究算例为50个需求点,6种车型。从表 8可以看出, 6种车型中使用了5种车型,根据不同车型的使用次数,在保证可靠性、总成本最小情况下,得出的线路走向共有12条。即使是相同车型,可靠性也有差异,其经过的节点也不同,这主要是因为每个需求点的乘客对车型的要求和到达目的地的可靠性是不同的。同时遗传算法在迭代到50次时求得的最优解仍有波动,因为算法规模及可靠性对目标函数有所影响,增加了算法的复杂度,同时也证明了遗传算法在求解大规模优化问题上的优势。
| 车型 | 线路 | 可靠度 |
| 1 | 1→5→20→17→4→24→7→34→36→50 | 0.91 |
| 1 | 1→5→3→2→6→33→18→8→45→48 | 0.95 |
| 1 | 1→31→9→10→26→8→7→43→50 | 0.93 |
| 2 | 1→27→12→35→48 | 0.965 |
| 2 | 1→21→15→46→50 | 0.966 |
| 2 | 1→28→11→19→13→38→50 | 0.96 |
| 3 | 1→30→32→44→50 | 0.97 |
| 3 | 1→16→40→50 | 0.976 |
| 4 | 1→22→14→4→39→50 | 0.98 |
| 4 | 1→25→41→50 | 0.988 |
| 5 | 1→23→42→50 | 约为1 |
| 5 | 1→6→29→37→48 | 约为1 |
3.3 可靠性和舒适性对线路的影响
对响应式定制公交线路来说,可靠性和舒适性会在某种程度上影响其线路的生成。为了分析可靠性和舒适性对其线路生成的影响,将不考虑可靠性和舒适性要求与考虑两者要求的线路生成模型结果进行对比。首先,将模型中的可靠性要求(约束2中的βk)取值为零,即为不考虑可靠性的模型;当只有一种车型可供选择时,即为不考虑舒适性的模型;当两者同时满足时,即为不考虑可靠性和舒适性要求的响应式定制公交线路生成模型。其次,分别用两种模型对前述13个点的算例进行求解,求解结果如表 9所示。
| 线路 | 不考虑可靠性和舒适性 | 仅考虑舒适性 | 仅考虑可靠性 | 同时考虑可靠性和舒适性 |
| L1 | 1-8-5-6-2-7-4-10 | — | 1-3-5-6-12 | 1-9-8-5-4-10 |
| L2 | 1-9-4-3-5-13 | 1-9-7-4-2-8-5-6-12 | 1-9-8-5-4-10 | 1-2-7-6-12 |
| L3 | — | 1-4-3-5-13 | 1-7-2-4-10 | 1-3-5-4-10 |
| 总成本/元 | 1 467 | 1 780 | 1 937 | 2 248 |
可以看出,需要3条线路才能满足可靠性和舒适性的要求,用2 248元才能完成运输任务;仅考虑舒适性的情况下,只需要2条线路,用1 780元就能完成运输任务;仅考虑可靠性要求时,需要3条线路,用1 937元才能完成相同的运输任务;不考虑可靠性和舒适性要求时,只需要2条线路,用1 467元就能完成相同的运输任务。由此可见,从线路生成和运营成本的角度来说,响应式定制公交线路的生成和运营成本受可靠性和舒适性的影响很明显,而且可靠性对线路路径的影响比舒适性大,舒适性对成本的影响比可靠性大。
4 结论响应式定制公交作为一种新型的公共交通方式,填补了传统公共交通服务的空白,不同出行者可以通过这种方式来满足各自的出行需求。由于其一站式到达、舒适的乘车环境而倍受乘客的青睐,研究响应式定制公交线路设计问题,对于提高定制公交企业的运营效益和满足乘客的多样化需求有重要意义。本研究结合可靠性和舒适性要求,在最低运营成本的基础上,构建了响应式定制公交线路的数学模型。在求解过程中,运用精确算法和遗传算法对所构建的线路生成模型进行求解,并对两种算法得出的结论做了比较。通过对不同规模算例进行分析,得到以下结论:(1)本研究建立的数学模型是有效的,求解模型的遗传算法是可行的;(2)在运算效率上,遗传算法有显著优势,可用于实际规模算例的求解;(3)可靠性和舒适性要求对响应式定制公交线路的生成和运营成本有明显影响,但两者的影响程度不同。在未来的研究中,可以进一步考虑多个出发车场和多个终点车场的情况,还可以在模型中考虑加入票价决策变量,使得模型能更好地满足实际的需求。
| [1] |
NELSON J D, WRIGHT S, MASSON B, et al. Recent Developments in Flexible Transport Services[J]. Research in Transportation Economics, 2010, 29(1): 243-248. |
| [2] |
沈昱, 关函非. 响应需求公交系统分析与实施要点研究[J]. 交通与运输, 2010, 26(增2): 75-78. SHEN Yu, GUAN Han-fei. Study on Demand Responsive Transport System and Implementation Issues[J]. Traffic & Transportation, 2010, 26(S2): 75-78. |
| [3] |
PRATT R, PARK G. Traveler Response to Transportation System Changes Interim Handbook[R]. Washington, D.C.: Transit Cooperative Research Program, 2000.
|
| [4] |
柳波, 余红红. 基于可靠性的快速公交线路评价体系[J]. 交通科学与工程, 2012, 28(3): 90-94. LIU Bo, YU Hong-hong. Evaluation System of Bus Rapid Transit Lines Based on Reliability[J]. Journal of Transport Science and Engineering, 2012, 28(3): 90-94. |
| [5] |
席姣姣.常规公交服务水平指标体系与评价方法研究[D].长春: 吉林大学, 2013. XI Jiao-jiao. Index System and Evaluation Method of Regular Transit Service Level[D]. Changchun: Jilin University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10183-1013192859.htm |
| [6] |
MCKNIGHT C E, PAASWELL R E. The Potential of Private Subscription Bus to Reduce Public Transit Subsidies[R]. Washington, D.C.: TRB, 1985.
|
| [7] |
BRAKE J, NELSON J D, WRIGHT S. Demand Responsive Transport:Towards the Emergence of a New Market Segment[J]. Journal of Transport Geography, 2004, 12(4): 323-337. |
| [8] |
刘毅.城市定制公交线路规划及发展评价研究[D].西安: 西安建筑科技大学, 2015. LIU Yi. Evaluation of Planning and Development of Urban Customized Shuttle Bus[D]. Xi'an: Xi'an University of Architecture and Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10703-1015994491.htm |
| [9] |
李艳梅.定制公交系统浅网构建方法硏究[D].成都: 西南交通大学, 2016. LI Yan-mei. Research on Shallow Network Construction Method of Customized Public Transport System[D]. Chengdu: Southwest Jiaotong University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10613-1016168503.htm |
| [10] |
CEDER A, WILSON N H M. Bus Network Design[J]. Transportation Research Part B:Methodological, 1986, 20(4): 331-344. |
| [11] |
GAO Z, SUN H, SHAN L L. A Continuous Equilibrium Network Design Model and Algorithm for Transit Systems[J]. Transportation Research Part B:Methodological, 2004, 38(3): 235-250. |
| [12] |
CHEN Q, WANG X, LI W Q. Evaluation Method on Bus Arrival Headway Reliability[J]. Journal of Southeast University, 2013, 29(3): 316-321. |
| [13] |
YIN Y, LAM W, IEDA H. Reliability Assessment on Transit Network Services[C]//Proceedings of the 1st International Symposium on Transportation Network Reliability (INSTR). Kyoto: TRB, 2003.
|
| [14] |
TUMQUIST M A. Strategies for Improving Bus Transit Service Reliability[R]. Washington, D.C.: TRB, 1981.
|
| [15] |
BOTZOW H. Level-of-service Concept for Evaluating Public Transport[J]. Transportation Research Record, 1974, 519: 73-84. |
| [16] |
余芯璇.城市快速公交系统(BRT)服务水平评价研究[D].重庆: 重庆交通大学, 2017. YU Xin-xuan. Research on Service Level Evaluation of Bus Rapid Transit(BRT)[D]. Chongqing: Chongqing Jiaotong University, 2017. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y3225753 |
| [17] |
雷英杰. MATLAB遗传算法工具箱及应用[M]. 西安: 西安电子科技大学出版社, 2014. LEI Ying-jie. MATLAB Genetic Algorithm Toolbox and Its Application[M]. Xi'an: Xidian University Press, 2014. |
| [18] |
汪定伟. 智能优化方法[M]. 北京: 高等教育出版社, 2007. WANG Ding-wei. Intelligent Optimization Method[M]. Beijing: Higher Education Press, 2007. |
 2019, Vol. 36
2019, Vol. 36
