扩展功能
文章信息
- 杜玲丽, 胡骥, 赵怀明, 刘海旭, 蒯佳婷
- DU Ling-li, HU Ji, ZHAO Huai-ming, LIU Hai-xu, KUAI Jia-ting
- 考虑出行者偏好和经验的路径选择行为研究
- Study on Route Choice Behavior Considering Traveler's Preference and Experience
- 公路交通科技, 2019, 36(5): 138-144, 151
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(5): 138-144, 151
- 10.3969/j.issn.1002-0268.2019.05.019
-
文章历史
- 收稿日期: 2018-05-04
2. 中铁二院工程集团有限责任公司, 四川 成都 610031
2. China Railway Eryuan Engineering Group Co., Ltd., Chengdu Sichuan 610031, China
研究出行者的路径选择行为,有助于使现有路网资源得到充分利用,提高交通运输系统的运行效率,该问题一直是交通领域的研究热点。城市交通网络中,出行者的日常路径选择行为既受到交通信息[1-2]、交通管制[3]等因素的影响,也与出行者的性格、偏好等自身特性[4-6]有关。本研究的重点为出行者偏好对路径选择行为的影响。
出行者对可行路径的偏好不是一成不变的,它会在过去出行经验的基础上,随着出行感知成本不断更新变化。路径偏好形成过程是一个动态的学习与更新过程,在众多学习模型中,最为经典的是信念学习(Belief Learning)模型和强化学习(Reinforcement Learning)模型,但信念学习忽略了参与者过去成功策略的影响,强化学习忽略了参与者未选策略的影响。为此,Camerer等[7]结合试验数据提出了经验-加权吸引力(Experience-weighted Attraction,EWA)学习模型。该模型将信念学习和强化学习有机结合,综合考虑成功经验和策略信念的影响,可估计和解释其他模型忽略的敏感特征,被认为是最适合描述和评估有限信息条件下人们如何快速学习的工具[8]。国内对学习模型的研究主要是将强化学习模型应用于自动化[9]与人工智能[10]方面,关于EWA学习模型的应用研究较少,主要集中在行为博弈领域[11-12]。现实生活中,当出行者过去的成功出行经验及其他未被选择路径的收益等信息可用时,出行者会加以考虑并据此形成和更新路径偏好。EWA模型能够综合考虑上述信息,因此,将EWA学习模型应用于刻画出行者的路径偏好是合理的。
Logit模型作为目前应用最广的离散选择模型,存在着一些缺陷:(1)非相关选择方案相互独立,即选择方案的概率之比不受其他选择方案的影响;(2)喜好随机性限制,即Logit模型无法体现不同个体对备选方案的偏好异质性特征。Gaudry等[13]在多项Logit模型基础上提出了Dogit模型,摒弃了Logit模型的上述缺陷,可体现偏好、忠诚度等个体异质性特征[14]。Gaudry等[15]进一步证实了在不考虑解释变量变换时,Dogit模型相比Logit模型具有一定的优越性。Li等[16]通过Dogit模型考虑司机对特定工作的偏好程度,分析了司机在各种政策干预下的就业选择行为。Bordley[17]证实了Dogit模型在用户对某备选方案不完全忠诚时同样适用。
考虑到以往研究[18]较少考虑出行者偏好动态更新对路径选择行为的影响,本研究基于EWA学习模型,建立出行者路径偏好的动态更新规则,通过Dogit模型将偏好这一心理影响因素纳入出行者的路径选择决策,以研究在出行者偏好动态更新下,个体路径选择行为对网络交通流演化的影响。
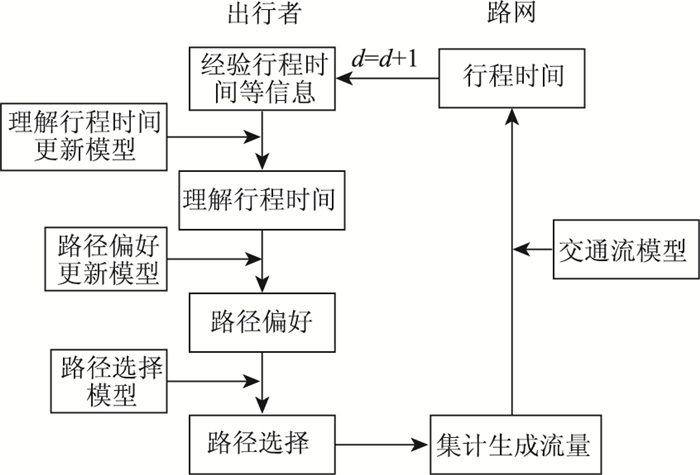
1 出行者路径选择过程分析本研究将出行者的路径选择考虑为如下过程,如图 1所示[19]。
|
| 图 1 出行者路径选择过程 Fig. 1 Traveler's route choice process |
| |
选择过程主要可分为3个步骤:(1)出行者根据获取的路网信息估计各路径的行程时间,形成对各路径的理解行程时间;(2)出行者在各路径的理解行程时间及以往出行经验的基础上形成对各路径的偏好;(3)出行者通过一定的择路机制综合考虑理解行程时间、路径偏好等因素后选择某条路径出行。
假定路网中所有出行者同时选择路径出行,个体路径选择结果集计到路网中形成交通流,各路径的实际行程时间由交通流模型(行程时间关于路段流量的函数)得出。路网更新信息,出行者重复上述路径选择过程。
2 模型构建 2.1 理解行程时间及其更新模型[6]实际出行中,出行者无法准确预知各路径的实际出行时间。因此,出行者的择路依据是其对各路径的理解行程时间而非实际出行时间。将出行者对路径的理解行程时间表示为:
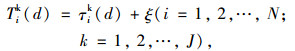
|
(1) |
式中,Tik (d)为第d天出行者i对路径k的理解行程时间;τik (d)为理解行程时间的确定项;ξ为理解行程时间的随机项;N为出行者总数;J为可选路径总数。假设随机项ξ的均值为0,则τik (d)为出行者i在第d天对路径k理解行程时间的期望值。
本研究假设出行者从路网中获取的信息为不完全历史信息,即出行者只知道自己所选路径的实际行程时间,未选路径的实际行程时间则未知。在此假设下,路径理解行程时间的更新规则为:若出行者在第d天选择了路径k,则第d+1天出行者对其理解行程时间期望值更新为前一天的期望时间与实际行程时间的加权和,否则理解行程时间期望值保持前一天的期望时间不变。具体表示为:

|
(2) |
式中,γik (d)为出行者i在第d天所选路径k的实际行程时间;ϕ为出行者对前一天所选路径实际行程时间的依赖程度(0≤ϕ < 1),是一固定参数。考虑到出行者在第1天没有历史经验,仿真试验中,将出行者在第1天对各路径的理解行程时间期望值初始化为各路径的自由流行程时间。
2.2 基于EWA学习的路径偏好更新模型出行者的路径选择行为既受自身过去成功出行经验的影响,也与其他未选路径的收益有关。EWA模型能够综合考虑这些因素,赋予每条路径一个“吸引力值”,以表示出行者对该路径的偏好。其具体模型为[7]:
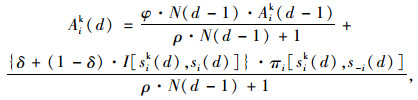
|
(3) |
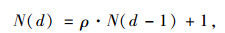
|
(4) |
式中,Aik (d)为路径吸引力值,表示第d天出行者i对路径k的偏好程度;φ为吸引力值衰退系数(φ∈[0, 1]),表示由于遗忘、交通环境的变化等原因,某路径被选择的有效性随时间下降的特性;N (d-1)为经验权重,表示在计算第d天的路径吸引力值时,赋予前一天出行经验的权重;ρ为吸引力值增长控制系数,用以控制某路径对出行者的吸引力值增长率,反映出行者的学习能力;δ为赋予未选路径的收益权重(δ∈ (0, 1)),表示受到被放弃路径收益的影响;I[sik (d), si (d)]为关联函数,表示路径k在第d天是否被出行者i选择,当出行者i在第d天选择了路径k,则指标函数I=1,否则I= 0;πi[sik (d), s-i(d)]为第d天当其他出行者选择路径集合s-i(d)时,出行者i选择路径k的收益。
当N (0)=1,ρ=0,δ=0时,吸引力值由式(5)更新,此时EWA模型相当于累计强化学习模型,赋予每轮学习的经验权重N (d)恒定为1。
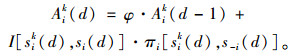
|
(5) |
本研究中,以出行者i在第d天对路径k的理解行程时间来表示收益πi [sik (d), s-i (d)],因此,Aik (d)表示出行者i在第d天对路径k的排斥值。而出行者i对路径k的排斥值Aik (d)可通过式(6)转化为偏好程度θik (d):
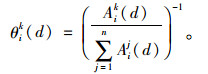
|
(6) |
一般而言,将OD对间可供出行者选择的路径称为“选择枝”,其令人满意的程度称为“效用”。假设出行者的日常择路行为遵循“效用最大化”原则。出行者关于可行路径的效用值由个人自身特性和选择枝特性共同决定。由于在实际交通环境中无法测量出出行者效用的全部影响因素,因此,在出行者i选择路径k的实际效用值Vik与出行者对其效用估计值Uik之间总是存在着一定的随机误差εik,即:
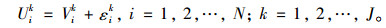
|
(7) |
假设εik服从某独立极值分布。由于出行者在路径选择过程中较多关注的是出行成本,因此将出行者的感知成本作为负效用,即令Vik (d)=-Cik (d),Cik (d)为出行者i第d天经路径k的出行感知成本,在忽略现金成本的影响下,以出行者i在第d天对路径k的理解行程时间来表示出行感知成本,即:
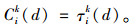
|
(8) |
时间作为路径选择影响因素的一个综合指标,可综合考虑出行距离、通行质量等因素。出行距离越长,时间也越长;通行质量低,时间耗费多。因此,将理解行程时间作为影响出行者形成路径偏好的一个主要因素具备合理性。
出行者在选择路径时,依据的是自己对各路径的效用主观估计值,而非实际效用值。如果Uik=maxUij (j∈J),则出行者必定选择路径k出行。由于Uik是不确定的,因此出行者只能以某一概率Pik选择路径k。在Dogit模型框架下,出行者i在第d天选择路径k的概率可表示为:
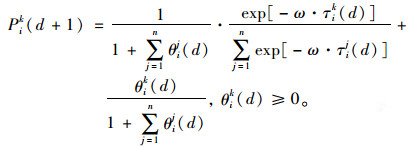
|
(9) |
该模型将选择划分为两部分,第1项表示自由选择部分,由Logit模型决定;第2项为强迫选择部分,指所选路径k中满足基本必要需求的部分。参数θik (d)表示各路径强迫选择部分与自由选择部分总量的比例,这里解释为出行者i在第d天对路径k的偏好程度[20]。参数ω为出行者路径选择行为的理智程度。可以看出,当路径偏好θik (d)为0时,Dogit模型转化为MNL模型。仿真中,出行者的路径选择采用比例选择方法,路径的选择概率越大,出行者最终选择该路径出行的概率也越大。具体方法为:首先,由式(9)计算出出行者i对每条路径的选择概率,假定计算结果为:p1, p2, p3, …, pJ;然后,计算出每条路径被选择的累积概率:qk=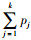
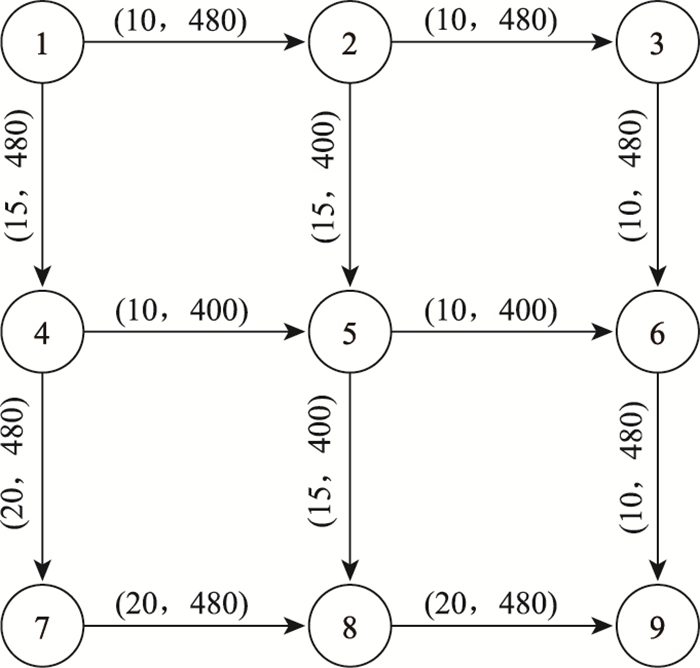
算例路网如图 2所示。网络中只有1对OD,起点为节点1,讫点为节点9。路网中共有12条路段,各路段的自由流行程时间t0和通行能力c的取值依次标在图 2中各路段上方的括号里。出行者有6条可行路径,分别为路径1:1-2-3-6-9;路径2:1-2-5-6-9;路径3:1-2-5-8-9;路径4:1-4-5-6-9;路径5:1-4-5-8-9;路径6:1-4-7-8-9,6条路径的自由流行程时间大小为:路径6>路径5>路径4>路径3>路径2>路径1。路段的行程时间t关于路段流量q的函数采用经典的BPR函数,表示为:
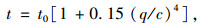
|
(10) |
式中,t0为路段的自由流行程时间;c为路段的通行能力。
|
| 图 2 路网示意图 Fig. 2 Schematic diagram of road network |
| |
3.2 结果分析
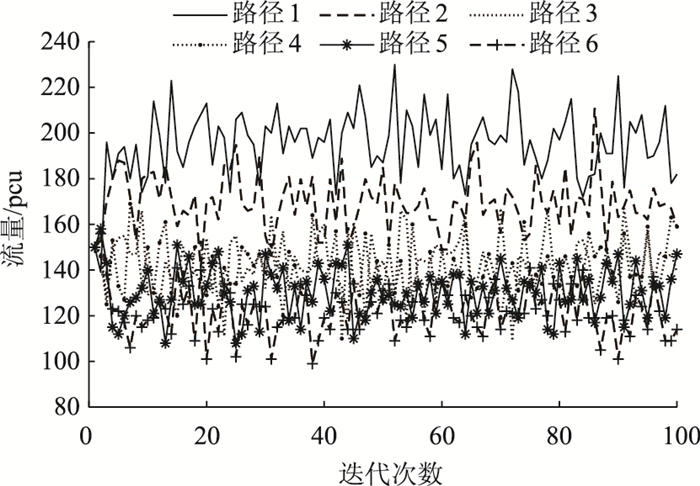
假设出行者在初始阶段对6条路径的选择偏好无明显差异,各路径的初始偏好值为0,出行者在初始阶段对各路径的选择概率均为1/6。由文献[21],令ρ=0.92,φ=0.86,δ=0.76,引入经验权重N (0)的目的是允许出行者有初始优先选择权,由于仿真试验中给定6条路径在初始阶段的被选择概率均为1/6,故在此令经验权重N (0)=1。此外,令ϕ=0.9,ω=0.176 8, 得到在路径偏好动态更新情况下及路径偏好值固定(数值为第2天的偏好值)、未考虑路径偏好情况下6条路径的流量演化曲线,分别如图 3~图 5所示。为使图片内容尽可能清晰可见,图 3~图 5的纵坐标根据路径流量的最大值而定。4种情形下,程序运行时间从长到短为:基于累计强化学习模型更新路径偏好>基于EWA学习模型更新路径偏好>偏好为固定值>不考虑路径偏好,最长与最短之间相差2.762 755 s,在可接受范围内,因此,在程序的运行时间上,4种情形不存在较大差异。对比图形可知,在考虑路径偏好时,只有路径1的均衡流量明显高于其他路径,但各路径之间均衡流量的差异较小,出行者在不同路径间的流量分配结果更为均衡;不考虑路径偏好时,Logit模型会高估路径之间的差异性,从而导致6条路径的均衡流量结果差距较大。

|
| 图 3 路径偏好动态更新情况下各路径的均衡流量 Fig. 3 Route equilibrium volumes under route preference dynamic update |
| |
|
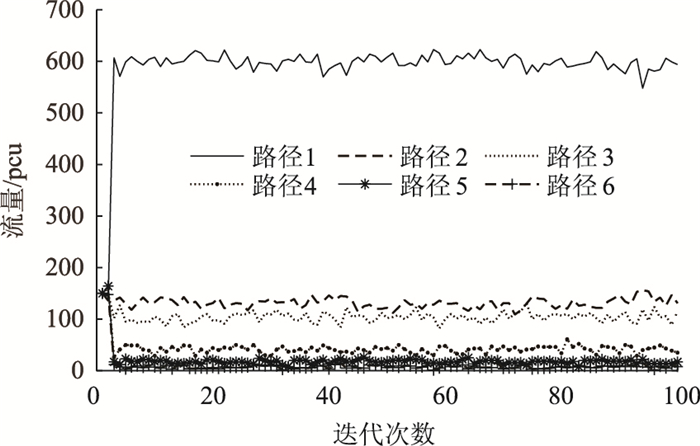
| 图 4 路径偏好为固定值时各路径的均衡流量 Fig. 4 Route equilibrium volumes when route preference is a fixed value |
| |
|
| 图 5 未考虑路径偏好时各路径的均衡流量 Fig. 5 Route equilibrium volumes without considering route preference |
| |
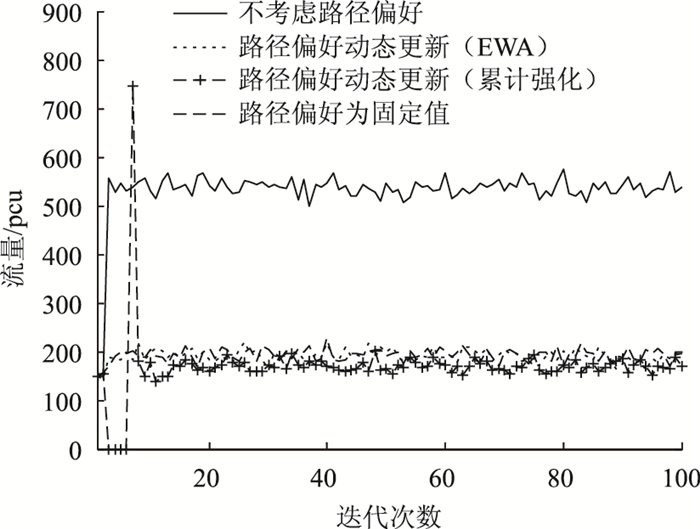
为进一步比较出行者路径偏好动态更新时与为固定值时对路径均衡流量的影响,选取路径1的均衡流量作为比较对象,得到4种不同路径偏好情况下路径1的均衡流量演化结果,如图 6所示。计算得到在不考虑路径偏好、路径偏好为固定值、基于EWA学习模型更新路径偏好和基于累计强化学习模型更新路径偏好4种情况下路径1的流量均值分别为441, 191, 197, 168 pcu。总体而言,考虑路径偏好与不考虑路径偏好下,路径1的均衡流量差异较大。考虑路径偏好时,3种偏好情况下路径1的均衡流量差异较小,偏好为固定值时路径1的均衡流量介于两种偏好更新规则下路径1的均衡流量之间。
|
| 图 6 不同路径偏好情况下路径1的均衡流量 Fig. 6 Equilibrium volume for route 1 with different route preferences |
| |
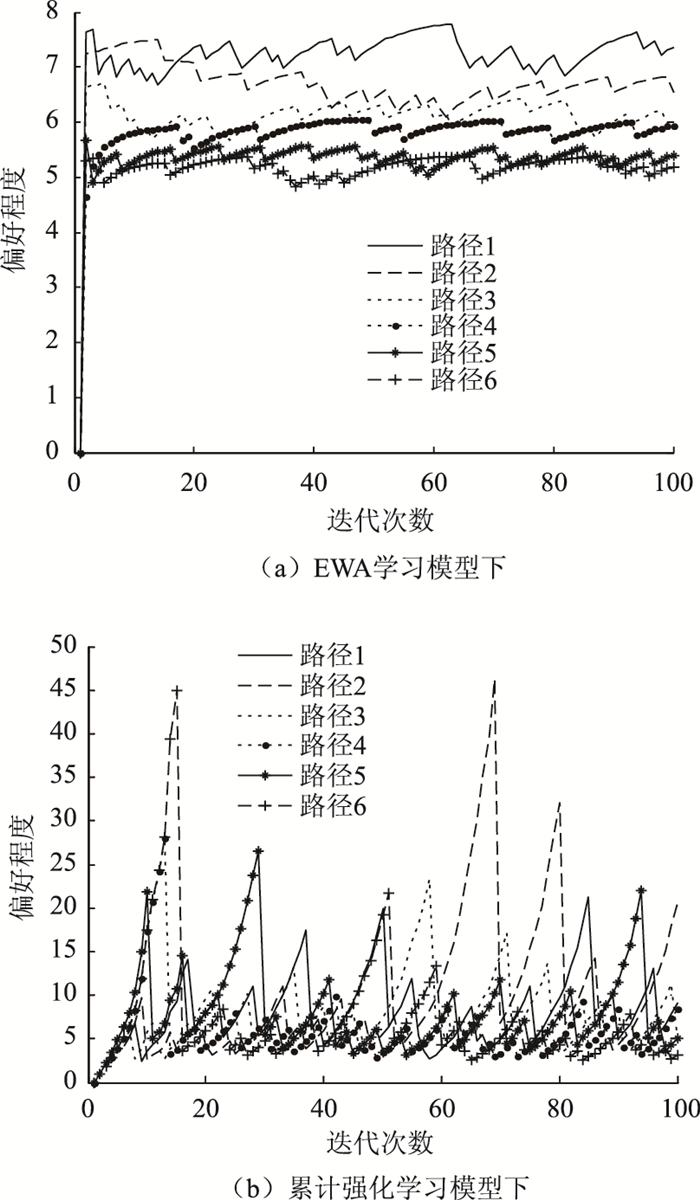
为判别EWA学习模型和累计强化学习模型动态刻画出行者路径偏好的有效性,随机选取1位出行者,图 7展示了在不同学习模型下出行者对6条路径的偏好变化情况。图 7(a)中,出行者对6条路径的偏好各自都在一个相对稳定的值附近波动,这是因为基于EWA学习的路径偏好模型是在出行个体对每次出行的理解行程时间以及上次出行经验的基础上进行更新,既对已选择路径进行更新,也对未选择路径进行更新。出行者对6条路径的偏好大小情况为:路径1>路径2>路径3>路径4>路径5>路径6。通过计算得到,在基于EWA学习的路径偏好模型下,各路径的路径偏好均值分别为8.35,6.36,5.92,5.50,5.22,5.00,说明建立的偏好动态更新规则确实能在一定程度上捕捉出行个体的真实路径偏好。而由图 7(b)无法明确判断出出行者的路径偏好大小,计算得出的各路径偏好均值分别为7.85,7.67,7.30,6.64,8.58,6.20,路径偏好均值无法准确反映出行个体的路径偏好,这是由于在累计强化学习模型中,出行者对当期选择路径的偏好是依据以往出行经验以及当期对该路径的理解行程时间进行更新,而未选择路径的偏好则基本上不更新,由于路径选择过程存在一定的随机性,造成同一路径的偏好波动性较大。因此,从对出行者路径偏好刻画有效性的角度来看,EWA模型优于累计强化学习模型。但在图 3中,累计强化学习下各路径的流量分配结果比EWA学习下的流量分配结果更为均衡,这是由于在累计强化学习模型下,不考虑未选择路径的理解行程时间,出行者对未选择路径的偏好相对增大,即处于“劣势”路径的选择偏好相对增加,路径之间的偏好差异减小,因此,路径流量分配结果更为均衡。
|
| 图 7 不同学习模型下出行者的路径偏好 Fig. 7 Traveler's route preference using different learning models |
| |
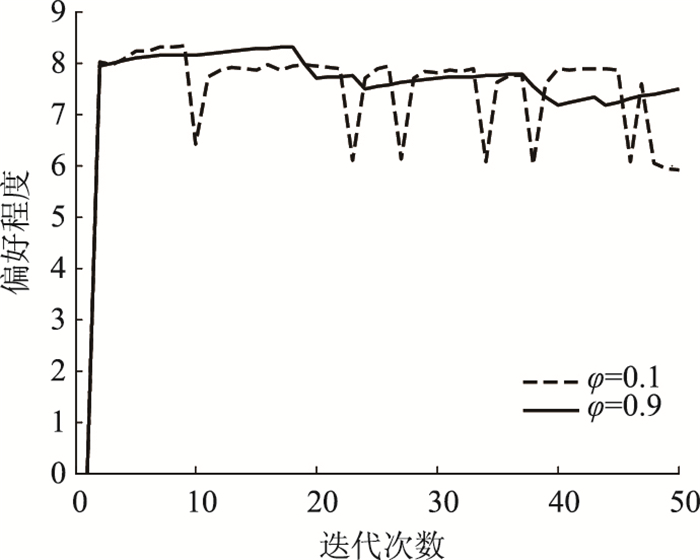
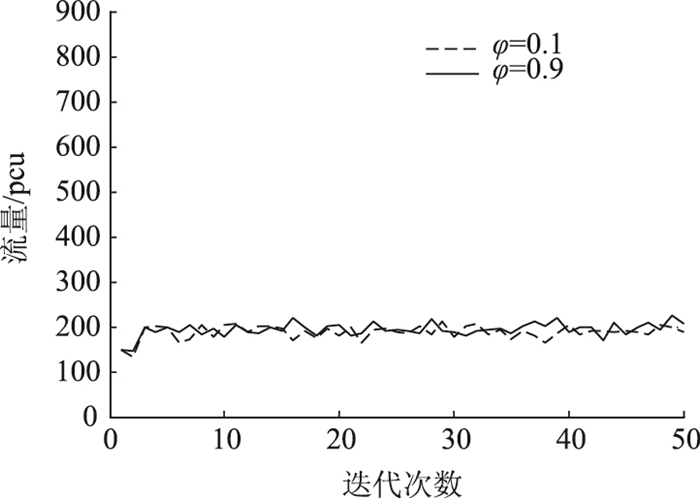
为分析衰退系数φ对偏好程度及均衡流量的影响,图 8展示了当φ分别取0.1和0.9时出行者对路径1偏好程度的变化情况,图 9为φ取不同值时,路径1流量的变化情况。可以看出,φ值越大,偏好程度的演化更为稳定,即当人们对路径选择的有效性随时间、交通环境等因素下降越慢时,越容易形成稳定的路径偏好。但改变φ值带来的路径偏好波动性对路径均衡流量波动的影响并不大。
|
| 图 8 φ取不同值下出行者对路径1偏好的演化 Fig. 8 Evolution of traveler's preference for route 1 under different φ values |
| |
|
| 图 9 φ取不同值下路径1流量的演化 Fig. 9 Evolution of volumes of route 1 under different φ values |
| |
4 结论
本研究通过分析个体路径偏好对日常路径流量演化轨迹的影响,得出以下结论:
(1) 在不考虑路径偏好、路径偏好为固定值、基于EWA学习模型更新路径偏好和基于累计强化学习模型更新路径偏好4种不同偏好情况下,利用Dogit模型考虑路径偏好的流量分配结果均比利用Logit模型不考虑路径偏好的流量分配结果更为均衡,说明Logit模型会高估路径之间的差异性,使得路径流量间的差异显著。
(2) 在考虑偏好情况下,基于EWA学习的路径偏好动态更新模型较累计强化学习模型能更好地捕捉出行个体的路径偏好,但由累计强化学习模型得到的路网流量分配结果更为均衡。
(3) 在考虑偏好时,路径偏好为固定值、基于EWA学习模型更新路径偏好和基于累计强化学习模型更新路径偏好3种情况下路径的均衡流量间差距较小,偏好为固定值时路径的均衡流量介于EWA学习模型和累计强化学习模型两种偏好动态更新规则下路径的均衡流量之间。
(4) 衰退系数φ的值关系着出行个体路径稳定偏好的形成,但由其值带来的路径偏好的波动性对路径均衡流量并无显著影响。
本研究主要考虑了出行感知成本中的行程时间对出行者偏好形成的影响,其他一种或多种因素对出行者偏好形成的影响以及其他个体异质特征对路径选择行为的影响是下一步的研究方向。
| [1] |
CHORUS C G, MOLIN E J E, ARENTZE T A, et al. Validation of a Multimodal Travel Simulator With Travel Information Provision[J]. Transportation Research Part C:Emerging Technologies, 2007, 15(3): 191-207. |
| [2] |
李志纯, 黄海军. 先进的旅行者信息系统对出行者选择行为的影响研究[J]. 公路交通科技, 2005, 22(2): 95-99. LI Zhi-chun, HUANG Hai-jun. Modeling the Impacts of Advanced Traveler Information Systems on Travelers' Travel Choice Behaviors[J]. Journal of Highway and Transportation Research and Development, 2005, 22(2): 95-99. |
| [3] |
肖浩汉, 蒋慧园, 刘义, 等. 城市道路拥挤收费下路径选择的演化博弈分析[J]. 武汉理工大学学报, 2015, 37(9): 53-59. XIAO Hao-han, JIANG Hui-yuan, LIU Yi, et al. Evolutionary Game Analysis of Route Choices under Urban Road Congestion Charging[J]. Journal of Wuhan University of Technology, 2015, 37(9): 53-59. |
| [4] |
VERPLANKEN B, AARTS H. Habit, Attitude, and Planned Behavior:Is Habit an Empty Construct or an Interesting Case of Goal-directed Automaticity?[J]. European Review of Social Psychology, 1999, 10(1): 101-134. |
| [5] |
XIE C, LIU Z. On the Stochastic Network Equilibrium with Heterogeneous Choice Inertia[J]. Transportation Research Part B:Methodological, 2014, 66: 90-109. |
| [6] |
刘诗序, 关宏志. 出行者有限理性下的逐日路径选择行为和网络交通流演化[J]. 土木工程学报, 2013, 46(12): 136-144. LIU Shi-xu, GUAN Hong-zhi. Travelers' Day-to-day Route-choice Behavior and Evolution of Network Traffic Flow Based on Bounded Rationality[J]. China Civil Engineering Journal, 2013, 46(12): 136-144. |
| [7] |
CAMERER C, HO T H. Experience-weighted Attraction Learning in Normal Form Games[J]. Econometrica, 1999, 67(4): 827-874. |
| [8] |
CHEN Y, KHOROSHILOV Y. Learning under Limited Information[J]. Games and Economic Behavior, 2003, 44(1): 1-25. |
| [9] |
夏新海.面向城市自适应交通信号控制的强化学习方法研究[D].广州: 华南理工大学, 2013. XIA Xin-hai. Study of Reinforcement Learning Towards Urban Self-adaptive Traffic Signal Control Environment[D]. Guangzhou: South China University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10561-1014153505.htm |
| [10] |
段勇, 徐心和. 基于多智能体强化学习的多机器人协作策略研究[J]. 系统工程理论与实践, 2014, 34(5): 1305-1310. DUAN Yong, XU Xin-he. Research on Multi-robot Cooperation Strategy Based on Multi-agent Reinforcement Learning[J]. Systems Engineering-Theory & Practice, 2014, 34(5): 1305-1310. |
| [11] |
徐超, 周宗放. 基于EWA学习机制的联保贷款组织还款策略选择行为[J]. 系统工程, 2015, 33(6): 111-116. XU Chao, ZHOU Zong-fang. Repayment Strategy Behavior of Guaranteed Loan Organizations Based on EWA Learning Model[J]. Systems Engineering, 2015, 33(6): 111-116. |
| [12] |
宋妍. 基于EWA学习的共享资源捐赠习俗演化仿真研究[J]. 系统科学学报, 2013, 21(4): 78-81. SONG Yan. Simulation Research for the Contribution Convention Evolutionary of Shared Resource Based on EWA Learning[J]. Journal of Systems Science, 2013, 21(4): 78-81. |
| [13] |
GAUNDRY M J I, DAGENAIS M G. The Dogit Model[J]. Transportation Research Part B:Methodological, 1979, 13(2): 105-111. |
| [14] |
BEN-AKIVA M. Choice Models with Simple Choice Set Generating Processes[R]. Cambridge: MIT, 1977.
|
| [15] |
GAUDRY M J I, WILLS M J. Testing the Dogit Model with Aggregate Time-series and Cross-sectional Travel Data[J]. Transportation Research Part B:Methodological, 1979, 13(2): 155-166. |
| [16] |
LI G, ZHANG J, NUGROHO S B, et al. Analysis of Paratransit Drivers' Stated Job Choice Behavior under Various Policy Interventions Incorporating the Influence of Captivity:A Case Study in Jabodetabek Metropolitan Area, Indonesia[J]. Journal of the Eastern Asia Society for Transportation Studies, 2011, 9: 1144-1159. |
| [17] |
BORDLEY R F. The Dogit Model Is Applicable Even without Perfectly Captive Buyers[J]. Transportation Research Part B:Methodological, 1990, 24(4): 315-323. |
| [18] |
刘新民, 鲁晓燕, 孙秋霞. 基于不同偏好的出行者路径选择行为研究[J]. 重庆交通大学学报:自然科学版, 2017, 36(10): 102-106. LIU Xin-min, LU Xiao-yan, SUN Qiu-xia. Traveler's Behavior of Path Selection Based on Different Preferences[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2017, 36(10): 102-106. |
| [19] |
刘诗序, 关宏志, 严海. 预测信息下的驾驶员逐日路径选择行为与系统演化[J]. 北京工业大学学报, 2012, 38(2): 269-274. LIU Shi-xu, GUAN Hong-zhi, YAN Hai. Driver's Day-to-day Route Choice Behavior and System Evolution under Forecast Information[J]. Journal of Beijing University of Technology, 2012, 38(2): 269-274. |
| [20] |
田丽君, 江晓岚, 刘天亮, 等. 基于Dogit模型考虑路径偏好的日常出行行为研究[J]. 交通运输系统工程与信息, 2016, 16(6): 228-235. TIAN Li-jun, JIANG Xiao-lan, LIU Tian-liang, et al. Day-to-day Route Choice Behavior Considering Route Preference in a Dogit Model[J]. Journal of Transportation System Engineering and Information Technology, 2016, 16(6): 228-235. |
| [21] |
曾鹦.考虑乘客选择行为的城市公交客流分配及系统演化[D].成都: 西南交通大学, 2014. ZENG Ying. Urban Public Transit Assignment and System Evolution Considering Passengers' Choice Behavior[D]. Chengdu: Southwest Jiaotong University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10613-1015348675.htm |
 2019, Vol. 36
2019, Vol. 36
