扩展功能
文章信息
- 石丽娜, 张玺, 石超峰
- SHI Li-na, ZHANG Xi, SHI Chao-feng
- 城市中心路内停车次优容量研究
- Study on Sub-optimal Capacity of On-street Parking in Urban Center
- 公路交通科技, 2019, 36(5): 113-120
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(5): 113-120
- 10.3969/j.issn.1002-0268.2019.05.016
-
文章历史
- 收稿日期: 2017-12-13
2. 重庆交通大学 交通运输学院, 重庆 400074
2. School of Traffic and Transportation, Chongqing Jiatong University, Chongqing 400074, China
合理的路内停车容量是衡量城市中心路内停车泊位最佳服务能力的一个重要指标。近年来,城市中心所面临的停车问题越来越严重。例如机动车的停车需求正逐渐逼近停车设施供应能力的上限;城市中心路内停车规划不合理导致车辆任意停放的现象越来越严重;低速的巡航车辆加重了城市交通拥堵等。针对这些问题,相关学者分别从停车价格、停车影响以及停车管理等方面做出了研究。例如,Shoup[1-2]认为路边停车收费价格的设置应该使平均泊位占用率达到85%的水平。Das D[3]等指出可以通过有效的停车系统来控制路内停车所造成的拥挤问题。Dey [4-5]将研究的重点集中于提高路内停车利用率等方面。田琼[6]等研究了延误时间成本作用下,出行者面对路边停车空位随机分布的寻位策略选择。丁浣等[7]研究了停车价格对出行者巡航停车行为的影响情况。王姝春[8]等针对路内停车设施提出一种多层次、多目标优化模型。韦兰香[9]等通过数值模拟证实了待停车辆的比例系数越大,交通堵塞现象就越明显。戴帅[10]等指出要加大对路内停车末端环节的管理。
针对路内停车容量的研究,Arnott[11-13]假设进入市区的车辆均进行停车,对出行成本分析时仅考虑了旅行时间成本、巡航停车时间成本以及停车费三大成本要素,并以特定停车时长为例,对路内停车容量进行求解。由于企图进行路内停车的车辆处于相对低速的状态,在此过程中所造成的能源消耗问题较为严重,该部分燃油消耗成本在整个出行成本中占有一定的比例,属于不可忽视的部分。因此,本研究在Arnott对路内停车问题分析的基础上,考虑了燃油消耗成本,进一步优化了路内停车容量次优求解算法,数值算例中验证了算法的有效性及可行性。
1 路内停车的一般原理(1) 次优容量
在西方经济学中,“次优理论”是1956年由经济学家R.G.Lipsey和K.Lancaster创立的。“次优理论”是指在一般均衡体系中,如果存在某些情况,使得帕累托最优的某个条件遭到破坏,那么剩余的所有条件所能达到的最优结果即为次优。西方经济学者认为受公共物品(如公路)、外部效应(如污染)以及垄断等因素的影响,市场失灵,完全竞争下最优的资源配置很难达到,但是可以让政府参与进来,通过运用合适的经济政策使其接近最优状态。停车价格是影响路内停车的一个重要因素。例如,路内停车价格较低,美国洛杉矶Westwood每年因车辆巡航所增加的行驶里程将近161万km;而通过对路内停车合理定价,能够使美国旧金山Redwood每年获得100万美元的停车收益[1]。因此,区别于市场有效定价下可产生路内停车最优容量的情况,这里假设路内停车收费是给定的,探讨此时产生的次优容量问题。
(2) 供需均衡
路内停车容量求解问题可以利用经济学中的供需平衡理论进行探讨。交通流率是影响出行成本的重要因素。由于总出行成本除了包含旅行时间成本、巡航时间成本和停车费外,还需要考虑燃油消耗成本。因此,总出行成本F可以进一步表示为:
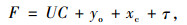
|
(1) |
式中,UC为旅行时间成本,下面称之为用户成本;yo为巡航时间成本;xc为燃油消耗成本;τ为停车费用,这里UC和xdc均为旅行时间t的函数。结合交通流理论的知识可推导出旅行时间t是密度K的一个函数,又由于密度K是交通流率r的函数,因此,最终出行成本与交通流率成非线性关系,这里便以出行成本F表示供给曲线。
由于整个交通系统中,一定时间内,交通流率受出行成本的影响,呈现出一定的需求弹性。因此,这里将需求函数表示为:

|
(2) |
式中,D0为需求强度;a为需求弹性。
在经济学中,供给曲线与需求曲线的交点即是均衡点,此时所对应的停车资源能够得到高效利用,社会剩余达到最大[14]。满足路内停车容量次优的均衡点即是所要求的最佳点,如图 1所示,图中B为出行成本,D为需求曲线,S为供给曲线,e1和e2为均衡点。
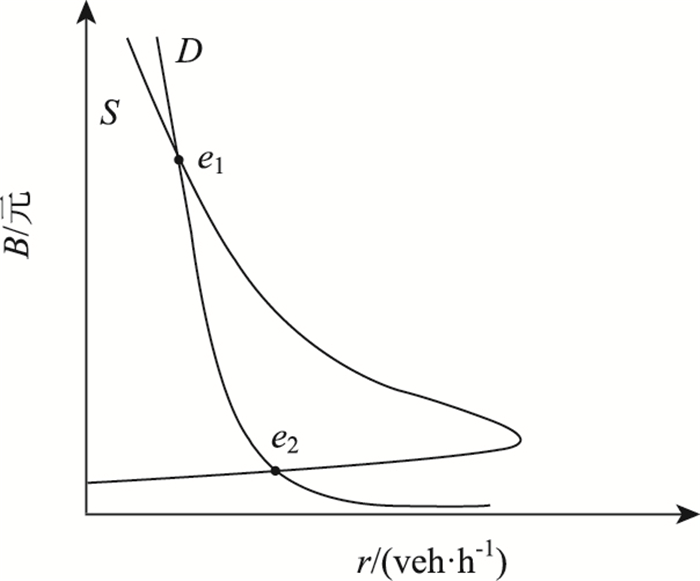
|
| 图 1 供需均衡 Fig. 1 Equilibrium of supply and demand |
| |
2 短期次优流率问题 2.1 模型假设及问题描述
假设1:停车者是同质的,交通工具均采用小汽车。
假设2:城市道路是各向同性的且为单向车道。
假设3:路内停车设置在道路的一侧。
经济学中,短期是指生产要素仅作为一个固定量,其投入数量不能调整。因而,在短期情况下,城市中心路内停车容量保持不变,此时,以次优流率作为研究基础对城市中心路内停车率进行分析。
与市场定价时追求经济效益最大化不同,政府在指导路内停车定价时更多的是追求社会效益最大化,路内停车泊位的价格与市场定价下的真实价格存在着一定的差异。路内停车次优流率问题因而存在了两种扭曲:一是不收取拥堵费,即路内停车费中不包含拥堵外部性成本;二是路内停车费不是最优的,而是满足了准公共物品低价的性质。此时,短期次优流率问题即是在路内停车容量与停车费用保持一定时,使得满足容量约束条件的社会剩余实现最大化。根据微观经济学中的分析,均衡点处产生最大的社会剩余,因此次优点即在均衡处。
为了方便描述,下文将用到的符号含义如表 1所示:
| 符号 | 含义 | 单位 |
| ρ | 时间价值 | 元/h |
| m | 旅行距离 | km |
| T | 正常行驶车辆密度 | veh/km |
| C | 巡航车辆行驶密度 | veh/km |
| P | 路内停车容量 | veh |
| Pmax | 路内停车容量所能达到的最大值 | veh |
| l | 停车时长 | h |
| f | 停车费 | 元/h |
| t | 出行者行驶1 km所用时间 | h |
| Ω | 无路内停车时堵塞密度 | veh/km |
| α | 需求强度 | |
| u | 小汽车每小时燃油消耗成本 | 元/h |
2.2 均衡
前面提到出行者行驶1 km所用时间t与交通密度有一定的关系,进一步将其表示为:
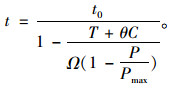
|
(3) |
(1) 路内停车为非饱和状态下的均衡
当仍有路内停车位可被利用时,路内停车处于非饱和状态,此时不考虑巡航停车行为,即C=0。
那么,用户成本UC就表示为:
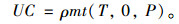
|
(4) |
燃油消耗成本xc为:

|
(5) |
路内停车费τ为:
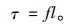
|
(6) |
而用户出行的总成本即是:
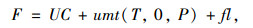
|
(7) |
式中,正常行驶车辆的密度T满足稳态条件:
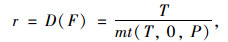
|
(8) |
即当达到稳定状态时,单位时间内由需求产生的初始出行数与正常行驶过程中产生的最终出行数相等。容量一定时,路内停车非饱和状态下用户成本曲线可进一步表示为UC(r;P),且在该种流率水平下,路内停车容量约束还未起到限制作用。而将非饱和状态下用户成本曲线向上平移fl个单位即得到供给曲线,供给曲线与需求曲线的交点就是路内停车非饱和状态下的均衡。
(2) 路内停车为饱和状态下的均衡
受路内停车容量约束条件的作用,路内停车位被充分利用后达到饱和状态,此时考虑出行者巡航停车行为。在分析均衡时,需要同时考虑两个密度变量,即正常行驶车辆的密度T以及巡航停车的车辆密度C,而这两个未知变量可由两个均衡条件推导出来。
第1个是考虑巡航停车后的稳态条件,关系式为:
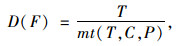
|
(9) |
式中,出行总成本F包含正常行驶过程中所产生的旅行时间成本、巡航停车时间成本以及路内停车费,即:
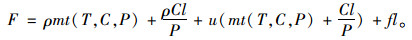
|
(10) |
第2个是巡航停车均衡条件。巡航停车均衡条件的意义在于单位时间内,车辆脱离正常行驶的状态进入巡航停车状态,并最终可以找到能够利用的停车位。其中,从正常行驶状态中退出的车辆数与进入巡航停车状态的车辆数相等,而从巡航停车状态退出的车辆数最终与单位时间内可供利用的路内停车位数相等,即:
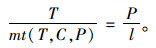
|
(11) |
其中,式(9)、(11)是关于T和C的两个非线性等式,通过等式(9)~(11)联立可对T和C进行求解。
2.3 图示分析短期情况下次优流率就可以用图 2来进行描述。其中供给曲线是由用户成本曲线向上平移fl个单位得到,由于受容量约束的影响,这里将分析的重点集中在容量约束左侧的供给曲线上,从图中可以看出,供给曲线包括3部分,一部分为供给曲线向上倾斜至容量约束线处,记为S1;一部分为从容量约束线开始向后弯曲的部分记为S2;另外一部分是容量约束线被这两段曲线所截取的部分,记为S3。D1,D2,D3为低、中、强3种需求强度下所对应的具有代表性的3条需求曲线。其中,需求曲线D1与供给曲线S分别交S1于均衡点E1,交S3于均衡点E2,另外还有一种均衡没有在图中描述出来,即零流均衡;需求曲线D2与供给曲线S分别交S2于均衡点E3,交S3于均衡点E4,另有零流均衡;而对于较高需求强度的需求曲线D3而言,仅有零流均衡。从微观经济学的理论出发,可以从图中得出:每一种需求曲线下,对应最低出行成本的均衡点处社会剩余最大。因此,短期情况下,次优点在E1,E3处。
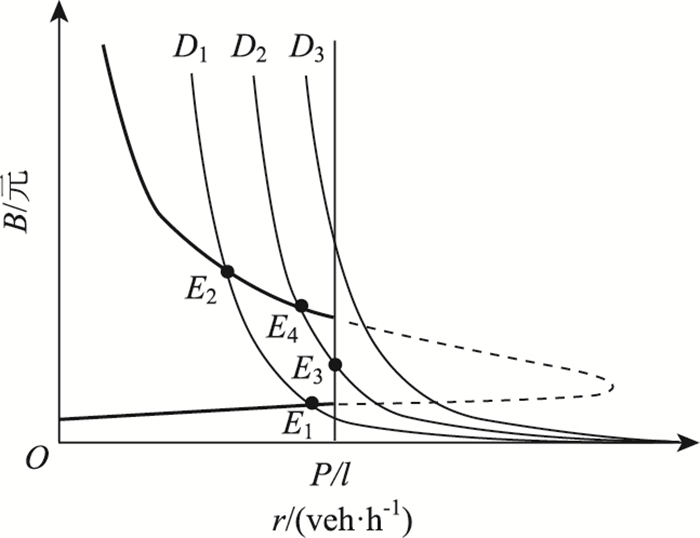
|
| 图 2 短期情况下的次优流率 Fig. 2 Sub-optimal flow rate in short term |
| |
以E3点为例。已知该点为需求曲线与容量约束线的交点,所对应的为路内停车饱和状态下的均衡。
那么,由等式(9)可得:
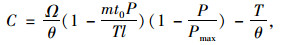
|
(12) |
式(9)~(11)联立得:
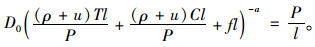
|
(13) |
将式(12)代入等式(13)可以得到关于T的一元二次方程,通过求根公式,取T的最小解,此时对应的出行成本最低。
3 长期次优容量问题 3.1 图解分析陈群[15-16]等从静态的角度出发,指出设置合理的路内停车泊位数量,以最大限度满足停车需求,并有效避免交通堵塞。本研究从动态的角度考虑,通过寻求合理的路内停车容量,以使停车率达到最优,进而整个交通系统处于最优状态。经济学中,长期是指生产要素的投入能够灵活地调整,作为一个决策变量。对路内停车容量的研究是对短期次优流率问题的一个延伸分析。由于短期情况下,在次优流率处满足了社会剩余最大化。那么,从长期的角度来看,一定需求下,路内停车次优容量处也应满足社会剩余最大。
经济学中,社会剩余等于消费者剩余加上路内停车费所带来的社会收入。结合图 2可以看出短期次优点在需求曲线与供给曲线的最低交点处。此时,在同一价格水平下,路内停车容量变化时,供给曲线移动(比较静态分析),存在以下几种情况:
(1) 如果在短期次优点处,路内停车是饱和的,且路网中存在巡航停车,那么,社会剩余随路内停车容量的增加而增加。在这种情况下,供给曲线中垂直部分将会向右移动,流率增加,消费者剩余和停车费收入也随之增加。
(2) 如果在短期次优点处,路内停车是不饱和的,社会剩余随路内停车容量的减少而增加。在该种情况下,短期次优点在供给曲线中又包含了两种可能:第1种是短期次优点位于供给曲线中向上倾斜的部分,这时,减少路内停车容量将会使该部分曲线向下移动,以使流量增加,消费者剩余与停车收入增加。第2种是短期次优点位于供给曲线中向后弯曲的部分,此时只有S1与S3交点处符合条件,在这种情况下,减少路内停车容量会使得该部分曲线向右移动,此时均衡点是随着需求曲线向下移动,与此同时,社会剩余逐渐增加。
综上所述,路内停车容量可变时,供给曲线发生了移动,从而致使均衡点也产生了移动,其中随着流率的增加,在路内停车容量约束刚起作用处,社会剩余最大。因此,在长期情况下,次优状态的一个重要特性即是均衡处路内停车容量约束刚起作用。
3.2 次优容量的求解方法该问题的解决方法实则是在短期次优流率分析的基础上,以确定满足社会剩余最大化的均衡点的位置来确定长期次优流率,进而确定长期情况下次优路内停车容量。
由于容量可变时,社会剩余产生于容量约束刚起作用时,因此用户成本曲线可进一步表示为:
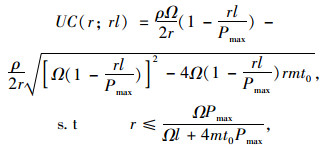
|
(14) |
式中,
将用户成本曲线向上移动fl个单位即可得到长期供给曲线LRS (r):
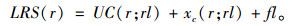
|
(15) |
由于逆需求函数为:
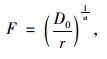
|
(16) |
则通过LRS (r)=F,所求得的需求曲线与供给曲线的最低交点E* *即是长期情况下的次优点,该点所对应的流率即是长期次优流率r* *(如图 3所示)因此,长期次优路内停车容量为P* *=r* *l。
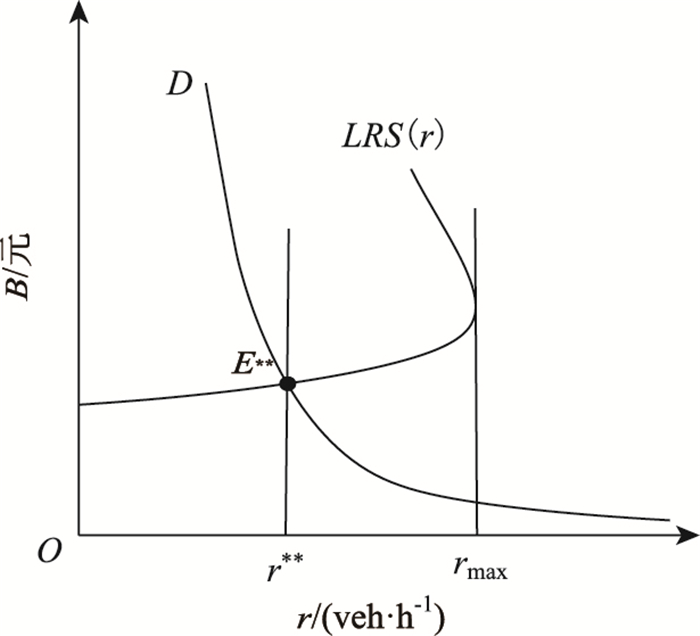
|
| 图 3 长期次优流率 Fig. 3 Sub-optimal flow rate in long term |
| |
3.3 路内停车次优容量算法改进
叶晓飞等[17]采用交通冲突分析技术,路内停车使得非机动车道的通行能力降低了14.04%。除此之外,路内停车泊位的设置减少了用于车辆通行的道路空间,使得道路的有效宽度得以减少,也进一步影响了机动车道的通行能力。而我国城市中心交通现状表明,由于用户出行目的的多样性,进入市区的车辆存在一部分为过境车辆,其目的地在城市中心以外,它们仅是路过市区。所以,车辆混合行驶时,需要考虑单位时间内停车量上限,进一步增加通行能力限制的约束条件,使得城市中心总的交通量小于道路的通行能力。因此,这里在路内停车次优容量的整体分析中,放松了Arnott关于进入城市中心车辆均停车的假设,设定进入城市中心的车辆中选择路内停车的车辆所占比例为k(0 < k < 1)。若车道宽度为W,侧向净宽即路内停车相邻车道右(左)边缘至拟停放车辆左(右)边缘的横向距离为N,不存在路内停车时道路通行能力为M(i),有路内停车时道路通行能力为M(j),停车后其余车道对通行能力的修正系数为β,侧向净宽对通行能力的修正系数为γ,则有:
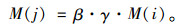
|
(17) |
那么,路内停车次优容量求解时还应满足以下约束条件:
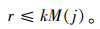
|
(18) |
综上,路内停车次优容量求解过程中应满足:
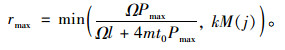
|
(19) |
本节用算例验证以上模型,参照城市道路路内停车泊位设置规范(GA/T 850—2009),对模型中的相关参数进行赋值,以计算出次优路内停车容量。因此这里假设ρ=20,u=10,f=5,Ω=1 500,Pmax =6 000,m=2,t0=0.08,θ=1.5,k=0.4,M (i )=1 800 veh/h,W=3.5 m,N=0.75 m,该种车道宽度和侧向净宽下所对应的β=1.87,γ=0.84,此时得出kM (j)=1 130。
4.1 短期次优流率问题的求解当D2所对应的需求强度为D0=1 500,P=1 620,l=2时,以E3为例,可知r=810,通过式(12)与(13)联立可得:
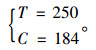
|
由此可进一步得出正常行驶过程中的旅行时间成本6.17元,巡航停车的时间成本为4.54元,路内停车费为10元,燃油消耗成本为3.08元,出行的总成本为23.79元。
4.2 长期次优容量问题的求解(1) 固定需求下,停车时长一定时,求解路内停车次优容量。
当停车时长l=2时,由式(10)可得:
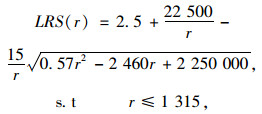
|
(20) |
此时,rm=1 315,则rmax=min (1 315, 1 130)=1 130。
由需求函数r=D (F )=D0F-a得:

|
此时令F=LRS (r),得出r**=866 < 1 130。进一步,可得出路内停车次优容量P**=r**l=1 732。
(2) 停车需求或与停车时长其中之一发生变化时,对比分析不考虑油耗成本与考虑油耗成本时的路内停车次优容量。
由于一种需求强度对应一种停车需求,因此,根据需求强度的大小来衡量停车需求。分别以需求强度D0=1 500,D0=1 800,D0=2 000为分析对象,将停车时长在(0,2.5 h)区间内,以0.5 h为间隔进行取值,然后按照(1)中的步骤进行求解。表 2、表 3分别给出算法改进前未考虑燃油消耗成本时与算法改进后考虑燃油消耗成本时运用Matlab求解出的路内停车次优容量。
| 停车时长l/h | 需求强度D0=1 500 | 需求强度D0=1 800 | 需求强度D0=2 000 | ||||||
| 次优流率r**/(veh·h-1) | 出行成本F(r**)/元 | 次优容量P**/veh | 次优流率r**/(veh·h-1) | 出行成本F(r**)/元 | 次优容量P**/veh | 次优流率r**/(veh·h-1) | 出行成本F(r**)/元 | 次优容量P**/veh | |
| 0.5 | 1 040 | 6.22 | 520 | 1 241 | 6.4 | 620 | 1 372 | 6.55 | 686 |
| 1 | 972 | 8.44 | 972 | 1 161 | 8.94 | 1 161 | 1 285 | 9.13 | 1 285 |
| 1.5 | 924 | 11.27 | 1 386 | 1 104 | 11.52 | 1 656 | 1 220 | 11.76 | 1 830 |
| 2 | 887 | 13.8 | 1774 | 1 060 | 14.13 | 2 120 | 1 172 | 14.49 | 2 342 |
| 2.5 | 856 | 16.36 | 2 140 | 1 024 | 16.8 | 2 560 | 1 128 | 19.56 | 2 820 |
| 停车时长l/h | 需求强度D0=1 500 | 需求强度D0=1 800 | 需求强度D0=2 000 | ||||||
| 次优流率r**/(veh·h-1) | 出行成本F(r**)/元 | 次优容量P**/veh | 次优流率r**/(veh·h-1) | 出行成本F(r**)/元 | 次优容量P**/veh | 次优流率r**/(veh·h-1) | 出行成本F(r**)/元 | 次优容量P**/veh | |
| 0.5 | 988 | 8.03 | 494 | 1 130 | 10.26 | 565 | 1 130 | 17.36 | 565 |
| 1 | 936 | 10.56 | 936 | 1 117 | 10.83 | 1 117 | 1 130 | 17.36 | 1 130 |
| 1.5 | 896 | 13.1 | 1 344 | 1 070 | 13.45 | 1 605 | 1 130 | 17.36 | 1 695 |
| 2 | 866 | 15.56 | 1 732 | 1 035 | 15.87 | 2 070 | 1 130 | 17.36 | 2 260 |
| 2.5 | 838 | 18.2 | 2 095 | 1 000 | 18.82 | 2 500 | 1 102 | 19.56 | 2 755 |
(1) 考虑油耗成本与不考虑油耗成本时均存在需求一定,停车时长越长,所允许的路内停车次优容量越大。
(2) Arnott算法改进前未考虑油耗成本时,停车时长一定,需求越大所要求的次优路内停车容量越高,但单位时间内的停车量却减少了,也就是说停车时长越长严重影响了单位时间内的路内停车效率。其中当r* *=rmax时,此时的次优路内停车容量达到最大,且能满足的停车需求最高。当需求超过该限制时,无法在该种情况下设置合理的路内停车容量以满足停车需求。
(3) 算法改进后考虑燃油消耗成本时,所求得的结果小于不考虑油耗成本时的次优容量。
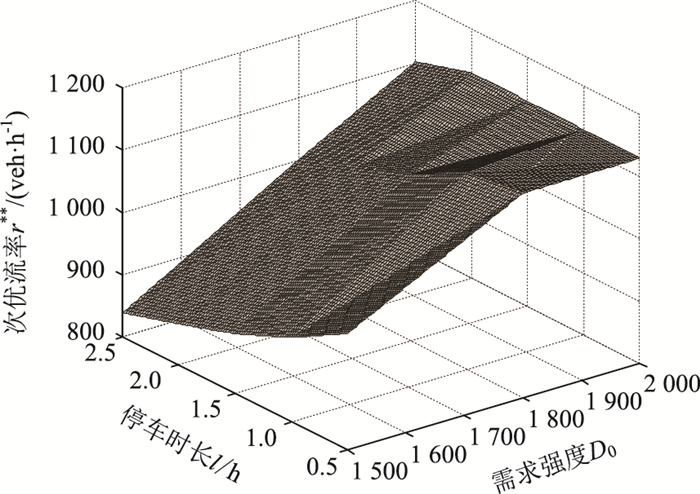
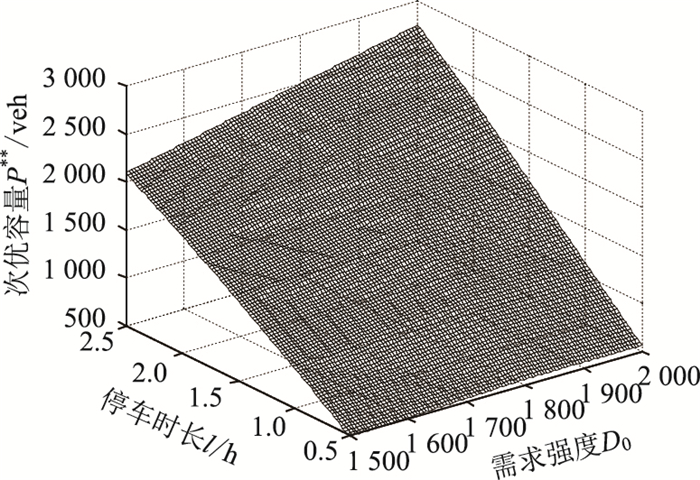
小汽车出行的用户对其出行成本较为敏感,而油耗成本的引入增加了出行成本,间接地改变了出行者的出行行为,使得城市中心交通流率重新分配[18]。因此,该种情况下所求得的结果小于不考虑油耗成本时的次优容量,这样更加符合了城市中心路内停车的实际情况。此外,通过算法改进,在停车活动活跃下,考虑道路条件及过境车辆的影响,可有效避免交通拥堵。进一步,在D0∈ (1 500, 2 000),l∈ (0, 2.5 h)时,根据次优流率及路内停车次优容量随停车时长与停车需求的变化规律,得到相应的关系图,如图 4和图 5所示。
|
| 图 4 停车时长、需求强度与次优流率之间的关系图 Fig. 4 The relationship between parking length, demand intensity and sub-optimal throughput |
| |
|
| 图 5 停车时长、需求强度与次优容量之间的关系图 Fig. 5 Relationship among parking length, demand intensity and sub-optimal capacity |
| |
图 4和图 5所示的关系图说明:停车平均时长一定,可以得出该种状态下能够满足社会剩余最大化的次优容量,但是这种人为限定停车费的情况下,路内停车时长越长,次优容量虽达到最大,而效率不是最好,因此,还有待于路内停车费进一步市场化。
综上,虽然一定停车需求下,针对给定时长,路内停车次优求解符合了Arnott对于路内停车的研究,但考虑燃油消耗成本后,使得路内停车次优容量求解算法更符合实际交通现状。通过数值分析的结果可以看出,在受过境车辆的影响且停车活动相对活跃的情况下,合理限制市区内的交通量,使得路内停车次优容量的求解更加符合交通现状,还可以有效地避免交通拥堵。除此之外,通过对路内停车次优容量在不同停车时长下的比较分析,进一步验证了短时停车对提高路内停车效率的重要意义。
5 结论路内停车容量能够有效的反映城市中心路内停车的服务水平,对城市中心路内停车容量进行优化有助于科学地管理城市交通。本研究从政府指导定价的角度出发,探讨了区别于市场定价的路内停车次优容量,并结合供需均衡的理论,在引入燃油消耗成本后,给出了路内停车次优容量的具体计算方法。通过数值算例,验证了特定停车时长下计算方法的可行性;在分析路内停车次优容量与停车时长和停车需求的关系时,明确了进行路内短时停车的意义。文章放松了Arnott关于进入城市中心的车辆均进行停车的假设,并引入油耗成本,改进了成本函数,通过对路内停车次优容量算法进行优化,为科学地研究路内停车次优容量提供了参考价值。在下一步研究中,将考虑停车者是异质的情况,并结合实证研究工作标定模型参数,使其与实际交通现状更加吻合。
| [1] |
SHOUP D C. Cruising for Parking[J]. Transport Policy, 2006, 13(6): 479-486. |
| [2] |
SHOUP D C. The High Cost of Free Parking[J]. Journal of Planning Education & Research, 1997, 17(1): 3-20. |
| [3] |
DAS D, AHMED M A. Level of Service for On-street Parking[J]. KSCE Journal of Civil Engineering, 2017(1): 1-11. |
| [4] |
DEY S S, DANCE C R, DARST M, et al. To Demarcate or Not to Demarcate:Analysis of Marked Versus Unmarked On-Street Parking Efficiency[J]. Transportation Research Record, 2016, 2562: 18-27. |
| [5] |
DEY S S, DOCK S, PATTERSON E. Implications of Changing Dynamics for Metered On-street Parking[J]. Transportation Research Board, 2015, 2500: 17-25. |
| [6] |
田琼, 罗婷, 杨丽. 考虑延误时间成本的最优路边停车策略研究[J]. 管理科学学报, 2016, 19(7): 50-59. TIAN Qiong, LUO Ting, YANG Li. The Optimal Curbside Parking Strategies with Schedule Delay[J]. Journal of Management Sciences In China, 2016, 19(7): 50-59. |
| [7] |
丁浣, 郭宏伟, 张余杰, 等. 考虑时间价值的路内停车巡航行为建模[J]. 交通运输系统工程与信息, 2015, 15(4): 187-191. DING Huan, GUO Hong-wei, ZHANG Yu-jie, et al. Modeling Behavior of Cruising for On-street Parking Based on Time Value[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(4): 187-191. |
| [8] |
王姝春, 陈峻, 张辉. 与路外停车场协调的城市路内停车设施选址优化模型[J]. 公路交通科技, 2009, 26(5): 97-102. WANG Shu-chun, CHEN Jun, ZHANG Hui. A Location Optimization Model for Curb Parking Facilities Coordinating with Off-street Parking Facilities[J]. Journal of Highway and Transportation Research and Development, 2009, 26(5): 97-102. |
| [9] |
韦兰香, 梁玉娟. 考虑路内停车的元胞自动机交通流能耗模型[J]. 科技通报, 2017, 33(1): 216-220. WEI Lan-xiang, LIANG Yu-juan. Cellular Automaton Traffic Flow Energy Loss Model Considering Curb Parking[J]. Bulletin of Science and Technology, 2017, 33(1): 216-220. |
| [10] |
戴帅, 刘金广, 朱建安, 等. 城市路内停车管理战略及实践[J]. 城市交通, 2014(1): 6-11. DAI Shuai, LIU Jin-guang, ZHU Jian-an, et al. On-street Parking Management Strategies and Practice[J]. Urban Transport of China, 2014(1): 6-11. |
| [11] |
ARNOTT R, INCI E, ROWSE J. Downtown Curbside Parking Capacity[J]. Journal of Urban Economics, 2015, 86: 83-97. |
| [12] |
ARNOTT R, INCI E. The Stability of Downtown Parking and Traffic Congestion[J]. Journal of Urban Economics, 2010, 68(3): 260-276. |
| [13] |
ARNOTT R, ROWSE J. Curbside Parking Time Limits[J]. Transportation Research Part A:Policy and Practice, 2013, 55(9): 89-110. |
| [14] |
耿克姣. 城市路内停车的必然性和供求规划模型分析[J]. 交通标准化, 2013(3): 42-44. GENG Ke-jiao. Necessity and Model about Supply and Demand Planning of Urban Curb Parking[J]. Transportation Standardization, 2013(3): 42-44. |
| [15] |
陈群, 史峰, 晏克非. 停车泊位有限供给条件下最佳停车泊位规模[J]. 同济大学学报:自然科学版, 2010, 38(12): 1758-1762. CHEN Qun, SHI Feng, YAN Ke-fei. Optimum Berth Scale Under a Restricted Supply of Parking Berths[J]. Journal of Tongji University:Natural Science Edition, 2010, 38(12): 1758-1762. |
| [16] |
陈群, 晏克非. 基于路网容量约束的停车设施泊位规模优化[J]. 北京工业大学学报, 2012, 38(4): 553-557. CHEN Qun, YAN Ke-fei. Parking Berth Scale Optimization Based on Road Network Capacity Restriction[J]. Journal of Beijing University of Technology, 2012, 38(4): 553-557. |
| [17] |
叶晓飞, 邓社军, 陈峻, 等. 路内停车对非机动车道通行能力的影响[J]. 西南交通大学学报, 2015, 50(3): 529-535. YE Xiao-fei, DENG She-jun, CHEN Jun. Impact of Curbside Parking on Bicycle Lane Capacity[J]. Journal of Southwest Jiaotong University, 2015, 50(3): 529-535. |
| [18] |
林湛, 四兵锋, 胡卉, 等. 基于均衡流量的城市停车费用优化模型[J]. 交通运输工程学报, 2014(5): 82-89. LIN Zhan, SI Bing-feng, HU Hui, et al. Optimization Model of Urban Parking Fare Based on Equilibrium Flow[J]. Journal of Traffic and Transportation Engineering, 2014(5): 82-89. |
 2019, Vol. 36
2019, Vol. 36
