扩展功能
文章信息
- 李彦瑾, 罗霞
- LI Yan-jin, LUO Xia
- 基于路网压缩的城市路网脆弱路段识别
- Identification of Urban Road Vulnerability Based on Road Network Compression
- 公路交通科技, 2019, 36(5): 104-112
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(5): 104-112
- 10.3969/j.issn.1002-0268.2019.05.015
-
文章历史
- 收稿日期: 2018-02-01
交通事故、灾害天气、恐怖袭击等突发事件具有很强的随机性,并且涉及面很广。如果城市道路交通网络出现了这类突发事件,则极易引起相关路段或交叉口出现继发性拥堵,进而造成大面积交通瘫痪,这极大地影响了道路交通系统的运转,阻碍了灾后应急救援的实施。因此,对突发条件下的路网脆弱路段识别,有助于交管部门提前做好应急预案,提升道路交通网络防灾抗灾能力。
路网脆弱性识别的基础是进行脆弱路段的识别,传统做法沿用了Berdica[1]的研究思路,即:首先结合路网几何形态和交通状态构建脆弱性评估指标,然后遍历网络中的所有交通单元(路段或交叉口),通过计算删除特定单元后路网脆弱性指标的变化来评估该交通单元对路网脆弱性的影响程度。基于此种思路,Sullivan等[2-4]先后运用鲁棒性指数、路段重要度和网络效率等指标来进行脆弱路段识别。这类方法虽可比较拓扑形态各异的道路交通网络,但需要遍历路网中的所有路段,效率很低。
对此,Taylor等[5-6]发展出潜在脆弱路段的概念。他们认为,进行路网脆弱性研究不能逐一遍历所有路段,而应将研究重点放在潜在的脆弱路段上,比如路段饱和度或占用率较高(V/C比)的路段。但是,Knoop等[7]认为Scott提出的潜在脆弱路段没有较好地考虑突发环境下出行者的路径选择行为。于是,国内的李小静等[8-10]先后运用前景理论、可靠性理论和鲁棒性理论等,尝试对Knoop提出的问题予以改善,但改进后的模型均较为复杂,求解过程繁琐,不适用于大规模路网。
由于突发环境下的城市路网在鲁棒性、出行者行为、交通流量分布等方面的不确定性变化,使得现有研究无法较好地评估其脆弱性。因此,本研究尝试从网络鲁棒性入手,提出一种基于可达性的路网矩阵压缩算法;然后在压缩后的子路网上构建一个考虑出行者路径选择行为的多用户随机均衡(Stochastic User's Equilibrium,SUE)模型;再通过设计一个新的脆弱性指标来识别子路网的脆弱路段;最后,通过SP(Stated Preference)调查数据并结合实际算例完成模型验证。
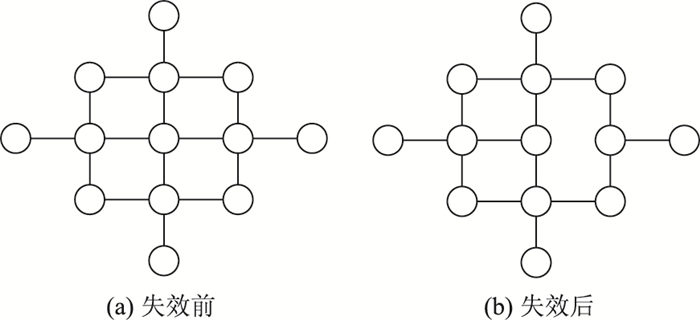
1 路网鲁棒性分析 1.1 突发环境下的路网拓扑变化暂不考虑路网上的交通流量分布,假定突发事件后事发路段将立即失效,则此时路网的拓扑变化如图 1所示。
|
| 图 1 路网拓扑变化 Fig. 1 Road network topological changes |
| |
图 1从中观层面表征了突发环境下的路网拓扑变化。进一步地,由于突发事件具有很强的不确定性,若将其视为对路网的随机攻击,则可利用鲁棒性指标来评估该情景下的路网拓扑变化。
1.2 路网鲁棒性指标路网的鲁棒性表征了路网抵抗随机攻击或蓄意攻击的能力,常用鲁棒性指标刻画。若指标变化量大,则说明路网鲁棒性受到的影响越大[10]。现选取网络效率E、最大连通子图V来进行路网鲁棒性分析。
(1) 网络效率
网络效率从最短路的角度评价路网的鲁棒性能。若在路段失效后,网络效率的变化量ΔE越大,则说明此路段失效对路网鲁棒性的影响越显著。网络效率的变化量ΔE按式(1)计算:
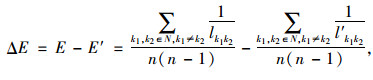
|
(1) |
式中,E和E′分别为路段失效前、后的网络效率;n为节点数量;N为节点集;lk1k2和l′k1k2分别为路段失效前后节点k1,k2的最短路径。
(2) 最大连通子图
最大连通子图是一类以尽可能少的路段连接网络中尽可能多的节点的拓扑图[10]。若在路段失效后,最大连通子图的变化量越大,则说明此失效路段对路网拓扑变化的影响越大。最大连通子图的变化量ΔS按式(2)计算:
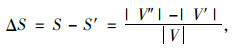
|
(2) |
式中,S和S′分别为路段失效前、后的最大连通子图大小;|V|为原路网节点数量;|V′|和|V″|分别路段失效前、后为最大连通子图节点数量。
对于路网G (N, L),N= {ni|i=1, 2, …, n}为交叉口集合,L= {lj|j=1, 2, …, m}为路段集合。通过遍历法,逐一删除路段集合L= {lj|j=1, 2, …, m}中的路段,并按照式(1)、式(2)计算鲁棒性指标的变化量ΔE和ΔS。然后,筛选出ΔE,ΔS值均较大的路段,用它们构成潜在脆弱路段集L′。
2 路网压缩算法的设计基于潜在脆弱路段集合L′,结合复杂网络理论[11]设计出一种基于可达性原理的路网压缩算法。算法的具体设计流程如下。
算法A
Step 0 获取潜在脆弱路段集L′中各个路段的关联节点,以此构建初始节点集合N′={np|1≤p≤n},N′⊆N。
Step 1 在路网G (N, L)中,从节点n1出发,若该节点可与节点集N′中的节点np邻接,则将其标记为“1”,否则为“0”。遍历N′的节点,得到一个关于节点n1的0-1向量。
Step 2 在节点n1的0-1向量中,记录所有“1”元素,并按照Step 1构造出这些“1”元素所对应的节点0-1向量。
Step 3 反复执行Step 1~Step 2,直至构造出路网G (N, L)中所有节点与集合N′中所有节点相对应的0-1向量。
Step 4 搜索出节点n1所有0-1向量中的非“1”元素并将它们全部置“0”,进而生成出一个关于节点n1的邻接矩阵MA。
Step 5 将路网G (N, L)反向,得到一个由反向路段组成的路网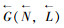
Step 6 在反向路网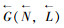
Step 7 进行转置矩阵MBT与邻接矩阵MA的交集运算:M A*= MA∩ MBT。根据矩阵M A*中各元素的0-1关系便可得到子路网:Gh* (N*, L*), h≥1,完成路网压缩。
注意:由于集合L′中的路段在几何拓扑层面上并不相邻,故由算法A获取的压缩子路网Gh* (N*, L*)可能不止一个(数量设为h),它们彼此间满足:
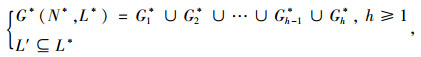
|
(3) |
式中,G* (N*, L*)为各个子路网的并集,可完全覆盖子路网;h为子路网个数。
通过式(3)可以看出,算法A实质上采用了“分治法”,在包含潜在脆弱路段集L′的基础上,将初始路网G (N, L)分成了h个彼此连通可达的子路网。由于子路网Gh* (N*, L*)的规模较小,这便于接下来路网脆弱性分析的开展。
3 多用户SUE模型考虑出行者对路段阻抗的随机偏差估计与路径选择概率,据此构建多用户随机均衡配流模型。具体而言,按照路段阻抗、路径阻抗、路径选择概率、目标函数4部分建模。
3.1 路段阻抗在突发环境下,假定路网G (N, L)共有D类不同类型的出行者,则第d (d∈D)类出行者对路段a的路段阻抗估计值Tad为:

|
(4) |
式中,xa为路段a的交通流量;ta (xa)为路段a的基本阻抗,它是关于路段a流量的增函数;εad为第d类出行者对路段a阻抗的随机偏差估计。
式(4)表明,在突发环境下的路段阻抗Tad是一个随机变量。
3.2 路径阻抗在路网G (N, L)中,假定OD对rs间的有效路径集合为Krs,则第d类出行者对第k条有效路径的路径阻抗估计值Cd, krs为:
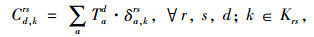
|
(5) |
式(5)中,δa, krs为表征路段a与路径k关系的0-1变量,若路段a被第k条路径利用,则δa, krs=1,否则δa, krs=0。
由于路径阻抗是由路段阻抗累加而成的,故路径阻抗Cd, krs也是一个随机变量,并且满足E [Cd, krs]=cd, krs,即:
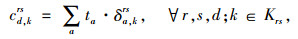
|
(6) |
式中cd, krs为路径阻抗Cd, krs的期望。
3.3 路径选择概率根据随机用户均衡的基本假设,第d类出行者选择第k条路径的概率Pd, krs即是路径k为rs间最短路径(路径阻抗值Cd, krs最小)的概率[8],即:
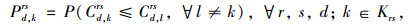
|
(7) |
式中Cd, lrs为OD对rs间第l条路径的阻抗。
若路段a阻抗的随机估计偏差εad服从Gumbel分布,则式(7)可按Logit模型进行标定,即:
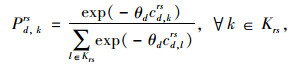
|
(8) |
式中θd为第d类出行者在Logit模型中的待定参数,一般可通过SP调查数据拟合得到。
因此,通过引入多用户的路径选择概率Pd, krs,OD对rs之间的第k条路径流量fd, krs与其交通需求量qrs满足:
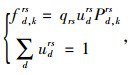
|
(9) |
式中udrs为第d类出行者在OD对rs之间所占的比例。
3.4 目标函数通过分析总结式(4)~式(9)可得:多用户SUE模型是一个通过Logit模型参数θd来定量反映出行者路径选择概率的交通分配问题。因此,可将目标函数构造成关于路径流量fd, krs与路段流量w的函数[12],即:
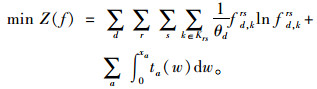
|
(10) |
而模型的约束条件,由于考虑了不同的出行者类型d、路径选择概率Pd, krs、出行者比例udrs等多个用户出行特征变量,因此应在静态均衡配流模型的基础上,将对应的约束条件改为:
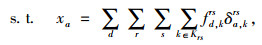
|
(11) |
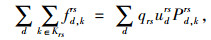
|
(12) |
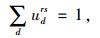
|
(13) |

|
(14) |
式(11)~式(14)分别对应多用户SUE模型的路段流量xa、路径流量fd, krs、出行者比例udrs和非负约束等约束条件。
进一步观察发现,在模型参数qrs,udrs,θd由SP调查数据拟合标定以后,目标函数式(10)将退化为一个关于路径流量fd, krs的凸函数,而且模型的约束条件均是线性的,故其解集为紧凸集。同时,根据变分不等式理论[12],目标函数是具有可解性的,故此模型拥有路径均衡流量解。
4 脆弱路段识别指标的构建突发环境下,子路网Gh* (N*, L*)内部的交通分布状态将会突变,从而导致其路网总阻抗发生改变。上述SUE模型中,路网总阻抗一般以路径阻抗形式给出,即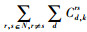
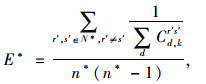
|
(15) |
式(15)中,Cd, kr′s′为第d类出行者选择第k条路径作为最优路径的路径阻抗,可按式(5)进行计算;r′, s′, N*, n*分别为子路网Gh* (N*, L*)的起、终点、节点集与节点数量。
不难发现,新的脆弱性识别指标E*利用出行者在rs间的路径总阻抗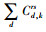
因此,本研究用指标E*在突发事件前后的变化量ΔEa*来识别子路网Gh* (N*, L*)的脆弱路段a:
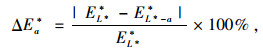
|
(16) |
式中,EL**和EL*-a*分别为子路网Gh* (N*, L*)在路段a失效前、后的脆弱性评价指标。该式以变化率的形式刻画路网脆弱性,这样做主要是为了使识别结果有更好的区分度,并尽量弱化路段通行能力统计分布特征的不同对识别效果的影响。
最后,将基于多用户SUE模型的脆弱路段识别流程阐述如下。
算法B
Step 0 利用MSA配流法将OD对rs间的需求量qrs加载到原始路网G (N, L)中,得到各路段的初始流量xi (i∈L)。
Step 1 通过算法A进行路网压缩,得到第h个子路网:Gh* (N*, L*), 1≤h≤hm。
Step 2 针对第h个子路网Gh* (N*, L*),计算其初始需求量qrsh和内部各路段的路段流量xah(a∈L*)。
Step 3 按照式(5)、式(15)分别计算子路网Gh* (N*, L*)的初始总阻抗
Step 4 将路段a从子路网Gh* (N*, L*)中予以删除,得到更新后的子路网Gh* (N*, L*-a)。
Step 5 利用MSA配流法将需求量qrsh重新加载到更新后的子路网Gh* (N*, L*-a)中,得到各条路段的更新流量x′i (i∈L*-a)。
Step 6 再次按照式(5)、式(15)计算Gh*(N*, L*-a)的总阻抗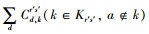
Step 7 按照式(16),计算路段a的脆弱性识别指标变化率ΔEa*。
Step 8 如果已更新子路网Gh* (N*, L*)中的所有路段,则h=h+1,转入Step 9;否则,删除子路网Gh* (N*, L*)中的另一条路段,转至Step 4。
Step 9 若h≥hm,终止算法,输出脆弱性识别结果;否则,转至Step 2。
5 案例分析 5.1 数据收集与参数标定[13]模型参数θd和udrs需结合实际路网通过SP调查获取。在此,以成都市锦江区某地的道路网络G (N, L)为调查对象进行案例分析,其几何拓扑形态如图 2所示。具体的路网设计参数如表 1所示。
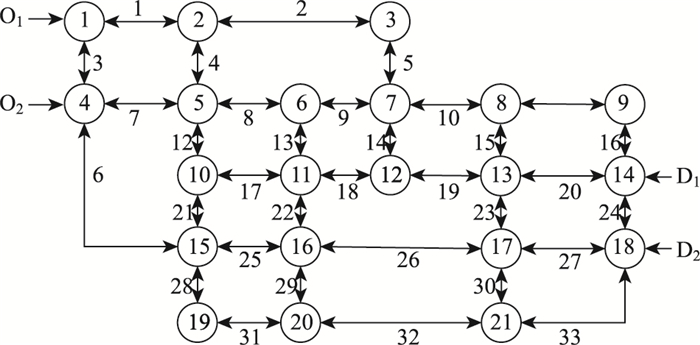
|
| 图 2 路网算例[17] Fig. 2 Example of road network 注:路网G (N, L)上的OD对分别为1→14,4→14,1→18,4→18。 |
| |
| 编号 | 通行能力/(veh·h-1) | 初始阻抗/h | 编号 | 通行能力/(veh·h-1) | 初始阻抗/h |
| 1 | 1 000 | 0.12 | 18 | 700 | 0.12 |
| 2 | 1 300 | 0.12 | 19 | 1 000 | 0.12 |
| 3 | 700 | 0.12 | 20 | 1 000 | 0.12 |
| 4 | 700 | 0.12 | 21 | 500 | 0.2 |
| 5 | 700 | 0.12 | 22 | 500 | 0.2 |
| 6 | 1 300 | 0.15 | 23 | 600 | 0.2 |
| 7 | 1 000 | 0.12 | 24 | 600 | 0.2 |
| 8 | 700 | 0.12 | 25 | 700 | 0.12 |
| 9 | 700 | 0.12 | 26 | 1 300 | 0.12 |
| 10 | 1 000 | 0.12 | 27 | 1 000 | 0.12 |
| 11 | 1 000 | 0.12 | 28 | 700 | 0.12 |
| 12 | 600 | 0.2 | 29 | 700 | 0.12 |
| 13 | 600 | 0.2 | 30 | 700 | 0.12 |
| 14 | 600 | 0.2 | 31 | 700 | 0.12 |
| 15 | 600 | 0.2 | 32 | 1 300 | 0.12 |
| 16 | 600 | 0.2 | 33 | 1 300 | 0.12 |
| 17 | 700 | 0.2 | |||
| 注:按《城市道路交通规划设计规范》[13]取值。 | |||||
然后,采集路网OD需求量与出行者特征数据,得到各OD对间的需求量,如表 2所示。之后,通过对出行者特征数据的非集计处理,得到3种出行特征各异的出行者类型:不理性型、部分理性型和完全理性型,3者的比例udrs与Logit模型参数θd如表 3所示。
采用BPR函数刻画路网G (N, L)的道路阻抗[15]:
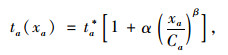
|
(17) |
式中,xa为路段a流量;ta*为路段a的初始自由流阻抗;Ca为路段a的道路通行能力;参数α,β根据实际调查数据用非线性回归[15]拟合,取值为α=0.351,β=3.089。
对获取的数据进行一致性验证。一方面,通过表 1计算出路网中各路段的平均路段阻抗在区间[0.10 h, 0.27 h]波动,这与实际调查得到的机动车平均行驶时间一致;另一方面,利用表 2、表 3进行模型参数的标定,其计算得到的各种类型出行者在路网中所占的比例也与实际的交通调查结果相近。
下面,将突发环境下的路网脆弱性分析分为潜在脆弱路段集获取、路网压缩、脆弱路段3个阶段进行识别。
5.2 潜在脆弱路段集获取遍历删除路网G (N, L)中的路段,并按式(1)、式(2)分别计算突发环境下路网鲁棒性指标的变化量ΔE,ΔS,结果如图 3所示。
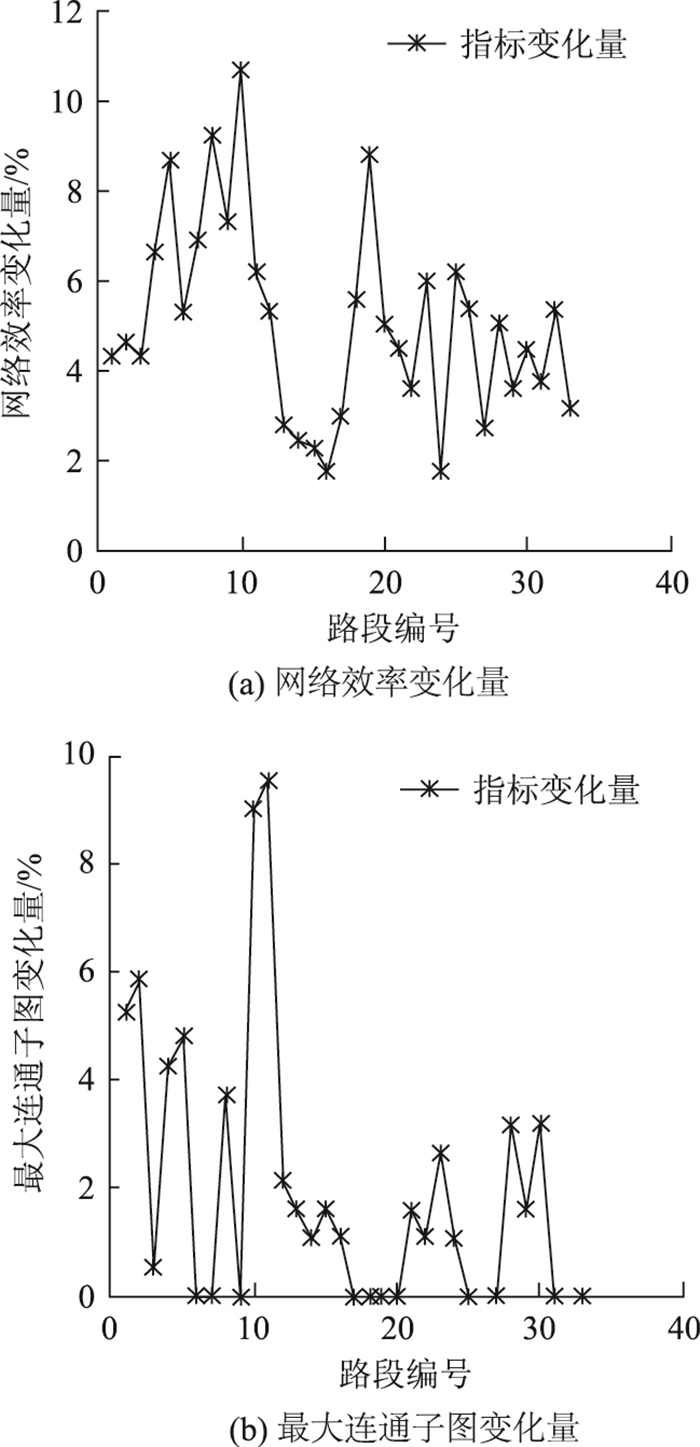
|
| 图 3 路网鲁棒性指标的变化 Fig. 3 Variation of road network robustness indicators |
| |
将图 3中ΔE与ΔS的均值ΔE =5.04%和ΔS =1.96%作为路网潜在脆弱路段的筛选条件,选择指标变化量均大于ΔE和ΔS的路段构成潜在脆弱路段集合L′:
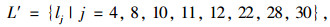
|
(18) |
式中j为潜在路段的编号。
5.3 路网压缩在潜在脆弱路段集L′的基础上,通过算法A进行路网G (N, L)的压缩,结果如图 4所示。
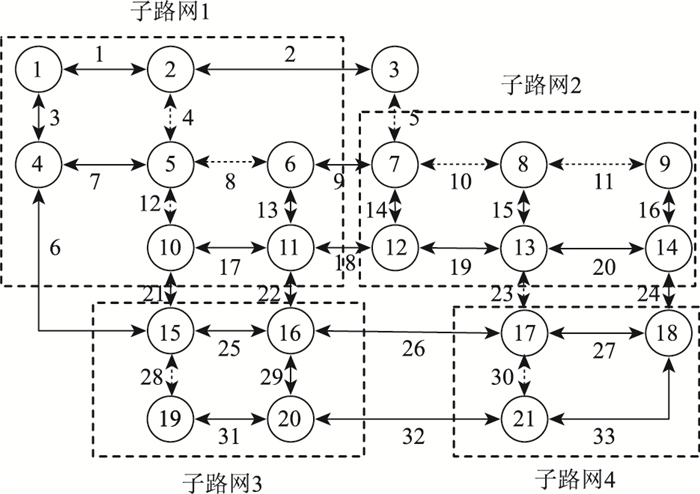
|
| 图 4 子路网分区 Fig. 4 Road sub-network partition 注:潜在关键路段用虚线。 |
| |
由图 4可得,算法A将路网G (N, L)压缩为G1* (N*, L*),G2* (N*, L*),G3* (N*, L*),G4* (N*, L*)等4 (hm=4)个子路网,它们均为简单回路,便于进行交通流量分析与计算机编程。
5.4 脆弱路段识别执行算法B的Step 0。通过MSA法完成路网初始配流,设MAS法的收敛精度e为0.01。通过计算,可得模型收敛情况与各路段的初始流量分配结果,如图 5所示。
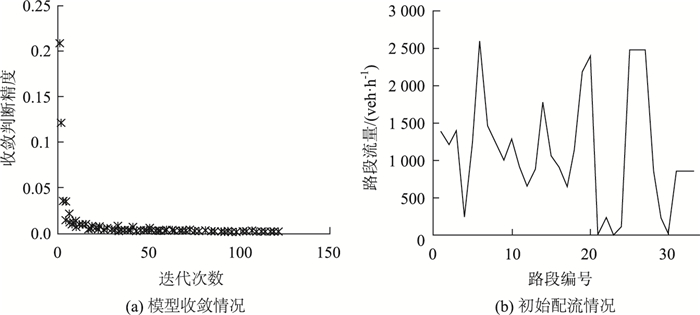
|
| 图 5 初始配流结果 Fig. 5 Initial flow assignment result |
| |
由图 5可得,算法在进行到第127次时收敛,该过程耗时为103.604 s。可以推断,如果采用遍历法逐一删除33条路段进行脆弱性识别,则整个识别过程将耗时3 418.932 s (约1 h,33×103.604 s)。显然,常规计算机的计算速度不足以在短时间内求得模型结果。因此通过算法A压缩路网规模。
在每个压缩后的子路网Gh* (N*, L*)上,运用matlab2012a完成算法B,得到各子路网Gh* (N*, L*)的脆弱性分析指标ΔEa*,结果如图 6所示。
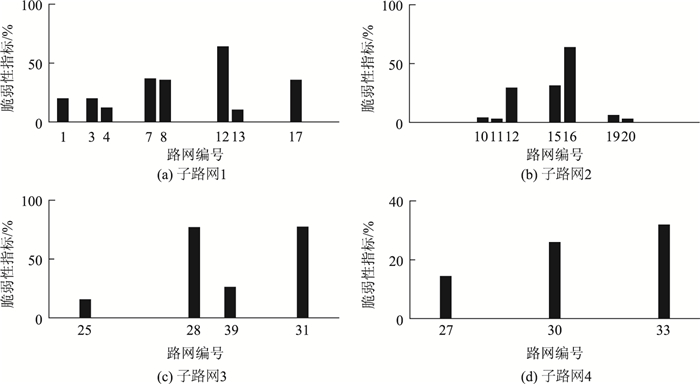
|
| 图 6 子路网脆弱性指标 Fig. 6 Vulnerability indicators of road sub-networks 注:该过程耗时为20.004 s。 |
| |
从图 6可知,用脆弱性指标ΔEa*识别出子路网1~4的脆弱路段分别为:路段12、路段16、路段31和路段33,且如果突发事件导致这4条路段完全失效,则它们分别会对子路网1~4造成61.97%,62.68%,75.74%和29.75%的负面影响。
最后,尝试将本研究模型与传统的遍历法识别模型[16-18]进行对比,结果如表 4所示。
| 方法 | 脆弱性排序 | 编号 | 变化量ΔEa*/% | |
| 多用户SUE模型(算法A+算法B) | 子路网1 | 1 | 12 | 61.973 |
| 2 | 7 | 33.851 | ||
| 3 | 17 | 32.740 | ||
| 子路网2 | 1 | 16 | 62.684 | |
| 2 | 15 | 28.218 | ||
| 3 | 14 | 26.380 | ||
| 子路网3 | 1 | 31 | 75.741 | |
| 2 | 28 | 75.741 | ||
| 3 | 29 | 23.924 | ||
| 子路网4 | 1 | 33 | 29.745 | |
| 2 | 30 | 22.779 | ||
| 3 | 27 | 11.418 | ||
| 方法 | 脆弱性排序 | 编号 | 变化量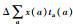 /(veh·h) /(veh·h) |
|
| 遍历法 | 1 | 28 | 91.561 | |
| 2 | 16 | 83.339 | ||
| 3 | 6 | 62.948 | ||
| 4 | 12 | 60.530 | ||
| 5 | 31 | 40.177 | ||
| 注:两种方法识别结果一致的路段用黑体标出。 | ||||
从表 4可得,本研究模型的识别结果与传统模型基本一致,但脆弱性识别指标间的区分度(方差)高出传统模型约24.46%。此外,本研究模型的识别过程耗时更短。具体而言,算法A加算法B总耗时仅为:2.053+123.608(103.604+20.004)=125.661 s(约2 min),而传统模型需采用遍历法识别脆弱路段,全程耗时将近1 h。
值得注意的是,本研究模型未识别出路段6,原因在于路段6并不在潜在脆弱路段集合(式(18))中,进而无法出现在子路网里,故无法得到路段6的配流与识别结果。这一现象表明,突发环境下路网鲁棒性与脆弱性虽具有一定的正相关关系[10](最脆弱路段如路段28、路段16、路段33等同时也是对路网鲁棒性影响较大的路段),但并非简单的线性相关[17],需综合考虑两种方法的识别结果,避免对脆弱路段的“漏判”。
6 结论为更高效地实现突发条件下的路网脆弱路段识别,本研究以网络鲁棒性分析为出发点,构建多用户SUE模型,得到相关结论如下:
(1) 考虑了突发环境下不同类型出行者的路径选择行为,提出的多用户SUE模型能够刻画路网交通流分布的随机特性。
(2) 基于可达性原理,设计了路网压缩的矩阵算法,将路网分割成多个彼此连通的子路网,各子路网可完整覆盖潜在脆弱路段集合,并显著降低模型求解的时间。
(3) 模型的参数标定需要利用大量的基础调研数据。这些数据往往具有时变特性,而本研究模型是基于静态路网的,如何融入这些数据的时变特性,是下一阶段的工作。
| [1] |
BERDICA K. An Introduction to Road Vulnerability:What Has Been Done, Is Done and Should Be Done[J]. Transport Policy, 2002, 9(2): 0-127. |
| [2] |
SULLIVAN J L, NOVAK D C, AULTMAN-HALL L, et al. Identifying Critical Road Segments and Measuring System-wide Robustness in Transportation Networks with Isolating Links:A Link-based Capacity-reduction Approach[J]. Transportation Research Part A:Policy & Practice, 2010, 44(5): 323-336. |
| [3] |
JENELIUS E, PETERSEN T, MATTSSON L G. Importance and Exposure in Road Network Vulnerability Analysis[J]. Transportation Research Part A:Policy & Practice, 2006, 40(7): 537-560. |
| [4] |
D'ESTE G M, TAYLOR M A P. Network Vulnerability:An Approach to Reliability Analysis at the Level of National Strategic Transport Networks[R]. New York:Pergamon Press, 2003:23-44.
|
| [5] |
TAYLOR M A P, SEKHAR S V C, D'ESTE G M. Application of Accessibility Based Methods for Vulnerability Analysis of Strategic Road Networks[J]. Networks and Spatial Economics, 2006, 6(3/4): 267-291. |
| [6] |
SCOOT D M, NOVAK D C, AULTMAN-HALL L. Network Robustness Index:A New Method for Identifying Critical Links and Evaluating the Performance of Transportation Networks[J]. Journal of Transport Geography, 2006, 14(3): 215-227. |
| [7] |
KNOOP V, VAN ZUYLEN H, HOOGENDOORN S. The Influence of Spillback Modelling When Assessing Consequences of Blockings in a Road Network[J]. European Journal of Transport and Infrastructure Research, 2008, 8(4): 287-300. |
| [8] |
李小静, 刘林忠. 基于累计前景理论的通勤者路径选择模型[J]. 交通运输系统工程与信息, 2015, 15(1): 173-178. LI Xiao-jing, LIU Lin-zhong. Route Choice Model for Commuters Based on Cumulative Prospect Theory[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(1): 173-178. |
| [9] |
CHEN B Y, LAM W H K, SUMALEE A, et al. Vulnerability Analysis for Large-scale and Congested Road Networks with Demand Uncertainty[J]. Transportation Research Part A:Policy and Practice, 2012, 46(3): 501-516. |
| [10] |
李彦瑾, 罗霞, 车国鹏. 突发拥挤条件下城市道路网脆弱性识别[J]. 公路交通科技, 2017, 34(5): 129-136. LI Yan-jin, LUO Xia, CHE Guo-peng. Vulnerability Identification of Urban Road Network under Abrupt Congestion Condition[J]. Journal of Highway and Transportation Research and Development, 2017, 34(5): 129-136. |
| [11] |
刘思峰, 万寿庆, 陆志鹏, 等. 交通网络中救援点与事故点的路段重要性评价模型研究[J]. 中国管理科学, 2009, 17(1): 119-124. LIU Si-feng, WAN Shou-qing, LU Zhi-peng, et al. The Importance of Highway Section Evaluation Model in Complex Network between Accident Point and Rescue Point in the Emergency Situations[J]. Chinese Journal of Management Science, 2009, 17(1): 119-124. |
| [12] |
黄海军. 城市交通网络平衡分析:理论与实践[M]. 北京: 人民交通出版社, 1994: 57-69. HUANG Hai-jun. Urban Transportation Network Equilibrium Analysis:Theory and Practice[M]. Beijing: China Communications Press, 1994: 57-69. |
| [13] |
李彦瑾, 罗霞, 徐沙.突发环境下城市道路网脆弱性识别[C]//2018世界交通运输大会.北京: 人民交通出版社, 2018: 789-802. LI Yan-jin, LUO Xia, XU Sha. Vulnerability Identification of Urban Road Network under Emergency Environment[C]//2018 World Transportation Conference. Beijing: China Communications Press, 2018: 789-802. |
| [14] |
北京市市政工程设计研究总院. 城市道路设计规范[M]. 北京: 中国建筑工业出版社, 2012. Beijing General Municipal Engineering Design & Research Institute. Code for Design of Urban Road Engineering[M]. Beijing: China Architecture & Building Press, 2012. |
| [15] |
陆化普. 交通规划理论与方法[M]. 2版. 北京: 清华大学出版社, 2006: 251-258. LU Hua-pu. Theory and Method in Transportation Planning[M]. 2nd ed. Beijing: Tsinghua University Press, 2006: 251-258. |
| [16] |
王玮强, 张春民, 朱昌锋. 基于累积前景理论的应急物流路径选择方法[J]. 中国安全科学学报, 2017, 27(3): 169-174. WANG Wei-qiang, ZHANG Chun-min, ZHU Chang-feng. Route Selection Method for Emergency Logistics Based on Cumulative Prospect Theory[J]. China Safety Science Journal, 2017, 27(3): 169-174. |
| [17] |
张勇, 屠宁雯, 姚林泉. 城市道路交通网络脆弱性识别方法[J]. 中国公路学报, 2013, 26(4): 154-161. ZHANG Yong, TU Ning-wen, YAO Lin-quan. Urban Road Traffic Network Vulnerability Identification Method[J]. China Journal of Highway and Transport, 2013, 26(4): 154-161. |
| [18] |
李彦瑾, 罗霞. 基于Logistic曲线的路网脆弱性动态识别[J]. 中国安全科学学报, 2018, 28(2): 28-33. LI Yan-jin, LUO Xia. Dynamic Vulnerability Identification of Road Network Based on Logistic Curve[J]. China Safety Science Journal, 2018, 28(2): 28-33. |
 2019, Vol. 36
2019, Vol. 36
