扩展功能
文章信息
- 王世波, 赵金楼, 郑继兴
- WANG Shi-bo, ZHAO Jin-lou, ZHENG Ji-xing
- 基于复杂网络的城市交通堵塞载荷再分配控制
- Urban Traffic Congestion Load Redistribution Control Based on Complex Network
- 公路交通科技, 2019, 36(5): 98-103
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(5): 98-103
- 10.3969/j.issn.1002-0268.2019.05.014
-
文章历史
- 收稿日期: 2018-05-04
2. 哈尔滨工程大学 经济管理学院, 黑龙江 哈尔滨 150001
2. School of Economics and Management, Harbin Engineering University, Harbin Heilongjiang 150001, China
现实世界中存在着很多复杂网络系统,这些系统大多都可以用构建的网络模型来刻画[1],如因特网、蛋白质网、电力网络、科研合作网络、交通网络、金融网络等,这些网络中存在大量的节点并且节点之间有复杂的联系,与我们的日常生活紧密关联。随着复杂网络的无标度特性[2]和小世界效应[3]的发现,对于复杂网络的研究逐渐成为研究的热点问题[4],越来越多的学者开始研究复杂网络,其中网络节点(或边)故障引发的网络级联失效及控制是一个重要的研究方向。城市交通网络是城市经济运行的大动脉,是城市系统中重要的子系统,如何降低城市交通网络级联失效的概率、提升网络的抗击毁性,具有重要的研究意义[5-6]。
复杂网络的抗击毁性研究主要包括两个方面。一方面是不考虑网络中节点的载荷,即不考虑一个节点失效后对整个网络带来的级联效应[7],然而,现实中的大部分网络都有不同形式的载荷,如信息、流量、物质、能源等,需要考虑载荷对网络抗击毁性的影响。另一方面是考虑网络中节点的载荷,尤其是当网络拓扑结构发生变化时(网络中的节点或边失效后从网络中移除),网络中的载荷会被重新分配,这样就会因为节点容量有限而载荷重新分配使得网络的抗击毁性变得异常复杂。如一个节点的失效导致载荷会被重新分配,这就可能会使得某些节点因为新加入的载荷使得载荷总量超过其容量,引发这些节点失效,继而扩散开来,引发级联失效,导致网络堵塞[8-9]。
城市交通网络与其他网络一样,也存在级联失效的现象。目前学者们针对交通网络的研究多集中在路段(边)失效所带来的级联影响,主要采用排队模型[10-11]和交通波模型[12-13]。针对节点失效带来的级联影响主要采用耦合映像格子模型[14]来仿真分析网络拓扑结构、路段移除方式与外部扰动等因素对网络级联失效的影响规律。城市交通网络级联失效主要影响因素包括容量、载荷及载荷再分配策略,其中载荷再分配策略是影响级联失效效果的关键。Motter[15]在2002年提出了ML模型,设定节点的容量正比于其初始载荷,在复杂网络的研究中引入了过载机制。随后,Wang等[16]在ML模型基础上提出了WK模型, 认为初始载荷高的节点应赋予更大的容量。认为LW模型[17]的节点容量应和节点自身的度相关。黄英艺[18]提出了物流网络带有边权的节点重要度测量方法,在此基础上建立了对应的级联失效模型,以分析网络结构对物流网络级联失效的影响。Lehmann[19]提出了随机载荷重分配策略,将失效节点的载荷随机分配到余下的节点上。Kim[20]则提出了将失效节点载荷完全等分到其他完好节点。Wang[21]提出了近邻载荷重分配模型,将失效边上的载荷分到近邻节点上。这些学者都从不同的角度对网络级联失效进行了研究,节点或边失效后的载荷采用的全局分配、近邻分配、同质分配、异质分配都属于载荷分配的特殊情况,现实中的不同网络使得应采取的载荷分配策略亦应不同。本研究提出载荷可调节的级联失效非线性模型,针对城市交通网络节点失效后的载荷进行重新分配,并对网络展开随机攻击和蓄意攻击,对比网络抗毁性的差异,以寻求提升网络抗毁性的载荷重分配策略,提升城市交通网络的效能,保障其良好运行。
1 基于节点载荷再分配的级联失效非线性模型 1.1 节点的初始载荷分配与节点容量在级联失效模型中, 初始载荷分配是基于节点重要性的[22],将节点i的初始载荷定义为:
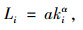
|
(1) |
式中,a和α为调整参数;ki为节点i的度数,即初始载荷基于节点的赋予中心度。
节点容量是指节点能够处理的最大量,在人造网络中,节点容量明显受到成本的限制,因此,假设节点容量Ci正比于其初始载荷, 即:
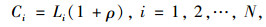
|
(2) |
式中,ρ为大于等于0的容量系数;N为初始节点数量。
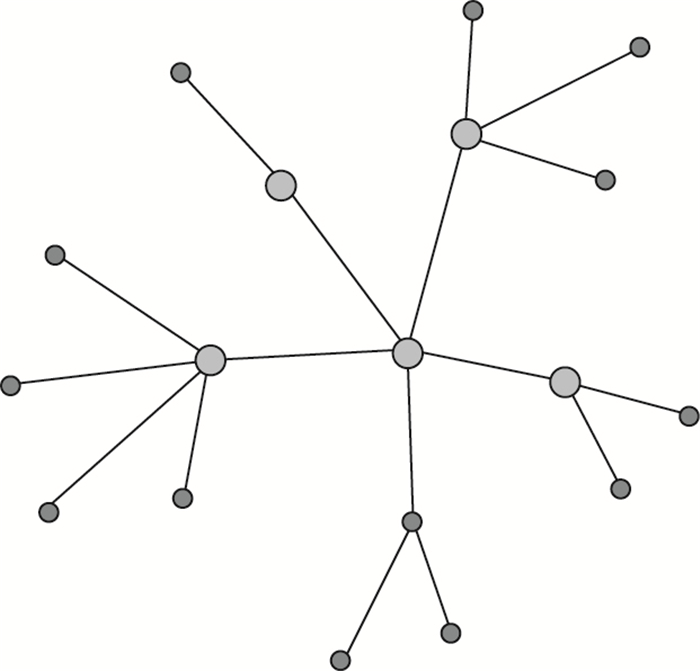
1.2 节点载荷再分配级联失效模型城市交通网络中的交叉路口(节点)出现堵塞或发生事故后,原本打算经过该点的车流就会重新规划行车路线,在未提前获得该路口堵塞状态的情况下,可选择的节点只能是失效路口节点的近邻路口节点,这些近邻路口节点的容量各有不同,车辆选择经过的情况亦不相同。本研究围绕节点失效后的载荷再分配问题展开,构建失效节点载荷再分配模型, 如图 1所示。当某节点i失效后,原本由其承载的载荷会按照一定的分配原则被分配到与之近邻的完好节点上,这种变化使得这些近邻节点的载荷发生一次变化。
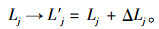
|
(3) |
|
| 图 1 失效节点载荷再分配模型 Fig. 1 Failure node load redistribution model |
| |
假设近邻完好节点所获得的载荷分配增量ΔLj与失效节点的载荷成正比,比例系数为L(Kj, r):
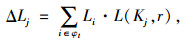
|
(4) |
式中,φt为t时间步时失效节点的集合;Kj为节点的度;r为载荷再分配系数。
在节点i失效后,其近邻节点j分担其载荷时的权重为Kj的函数,即ηj=bKjr,b为权重系数,可以得到失效节点分配到节点j的载荷的比例为:
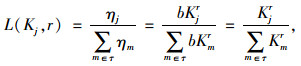
|
(5) |
式中,m为节点i的近邻完好节点的集合,r∈[-∞, ∞],r=0时为最近邻均匀共享载荷,r≠0时为非均匀载荷,r>0时侧重于度大的节点,r < 0时侧重于度小的节点。
将式(5)代入式(3)和式(4),得到某节点失效后其近邻完好节点的新载荷Lj′,这样就可以通过判断Lj′与节点容量Cj之间的大小关系来确定此步长时刻节点j是否堵塞失效。若Lj′>Cj,则节点处于堵塞状态,引发新一轮的载荷再分配;若Lj′≤Cj,则节点处于正常状态,不会引发新的载荷再分配,直到整个网络中所有节点的载荷都小于等于其自身容量,级联失效过程结束。
2 仿真分析 2.1 仿真环境与方法同许多其他网络一样,城市交通网络也处于不断完善和发展的过程中,其网络拓扑结构也不断发生变化。又由于城市交通网络不仅包括公交网络,还包括铁路网络,因而属于异质性的网络,符合无标度网络特征,可以使用BA模型来刻画[23]。
位于黑龙江省西北部地区的齐齐哈尔市,下辖7个区、9个县,主城区包括建华、龙沙、铁锋3个区,目前共计有主要交通路口280余个,主城区中通有客运和货运铁路,共涉及到铁路道口近20处。城区交通道路与货运铁路交汇,随着城市发展,未来还可能引入轻轨建设,属于典型的异质性网络。
仿真方法采用上述的节点载荷再分配级联失效模型方法,将每个交通路口定义为一个节点,初始节点容量与节点度数相关。当节点发生拥堵或者因施工需关闭而触发级联反应时,该节点的载荷向近邻节点分配,分配的规则通过调节模型中的参数r的值来实现,r=0时为最近邻均匀共享载荷,r≠0时为非均匀载荷,r>0时侧重于度大的节点,r < 0时侧重于度小的节点。
2.2 初始条件设定数值仿真以构建的齐齐哈尔市真实交通网络邻接矩阵展开,节点规模为280,平均度为3.8,采取的攻击方式为随机攻击和蓄意攻击两种方式,随机攻击进行50次,取平均值;蓄意攻击选择网络中载荷最大节点和度最大节点进行。设定载荷调节系数a=30, α=0.2, 模型的容量系数ρ分别为0.2,0.5,0.8。
2.3 不同仿真约束的仿真结果网络抗击毁性测度通常有两种方法。一种是基于网络连通特性的,即测度网络攻击前后最大连通子图的变化,用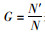
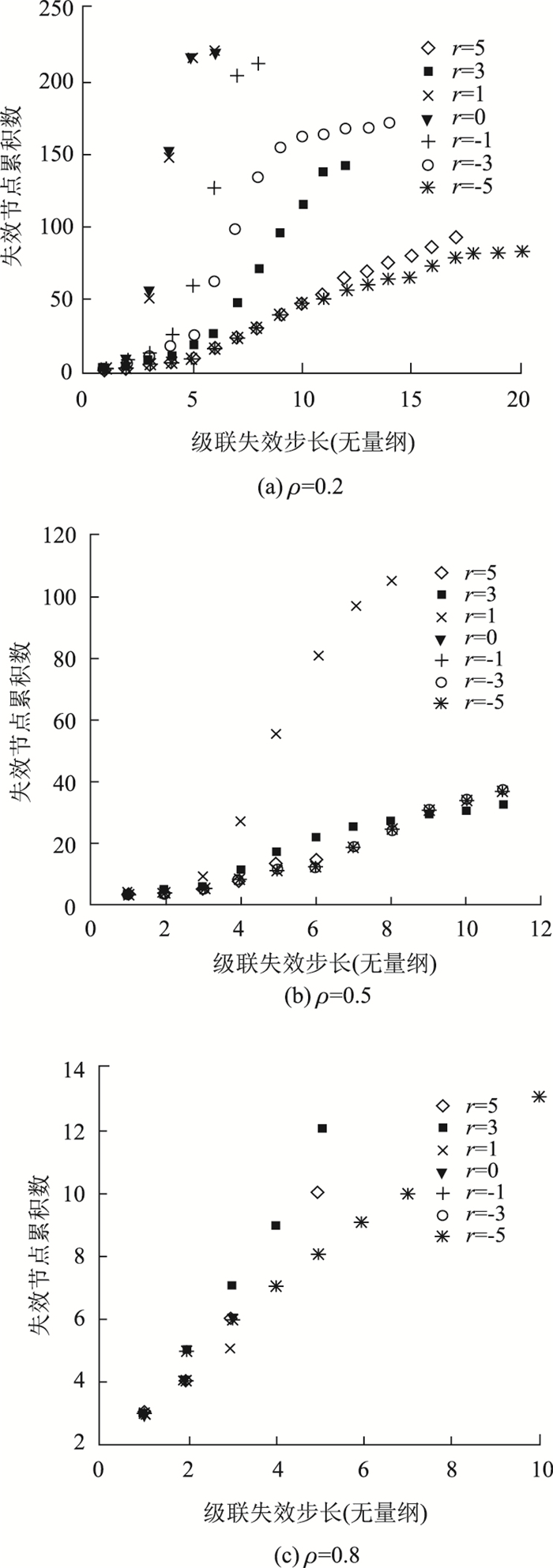
首先进行随机攻击,对不同载荷重分配策略下的网络抗毁性进行了仿真, 结果见图 2。由图 2可以发现,在网络容量固定的情形下,通过适当调节载荷再分配系数r(控制载荷分配的均匀性)可以保证网络的抗毁性处在一个较高的水平,即失效节点累积数相对较少, 大多数局部失效可以被系统吸收和消化,并不一定会导致级联失效。当ρ=0.2,r>0时,减小r的值会使网络失效的累积节点数上升,反映对网络的破坏程度变大;当r < 0时,继续减小r的值会使网络失效的累积节点数下降,网络的抗毁性得到了提升;当ρ=0.5时,r取较小的负数能很好地提升网络的抗毁性;当ρ=0.8时,由于容量的提升,失效节点累积数量变小,网络抗毁性更强,r取-3~0之间的值都会使网络的抗毁性提升,但超过了这个区间,局部失效就会产生并经过较小步长的蔓延。
|
| 图 2 随机攻击网络抗毁性 Fig. 2 Random attack network robustness |
| |
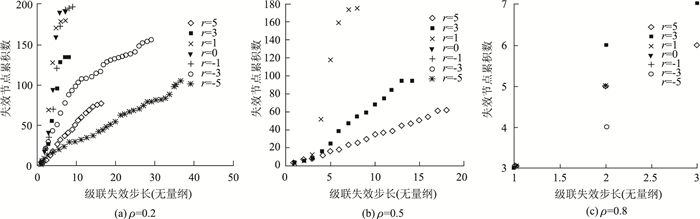
然后针对网络载荷较大节点蓄意攻击,得到不同载荷重分配策略下容量系数ρ分别为0.2,0.5,0.8时的网络抗击毁性仿真图(图 3)。由图 3同样可以发现,适当调节载荷再分配系数r也可以保证网络的抗毁性处在一个较高的水平,从而避免网络级联失效的大范围发生。对比同容量系数情况下的随机攻击与蓄意攻击发现,在容量系数较小的时刻(ρ < =0.5),随机攻击的级联失效步长明显小于蓄意攻击,而且累积失效节点数也相对偏少,但当容量系数较大的时刻(ρ=0.8),蓄意攻击的级联失效步长小于随机攻击,而且失效节点累积数也相对偏少,发生这样的情况主要是因为网络的拓扑特性造成的。当展开蓄意攻击的时候,攻击的都是载荷较大的节点。按照节点载荷计算公式可以发现,这样的点度数都相对比较大,即它的邻居节点相对较多,这样其载荷在重新非配时就更为分散,每个邻居节点分配的载荷相对就会较少,而邻居节点容量相对较大,故而不容易触发进一步失效。随机攻击却因为攻击的节点载荷重新分配到较少的邻居节点而相对容易使得邻居节点载荷超出其容量,引发局部失效,但这个过程也不会太长,很快就会因为节点容量系数大而被系统吸收消化。
|
| 图 3 蓄意攻击网络抗毁性 Fig. 3 Intentional attack network robustness |
| |
3 结论
在对复杂网络系统级联失效及演化机理的研究过程中,过载机制得到了更好的研究应用,但在载荷重新分配的策略上,经典模型和方法要么是将失效节点载荷随机分配到其他节点上,要么是均匀分配到其他节点上,更有将其分配到剩余节点上的全局分配策略。这些方法在各自研究的问题上有合理性,但针对城市交通网络并不完全适用,城市交通网络在节点失效时只能够采用近邻分配策略。本研究基于这一特点,提出了堵塞失效节点载荷再分配的可调分配策略,并进行了数值仿真,针对仿真结果进行了分析。从仿真的结果可以发现,交通堵塞载荷再分配策略的确能对网络的抗毁性产生影响。诚然,容量系数ρ在较大的时候,城市交通网络抗毁性会更强,但现实生活中,人们由于各种条件的限制,不可能无限制地加大容量系数ρ,因此只能在有限的范围内增加它。这样在网络规模和容量系数已定的情况下,可以针对载荷再分配的均匀性进行控制来提升网络抗毁性,避免网络级联失效发生,保障城市交通良好运行。
本研究有利于城市交通管理部门针对相应的城市交通网络展开交通堵塞载荷的再分配控制,不管是随机的节点失效还是载荷大的节点失效,都可以通过调节载荷再分配系数来有效提升城市交通网络抗毁性,保障城市交通,具有广阔的应用前景。目前研究的网络属于无向赋权网络,而现实中有些网络是带有方向性的,尤其是城市群复合交通网络更为复杂,影响更为广泛,城市群复合有向赋权网络的载荷再分配策略将是后续的研究方向。
| [1] |
NEWMAN M E J. The Structure and Function of Complex Networks[J]. SIAM Review, 2003, 45(2): 167-256. |
| [2] |
WATTS D J, STROGATZ S H. Collective Dynamics of "Small-world" Networks[J]. Nature, 1998, 393: 440-442. |
| [3] |
BARABASI A L, ALBERT R. Emergence of Scaling in Random Networks[J]. Science, 1999, 286(5439): 509-512. |
| [4] |
WANG S B, ZHAO J L. Multi-attribute Integrated Measurement of Node Importance in Complex Networks[J]. Chaos:An Interdisciplinary Journal of Nonlinear Science, 2015, 25(11): 113105. |
| [5] |
谭跃进, 吴俊, 邓宏钟, 等. 复杂网络抗毁性研究综述[J]. 系统工程, 2006, 24(10): 1-5. TAN Yue-jin, WU Jun, DENG Hong-zhong, et al. Invulnerability of Complex Networks:A Survey[J]. Systems Engineering, 2006, 24(10): 1-5. |
| [6] |
汪秉宏, 周涛, 何大韧. 统计物理与复杂系统研究最近发展趋势分析[J]. 中国基础科学, 2005, 7(3): 37-43. WANG Bing-hong, ZHOU Tao, HE Da-ren. The Trend of Recent Research on Statistical Physics and Complex Systems[J]. China Basic Science, 2005, 7(3): 37-43. |
| [7] |
ALBERT R, JEONG H, BARABASI A L. Error and Attack Tolerance of Complex Networks[J]. Nature, 2000, 406(6794): 378-382. |
| [8] |
MOTTER A E. Cascade Control and Defense in Complex Networks[J]. Physical Review Letters, 2004, 93(9): 098701. |
| [9] |
CRUCITTI P, LATORA V, MARCHIORI M. A Model for Cascading Failures in Complex Networks[J]. Physical Review E:Statistical Nonlinear & Soft Matter Physics, 2003, 69(4): 045104. |
| [10] |
何斌, 王若恩. 物元演绎推理[J]. 系统工程理论与实践, 1998, 18(1): 85-92. HE Bin, WANG Ruo-en. Matter-element Deductive Inference[J]. Systems Engineering-Theory & Practice, 1998, 18(1): 85-92. |
| [11] |
周鸣争, 杨益民. 菱形思维的可拓神经网络实现[J]. 系统工程理论与实践, 2000, 20(6): 123-130. ZHOU Ming-zheng, YANG Yi-min. Implementation of Extension Neural Network for Rhombus-thinking Process[J]. Systems Engineering Theory & Practice, 2000, 20(6): 123-130. |
| [12] |
洪筠, 张波. 仿生生物信息可拓数据挖掘研究[J]. 情报科学, 2009(4): 622-625. HONG Yun, ZHANG Bo. Biological Information of Bionics and Extension Data Mining[J]. Information Science, 2009(4): 622-625. |
| [13] |
陈文伟. 基于本体的可拓知识链获取[J]. 智能系统学报, 2007, 2(6): 68-71. CHEN Wen-wei. Acquisition of an Extensional Knowledge Chain Based on Ontology[J]. CAAI Transactions on Intelligent Systems, 2007, 2(6): 68-71. |
| [14] |
尹洪英, 权小锋. 交通运输网络级联失效影响规律及影响范围[J]. 系统管理学报, 2013, 22(6): 869-881. YIN Hong-ying, QUAN Xiao-feng. The Cascading Influence Law and Influence Scope of a Failure in Transportation Networks[J]. Journal of Systems & Management, 2013, 22(6): 869-881. |
| [15] |
MOTTER A E, LAI Y C. Cascade-based Attacks on Complex Networks[J]. Physical Review E:Statistical, Nonlinear, and Soft Matter Physics, 2002, 66(6): 065102. |
| [16] |
WANG B, KIM B J. A High-robustness and Low-cost Model for Cascading Failures[J]. Europhysics Letters, 2007, 78(4): 48001. |
| [17] |
LI P, WANG B H, SUN H. A Limited Resource Model of Fault-tolerant Capability Against Cascading Failure of Complex Network[J]. European Physical Journal B, 2008, 62(1): 101-104. |
| [18] |
黄英艺, 金淳, 荣莉莉. 考虑节点综合重要度的物流网络级联失效模型[J]. 运筹与管理, 2014(6): 108-114. HUANG Ying-yi, JIN Chun, RONG Li-li. Cascading Failure Model on Logistics Network Based on the Overall Importance of Nodes[J]. Operations Research and Management Science, 2014(6): 108-114. |
| [19] |
LEHMANN J, BERNASCONI J. Stochastic Load-redistribution Model for Cascading Failure Propagation[J]. Physical Review E:Statistical, Nonlinear, and Soft Matter Physics, 2010, 81(3): 031229. |
| [20] |
KIM D H, KIM B J, JEONG H. Universality Class of the Fiber Bundle Model on Complex Networks[J]. Physical Review Letters, 2005, 94(2): 025501. |
| [21] |
WANG W X, CHEN G. Universal Robustness Characteristic of Weighted Networks against Cascading Failure[J]. Physical Review E:Statistical, Nonlinear & Soft Matter Physics, 2008, 77(2): 026101. |
| [22] |
袁铭. 带有层级结构的复杂网络级联失效模型[J]. 物理学报, 2014, 63(22): 73-80. YUAN Ming. A Cascading Failure Model of Complex Network with Hierarchy Structure[J]. Acta Physica Sinica, 2014, 63(22): 73-80. |
| [23] |
AILING H, MICHAEL Z H, WEI G, et al. Cascading Failures in Weighted Complex Networks of Transit Systems Based on Coupled Map Lattices[J]. Mathematical Problems in Engineering, 2015, 2015: 1-16. |
 2019, Vol. 36
2019, Vol. 36
