扩展功能
文章信息
- 何雅琴, 容煜伦, 柳祖鹏, 杜胜品
- HE Ya-qin, RONG Yu-lun, LIU Zu-peng, DU Sheng-pin
- 基于车速比的城市交通事故交通影响程度评价
- Evaluation of Traffic Influence Degree of Urban Traffic Accident Based on Speed Ratio
- 公路交通科技, 2019, 36(5): 91-97
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(5): 91-97
- 10.3969/j.issn.1002-0268.2019.05.013
-
文章历史
- 收稿日期: 2017-12-04
城市道路交通事故的发生除了造成人员伤亡和财产损失外,也会使道路通行能力降低,造成交通拥堵甚至大范围的交通受阻,而在交通事故的处置过程中,良好的交通系统是保证及时救援的重要条件。基于此,分析城市道路交通事故对交通的影响程度,制订有效的应急措施,显得尤为重要。
交通事件对交通的影响研究分定性和定量两个方面[1-6],而定量研究主要集中在影响时间和影响范围。文献[7]采用排队论研究了交通事件背景下的交通流运行特性。文献[8]利用加速失效时间模型构建了事故持续时间模型。文献[9-10]构建了参数加速失效时间生存模型,对快速路交通事件影响时间进行了研究。文献[11]建立了交通事件持续时间的竞争风险混合模型。文献[12]利用生存模型研究了事故清理时间。文献[13]利用交通波理论,对交通事件下的车流集结排队和消散过程的变化进行了分析。文献[14]建立了高速公路事故持续时间多元线性回归模型。文献[15]建立了时变的拥堵蔓延速度模型,对交通事件拥堵蔓延疏散的时空范围进行了研究。文献[16]基于非参数回归方法,对交通事件影响范围进行了预测。文献[17]利用随机生存森林模型研究了快速路交通事件持续时间。
上述研究中多以高速公路和快速路为研究对象,缺少对城市道路的研究。而城市道路由于节点多,一旦发生交通事故,若处理不及时,排队车辆会向四周扩散而非仅仅沿主线延伸,以至于影响整个周边路网的交通运行,这与向水里扔石头产生的水波涟漪现象类似[18]。水波涟漪现象是指往平静的湖水中扔一块石头,产生的水波会均匀向外传播,传播过程中能量减小,使得传播速度逐渐降低,影响逐渐减小。城市道路上的交通事故带来的影响与水波涟漪效应类似,也会向外传播,且影响会逐渐衰减。基于此,本研究类比水波涟漪现象,利用事故发生后和无事故时的道路车速比值来分析交通事故的交通影响。
1 交通影响分析 1.1 交通影响系数提出定量指标“交通影响系数”来表征交通事故的交通影响,定义为交通事故发生后某一瞬时,影响区域内道路上某一断面面向事故点行驶方向的平均车速与正常运行状态下该断面同方向的平均车速的比值,用γ表示。
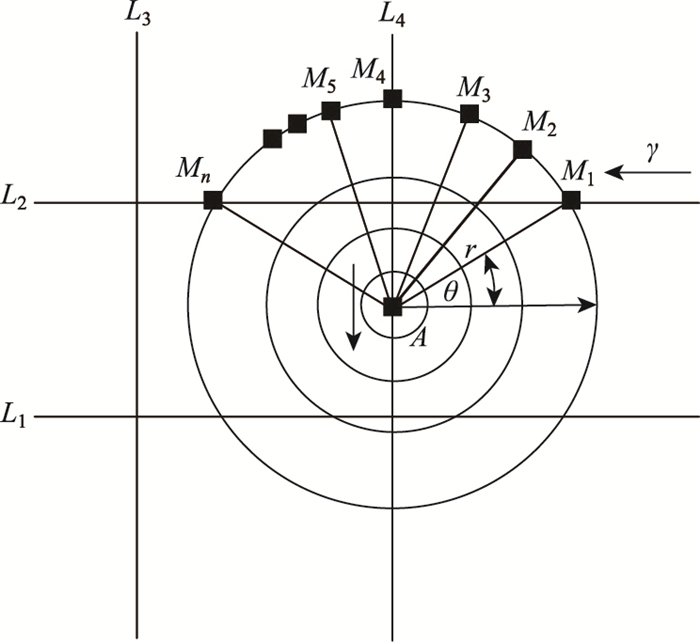
基于水波涟漪现象,交通事故对交通的影响形式可以表示为以事故地点为圆心的同心圆环,如图 1所示。道路用Li表示,事故地点为A,离事发点A距离(圆环半径)为r,极角为θ的道路断面用Mi表示。如无其他因素干扰, 则事故发生后t时刻,断面M1(半径为r,极角为θ)的瞬时交通影响系数为γr, θ(t),γr, θ(t)∈[0, 1],其中t∈[0, T];r∈[0, R];T为事故的影响时间;R为事故影响范围半径。γr, θ(t)越大,表示影响越小,反之亦然。
|
| 图 1 交通事故影响示意图 Fig. 1 Schematic diagram of influence of traffic accident |
| |
1.2 基本交通影响系数分析
假设图 1中圆环上每个点都认为是一个道路断面,则t时刻半径为r的圆环上的n个断面M1,M2,…,Mn的交通影响系数γM1(r, t),γM2(r, t),…,γMn(r, t)显然是不同的,这种不同是方向(极角θ)的不同引起的,但在实际路网下主要是由于该断面受影响的车辆数不同造成的。为了简化计算,提出“交通量修正系数λ”对极角θ进行修正,其定义为从某断面驶向事故点的车辆数与该断面面向事故点方向总行驶车辆数的比值。因此,在不考虑方向,只考虑时间和距离的情况下,t时刻半径为r的圆环上各断面的基本交通影响系数γ(r, t)为:
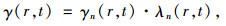
|
(1) |
式中,γ(r, t)为半径为r的断面基本交通影响系数;γn(r, t)为半径为r的断面n的实测交通影响系数;λn(r, t)为半径为r的断面n的交通量修正系数,是与时间有关的变量。
则在ti时刻,半径为rj的断面交通影响系数γ(rj, ti)为:
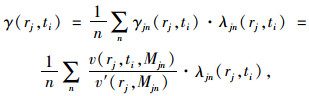
|
(2) |
式中,γ(rj, ti)为ti时刻半径为rj的断面交通影响系数,也是半径为rj的圆环在ti时刻的平均交通影响系数;λjn(rj, ti)为事故发生后ti时刻,半径为rj环上Mn断面的交通量修正系数;v(rj, ti, Mjn)为事故发生后ti时刻,半径为rj环上Mn断面的平均车速;v′(rj, Mjn)为正常状态下,半径为rj环上Mn断面的平均车速。
根据调查所得的车速和交通量数据,可以计算得到一系列的γ(rj, ti)值,从而构建出瞬时交通影响系数γ的函数:
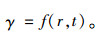
|
(3) |
首先假定某一类型的交通事故作为建模的基础,其条件为发生时间为高峰期间两车追尾,事故地点处于两交叉口之间路段中间位置,路段单向3车道,事故占用道路1条车道(最内侧车道),无人员伤亡,道路中间有分隔带,选取与假定事故条件类似的35起事故数据进行分析建模。筛选出事故各影响路段事发当天及事故前10 d的每5 min为间隔的车速(面向事故方向)。将事故开始时刻所在的5 min间隔记为0时刻,以此类推,得到事故发生后各影响路段每5 min为间隔的平均车速;将事故前10 d对应时刻的车速平均值作为正常运行状态下的车速,从而得到各影响路段每5 min为间隔的事故发生后与无事故发生时的车速比值,然后根据各断面的交通量修正系数λ(为了简化计算,此处λ取定值),得到每5 min为间隔的各点的基本交通影响系数,即得到一系列的γ(ri, tj)值。
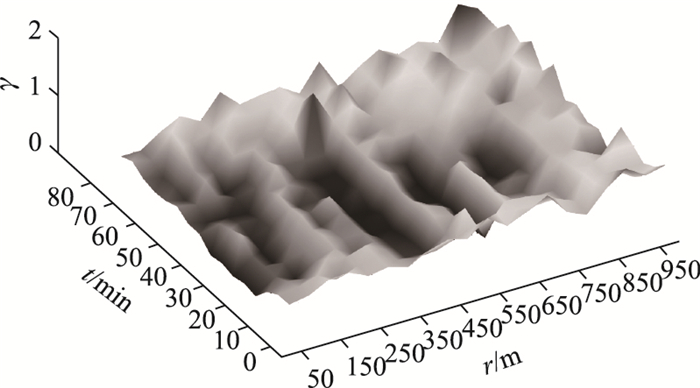
2.1.2 模型构建利用MATLAB绘制γ(ri, tj)的时空分布图,如图 2所示。
|
| 图 2 γ的时空分布 Fig. 2 Time-space distribution of γ |
| |
图 2中极少数点的γ值会出现大于1的情况。原因的一方面是这些点受影响的开始时刻有延迟或提前恢复交通,另一方面是由于车速会受到除交通事故外很多其他不确定因素的影响,从而造成事发前10 d某时刻的平均车速偏低,导致γ值大于1,与理论不符。为了能够对该图像进行拟合,构建数学模型,先分别观察γ与r和t的大致变化规律,在此采取控制变量法,对各影响点系数值分别进行逐步平均。
(1) γ与r的关系
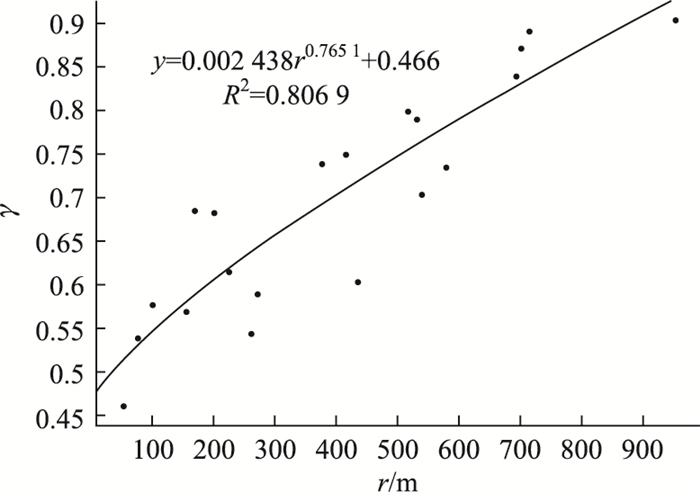
对同一距离r的影响点不同时刻的影响系数取平均值,可以得到γ与r的关系图,如图 3所示。可以发现两者呈幂函数关系,距离事发点距离越远,γ越大,交通影响越小。
|
| 图 3 γ与r的关系 Fig. 3 Relationship between γ and r 注:R2为决定系数,判定曲线拟合程度指标。 |
| |
(2) γ与t的关系
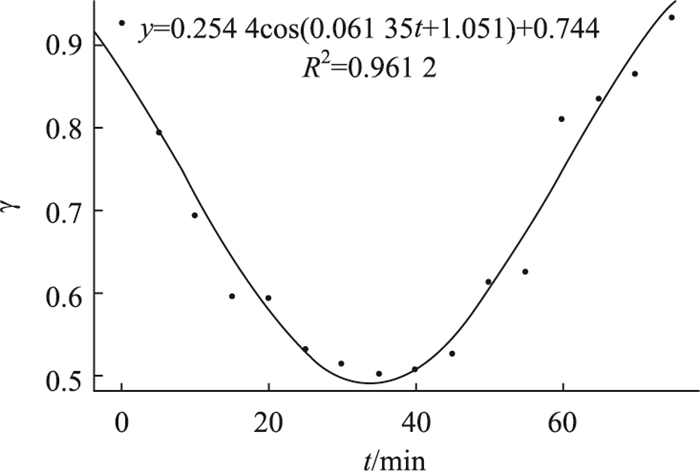
对同一时间t的各影响点的影响系数取平均值,可以得到γ与t的关系图,如图 4所示。随着时间t的增加,γ值逐渐减小直至达到最低点,随后又逐渐增大至接近于1。这主要是由于事故刚发生时,影响有延迟性,车速不可能立即减小至0,随着后续到达排队车辆越来越多,车速降至最低,而后交通疏导措施的介入使得交通慢慢恢复。
|
| 图 4 γ与t的关系 Fig. 4 Relationship between γ and t |
| |
(3) γ与r和t的关系
根据上述γ与r和γ与t的关系曲线,在MATLAB中输入三角函数与幂函数的组合模型,对图 2中曲面进行拟合,拟合结果见图 5和式(4)。
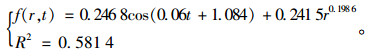
|
(4) |

|
| 图 5 γ与r及t的关系 Fig. 5 Relationship among γ, r and t |
| |
从图 5中可以发现,交通影响系数与时间总体上先减小直至最低点,然后再逐渐恢复至正常状态,而随着距离的增加,交通影响系数整体向上增长。
2.2 事件源修正构建上述γ=f(r, t)模型时仅仅考虑了车速和交通量,但是每起事故特性的差异性(如事故占道情况、事故延迟时间差异)也会使造成的交通影响不尽相同,因此,需要引入系数β对事件源进行修正,即有:
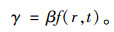
|
(5) |
β主要与事件伤亡情况,延迟时间、事件占道情况有关。此处仅考虑不同事故占道情况对交通的影响差异,反映为事故发生后事故点剩余通行能力的差异性。根据城市道路车道利用系数(表 1)[19]及车道数修正系数(表 2),可以计算事故下的有效通行能力比例。例如,单向3车道路段,事故占用车道①,则有效通行能力的比例为(0.845+0.675)/ 2.57=0.591。按照相同的方法得到各种占道情况下的有效通行能力比例,结果见表 3。
| 车道 | ① | ② | ③ | ④ |
| 车道利用系数 | 1 | 0.8~0.89 | 0.65~0.70 | 0.5~0.65 |
| 平均值 | 1 | 0.845 | 0.675 | 0.575 |
| 注:从道路中心线到路边依次为车道①,②,③,④。 | ||||
| 车道数 | 1 | 2 | 3 | 4 |
| 车道数修正系数 | 1 | 1.8~1.89 | 2.5~2.63 | 3.07~3.22 |
| 平均值 | 1 | 1.85 | 2.57 | 3.15 |
| 单向车道数 | 2 | 3 | 4 | |
| 事故占用车道情况 | ① | 0.457 | 0.591 | 0.665 |
| ② | 0.541 | 0.65 | 0.714 | |
| ③ | — | 0.718 | 0.768 | |
| ④ | — | — | 0.8 | |
| ①② | 0 | 0.263 | 0.397 | |
| ②③ | — | 0.389 | 0.5 | |
| ③④ | — | — | 0.586 | |
| ①②③ | — | 0 | 0.183 | |
| ②③④ | — | — | 0.317 | |
用表 3中所得各种情况下有效通行能力比例除以建模采用的特定事故(3车道占用车道①)的有效通行能力比例(0.591),得到不同占道情况下的事故源修正系数β,结果见表 4。
| 单向车道数 | 2 | 3 | 4 | |
| 事故占用车道情况 | ① | 0.773 | 1.000 | 1.125 |
| ② | 0.915 | 1.100 | 1.208 | |
| ③ | — | 1.215 | 1.299 | |
| ④ | 0.000 | — | 1.354 | |
| ①② | — | 0.445 | 0.672 | |
| ②③ | — | 0.658 | 0.846 | |
| ③④ | — | — | 0.992 | |
| ①②③ | — | 0.000 | 0.310 | |
| ②③④ | — | — | 0.536 | |
2.3 综合交通影响程度分析
突发事件交通影响程度是指事件对周边路网的综合交通影响程度,用γtotal表示,定义为在交通事故影响时空区域各影响断面交通影响程度的平均值。虽然在实际路网下不是所有影响点都对应道路,但是为了简化计算模型,在此假设各影响点是连续的,则γtotal可以用下式表示:
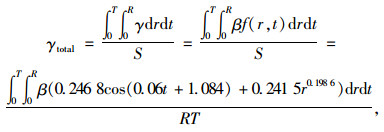
|
(6) |
式中,γtotal为综合交通影响程度,γtotal∈[0, 1];S为表示时空曲面在r-t平面的投影面积,S=RT;R为事故影响范围半径;T为事故的影响时间; β为事件源修正系数;γ为理想交通影响系数,是关于r和t的函数。
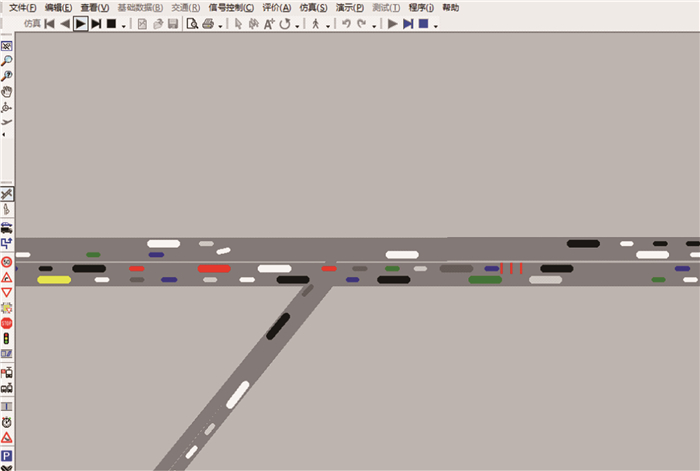
3 案例分析 3.1 案例背景假设有一起两车追尾事故发生在某双向4车道路段上,事故占用了中间车道①,该事故持续时间20 min。采用VISSIM仿真软件对该事故进行交通模拟,交通事故则利用信号控制来实现。给定运行时间4 800 s为周期;0~1 200 s和2 400~4 800 s为绿灯时间,分别表示事故未发生和已经结束;1 200~2 400 s为红灯时间,代表事故延迟时间。设置3组信号灯,表示事故车辆所占用的道路长度(图 6)。在事故周边道路断面设置数据采集点,收集通过各断面的车辆的车速数据。
|
| 图 6 仿真运行图 Fig. 6 Running simulation graph |
| |
3.2 综合影响程度计算
方法1: 对仿真所得车速数据按照上文所述方法进行处理分析,用MATLAB构建模型,可得到式(7)。
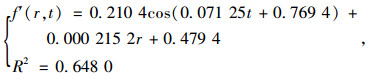
|
(7) |
式中f′(r, t)为由仿真数据构建的γ与t, r的函数。
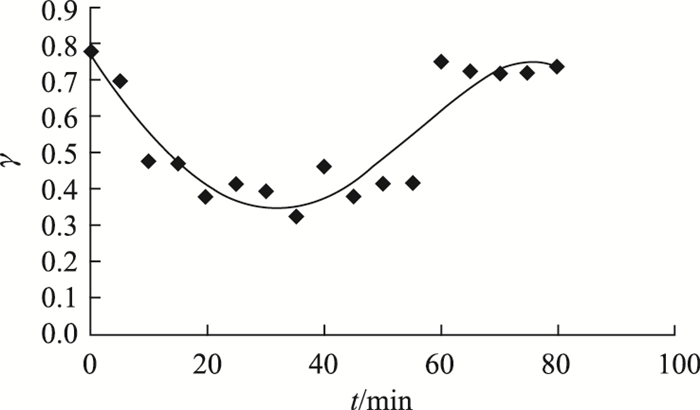
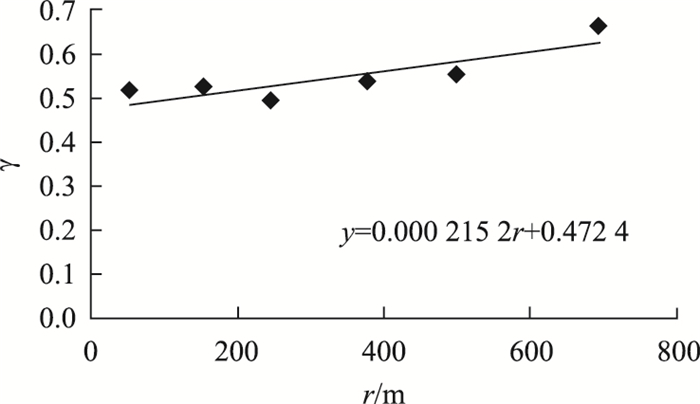
同时可根据γ与t(图 7)、γ与r的关系曲线(图 8),令γ=1,得到R为2 451 m,T为70 min。则交通事故的综合影响程度值为:
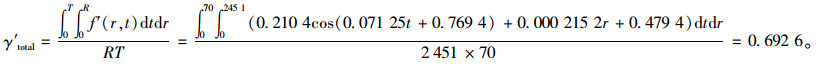
|
(8) |
|
| 图 7 γ随t的变化曲线 Fig. 7 Relationship between γ and t |
| |
|
| 图 8 γ随距离的变化图 Fig. 8 Relationship between γ and distance |
| |
方法2: 根据表 4中修正系数,可取β值为0.773,由上文所构建的基准模型(式6)来求解,则有:
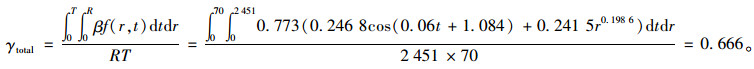
|
(9) |
从上述计算结果(0.648和0.666)可以认为该起事故对交通系统影响一般,与事故仿真运行状态基本一致。虽然两种方法计算值存在一定的误差(3.8%),但是误差在可以接受的范围。因此,本研究所构建的交通影响程度评价模型是可行的。
4 结论(1) 本研究借助于水波涟漪现象,采用事故发生后和无事故时道路平均车速的比值建立了交通影响系数模型,采用车道利用系数计算得到了不同事故占道情况下的事故源修正系数,最后利用二重积分得到了交通影响程度值。与影响时间和影响范围相比,该值不仅能更直观地体现交通事故的交通影响,而且能够为评价交通应急级别并采取相应等级的应急对策提供更直接的依据。
(2) 在建模时给定了一些假设条件,且事故样本较少,造成模型精度不高,给模型的实际应用带来一定的局限性,如何消除假设引起的误差,提高模型精度还有待更进一步的研究。
(3) 事件源修正系数取值仅考虑事故占道情况,根据车道利用系数计算得到,只适用于单向不多于4车道的城市道路,且对于所有车道被占用的事故不适用,没有考虑事故其他特性的差异性。因此,如何得到精确的事件源修正系数也将是下一步的研究重点。
(4) 本研究仅根据构建的模型计算了交通事故交通影响程度值,对于划分事故交通影响等级区间,明确其交通影响等级还有待下一步的深入研究。
| [1] |
CHIEN S J, GOULIAS D G, YAHALON S, et al. Simulation-based Estimates of Delays at Freeway Work Zones[J]. Journal of advanced Transportation, 2002, 36(2): 131-156. |
| [2] |
余贵珍, 刘玉敏, 金茂菁. 基于交通波的高速公路事故的交通影响分析[J]. 北京航空航天大学学报, 2012, 38(10): 1420-1424. YU Gui-zhen, LIU Yu-min, JIN Mao-jing. Traffic Impact Analysis of Highway Accident Based on the Shockwave Theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(10): 1420-1424. |
| [3] |
俞斌, 陆建, 陶小伢. 道路交通事故的影响范围算法[J]. 城市交通, 2008, 6(3): 82-86. YU Bin, LU Jian, TAO Xiao-ya. Method to Determine the Influence Area of Street Accidents[J]. Urban Transport of China, 2008, 6(3): 82-86. |
| [4] |
马剑, 李文勇, 梁满朝. 基于卡尔曼滤波的交通突发事件影响范围预测研究[J]. 长沙大学学报, 2012, 26(5): 86-89. MA Jian, LI Wen-yong, LIANG Man-chao. Prediction of Traffic Emergency Impact Scope Based on Kalman Filtering[J]. Journal of Changsha University, 2012, 26(5): 86-89. |
| [5] |
丛浩哲, 王俊骅, 童世鑫. 高速公路网络交通突发事件辐射范围预测模型[J]. 同济大学学报:自然科学版, 2012, 40(3): 414-422. CONG Hao-ze, WANG Jun-ye, TONG Shi-xin. Prediction Model of Freeway Network Traffic Incident Radiation Scope[J]. Journal of Tongji University:Natural Science Edition, 2012, 40(3): 414-422. |
| [6] |
曹志远, 郭忠印, 张起森. 高速公路重大交通事故时空影响范围研究[J]. 公路工程, 2011, 36(6): 55-58. CAO Zi-yuan, GUO Zhong-yin, ZHANG Qi-sen. Research on Time and Spatial Extent of Terrible Traffic Accident on Highway[J]. Highway Engineering, 2011, 36(6): 55-58. |
| [7] |
BAYKAL-GURSOY M, XIAO W, OZBAY K. Modeling Traffic Flow Interrupted by Incidents[J]. European Journal of Operational Research, 2009, 195(1): 127-138. |
| [8] |
CHUNG Y. Development of an Accident Duration Prediction Model on the Korean Freeway Systems[J]. Accident Analysis & Prevention, 2010, 42(1): 282-289. |
| [9] |
HOJATI A T, FERREIRA L, WASHINGTON S, et al. Modelling Total Duration of Traffic Incidents Including Incident Detection and Recovery Time[J]. Accident Analysis & Prevention, 2014, 71: 296-305. |
| [10] |
HOJATI A T, FERREIRA L, WASHINGTON S, et al. Hazard Based Models for Freeway Traffic Incident Duration[J]. Accident Analysis & Prevention, 2013, 52: 171-181. |
| [11] |
LI R M, PEREIRA F C, BEN-AKIVA M E. Competing Risk Mixture Model and Text Analysis for Sequential Incident Duration Prediction[J]. Transportation Research Part C:Emerging Technologies, 2015, 54: 74-85. |
| [12] |
ALKAABI A, DISSANAYAKE D, BIRD R. Analyzing Clearance Time of Urban Traffic Accidents in Abu Dhabi, United Arab Emirates, with Hazard-based Duration Modeling Method[J]. Transportation Research Record, 2011, 2229: 46-54. |
| [13] |
孙明玲, 杨峰, 贝登荣. 基于交通波动理论的排队消散时效分析[J]. 公路交通科技, 2013, 30(10): 112-116. SUN Ming-ling, YANG Feng, BEI Deng-rong. Analysis of Queue Dissipation Time Effect Based on Traffic Wave Theory[J]. Journal of Highway and Transportation Research and Development, 2013, 30(10): 112-116. |
| [14] |
刘伟铭, 管丽萍, 尹湘源. 基于多元回归分析的事件持续时间预测[J]. 公路交通科技, 2005, 22(11): 126-129. LIU Wei-ming, GUAN Li-ping, YIN Xiang-yuan. Prediction of Incident Duration Based on Multiple Regression Analysis[J]. Journal of Highway and Transportation Research and Development, 2005, 22(11): 126-129. |
| [15] |
臧金蕊, 宋国华, 万涛, 等. 交通事件下快速路拥堵蔓延消散时空范围模型[J]. 交通运输系统工程与信息, 2017, 17(5): 179-185. ZANG Jin-rui, SONG Guo-hua, WAN Tao, et al. A Temporal and Spatial Model of Congestion Propagation and Dissipation on Expressway Caused by Traffic Incidents[J]. Journal of Transportation System Engineering and Information Technology, 2017, 17(5): 179-185. |
| [16] |
荣福香, 齐月荣, 蔡琳琳. 基于非参数回归的交通事件影响范围预测[J]. 测绘与空间地理信息, 2015, 38(8): 102-103. RONG Fu-xiang, QI Yue-rong, CAI Lin-lin. Calculate the Affected Area of Traffic Incident Base on Non-parametric Regression[J]. Geomatics and Spatial Information Technology, 2015, 38(8): 102-103. |
| [17] |
高珍, 柯阿香, 余荣杰, 等. 基于随机生存森林的交通事件持续时间预测[J]. 同济大学学报:自然科学版, 2017, 45(9): 1304-1310. GAO Zhen, KE A-xiang, YU Rong-jie, et al. Urban Expressway Traffic Incident Duration Prediction Based on Random Survival Forests[J]. Journal of Tongji University:Natural Science Edition, 2017, 45(9): 1304-1310. |
| [18] |
何雅琴, 容煜伦, 柳祖鹏, 等. 基于水波原理的城市突发事件交通影响程度研究[J]. 交通运输系统工程与信息, 2017, 17(5): 151-156. HE Ya-qin, RONG Yu-lun, LIU Zu-peng, et al. Traffic Influence Degree of Urban Traffic Emergency Based on Water Wave Principle[J]. Journal of Transportation System Engineering and Information Technology, 2017, 17(5): 151-156. |
| [19] |
王玮, 过秀成. 交通工程学[M]. 2版. 南京: 东南大学出版社, 2011. WANG Wei, GUO Xiu-cheng. Traffic Engineering[M]. 2nd ed. Nanjing: Southeast University Press, 2011. |
 2019, Vol. 36
2019, Vol. 36
