扩展功能
文章信息
- 梁志磊, 宋一凡, 闫磊
- LIANG Zhi-lei, SONG Yi-fan, YAN Lei
- 悬索桥基准索股定位与调整方法研究
- Study on Positioning and Adjusting Method of Datum Strands for Suspension Bridge
- 公路交通科技, 2019, 36(5): 84-90
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(5): 84-90
- 10.3969/j.issn.1002-0268.2019.05.012
-
文章历史
- 收稿日期: 2018-04-26
悬索桥基准索股线形的控制是施工控制的关键环节。然而施工现场的索股线形随着温度、跨度(塔偏)和高差(主塔预抬量)的变化而变化,且调索时需要根据当前测定参数在短时间内进行索长调整,即悬索桥基准索股架设控制计算有两大关键点,一是快速确定当前条件下索股理论垂度;二是根据实测垂度与理论垂度之差快速计算索长调整量。
目前,基准索股线形控制计算普遍采用的方法[1-7]是:先用解析法软件计算设计空缆状态下的索股线形,然后运用抛物线理论推导索股跨中标高在温度、跨度、高差变化下的影响公式和无应力索长对跨中标高的影响公式。已有研究[6-8]指出对于矢跨比适中的索股,抛物线公式能保证计算精度,但是当矢跨比较小或较大时,误差较大。
有学者[9-13]基于悬链线理论推导了索股跨中垂度影响公式和调索公式,因为公式中含有参数c,c为变量,且与索股两端水平力有关,需迭代求解[7, 14],所以公式推导在有些情况下也无法获得精确结果。
无论抛物线公式还是悬链线公式,均无法考虑索鞍切点位置的变化,而现场实际中,随着索股温度、跨度、高差的变化,索股在鞍槽内切点的位置也在变化,因此建立基于悬链线理论考虑索鞍切点位置变化的索股跨中标高影响公式和调索公式,势在必行。
文献[8]提出了一种考虑索鞍切点修正的索股线形计算方法,具有较高的精度,但实际运用时其迭代过程较复杂。本文对其迭代过程进行了优化,提出一套高效的索股线形计算方法,并在此基础上建立基于悬链线理论的索股跨中标高影响公式和调索公式,从而总结出一套实用、高效的基准索股施工控制计算方法。
1 考虑切点变化的悬链线索股线形求解法在索鞍预偏量计算确定的情况下,根据两索鞍控制点间无应力长度不变原理,通过迭代索股在鞍槽内的切点位置,使得索端力倾角与索鞍圆弧切点的切线角相吻合,则切点位置确定。然后根据切点与索鞍控制点的几何关系和悬索段平衡方程可确定任意里程处索股的高程。
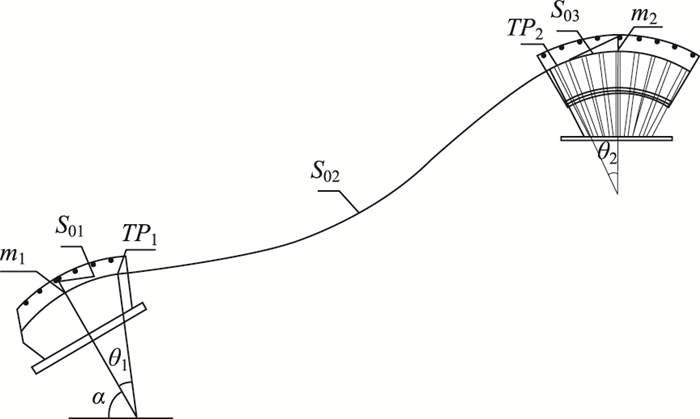
1.1 计算思路及流程根据两索鞍控制点间索股无应力长度S0不变原理,将相邻两索鞍间的索股分成3段,索鞍控制点m1与切点PT1之间索段长度为S01,切点TP1与切点TP2之间自由悬挂的索段长度为S02,切点TP2与索鞍控制点m2之间索段长度为S03,假定索段S01和S02的有应力长度等于无应力长度(经计算,空缆状态二者相差很小,误差可忽略不计),则S0=S01+S02+S03。对相邻切点间的自由悬挂索股段S02,当两端点间水平距离l、高差h和无应力索长S02确定时,索股线形唯一,并满足式(1)、式(2)组成的悬链线方程组[15]。索股切点分段计算如图 1所示。通过迭代S01,S03长度,修正切点位置,当索鞍切点处切线角与索股索端力倾角相一致时,就确定了切点位置。然后根据悬链线线形公式[14, 16]即可确定任意里程处索股的高程。
|
| 图 1 索股切点分段计算简图 Fig. 1 Segmented calculation diagram of cable strands at tangent points |
| |
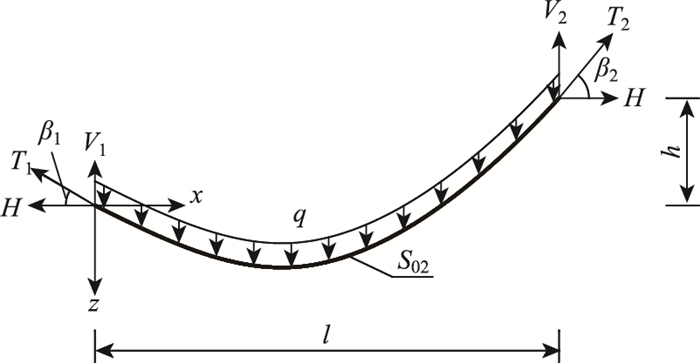
悬链线索股计算模型如图 2所示,索的自重均布荷载为q,无应力长度为S02,抗拉刚度为EA,两支点跨度为l,高差为h,水平张力为H。索股左端竖向反力为V1,索力与水平方向夹角为β1。索股右端竖向反力为V2=qS02-V1,索力与水平方向夹角为β2。则满足边界条件的曲线表达式为:
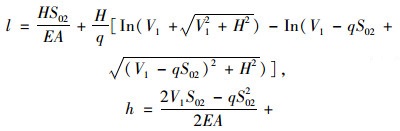
|
(1) |
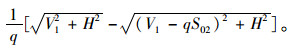
|
(2) |
|
| 图 2 悬链线索股计算模型 Fig. 2 Catenary cable calculation model |
| |
自由悬索,以左端点为原点,建立直角坐标系,如图 2所示悬链线索股计算模型,则悬索的线形方程为:
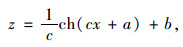
|
(3) |
式中,c=q/H; a,b为积分常数,与悬索的边界条件有关。
在图 2所示的坐标系中,将x=0,z=0代入式(3)得:
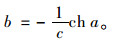
|
(4) |
将x=l,z=h代入式(3)得:
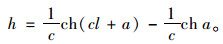
|
(5) |
变换式(5)得:
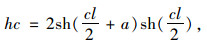
|
(6) |
则:
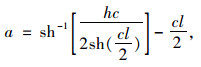
|
(7) |
因此:
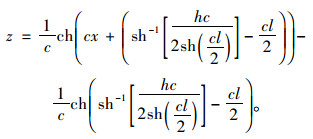
|
(8) |
具体计算如下:(1)以悬索桥成桥状态切点位置及S01,S03为初值,计算S02,h,l;(2)将S02,h,l,q代入非线性方程组(1)、(2),迭代求解索端力H和V1,从而求得索股端点处切线与水平方向夹角β1和β2;(3)分别将β1与90°-α-θ1,β2与θ2进行比较,若二者差值大于10-3,则修正θ1,θ2及S01,S03,回到步骤(1)重新进行计算;直到β1与90°-α-θ1, β2与θ2的差值小于10-3,此时的TP1, TP2即为当前状态下索股与索鞍的切点位置。切点位置确定后,根据式(8)就可以确定基准索股任意点的坐标。
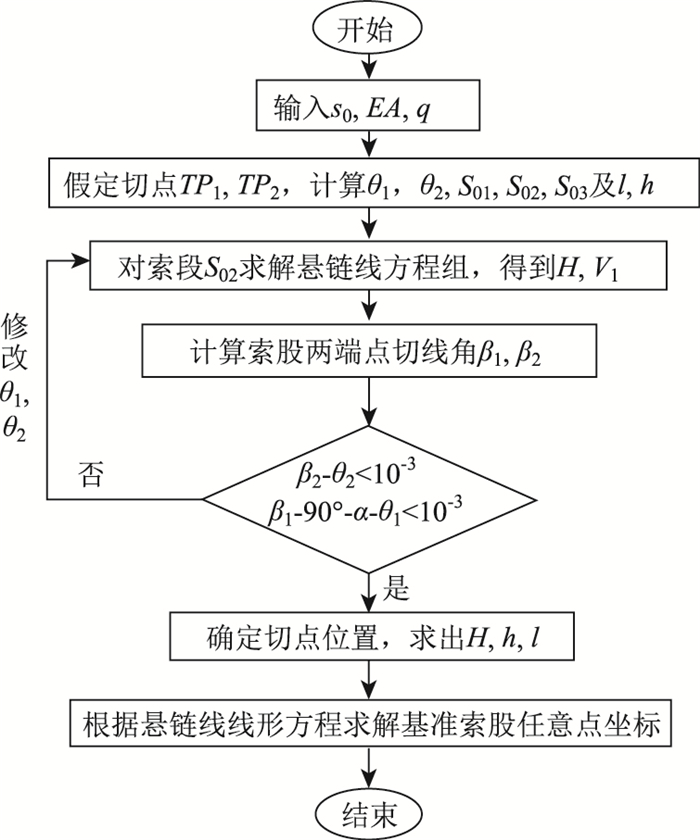
基准索股线形求解法的计算流程如图 3所示,根据计算流程运用MATLAB语言可编写索股线形求解程序。
|
| 图 3 考虑切点变化的索股线形求解法计算流程 Fig. 3 Calculation process of cable strand geometric shape considering change of tangent point |
| |
1.2 算例验证
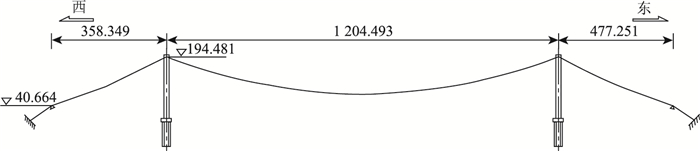
为验证本文基准索股线形求解法的正确性,以图 4所示的某悬索桥为例,计算空缆线形。该桥基准索股参数如下:截面积为2.697×10-3 m2,线荷载为0.207 2 kN/m,弹性模量为2.0×108 kN/m2。空缆状态西索鞍西偏1.697 m,东索鞍东偏2.796 m,基准索股西边跨、中跨无应力长度分别为388.674, 1 230.87 m。
|
| 图 4 某悬索桥空缆状态布置图 (单位:m) Fig. 4 Free cable state layout of a suspension bridge (unit: m) |
| |
线形计算结果与设计悬链线空缆线形比较见表 1。从表 1可以看出本文计算结果与设计结果吻合较好,证明了本文方法具有较高的精度。
| 纵桥向位置 | 本文求解法高程/m | 设计悬链线空缆高程/m | 误差/mm | 误差/% | |
| 西边跨 | L/4 | 109.936 0 | 109.932 2 | 3.8 | 0.003 5 |
| 跨中 | 82.324 0 | 82.319 0 | 5 | 0.006 1 | |
| 3L/4 | 109.841 1 | 109.837 2 | 3.9 | 0.003 6 | |
| 中跨 | L/4 | 71.895 3 | 71.890 1 | 5.2 | 0.007 2 |
| 跨中 | 108.435 9 | 108.429 0 | 6.9 | 0.006 4 | |
| 3L/4 | 149.806 6 | 149.801 5 | 5.1 | 0.003 4 | |
| 注:L为悬索桥各跨跨径。 | |||||
2 基于悬链线理论的索股跨中标高影响公式和调索公式
索股线形的调整采用垂度调整法[6, 17-18],一般在夜间环境稳定时进行,每次调整之前需要对当前条件下相关几何参数进行重新测定,然后计算索股的跨中理论标高,再根据实测标高与理论标高的差值计算索鞍处索长调整量,以使基准索股线形满足要求,即悬索桥基准索股架设控制计算有两大关键点:一是快速确定当前条件下索股理论垂度;二是根据实测垂度与理论垂度之差快速计算索长调整量。
为了减少现场重复调索工作,提高基准索股架设的精度和效率,运用本文考虑索鞍切点变化的悬链线索股线形求解程序,进行参数分析,确定索股跨中标高影响系数,建立索股跨中标高影响公式和调索公式,现场可方便快捷地实现索股架设线形的定位。
2.1 跨中标高影响公式由式(8)可知,索股任意一点的标高z与参数c,l和h有关,而c与式(1)、(2)中的l,h,S有关,需迭代求解。根据无应力长度不变原则,S随着现场温度T的变化而发生变化,且温度变化会改变索塔的高度。因此影响索股任意一点标高z的因素是:索股两端点的跨度l、高差h和温度T。
把索股跨中标高z0.5l看做l,h,S的函数,且l,h,S为相互独立变量,则有:
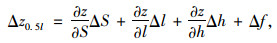
|
(9) |
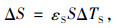
|
(10) |
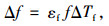
|
(11) |
式中,z0.5l为参数变化引起索股跨中标高的变化量;ΔS为温度变化引起的索长变化;Δl为桥塔偏位、温度变化引起的索跨度的变化;Δh为桥塔预抬高及不均匀温度引起的索两端高差的变化;Δf为平均温度变化引起的索鞍控制点高程的变化;S, f分别为基准温度下索股的无应力长度和索鞍以下桥塔的高度;εS, εf分别为索股温度膨胀系数、桥塔温度膨胀系数;ΔTS, ΔTf分别为索股平均温度变化量、桥塔平均温度变化量。
式(9)即基准索股跨中标高变化量Δz0.5l的影响公式,ΔTS,Δl,Δh和ΔTf为影响因素,而∂z/∂S,∂z/∂l,∂z/∂h为基于悬链线理论考虑索鞍切点变化的索股跨中标高影响系数。
影响系数的取值通过索股线形求解程序进行参数分析,建立影响系数与影响因素的关系曲线。其中,索股温度变化引起索股长度的变化,但索股的总质量不变,即索股的自重荷载集度q和索股截面面积A也会随着索股温度的变化而变为q′和A′,如式(12)、(13)所示。
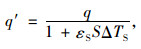
|
(12) |
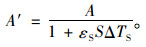
|
(13) |
现场调索计算时,根据上述方法建立的曲线确定影响因素变化量所对应的影响系数,确定当前条件相对设计状态基准索股跨中标高的理论变化量Δz0.5l,根据式(14)准确定位当前索股跨中理论标高。
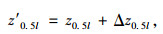
|
(14) |
式中, z0.5l为设计空缆状态下索股跨中标高; z′0.5l为当前索股跨中理论标高。
2.2 调索公式将索股当前跨中标高实测值z0.5l测与理论值做差,即得垂度差,根据式(15)所示索股无应力索长变化对跨中标高的影响公式,即可知基准索股索长调整量ΔS。其中∂S/∂z是无应力索长对跨中标高的影响系数,可通过索股线形求解程序进行参数分析获得影响曲线。
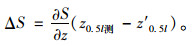
|
(15) |
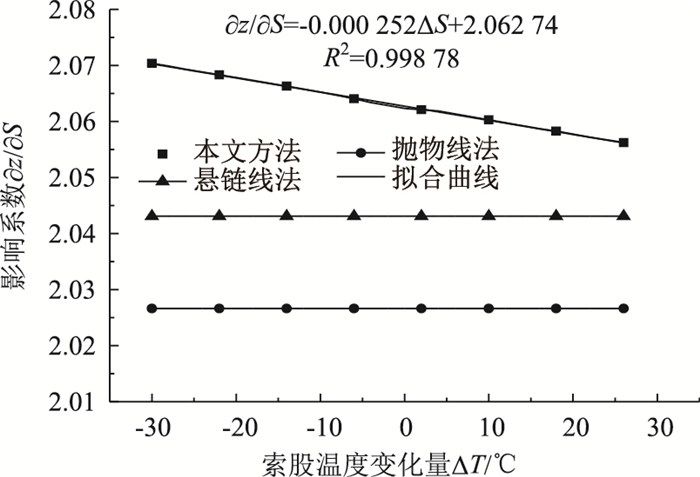
以图 4所示某悬索桥为例,以设计状态为基准,对索股线形进行参数分析,建立影响曲线。在一定的影响因素变化范围内,运用本文的影响公式和调索公式计算索股线形,并与近似抛物线公式和悬链线公式进行比较,如图 5~图 8所示。关于悬链线公式,目前已有文献中仅有索长与跨中标高之间的微分关系式,如图 5、图 8所示。
|
| 图 5 索股温度变化对跨中标高的影响系数 Fig. 5 Influence coefficient of cable strand temperature change on mid-span elevation |
| |
|
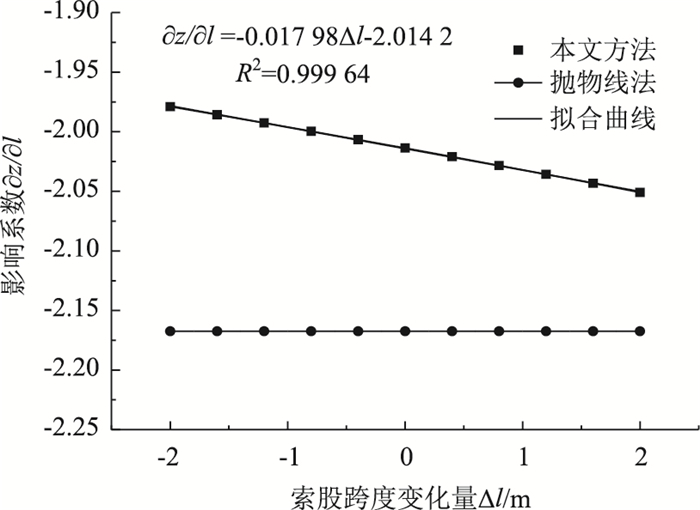
| 图 6 索股跨度变化对跨中标高的影响系数 Fig. 6 Influence coefficient of cable strand span change on mid-span elevation |
| |
|
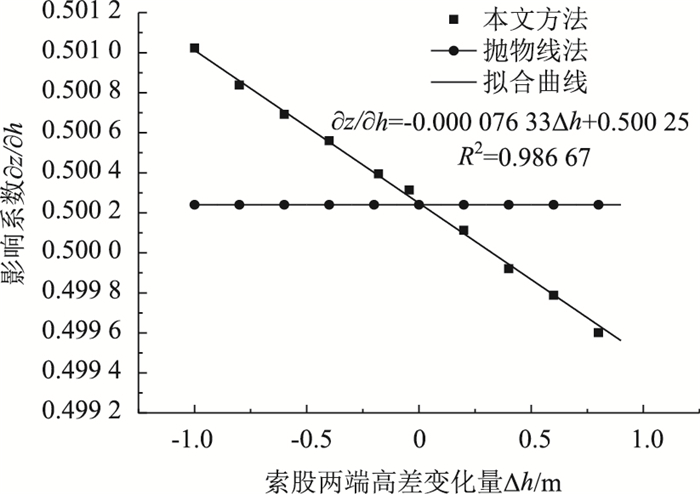
| 图 7 索股两端高差变化对跨中标高的影响系数 Fig. 7 Influence coefficient of height difference at two ends of cable strand change on mid-span elevation |
| |
|
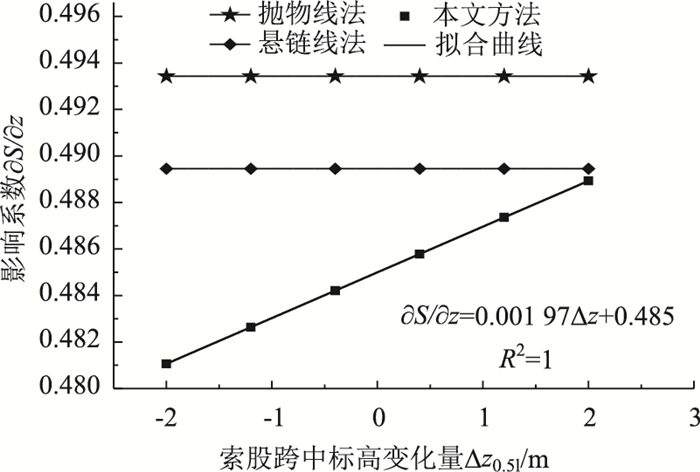
| 图 8 索股索长变化对跨中标高的影响系数 Fig. 8 Influence coefficient of cable strand length change on mid-span elevation |
| |
(1) 基于悬链线理论考虑索鞍切点位置的变化所得索股跨中标高影响系数随影响因素的变化而变化,可近似斜直线处理。经分析该桥各影响系数公式如下:
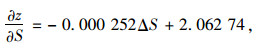
|
(16) |
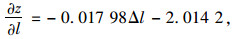
|
(17) |
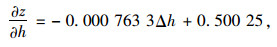
|
(18) |
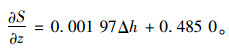
|
(19) |
由式(16)~(19)可以计算该桥基准索股任意影响因素发生任意变化时所对应的影响系数。
(2) 温度变化引起索长变化和索股两端跨度变化对垂度的影响系数较大,大于2.0, 即索股跨中标高对温度和两索鞍间距离比较敏感。施工时因对索鞍绝对预偏量和温度进行严格的监测,必要时采取相应调整措施。
(3) 与本文方法相比,抛物线公式计算的影响系数偏差较大,其中当跨度变化较大时,跨度变化对垂度的影响系数偏差最大达9%,其余影响因素偏差在2.5%以内。即索股两端点的跨度变化时,抛物线公式误差较大。
取施工现场与设计基准条件偏差如表 2所示,基准索股平均升温2~6 ℃,桥塔偏位导致索股跨度变化-0.1~-0.3 m,桥塔预抬高使得索股两端点高差变化0.1~0.3 m,根据上文各影响系数公式,分别计算单因素和多因素组合影响下基准索股跨中标高的变化量,计算误差并与抛物线公式计算结果进行比较,见表 2。
| ΔT/ ℃ | Δl/ m | Δh/ m | 理论解Δz/m | 影响公式法 | 抛物线法 | |||
| Δz/m | 误差/% | Δz/m | 误差/% | |||||
| 2 | — | — | 0.060 6 | 0.060 6 | -0.03 | 0.059 6 | -1.73 | |
| 4 | — | — | 0.121 3 | 0.121 2 | -0.03 | 0.119 2 | -1.71 | |
| 6 | — | — | 0.181 8 | 0.181 8 | -0.02 | 0.178 8 | -1.68 | |
| — | -0.1 | — | 0.201 2 | 0.201 3 | 0.05 | 0.216 7 | 7.72 | |
| — | -0.2 | — | 0.402 0 | 0.402 3 | 0.06 | 0.433 5 | 7.82 | |
| — | -0.3 | — | 0.602 5 | 0.602 9 | 0.06 | 0.650 2 | 7.92 | |
| — | — | 0.1 | 0.050 0 | 0.050 0 | -0.04 | 0.050 0 | -0.02 | |
| — | — | 0.2 | 0.100 0 | 0.100 0 | -0.02 | 0.100 0 | 0.02 | |
| — | — | 0.3 | 0.150 0 | 0.150 0 | 0.00 | 0.150 1 | 0.05 | |
| 2 | -0.1 | 0.1 | 0.311 8 | 0.312 0 | 0.06 | 0.326 4 | 4.68 | |
| 4 | -0.2 | 0.2 | 0.622 9 | 0.623 5 | 0.10 | 0.652 7 | 4.79 | |
| 6 | -0.3 | 0.3 | 0.933 4 | 0.934 7 | 0.13 | 0.979 1 | 4.89 | |
由表 2可知,运用本文影响公式所计算的索股跨中标高变化量不管在单因素影响下还是多因素组合影响下都有较高的精度,误差不超过0.15%。索股跨中标高变化量对跨度变化最为敏感,因此计算误差也较大,其中抛物线公式误差达到8%,已经不能满足施工精度的要求。因此在实桥基准索股调整过程中,运用本文影响公式法可以实现对基准索股跨中标高的准确定位。
已知基准索股垂度差见表 3,运用本文的调索影响公式计算调索量ΔS,将其误差与抛物线公式和悬链线公式进行比较。
| 垂度差/m | 理论解ΔS/m | 影响公式法 | 悬链线法 | 抛物线法 | |||||
| ΔS/m | 误差/% | ΔS/m | 误差/% | ΔS/m | 误差/% | ||||
| 0.2 | 0.097 1 | 0.097 1 | -0.02 | 0.097 9 | 0.81 | 0.098 7 | 1.63 | ||
| 0.4 | 0.194 3 | 0.194 3 | 0.01 | 0.195 8 | 0.76 | 0.197 4 | 1.58 | ||
| 0.6 | 0.291 7 | 0.291 7 | 0.01 | 0.293 7 | 0.68 | 0.296 1 | 1.49 | ||
| 0.8 | 0.389 3 | 0.389 3 | -0.01 | 0.391 6 | 0.58 | 0.394 7 | 1.40 | ||
| 1 | 0.487 | 0.487 0 | 0.00 | 0.489 5 | 0.50 | 0.493 4 | 1.32 | ||
由表 3可知,无论垂度差多大,本文影响公式所得结果都有非常高的精度,误差不超过0.02%,悬链线法误差不超过1%,抛物线法误差不超过2%,均能满足施工精度要求。随着垂度差的增大,悬链线法和抛物线法更接近于精确解,这是由于无应力索长对垂度的影响系数随着垂度差的增大而增大,如图 8所示。
4 结论本文考虑索股在索鞍内切点位置的变化对索股线形的影响,改进索股线形计算方法及流程,编写了相应的计算程序,并建立了基于悬链线理论的索股跨中标高影响公式和调索公式,通过对实桥算例进行参数影响分析,并与传统抛物线、悬链线公式对比,得到的研究结论如下:
(1) 传统抛物线、悬链线公式的索股跨中标高影响系数随着影响因素的变化为恒定值,而考虑索股在索鞍内切点位置变化的索股跨中标高影响系数随着影响因素的变化而变化,可近似斜直线处理。
(2) 索股跨中标高对温度和索股两端间距离的变化比较敏感,施工时应对桥塔偏位(索鞍绝对预偏量)和温度进行严格的监测,必要时采取相应调整措施。
(3) 在任意影响因素发生任意变化时,本文影响公式和调索公式都能保证一定的精度,对实桥基准索股的施工控制具有指导意义。
| [1] |
贺拴海. 桥梁结构理论与计算方法[M]. 北京: 人民交通出版社, 2017. HE Shuan-hai. Bridge Structure Theory and Calculation Method[M]. Beijing: China Communications Press, 2017. |
| [2] |
唐茂林.大跨度悬索桥几何非线性分析及软件开发[D].成都: 西南交通大学, 2003. TANG Mao-lin. Geometric Nonlinear Analysis and Software Development of Long Span Suspension Bridge[D]. Chengdu: Southwest Jiaotong University, 2003. http://cdmd.cnki.com.cn/Article/CDMD-10613-2004020320.htm |
| [3] |
王建金, 叶贵如. 自锚式悬索桥基准索股架设线形推导与验证[J]. 华东公路, 2013(6): 46-49. WANG Jian-jin, YE Gui-ru. Derivation and Verification of Alignment of Datum Strands of Self-anchored Suspension Bridge[J]. East China Highway, 2013(6): 46-49. |
| [4] |
郭福, 乔卫华. 悬索桥基准索股架设若干影响因素分析与控制[J]. 筑路机械与施工机械化, 2014, 31(3): 71-73. GUO Fu, QIAO Wei-hua. Analysis and Control of Factors Affecting Erection of Datum Strand of Suspension Bridge[J]. Road Machinery & Construction Mechanization, 2014, 31(3): 71-73. |
| [5] |
王达, 张永健, 黄平明. 大跨度悬索桥主缆施工温度时变效应研究[J]. 公路交通科技, 2010, 27(12): 72-77. WANG Da, ZHANG Yong-jian, HUANG Ping-ming. Research on Temperature Time-varying Effect of Long-span Suspension Bridge during Main Cable Construction[J]. Journal of Highway and Transportation Research and Development, 2010, 27(12): 72-77. |
| [6] |
王达, 张永健, 杨琴, 等. 大跨度悬索桥施工期主缆索股线形区域分段控制法[J]. 长安大学学报:自然科学版, 2015, 35(5): 57-64. WANG Da, ZHANG Yong-jian, YANG Qin, et al. Sub-regional and Subsection Linear Control Method during the Construction of Main Cables Strands for Long-span Suspension Bridge[J]. Journal of Chang'an University: Natural Science Edition, 2015, 35(5): 57-64. |
| [7] |
王建金.独塔空间主缆自锚式悬索桥缆索系统施工计算分析[D].杭州: 浙江大学, 2014. WANG Jian-jin. Cable System Construction Calculation and Analysis of Single Tower Space Main Cable Self-anchored Suspension Bridge[D]. Hangzhou: Zhejiang University, 2014. http://cdmd.cnki.com.cn/article/cdmd-10335-1014171275.htm |
| [8] |
柯红军.复杂悬索桥合理设计及合理施工状态确定[D].长沙: 长沙理工大学, 2014. KE Hong-jun. Determining the Reasonable Design State and Reasonable Construction State of Complex Suspension Bridges[D]. Changsha: Changsha University of Science & Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10536-1015393312.htm |
| [9] |
魏建东. 悬链线解答在悬索垂度调整中的应用[J]. 钢结构, 2006, 21(6): 40-43. WEI Jian-dong. Application of Catenary Solution in SAG Adjustment of Suspension Cable[J]. Steel Construction, 2006, 21(6): 40-43. |
| [10] |
孙全胜, 孙航, 张清晨. 基于影响矩阵的自锚式悬索桥基准索股架设监控分析[J]. 中外公路, 2012, 32(4): 117-122. SUN Quan-sheng, SUN Hang, ZHANG Qing-chen. Monitoring Analysis of Datum Strands Erection of Self-anchored Suspension Bridge Based on Impact Matrix[J]. Journal of China & Foreign Highway, 2012, 32(4): 117-122. |
| [11] |
谭红梅, 袁帅华, 肖汝诚. 大跨度悬索桥的基准索股调整[J]. 中国铁道科学, 2010, 31(1): 38-43. TAN Hong-mei, YUAN Shuai-hua, XIAO Ru-cheng. The Adjustment of Datum Strand of Long-span Suspension Bridges[J]. China Railway Science, 2010, 31(1): 38-43. |
| [12] |
刘来君, 贺拴海. 索鞍无预偏施工悬索桥主缆的温度效应[J]. 长安大学学报:自然科学版, 2007, 27(1): 40-44. LIU Lai-jun, HE Shuan-hai. Temperature Effect on Suspension Bridge with Non-pre-bias of Cable-saddle[J]. Journal of Chang'an University: Natural Science Edition, 2007, 27(1): 40-44. |
| [13] |
刘世忠, 贾一全, 王苍和, 等. 大温差影响下刘家峡大桥基准索股的调整[J]. 桥梁建设, 2014, 44(3): 51-56. LIU Shi-zhong, JIA Yi-quan, WANG Cang-he, et al. Adjusting of Datum Strand of Liujiaxia Bridge Influenced by Great Temperature Difference[J]. Bridge Construction, 2014, 44(3): 51-56. |
| [14] |
何湘峰.大跨度悬索桥缆索系统分析与施工控制[D].西安: 长安大学, 2007. HE Xiang-feng. Analysis and Construction Control of Cable System of Long-span Suspension Bridges[D]. Xi'an: Chang'an University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-11941-2009211955.htm |
| [15] |
唐茂林, 沈锐利, 强士中. 大跨度悬索桥丝股架设线形计算的精确方法[J]. 西南交通大学学报, 2001, 36(3): 303-307. TANG Mao-lin, SHEN Rui-li, QIANG Shi-zhong. An Accurate Calculation Method for Erecting Curves of Wire Strands of Long Suspension Bridges[J]. Journal of Southwest Jiaotong University, 2001, 36(3): 303-307. |
| [16] |
汪东林, 张伟. 悬索桥主缆温度场计算模型构建分析[J]. 公路交通科技, 2015, 32(8): 66-71. WANG Dong-lin, ZHANG Wei. Analysis of Temperature Field Calculation Modelling of Main Cables of Suspension Bridge[J]. Journal of Highway and Transportation Research and Development, 2015, 32(8): 66-71. |
| [17] |
梅葵花.悬索桥主缆施工监控的研究[D].西安: 长安大学, 2000. MEI Kui-hua. Research on Construction Monitoring of Main Cable of Suspension Bridge[D]. Xi'an: Chang'an University, 2000. http://cdmd.cnki.com.cn/Article/CDMD-11941-2000002038.htm |
| [18] |
何辉剑.大跨度悬索桥施工监控若干关键问题研究[D].长沙: 长沙理工大学, 2012. HE Hui-jian. Study on Several Key Issues in Construction Control to Long-span Suspension Bridge[D]. Changsha: Changsha University of Science & Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10536-1012347884.htm |
 2019, Vol. 36
2019, Vol. 36
