扩展功能
文章信息
- 李刚, 冯霄暘
- LI Gang, FENG Xiao-yang
- 低温条件下大跨径混合梁斜拉桥合龙顶推技术研究
- Study on Jacking Technology for Closure of Long-span Hybrid Girder Cable-stayed Bridge at Low Temperature
- 公路交通科技, 2019, 36(5): 69-77
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(5): 69-77
- 10.3969/j.issn.1002-0268.2019.05.010
-
文章历史
- 收稿日期: 2018-05-31
2. 西南交通大学, 四川 成都 610031
2. Southwest Jiaotong University, Chengdu Sichuan 610031, China
混合梁斜拉桥集钢主梁和混凝土主梁各自优点于一体,满足了大跨度桥梁的建设条件及经济要求,在千米级乃至更大跨度斜拉桥方案中具有独特的竞争优势,而中跨合龙为斜拉桥建设过程中的控制性环节,就显得尤为重要[1]。本研究以重庆高家花园轨道环线专用桥为例,对低温条件下的大跨径混合梁斜拉桥中跨合龙技术进行研究。
重庆高家花园轨道环线专用桥桥跨布置为(52+68+340+66.5+50.5)m,五跨连续半漂浮体系的双塔双索面混合梁斜拉桥,中跨为钢箱梁,边跨为混凝土箱梁,桥型布置图如图 1所示。钢混结合部位于中跨一侧距主塔中心6 m处,边跨混凝土箱梁采用满堂支架现浇施工,中跨钢箱梁段采用对称悬臂拼装施工。该桥是当今国内轨道专用桥中跨径最大的斜拉桥,主跨达340 m。

|
| 图 1 桥型布置图 (单位:cm) Fig. 1 Bridge layout (unit:cm) |
| |
1 高家花园轨道环线专用桥合龙方案
经过详细对比分析温度配切合龙法[2-4]及缝接合龙法[5]在不同合龙温度下对成桥状态的影响,选定缝接合龙法作为高家花园轨道环线专用桥的合龙方案,该法不仅可以有效消除合龙温差对成桥索力、成桥主梁应力、主梁线形及主塔偏移的影响,而且该法的施工工艺也方便、快捷。该法是一种新型合龙法,基于几何控制原理,提出通过精确控制合龙缝代替合龙段的思路,来实现中跨梁体精准合龙的施工方法,即使用桥面吊机先行起吊合龙段,并使其与一侧主梁匹配焊接,形成合龙缝,再通过主梁顶推、桥面吊机调整合龙缝线形高差,实现合龙缝合龙[5-6]。
缝接合龙法的关键参数为合龙顶推位移量和合龙顶推力,两个关键参数数值计算准确,才能确保主梁移动位移精准,合龙缝精确合龙,成桥状态良好。
本研究是基于高家花园轨道环线专用桥合龙施工控制,来对合龙顶推位移量和合龙顶推力展开研究计算的。该桥设计合龙温度20 ℃,现场合龙温度0~10 ℃,合龙温差为10~20 ℃,所以本研究拟定现场合龙温度分别为0,5,10,15 ℃来进行研究分析。
2 有限元模型建立高家花园轨道环线专用桥由主梁、索塔、斜拉索、辅助墩4部分组成,全桥借助MIDAS/Civil2015有限元软件建立模型,如图 2所示。

|
| 图 2 MIDAS/Civil有限元模型 Fig. 2 MIDAS/Civil finite element model |
| |
3 合龙顶推位移量计算研究
合龙顶推位移量由合龙温差引起的中跨梁体伸缩量,预留合龙缝焊接宽度及合龙段下料长度3部分组成[7-8]。后两者无需进行理论计算和数值模拟,只需结合现场施工累计误差和设计要求确定。梁体伸缩量需根据不同合龙温差,借助数值模拟和理论计算相互对比确定,本研究关于梁体伸缩量的计算研究,如下文所示。
3.1 梁体伸缩量计算理论本研究是基于刚性支撑连续梁法原理[9],对斜拉桥最大悬臂结构进行研究分析的。刚性支撑连续梁法是指在成桥状态下,斜拉桥主梁的弯曲应力和刚性支撑连续梁的内力状态一致[9]。因此可将斜拉桥最大悬臂结构等效成刚性支撑连续梁结构进行处理。
本研究拟将斜拉桥在最大悬臂状态下的结构体系等效成刚性支撑连续梁处理,等效前后的结构分别如图 3和图 4所示。图中P2为固定支座,顶推前P3支座临时固结,顶推时解除临时固结变为纵向活动支座,其余支座均为纵向活动支座。因结构体系是对称的,取单侧结构分析即可,如图 5所示。

|
| 图 3 最大悬臂状态结构 Fig. 3 Structure of maximum cantilever state |
| |

|
| 图 4 最大悬臂状态刚性支撑连续梁 Fig. 4 Rigid support continuous girder of maximum cantilever state |
| |

|
| 图 5 单侧最大悬臂状态刚性支撑连续梁 Fig. 5 Rigid support continuous girder of unilateral maximum cantilever state |
| |
依据结构温度作用位移公式[10],可得出梁体在不同温差下的伸缩值Δ,如下所示。
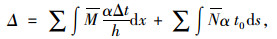
|
(1) |
式中,M为虚设单位力弯矩;N为虚拟单位力轴力;h为杆件截面厚度;ds为杆件轴线方向单元长度微分;α为材料线膨胀系数;预应力混凝土、钢筋混凝土及混凝土为0.000 010,钢材为0.000 012;Δt=t2-t1,t2为梁体下缘温度值;t1为梁体上缘温度值;t0为梁体形心轴温度变化值[10]。
3.2 梁体伸长收缩量计算分析 3.2.1 力学理论计算结合上述式(1),以高家花园轨道环线专用桥为例展开分析计算。由于P3支座的纵向约束在主梁顶推之前没有解除,因此中、边跨梁体将分别以P3支座为基准点进行伸缩变形,所以中跨梁体的伸缩量计算过程如下所示[11-12]。
以现场合龙温度0 ℃为例展开计算,中跨主梁由钢箱梁和混凝土箱梁两部分组成,其中单侧钢箱梁长度为160 m,混凝土箱梁长度为6 m。
所以,单侧梁体收缩量为Δ=1×0.000 012×160×20+1×0.000 01×6×20=0.039 6 m。同理,可计算得出单侧梁体在合龙温度为15,10,5 ℃时,梁体收缩量分别为0.009 9,0.019 8,0.029 7 m,进而得出最终中跨梁体收缩量2Δ,即0.019 8,0.039 6,0.059 4 m。
3.2.2 有限元模型计算借助Midas/Civil 2015有限元软件,通过在全桥模型中依据不同合龙温度施加对应的单元温度荷载,来仿真模拟梁体在不同合龙温差下的伸缩变化情况。
为确定顶推位移量的准确性,将不同合龙温度下的中跨梁体收缩量的力学理论计算值和有限元模型计算值进行对比,如图 6所示。

|
| 图 6 梁体收缩位移量对比图 Fig. 6 Contrast of shrinkage displacements of girder body |
| |
由图 6可得,有限元模型计算值与力学理论计算值均与合龙温度呈线性关系,且均随合龙温度的升高而减小。且在相同合龙温度下,两者数值差在7 mm以内,这表明,基于刚性支撑连续梁法原理对斜拉桥中跨梁体计算温差伸缩量的理论计算方法是可行的,同时验证了理论计算值与有限元模型计算值的可靠性。因有限元模型作为桥梁施工控制的指导工具,所以采用有限元模型计算值作为梁体温差伸缩量值[13-14]。
4 合龙顶推力计算研究 4.1 顶推力计算理论中跨主梁在顶推过程中,主要受到中、边跨索力不平衡拉索水平分量和支座摩阻力影响[4],详见图 7。

|
| 图 7 顶推力分析示意图 Fig. 7 Schematic diagram of jacking force analysis |
| |
根据上述分析,顶推力P的计算公式为:
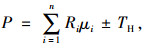
|
(2) |
式中,Ri为支座i的支反力;μi为摩擦系数;TH为中、边跨不平衡拉索水平分量[15-16]。
4.2 顶推力计算分析结合上述式(2),以现场合龙温度5 ℃为例展开计算分析。
首先对支座摩擦系数进行分析,本桥使用球型钢支座,参考相关试验研究[7],球型钢支座的摩擦系数不可避免地存在较大的离散性。为确保主梁顶推顺利进行,根据《桥梁球型支座》规范,支座动、静摩擦系数统一取较大值0.1[7],即顶推力计算公式可如下所示。
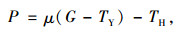
|
(3) |

|
(4) |
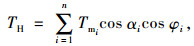
|
(5) |
式中,G为主梁竖向荷载;TY为索力竖向分量;Tmi为i号斜拉索目标索力;αi为i号斜拉索梁端立面夹角;φi为i号斜拉索梁端平面夹角。
综合上述式(3)~(5)可知,计算顶推力P的关键在于如何得出目标索力Tm,关于Tm值计算研究如下文所示。
本研究提出借助影响矩阵来计算目标索力Tm值,即已知初始索力Tc和施调索力位移量Δs,通过影响矩阵原理计算出目标索力Tm。
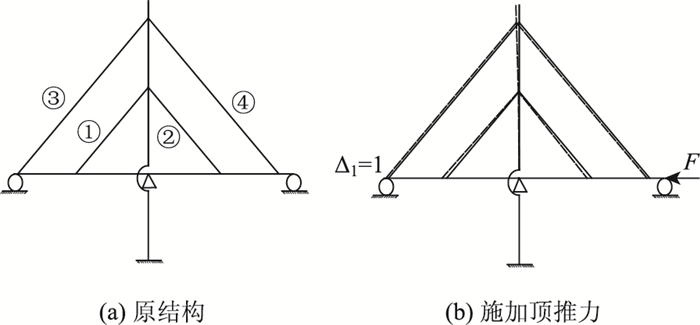
本研究以一座斜拉桥为例,说明影响矩阵的构成,如图 8所示。
|
| 图 8 影响矩阵法原理 Fig. 8 Principle of influence matrix method |
| |
对主梁单侧梁端施加顶推力F时,使其产生单位水平位移Δ1=1,此时斜拉索1,2,3,4相应的索力增量为{Ti}(i=1, 2, 3, 4),即可得出关于斜拉索1,2,3,4的索力影响矩阵MΔ:

|
也可得出关键截面C1,C2,…,Cn应力影响矩阵为Mσ:
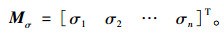
|
(2) 斜拉索目标索力计算
由上述计算方法计算出索力影响矩阵MΔ,MΔ为n×1阶的矩阵,其中的元素Mi表示主梁产生单位水平位移时,i号索索力的增量。
已知初始索力值Tc和梁端施调位移量Δs,Δs为n×n阶的对角矩阵,对角元素为施调位移值,则可得目标索力Tm为

|
(6) |
结合上式,计算该桥的目标索力Tm。
该桥北岸侧主梁为顶推侧,顶推前的最大悬臂状态为初始索力状态,结合前文计算得出的梁体伸缩量,拟计算主梁顶推移动1,2,3,4,5,6 cm时,斜拉索的目标索力Tm。
借助Midas/Civil 2015有限元软件,通过对北岸侧主梁梁端施加水平荷载,迫使主梁产生单位水平位移,进而可得出北岸侧26对52根斜拉索的索力影响矩阵MΔ。同时施调位移量Δs依次为

|
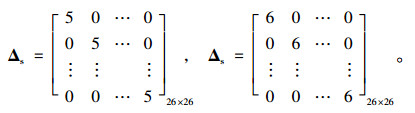
|
借助Matlab软件,可计算出不同顶推位移下的目标索力Tm,限于篇幅仅列出部分斜拉索的目标索力,如表 1所示。
| 索号 | 目标索力/kN | ||||||
| 初始状态 | 顶推1 cm | 顶推2 cm | 顶推3 cm | 顶推4 cm | 顶推5 cm | 顶推6 cm | |
| BZ1 | 3 258 | 3 425 | 3 592 | 3 759 | 3 926 | 4 092 | 4 259 |
| BZ2 | 2 496 | 2 538 | 2 579 | 2 621 | 2 663 | 2 704 | 2 746 |
| BZ3 | 2 139 | 2 145 | 2 152 | 2 159 | 2 165 | 2 172 | 2 179 |
| BZ4 | 1 884 | 1 878 | 1 871 | 1 865 | 1 859 | 1 853 | 1 847 |
| BZ5 | 1 751 | 1 740 | 1 730 | 1 720 | 1 709 | 1 699 | 1 688 |
表 1得出目标索力Ti后,可计算TY, TH,如表 2所示。
| 索力分量 | 初始状态 | 顶推1 cm | 顶推2 cm | 顶推3 cm | 顶推4 cm | 顶推5 cm | 顶推6 cm |
| TY/kN | 59 488.78 | 59 159.12 | 58 836.78 | 58 511.04 | 58 181.12 | 57 858.78 | 57 531.56 |
| TH/kN | -4 882.18 | -3 925.04 | -2 977.38 | -2 016.48 | -1 067.84 | -120.18 | 833.8 |
| 注:“-”表示,TH方向为中跨方向。 | |||||||
结合前文式(3)可计算出主梁顶推过程中的顶推力数值,如表 3所示。
| 顶推力/kN | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| 顶推位移量/mm | -111 | 878 | 1 858 | 2 852 | 3 833 | 4 813 | 5 800 |
由表 3可以看出,解除P3支座的临时固结时,主梁将自动向中跨侧移动,但使主梁达到拟定顶推位移量,需持续增加顶推力。
5 高家花园轨道环线专用桥合龙技术 5.1 合龙顶推施工装置合龙顶推施工装置包括主梁顶推限位装置和顶推力加载装置两个部分,限位装置如图 9和图 10所示。

|
| 图 9 顶推顺桥向限位装置 Fig. 9 Jacking limit device in bridge direction |
| |

|
| 图 10 顶推竖向限位装置 Fig. 10 Jacking limit device in vertical direction |
| |
主梁的顶推力加载装置可根据现场实际情况确定,一般可设置在主梁梁端处或者塔梁支座处。本桥的顶推装置设置在北岸主梁梁端,布设在A5桥台后侧,如图 11所示。

|
| 图 11 顶推装置 (单位:m) Fig. 11 Jacking device (unit:m) |
| |
5.2 合龙顶推位移量及顶推力确定
合龙段起吊前先对合龙口宽度进行现场监测,合龙口处的梁体实际收缩量,与理论值对比情况如图 12所示。

|
| 图 12 梁体收缩量理论值与实测值对比 Fig. 12 Contrast of theoretical and measured values of shrinkage displacement of girder body |
| |
由图 12可得,梁体伸缩量的实测值与理论计算值均与合龙温度呈线性关系,即均随合龙温度增大而减小,且两者线性变化率基本相同,实测值变化率约4.0 mm/℃,理论值变化率约3.8 mm/℃,这表明两者关于梁体温差伸缩量变化率是相同的,即在同等温差条件下,两者引起的梁体伸缩量是相同的,从而验证了本研究3.2节关于梁体温差伸缩量计算理论的可行性。
但实测值未与理论值保持一致,在相同合龙温度下两者均相差19 mm。究其原因,施工累积误差造成两者在初始状态(设计合龙温度)存在19 mm的误差,进而得出:梁体收缩量实测值=梁体收缩量理论值-施工累积误差值。
依据上文计算方法得出梁体温度收缩量实测值,再结合现场情况,得到如表 4所示的主梁顶推位移量及顶推力。
| 合龙温度/℃ | 梁体收缩量实测值 (①)/mm |
焊缝宽度 (②)/mm |
合龙段切割长度 (③)/mm |
顶推位移量 (④=①-②+③)/mm |
顶推力/kN |
| 4 | 39 | 20 | 25 | 44 | 4 000 |
| 5 | 35 | 20 | 25 | 40 | 3 700 |
| 6 | 31 | 20 | 25 | 36 | 3 300 |
5.3 主梁顶推移动监测分析
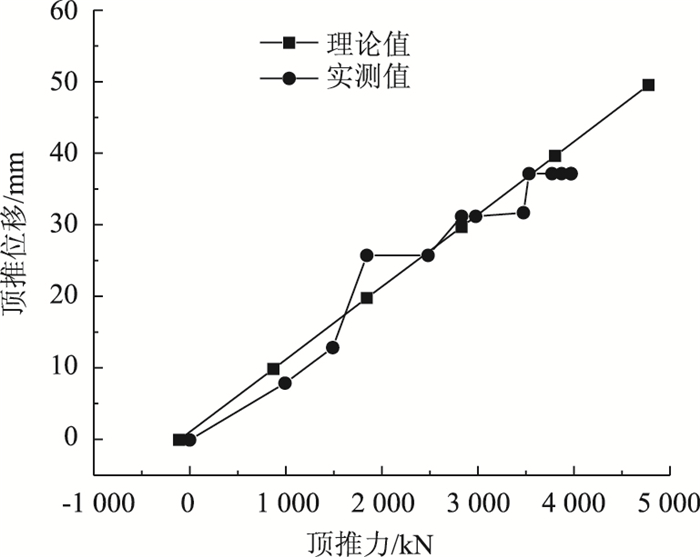
2016年1月29日凌晨6时合龙段施工正式开始,前后历时6 h,合龙施工过程十分顺利,通过现场实时监测得到主梁顶推力与位移实测值,并将其与理论值进行对比,如图 13所示。
|
| 图 13 顶推力理论值与实测值对比 Fig. 13 Contrast of theoretical and measured values of jacking force |
| |
由图 13可得,顶推力与位移理论值呈线性增长规律,而顶推力与位移实测值呈台阶式增长规律。实侧值均匀分布在理论值折线的两侧,未在理论值折线两侧剧烈变化或者只分布在折线某一侧,说明实测值与理论值之间是有关系的,理论值具有一定的指导作用。
针对实测值与理论值差别的原因进行分析,得出了以下两个影响因素:(1)支座摩擦系数取值不准确,未能反映真实情况,既而得出的顶推力理论值不够准确;(2)斜拉索初始索力存在误差,因本研究所取索力值为有限元模型计算索力,与现场实际索力有误差,这就导致计算中、边跨不平衡索力水平分量有误差,进而影响到顶推力结果的精确性。
6 成桥状态验证缝接合龙方案实施后,借助已建立的全桥有限元计算模型,分别从成桥线形、拉索索力、主梁应力等方面验证成桥状态与设计状态的相符情况,如图 14~图 15及表 5所示。

|
| 图 14 成桥索力附加比率 Fig. 14 Additional ratio of cable forces of completed bridge |
| |
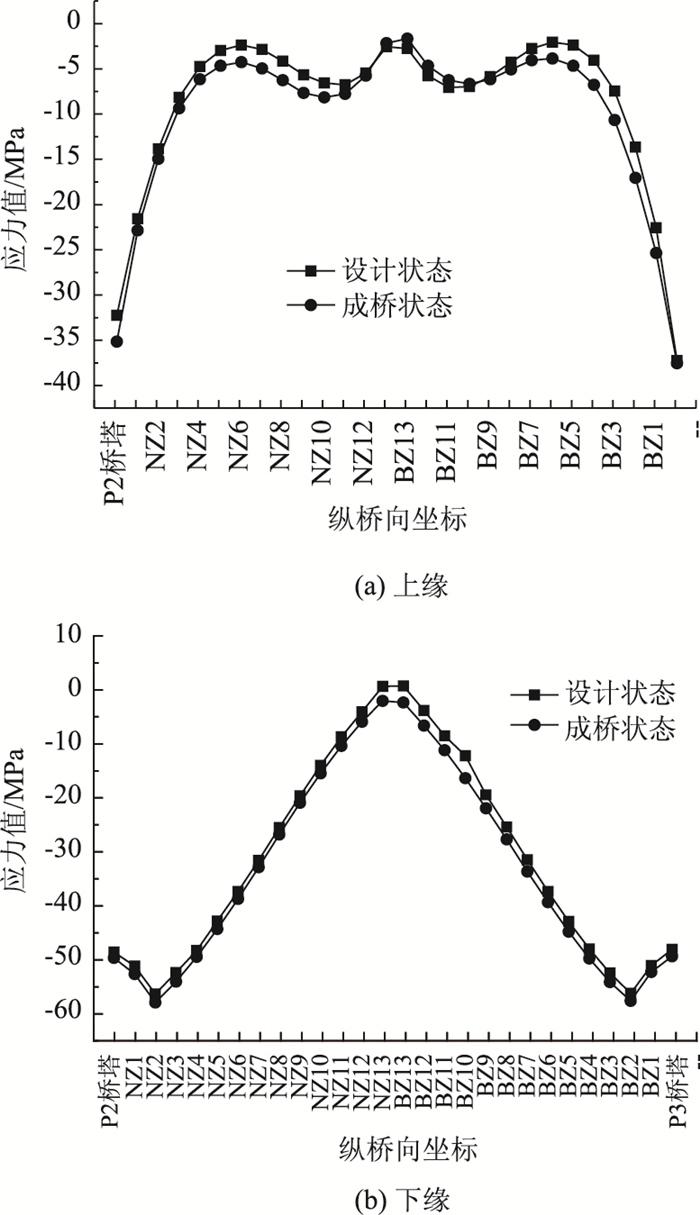
|
| 图 15 钢箱梁中跨应力对比 Fig. 15 Contrast of stresses of middle span of steel box girder |
| |
| 项目 | 最大附加位移/mm | |
| 南岸边跨 | 混凝土箱梁顺桥向 | 4 |
| 混凝土箱梁竖向 | 1 | |
| 中跨 | 钢箱梁顺桥向 | 10 |
| 钢箱梁竖向 | 17 | |
| 北岸边跨 | 混凝土箱梁顺桥向 | 16 |
| 混凝土箱梁竖向 | 6 | |
| 桥塔 | P2顺桥向 | 6.5 |
| P3纵向 | 19 |
由图 14可得出,全桥拉索的附加索力比率基本控制在8%之内;从图 15可以看出,成桥状态下的钢箱梁应力与设计状态的应力误差控制3 MPa范围之内,且普遍较设计状态偏大;从表 5可以看出,成桥状态下主塔偏移、主梁线形控制较好,与设计状态偏差较小。
7 结论(1) 依托高家花园轨道环线专用桥,分别运用力学理论和有限元软件两种方法计算梁体温差伸缩量,两种方法计算的结果基本相同,且将其与现场实测值对比,得出关于梁体温差伸缩量变化率的理论计算方法是正确的,梁体温差伸缩量理论值与实测值保持一致,既而有效指导了现场合龙施工。
(2) 通过对主梁顶推过程进行受力分析,得出了合龙顶推力的计算方法,进而确定出顶推位移与顶推力数值变化关系,为现场顶推力加载提供了理论指导。
(3) 实际情况下的顶推位移与顶推力呈台阶式增长关系,理论值呈线性变化规律,两者虽未完全吻合,但实测值均匀地分布在理论值的两侧,侧面验证了本研究关于顶推力计算方法的可行性。
| [1] |
陈开利, 余天庆, 习刚. 混合梁斜拉桥的发展与展望[J]. 桥梁建设, 2005, 35(2): 1-4. CHEN Kai-li, YU Tian-qing, XI Gang. Development and Prospective of Hybrid Girder Cable-stayed Bridge[J]. Bridge Construction, 2005, 35(2): 1-4. |
| [2] |
易云焜, 严和仲, 赵鹍鹏, 等. 厦漳跨海大桥北汊主桥配切-顶推合龙技术[J]. 桥梁建设, 2013, 43(4): 49-53. YI Yun-kun, YAN He-zhong, ZHAO Kun-peng, et al. Technique of Cutting-pushing Closure for North Main Bridge of Xiazhang Sea-crossing Bridge[J]. Bridge Construction, 2013, 43(4): 49-53. |
| [3] |
涂国平, 张喜刚, 刘玉擎, 等. 混合梁斜拉桥[M]. 北京: 人民交通出版社, 2013: 7-8. TU Guo-ping, ZHANG Xi-gang, LIU Yu-qing, et al. Hybrid Girder Cable-stayed Bridge[M]. Beijing: China Communications Press, 2013: 7-8. |
| [4] |
刘琳.大跨度混合梁斜拉桥施工期主梁应力控制与合龙技术研究[D].成都: 西南交通大学, 2013. LIU Lin. Girder Stress Control and Closure Technique in Construction Period of Long-span Hybrid Girder Cable-stayed Bridges[D]. Chengdu: Southwest Jiaotong University, 2013. http://cdmd.cnki.com.cn/article/cdmd-10613-1014257907.htm |
| [5] |
万华. 荆岳长江公路大桥中跨基于缝接合龙法的合龙施工技术[J]. 中外公路, 2011, 31(4): 104-107. WAN Hua. Closure Construction Technique for Jingyue Yangtze River Highway Bridge Based on Seaming Closure Metho[J]. Journal of China & Foreign Highway, 2011, 31(4): 104-107. |
| [6] |
周晟.大跨径混合梁斜拉桥中跨合龙施工控制研究[D].长沙: 长沙理工大学, 2011. ZHOU Sheng. Research on Mid-span Closure Construction Control of Long-span Hybrid Girder Cable-stayed Bridge[D]. Changsha: Changsha University of Science & Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10536-1012274353.htm |
| [7] |
杨飞, 向学建, 刘殿元, 等. 瓯江特大桥钢箱梁合龙控制研究[J]. 公路交通科技, 2014, 31(4): 94-99. YANG Fei, XIANG Xue-jian, LIU Dian-yuan, et al. Steel Box Girder Closure Control Research of Oujiang Grand Bridge[J]. Journal of Highway and Transportation Research and Development, 2014, 31(4): 94-99. |
| [8] |
李宏江, 李万恒, 张劲泉, 等. 既有PC斜拉桥合龙段拆除的施工控制[J]. 公路交通科技, 2008, 25(8): 61-66. LI Hong-jiang, LI Wan-heng, ZHANG Jin-quan, et al. Construction Control for Removal of the Closure Segment in an Existing Prestressed Concrete Cable-stayed Bridge[J]. Journal of Highway and Transportation Research and Development, 2008, 25(8): 61-66. |
| [9] |
项海帆. 高等桥梁结构理论[M]. 北京: 人民交通出版社, 2001: 284-285. XIANG Hai-fan. Structural Theory of High Grade Bridges[M]. Beijing: China Communications Press, 2001: 284-285. |
| [10] |
崔清洋, 张大华, 朱华. 结构力学[M]. 武汉: 武汉理工大学出版社, 2010: 113-114. CUI Qing-yang, ZHANG Da-hua, ZHU Hua. Structural Mechanics[M]. Wuhan: Wuhan University of Technology Press, 2010: 113-114. |
| [11] |
吴明威, 华勇, 向梨梨, 等. 大跨度钢桁结合梁斜拉桥合龙施工技术[J]. 施工技术, 2016, 45(增1): 294-297. WU Ming-wei, HUA Yong, XIANG Li-li, et al. Closure Construction Technology of Cable-stayed Bridge with Large Span Steel Truss Composite Girder[J]. Construction Technology, 2016, 45(S1): 294-297. |
| [12] |
何承海, 彭琳琳. 嘉绍大桥合龙工艺研究[J]. 施工技术, 2014, 43(23): 58-60. HE Cheng-hai, PENG Lin-lin. Study on Closure Technology of Jiashao Bridge[J]. Construction Technology, 2014, 43(23): 58-60. |
| [13] |
吴运宏, 岳青, 朱利明, 等. 金塘大桥主通航孔斜拉桥合龙控制措施[J]. 施工技术, 2011, 40(3): 15-17. WU Yun-hong, YUE Qing, ZHU Li-ming, et al. Control Measures for Closure Construction of Jintang Primary Fairway Bridge[J]. Construction Technology, 2011, 40(3): 15-17. |
| [14] |
贾少敏, 赵雷, 杨兴旺. 嘉绍大桥主航道桥几何合龙控制[J]. 公路交通科技, 2014, 31(4): 87-93. JIA Shao-min, ZHAO Lei, YANG Xing-wang. Geometry Closure Control of Main Channel Bridge of Jiaxing-Shaoxing Bridge[J]. Journal of Highway and Transportation Research and Development, 2014, 31(4): 87-93. |
| [15] |
陈鸣, 罗承斌, 张永涛, 等. 苏通大桥主桥中跨顶推辅助合龙技术[J]. 中外公路, 2008, 28(5): 132-138. CHEN Ming, LUO Cheng-bin, ZHANG Yong-tao, et al. Assistant Pullback Technique for Main Span Closure of Sutong Bridge[J]. Journal of China & Foreign Highway, 2008, 28(5): 132-138. |
| [16] |
陈荣刚. 六跨连续刚构组合梁桥合龙方案研究[J]. 公路交通科技, 2014, 31(7): 91-96. CHEN Rong-gang. Study on Closure Scheme of Six-span Continuous Rigid Frame Composite Girder Bridge[J]. Journal of Highway and Transportation Research and Development, 2014, 31(7): 91-96. |
| [17] |
刘明虎, 谭皓, 徐国平, 等. 大跨径混合梁斜拉桥合龙技术研究与实践[J]. 桥梁建设, 2011, 41(4): 83-87. LIU Ming-hu, TAN Hao, XU Guo-ping, et al. Research and Practice of Closure Techniques for Long Span Hybrid Girder Cable-stayed Bridge[J]. Bridge Construction, 2011, 41(4): 83-87. |
| [18] |
肖汝诚, 郭文复. 结构关心截面内力, 位移混合调整计算的影响矩阵法[J]. 计算力学学报, 1992, 9(1): 91-99. XIAO Ru-cheng, GUO Wen-fu. Influence Matrics Method for Structural Adjustment Calculation of Internal Forces and Displacements of Concern Sections[J]. Chinese Journal of Computational Mechanics, 1992, 9(1): 91-99. |
| [19] |
肖汝诚, 项海帆. 斜拉桥索力优化的影响矩阵法[J]. 同济大学学报:自然科学版, 1998, 26(3): 235-240. XIAO Ru-cheng, XIANG Hai-fan. Influence Matrix Method of Cable Tension Optimization for Cablo-stayed Bridges[J]. Journal of Tongji University:Natural Science Edition, 1998, 26(3): 235-240. |
 2019, Vol. 36
2019, Vol. 36
