扩展功能
文章信息
- 马楠, 陈砚, 朱锋
- MA Nan, CHEN Yan, ZHU Feng
- 无应力长度正装迭代法在无背索斜拉桥工程中应用
- Application of Cable-stayed Bridge without Backstay of Forward Iterative Method Based on Unstressed Length
- 公路交通科技, 2019, 36(5): 64-68
- Journal of Highway and Transportation Research and Denelopment, 2019, 36(5): 64-68
- 10.3969/j.issn.1002-0268.2019.05.009
-
文章历史
- 收稿日期: 2018-03-20
2. 北京迈达斯技术有限公司, 北京 100000
2. MIDAS Information Technology Co., Ltd., Beijing 100000, China
无背索斜拉桥是一种较新型的斜拉桥形式,此种桥型具有造型独特、受力清晰、美观简洁等特点。但因单侧无背索,同时主塔一般做成倾斜,施工难度较大,目前为止国内外已建成的无背索斜拉桥数量较少。同时对于无背索斜拉桥的施工控制要求较高,其中拉索是结构合理受力的重要组成结构,施工过程中索力确定与优化是直接影响最终内力和线型达到合理成桥状态的关键因素[1-3]。
对于斜拉桥的施工过程分析,先倒拆得到施工过程索力再进行正装模拟,是斜拉桥施工控制与施工过程索力求解常用的方法。通过拟定合理的成桥状态,然后建立分析模型,通过定义单元的生死,来实现结构或者构件的激活与钝化,而后通过钝化单元后,实现拆除结构,进而可以求得每个施工阶段对应的拉索索力。这个过程是逆向的,由于我们考虑混凝土的收缩徐变是正向分析,因此在倒拆过程中没法考虑收缩徐变,故由倒拆得到的索力代入正装模型后,得到的结果与目标状态不一致,这样的情况也就比较容易理解了[4-6]。
对于施工过程中考虑无应力长度与无应力曲率,保证施工过程中的荷载、边界条件与成桥状态一致,同时控制拉索的锚头拔出量,以及平曲线合龙,这样的方法就是基于无应力长度的施工正装。拉索的索力与其无应力长度是可以相互转化,因此可以结合正装迭代的思路,引入拉索的无应力长度作为变量,同时考虑混凝土的徐变收缩等影响,最后通过替换索力方式,修正拉索的无应力长度,而后将新的无应力索长重新代入正装模型进行计算,直到满足一定工程精度要求,得到最终合理的成桥状态。
1 无背索斜拉桥内力平衡状态无背索斜拉桥的受力特点比较特殊,与常规斜拉桥的受力有较大差别,实际设计中,主塔的刚度较大,同时需要用主塔部分的荷载与主梁的荷载进行平衡[7-9]。
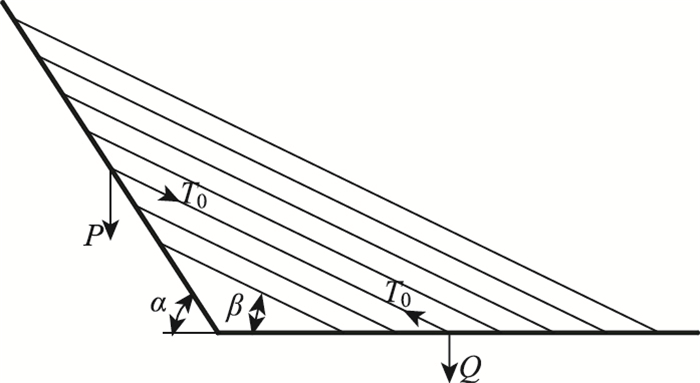
对于无背索斜拉桥平衡状态,由图 1所示,主塔的重量节段荷载为P,主梁上均布荷载为Q(平衡状态时往往考虑一半的活载),同时拉索的索力T0,三者若满足平衡状态,需要满足式(1)要求。
|
| 图 1 无背索斜拉平衡示意图 Fig. 1 Illustration of balance of cable-stayed bridge without backstay |
| |
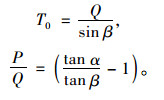
|
(1) |
对于结合无应力长度的施工正装迭代分析,首先一般是利用零位移法进行成桥调索,再利用最小弯曲能法进行索力优化,进行合理成桥状态求解,而后通过成桥索力求解相应拉索的无应力长度,再考虑施工顺序进行正装模拟,考虑各种施工荷载,包括恒荷载,预应力荷载,二期荷载。混凝土的收缩徐变影响,包括分阶段拉索张拉模拟,这样就可以得到最终的索力状态,而且参考之前的目标索力状态,两者比较后得到差值,利用最小二乘法进行修正,这样就得到新索的无应力长度,而后代入计算模型中重新进行正装分析,直到满足工程精度要求,计算终止。
2.1 最小弯曲能状态描述最小弯曲能法是斜拉桥常用的获得合理成桥状态初始调索方法之一。以最小的主塔、主梁弯曲与拉压应变能为目标,获得斜拉桥的一种合理成桥状态。这种分析方法可以综合考虑主梁与主塔的受力,同时求解得到成桥索力总体比较均匀,斜拉桥成桥内力状态更加合理,具体描述如式(2)所示。
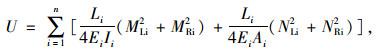
|
(2) |
式中,n为单元总数;Li,Ei,Ii,Ai分别为第i号单元长度、弹性模量、截面惯性矩和截面面积;MLi,MRi,NLi,NRi分别为左右端弯矩及轴力。
2.2 无应力长度的求解与描述对于无应力长度的求解,具体描述如式(3)所示,首先得到拉索单位无应力长度对结构内力状态的影响向量,从而得到相应的影响矩阵。
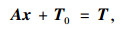
|
(3) |
式中,A为拉索单位无应力长度作用下斜拉桥内力的影响矩阵;x为斜拉索的无应力长度列阵;T0为结构在其他荷载作用时的内力或位移相应列阵;T为结构在索力作用与其他荷载作用下的相应列阵。
对于斜拉索的无应力长度,只有在进行索力张拉时才会有变化。对于结构体系、边界条件以及荷载工况确定的斜拉桥结构,拉索的无应力长度变化与其索力变化则存在线性关系[3]。
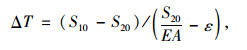
|
(4) |
式中,ΔT为斜拉索张力增量;S10为无应力长度;S20为无应力长度;E为斜拉索的弹性模量;A为斜拉索面积;ε为几何应变。
对于斜拉桥施工阶段模拟,拉索无应力长度调整与索力变化关系可由式(4)确定。
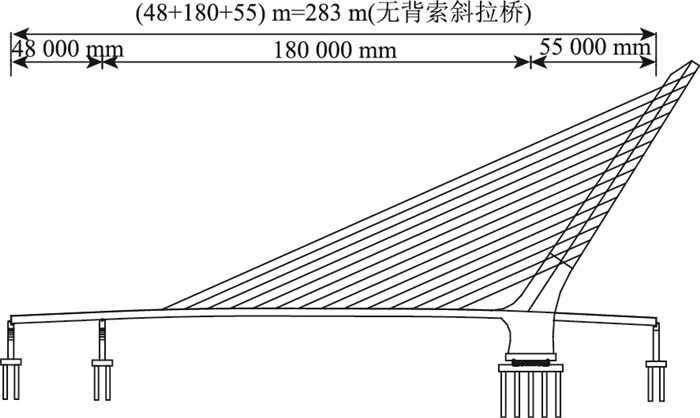
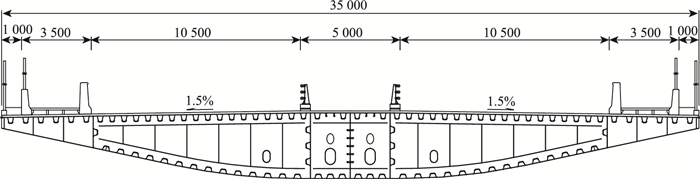
3 工程实例 3.1 工程概况工程位于四川省成都市东部,横跨成渝铁路,结构采用无背索斜塔单索面钢混组合斜拉桥形式,塔墩梁固结体系,跨径组合(48+180+55)m,桥面宽度35 m,其结构总体布置图见图 2,主梁标准断面见图 3。
|
| 图 2 桥梁总体布置图 Fig. 2 General arrangement of bridge |
| |
|
| 图 3 主梁标准横断面 (单位:mm) Fig. 3 Standard cross-section of main girder (unit:mm) |
| |
3.2 计算模型
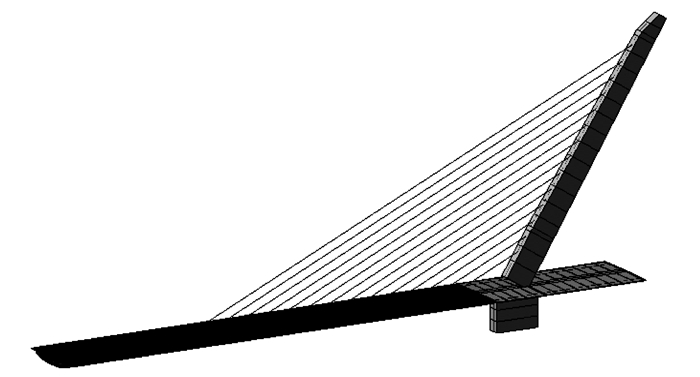
利用MIDAS Civil有限元软件建立全桥三维模型(图 4),塔、梁采用梁单元建立,拉索采用索单元,定义施工过程,包括荷载的激活与钝化,边界的转换等,全桥共计节点65个,单元77个。按实际施工步骤,需模拟施工过程中斜拉索多次张拉调整结构内力的过程,利用软件的单元激活与钝化功能,设置双斜拉索单元,分别赋予初拉力与无应力长度,这样就可以实现基于无应力长度正装迭代法的计算[5-6]。
|
| 图 4 空间计算模型 Fig. 4 Spatial calculation model of bridge |
| |
计算模型考虑结构自重、索力荷载、主梁预应力荷载、挂篮荷载、二期铺装等,同时考虑混凝土10 a的收缩徐变作用。
3.3 合理成桥状态确定对于无背索单索面斜拉桥确定合理的成桥状态,采用零位移法与最小弯曲能法结合方式,需要考虑自重、二期恒载、二分之一活载等的影响。零位移法控制主梁与拉索相接节点位移尽量小,对于最小弯曲能法,将拉索、主塔与主梁的轴向刚度放大105倍,得到初调索力,然后通过调整局部单元的抗弯刚度以及拉索轴向刚度,不断优化成桥目标状态,最后得到斜拉桥成桥合理状态[10-13]。
3.4 施工索力优化对于施工过程模拟,在首次正装迭代计算中,按照最小二乘法原理,根据初始索力求解出斜拉索初始无应力长度,输入到索单元并对比最终状态与目标状态的差异,重新修正索单元的无应力长度[14-18]。
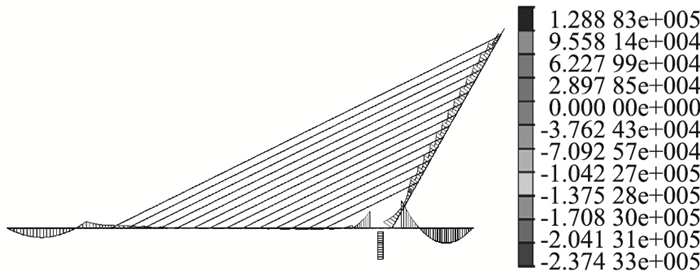
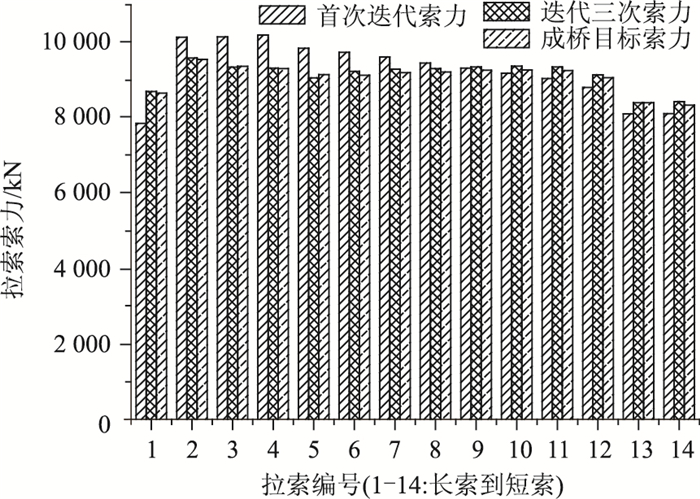
再次建立正装模型,重新进行正装模拟。依据多次上述迭代过程,直到最后状态与目标状态相差值不超过3%的要求,最后得到成桥索力如表 1所示,全桥内力图如图 5所示。基于无应力长度正装迭代分析得到成桥索力与目标状态索力比较, 如图 6所示。由图 6可以看出,最终状态与目标成桥索力最大差值不超过89 kN,最大误差为0.96%,满足工程精度要求。
|
| 图 5 主梁合理成桥弯矩云图 (单位:mm) Fig. 5 Nephogram of bending moment of main girder in reasonable bridge completion state (unit:mm) |
| |
|
| 图 6 正装迭代计算索力与目标索力比较 Fig. 6 Comparison of cable force calculated by forward iteration method and target cable force |
| |
| 索号 | 首次正装索力/kN | 迭代三次后索力/kN | 成桥目标索力/kN | 差值/kN | 误差/% |
| 1 | 7 865 | 8 697 | 8 688 | 9 | 0.10 |
| 2 | 10 137 | 9 586 | 9 549 | 36 | 0.38 |
| 3 | 10 160 | 9 376 | 9 357 | 19 | 0.20 |
| 4 | 10 188 | 9 318 | 9 305 | 12 | 0.13 |
| 5 | 9 855 | 9 086 | 9 167 | -81 | -0.89 |
| 6 | 9 739 | 9 219 | 9 152 | 67 | 0.74 |
| 7 | 9 604 | 9 269 | 9 202 | 68 | 0.73 |
| 8 | 9 459 | 9 315 | 9 241 | 74 | 0.81 |
| 9 | 9 318 | 9 354 | 9 271 | 83 | 0.89 |
| 10 | 9 190 | 9 375 | 9 286 | 89 | 0.96 |
| 11 | 9 051 | 9 341 | 9 258 | 83 | 0.90 |
| 12 | 8 810 | 9 139 | 9 083 | 56 | 0.61 |
| 13 | 8 122 | 8 413 | 8 393 | 20 | 0.24 |
| 14 | 8 115 | 8 433 | 8 354 | 79 | 0.95 |
4 结论
近年来, 我国修建了一些独塔无背索斜拉桥, 而且跨径有较大的提高,但是由于独塔无背索斜拉桥的不对称性和无背索状态, 所以还有一些具体的问题尚未能很好解决,施工过程索力求解及施工控制就是其中一个问题。
本研究采用基于无应力长度的正装迭代方法,以无背索斜拉桥的施工控制过程为工程背景进行研究。采用零位移法与最小弯曲能法结合,得到一种斜拉桥合理成桥状态,而后采用拉索无应力长度对结构进行正装分析,利用正装迭代思路,对于最后拉索的无应力长度进行修正,而后进行迭代计算,直到满足工程精度要求,这种方法操作简单,思路清晰,对无背索斜拉桥合理成桥状态索力及合理施工过程索力优化提供了一定参考,具有一定的推广价值。
| [1] |
王永安, 刘世同, 谭红梅. 斜拉桥索力优化理论研究[J]. 公路, 2006(5): 31-34. WANG Yong-an, LIU Shi-tong, TAN Hong-mei. Theoretical Study on Optimization of Cable Force in Cable-stayed Bridge[J]. Highway, 2006(5): 31-34. |
| [2] |
RUIZ-TERAN A M, APARICIO A C. Structural Behavirour and Design Criteria of Under-deck Cable-stayed Bridges and Combined Cable-stayed Bridges.Part 2:Multispan Bridges[J]. Canadian Journal of Civil Engineering, 2008, 35(9): 951-962. |
| [3] |
SHAO X D, ZHAO H, LI L F, et al. Design and Experimental Study of a Harp Shaped Single Span Sable-stayed Bridge[J]. Journal of Bridge Engineering, 2005, 10(6): 658-665. |
| [4] |
邵旭东. 桥梁工程[M]. 北京: 人民交通出版社, 2005. SHAO Xu-dong. Bridge Engineering[M]. Beijing: China Communications Press, 2005. |
| [5] |
秦顺全. 斜拉桥安装无应力状态控制法[J]. 桥梁建设, 2003(2): 31-34. QIN Shun-quan. Control Method of Stress-free Status for Erection of Cable-stayed Bridges[J]. Bridge Construction, 2003(2): 31-34. |
| [6] |
贾丽君, 肖汝诚, 孙斌, 等. 确定斜拉桥施工张拉力的影响矩阵法[J]. 苏州城建环保学院学报, 2003, 13(4): 21-27. JIA Li-jun, XIAO Ru-cheng, SUN Bin, et al. Influence Matrix Method Determining Construction Cable Tensions for Cable-stayed Bridges[J]. Journal of Suzhou Institute of Urban Construction and Environmental Protection, 2003, 13(4): 21-27. |
| [7] |
黄侨, 吴江林, 杨大伟. 确定斜拉桥成桥索力多约束条件下最小能量法[J]. 哈尔滨工业大学学报, 2007, 39(2): 288-291. HUANG Qiao, WU Jiang-lin, YANG Da-wei. Minimum Energy Method with Multi-restrictions to Decide the Rational Completed Stage Force[J]. Journal of Harbin Institute of Technology, 2007, 39(2): 288-291. |
| [8] |
王伯惠. 斜拉桥结构发展和中国经验(上册)[M]. 北京: 人民交通出版社, 2003. WANG Bo-hui. Structural Development and Chinese Experiences of Cable-stayed Bridges (Volume Ⅰ)[M]. Beijing: China Communications Press, 2003. |
| [9] |
周孟波. 斜拉桥手册[M]. 北京: 人民交通出版社, 2004. ZHOU Meng-bo. Cable-stayed Bridge Handbook[M]. Beijing: China Communications Press, 2004. |
| [10] |
张建民, 肖汝诚. 五河口预应力混凝土斜拉桥施工过程计算分析[J]. 公路交通科技, 2007, 24(1): 60-63. ZHANG Jian-min, XIAO Ru-cheng. Construction Process Calculation Analysis for a Prestressed Concrete Cable-stayed Bridge at Wuhekou[J]. Journal of Highway and Transportation Research and Development, 2007, 24(1): 60-63. |
| [11] |
周恒武, 熊守富. 天津南仓道立交桥主桥斜拉索调索优化方案[J]. 桥梁建设, 2010(3): 36-39. ZHOU Heng-wu, XIONG Shou-fu. Optimization Scheme of Stay Cable Adjustment for Main Bridge of Nancang Avenue Interchange in Tianjin[J]. Bridge Construction, 2010(3): 36-39. |
| [12] |
梁鹏, 肖汝城, 徐岳. 超大跨度斜拉桥施工过程随机模拟分析[J]. 中国公路学报, 2006, 19(4): 52-58. LIANG Peng, XIAO Ru-cheng, XU Yue. Random Simulation Analysis of Construction Process for Super Long-span Cable-stayed Bridges[J]. China Journal of Highway and Transport, 2006, 19(4): 52-58. |
| [13] |
杨煊, 周水兴. 斜拉桥施工阶段初张索力计算方法研究[J]. 重庆交通大学学报:自然科学版, 2008(1): 32-36. YANG Xuan, ZHOU Shui-xing. Method to Determine Construction Cable Tension Force of Cable-stayed Bridge[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2008(1): 32-36. |
| [14] |
颜东煌.斜拉桥合理设计状态确定与施工控制[D].长沙: 湖南大学, 2001. YAN Dong-huang.Determination of Rational Design Status and Construction Control of Cable-stayed Bridges[D].Changsha: Hunan University, 2001. http://cdmd.cnki.com.cn/Article/CDMD-10532-2001008355.htm |
| [15] |
钟继卫. 斜拉桥合龙后索力最优调整的实现[J]. 世界桥梁, 2002(4): 43-44. ZHOU Ji-wei. Realizing of Cable Force Optimum Adjustment after Closure of Cable-stayed Bridge[J]. Foreign Bridges, 2002(4): 43-44. |
| [16] |
封洁纯, 戴英樟. 斜拉索无应力长度计算[J]. 公路, 2012(5): 143-147. FENG Jie-chun, DAI Ying-zhang. Calculation of Non-Stress Length of Cable in Cable-stayed Bridge[J]. Highway, 2012(5): 143-147. |
| [17] |
田俊, 王文炜, 宋一凡. 大跨度斜拉桥斜拉索无应力长度计算方法[J]. 建筑科学与工程学报, 2016, 33(2): 71-76. TIAN Jun, WANG Wen-wei, SONG Yi-fan. Calculation Method for Unstressed Length of Stay Cables in Long-span Cable-stayed Bridges[J]. Journal of Architecture and Civil Engineering, 2016, 33(2): 71-76. |
| [18] |
郝超, 裴岷山, 强士中. 大跨度斜拉桥拉索无应力长度的计算方法比较[J]. 重庆交通学院学报, 2001, 20(3): 1-3. HAO Chao, PEI Min-shan, QIANG Shi-zhong. Comparison of Algorithm for Calculating Non-stress Length of Cable in Long-span Cable-stayed Bridges[J]. Journal of Chongqing Jiaotong University, 2001, 20(3): 1-3. |
 2019, Vol. 36
2019, Vol. 36
